避雷针保护范围的计算方法
避雷针保护范围及其计算
避雷针保护范围及其计算避雷针,又名防雷针,是用来保护建筑物、高大树木等避免雷击的装置。
当雷云放电接近地面时它使地面电场发生畸变。
在避雷针的顶端,形成局部电场集中的空间,以影响雷电先导放电的发展方向,引导雷电向避雷针放电,再通过接地引下线和接地装置将雷电流引入大地,从而使被保护物体免遭雷击。
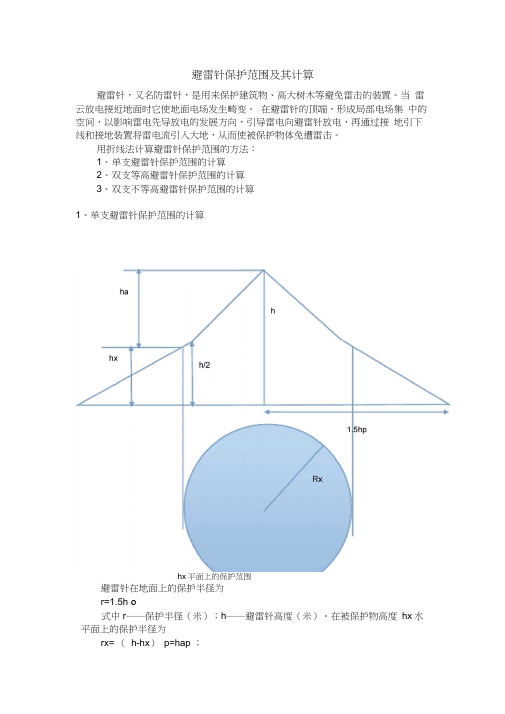
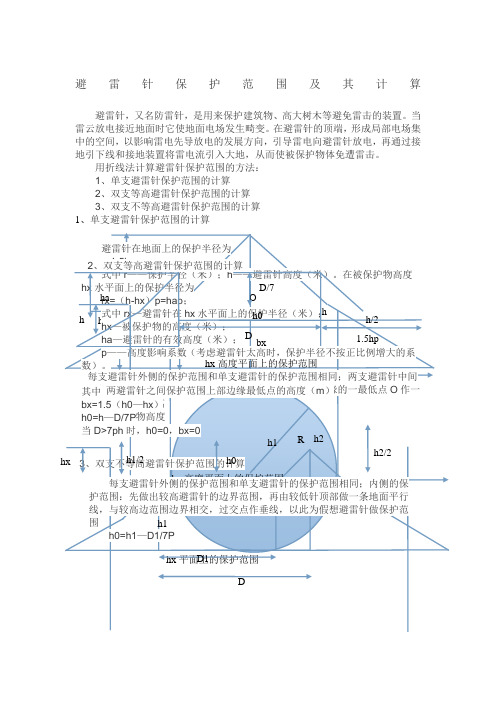
用折线法计算避雷针保护范围的方法:1、单支避雷针保护范围的计算2、双支等高避雷针保护范围的计算3、双支不等高避雷针保护范围的计算1、单支避雷针保护范围的计算hx平面上的保护范围避雷针在地面上的保护半径为r=1.5h o式中r――保护半径(米);h――避雷针高度(米)。
在被保护物高度hx水平面上的保护半径为rx= (h-hx)p=hap ;式中rx—避雷针在hx水平面上的保护半径(米);hx—被保护物的高度(米);ha —避雷针的有效高度(米);p――高度影响系数(考虑避雷针太高时,保护半径不按正比例增大的系数)0h< 30 米时,p=1 o2、双支等高避雷针保护范围的计算每支避雷针外侧的保护范围和单支避雷针的保护范围相同;两支避雷针中间的保护范围由通过两避雷针的顶点以及保护范围上部边缘的一最低点0作一圆弧来确定。
h0 :两避雷针之间保护范围上部边缘最低点的高度(m)D:避雷针之间距离hx:被保护物高度bx:宽度其中bx=1.5 (hO —hx)hO=h —D/7P当D>7ph 时,h0=0, bx=0 3、双支不等高避雷针保护范围的计算每支避雷针外侧的保护范围和单支避雷针的保护范围相同;内侧的保护范围:先做出较高避雷针的边界范围,再由较低针顶部做一条地面平行线,与较高边范围边界相交,过交点作垂线,以此为假想避雷针做保护范围hO=h1 —D1/7P。
避雷针的防护范围计算方法

避雷针的防护范围计算方法常用避雷针(这里仅指单针)保护范围的计算方法主要有折线法和滚球法,为此,就“折线法”和“滚球法”的计算进行了初步的分析和探讨,得出:“折线法”的主要特点是设计直观,计算简便,节省投资,但建筑物高度大于20 m以上不适用;“滚球法”的主要特点是可以计算避雷针(带)与网格组合时的保护范围,但计算相对复杂,投资成本相对大。
在避雷针保护范围的计算方法中,“折线法”是比较成熟的方法。
近几年来,国标中规定的“滚球法”也开始得到同行的认同,但在实际运用中,“滚球法”也碰到一些问题,特别是在计算天面避雷针保护范围的时候。
因此有必要对电力系统常用的“折线法”和国标的“滚球法”进行比较分析,发现其中存在的问题。
1“折线法”避雷保护计算“折线法”在电力系统又称“规程法”,即单支避雷针的保护范围是一个以避雷针为轴的折线圆锥体。
L/ 620—997《交流电气装置的过电压保护和绝缘配合》标准就规定了单支避雷针的保护范围,见图。
1.1避雷针在地面上保护半径的计算计算避雷针在地面上的保护半径可用公式式中:Rp——保护半径;h——避雷针的高度;P——高度影响因数。
其中,P的取值是:当h≤30 m,P=1;当30 m的h的纯数值;当h>20 m时,只能取h=120 m。
1.2被保护物高度hp水平面上保护半径的计算a)当hp≥0.5h时,被保护物高度hp水平面上的保护半径式中:Rp——避雷针在hp水平面上的保护半径;hp——被保护物的高度;ha——避雷针的有效高度。
b)当hp<0.5h时,被保护物高度hp水平面上的保护半径2“滚球法”避雷保护计算“滚球法”是国际电工委员会(IEC)推荐的接闪器保护范围计算方法之一。
我国建筑防雷规范G 50057—994(2000年版)也把“滚球法”强制作为计算避雷针保护范围的方法。
滚球法是以hR为半径的一个球体沿需要防止击雷的部位滚动,当球体只触及接闪器(包括被用作接闪器的金属物)或只触及接闪器和地面(包括与大地接触并能承受雷击的金属物),而不触及需要保护的部位时,则该部分就得到接闪器的保护。
避雷针保护范围

避雷针保护范围的计算r=1.5h。
式中r——保护半径(米);h——避雷针高度(米)。
在被保护物高度hx水平面上的保护半径为rx=1.5(h-hx)p。
式中rx—避雷针在hx水平面上的保护半径(米);hx—被保护物的高度(米);p——高度影响系数(考虑避雷针太高时,保护半径不按正比例增大的系数)这里取p=1两针间的保护范围,上限最低高度:H0 =H-D/7PD---两避雷针之间的距离m井架上两支避雷针的高度为38米,天轮最高点位置按30米计算,两避雷针之间的距离为9.05米,变电所旁及主提绞车房旁的避雷针高均为18米,井架避雷针到两个绞车房的距离均按60米计算,井架到机厂的最远距离按50米计算,绞车房的高度为6米,机厂宿舍的高度为3米。
H0 =38-9.05/7=36.7>30井架上避雷针在绞车房屋顶平面上的保护范围r1=1.5×(38-6)×1=48米主提绞车房旁的避雷针在绞车房屋顶平面上的保护范围r2=1.5×(18-6)×1=18米变电所旁的避雷针在绞车房屋顶平面上的保护范围r3=1.5×(18-6)×1=18米井架上避雷针在机厂屋顶平面上的保护范围r4=1.5×(38-3)×1=52.5米由以上计算与避雷针到各场所的实际距离相比较,可得出结论:各场所均在避雷针的保护范围之内。
生活区两个避雷针的高度均为15米,宿舍高度为3米,生活区到避雷针的最远距离为15米,两避雷针之间的距离为10米。
生活区避雷针在宿舍屋顶平面上的保护范围r5=1.5×(15-3)=18米两针的保护范围,上限最低高度H0= H-D/7P=15-10/7=13.57>3米由以上计算与避雷针到各场所的实际距离相比较,可得出结论:生活区各场所均在避雷针的保护范围之内。
用折线法滚球法对避雷针保护范围计算

避雷针的保护范围计算在避雷针保护范围的计算方法中,“折线法”是比较成熟的方法。
近几年来, 国标中规定的“滚球法”也开始得到同行的认同。
下面分别介绍计算过程。
一、 折线法1,1单支避雷针h 为避雷针的高度(m );h x 为被保护物体的高度(m );r x 为在高度为h x 的水平面上的保护半径(m 针离设备至少5m避雷针在地面上的保护半径为r=1.5h在被保护高度h x 当h x ≥ h /2 r x =(h -h x )×p =h a ×p当h x <h /2 r x =(1.5h -2h x )×p p —高度影响系数 h ≤ 30m 时,p =1 ;30<h ≤ 120 m 时1.2两只避雷针1.2.1两支避雷针高度相同随着所要求保护的范围增大。
单支避雷针的高度要升高,但如果所要求保护的范围比较狭长(如长方形),就不宜用太高的单支避雷针,这时可以采用两支较矮的避雷针采用两针后,外侧的保护范围与单针保护范围的确定方法相同,针的内侧部分的确定方法为:令D 为两针间距离;2b x 等于在高度为h x 水平面上保护范围的最小宽度,它位于两针的连接线的中点,即距每针的距离为D/2。
b x=1.5(h o—h x ) 两针间距离与针高之比D/h 不宜大于5h o 为两针间保护范围上部边缘最低点的高度(m)h o=h ‐D/7p 当D=7p ×h a 时, b x=01.2.1两支避雷针高度不同俩针外侧的保护范围仍按单针的方法确定,俩针内侧的保护范围:先作出较高针的保护范围的边界,之后由较低针的针顶部作一条与地面平行线,这两者的交点对地面作垂线,将此垂线看作一假想避雷针,再作它与较低针的保护范围,这样2和3就是相当于俩根等高避雷针的保护范围。
图中 f=D1/7p1.2.3三支或四支避雷针的保护范围可以两两当作两只避雷针确定保护范围二、 滚球法所谓“滚球法”(roll‐ball method),就是选择一个半径为hr(滚球半径)的球体,沿需要防护直击雷的部位滚动,如果球体只接触到避雷针(线)或避雷针(线)与地面,而不触及需要保护的部位,则该部位就在避雷针(线)的保护范围之内。
单支避雷针保范围计算方式

1.滚球法计算单只避雷针的保护范围应按下列方法
确定
1)当单只避雷针高度h小于或等于hr(滚球半径)时:
①距地面hr处作一平行于地面的平行线;
②以针尖为圆心,hr为半径,作弧线交于平行线的A、B两点;
③以A、B为圆心,hr为半径作弧线,该弧线与针尖相交并与地面相切。
从此弧线起到地面止就是保护范围。
保护范围是一个对称的锥体;
④避雷针在hx高度的xxˊ平面上和在地面上的保护半径,按下列计算式确定:
(附4.1)
(附4.2)
式中:rx──避雷针在hx高度的xx′平面上的保护半径(m);
hr──滚球半径,按本规范表5.2.1确定(m);
hx──被保护物的高度(m);
r0──避雷针在地面上的保护半径(m)。
(2)当避雷针高度h大于hr时,在避雷针上取高度hr的一点代替单支避雷针针尖作为圆心。
其余的做法同本款第(1)项。
(附4.l)和(附4.2)式中的h用hr代人。
避雷针折线法与滚球法

b)当hp v0.5h时,被保护物高度hp水平面上的保护半径2“滚球法”避雷保护计算“滚球法”是国际电工委员会(IEC)推荐的接闪器保护范围计算方法之一。
我国建筑防雷规范G 50057—994(2000年版)也把“滚球法”强制作为计算避雷针保护范围的方法。
滚球法是以hR为半径的一个球体沿需要防止击雷的部位滚动,当球体只触及接闪器(包括被用作接闪器的金属物)或只触及接闪器和地面(包括与大地接触并能承受雷击的金属物),而不触及需要保护的部位时,则该部分就得到接闪器的保护。
滚球法确定接闪器保护范围应符合规范规定,见表。
应用滚球法,避雷针在地面上的保护半径的计算可见以下方法及图2。
a)避雷针高度h< hR时的计算距地面hR处作条平行于地面的平行线。
以针尖为圆心、hR为半径作弧线交于平行线A,两点。
以A,为圆心,hR为半径作弧线,该弧线与针尖相交并与地面相切,这样,从弧线起到地面就是保护范围。
保护范围是一个对称的锥体。
避雷针在hP高度的xx'平面上和在地面上的保护半径,按公式[2](4)计算确定式中:Rp――避雷针保护高度xx'平面上的保护半径;hR ――滚球半径,按表确定;hp ――被保护物的高度;R0 ――避雷针在地面上的保护半径。
b)当避雷针高度h> hR时的计算在避雷针上取高度hp的一点代替单支避雷针针尖并作为圆心,亦可见图2。
3“滚球法”计算天面避雷针保护范围存在的问题3.1用“滚球法”计算避雷针在地面上的保护,保护范围可以很好地得到确认,但用“滚球法”计算天面避雷针保护范围时却存在较大的误差。
“滚球法”是以避雷针和被保护物所在平面为一无限延伸的平面作为前提的,当被保护物位于屋顶天面时,天面不是一个无限延伸的平面,况且,当滚球同时与避雷针尖和天面避雷带接触时,滚球和天面之间不存在确定的相切关系。
因此《建筑物防雷设计规范》中给出的计算公式将不能直接运用。
在这种情况下,我们怎样计算其保护范围呢?由于天面不可延伸且形状不规则,因此,根据滚球法计算保护范围的原理,当避雷针位置确定后,滚球在以避雷针尖作为一个支点,以避雷带上任一点作为另一支点滚动时,它在一定高度的保护范围也将是一个不规则的图形。
避雷针保护范围及其计算
避雷针保护范围及其计算
避雷针,又名防雷针,是用来保护建筑物、高大树木等避免雷击的装置。
当雷云放电接近地面时它使地面电场发生畸变。
在避雷针的顶端,形成局部电场集中的空间,以影响雷电先导放电的发展方向,引导雷电向避雷针放电,再通过接地引下线和接地装置将雷电流引入大地,从而使被保护物体免遭雷击。
用折线法计算避雷针保护范围的方法:
1、单支避雷针保护范围的计算
2、双支等高避雷针保护范围的计算
3、双支不等高避雷针保护范围的计算
1、单支避雷针保护范围的计算。
避雷针保护范围计算公式

避雷针保护范围计算公式文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]避雷针保护范围计算公式Rx=√H(2Hr-H)-√Hx(2Hr-Hx)Rd=√H(2Hr-H)其中:Rx-----避雷针在Hx高度平面上的保护半径MHr-----滚球半径MHx――被保护物体高度MH―――避雷针的计算高度MRd―――避雷针在地面上的保护半径MRx=1.6Ha/(1+Hx/H)Rx-----避雷针在Hx高度平面上的保护半径MHx――被保护物体高度MH―――避雷针的计算高度MHa=H-Hx―――避雷针的有效高度避雷针的保护范围众所周知,雷是一种常见的自然现象。
雷电击中物体会产生强烈的破坏作用。
防雷是人类同自然斗争的一个重要课题。
安装避雷针是人们行之有效的防雷措施之一。
避雷针由接受器、接地引下线和接地体(接地极)三部分串联组成。
避雷针的接受器是指避雷针顶端部分的金属针头。
接受器的位置都高于被保护的物体。
接地引下线是避雷针的中间部分,是用来连接雷电接受器和接地体的。
接地引下线的截面积不但应根据雷电流通过时的发热情况计算,使其不会因过热而熔化,而且还要有足够的机械强度。
接地体是整个避雷针的最底下部分。
它的作用不仅是安全地把雷电流由此导入地中,而且还要进一步使雷电流在流入大地时均匀地分散开去。
避雷针的工作原理就其本质而言,避雷针不是避雷,而是利用其高耸空中的有利地位,把雷电引向自身,承受雷击。
同时把雷电流泄入大地,起着保护其附近比它矮的建筑物或设备免受雷击的作用。
避雷针保护其附近比它矮的建筑物或设备免受雷击是有一定范围的。
这范围像一顶以避雷针为中心的圆锥形的帐篷,罩在帐篷里面空间的物体,可以免遭雷击,这就是避雷针的保护范围。
单支避雷针的保护范围如图1所示,它的具体计算通常采取下列方法(这种方法是从实验室用冲击电压发生器作模拟试验获得的)。
避雷针在地面上的保护半径为r=1.5h。
式中r——保护半径(米);h——避雷针高度(米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
避雷针保护范围的计算方法避雷针保护范围的计算方法卢伟辉1,黄旭丹21.广东粤华发电有限责任公司,广东广州 510731;2.广东电力设计研究院广东广州 510600)摘要:常用避雷针(这里仅指单针)保护范围的计算方法主要有折线法和滚球法,为此,就“折线法”和“滚球法”的计算进行了初步的分析和探讨,得出:“折线法”的主要特点是设计直观,计算简便,节省投资,但建筑物高度大于20 m以上不适用;“滚球法”的主要特点是可以计算避雷针(带)与网格组合时的保护范围,但计算相对复杂,投资成本相对大。
关键词:避雷针;折线法;滚球法;保护范围Calculation methods of lightning conductor protective rangeLU Weihui,UANG Xudan2(1.Guangdong Yuehua Power Co.,Ltd.,Guangzhou 510731,China;2.Guangdong Electric PowerDesign Institute,Guangzhou 510600,China)Abstract:he common calculation methods of lightning rod (single rod only)protective range are the“polygon method” and the“rolling ball method”. his paper makes a primary discussion on these two methods,drawing a conclusion that the “polygon method” is of intuitionistic design,simple computation,economic costs,but it is inapplicable to buildings higher than 20 m; the “rolling ball method” can figure out the protective range of a lightning rod combined with gridding,yet the computation is more complicated and the investment is higher.Keywords:polygon method; rolling ball method; lightning rod; protective range在避雷针保护范围的计算方法中,“折线法”是比较成熟的方法。
近几年来,国标中规定的“滚球法”也开始得到同行的认同,但在实际运用中,“滚球法”也碰到一些问题,特别是在计算天面避雷针保护范围的时候。
因此有必要对电力系统常用的“折线法”和国标的“滚球法”进行比较分析,发现其中存在的问题。
1“折线法”避雷保护计算“折线法”在电力系统又称“规程法”,即单支避雷针的保护范围是一个以避雷针为轴的折线圆锥体。
L/ 620—997《交流电气装置的过电压保护和绝缘配合》标准就规定了单支避雷针的保护范围,见图。
1.1避雷针在地面上保护半径的计算计算避雷针在地面上的保护半径可用公式式中:Rp——保护半径;h——避雷针的高度;P——高度影响因数。
其中,P的取值是:当h≤30 m,P=1;当30 m的h的纯数值;当h>20 m时,只能取h=120 m。
1.2被保护物高度hp水平面上保护半径的计算a)当hp≥0.5h时,被保护物高度hp水平面上的保护半径式中:Rp——避雷针在hp水平面上的保护半径;hp——被保护物的高度;ha——避雷针的有效高度。
b)当hp<0.5h时,被保护物高度hp水平面上的保护半径2“滚球法”避雷保护计算“滚球法”是国际电工委员会(IEC)推荐的接闪器保护范围计算方法之一。
我国建筑防雷规范G 50057—994(2000年版)也把“滚球法”强制作为计算避雷针保护范围的方法。
滚球法是以hR为半径的一个球体沿需要防止击雷的部位滚动,当球体只触及接闪器(包括被用作接闪器的金属物)或只触及接闪器和地面(包括与大地接触并能承受雷击的金属物),而不触及需要保护的部位时,则该部分就得到接闪器的保护。
滚球法确定接闪器保护范围应符合规范规定,见表。
应用滚球法,避雷针在地面上的保护半径的计算可见以下方法及图2。
a)避雷针高度h≤hR时的计算距地面hR处作条平行于地面的平行线。
以针尖为圆心、hR为半径作弧线交于平行线A,两点。
以A,为圆心,hR为半径作弧线,该弧线与针尖相交并与地面相切,这样,从弧线起到地面就是保护范围。
保护范围是一个对称的锥体。
避雷针在hP高度的xx'平面上和在地面上的保护半径,按公式[2](4)计算确定式中: Rp——避雷针保护高度xx'平面上的保护半径; hR——滚球半径,按表确定;hp——被保护物的高度;R0——避雷针在地面上的保护半径。
b)当避雷针高度h>hR时的计算在避雷针上取高度hp的一点代替单支避雷针针尖并作为圆心,亦可见图2。
3“滚球法”计算天面避雷针保护范围存在的问题3.1 存在问题用“滚球法”计算避雷针在地面上的保护,保护范围可以很好地得到确认,但用“滚球法”计算天面避雷针保护范围时却存在较大的误差。
“滚球法”是以避雷针和被保护物所在平面为一无限延伸的平面作为前提的,当被保护物位于屋顶天面时,天面不是一个无限延伸的平面,况且,当滚球同时与避雷针尖和天面避雷带接触时,滚球和天面之间不存在确定的相切关系。
因此《建筑物防雷设计规范》中给出的计算公式将不能直接运用。
在这种情况下,我们怎样计算其保护范围呢?由于天面不可延伸且形状不规则,因此,根据滚球法计算保护范围的原理,当避雷针位置确定后,滚球在以避雷针尖作为一个支点,以避雷带上任一点作为另一支点滚动时,它在一定高度的保护范围也将是一个不规则的图形。
从理论上讲,要想知道被保护物体能否得到全面保护,我们需要计算出以避雷针尖为一个滚球支点,以避雷带上的所有点作为另一个滚球支点时,用避雷针在一定高度的所有保护半径来确定被保护物体能否完全得到保护。
这种计算方法在实际应用中有一定的偏差。
因此,我们需要寻找一种简便的方法来计算被保护物体能否得到避雷针的完全保护。
从滚球法计算保护范围的原理中,我们可以得出如下推论:a)以避雷针的顶点为一个支点,另一个支点距避雷针基点的垂直距离越近时,其在一定高度的保护半径越小,反之,另一个支点距避雷针的基点垂直的距离越远(不能超过滚球半径)时,其在一定高度的保护半径越大。
b)当被保护物体最高点垂直于避雷针的平面上,计算出的保护半径大于被保护物体上最远点距避雷针的垂直距离时,该被保护物体可得到避雷针的全面保护。
根据以上推论,我们只要计算出避雷带上距避雷针基点最近(指以避雷针基点作为起点,经被保护物体在天面上的正投影与避雷带上各点连线中的最短距离)的点作为支点时,一定高度的保护距离,即可判断出该物体能否得到全面保护(当计算出的保护距离大于该被保护物体到避雷针的垂直距离的最大值时,被保护物体得到全面保护,反之,则相反)。
3.2举例说明假设天面有一物体,物体的高度为3 m,其最远点距避雷针基点的垂直距离为7 m,避雷带上距避雷针基点最近的点(该支点与避雷针基点的连线经过被保护物体在天面的正投影)距避雷针的垂直距离为5 m。
避雷针设多高才能对该物体进行全面保护?根据以上条件,假设避雷针的基点为O点,被保护物体上距避雷针的最远点设为A点,滚球的另一个支点为点,依据滚球法的原理,可作图3。
a)分别以A,两点为圆心,以hR为半径划圆弧,则圆弧相交于E点,E点即为滚球的圆心。
b)以E点为圆心,以hR为半径划圆,则该圆一定经过A,两点且与避雷针相交于C点(当E点距避雷针的垂直距离大于hR时,无交点),OC即为所求避雷针的高度。
c)经过滚球中心点E点作垂直于O的直线,与O的延长线相交于F点。
连接EA,EB,EC,则线段EA,EB,EC相等且等于滚球半径。
经A,C两点作垂直于EF的直线,与EF相交于I,H两点。
d)设F=x,EF=y,避雷针高度OC=h,滚球半径取45m,则可得方程组y=43.95 m。
避雷针的高度应取一定的裕量,所以取高度为7.5m,可对物体进行全面保护。
如果用G50057—994标准给出的滚球法计算公式进行计算,所得结果为h= 6.4m,被保护对象可能得不到全面保护,存在一定雷电绕击概率。
4实例比较下面以发电厂一些常见建筑物的保护面积来比较两种计算方法(由于电厂的建筑物多数属于第三类防雷建筑物,所以滚球半径按第三类防雷建筑物选择,即hR=60 m)。
某电厂油区有两种规格的油罐,油罐保护高度hP分别为8 m和25 m,都设置了同样高度的避雷针,避雷针高度h=40 m,油罐保护半径分别以折线法和滚球法进行计算。
4.1折线法根据公式(1),油罐保护高度8m的地面保护半径等于油罐保护高度25 m的地面保护半径,R=5hP=52.2 m。
这是因为保护高度hP=8 m<0.5h=20 m,而保护高度hP=25 m>0.5h=20 m。
油罐保护高度8 m水平面上的保护半径Rp=(1.5h-2hp)P=20.88 m。
油罐保护高度25 m水平面上的保护半径Rp=(h-hp)P= 13.05 m。
4.2滚球法因为避雷针高度h=40 m,滚球半径hR= 60m,h<hR,根据公式[2](4),油罐保护高度8 m的地面保护半径等于油罐保护高度25 m的地面保护对比以上数据,可以看出,在相同的条件下(滚球半径按第三类防雷建筑物选),用“滚球法”计算出来的建筑物高度水平面的保护半径(13.72 m和7.84 m)要比“折线法”计算出来的保护半径(20.88 m和13.05 m)要小,换言之,要达到相同的保护半径,用“滚球法”计算出的避雷针高度要比“折线法”计算出来的高度要高,可见“滚球法”要比“折线法”对独立避雷针的要求略高一些。
只有第三类防雷建筑物的高度低于20 m时,“滚球法”算出的避雷针保护范围才与“折线法”算出的保护范围相似。
5结论综上所述,可以得出以下几点结论:a)“折线法”的主要特点是设计直观、计算简便、节省投资,但只适用于20 m以下的避雷高度,不能计算高度20 m以上建筑物的保护范围,而且计算结果与雷电流大小无关。
b)“滚球法”的主要特点是可以计算避雷针(带)与网格组合时的保护范围。
凡安装在建筑物上的避雷针、避雷线(带),不管建筑物的高度如何,都可采用滚球法来确定保护范围,并且保护范围与雷电流大小有关,但独立避雷针、避雷线受相应的滚球半径限制(60 m),其高度和计算相对复杂,比“折线法”要增大投资。
