扩散系数计算
扩散系数计算

扩散系数计算WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、 气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ;T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯式7-19的相对误差一般小于10%。
二、 液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K; μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水;甲醇;乙醇;苯、乙醚等不缔合的溶剂为;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数计算
7.2.2扩散系数费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为5210/m s -。
通常对于二元气体A、B 的相互扩散,A在B 中的扩散系数和B 在A 中的扩散系数相等,因此可略去下标而用同一符号D表示,即AB BA D D D ==。
表7-1给出了某些二元气体在常压下(51.01310Pa ⨯)的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:1/31/32[()()]A B D P v v =+∑∑ (7-19)式中,D -A、B 二元气体的扩散系数,2/m s ;P -气体的总压,Pa ; T -气体的温度,K;A M 、B M -组分A、B 的摩尔质量,/kg kmol ;Av∑、Bv∑-组分A、B 分子扩散体积,3/cm mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
51.01310Pa ⨯式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得多,其量级为9210/m s -。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
对于很稀的非电解质溶液(溶质A+溶剂B),其扩散系数常用Wilke-Chang 公式估算:150.6()7.410T B AB A M TD V -φ=⨯μ 2/m s (7-21)式中,AB D -溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数),2/m s ;T -溶液的温度,K;μ-溶剂B的粘度,.Pa s ;B M -溶剂B的摩尔质量,/kg kmol ;φ-溶剂的缔合参数,具体值为:水2.6;甲醇1.9;乙醇1.5;苯、乙醚等不缔合的溶剂为1.0;A V -溶质A 在正常沸点下的分子体积,3/cm mol ,由正常沸点下的液体密度来计算。
扩散系数计算

它表达某个组分在介质中扩 0.0101T 1.75(7—19)722扩散系数费克定律中的扩散系数D 代表单位浓度梯度下的扩散通量, 散的快慢,是物质的一种传递性质。
一、气体中的扩散系数气体中的扩散系数与系统、温度和压力有关,其量级为10 m 2/s 。
通常对于二元气体A 、B 的相互扩散,A 在 B 中的扩散系数和 B 在A 中的扩散系数相等,因此可略去下标而用同一符号D 表示,即 D AB = D BA =D。
表7 — 1给出了某些二元气体在常压下(1.013 105Pa )的扩散系数。
对于二元气体扩散系数的估算,通常用较简单的由富勒(Fuller )等提出的公式:p[c V A )1/3 e V B )1/3]22式中,D —A 、B 二元气体的扩散系数,m /s ;P —气体的总压,Pa ;T —气体的温度,K ;MA 、MB —组分A 、B 的摩尔质量,kg/kmol ;7 V A 7 V B3、—组分A 、B 分子扩散体积,cm 3/mol 。
一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,某些简单物质则在表7-2种直接列出。
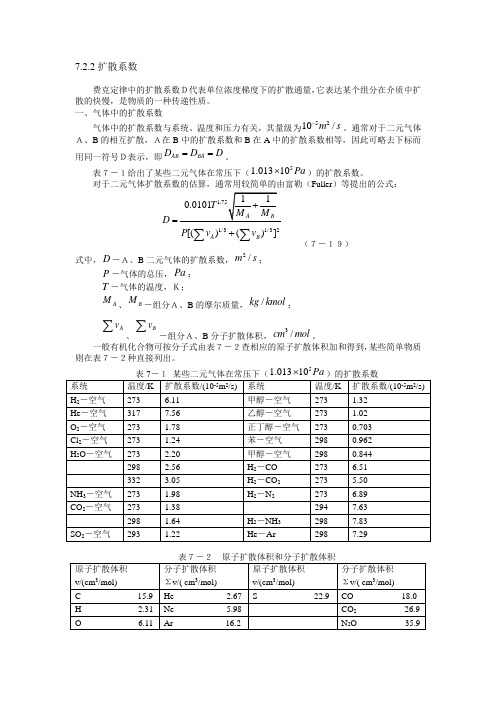
表7-1某些二元气体在常压下(5)的扩散系数系统温度/K 扩散系数/(10-5m 2/s)系统温度/K-5 2扩散系数/(10 m/s)H 2—空气 273 6.11 甲醇一空气 273 1.32 He —空气 317 7.56 乙醇一空气 273 1.0202—空气 273 1.78 正丁醇-空气 273 0.703 Cl 2 —空气 273 1.24 苯-空气 298 0.962 H 2O —空气273 2.20 甲醇一空气298 0.844 298 2.56 H 2— CO 273 6.513323.05 H 2— CO 2 273 5.50 NH 3 —空气 273 1.98H 2— N 2 273 6.89 CO 2 —空气273 1.38294 7.632981.64 H 2— NH 3 298 7.83 SO 2 —空气 2931.22He — Ar2987.297-2 原子扩散体积3v/(cm /mol) 分子扩散体积 3工 V /( cm /mol)原子扩散体积3v/(cm /mol)分子扩散体积3工 V /( cm /mol)C15.9 He 2.67 S22.9CO 18.0,其扩散系数常用 Wilke-Cha ng 公式估算:2 /m/S(7 — 21)AB= 7.4 10‘5(M B )T T 」V A 0.6式7 — 19的相对误差一般小于1 0%。
多巴胺扩散系数计算公式

多巴胺扩散系数计算公式多巴胺是一种重要的神经递质,它在人体内起着重要的调节作用。
多巴胺扩散系数是描述多巴胺在生物组织中扩散速度的参数,它对于研究多巴胺在神经系统中的传递和调节具有重要意义。
本文将介绍多巴胺扩散系数的计算公式及其在神经科学研究中的应用。
多巴胺扩散系数的计算公式如下:D = kT/6πηr。
其中,D为多巴胺的扩散系数,k为玻尔兹曼常数,T为温度,η为介质的粘度,r为多巴胺分子的半径。
这个公式描述了多巴胺在生物组织中扩散的速度与温度、介质粘度和分子半径之间的关系。
多巴胺扩散系数的计算需要考虑多种因素,其中温度是一个重要的影响因素。
在生物体内,温度的变化会直接影响多巴胺的扩散速度。
一般来说,温度越高,多巴胺的扩散速度越快。
而介质的粘度也会影响多巴胺的扩散速度,粘度越大,多巴胺的扩散速度越慢。
此外,多巴胺分子的半径也会对扩散系数产生影响,分子半径越大,扩散系数越小。
多巴胺扩散系数的计算公式为神经科学研究提供了重要的工具。
通过测量多巴胺在不同温度、不同介质粘度和不同分子半径下的扩散系数,可以更深入地了解多巴胺在神经系统中的传递和调节机制。
例如,研究人员可以通过测量多巴胺在不同温度下的扩散系数来研究多巴胺在不同生理状态下的传递速度。
另外,通过测量多巴胺在不同介质粘度下的扩散系数,可以研究多巴胺在不同病理状态下的传递速度。
此外,通过测量多巴胺在不同分子半径下的扩散系数,可以研究多巴胺与其他分子之间的相互作用。
多巴胺扩散系数的研究还可以为神经系统疾病的治疗提供重要的参考。
例如,通过研究多巴胺在不同介质粘度下的扩散系数,可以为治疗帕金森病等多巴胺相关疾病提供新的思路。
另外,通过研究多巴胺在不同分子半径下的扩散系数,可以为设计新的多巴胺类药物提供参考。
总之,多巴胺扩散系数的计算公式为神经科学研究提供了重要的工具,它可以帮助研究人员更深入地了解多巴胺在神经系统中的传递和调节机制,为神经系统疾病的治疗提供新的思路。
扩散系数的公式

扩散系数的公式扩散系数(Diffusion coefficient)是描述物质扩散能力的物理量。
一、菲克定律与扩散系数。
1. 菲克第一定律。
- 表达式为J = -D(dc)/(dx),这里J是扩散通量(单位时间内通过单位面积的物质的量),D就是扩散系数,(dc)/(dx)是浓度梯度(沿x方向的浓度变化率)。
- 由该定律可以推导出扩散系数D=(-J)/(frac{dc){dx}}(在已知扩散通量J和浓度梯度(dc)/(dx)的情况下)。
2. 菲克第二定律。
- 表达式为(∂ c)/(∂ t)=Dfrac{∂^2c}{∂ x^2}(在一维扩散情况下),其中c是浓度,t是时间,x是空间坐标。
- 在一些特定的初始条件和边界条件下,通过求解菲克第二定律的方程,可以得到扩散过程中浓度随时间和空间的分布,进而可以确定扩散系数D的值。
例如在简单的扩散问题中,假设扩散物质初始时局限于某一区域,随着时间的推移,根据浓度分布的变化情况来计算D。
- 如果已知浓度c随时间t和空间x的函数关系c(x,t),可以通过对(∂ c)/(∂ t)和frac{∂^2c}{∂ x^2}求导,然后根据菲克第二定律计算D=(frac{∂ c)/(∂ t)}{frac{∂^2c}{∂ x^2}}。
二、爱因斯坦 - 斯托克斯方程(适用于稀溶液中的球形粒子扩散)1. 公式为D = (kT)/(6πeta r),其中k是玻尔兹曼常量(k = 1.38×10^-23J/K),T 是绝对温度,eta是溶剂的粘度,r是球形粒子的半径。
2. 这个公式的推导基于分子运动论和流体力学原理。
它表明扩散系数与温度成正比,与溶剂粘度和粒子半径成反比。
例如,在研究胶体溶液中球形胶粒的扩散时,可以通过测量温度T、溶剂粘度eta以及已知胶粒半径r,利用该公式计算扩散系数D。
科特雷尔方程计算扩散系数

科特雷尔方程计算扩散系数
我们要找出使用科特雷尔方程如何计算扩散系数。
首先,我们需要了解科特雷尔方程是什么以及它与扩散系数的关系。
科特雷尔方程是一个描述物质扩散过程的方程,其形式如下:
dc/dt = D × (dc/dx)
其中:
dc/dt 是物质浓度的变化率,
D 是扩散系数,
dc/dx 是物质浓度随空间位置的变化率。
这个方程告诉我们,物质浓度的变化率与扩散系数和浓度随空间位置的变化率成正比。
为了求出扩散系数D,我们通常需要解这个方程,并从中提取D的值。
计算结果为:扩散系数D = cm^2/s。
所以,使用科特雷尔方程计算得到的扩散系数是 cm^2/s。
活性染料扩散系数计算公式

活性染料扩散系数计算公式活性染料是一种广泛应用于纺织品、皮革、纸张等领域的染料,它具有良好的亲和力和扩散性能,能够在材料表面均匀分布并与材料发生化学反应,从而实现着色的效果。
活性染料的扩散系数是评价染料扩散性能的重要参数,它能够反映染料在材料中的扩散速率和扩散程度,对于染料的选择和应用具有重要的指导意义。
本文将介绍活性染料扩散系数的计算公式及其相关知识。
一、活性染料扩散系数的定义。
活性染料在材料中的扩散过程可以用Fick定律来描述,Fick定律表明了扩散通量与浓度梯度之间的关系。
在一维情况下,Fick定律可以表示为:\[ J = -D \frac{dC}{dx} \]其中,J为扩散通量,单位为mol/(m^2·s);D为扩散系数,单位为m^2/s;C 为染料浓度,单位为mol/m^3;x为扩散方向,单位为m。
根据Fick定律,活性染料在材料中的扩散过程可以通过扩散系数D来描述。
二、活性染料扩散系数的计算公式。
活性染料扩散系数的计算通常采用扩散实验的方法,通过实验数据来确定扩散系数的数值。
一般情况下,可以采用扩散系数的计算公式来进行计算,常用的计算公式有以下几种:1. Fick第一定律。
Fick第一定律是描述非稳态扩散过程的定律,它可以表示为:\[ D = \frac{1}{2} \frac{dC}{dt} \frac{l^2}{C_0} \]其中,D为扩散系数,单位为m^2/s;dC/dt为浓度变化率,单位为mol/(m^3·s);l为材料厚度,单位为m;C0为染料初始浓度,单位为mol/m^3。
Fick第一定律的计算公式可以通过测量不同时间下染料浓度的变化来确定扩散系数的数值。
2. Fick第二定律。
Fick第二定律是描述稳态扩散过程的定律,它可以表示为:\[ D = \frac{Ql}{At} \]其中,D为扩散系数,单位为m^2/s;Q为扩散通量,单位为mol/s;l为材料厚度,单位为m;A为扩散截面积,单位为m^2;t为扩散时间,单位为s。
二维核磁扩散系数计算公式

二维核磁扩散系数计算公式
二维核磁扩散系数的计算公式如下:
D = (πΔδ)^2 / (4γ^2G^2δ^2(Δ - δ/3))
其中,
D 为核磁扩散系数(单位:m^2/s);
Δ为梯度脉冲的总持续时间(单位:s);
δ为梯度脉冲的单个脉冲宽度(单位:s);
γ为核的旋磁比(单位:rad/(T·s));
G 为梯度强度(单位:T/m)。
这个公式描述了二维核磁共振(NMR)中自旋扩散的现象,其中梯度脉冲用于引入空间坐标信息。
通过测量核磁共振信号的强度随时间变化的方式,可以计算出样品中分子的扩散系数。
这个公式是基于经典的自旋扩散理论推导得到的,适用于二维核磁扩散实验的数据处理和解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
7.2.2扩散系数
费克定律中的扩散系数D代表单位浓度梯度下的扩散通量,它表达某个组分在介质中扩散的快慢,是物质的一种传递性质。
一、气体中的扩散系数
?52s10m/。
通常对于二元气体气体中的扩散系数与系统、温度和压力有关,其量级为中的扩散系数相等,因此可略去下标而B在AA、B的相互扩散,A在B中的扩散系数和D?D?D。
用同一符号D表示,即BAAB5Pa?101.013)的扩散系数。
表7-1给出了某些二元气体在常压下(Fuller)等提出的公式:对于二元气体扩散系数的估算,通常用较简单的由富勒
??1/321/3]vv))?(P[(BA(7-19)(111.75?0.0101TMM BA?D
2m/sD;二元气体的扩散系数,式中,-A、B PaP;-气体的总压,T-气体的温度,K;MMkg/kmol;的摩尔质量,、-组分A、B BA??vv BA3molcm/、-组分A、B分子扩散体积,。
某些简单物质一般有机化合物可按分子式由表7-2查相应的原子扩散体积加和得到,则在表5
表7-2原子扩散体积和分子扩散体积
1 / 4
.
注:已列出分子扩散体积的,以后者为准。
式7-19的相对误差一般小于10%。
二、液体中的扩散系数由于液体中的分子要比气体中的分子密集得多,因此也体的扩散系数要比气体的小得2?9s10m/。
表7-3给出了某些溶质在液体溶剂中的扩散系数。
多,其量级为表7-3溶质在液体溶剂中的扩散系数(溶质浓度很低)
Wilke-Chang公式估算:(溶质A+溶剂B),其扩散系数常用对于很稀的非电解质溶液
T T?M)(15?B10?7.4D?AB0.6V?2sm/(7-21)A D2sm/-溶质A在溶剂B中的扩散系数(也称无限稀释扩散系数);,式中,AB
T-溶液的温度,K;
?sPa.-溶剂B的粘度,;Mkmol/kg;-溶剂B的摩尔质量,B?;苯、乙醚等不缔合的溶剂;乙醇1.91.5-溶剂的缔合参数,具体值为:水2.6;甲醇 1.0;为V3molcm/,由正常沸点下的液体密度来计-溶质A在正常沸点下的分子体积,A1.048VV0.285V?为物质的方法估算:则可采用算。
若缺乏此密度数据,Tyn-Calus,其中cc2 / 4
.
3C
与溶质B在溶质A中的扩散从(7-21)可见,溶质A在溶剂B中的扩散系数AB不相等,这一点与气体扩散系数的特性明显不同,需引起注意。
系数BA TDDTTT相差不大)和下的扩散系数(要求推算,下的对给定的系统,可由温度111222如下:
T?12)D(D?12T?(7-22)?1三、生物物质的扩散系数
表7-5给出了一些生物溶质在水溶液中的扩散系数。
表7—5 生物溶质在水溶液中的扩散系数
.
或其分子体对于水溶液中生物溶质扩散系数的估算,当溶质相对于分子质量小于10003molcm/,Polson方法)积小于500时,可用式(7-21);否则,宜用式(7-23)(15?T9.40?10?D AB1/3)?(M2sm/(7-23)A?s.Pa其中,;-镕基的粘度,M-生物溶
质的摩尔质量。
A四、四、固体中的扩散系数一般是用渗对于气体在固体中的扩散,表7-6给出了某些物质在固体中的扩散系数。
P,两者间的关系为permeability)来代替扩散系数透率D (M SDP?(7-24)ABM p/S?c33mm((标准状态),其中,S为气体溶质A在固相中的溶解度,单位为/溶质AA。
.atm)固体固体中的扩散系数和渗透率表7—6
33;固体?atm)m* S的单位:溶质(标准状态)/(m23)ms的单位:** Pm溶质(标准状态)/(??atm/m。
M4 / 4。
