大学物理习题答案_吴百诗
北邮 大学物理 吴百诗 Chapter-6-热力学基础

p
o
等 体 降 p2 压
p1
1 ( p1,V , T1 )
( p2 ,V , T2 )
V
2
V
V
V
o
QV
E1
E2
QV
E1
E2
30
二 等压过程 摩尔定压热容
特性
p 常量
过程方程 VT 1 常量 p ( p,V1, T1 ) ( p,V2 ,T2 ) p 功 W p(V2 V1 ) 2 1 由热力学第一定律 W
18
热力学理论
19
一 热力学第一定律
p
1*
*2
Q E2 E1 W
系统从外界吸收的热 量,一部分使系统的内能 增加,另一部分使系统对 外界做功 .
o
V1
V2 V
Q E2 E1 W E W
20
准静态过程
Q E
微变过程
V2
V1
pdV
dQ dE dW dE pdV
dp pA ( )T dV VA
pA
o
V A V V B
V
绝热线的斜率大于等温线的斜率.
48
例1 设有 5 mol 的氢气,最初温度20 C , 压强 1.013105 Pa ,求下列过程中把氢气压缩 为原体积的 1/10 需作的功: (1)等温过程 (2)绝热过程 (3)经这两过程后,气体的 p 2 压强各为多少? T T' T
o V1 dV
dE CV ,mdT
绝热的汽缸壁和活塞
41
W pdV
V1
V2
CV ,mdT
T1
西安交大大学物理学 吴百诗ch4-3

例 在恒星系中,两个质量分别为 m1 和 m2 的星球,原来为静 止,且相距为无穷远,后在引力的作用下,互相接近,到
相距为 r 时。 求 它们之间的相对速率为多少? 解 由动量守恒,机械能守恒
m1
mv1 mv 2 0
1 1 m1m2 2 2 m1v1 m2v 2 G 0 2 2 r
Fy 0 miv iy Py 常量
例 如图所示,两部运水的卡车A、B在水平面上沿同一方向运 动,B的速度为u ,从B上以6kg/s的速率将水抽至A上,水 从管子尾部出口垂直落下,车与地面间的摩擦不计,时刻 t 时,A车的质量为M,速度为v 。 求 时刻 t ,A 的瞬时加速度 解 选A车M和t时间内抽至A 车的水 m 为研究系统, 水平方向上动量守恒 A A B
解得
O
v1
v2
m2
x
v1 m2
2G (m1 m2 )r
2G v 2 m1 (m1 m2 )r
相对速率 v12 v1 v 2 m2
2G 2G m1 (m1 m2 )r (m1 m2 )r
§4.3 质点系动量守恒定律
当
Fi 0
i
d miv i 0 miv i 常矢量
质点系动量守恒定律 动量守恒的分量表述
Fx 0 miv ix Px 常量 Fz 0 miv iz Pz 常量
说明 (1) 动量守恒定律适用于惯性系 (2) 动量守恒定律也适用于高速,微观领域
v
u
Mv mu ( M m)v
Mv mu v M m m u v v M
mu v v v v M m v dm u v 6 a lim
大学物理(吴百诗)第三版答案

大学物理习题及解答第一章1-1 |r ∆|与r ∆有无不同?t d d r 和t d d r有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明. 解:(1)r∆是位移的模,∆r 是位矢的模的增量,即r ∆12r r -=,12r r r-=∆; (2)t d d r 是速度的模,即t d d r ==v tsd d . t rd d 只是速度在径向上的分量.∵有r r ˆr =(式中r ˆ叫做单位矢),则t ˆrˆt r t d d d d d d r r r +=式中t rd d 就是速度径向上的分量,∴t rt d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模,即t v a d d=,t vd d 是加速度a 在切向上的分量.∵有ττ (v =v 表轨道节线方向单位矢),所以t v t v t v d d d d d d ττ =式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂,超出教材规定,故不予讨论)1-2 设质点的运动方程为x =x (t ),y =y (t ),在计算质点的速度和加速度时,有人先求出r =22y x +,然后根据v =t rd d ,22d d t r v =22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确?为什么?两者差别何在?解:后一种方法正确.因为速度与加速度都是矢量,在平面直角坐标系中,有j y i x r +=,jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x yx而前一种方法的错误可能有两点,其一是概念上的错误,即误把速度、加速度定义作22d d d d t r a t r v == 其二,可能是将22d d d d t r t r 与误作速度与加速度的模。
大学物理复习题解析-吴百诗

物理学练习§1-1(总1)一、进择题:1. 某质点的运动方程为)(3723SI t t x +-=,则该质点作(A)匀加速直线运动,加速度沿X 轴正方向; (B)匀加速直线运动,加速度沿X 轴负方向; (C)变加速直线运动,加速度沿X 轴正方向;(D)变加速直线运动,加速度沿X 轴负方向。
( )解答:)(3723SI t t x +-= t -t x 2212 d d ==∴v t tva 21 d d -== ( D ) 3. 以下五种运动形式中,a保持不变的运动是(A)单摆的运动; (B)匀速率圆周运动;(C)行星的椭圆轨道运动; (D)抛体运动; (E) 圆锥摆运动。
( )解答:a 为矢量,a 保持不变说明a的大小和方向都不变(A )a 的大小和方向都变 (B )a的大小不变,方向变(C )a 的大小和方向都变 (D )a的大小和方向都不变(E )a的大小不变,方向变 (D )4.对于沿曲线运动的物体,以下几种说法中哪一种是正确的: (A)切向加速度必不为零;(B)法向加速度必不为零(拐点处除外);(C)由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零; (D)若物体作匀速率运动,其总加速度必为零;(E)若物体的加速度a为恒矢量,它一定作匀变速率运动。
( )解答:根据t n a a a+=(A )0≠t a说明物体作曲线运动时速度的大小改变,但是匀速率圆周运动的速度大小不变,因此该说法错误。
(B )题目给出物体作曲线运动,说明速度的方向是变化的即0≠n a,因此该说法正确。
(C )物体作曲线运动,速度的方向是变化的, 0≠n a,错误。
(D )物体作曲线运动,速度的方向改变0≠n a ,所以虽然速度的大小不变,即 0=t a ,仍有0≠+=t n a a a,该说法错误。
(E )该说法错误,例如斜抛运动,a是恒量,但做变速率运动。
(B )二、填空题,1.一质点沿X 方向运动,其加速度随时间变化关系为)(24SI t a +=,如果初始时质点的速度0υ为7m ·s -1,则当t为4s 时,质点的速度=υ 米/秒。
大学物理 吴百诗主编5-7
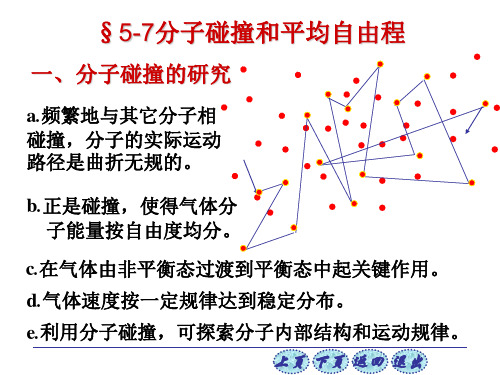
d
围绕分子的中心,以d为半径画出的 球叫做分子的作用球。
d
d 围绕分子的中心,以d为半径画出的截 面叫做分子的碰撞截面。 πd 2
以A分子中心的运动轨迹为轴线,以d为半径作 一曲折的圆柱体。
2d A d
上页 下页 返回 退出
在t 时间内,分子A走过的路程为:
u t
二、平均碰撞频率 Z
单位时间内一个分子和其它分子碰撞的平均次数。
三、 平均自由程 公式
每两次连续碰撞之间一个分子自由运动的平均路程。 设分子的平均速率为 v ,则
v . Z
d
(1)假定每个分子都是直径为d 的刚性小球;
(2)假定一个A分子以相对速率 u 运动,其他分子都静 止不动; 当A分子与其他分子作一次弹性碰撞 时,两个分子的中心相隔距离就是d。
Байду номын сангаас
因为 所以
u 2v
Z n u 2nπd v
2
2d A d
上页 下页 返回 退出
平均自由程:
v Z
因为
1 2 2nπd
p nkT
kT 2 2πd p
平均自由 程公式
所以
所以平均自由程与温度成正比,与压强成反比。
上页 下页 返回 退出
例题5-7
求氢在标准状态下,在1s 内分子的平均
碰撞次数。已知氢分子的有效直径为210-10m。 解:按气体分子算术平均速率公式得
8RT 3 1.70 10 m/s v πM mol
按公式 p=nkT 可知单位体积中分子数为
p 25 3 n 2.69 10 m kT
上页 下页 返回 退出
因此
大学物理吴百诗科学社 课后习题答案

q
4πε 0 r
( r ≥ R2 )
ε0S
d d′ 2πε 0
,
1 ε 0 Sd ′ 2 U0 2 2 (d d ′)
R1 R2 U2 R2 R1
1.0 × 10 7 C, 2.0 × 10 7 C, 2.3 × 10 3 V, 2.1 × 10 7 C, 8.6 × 10 8 C, 9.7 × 10 2 V
第九章
9.1 9.2
9.4 9.12 9.14 9.16 9.18 9.20 9.24 9.26 9.28 9.30
(1) D (1)
(2) B
(2)
3 q 3 σ a+b ln , 2πε 0 2
q 2πε 0 a 2
r i
σ b arctan πε 0 2h
13.6 eV
等势线是中垂面内半径为 x 的圆,圆心在两电荷连线的中点
9.32 9.34 9.36
0,0;3.5×10-8 C/m2,8.0×102 N/C;1.3×10-8 C/m2,1.4×103 N/C; 5.4×102 V;4.8×102 V;3.6×102 V 2.7×10-5 C/m2 (1)
U 0ε 0 S d
(2)
U 0ε 0 U0 , d εrd
(3)
IBR (5)
0 NI 0 NIh D1 , ln 2π r 2π D2
2.86×1014 m-3,n
0 I
r
1
10.6
10.8
10.10 10.12
λω 0 a + b λω ln , [(a + b) 3 a 3 ] 4π a 6 0 I r 0 I 0 I ( r32 r 2 ) (r < r1 ), (r1 < r < r2 ), (r2 < r < r3 ), 0 (r > r3 ) 2π r 2π r12 2π ( r32 r22 )r
大学物理(吴百诗)习题答案3运动守恒定律汇编
冲量和动量定理3-1质量m =10kg 的物体在力F x =30+4t N 的作用下沿x 轴运动,试求(1)在开始2s 内此力的冲量I ;(2)如冲量I =300N·s ,此力的作用时间是多少?(3)如物体的初速v 1=10m/s ,在t =6.86s 时,此物体的速度v 2为多少? 解:(1) s N 68d )430(d 2020⋅=+==⎰⎰t t t FI xx(2) 300230d )430(d 2=+=+==⎰⎰tt t t t F I tt x t ,s 86.6=t(3) 1212mv mv p p I -=-=,s 86.6=t ,s N 300⋅=I ,m/s 20)1010300(101)(112=⨯-=-=mv I m v 3-2质量m =1kg 的物体沿x 轴运动,所受的力如图3-2所示。
t =0时,质点静止在坐标原点,试用牛顿定律和动量定理分别求解t =7s 时此质点的速度。
解:(1) ⎩⎨⎧≤≤+-≤≤=75355502t t t t F 50≤≤t ,t tv m2d d =,⎰⎰=500d 2d 1t t v m v ,(m/s)25251==m v75≤≤t ,355d d +-=t tvm ,⎰⎰+-=75d )355(d 21t t v m v v ,(m/s)352=v(2) s)(N 35)107(21d 7⋅=⨯==⎰t F I ,212mv mv mv I =-=,(m/s)352=v动量守恒定律3-3两球质量分别为m 1=3.0g , m 2=5.0g ,在光滑的水平桌面上运动,用直角坐标xOy 描述运动,两者速度分别为cm /s 81i v ϖϖ=,cm /s )168(2j i v ϖϖϖ+=,若碰撞后两球合为一体,则碰撞后两球速度v ϖ的大小为多少?与x 轴的夹角为多少?解:系统动量守恒 j i v m v m v m m ϖϖϖϖϖ8064)(221121+=+=+, j i v ϖϖϖ108+=cm/s 8.1210822=+==v v ϖ,与x 轴夹角 ︒==3.51810arctan α3-4如图3-4所示,质量为M 的1/4圆弧滑槽停在光滑的水平面上,一个质量为m 的小物体自圆弧顶点由静止下滑。
大学物理复习题解析-吴百诗
物理学练习§1-1(总1)一、进择题:1. 某质点的运动方程为)(3723SI t t x +-=,则该质点作(A)匀加速直线运动,加速度沿X 轴正方向; (B)匀加速直线运动,加速度沿X 轴负方向; (C)变加速直线运动,加速度沿X 轴正方向;(D)变加速直线运动,加速度沿X 轴负方向。
( )解答:)(3723SI t t x +-= t -t x 2212 d d ==∴v t tva 21 d d -== ( D ) 3. 以下五种运动形式中,a保持不变的运动是(A)单摆的运动; (B)匀速率圆周运动;(C)行星的椭圆轨道运动; (D)抛体运动; (E) 圆锥摆运动。
( )解答:a 为矢量,a 保持不变说明a的大小和方向都不变(A )a 的大小和方向都变 (B )a的大小不变,方向变(C )a 的大小和方向都变 (D )a的大小和方向都不变(E )a的大小不变,方向变 (D )4.对于沿曲线运动的物体,以下几种说法中哪一种是正确的: (A)切向加速度必不为零;(B)法向加速度必不为零(拐点处除外);(C)由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零; (D)若物体作匀速率运动,其总加速度必为零;(E)若物体的加速度a为恒矢量,它一定作匀变速率运动。
( )解答:根据t n a a a+=(A )0≠t a说明物体作曲线运动时速度的大小改变,但是匀速率圆周运动的速度大小不变,因此该说法错误。
(B )题目给出物体作曲线运动,说明速度的方向是变化的即0≠n a,因此该说法正确。
(C )物体作曲线运动,速度的方向是变化的, 0≠n a,错误。
(D )物体作曲线运动,速度的方向改变0≠n a ,所以虽然速度的大小不变,即 0=t a ,仍有0≠+=t n a a a,该说法错误。
(E )该说法错误,例如斜抛运动,a是恒量,但做变速率运动。
(B )二、填空题,1.一质点沿X 方向运动,其加速度随时间变化关系为)(24SI t a +=,如果初始时质点的速度0υ为7m ·s -1,则当t为4s 时,质点的速度=υ 米/秒。
《大物》下(吴百诗)作业答案
《大学物理》(下)(吴百诗)作业答案7.1 -1190J ; 7.2 B ; 7.3 A ;7.4 解:A=曲线下面积=(P1+P2)(V2-V1)/2P1V1=νRT1 P2V2=νRT2ΔE=νCv(T2-T1)= ν5R/2(P2V2/νR - P1V1/νR)=5(P2V2-P1V1)/2 Q=A+ΔE7.5 解:等压过程A=P ΔV=5*102JQ=A+ΔEΔE=Q-A=1.21*103J7.6 A ; 7.7 D ; 7.8 B ; 7.9 解:C V =5R/2;C p =7R/2;γ=7/5ab 等容过程 吸热a b b b a a a b V ab T T T P T P T T C Q 2,//),(==-=νbc 绝热过程 γγγγγ2/,,011b c c cbb bc T T T P T P Q ===----ca 等压过程 放热)(c a p ca T T C Q -=νabcaab Q Q Q +=η7.10 解:与老版答案相同AB 过程 吸热Q 1=vRT 1InV 2/V 1 BC 过程 放热 Q 2=vC V (T 2-T 1) CD 过程 放热Q 3=vRT 2InV 1/V 2 DA 过程 吸热Q 4=vC V (T 1-T 2)η=A/Q 吸=( Q 1+ Q 2+ Q 3+ Q 4)/(Q 1+ Q 4)=15%8.1 相同、相同、相同、不一定; 8.2 A ; 8.3 B ; 8.4 解:与老版答案相同n=N/V=P/kT=2.44*1025/m 3ρ=n μ=1.3kg/ m 3ε=3kT/2=6.21*10-21Jm n d 931045.3/1-⨯==8.5 解:PV=νRT T=PV/νR J kT 221089.32/3-⨯==ε8.6 理想气体分子速率大于最概然速率的概率理想气体分子平均平动动能 8.7 6; 8.8 B ;8.9 解:J RT M m E J n E kT P n J KT CON mol kg RT M sm P M RT v MRT p vRT PV K k K 33212322107.125)5(105.1,/)4(107.32/3)3(,/1028)494/(3)2(/494/3/3//,)1(⨯==⨯===⨯==⨯=======--εερρ8.10 解:s m v K T M RTv s m v v v M M MRTv pO H pH pH pO pH O H p /500,481,2/2000,,,222222222====><=12.1、C 12.2、D 12.3、 2π12.4 解:(1)波动方程y=0.05cos (100t-2x)= 0.05cos2π (50t/π-x/π)将上述方程与波动方程标准形式y=Acos2π (νt-x/λ)相比较,有: A=0.05(m),λ=π(m),T=1/ν=π/50(s),u=λ/T=50(m/s) (2)质点的振速度方程为=-0.05*100sin(100t-10) 故V m =0.05*100=5m/s各质点加速度方程为:a==-0.05*100*100 cos (100t-2x)故a m =0.05*100*100=500m/s 212.5 解:(1)设坐标原点的振动方程为:y=Acos (ωt+φ)由题意可知:A=0.1m ,ω=2π/T=πs -1; 由旋转矢量法可知φ=-π/2 故振动方程为:y=0.1cos(πt-π/2) 又u=λ/T=2/2=1m/s故波动方程为:y=0.1cos[π(t-x)- π/2](2)将x=0.5m 代入波动方程,得该质点的振动方程为:y=0.1cos(πt-π)tyv ∂∂=tv∂∂(3)将t=1.0s 代入波动方程,得此时各质点的位移为:y=0.1cos(π/2-πx)=0.1sin πx波形图为:12.6 解:(1)设坐标原点的振动方程为:y=Acos (ωt+φ)由图可知:A=0.10(m),λ=20 (m),ω=2πν=500πs -1由题意可知波沿OX 轴负方向传播,并可判断原点处质点将沿OY 轴的负方向运动,由旋转矢量法可知初相φ=π/3;故坐标原点的振动方程为:y=0.10cos (500πt+π/3) 又u=λν=5000(m/s)故波动方程为 y=0.10cos[500π(t+x/5000)+π/3]12.7 频率相同;振动方向相互平行;相位相同或相位差恒定。
北邮 大学物理 吴百诗第12章-机械振动
x1 A cos(t1 )
x2 A cos(t 2 )
(t2 ) (t1 )
t t 2 t1
(2)对于两个同频率的简谐运动,相位 差表示它们间步调上的差异(解决振动合成 问题).
x1 A1 cos(t 1 )
x2 A2 cos(t 2 )
(t 2 ) (t 1 )
2 1
2 1
0 同步
π 反相
为其它
超前 落后
x
x
t
x
t
o
o
o
t
例题. 质点作简谐振动A=4cm,=0.5Hz,t=1s时x= -2cm,且向 t=0s X正方向运动,写出振动表达式。 解:设振动表达式为
dx v A sin( t ) dt d2 x a 2 A 2 cos(t ) dt
简谐运动方程— 状态参量??
其中
v0 2 2 A x0 ( ) arctan( v 0 ) x0
x A cos(t )
=0
T t
4.初相 弹簧振子 的几个特 殊的初始 状态及相 应的振动 曲线:
(b)
m o
x0 = 0
A x o
= /2
T t
-A x A
(c)
m -A
x0 = -A
=
T t
o
x
o -A x A
= 3/2
T t
(d)
m
x0 = 0
o
x
o -A
讨论
已知
t 0, x 0, v0 0
2
