R案例分析_异方差
异方差检验案例

异方差检验案例那我就来给你讲个异方差检验的案例哈。
咱们就说有个超级好奇的经济学家,他想研究一下不同城市居民的消费和收入之间的关系。
这个经济学家啊,从各个城市收集了好多家庭的数据,比如说每个家庭的月收入,还有他们每个月的消费金额。
他就想着啊,用一个线性回归模型来看看收入和消费到底有啥联系。
于是他就开始噼里啪啦地在电脑上一顿操作,得出了一个初步的回归方程。
但是呢,这个经济学家可没那么容易就满足。
他就琢磨啊,这里面会不会有个捣蛋鬼叫异方差呢?啥是异方差呢?就好比每个城市的家庭,他们在消费这个事儿上的波动情况可能不一样,不是那种规规矩矩都一样的波动。
那他怎么去检验有没有异方差呢?他就用了怀特(White)检验。
这怀特检验啊,就像是给数据来个全面的体检。
他把各种可能影响消费和收入关系的变量都组合在一起,搞出了一些新的统计量。
比如说,他把家庭人数、城市的物价水平这些因素都考虑进去了。
然后计算这个怀特检验的统计量。
如果这个统计量的值很大很大,那就像是敲响了警钟,告诉他:“老兄,这里面很可能有异方差哦!”就像有个城市呢,是那种超大型的商业城市,里面有很多高收入人群,他们的消费可能就特别多样化。
今天去买个超级贵的限量版包包,明天又去参加个豪华游艇派对,消费的波动超级大。
而另外一个小县城呢,大家收入都差不多,消费也比较固定,就每天买买菜、偶尔添置个新衣服啥的,消费波动就小得多。
这种不同城市之间消费波动的差别,就可能导致异方差的出现。
如果这个经济学家发现真的有异方差,那他之前做的那个简单的线性回归模型可能就不太靠谱啦。
他就得想办法去调整,比如说用加权最小二乘法,给那些波动大的数据一些特殊的“照顾”,让模型更准确地反映收入和消费之间的关系。
这样呢,他就能更好地给政府出谋划策,告诉政府不同城市在消费和收入方面的真实情况,政府就能制定出更合适的经济政策啦。
怎么样,这个案例是不是还挺好理解的呀?。
异方差性的概念、类型、后果、检验及其修正方法含案例

Yi和Xi分别为第i个家庭的储蓄额和可支配收入。
在该模型中,i的同方差假定往往不符合实际情况。对高收 入家庭来说,储蓄的差异较大;低收入家庭的储蓄则更有规律 性(如为某一特定目的而储蓄),差异较小。
因此,i的方差往往随Xi的增加而增加,呈单调递增型变化 。
– 在选项中,EViews提供了包含交叉项的怀特检验“White Heteroskedasticity(cross terms)”和没有交叉项的怀特检 验“White Heteroskedasticity(no cross terms)” 这样两个 选择。
• 软件输出结果:最上方显示两个检验统计量:F统计 量和White统计量nR2;下方则显示以OLS的残差平 方为被解释变量的辅助回归方程的回归结果。
随机误差项具有不同的方差,那么: 检验异方差性,也就是检验随机误差项的方差与解
释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
路漫漫其修远兮, 吾将上下而求索
问题在于:用什么来表示随机误差项的方差? 一般的处理方法:
路漫漫其修远兮, 吾将上下而求索
2.图示检验法
路漫漫其修远兮, 吾将上下而求索
3.模型的预测失效
一方面,由于上述后果,使得模型不具有良好的统计性质;
【书上这句话有点问题】
其中 所以,当模型出现异方差性时,Y预测区间的建立将发生困 难,它的预测功能失效。
路漫漫其修远兮, 吾将上下而求索
三、异方差性的检验(教材P111)
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值,
(注意:其中的2完全可以是1)
r语言多元回归异方差检验并处理

r语言多元回归异方差检验并处理以下是关于r语言多元回归异方差检验并处理的文章:1. 引言在统计学中,多元回归分析是一种常用的技术,用于研究自变量对因变量的影响。
然而,在实际应用中,数据可能存在异方差的问题,即误差方差与自变量之间存在相关性。
本文将介绍如何使用R语言进行多元回归异方差检验并处理。
2. 异方差的概念异方差是指在多元回归分析中,误差项的方差不是恒定的,而是与自变量之间的差异有关。
这可能导致参数估计的不准确性,从而影响对因变量的预测和解释。
3. 多元回归异方差检验在R语言中,我们可以使用许多方法来检验多元回归模型中是否存在异方差。
其中最常用的方法是利用residuals()函数来获取模型的残差,然后使用对应的统计检验方法来检验残差的异方差性。
4. 处理异方差的方法一旦检测到存在异方差,就需要采取相应的处理方法。
在R语言中,可以使用诸如加权最小二乘法(WLS)或广义最小二乘法(GLS)等方法来处理异方差。
5. 个人观点与理解对于多元回归异方差检验并处理,我个人认为这是一个非常重要的统计问题。
在实际应用中,数据往往不满足经典统计假设,因此需要我们针对具体情况进行检验和处理,以确保模型的合理性和准确性。
6. 总结通过本文的介绍,我们了解了R语言中多元回归异方差检验并处理的基本方法和步骤。
在实际应用中,我们需要仔细对待数据的异方差问题,以确保多元回归模型的有效性和稳健性。
通过以上内容,我希望你能对r语言多元回归异方差检验并处理有更深入的了解和掌握。
如果还有任何问题或需要进一步解释,请随时与我联系。
多元回归分析是一种应用广泛的统计技术,它可以用来研究多个自变量对一个因变量的影响。
然而,在实际应用中,我们常常会遇到异方差的问题,即误差项的方差不是恒定的,而是与自变量之间的差异有关。
这可能会对参数估计和模型的预测产生影响。
在R语言中,我们可以使用许多方法来检验多元回归模型中是否存在异方差。
其中最常用的方法是利用residuals()函数来获取模型的残差,然后使用对应的统计检验方法来检验残差的异方差性。
异方差性的检验及处理方法
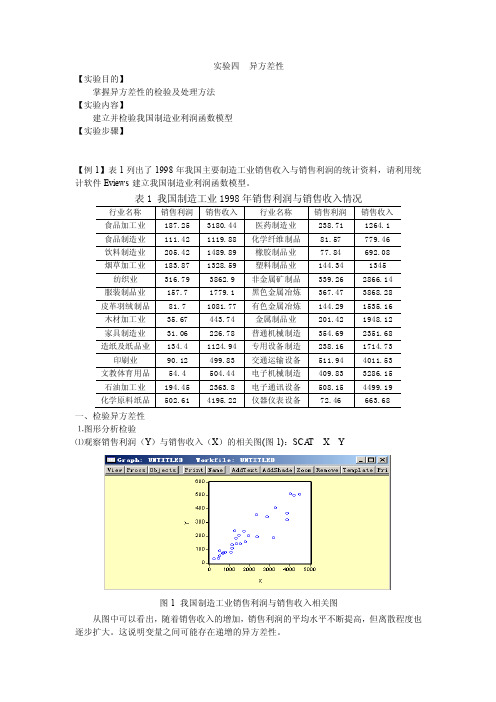
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
异方差及其处理

ei 0 1x i2 i
ei 0 1 x ji i
ei 0 1 1 i x ji
对本例进行Glezser test
异方差的诊断
2、正规的检验 (2)戈德菲尔德-匡特检验(GlodfeldQuandt test) 先给原始数据进行排序,然后。。。
戈德菲尔德-匡特检验(GlodfeldQuandt test)
3/8个样本
24,000 22,000
¼ 个样本
两个回归 可以产生 两个残差 平方和
20,000 18,000
CONS
16,000 14,000 12,000
同方差时, 两个残差 平方和应 该差不多!
10,000 8,000 12,000
1,200
ABRE
800 400
0 12,000
16,000
20,000
24,000
28,000
32,000
INC
案例:用截面数据估计消费函数
直观感受:
存在异方差 (heteroskedasticity)
Homoskedasticity (同方差)
Heteroskedasticity(异方差)
异方差的诊断
2、正规的检验 (3)怀特检验:
③ 由上述辅助方程的R2构成的统计量 nR2服从X2 (p)分布,可进行卡方检验; 大于临界值时,拒绝同方差假设 当然,也可以应用F检验。
案例:纽约的租金和收入
案例:纽约的租金和收入
因变量:RENT(n=108)
变量
C Income
系数
5455.48 0.06
所以,可进行F检验。
R案例分析_异方差

R案例分析_异方差异方差是指在统计分析中,随着自变量的不同取值,因变量的方差也随之发生变化的现象。
异方差问题在实际数据分析中经常遇到,其存在会对统计模型的准确性和效果产生重要影响。
本文将以一个实际案例为例,分析异方差问题及其解决办法。
假设我们是一家电商公司的数据分析师,负责分析产品销售情况。
在进行销售数据分析时,我们发现在不同的销售渠道下,产品的销售量存在差异。
为了更准确地分析销售情况,我们希望解决异方差问题。
首先,我们需要通过数据分析手段来确认异方差的存在。
我们可以绘制销售量和销售渠道的散点图,观察销售量在不同渠道下的分布情况。
如果不同渠道下的散点图呈现出不同的方差大小,则可以初步判断存在异方差问题。
确定存在异方差问题后,我们需要采取措施来解决。
以下是几种常见的异方差处理方法:1.数据变换:可以通过对因变量进行一些数学变换,如开方、取对数等。
这样可以将异方差问题转化为方差齐性问题,便于后续的数据分析。
但需要注意的是,变换后的数据在解释上可能会有所改变。
2. 加权最小二乘法(Weighted Least Squares, WLS):WLS是一种适用于异方差数据的回归分析方法。
其基本思想是根据异方差结构,对不同的观测值赋予不同的权重,从而修正回归模型的误差项。
3.方差分析(ANOVA):如果我们可以找到一些能够解释异方差的因素,可以通过方差分析来进行处理。
对于不同的因子水平,通过统计方法比较其差异性,进而确定是否存在异方差问题。
4. 偏最小二乘回归(Partial Least Squares Regression, PLS):PLS是一种非参数化的回归分析方法,可以在一定程度上克服异方差问题。
PLS通过找到主成分来降低变量间的相关性,从而改善模型的准确性。
在实际应用中,我们可以尝试使用上述方法中的一个或多个来解决异方差问题。
需要注意的是,不同的方法适用于不同的数据情况,选择合适的方法需要基于实际情况和数据分析的目的进行综合考虑。
异方差的例子

异方差的例子异方差指的是在统计分析中,不同观测值的方差不相等。
这种情况下,使用传统的线性回归模型可能会导致结果的偏差和误差。
因此,为了得到更准确的结果,需要采取一些方法来处理异方差性。
下面将列举一些常见的异方差的例子,并介绍相应的处理方法。
1. 股票价格波动:股票价格的波动通常呈现出非常明显的异方差性。
在股票市场中,有些股票的价格非常波动,而有些股票的价格相对稳定。
这种情况下,可以使用加权最小二乘法来处理异方差。
2. 学生考试成绩:学生考试成绩的方差通常也会存在异方差性。
一些学生的考试成绩波动较大,而一些学生的考试成绩相对稳定。
在分析学生的考试成绩时,可以考虑使用方差齐性检验来确定是否存在异方差,并选择相应的处理方法。
3. 经济增长率:经济增长率在不同的时间段和地区通常也会呈现出异方差性。
一些地区的经济增长率波动较大,而一些地区的经济增长率相对稳定。
在分析经济增长率时,可以使用异方差稳健标准误来处理异方差。
4. 气温变化:气温在不同的季节和地区通常也会呈现出异方差性。
一些地区的气温波动较大,而一些地区的气温相对稳定。
在分析气温变化时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
5. 金融市场波动:金融市场的波动性也会导致异方差的问题。
一些金融资产的价格波动较大,而一些金融资产的价格相对稳定。
在分析金融市场波动时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
6. 人口增长率:人口增长率在不同的国家和地区也会呈现出异方差性。
一些国家的人口增长率波动较大,而一些国家的人口增长率相对稳定。
在分析人口增长率时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
7. 网络流量:网络流量在不同的时间段和地区也会呈现出异方差性。
一些地区的网络流量波动较大,而一些地区的网络流量相对稳定。
在分析网络流量时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
8. 土地价格:土地价格在不同的地区和时间段也会呈现出异方差性。
第六章异方差的性质-PPT课件

(一)残差序列分析 (二)戈德菲尔德-夸特检验 (三)戈里瑟检验 (四)怀特检验
(一)残差序列分析
(a)
e
i
X k
(b)
eห้องสมุดไป่ตู้
i
X k
(c)
e
i
X k
(d)
e
i
X k
(e)
e
i
X k
(f)
e
i
X k
(二)戈德菲尔德-夸特检验
戈德菲尔德-夸特检验是最常用的异方差专门检 验方法之一。这种方法适合于检验样本容量较大 的线性回归模型的递增或递减型异方差性。 对于存在递增异方差模型,步骤:首先将样本按 X值的大小顺序将观测值排列,然后略去居中的C 个观测值,并将其余的(n-C)个观测值分成两组, 每组(n-C)/2个,分别对两个子样本进行回归, 并分别获得残差平方和,自由度都为(n-C)/2K-1。
普遍性:两类数据都有,横截面数据更多。 原因:
1.按照边错边改学习模型,人们在学习过程中,其行为误 2 差随时间而减少。在这种情形下,方差 i 会逐渐变小。 例如,随着打字练习小时数的增加,不仅平时打错的个 数而且打错的方差都有所下降。 2.随着收入的增长,人们有更多的备用收入,从而如何支 配他们的收入有更大的选择范围。因此,在作出储蓄对 收入的回归时,很可能发现,由于人们对其储蓄行为有 更多的选择, i2 与收入俱增。因此,以增长为导向的公 司比之于已发展定型的公司在红利支付方面也可能表现 更多的变异。
(二)戈德菲尔德-夸特检验
计算统计量:
F e
i2 2 i2
2 e i1 i1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 案例分析
一、问题的提出和模型设定
为了分析不同省份或城市的交通和通讯支出的规划提供依据,分析交通和通讯支出与可支配收入的关系,建立交通和通讯支出与可支配收入的回归模型。
假定交通和通讯支出与可支配收入满足线性约束,则理论模型设定为
i i i cum income u αβ=+⋅+ (1) 其中i cum 表示交通和通讯支出,i income 表示可支配收入。
由1999年《中国统计年鉴》得到如下数据
注:见数据文件cumexp_income.csv
二、参数估计
利用最小二乘法估计模型(1)的参数:
mydata.lm <- lm(cumexp ~ income)
summary(mydata.lm)
R 软件输出的结果为:
Call:
lm(formula = cumexp ~ income)
Residuals:
Min 1Q Median 3Q Max
-97.465 -19.986 -5.111 15.532 184.115
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -56.91798 36.20624 -1.572 0.127
income 0.05808 0.00648 8.962 1.02e-09 ***
---
Signif. codes : 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 50.48 on 28 degrees of freedom
Multiple R-squared: 0.7415, Adjusted R-squared: 0.7323
F-statistic: 80.32 on 1 and 28 DF, p-value: 1.021e-09
估计结果为:
ˆ56.920.06(36.21)(0.01)
cum income =-+ 20.74
..504880.32R s e F ===
括号内为标准差。
三、检验模型的异方差
(一)图示法
par(mfrow=c(1,2))
plot(cumexp ~ income, col="red")
abline(mydata.lm)
plot(residuals(mydata.lm)^2 ~ income,col="blue")
从上图可以看出,残差平方对解释变量X 的散点图主要分布在图形中的下三角部分,大40006000
8000200300400500
600
a.散点图及回归线income c u m e x
p 4000600080000500010000200003000
0 b.残差平方的散点图
income r e s i d u a l s (m y d a t a .l m )^2
致看出残差平方随可支配收入的变动呈增大的趋势,因此,模型很可能存在异方差。
但是否确实存在异方差还应通过更进一步的检验。
(二)white异方差检验
根据white检验的步骤,计算出white检验的统计量及置信水平为1%的临界值,判读模型是否存在异方差。
u2 <- residuals(mydata.lm)^2
summary(lm(u2 ~ income + income^2)) #辅助回归
R值。
nrow(mydata)*0.341 #white 统计量,数据来自于辅助回归中的2
qchisq(0.01,df=2, lower.tail=F) #计算对应的临界值。
输出结果为:
Call:
lm(formula = u2 ~ income + income^2)
Residuals:
Min 1Q Median 3Q Max
-8511.0 -2362.2 -79.0 741.5 22735.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.143e+04 3.752e+03 -3.047 0.004999 **
income 2.556e+00 6.716e-01 3.806 0.000705 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5232 on 28 degrees of freedom
Multiple R-squared: 0.341, Adjusted R-squared: 0.3174
F-statistic: 14.49 on 1 and 28 DF, p-value: 0.0007047
> nrow(mydata)*0.341 #white 统计量
[1] 10.23
> qchisq(0.01,df=2, lower.tail=F)
[1] 9.21034
有输出结果可以看出,white统计量大于临界值,我们拒接模型存在异方差,接受备择假设。
(三)Goldfeld-Quanadt检验
library(lmtest)
gqtest(mydata.lm)
输出结果为:
Goldfeld-Quandt test
data: mydata.lm
GQ = 9.2707, df1 = 13, df2 = 13, p-value = 0.0001458
根据p值,在1%的置信水平下显著,拒接原假设,模型中的残差项存在异方差,而且方差是逐渐增大的。
