微波技术习题
微波技术与天线总复习题及其答案

微波技术与天线基础总复习题一、填空题1、微波是一般指频率从 至 范围内的电磁波,其相应的波长从 至 。
并划为 四个波段;从电子学和物理学的观点看,微波有 、 、 、 、 等重要特点。
2、无耗传输线上的三种工作状态分别为: 、 、 。
3、传输线几个重要的参数:(1) 波阻抗: ;介质的固有波阻抗为 。
(2) 特性阻抗: ,或 ,Z 0=++I U 其表达式为Z 0= ,是一个复数; 其倒数为传输线的 .(3) 输入阻抗(分布参数阻抗): ,即Z in (d)= 。
传输线输入阻抗的特点是: a) b) c) d)(4) 传播常数:(5) 反射系数:(6) 驻波系数:(7) 无耗线在行波状态的条件是: ;工作在驻波状态的条件是: ;工作在行驻波状态的条件是: 。
4、负载获得最大输出功率时,负载Z 0与源阻抗Z g 间关系: 。
5、负载获得最大输出功率时,负载与源阻抗间关系: 。
6、史密斯圆图是求街均匀传输线有关 和 问题的一类曲线坐标图,图上有两组坐标线,即归一化阻抗或导纳的 的等值线簇与反射系数的 等值线簇,所有这些等值线都是圆或圆弧,故也称阻抗圆图或导纳圆图。
阻抗圆图上的等值线分别标有 ,而 和 ,并没有在圆图上表示出来。
导纳圆图可以通过对 旋转180°得到。
阻抗圆图的实轴左半部和右半部的刻度分别表示 或 和 或 。
圆图上的电刻度表示 ,图上0~180°是表示 。
7、阻抗匹配是使微波电路或系统无反射运载行波或尽量接近行波的技术措施,阻抗匹配主要包括三个方面的问题,它们是:(1);(2);(3)。
8、矩形波导的的主模是模,导模传输条件是,其中截止频率为,TE10模矩形波导的等效阻抗为,矩形波导保证只传输主模的条件是。
9、矩形波导的管壁电流的特点是:(1)、(2)、(3)。
10、模式简并现象是指,主模也称基模,其定义是。
单模波导是指;多模传输是。
11、圆波导中的主模为,轴对称模为,低损耗模为。
微波技术基础期末复习题

《微波技术基础》期末复习题第2章 传输线理论1. 微波的频率范围和波长范围频率范围 300MHz ~ 3000 GHz 波长范围 1.0 m ~ 0.1mm ;2. 微波的特点⑴ 拟光性和拟声性;⑵ 频率高、频带宽、信息量大;⑶ 穿透性强;⑷ 微波沿直线传播;3. 传输线的特性参数⑴ 特性阻抗的概念和表达公式特性阻抗=传输线上行波的电压/传输线上行波的电流 1101R j L Z G j C ⑵ 传输线的传播常数传播常数 j γαβ=+的意义,包括对幅度和相位的影响。
4. 传输线的分布参数:⑴ 分布参数阻抗的概念和定义⑵ 传输线分布参数阻抗具有的特性()()()in V d Z d I d =00ch sh sh ch L L L L V d I Z d V d I d Z γγγγ+=+000th th L L Z Z d Z Z Z d γγ+=+① 传输线上任意一点 d 的阻抗与该点的位置d 和负载阻抗Z L 有关; ② d 点的阻抗可看成由该点向负载看去的输入阻抗;③ 传输线段具有阻抗变换作用;由公式 ()in Z d 000th th L L Z Z d Z Z Z dγγ+=+ 可以看到这一点。
④ 无损线的阻抗呈周期性变化,具有λ/4的变换性和 λ/2重复性; ⑤ 微波频率下,传输线上的电压和电流缺乏明确的物理意义,不能直接测量;⑶ 反射参量① 反射系数的概念、定义和轨迹;② 对无损线,其反射系数的轨迹?;③ 阻抗与反射系数的关系;in ()1()()()1()V d d Z d I d d 01()1()d Z d ⑷ 驻波参量① 传输线上驻波形成的原因?② 为什么要提出驻波参量?③ 阻抗与驻波参量的关系;5. 无耗传输线的概念和无耗工作状态分析⑴ 行波状态的条件、特性分析和特点;⑵ 全反射状态的条件、特性分析和特点;⑶ 行驻波状态的条件、特性分析和特点;6. 有耗传输线的特点、损耗对导行波的主要影响和次要影响7. 引入史密斯圆图的意义、圆图的构成;8. 阻抗匹配的概念、重要性9. 阻抗匹配的方式及解决的问题⑴ 负载 — 传输线的匹配⑵ 信号源 — 传输线的匹配⑶ 信号源的共轭匹配10. 负载阻抗匹配方法⑴ λ/4阻抗匹配器⑵ 并联支节调配器⑶ 串联支节调配器第3章 规则金属波导1. 矩形波导的结构特点、主要应用场合;2. 矩形波导中可同时存在无穷多种TE 和TM 导模;3. TE 和TM 导模的条件;TE 导模的条件:00(,,)(,)0j z z z z E H x y z H x y e β-==≠TE 导模的条件:00(,,)(,)0j z z z z H E x y z E x y e β-==≠4. 关于矩形波导的5个特点;5. 掌握矩形波导TE 10模的场结构,并在此基础上掌握TE m0模的场结构;6. 管壁电流的概念;7. 管壁电流的大小和方向;8. 矩形波导的传输特性(导模的传输条件与截止);9. 圆形波导主模TE11模的场结构。
微波技术基础课后参考答案 (田加胜版)

微波技巧基本课后习题答案1 第一章1.7 终端反射系数0050505050125050501005025L L L Z Z j j j j Z Z j j j ------Γ=====+-+--,125L j -Γ==终端驻波比1115LL L ρ+Γ===-Γ; 000505050tantan 504()5010(2)8tan 250(5050)tan 4L in L j j Z jZ d Z Z j Z jZ d j j j πβλπβ-++====-+++-. 1.11 终端反射系数00250-50011=-=250+50033j L L L Z Z e Z Z π-Γ==+,终端反射系数模值13L Γ=,相角=L φπ.依据行驻波状况时电压的变更纪律可知:=L φπ时,若1n =,则4234L n φλπλλ+=,电压处于波腹点,是以在输入端电压处于波腹点.max (1)500L L U U V +=+Γ=,所以1500=3754L U V V +=,min (1)250L L U U V +=-Γ=;max500(1)1500L L U IA Z +=+Γ==,min250(1)0.5500L L U IA Z +=-Γ==. 因为0L R Z <,负载处为电压波节点;驻波比11+1+3==211-1-3L L ρΓ=Γ,0min 250Z R ρ==Ω,max 01000R Z ρ==Ω.1.13 (1)负载1z 处的反射系数122821()0.5pp j j z L L L z e e j j λπλβ-⋅⋅-Γ=Γ=Γ=-Γ=,是以0.5L Γ=-.随意率性不雅察点z 处的反射系数22()0.5j z j z L z e e ββ--Γ=Γ=-;等效阻抗2021()10.5()501()10.5j zj zz e Z z Z z e ββ--+Γ-==-Γ+.(2)已知0L L L Z Z Z Z -Γ=+,050Z =Ω;(1)中求得0.5L Γ=-,可解出50/3L Z =Ω.(3)由等效阻抗公式2210.5()5010.5j zj ze Z z e ββ---=+,取z=0,得10.55050/310.5L Z -==Ω+. 1.14 min122()444422LLLl φλπφφλππββππΓΓΓ=+=+=+, 所以min1sin()sin()cos()222LLl φφπβΓΓ=+=,min1cos()cos()sin()222L L l φφπβΓΓ=+=-.或:在min1l 处的输入阻抗为()00min1min100min1tan tan L L Z Z jZ l Z l Z Z jZ l βρβ+==+所以()0min10min1tan tan L L Z jZ l Z jZ l βρβ+=+ 1.15(a )终端短路:0L Z =,2200()j zj zL L Z Z z e e Z Z ββ---Γ==-+,23223()12j e πλλλ-⋅⋅Γ=-=-,033()tan()022Z jZ λβλ=⋅=或031()32()0321()2Z Z λλλ+Γ==-Γ. (b )终端开路:L Z =∞,2200()j zj zL L Z Z z e e Z Z ββ---Γ==+,2142551()5j j e e πλπλλ-⋅⋅-Γ==,0112()cot()cot 555Z jZ j λβλπ=-⋅=-. (c )虚线右半部分:负载为0Z ,长度为5λ传输线的输入阻抗000in 000000tan tan tan tan L L Z jZ d Z jZ dZ Z Z Z Z jZ d Z jZ dββββ++===++;是以,从最左端看去,负载为两个0Z 并联,等效负载阻抗为02Z .传输线输入端阻抗00in 0000tan 242tan 24Z jZ Z Z Z Z Z j λβλβ+==+, 反射系数002204000112()=-=332j j zj L L Z Z Z Z z ee e Z Z Z Z λββπ-----Γ==++. (d )终端短路的/4λ传输线输入阻抗为∞,终端匹配的/2λ传输线输入阻抗为0Z ,所以支节点处等效输入阻抗为00||Z Z ∞=;再经/2λ阻抗变换得输入端输入阻抗为0Z ,反射系数-j200200e =0Z Z Z Z λβ-Γ=+;(e )终端阻抗02Z 经由两个/2λ阻抗变换之后输入阻抗仍为02Z ,另一歧路在支节点处输入阻抗仍为0/2Z ,所以支节点处等效输入阻抗为0002Z ||Z /22Z /5=;再经/4λ阻抗变换得输入端输入阻抗为20005/22/5Z Z Z =,反射系数-j2-j 004002/533e =-e 2/577Z Z Z Z λβπ-Γ==+; (f )主线上第一节点处输入阻抗为0Z ,支线支节点处00in 0000tan 8tan 8Z jZ Z Z Z Z jZ λβλβ+==+,支节点等效输入阻抗000Z ||Z Z /2=,输入端等效阻抗仍为0/2Z ,反射系数-j200200/21e =/23Z Z Z Z λβ-Γ=-+;(g )支节点处输入阻抗0002Z ||2Z Z =,输入端输入阻抗0Z ,反射系数-j200200e =0Z Z Z Z λβ-Γ=+.1.160025-j25-5025251=0.20.425-j25+5075253L L L Z Z j jj Z Z j j-----Γ====--+--,1+2.6171-2ρΓ==≈Γ,距离负载0.375λ处阻抗in003tan252550850350(2525)tan825755050(2)2525LLLLZ jZ Z jZ j jZ Z ZZ jZ j jZ jZjjjλβλβ+---===---+-==--11125255050LY jj==+-,LY的实部等于01=50Y,依据传输线导纳公式:依据单支节在传输线上的匹配前提:()inY z的实部应为01=50Y,是以:()2211tan1zβ=-+,tan0zβ=或2当tan0zβ=时,单支线在主线0d=处(即终端负载处),此处()115050inY z j=+.是以短路支节导纳为11-=50j50tanjdβ,所以tan1dβ=,支节长度/8lλ=.当tan2zβ=时,单支线在主线arctan22dλπ=处,此处()115025inY z j=-.所以短路支节导纳为11=25j50tanjdβ,所以tan0.5dβ=-,支节长度()arctan0.52lλπ=-.1.17 已知1+51-ρΓ==Γ,所以-12+13ρρΓ==;相邻电压波节点之间的距离=452cmλ,所以=90cmλ;第一电流波腹点(电压波节点)设为min1l,则min12-LlβφπΓ=,所以min1=44LlφλλπΓ+,由=90cmλ,min1=20cml得-9LπφΓ=,所以923LjjL Le eπφΓ-Γ=Γ=,进而可求出9921+13=250725.19595.271213j LL jL e Z Z j e ππ--+Γ=≈-Ω-Γ-. 1.21(1)将负载阻抗归一化得30150.60.350L j z j +==+,对应圆图上点A;在等反射系数圆上往电源偏向顺时针扭转/6λ(120度)得到点B;读取B 点的阻抗为91.5493+j13.4512Ω; (2)将输入阻抗归一化得6055111+j 6012L j z +==,对应圆图上点A;从A点做OA 射线,得角度为65.3785;从A 点做等反射系数圆与X 轴右半轴交点,读出=2.4ρ;依据-10.4167+1ρρΓ=≈; (3)在X 轴左半轴读出1==0.42.5ρ的地位,对应圆图点A;在圆图等反射系数圆上,往负载偏向逆时针扭转0.15λ(108度),读出归一化负载阻抗为0.88-j0.91L z =,0(0.88-j0.91)52.854.6L Z Z j ==-Ω.1.22 将负载阻抗归一化0.5+j0.5L z =,对应圆图点A;从点A 沿电源偏向扭转2圈,得到'BB 处输入阻抗'0.50.5BB z j =+,''05050BB BB Z Z z j =⋅=+Ω’;再将'BB z 归一化对应圆图上点B,扭转4圈得到'0.250.25AA z j =+,''0200(0.250.25)5050AA AA Z Z z j j =⋅=⋅+=+Ω.2 第二章2.6 7.214a cm =,3.404b cm =,矩形波导的截止波长c λ=;对于10TE 模,m=1,n=0,214.428c a cm λ===,83310 2.0792914.42810c c cf GHz λ-⨯==≈⨯,故c f f <,不消失10TE 模; 对于01TE 模,m=0,n=1,2 6.808c b cm λ===,83310 4.406586.80810c c cf GHz λ-⨯==≈⨯,c f f <,也不消失01TE 模; 显然11TE 和22TE 模的截止频率大于10TE 和01TE ,也不成能消失11TE 模和22TE 模.2.7 10a mm =,6b mm =,对10TE 模,220c a mm λ===;对于01TE 模,212c b mm λ===;对于11TE 模,210.29c mm λ-===≈.2.9 22.8a mm =,10.15b mm =,工作波长12mm λ=.10TE 模:245.6c a mm λλ==>,可以消失; 01TE 模:220.3c b mm λλ==>,可以消失; 02TE模:10.15c b mm λλ===<,不成以消失;11TE (11TM )模:18.5454c mm λλ===≈>,可以消失;12TE (12TM ):9.9075c mm λλ===≈<,不消失;21TE (21TM )模:15.1641c mm λλ===≈>,可以消失;20TE模:22.8c a mm λλ===>,可以消失; 30TE模:215.23c a mm λλ===>,可以消失; 40TE模:111.42c a mm λλ===<,不成以消失; 31TE (31TM ):12.167c mm λλ===≈>,可以消失.2.15 圆波导的主模为11TE 模,其截止波长3.41 3.41310.23c R cm cm λ==⨯=;截止频率892310 2.931010.2310c f Hz -⨯==⨯⨯;波导波长2247.426w cm λ--====≈;波形阻抗111787TE Z ===Ω. 2.16 11TE 模 3.41 3.413c R cm cm λ==>,01TM 模 2.61 2.613c R cm cm λ==<,所以只能传输11TE 模.2.18 β=因为波在两波导中传输时β和K 都相等,所以截止波束c K 也相等,即两个波导中截止波长相等.矩形波导中10TE 模c K aπ=,22c ca K πλ==,圆波导01TE 模 1.64c R λ=,所以圆波导半径327.11108.671.64m R mm -⨯⨯=≈.2.21 衰减20lg 100c lL edB α-=-=,求出5ln1011.513115.13/0.1c dB m l α--===;已知8.686280)c παλ=⋅--,tan 0.001δ=,8931031010m cm λ⨯==⨯,由以上解得 3.00 3.41c cm R λ≈=,所以圆波导的半径0.88R cm =. 3 第三章3.5 微带线传输的主模是准TEM 模;现实上微带传输线的准TEM 模的场部分在空气中,部分在介质中,一般用等效介电常数eff ε来暗示这种情形对传输特征的影响.eff ε的界说如下:eff CC ε=,0C 为无介质填充时微带传输线单位长度的散布电容,C 为现实上部分填充介质时微带传输线的单位长度上的散布电容.介质填充系数1/2110[1(1)]2h q w-=++.当/1w h 时,1(1)eff r q εε≈+-.3.10 w/h=0.95<1,疏忽导带厚度,00860ln()460ln(8.4210.2375)129.5125h w Z w h=+=+=Ω,1/2110[1(1)]0.64732h q w-=++=,1(1)10.6473(9.51) 6.5eff r q εε≈+-=+⨯-=;050.79Z ===Ω. 4 第四章4.1 微波谐振器和低频谐振器回路重要有3点不合:1)LC 回路为集总参数电路,微波谐振器属于散布参数电路,所以LC 回路能量只散布在LC 上,而微波谐振器的能量散布在全部腔体中;2)LC 回路在L 及C 一准时,只有一个谐振频率,而微波谐振器有无穷多个谐振频率,这称为微波谐振器的多谐性;3)微波谐振腔储能多,损耗小,是以微波谐振器品德因数很高,比LC 回路的Q 值高许多. 4.40.1mλ=,3a 10m-=,21.510b m-=⨯,特征阻抗060ln 366bZ a=≈Ω; 810r 231022/ 1.885100.1r f v πωππλ⨯⨯===≈⨯;10110-9-521l 220.110.1=2 1.88510106621.2810+p 510r r r tg p CZ tg p mλλπωπ---=++⨯⨯⨯≈⨯⨯⨯. 4.9已知r f =f 3r GHz =时,有9310⨯=;f 6r GHz =时,有9610⨯=解得a 6.3cm =≈,l 8.2cm =≈,b<a. 4.12 l 10cm =时,l/R=2<2.1,最低谐振模式为010TM 模,谐振波长2.61 2.61513.05R cm cmλ==⨯=;l15cm=时,l/R=3>2.1,最低谐振模式为111TE模,谐振波长14.8cm λ=≈.。
微波技术习题解

《微波技术》习题解(一、传输线理论)(共24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--机械工业出版社《微 波 技 术》(第2版) 董金明 林萍实 邓 晖 编著习 题 解一、 传输线理论1-1 一无耗同轴电缆长10m ,内外导体间的电容为600pF 。
若电缆的一端短路, 另一端接有一脉冲发生器及示波器,测得一个脉冲信号来回一次需s ,求该电缆的特性阻抗Z 0 。
[解] 脉冲信号的传播速度为tlv 2=s /m 102101.010286⨯=⨯⨯=-该电缆的特性阻抗为 00C L Z =00C C L =lC εμ=Cv l =8121021060010⨯⨯⨯=-Ω33.83= 补充题1 写出无耗传输线上电压和电流的瞬时表达式。
[解] (本题应注明z 轴的选法)如图,z 轴的原点选在负载端,指向波源。
根据时谐场传输线方程的通解()()()()()())1()(1..210...21.⎪⎪⎩⎪⎪⎨⎧+=-=+=+=--z I z I e A e A Z z I z U z U e A e A z U r i zj z j r i zj z j ββββ 。
为传输线的特性阻抗式中02.22.1;;,Z U A U A r i ==:(1),,212.2.的瞬时值为得式设ϕϕj r j i e U U eU U -+==⎪⎩⎪⎨⎧+--++=+-+++=-+-+)()cos()cos([1),()()cos()cos(),(21021A z t U z t U Z t z i V z t U z t U t z u ϕβωϕβωϕβωϕβω1-2 均匀无耗传输线,用聚乙烯(εr =作电介质。
(1) 对Z 0=300 Ω的平行双导线,导线的半径 r =,求线间距D 。
(2) 对Z 0 =75Ω的同轴线,内导体半径 a =,求外导体半径 b 。
[解] (1) 对于平行双导线(讲义p15式(2-6b ))0C L Z =rD r D ln ln πεπμ=r D ln 1εμπ=r D rln 120ε=300= Ω 得52.42=rD, 即 m m 5.256.052.42=⨯=D (2) 对于同轴线(讲义p15式(2-6c ))Z LZ 0○ ~ z补充题1图示0C L Z =dD d D ln 2ln2πεπμ=d D r ln 60ε=ab r ln 60ε=75= Ω 得52.6=ab, 即 mm 91.36.052.6=⨯=b 1-3 如题图1-3所示,已知Z 0=100Ω, Z L =Z 0 ,又知负载处的电压瞬时值为u 0 (t)=10sin ωt (V), 试求: S 1 、S 2 、S 3 处电压和电流的瞬时值。
微波技术习题答案5.docx
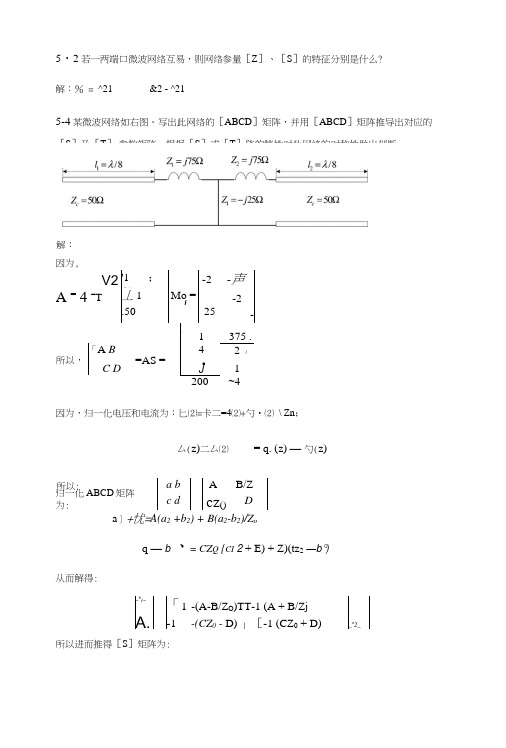
5・2若一两端口微波网络互易,则网络参量[Z ]、[S ]的特征分别是什么?解:% = ^21&2 - ^21因为,V2 '1 ;50__-2 -声 A = 4 =T 丄1 Mo = J-2.50_25 -一1 375 .「A B4 2」 所以, C D =AS =■J1 200 ~4因为,归一化电压和电流为:匕⑵=卡二=4⑵+勺•⑵ \ Zn ;厶(z)二厶⑵= q. (z) — 勺(z)a 〕+忧=A(a 2 +b 2) + B(a 2-b 2)/Z oq — b、= CZ Q {CI 2 + E) + Z)(tz 2—b°)从而解得:~b i~「1 -(A-B/Z O )TT-1 (A + B/ZjA.-1 -(CZ 0 - D)」[-1 (CZ 0 + D)_a 2_所以进而推得[S ]矩阵为:a b_AB/Z (「c dcz () D 归一化ABCD 矩阵为:所以:5-4某微波网络如右图。
写出此网络的[ABCD ]矩阵,并用[ABCD ]矩阵推导出対应的[S ]及[T ] 参数矩阵。
根据[S ]或[T ]阵的特性对此网络的对称性做出判断。
解:2(AD-BC )—A + B / Z ()— CZ ()+ D乙+Zc — K z _7 U 乙+Z 』v[Z][/] = [V]⑸一 A + B/Z ()+CZo + D_ A + B/ Z ()—CZ Q — D2 由(3)式解得[S] -1 1 ~—- + 4/ 27 . 27所以, b\ _ 1~ 2A —B / Z° — CZ ()+DA —B / Z ()+ CZ 1 A + B / Z° — CZ Q — D A — B / Z° — CZ°+ D2 A + B/Zo + CZo + D A-B/Z +CZ -D7 .—/21力• ----- 4 j 2----- 4 j 2 7 . * (9)因为[s ]阵的转置矩阵[sy 二[S ],所以,该网络是互易的。
微波技术基础课后习题(A)

杜 英
2011.5.1
第二章 传输线理论
2-6 如图所示为一无耗传输线,已知工作频率
Z L 1 5 0 j 5 0
f 3G H z , Z 0 1 0 0
Z 01
,
,欲使 A 处无反射,试求 l 和
。
答案:由输入阻抗定义知
Z in A Z 0 1 Z L jZ 0 1 tan l Z 0 1 jZ 位面沿轴向移动的速
vp
度,公式表示为
p
p
2
相波长 是等相位面在一个周期T内移动的距离,有
欲使电磁波传输信号,必须对波进行调制,调制后的波不再是单一频 率的波,而是一个含有多种频率的波。这些多种频率成分构成一个“波群”
2 又称为波的包络,其传播速度称为群速,用 v g 表示,即 v g v 1 c
c
、 ,随着频率的变化,传播长数 可能为虚数,也可能为实
0
数,还可以等于零。当
时,系统处于传输与截止状态之间的临界状态,此
时对应的波长为截止波长。
当 c 时,导波系统中传输该种波型。
当 c 时,导波系统中不能传输该种波型。
第三章 微波传输线
3-3 什么是相速、相波长和群速?对于TE波、TM波和TEM波,它们的相速 相波长和群速有何不同? 答案: 相速
0.125
0.188
D
A
0 0.5
D
0.25
B
0.15
0.2
C
0.375
0.361
0.338
第三章 微波传输线
3-2 何谓波导截止波长 c ?工作波长 大于 c 或小于 c 时,电磁波的特性有
微波的技术习题

微波技术习题思考题1.1 什么是微波?微波有什么特点?1.2 试举出在日常生活中微波应用的例子。
1.3 微波波段是怎样划分的?1.4 简述微波技术未来的发展状况。
2.1何谓分布参数?何谓均匀无损耗传输线?2.2 传输线长度为10cm,当信号频率为9375MHz时,此传输线属长线还是短线?2.3传输线长度为10cm,当信号频率为150KHz时,此传输线属长线还是短线?2.4传输线特性阻抗的定义是什么?输入阻抗的定义是什么?2.5什么是反射系数、驻波系数和行波系数?2.6传输线有哪几种工作状态?相应的条件是什么?有什么特点?3.1何谓矩形波导?矩形波导传输哪些模式?3.2何谓圆波导?圆波导传输哪些模式??3.3矩形波导单模传输的条件是什么?3.4何谓带状线?带状线传输哪些模式?3.5何谓微带线?微带线传输哪些模式?3.6 何谓截止波长?何谓简并模?工作波长大于或小于截止波长,电磁波的特性有何不同?3.7 矩形波导TE10模的场分布有何特点?3.8何谓同轴线?传输哪些模式?3.9为什么波导具有高通滤波器的特性?3.10 TE波、TM波的特点是什么?3.11何谓波的色散?3.12任何定义波导的波阻抗?分别写出TE波、TM波波阻抗与TEM波波阻抗之间的关系式。
4.1为什么微波网络方法是研究微波电路的重要手段?4.2微波网络与低频网络相比有哪些异同?4.3网络参考面选择的要求有什么?4.4表征微波网络的参量有哪几种?分别说明它们的意义、特性及其相互间的关系?4.5二端口微波网络的主要工作特性参量有哪些?4.6微波网络工作特性参量与网络参量有何关系?4.7常用的微波网络有哪些?对应的网络特性参量是什么?4.8微波网络的信号流图是什么?简要概述信号流图化简法则有哪些?5.1试述旋转式移相器的工作原理,并说明其特点。
5.2试分别叙述矩形波导中的接触式和抗流式接头的特点。
5.3试从物理概念上定性地说明:阶梯式阻抗变换器为何能使传输线得到较好的匹配。
《微波技术与天线》习题答案

第一章1-1解: f=9375MHz, / 3.2,/ 3.1251c f cm l λλ===> , 此传输线为长线。
1-2解: f=150kHz, 4/2000,/0.5101c f m l λλ-===⨯<< ,此传输线为短线。
1-3答: 当频率很高,传输线的长度与所传电磁波的波长相当时,低频时忽略的各种现象与效应,通过沿导体线分布在每一点的损耗电阻,电感,电容和漏电导表现出来,影响传输线上每一点的电磁波传播,故称其为分布参数。
用1111,,,R L C G 表示,分别称其为传输线单位长度的分布电阻,分布电感,分布电容和分布电导。
1-4 解: 特性阻抗050Z ====Ωf=50Hz X 1=ωL 1=2π×50×16.65×10-9Ω/cm=5.23×10-6Ω/cmB 1=ωC 1=2π×50×0.666×10×10-12=2.09×10-9S/cm 1-5 解: ∵ ()22j z j z i r Uz U e U e ββ''-'=+()()2201j z j z i r I z U e U e Z ββ''-'=- 将 2223320,2,42i r U V U V z πβλπλ'===⋅= 代入33223420220218j j z U eej j j Vππλ-'==+=-+=-()3412020.11200z I j j j A λ'==--=- ()()()34,18cos 2j te z uz t R U z e t V ωλπω'=⎛⎫''⎡⎤==- ⎪⎣⎦⎝⎭ ()()()34,0.11cos 2j te z i z t R I z e t A ωλπω'=⎛⎫''⎡⎤==- ⎪⎣⎦⎝⎭ 1-6 解: ∵Z L=Z 0∴()()220j z i r U z U e U β''==()()()212321100j j z z Uz e U z e πβ''-''==()()()()611100,100cos 6jU z e V u z t t V ππω'=⎛⎫=+ ⎪⎝⎭1-7 解: 210.20.2130j L e ccmfπρρλ-Γ=-=-==Γ+==由 011L L L Z Z +Γ=-Γ 得 0110.2100150110.2L LL Z Z -Γ+===Ω+Γ- 由 ()()()22max0.20.2j z j z L z e e z πββ-'-''Γ=Γ==Γ= 得 max1max120,7.54z z cm λπβ''-===1-8 解: (a) ()(),1inin Z z z ''=∞Γ=(b) ()()0100,0in in Z z Z z ''==ΩΓ=(c) ()()00012200,3in in in in Z Z Z z Z z Z Z -''==ΩΓ==+(d) ()()02200,1/3inin Z z Z z ''==ΩΓ=1-9 解: 1 1.21.510.8ρ+Γ===-Γmax 0min 75,33Z Z Z Z ρρ==Ω==Ω1-10 解: min2min124z z cm λ''=-=min1120.2,0.514L z ρππβρλ-'Γ===⨯=+ min1min120.2j z z L e β'-'Γ=-=Γ∴ 2420.20.2j jLeeππ⨯-Γ=-=1-11 解: 短路线输入阻抗 0in Z jZ tg l β= 开路线输入阻抗 0in Z jZ ctg l β=-a) 00252063inZ jZ tgjZ tgj πλπλ=⨯=Ω b) 002252033in Z jZ tg jZ tg j πλπλ=⨯=-Ωc) 0173.23inZ jZ ctgj π=-=-Ωd) 02173.23in Z jZ ctg j π=-=Ω1-12 解: 29.7502050100740.6215010013oj L L L Z Z j j e Z Z j -++Γ=Γ====++1-13 解: 表1-41-17 解: 1350.7j Le Γ=1-18 解: minmax0.6U K U == min143.2o z β'= 用公式求 min1min100min1min111L j tg z K jtg z Z Z Z jtg z jKtg z ρββρββ''--==''-- 0.643.25042.8522.810.643.2oojtg j j tg -==-Ω-⨯ 用圆图求 ()42.522.5LZ j =-Ω短路分支线的接入位置 d=0.016λ时()0.516B =-最短分支线长度为 l=0.174λ()0.516B =-1-19 解: 302.6 1.4,0.3,0.30.16100LL lZ j Y j λ=-===+由圆图求得 0.360.48in Z j =+ 1824in Z j =+Ω1.01 1.31in Y j =- ()0.020.026in Y j S =-1-20 解: 12LY j =+ 0.5jB j =()()()()0.150.6 1.460.150.60.960.20.320.380.2 1.311.54in in in in Y j Y jB j Y j Z j λλλλ=-+=-=+=-∴ 6577inZ j =-Ω 1-21 解: 11 2.5 2.50.20.2L L Y j j Z ===+- 并联支节输入导纳 min 2.5B ctg l β=-=- min 0.061l λ=此时 1/2.5LZ '= 500/2.5200LZ '==Ω(纯电阻)变换段特性阻抗 0316Z '==Ω 1-22 解: 1/0.851.34308.66o o Larctg ϕ=-=-= 由 max120L z ϕβ'=-= 得 max10.43z λ'= 由 min12Lz ϕβπ''=-=- 得 min10.1804L z ϕπλλπ+'== 1-23 解: 原电路的等效电路为由 1inZ j '+= 得 1inZ j '=-向负载方向等效(沿等Γ图)0.25电长度得 1inin Z Z ''='则 ininY Z '''=由inin in Y Y j Z ''''''=+= 得 12in inY Z j j ''''=-=-由负载方向等效0.125电长度(沿等Γ图)得12LY j =+ 0.20.4L Z j =-1-24 答: 对导行传输模式的求解还可采用横向分量的辅助标位函数法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微波技术习题思考题什么是微波?微波有什么特点?试举出在日常生活中微波应用的例子。
微波波段是怎样划分的?简述微波技术未来的发展状况。
何谓分布参数?何谓均匀无损耗传输线?传输线长度为10cm,当信号频率为9375MHz时,此传输线属长线还是短线?传输线长度为10cm,当信号频率为150KHz时,此传输线属长线还是短线?传输线特性阻抗的定义是什么?输入阻抗的定义是什么?什么是反射系数、驻波系数和行波系数?传输线有哪几种工作状态?相应的条件是什么?有什么特点?何谓矩形波导?矩形波导传输哪些模式?何谓圆波导?圆波导传输哪些模式??矩形波导单模传输的条件是什么?何谓带状线?带状线传输哪些模式?何谓微带线?微带线传输哪些模式?何谓截止波长?何谓简并模?工作波长大于或小于截止波长,电磁波的特性有何不同?矩形波导TE10模的场分布有何特点?何谓同轴线?传输哪些模式?为什么波导具有高通滤波器的特性?TE波、TM波的特点是什么?何谓波的色散?任何定义波导的波阻抗?分别写出TE波、TM波波阻抗与TEM波波阻抗之间的关系式。
为什么微波网络方法是研究微波电路的重要手段?微波网络与低频网络相比有哪些异同?网络参考面选择的要求有什么?表征微波网络的参量有哪几种?分别说明它们的意义、特性及其相互间的关系?二端口微波网络的主要工作特性参量有哪些?微波网络工作特性参量与网络参量有何关系?常用的微波网络有哪些?对应的网络特性参量是什么?微波网络的信号流图是什么?简要概述信号流图化简法则有哪些?试述旋转式移相器的工作原理,并说明其特点。
试分别叙述矩形波导中的接触式和抗流式接头的特点。
试从物理概念上定性地说明:阶梯式阻抗变换器为何能使传输线得到较好的匹配。
在矩形波导中,两个带有抗流槽的法兰盘是否可以对接使用?微波元件中的不连续性的作用和影响是什么?利用矩形波导可以构成什么性质的滤波器?试说明空腔谐振器具有多谐性,采用哪些措施可以使腔体工作于一种模式?欲用空腔谐振器测介质材料的相对介电常数,试简述其基本原理和方法。
什么是双极晶体管和场效应晶体管?各有什么优缺点?如何判断微波晶体管放大器的稳定性?设计小信号微波晶体管放大器依据的主要技术指标有哪些?什么是单向化设计?单向化设计优点是什么?什么是混频二极管的净变频损耗?如何降低这种损耗?什么是混频二极管的寄生参量损耗?如何减小这种损耗?什么是负阻效应?简述负阻型微波振荡器起振条件、平衡条件和稳定条件?习 题一根Ω75的无耗传输线,终端接有阻抗L L L jX R Z += 1) 欲使线上的电压驻波比等于3,则 L R 和L X 有什么关系? 2) 若Ω=150L R ,求L X 等于多少?3) 求在第二种情况下,距负载最近的电压最小点位置。
求下图所示电路的输入阻抗。
一根特性阻抗为Ω50、长度为2m 的无耗传输线工作于频率MHz 200,终端接有阻抗Ω+=3040j Z L ,试求其输入阻抗。
考虑一无损耗传输线,1)当负载阻抗(4030)L Z j =-Ω时,欲使线上驻波比最小,则线的特性阻抗应为多少?2)求出该最小的驻波比及相应的电压反射系数。
3)确定距负载最近的电压最小点的位置。
特性阻抗为50Ω的传输线终端接负载时,测得反射系数模Γ=,求线上电压波腹点和波节点处的输入阻抗。
均匀无损耗传输线终端接负载阻抗Z L 时,沿线电压呈行驻波分布,相邻波节点之间的距离为2cm ,靠近终端的第一个电压波节点离终端,驻波比为,求终端反射系数。
已知传输线特性阻抗050Z =Ω,负载阻抗1020L Z j =-Ω,用圆图确定终端反射系数2Γ。
特性阻抗为50Ω的传输线,终端负载不匹配,沿线电压波腹max U =10V ,波节min U =6V ,离终端最近的电压波节点与终端间距离为λ,求负载阻抗Z L 。
若用短路分支线进行匹配,题图0Z02Z4/λ4/λ4/λ4/λ0ZZ0Z0Z in Z0Z4/λ2/λ4/λ0Z 0Zin Z(a )(b ) (c )求短路分支线的并接位置和分支线的最短长度。
无耗均匀长线的特性阻抗Ω=500Z ,终端接负载阻抗Ω-=5.6686j Z L ,若用单支节匹配,试求单支节的长度l 及接入位置d 。
证明无耗传输线的负载归一化阻抗LZ %、行波系数K 和负载到第一个电压波节点的距离l min 三者之间满足下列关系式:min min1LK jtg l Z jKtg l ββ-=-% 均匀无损耗长线终接Z L =100Ω,信号频率为1000MHZ 时,测得终端电压反射系数的相角2ϕ=1800和电压驻波比ρ=。
计算终端电压反射系数Γ2、长线特性阻抗Z 0及距终端最近的一个电压波幅点的距离l max 。
一个感抗为jX L 的集中电感可以用一段长度为l e 的终端短路的传输线等效,试证明其等效关系为0()2L e X l arctg Z λπ=(Z 0为特性阻抗)。
一个容抗为jX C 的集中电容可以用一段长度为l e 的终端开路的传输线等效,试证明其等效关系为0()2C e X l arctg Z λπ=(Z 0为特性阻抗)。
用特性阻抗为600Ω的短路线代替电感为2×105H 的线圈,当信号频率为300MHZ 时,问短路线长度为多少?若用特性阻抗为600Ω的开路线代替电容量为的电容器,当信号频率为300MHZ 时,问开路线长度为多少?无耗长线的特性阻抗为300Ω,当线长度l 分别为l 1=6λ和l 2=3λ时,计算终端短路和开路条件下的输入阻抗。
均匀无损耗短路线,其长度如表所列,试用圆图确定传输线始端归一化输入阻抗in Z %及归一化输入导纳inY %。
均匀无损耗开路线,其长度如表所示,试用圆图确定传输线始端归一化输入阻抗in Z %及归一化输入导纳inY %。
根据表所给定的负载阻抗归一化值,用圆图确定驻波比ρ和反射系数模Γ。
表表表用BJ-100型矩形波导(a ×b =×),传输TE 10波,终端负载与波导不匹配,测得波导中相邻两个电场波节点之间的距离为,求工作波长λ。
BJ-100型矩形波导填充相对介电常数 2.1r ε=的介质,信号频率为f =10000MHz ,求TE 10波的相波长p λ和相速度p v 。
矩形波导截面尺寸为a ×b=72mm ×30mm ,波导内充满空气,信号源频率为3GHZ ,试求:1)波导中可以传播的模式 2)该模式的截止波长c λ、波数β、波导的波长p λ,相速p v 、群速g v 和波阻抗。
用BJ-32型矩形波导(a ×b=×)作馈线,试问:1)当工作波长为6cm 时,波导中能传输哪些模式?2)在传输TE 10模的矩形波导中,测得相邻两波节点的距离为,求0λ及p λ;3)当波导中传输工作波长为0λ=10cm 的TE 10模时,求c λ、p λ及g v 。
有一无限长的矩形波导,在z ≥0处填充相对介电常数为r ε的介质,其中TE 10波的波阻抗用Z 02表示,相波长为2p λ;在z <0的区域填充媒质为空气,其中TE 10波的波阻抗用Z 01表示,相波长为1p λ,电磁波由z <0的区域引入,试证明Z 02/ Z 01= 21p p λλ。
媒质为空气的同轴线外导体内直径D=7mm ,内导体直径d=,要求同轴线只传输TEM 波,问电磁波的最短工作波长为多少?已知带状线尺寸b=2mm 、t=、w=,介质的 2.1r ε=,求带状线的特性阻抗Z 0及传输TEM 容许的最高信号频率。
要求微带线特性阻抗Z 0=75Ω,介质的9r ε=,基片厚度h=,求微带线的宽度w 。
已知工作波长08mm λ=,采用矩形波导尺寸a ×b=×的TE 10模传输,现转换到圆波导TE 01模传输,要求两波导中相速度相等,问圆波导直径D 为多少? 当矩形波导工作在TE 10模时,试问图上哪些缝会影响波的传输?求如图所示二端口网络的阻抗参量。
如图所示,试求出网络的阻抗矩阵和导纳矩阵。
如图所示,试求出网络的转移矩阵。
求如图所示的T 型网络的[A]参量矩阵。
求下图电路的参考面T 1、T 2所确定的网络散射参量矩阵。
一线性互易无耗二端口网络终端接匹配负载时,证明输入端反射系数模值1Γ与传输参量2πθZ 0 Z 0Z 02T 1 1n2π2πZ 01 Z 02 Z 0 Z 0T 1T 2(a)(b)题 图1V 2V Ω12 Ω31I2I+ +--题 图1Z 2ZY题 图l βZ 0题 图Y 0Y 1Y 2θβ=l题 图11T 的模之间满足下列关系式2112111/)1(T T -=Γ。
如下图所示,二端口网络参考面T 2接归一化负载阻抗L Z ~。
证明参考面T 1的归一化输入阻抗为22211211~~~~~~~A Z A A Z A Z L L in ++=。
如图所示的二端口网络,试问: (1)归一化转移参量矩阵;(2)什么条件下插入此二端口网络不引起附加反射?测得矩形波导E 面的散射参量jj S +-=3111,j j S ++-=3)1(22若用上图电路等效,试求等效电路中的jb 与理想变压器的变比n 。
如下图微波网络系统,其中ab 、cd 段为理想传输线,其特性阻抗为Z 0,两段线间有一个由1jX 、2jX 构成的Γ型网络,且021Z X X ==,终端接负载02Z Z L =,试求: (1)此网络系统的[S]参量矩阵; (2)输入端'aa 的反射系数。
如下图所示,在网络系统中,1θ、2θ分别为一段理想传输线,其特性阻抗为01Z 、02Z ,jB为并联电纳,试求归一化的散射矩阵[S]。
L Z ~in Z ~题 图:~Z 1题 图题 图abcL题 图i x j x由参考面1T 、2T 所确定的二端口网络的散射参量为11S 、12S 、21S 及22S ,网络输入端传输线相移常数为β。
若参考面1T 外移距离1l 至'1T 处,求参考面'1T 、2T 所确定的网络的散射参量矩阵]['S 。
求图示流图从源节点i x 到j x 的传输量。
微波系统等效电路如下图所示,试计算此系统的插入衰减和插入相移。
试求在特性阻抗为Ω50的理想传输线上并联一个Ω-)5050(j 的阻抗所引起的插入衰减。
已知二端口网络的转移参量12211==A A ,012jZ A =,021=A ,网络外接传输线特性阻抗为0Z ,求网络输入驻波比ρ。
已知一个互易对称无耗二端口网络,输出端接匹配负载,测得网络输入端的反射系数为2/18.0πj e =Γ,试求:(1)11S 、12S 、22S ;(2)插入相移θ、插入衰减L 、电压传输系数T 和输入驻波比ρ。
