§3.3.1-1几何概型(一)
合集下载
3.3几何概型(1)
在 这 两个问题中 基 本 事 件有无限多个,虽然 , 类似于古典概型的 等可能性" 还存在着, 但是 " 显然不能用古典概型的 方法求解.怎么办呢? 考虑第一个问题, 如图, 记"剪得两段绳长都不 小于1 m " 为事件 A. 1 1
3 把经绳子三等分于是 , 当剪断位置处在中间一 段上时, 事件 A 发生.
1 12.22 P B 4 0.01. 1 1222 4
122cm
1 1222 cm2的大圆内, 4
从上面的分析可以看到对于一个随机试验 我们将每 , , 个基本事件理解为从某 个特定的几何区域内随 机地取 一点, 该区域中每一点被取到 的机会都一样 而一个随 ; 机事件的发生则理解为 恰好取到上述区域内的 某个指 定区域中的点这里的区域可以是线段 . 、平面图形、立 体图形等.用这种方法处理随机试 , 称为几何概型 验 geometric probabilit y mod el . 一般地, 在几何区域D中随机地取一点, 记事件" 该点落在 其内部一个区域 d 内"为事件 A, 则事件 A 发生的概率 d 的测度 P A . D 的测度 这里要求D的测度不为0, 其中 测度"的意义依D确定,当 " D分别是线段、平面图形 和立体图形时 相应的 测度" , " 分别是长度、面积和体 积等.
答 豆子落入圆内的概率为 . 4
例 2 在 1 L高产小麦种子中混入一 粒带麦锈 病的种子, 从中随机取出 mL, 含有麦锈病种 10 子的概率是多少 ? 分析 病种子在这1 L 种子中的分布可以看作 是 随 机的 , 取得的10 mL 种子可视作区域 d , 所 有种子可视为区域 D .
几何概型1
解：甲顾客购物的钱数在100元到 200元之间，可以获得一次转动转 盘的机会，转盘一共等分了20份， 其中1份红色、2份黄色、4份绿色， 因此对于顾客来说：
P(获得购物券)= 1 2 4 7 . 20 20
P(获得100元购物券)=
1 .
20
P(获得50元购物券)=
2 20
1 10
.
P(获得20元购物券)=
4 20
1 .
5
绿
黄
黄
绿
绿 绿红
ห้องสมุดไป่ตู้
课堂小结
1.古典概型与几何概型的区别. 相同：两者基本事件的发生都是等可能的； 不同：古典概型要求基本事件有有限个， 几何概型要求基本事件有无限多个.
2.几何概型的概率公式.
P( A)
构成事件A的区域长度（面积或体积） 试验的全部结果所构成的区域长度（面积或体积）
圆的面积 πa2 正方形面积 4a2
π 4
答 豆子落入圆内的概率为π4 .
数学拓展：模拟撒豆子试验估计圆周率
如果向正方形内撒 n 颗豆子，其中落在圆内的
豆子数为 m ，那么当 n很大时，比值 m ，
n
即频率应接近于 P( A) ，于是有
P( A) m . n
由此可得 4m
n
例3、某商场为了吸引顾客，设立了
6
在本例中，打开收音机的时刻X是随机的，可以是0~60之 间的任何一刻，并且是等可能的.我们称X服从[0,60]上的均匀分 布，X为[0,60]上的均匀随机数.
例2、取一个边长为2a的正方形及其内切圆，随机向正方 形内丢一粒豆子，求豆子落入圆内的概率.
2a
解: 记“豆子落在圆内”为事件A,
P(A)
3.3.1几何概型
三、意义建构 几何概型的概率公式：
P ( A ) 试
构 成 事 件 A 的 (面 区 积域 或) 长 体度 积 验的全部结 的果 区所 域 （ 构 长 面 成 度 积或体
几何概型的特点：
(1)试验中所有可能出现的结果(基本事件) 有无限多个.
(2)每个基本事件出现的可能性相等.
四、简单应用 1. 在区间[0，9]上任取一个整数，恰好取在区间
P(A) (60-50) 1. 60 6
0
50 60
即“等待报时的时间不超过10分钟”的概率
为1/6.
五、巩固深化 类型一:长度型几何概型
练习:方程x2+x+n=0(n∈(0,1))有实根的概率为________
五、巩固深化
类型二:面积型几何概型
例2.如图，矩形ABCD中，点E为边CD的中点，若在 矩形ABCD内部随机取一个点Q，则点Q取自△ABE 内部的概率等于（ ） A.1/4 B．1/3 C.1/2 D. 2/3
P Q RS
二、问题情境
【问题2】一根3米长的绳子，从任意一点处将绳子剪 断，如果剪得两段长都不小于1米，那灰太狼就可以不 去羊村，那么他不去羊村的概率是多少？
M PQN
三、意义建构
领悟归纳
几何概型的定义：
如果每个事件发生的概率只与构成该 事件区域的长度（面积或体积）成比例, 则称这样的概率模型为几何概率模型,简 称为几何概型.间[0，9]上任取一个实数，恰好取在区间 [0，3]上的概率为_______
五、巩固深化
类型一:长度型几何概型
例1.某人午觉醒来,发现表停了,他打开收音机,想 听电台报时,求他等待的时间不多于10分钟的概率.
解 : 设 A={ 等 待 的 时 间 不 多 于 10 分 钟 }. 事件A是打开收音机的时刻恰好位于 [50,60] 时 间 段 内 （ 如 图 ） ， 因 此 由 几 何概型的概率公式，得
331几何概型(共24张PPT)
全优69页变式训练
19:58
23
4.已知地铁列车每10min一班，在车站停1min， 则乘客到达站台立即乘上车的概率为______．
解析：由于地铁列车每10min一班， 则两班列车停靠车站之间时间可用长度为 10的线段表示．
而列车在车站停1min，乘客到达站台立即 乘上车的时间可用长度为1的线段表示．
19:58
20
解：
分析： 试验的基本事件是:
金币的中心投在由若干个小正
方形组成的阶砖面里. 3
S A
设事件A={金币不与小正方形 边相碰}
不妨先考虑金币与一块阶砖的关系.
3
Ａ={金币的中心要投在绿色小正方形内}
由几何概型的定义知：参加者获奖的概率为:
P( A)
n个A的面积 n个S的面积
A的面积 S的面积
则乘客到达站台立即乘上车的概率
19:58
全优71页基础夯实24
19:58
14
3.在半径为1的半圆内，放置一个边长为1/2的 正方形ABCD，向半圆内任投一点，该点落在 正方形内的概率为___________.
解析：本题只与面积有关
由几何概型的计算公式得
全优86页限时规范训练
19:58
15
2．如图所示的矩形，长为5，宽为2.在矩形内 随机地撒300颗黄豆，数得落在阴影部分的黄 豆数为138颗．则我们可以估计出阴影部分的 面积约为________．
在哪个房间，甲壳虫停留在黑砖上的概率大？
卧室
19:58
卧室
书房
4
（1）甲壳虫每次飞行,
停留在任何一块方砖上
的概率是否相同?
（2）图中共有10X10=100
块方砖，其中有10X2=20
3.3.1几何概型课件人教新课标B版
几何概型
复习
1.古典概型有哪些特点？
（1）所有可能出现的基本事件只有有限个(有限性) （2）每个基本事件出现的可能性相等（等可能性）
2.古典概型的概率公式是什么？
P(A)=
A包含的基本事件的个数 基本事件的总数
创设情境 引入新课
问题1：绳子上有均匀散布的10个点（如图）， 用剪刀随机的在A2----A9这8个点的位置剪， 求剪刀剪在下标为偶数点的概率？
基本事件
线段AB上的 任意一点
实所验有的基全本部事结件果 所的构集成合的是区？域 线段AB
事构件成A事对件应A的 集区合域是？
线段CD
3m
A
B
3m
A
B
1m
AC DB
创设情境 引入新课
很多同学喜欢玩飞镖游戏，飞镖盘有圆形的， 方形的，还有不规则图形的，丰富多彩的设 计给这项运动增添了很多乐趣，同时也引出 了一系列数学问题，下面我们来看看掷飞镖 掷出的数学问题。
基本事件
实验的全部结果 所构成的区域 构成事件A的 区域
大圆内任一点 大圆及其内部 小圆及其内部
问题3：在一个边长为2m的盛满水的正方体 容器中，一只小虫在容器中游动，记“它所 在的位置距离正方体中心不超过1m”为事件A， 那么事件A产生的概率是多少？
基本事件
实验的全部结果 所构成的区域 构成事件A的 区域
变式：取一根长度为3 m的绳子，拉直后在任 意位置剪断，那么“剪得两段的长都不小于1 m”为事件A,事件A产生的概率是多少？
Hale Waihona Puke 基本事件线段AB上的
3m
任意一点
A
B
问题1：这个问题的基本事件是什么？
问题2：是否满足古典概型？如果不满足，为什 么？
复习
1.古典概型有哪些特点？
（1）所有可能出现的基本事件只有有限个(有限性) （2）每个基本事件出现的可能性相等（等可能性）
2.古典概型的概率公式是什么？
P(A)=
A包含的基本事件的个数 基本事件的总数
创设情境 引入新课
问题1：绳子上有均匀散布的10个点（如图）， 用剪刀随机的在A2----A9这8个点的位置剪， 求剪刀剪在下标为偶数点的概率？
基本事件
线段AB上的 任意一点
实所验有的基全本部事结件果 所的构集成合的是区？域 线段AB
事构件成A事对件应A的 集区合域是？
线段CD
3m
A
B
3m
A
B
1m
AC DB
创设情境 引入新课
很多同学喜欢玩飞镖游戏，飞镖盘有圆形的， 方形的，还有不规则图形的，丰富多彩的设 计给这项运动增添了很多乐趣，同时也引出 了一系列数学问题，下面我们来看看掷飞镖 掷出的数学问题。
基本事件
实验的全部结果 所构成的区域 构成事件A的 区域
大圆内任一点 大圆及其内部 小圆及其内部
问题3：在一个边长为2m的盛满水的正方体 容器中，一只小虫在容器中游动，记“它所 在的位置距离正方体中心不超过1m”为事件A， 那么事件A产生的概率是多少？
基本事件
实验的全部结果 所构成的区域 构成事件A的 区域
变式：取一根长度为3 m的绳子，拉直后在任 意位置剪断，那么“剪得两段的长都不小于1 m”为事件A,事件A产生的概率是多少？
Hale Waihona Puke 基本事件线段AB上的
3m
任意一点
A
B
问题1：这个问题的基本事件是什么？
问题2：是否满足古典概型？如果不满足，为什 么？
3.3.1几何概型
A． B． C． D．
4.假设你家订了一份报纸，送报人可能在早上6：30～7：30之间把报纸送到你家，你父亲离开家去上班的时间为早上7：00～8：00之间，你父亲在离开家前能拿到报纸的概率为_______．
5.如图， ， ， ，在线段 上任取一点 ，
试求：(1) 为钝角三角形的概率；(2) 为锐角三角形的概率．
（四）达标检测
1.在区间(0,1)中随机地取出两个数，则两数之和小于5/6的概率是_____________.
2.已知地铁列车每10min一班，在车站停1min．则乘客到达站台立即乘上车的概率为_________________．
3.两人相约7点到8点在某地会面，先到者等候另一人20分钟，过时离去．则求两人会面的概率为（）
3.在区间 中任意取一个数，则它与 之和大于 的概率是（）
A． B． C． D．
4.同时转动如图所示的两个转盘，记转盘甲得到的数为x，转盘乙得到的数为y，构成数对（x，y），则所有数对（x，y）中满足xy＝4的概率为（）
A． B． C． D．
5．在长为10的线段AB上任取一点P，并以线段AP为边作正方形，这个正方形的面积介于25与49之间的概率为（）
A． B． C． D．
3.从一批羽毛球产品中任取一个，其质量小于4.8g的概率为0.3，质量小于4.85g的概率为0.32，那么质量在[4.8，4.85]（g）范围内的概率是（）A．0.62 B．0.38 C．0.02 D．0.68
4．一艘轮船只有在涨潮的Байду номын сангаас候才能驶入港口，已知该港口每天涨潮的时间为早晨 至 和下午 至 ，则该船在一昼夜内可以进港的概率是（）
A． B． C． D．
5.平面上画了一些彼此相距2a的平行线，把一枚半径r<a的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率（ ）
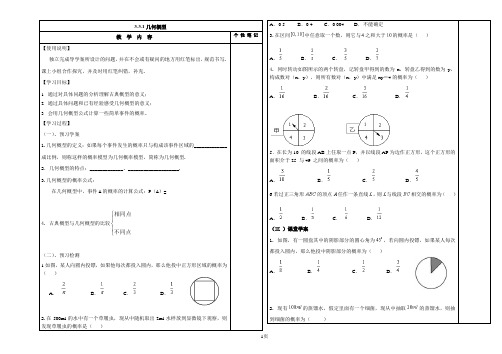
4.假设你家订了一份报纸，送报人可能在早上6：30～7：30之间把报纸送到你家，你父亲离开家去上班的时间为早上7：00～8：00之间，你父亲在离开家前能拿到报纸的概率为_______．
5.如图， ， ， ，在线段 上任取一点 ，
试求：(1) 为钝角三角形的概率；(2) 为锐角三角形的概率．
（四）达标检测
1.在区间(0,1)中随机地取出两个数，则两数之和小于5/6的概率是_____________.
2.已知地铁列车每10min一班，在车站停1min．则乘客到达站台立即乘上车的概率为_________________．
3.两人相约7点到8点在某地会面，先到者等候另一人20分钟，过时离去．则求两人会面的概率为（）
3.在区间 中任意取一个数，则它与 之和大于 的概率是（）
A． B． C． D．
4.同时转动如图所示的两个转盘，记转盘甲得到的数为x，转盘乙得到的数为y，构成数对（x，y），则所有数对（x，y）中满足xy＝4的概率为（）
A． B． C． D．
5．在长为10的线段AB上任取一点P，并以线段AP为边作正方形，这个正方形的面积介于25与49之间的概率为（）
A． B． C． D．
3.从一批羽毛球产品中任取一个，其质量小于4.8g的概率为0.3，质量小于4.85g的概率为0.32，那么质量在[4.8，4.85]（g）范围内的概率是（）A．0.62 B．0.38 C．0.02 D．0.68
4．一艘轮船只有在涨潮的Байду номын сангаас候才能驶入港口，已知该港口每天涨潮的时间为早晨 至 和下午 至 ，则该船在一昼夜内可以进港的概率是（）
A． B． C． D．
5.平面上画了一些彼此相距2a的平行线，把一枚半径r<a的硬币任意掷在这个平面上，求硬币不与任何一条平行线相碰的概率（ ）
3_3_1几何概型详案 (1)
3.3.1 几何概型（第一课时）【学习目标】1．了解几何概型的概念与基本特点；2．掌握简单的几何概型的概率运算.【重点与难点】重点：几何概型概念的建构.难点：几何概率模型中基本事件的确定，几何“测度”的选择；将实际问题转化为几何概型.【方法与手段】本节课以直观观察为主线，采用“引导发现、归纳猜想”为主的教学方法；以“课题性问题和导向性问题解决”作为教学路径，利用多媒体辅助教学手段.【活动方案】活动一：复习引入【以境激情，引出新知】试验1（幸运卡片）【设计意图】拉近师生距离，复习古典概型.班上有9位同学持有卡片，其中3张写着数学家的名言，老师随机选一张，恰好挑到写有名言的卡片的概率是多少？古典概型的特点：（1）所有的基本事件只有有限个；（有限性）（2）每个基本事件的发生都是等可能的.（等可能性）试验2（剪绳试验）【设计意图】丰富感性认知，表现长度测度.取一根长度为30cm的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不小于10cm的概率有多大？分析：一个基本事件：取到线段AB上某一点所有基本事件形成的集合：线段AB（除两端外）随机事件A（剪得两段的长度都不小于10cm）对应的集合：线段CD随机事件A发生(剪断位置处在中间一段CD上)的概率：试验3（射箭比赛）【设计意图】丰富感性认知，表现面积测度.射箭比赛的箭靶涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色，靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,黄心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少?分析：一个基本事件：在大圆面内取某一点所有基本事件形成的集合：直径为122cm的大圆面随机事件A（射中黄心）对应的集合：直径为12.2cm的小圆面随机事件A发生(中靶点落在黄心内)的概率：思考：【设计意图】引发认知冲突，引入几何概型.1．试验1是什么概率模型？有什么特点？是古典概型（有限性，等可能性）2．（1）试验2和试验3的一个基本事件是什么？试验2的基本事件：从每一个位置剪断都是1个基本事件，剪断位置能够是长度为30cm的绳子上除两端外的任意一点.（取到线段AB上某一点）试验3的基本事件：射中靶面上每一点都是1个基本事件，这个点能够是靶面直径为122cm的大圆内的任意一点.（在大圆面内取某一点）（2）试验2、试验3与试验1的本质区别是什么？有什么特点？试验1的基本事件是有限个，试验2、3的基本事件是无限个；每个试验的基本事件的发生都是等可能的.【互动交流，建构新知】活动二：了解几何概型的定义、特点及求解方法1．几何概型的特点：(1)试验中所有可能出现的结果(基本事件)有无限多个；(2)每个基本事件出现的可能性相等．2．几何概型的概念：设D是一个可度量的区域（例如线段、平面图形、立体图形等)，每个基本事件能够视为从区域D内随机地取一点，区域D内的每一点被取到的机会都一样；随机事件A的发生能够视为恰好取到区域D内的某个指定区域d中的点．这时，事件A发生的概率与d的测度（长度、面积、体积等）成正比，与d的形状和位置无关．我们把满足这样条件的概率模型称几何概型．3．几何概型的概率计算公式：的测度的测度DdAP=)(思考：【设计意图】即时回扣情境，完成新知建构结合“打靶问题”，若让你改造箭靶，你将如何设置黄色区域，仍使击中黄色区域的概率为1001呢？事件A 发生的概率与d 的测度（长度、面积、体积等）成正比，与d 区域的形状和位置无关.活动三：掌握简单的几何概型概率的求解例1：取一个边长为2a 的正方形及其内切圆(如图)，随机地向正方形内丢一粒豆子，求豆子落入圆内的概率．分析：基本事件：随机地向正方形内丢一粒豆子（在正方形内任取一点）；区域D ：正方形；区域d ：内切圆.（＂测度＂为面积）解：记“豆子落入圆内”为事件A ，因为是随机地丢豆子，故认为豆子落入正方形内任一点的机会都是均等的，可将边长为2a 的正方形看作区域D ，其内切圆为区域d .22()44a P A a ππ===圆面积正方形面积. 答：豆子落入圆内的概率为4π. 小结：试归纳解决几何概型问题的一般步骤：(1)设定事件A ；(2)判断是否为几何概型；(3)确定几何区域D 和d 的测度；(4)利用几何概型的概率计算公式；(5)应用题要作答.【设计意图】明晰思维路径，明确答题规范。
3.3.1几何概型1
柯希湖 何 鄂尔多斯市一中 概 型
一根长度为3米的绳子上,有A1、A2、A3、A4、 A5五个点将绳子均分成六段，从A1、A2、A3、 A4、A5中任选一点将绳子剪断，那么剪得 的两段均不小于1米的概率是多少？
A1 A2 A3 A4 A5
如果有10个点将绳子均分呢？
3 米 11
回马枪：取一根长度为3m的绳子，如果拉 直后在任意位置剪断，那么剪得两段的长 都不小于1m的概率有多大？
1m
C E 3m F
1m
D
例2.如图,转盘上有8个面积相等的扇形.
转动转盘,求转盘停止转动时指针落在阴
影部分的概率.(可选择不同的测度)
图一
图二
图三
例3.甲船在6:00-12:00的整点时分出港, 求甲船在8:00之前出港的概率.
几何概型的核心——“比例”， 每一份都均匀，即等可能性； 几何度量，即总数无限，求长度、面 积、体积的比值；
例1.取一个边长为2a的正方形及其内切圆， 若随机向正方形内撒一粒豆子，求豆子 落入圆内的概率. 2a
变式1：一个棱长为2a的正方体内有一个 内切球，若随机向正方体内任取一点， 求该点落入球内的概率.
几何概型定义:
事件A理解为区域Ω 的某一子区域A，A
的概率与 与A的位置和形状无关。 子区域A的几何度量 （长度、面积、体积）成正比；
A
满足以上条件的试验称为几何概型。
几何概型的特征 无限性。在一次试验中，可能出现的结 果有无限个，即有无限个不同的基本事 件； 等可能性。每个基本事件发生的可能性 是均等的。
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
取一根长度为3m的绳子，如果拉直后在任 意位置剪断，那么剪得两段的长都不小于 1m的概率有多大？
一根长度为3米的绳子上,有A1、A2、A3、A4、 A5五个点将绳子均分成六段，从A1、A2、A3、 A4、A5中任选一点将绳子剪断，那么剪得 的两段均不小于1米的概率是多少？
A1 A2 A3 A4 A5
如果有10个点将绳子均分呢？
3 米 11
回马枪：取一根长度为3m的绳子，如果拉 直后在任意位置剪断，那么剪得两段的长 都不小于1m的概率有多大？
1m
C E 3m F
1m
D
例2.如图,转盘上有8个面积相等的扇形.
转动转盘,求转盘停止转动时指针落在阴
影部分的概率.(可选择不同的测度)
图一
图二
图三
例3.甲船在6:00-12:00的整点时分出港, 求甲船在8:00之前出港的概率.
几何概型的核心——“比例”， 每一份都均匀，即等可能性； 几何度量，即总数无限，求长度、面 积、体积的比值；
例1.取一个边长为2a的正方形及其内切圆， 若随机向正方形内撒一粒豆子，求豆子 落入圆内的概率. 2a
变式1：一个棱长为2a的正方体内有一个 内切球，若随机向正方体内任取一点， 求该点落入球内的概率.
几何概型定义:
事件A理解为区域Ω 的某一子区域A，A
的概率与 与A的位置和形状无关。 子区域A的几何度量 （长度、面积、体积）成正比；
A
满足以上条件的试验称为几何概型。
几何概型的特征 无限性。在一次试验中，可能出现的结 果有无限个，即有无限个不同的基本事 件； 等可能性。每个基本事件发生的可能性 是均等的。
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
取一根长度为3m的绳子，如果拉直后在任 意位置剪断，那么剪得两段的长都不小于 1m的概率有多大？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§3.3.1-1几何概型(一)
重庆市万州高级中学 曾国荣 wzzxzgr@
§3.3.1-1几何概型(一)
复习 1、古典概型有哪两个基本特点？ （1）试验中所有可能出现的基本事件只有有限个； （2）每个基本事件出现的可能性相等（等可能性）.
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 14
60 50 1 P( A) , 60 6
§3.3.1-1几何概型(一)
练习：某路口红绿灯的时间设置为：红灯40秒,绿 灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到 哪一种灯的可能性最大?遇到哪一种灯的可能性最 小?根据什么? 遇到红灯,绿灯,黄灯的概率各是多少？为什么？
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 6
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
与扇形的弧长（或面积或圆心角）有关，与扇 形区域所在的位置无关.
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
4
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
以左边转盘为游戏工具时，甲获胜的概率为1/2 以右边转盘为游戏工具时，甲获胜的概率为3/5
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
17
§3.3.1-1几何概型(一)
例3：如图，甲转盘被分成３个面积相等的扇形，乙 转盘被分成了２个面积相等的扇形．小夏和小秋利用 它们来做决定获胜与否的游戏，规定小夏转甲盘一次， 小秋转乙盘一次为一次游戏（当指针指在边界线上视 为无效，重转） 小夏说：“如果 两个指针所指的区域内的数之和是６或７，则我胜； 否则你获胜”．按小夏设计的规则，请你写出两人获 胜的可能性分别是多少？
1
3
4
5
2
2013-8-15
甲盘
重庆市万州高级中学 曾国荣 wzzxzgr@
乙盘
18
§3.3.1-1几何概型(一)
小结 1、几何概率模型的定义 2、几何概型的特点 3、在几何概型中,事件A的概率的计算公式:
构成事件A的区域长度（面积或体积） P( A) 全部结果所构成的区域长度（面积或体积）
2
§3.3.1-1几何概型(一)
2、计算随机事件发生的概率，我们已经学习了哪 些方法? （1）利用古典概型的概率公式计算. （2）通过做试验或计算机模拟试验，用频率来近 似估计概率；
3、在现实生活中，常常会遇到试验的所有可能 结果是无穷多的情况，这时就不能用古典概型来计 算事件发生的概率.
2013-8-15
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
15
§3.3.1-1几何概型(一)
例2：甲乙两人相约上午8点到9点在某地会面，先 到者等候另一人20分钟，过时离去，求甲乙两人 能会面的概率. y 60
20
O 20 60 x
60 40 5 P( A) 2 9 60
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
9
§பைடு நூலகம்.3.1-1几何概型(一)
练习2：一个游戏转盘如图,让转盘自由转动,当转盘停 止转动后,指针落在哪个区域.这个随机事件是几何概型 吗？为什么？落在哪个区域的可能性最大?落在哪个区 域的可能性最小?有可能性相等的情况吗?为什么? 解：是几何概型， 因为事件发生的概 率只与构成该事件 区域的面积成比例,
13
§3.3.1-1几何概型(一)
例1:某人午觉醒来,发现表停了,他打开 收音机,想听电台报时,求他等待的时间 不多于10分钟的概率. 解:设A={等待的时间不多于10分钟}.我们所 关心的事件A恰好是打开收音机的时刻位于 [50,60]时间段内,因此由几何概型的求概率 的公式得
1 即“等待的时间不超过10分钟”的概率为 6
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 5
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
从结论来看，甲获胜的概率与字母B所在扇形区 域的哪个因素有关？哪个因素无关？
120º 90º
60º
90º
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
10
§3.3.1-1几何概型(一)
练习2：一个游戏转盘如图,让转盘自由转动,当转盘停 止转动后,指针落在哪个区域这个随机事件是几何概型 吗？为什么？落在哪个区域的可能性最大?落在哪个区 域的可能性最小?有可能性相等的情况吗?为什么?
2 2
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 16
§3.3.1-1几何概型(一)
练习：甲乙两人相约下午1时至2时在某公共汽车站 乘车，已知该站在下午1时30分和2时准点各发一班 车，假设因堵车的影响，甲乙两人在1时至2时之间 任一时刻到达车站的可能性相同，如果两人到车站 后见车就上，那么两人乘一辆车的概率是多少？
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
19
§3.3.1-1几何概型(一)
4、如果一个随机试验可能出现的结果有无限多个， 并且每个结果发生的可能性相等，那么该试验可以 看作是几何概型.通过适当设置，将随机事件转化 为几何问题，即可利用几何概型的概率公式求事件 发生的概率.
重庆市万州高级中学 曾国荣 wzzxzgr@
3
§3.3.1-1几何概型(一)
特定情形下，我们可以用几何概型来计算事件 发生的概率. 例如：一个人到单位的时间可能是8：00～9：00 之间的任何一个时刻；往一个方格中投一个石子，石 子可能落在方格中的任何一点上……这两个试验可能 出现的结果是有限个，还是无限个？若没有人为因素， 每个试验结果出现的可能性是否相等？
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 8
§3.3.1-1几何概型(一)
练习1：某班公交车到终点站的时间等可能是11： 30～12：00之间的任何一个时刻，那么“公交车 在11：40～11：50到终点站”这个随机事件是几 何概型吗？若是，怎样理解其几何意义？
解：落在红色区域 可能性最大，落在 蓝色区域可能性最 小，黄色和绿色可 能性相同,
120º 90º 60º 90º
这是几何概型，可以通过图形的面积判断.
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 11
§3.3.1-1几何概型(一)
对于具有几何意义的随机事件，或可以化归为 几何问题的随机事件，一般都有几何概型的特性， 我们希望建立一个求几何概型的概率公式. 在刚才的转盘游戏 中，落在各颜色区域 的概率各是多少？
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
20
§3.3.1-1几何概型(一)
课堂练习 <<教材>> P.140
练习1.2
书面作业
<<教材>> P.142 习题3.3 A组1
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
21
120º 90º
60º
90º
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
12
§3.3.1-1几何概型(一)
在几何概型中,事件A的概率的计算公式如下:
构成事件A的区域长度（面积或体积） P ( A) 全部结果所构成的区域长度（面积或体积）
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 7
§3.3.1-1几何概型(一)
几何概率模型的定义 如果每个事件发生的概率只与构成该事件区 域的长度(面积或体积)成比例,则称这样的概率模型 为几何概率模型,简称为几何概型. 几何概型的特点: (1)试验中所有可能出现的结果(基本事件)有无 限多个. (2)每个基本事件出现的可能性相等.
重庆市万州高级中学 曾国荣 wzzxzgr@
§3.3.1-1几何概型(一)
复习 1、古典概型有哪两个基本特点？ （1）试验中所有可能出现的基本事件只有有限个； （2）每个基本事件出现的可能性相等（等可能性）.
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 14
60 50 1 P( A) , 60 6
§3.3.1-1几何概型(一)
练习：某路口红绿灯的时间设置为：红灯40秒,绿 灯60秒,黄灯4秒.当人或车随意经过该路口时,遇到 哪一种灯的可能性最大?遇到哪一种灯的可能性最 小?根据什么? 遇到红灯,绿灯,黄灯的概率各是多少？为什么？
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 6
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
与扇形的弧长（或面积或圆心角）有关，与扇 形区域所在的位置无关.
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
4
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
以左边转盘为游戏工具时，甲获胜的概率为1/2 以右边转盘为游戏工具时，甲获胜的概率为3/5
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
17
§3.3.1-1几何概型(一)
例3：如图，甲转盘被分成３个面积相等的扇形，乙 转盘被分成了２个面积相等的扇形．小夏和小秋利用 它们来做决定获胜与否的游戏，规定小夏转甲盘一次， 小秋转乙盘一次为一次游戏（当指针指在边界线上视 为无效，重转） 小夏说：“如果 两个指针所指的区域内的数之和是６或７，则我胜； 否则你获胜”．按小夏设计的规则，请你写出两人获 胜的可能性分别是多少？
1
3
4
5
2
2013-8-15
甲盘
重庆市万州高级中学 曾国荣 wzzxzgr@
乙盘
18
§3.3.1-1几何概型(一)
小结 1、几何概率模型的定义 2、几何概型的特点 3、在几何概型中,事件A的概率的计算公式:
构成事件A的区域长度（面积或体积） P( A) 全部结果所构成的区域长度（面积或体积）
2
§3.3.1-1几何概型(一)
2、计算随机事件发生的概率，我们已经学习了哪 些方法? （1）利用古典概型的概率公式计算. （2）通过做试验或计算机模拟试验，用频率来近 似估计概率；
3、在现实生活中，常常会遇到试验的所有可能 结果是无穷多的情况，这时就不能用古典概型来计 算事件发生的概率.
2013-8-15
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
15
§3.3.1-1几何概型(一)
例2：甲乙两人相约上午8点到9点在某地会面，先 到者等候另一人20分钟，过时离去，求甲乙两人 能会面的概率. y 60
20
O 20 60 x
60 40 5 P( A) 2 9 60
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
9
§பைடு நூலகம்.3.1-1几何概型(一)
练习2：一个游戏转盘如图,让转盘自由转动,当转盘停 止转动后,指针落在哪个区域.这个随机事件是几何概型 吗？为什么？落在哪个区域的可能性最大?落在哪个区 域的可能性最小?有可能性相等的情况吗?为什么? 解：是几何概型， 因为事件发生的概 率只与构成该事件 区域的面积成比例,
13
§3.3.1-1几何概型(一)
例1:某人午觉醒来,发现表停了,他打开 收音机,想听电台报时,求他等待的时间 不多于10分钟的概率. 解:设A={等待的时间不多于10分钟}.我们所 关心的事件A恰好是打开收音机的时刻位于 [50,60]时间段内,因此由几何概型的求概率 的公式得
1 即“等待的时间不超过10分钟”的概率为 6
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 5
§3.3.1-1几何概型(一)
问题：有两个转盘，甲乙两人玩转盘游戏.规定当指 针指向B区域时，甲获胜，否则乙获胜.在两种情况下 分别求甲获胜的概率是多少？ B N B N N
B
N B
B
N
B
从结论来看，甲获胜的概率与字母B所在扇形区 域的哪个因素有关？哪个因素无关？
120º 90º
60º
90º
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
10
§3.3.1-1几何概型(一)
练习2：一个游戏转盘如图,让转盘自由转动,当转盘停 止转动后,指针落在哪个区域这个随机事件是几何概型 吗？为什么？落在哪个区域的可能性最大?落在哪个区 域的可能性最小?有可能性相等的情况吗?为什么?
2 2
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 16
§3.3.1-1几何概型(一)
练习：甲乙两人相约下午1时至2时在某公共汽车站 乘车，已知该站在下午1时30分和2时准点各发一班 车，假设因堵车的影响，甲乙两人在1时至2时之间 任一时刻到达车站的可能性相同，如果两人到车站 后见车就上，那么两人乘一辆车的概率是多少？
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
19
§3.3.1-1几何概型(一)
4、如果一个随机试验可能出现的结果有无限多个， 并且每个结果发生的可能性相等，那么该试验可以 看作是几何概型.通过适当设置，将随机事件转化 为几何问题，即可利用几何概型的概率公式求事件 发生的概率.
重庆市万州高级中学 曾国荣 wzzxzgr@
3
§3.3.1-1几何概型(一)
特定情形下，我们可以用几何概型来计算事件 发生的概率. 例如：一个人到单位的时间可能是8：00～9：00 之间的任何一个时刻；往一个方格中投一个石子，石 子可能落在方格中的任何一点上……这两个试验可能 出现的结果是有限个，还是无限个？若没有人为因素， 每个试验结果出现的可能性是否相等？
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 8
§3.3.1-1几何概型(一)
练习1：某班公交车到终点站的时间等可能是11： 30～12：00之间的任何一个时刻，那么“公交车 在11：40～11：50到终点站”这个随机事件是几 何概型吗？若是，怎样理解其几何意义？
解：落在红色区域 可能性最大，落在 蓝色区域可能性最 小，黄色和绿色可 能性相同,
120º 90º 60º 90º
这是几何概型，可以通过图形的面积判断.
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 11
§3.3.1-1几何概型(一)
对于具有几何意义的随机事件，或可以化归为 几何问题的随机事件，一般都有几何概型的特性， 我们希望建立一个求几何概型的概率公式. 在刚才的转盘游戏 中，落在各颜色区域 的概率各是多少？
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
20
§3.3.1-1几何概型(一)
课堂练习 <<教材>> P.140
练习1.2
书面作业
<<教材>> P.142 习题3.3 A组1
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
21
120º 90º
60º
90º
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
12
§3.3.1-1几何概型(一)
在几何概型中,事件A的概率的计算公式如下:
构成事件A的区域长度（面积或体积） P ( A) 全部结果所构成的区域长度（面积或体积）
2013-8-15
重庆市万州高级中学 曾国荣 wzzxzgr@
2013-8-15 重庆市万州高级中学 曾国荣 wzzxzgr@ 7
§3.3.1-1几何概型(一)
几何概率模型的定义 如果每个事件发生的概率只与构成该事件区 域的长度(面积或体积)成比例,则称这样的概率模型 为几何概率模型,简称为几何概型. 几何概型的特点: (1)试验中所有可能出现的结果(基本事件)有无 限多个. (2)每个基本事件出现的可能性相等.