Surfer中网格化方法的选取方法
Surfer软件使用教程
Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 （以下简称Surfer）是一款画三维图（等值线，image map，3d surface）的软件，是美国Golden Software公司的系列绘图软件之一。
该软件简单易学，可以在几分钟内学会主要内容，且其自带的英文帮助文件（help菜单）是相当完美且容易阅读的，对如何使用Surfer，解释的很详细，只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图（contour map），是具有插值功能的绘图软件，因此，即使你的数据是不等间距的，依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map，等形式的图形，其功能是比较强大的。
Surfer的安装比较简单（目前，只有Windows操作系统下的版本，最为常用的是8.0版本），只要按其提示缺省安装即可。
其安装软件的大小不到30M，一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后，其环境界面如图3－1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面·22·3.2 软件界面及命令菜单Surfer软件的界面非常友好，继承了Windows操作系统软件的特点。
从图3－1中可以看到，其最上方为命令菜单，在命令菜单的下方是命令菜单中的快捷工具栏（共两行），左侧的空白区域为目标管理窗口，用来更加方便的管理绘制的各个图形要素，右侧的空白区域为工作区，用来绘制图形，最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单（F）“文件菜单”如图3－2所示，主要是对文件进行操作，如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口，点击后即出现图3－1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
Surfer使用教程
第3章 Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 （以下简称Surfer）是一款画三维图（等值线，image map，3d surface）的软件，是美国Golden Software公司的系列绘图软件之一。
该软件简单易学，可以在几分钟内学会主要内容，且其自带的英文帮助文件（help菜单）是相当完美且容易阅读的，对如何使用Surfer，解释的很详细，只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图（contour map），是具有插值功能的绘图软件，因此，即使你的数据是不等间距的，依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map，等形式的图形，其功能是比较强大的。
Surfer的安装比较简单（目前，只有Windows操作系统下的版本，最为常用的是8.0版本），只要按其提示缺省安装即可。
其安装软件的大小不到30M，一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后，其环境界面如图3－1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面3.2 软件界面及命令菜单Surfer软件的界面非常友好，继承了Windows操作系统软件的特点。
从图3－1中可以看到，其最上方为命令菜单，在命令菜单的下方是命令菜单中的快捷工具栏（共两行），左侧的空白区域为目标管理窗口，用来更加方便的管理绘制的各个图形要素，右侧的空白区域为工作区，用来绘制图形，最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单（F）“文件菜单”如图3－2所示，主要是对文件进行操作，如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口，点击后即出现图 3－1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
surfer插值
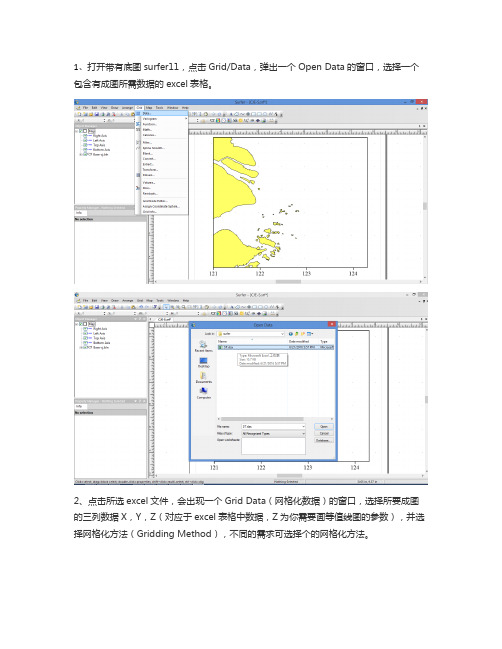
1、打开带有底图surfer11，点击Grid/Data，弹出一个Open Data的窗口，选择一个包含有成图所需数据的excel表格。
2、点击所选excel文件，会出现一个Grid Data（网格化数据）的窗口，选择所要成图的三列数据X，Y，Z（对应于excel表格中数据，Z为你需要画等值线图的参数），并选择网格化方法（Gridding Method），不同的需求可选择个的网格化方法。
3、选择存路径等，最后点击OK，就会输出一个grd文件并关闭Gridding Report, 得到插值的网格化grd.文件。
4、选择菜单栏Map/New/Contour Map，或者右击左边菜单栏里的Map/Add/Contour Layer，
5、找到上面的grd文件所在位置，点击打开，就得到所要的平面等值线图（未上色）。
如果等值线不够平滑，可以点击Contours...,在左下属性管理（Property Manager）选择General/Smoothing，进行None,Low,Medium,High四种不同程度地平滑
6、然后就是为等值线图上色；点击Contours...,在左下属性管理（Property Manager）选择Levels/Filled Contours/Fill Colors，勾选Fill Contours和Color Scale。
Res2dinv输出surfer格式的使用
Res2dinv输出surfer格式的使用Re2dinv反演软件完成反演后，可以将反演数据保存为urfer数据格式，以便在urfer软件中重新绘制。
选此项，直接保存电阻率值选此项，使用白化方法如要保存有地形的模型，选此项输出时会自动生成4个数据文件，一般生成模型数据格式为：原文件名_modre.dat原文件名_modre.bln原文件名_modre.lvl原文件名_modre_pot.datmod是模型的英文简写，re是电阻率的英文简写。
如下图如果是生成带地形的模型数据格式为原文件名_topre.dat原文件名_topre.bln原文件名_topre.lvl原文件名_topre_pot.dattop是地形的英文简写。
第一个文件是反演模型电阻率值的urfer格式数据文件。
第二个文件是模型值的urfer边界文件，是对网格文件做白化是用的。
第三个文件是urfer等级数据文件，用颜色来表示模型电阻率的大小。
第四个文件是张贴图数据文件，用于在地表面上表示斜距。
下面我们一步步使用这4个文件来把urfer等值线画出来。
假设原文件为TEST.DAT。
一，首先使用tet_topre.dat文件在urfer8中点击“网格”---“数据”—读入“tet_topre.dat”文件。
网格化数据时，网格化方法可选择克里格方法或自然邻近点法，克里格法在网格化较小数值时，容易插值出负值，而自然邻近点法则不会出现此问题。
网格线的间距要选小一点，即行数要多一些，这样做白化时，白化的边界不会出现很严重的锯齿状条纹。
当然，如果行数太大，计算量也较大，实际中根据情况灵活选择，满足要求即可。
可选择不同的网格化方法某,Y方向的网格线行数可选择多一点网格文件创建后，网格化插值算法会将数据文件插值为一个矩形的网格文件(以某，Y方向的最大值插满整个网格)如果直接绘制等值线图，会形成一个矩形的等值线图，这并不是我们需要的，因为反演后的模型数据不一定是矩形的，而且有地形的话，形状还会更复杂一些，这时，就需要使用网格白化的功能将没有实际数据的地方但又插值出的数据去掉。
surfer使用方法
8.00
7.00
6.00
5.00
4.00
3.00
2.00
1.00
化 探 数 据 基 本 处 理
0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00
0.00
-1.00 -1.00
21900
9
19600
8.5
8
17300
7.5
方法设置对话框
选项（Options）
允许为选择的方法指定网格化选项。对话框因 网格化的方法不同而不同。对所有方法都有两 项共同选项，即
各向异性（Anisotropy）
是指数据点之间的优 势方向，通过指定不同方向的不同半径来实现。 解释为给于一个方向轴上的点较大的权重，而 减弱另一个方向轴上的点权重。在许多情况下， 不必使用各向异性。
( 4.2, 8.1) ( 6.1, 7.9)
( 2.6, 7.2)
( 7.2, 6.6) ( 2.8, 6.3)
(6.2, 5.8) ( 4.8,5.6)
二、创建等值线图
等值线图是一种代表三维数据的平面图形，它是基本数据 文件[.dat]经 Surfer 的 Grid 命令生成网格化文件[.GRD]后 ，由Contour 命令生成。即，创建等值线图包括以下两个 步骤：
基本粘贴 Post 分类粘贴 ClassPost
x y labels 1 labels 2 … 2587 3264 Well 25 0.58 x y Ø ¿ Ö Æ Ö µ 2587 3264 100 labels 1 … 0.58
4 边界文件[.bna]
边界文件是用于存储封闭线、曲线、和点的ASCII 格式的文件。用于生成规则或不规则的边界线， 其扩展名为.bna。其要求的数据格式是：
Surfer
中禹科技信息 ２ ０ １ ５年第 ０ ７期
Hale Waihona Puke 信息技术推广 孟红 星
孟 红星
河 北 省 煤 田地 质 局 物 测 地 质 队
山地质 工程 师 Ｄ － Ｇ・ 克里 格 的名字 命 名的一 种插 值方 法 。 它是 以区域 化变 量理 论 为基础 ，以变差 函数 为 主要 工具 ， 在 保证 估计 计算 满足 无偏 性条 件和 最小 方差 条件 的 前提 下 求 得估值 ，是一 种特 定滑 动加 权平 均法 。克 里格 法极 为 灵 活 ，广 泛地 应用 于各 个科 学领 域 ，适用 于各 种类 型 的离 散 数据 ，网格 化精 度高 ，是 绘制地 质 图件 的一 种 常用插 值 方 法 。二是 步 长的 选取 ，横 向上 步长 选取 测点 距或 １ ／ ２测点 距 ，纵 向上 的步 长根 据断 面数据 的 纵 向分布 规律 和要 求 的 精度 来 选择 ，通 常 选 ５或 １ ０即可 ，步 长太 小 造成 网格 化 后 的数据 量太 大 ，影 响程序 运行 速度 ，步长 太大 ，数 据精 度会 降低 。
美 国 ＧｏＬ Ｄ Ｅ Ｎ软件 公司 的 Ｓ ｕ ｆ ｅ ｒ 软件 ， 以其 方便 、 直观 、 快 捷 、安装 简单 、对 系统 要求低 等优 点 得到 广大 用户 的青 睐 。Ｓ ｕ ｆ ｅ ｒ 是 一 套在 ｗｉ ｎ ｄ ｏ ｗｓ操作 环境 下 运行 的 二维 和 三维 图形 绘制 软件 ， 利用 它可 以绘制 等值 线 图 、 ３ Ｄ立体 图 、 阴影 地貌 图 、矢量 图等 。该 软件 自带 有数 据编 辑器 ，使 用 方法 和对 数 据的 处理 与 Ｍｉ ｃ ｒ ｏ ｓ ｏ ｌ ｆ Ｅ ｘ ｃ ｅ ｌ 大 致相 同 ，而 且 可 以 直接 处 理 Ｅ ｘ ｃ ｅ ｌ 文 件 ，能 迅 速 地 将 离 散 的 数据 通过 插值转换为连续的数据曲面 。 该软件提供了包括克里格法、 距 离 倒数 加权 法 、多元 回 归等 十 二种插 值 方法 ，可 以满足 不 同 应用 方 向的插值 需求 。 但是 像任 何软 件一样 ， Ｓ ｕ ｆ ｅ ｒ 提供 的功 能是 有 限的 ， 不 可能 满足 用 户多样 化 的需求 。由于我 们所 研究 的客 观世 界 的复 杂性 ，这 也决 定 了任何 软件 在功 能上 不可 能做 到面 面 俱到 。出于上 述原 因 ，我们 要对软 件 功能 进行 补充 ，即 利用 Ｓ ｕ ｆ ｅ ｒ 软 件 处 理 数据 和 自动 生 成 等 值线 图的 功 能 ， 然 后用 自编软 件２ － ， Ｊ － Ｓ ｕ ｒ ｆ ｅ ｒ 软件 图形数 据做 进一步 的处 理 。 通过 Ｓ ｕ ｆ ｅ ｒ 软 件 和 自编 软 件 相结 合 ，能够 达 到 快速 准 确 绘 制顺层 电性 切 片图 的 目的 。
surfer8.0_绘图教程(菜鸟入门)
Apart
Overlay） 29
从叠覆的复合图形中分离出所选的图形。
窗口(W)菜单
精选ppt课件
30
帮助(H)菜单
精选ppt课件
31
二）Surfer 创建基本等值线图
1、数据类型与准备 2、网格化数据 3、创建等值线图
精选ppt课件
32
1、数据类型与准备
基本数据文件[.dat]
网格文件[grd]
粘贴文件[.dat]
边界文件[.bna]
空白文件[.bln]
分级文件[.lvl]
精选ppt课件
33
基本数据文件[.dat]
基本数据文件是至少包括X、Y、Z三列数据 的文件,其后可增加Z1，Z2，….Zn列。
其中，X、Y是确定位置的坐标值，z是对应 于某坐标点的变量值（如油层厚度、有效 厚度、孔隙度、渗透率、百分含量等）。
基本数据文件在工作表中的格式是：
基本数据文件的精扩选pp展t课件名为.dat
34
网格文件[grd]
是绘制等值线图和表面图所必须的文件。 网格文件是由基本数据文件经网格化（Grid）
命令处理后得到的。 网格文件的扩展名为.Grd
精选ppt课件
35
粘贴文件[.dat]
在等值线图的数据点位置进行符号和数值标注所 需要的文件，分为Post 和 Class Post两种。
• 函数（Function）
根据用户指定的公式产生一个网 格文件。
• 数学（Math）
对已经存在的网格文件的Z值进 行数学变换，或者合并两个相同 网格文件的Z值。
• 微积分（Calculus）
精选ppt在课件网格化文件上进行微积分运24 算 。
• 网格滤波器（Filter）
Surfer中网格化方法的选取方法
克里格法（Kriging）
最初是由南非金矿地质学家克里格根据南非金矿的具体情况提出的计算矿产储 量的方法：按照样品与待估块段的相对空间位置和相关程度来计算块段品位及 储量，并使估计误差为最小。后来，法国学者马特隆对克里格法进行了详细的 研究，使之公式化和合理化。 克里格方法的基本原理是根据相邻变量的值（如若干样品元素含量值），利用 变差函数所揭示的区域化变量的内在联系来估计空间变量数值。 该方法总是尽可能地去描述原数据所隐含的趋势特征，以区域化变量理论为基 础，以变差函数为主要工具，在保证研究对象的估计值满足无偏性条件和最小 方差条件的前提下求得估计值。 对于高值数据点会使之沿某一“脊”分布，而不围绕该点孤立插值，不形成“ 公牛眼”等值线。 克里格法极为灵活，广泛地应用于各个科学领域，适于各种类型的离散数据， 网格化精度高，是极佳的网格化方法。
应用条件
数量小于２５０个点数据的网格化，对于２5０～ １０００个数据点，效果也不错 方法速度快，适合于大量（１０００个以上）数 据的网格化 适应范围类似克里格法 可以通过权重调整空间插值等值线的结构，计算 值容易受到数据点集群的影响，常出现孤立 点数据明显高于周围数据点 适合规则分布、或者大多数数据点位于网格节点 上的数据，更适合于均匀间隔的数据插值， 可以有效填充无值数据区域 方法速度快，适合中等数量、均匀分布的数据网 格化 实际上是一种趋势面分析作图程序，可用来确定 数据的大规模趋势和图案。被广泛应用于地 质科学。该方法具有速度快特点、然而其去 掉了原数据中的局部细节，不利于资料的详 细分析
11.4
12.6
13.8
15
16.2
-4.8
0.6
1.8
3
4.2
5.4
6.6
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
最小曲率法（Minimum curvature）
采用迭代的方法逐次求取网格节点数据，其插值面类似一个薄的、 线性—弹性形变板，该“板”经过所有的数据点，且每个数据点具 有最小曲率。 由于最小曲率法采用全区的数据进行网格化，因而比较适合于数据 分布不均匀的情况。在尽可能体现原数据的同时，最小曲率法产生 尽可能的光滑曲面，绘制的图件比较美观。 使用最小曲率法需要用最大偏差参数和最大循环次数参数来控制最 小曲率的收敛标准，且要求至少有4个点。 该方法速度快，适合于大量（1000个以上）数据的网格化，由于其 主要考虑曲面的光滑性，不能达到精确的插值结果，容易超出最大 值和最小值的范畴。
三角形剖分法 多项式回归法
实例
1、高密度电法温纳装置实例
0.6 -0.8 -1.6 -2.4 -3.2 -4 -4.8 0.6 1.8 3 4.2 5.4 6.6 7.8 9 10.2 11.4 12.6 13.8 15 16.2 1.8 3 4.2 5.4 6.6 7.8 9 10.2 11.4 12.6 13.8 15 16.2 -0.8 -1.6 -2.4 -3.2 -4 -4.8
-4.8
图1 高密度不同网格化方法视电阻率等值线图
此例子的高密度数据点553个。高密度电阻率法实测数据，取相同 的参数，采用不同的网格化方法绘制视电阻率等值线断面（图1A~F）， 可见效果不同。 采用三角剖分法网格生成的图1A，整个断面呈倒梯形，网格化的结果 是严格控制了实测数据边界，可清晰分辨出局部高阻异常，有利于局部异 常区的圈定和解释。
克里格法（Kriging）
最初是由南非金矿地质学家克里格根据南非金矿的具体情况提出的计算矿产储 量的方法：按照样品与待估块段的相对空间位置和相关程度来计算块段品位及 储量，并使估计误差为最小。后来，法国学者马特隆对克里格法进行了详细的 研究，使之公式化和合理化。 克里格方法的基本原理是根据相邻变量的值（如若干样品元素含量值），利用 变差函数所揭示的区域化变量的内在联系来估计空间变量数值。 该方法总是尽可能地去描述原数据所隐含的趋势特征，以区域化变量理论为基 础，以变差函数为主要工具，在保证研究对象的估计值满足无偏性条件和最小 方差条件的前提下求得估计值。 对于高值数据点会使之沿某一“脊”分布，而不围绕该点孤立插值，不形成“ 公牛眼”等值线。 克里格法极为灵活，广泛地应用于各个科学领域，适于各种类型的离散数据， 网格化精度高，是极佳的网格化方法。
网格化方法的特征及应用条件
网格化概念—是指通过一定的插值方法，将稀疏的、不规 则分布的数据插值加密为规则分布的数据，以适合绘图的 需要。 网格化方法—加权反距离法（Inverse distance to a power ）、克里格法（Kriging）、最小曲率法（Minimum curvature）、改进谢别德法（Modified shepard’s method ）、自然邻点法（Natural neighbor）、最近邻点法（ Nearest neighbor）、多项式回归法（Polynomial regression）、径向基函数法（radial basis function）、带 线性插值的三角剖分法（triangulation/liner interpolation ）、移动平均法（moving average ）、数据度量法（data metrics ）和局部多项式方法（local polynomial）。
-4.8
0.6 -0.8 -1.6 -2.4 -3.2 -4 -4.8 0.6
1.8
3
4.2
5.4
6.6
7.8
9
10.2
11.4
12.6
13.8
15
16.2 -0.8 -1.6 -2.4 -3.2 -4
50 46 42 38 34 30 26 22 18 14
1.8
3
4.2
5.4
6.6
7.8
9
10.2
表一：地球物理中常用的8种网格化方法及其特征 类型
克里格法 最小曲率法 径向基函数法 加权反距离插值 法 最近邻点法
特征
根据相邻变量的值，利用变差函数所揭示的区域变 量的内在联系来估计空间变量数值，网格化精度高 采用迭代的方法逐次求取网格节点数据 多个数据插值方法组合的、多形式的方法 认为任何一个观测值都对邻近的区域有影响，且影 响的大小随距离的增大而减小 采用距离网格节点最近的数据点的值来表明网格节 点的值 通过直线连接各数据点形成一系列互不相交的三角 形，每个三角形内的网格节点值由该三角平面决定 仅仅通过定义趋势面类型来表明原数据的大状态趋 势，并不增加未知的网格节点值
7.8
9
10.2
11.4
12.6
13.8
15
16.2
-4.8
0.6
1.8
3
4.2
5.4
6.6
7.8
9
10.2
11.4
12.6
13.8
15
16.2 -0.8 -1.6 -2.4 -3.2 -4
105 90 75 60 45
C— 反 距 离 加 权 D— 最 小 曲 率
-0.8 -1.6 -2.4 -3.2 -4 -4.8 0.6 1.8 3 4.2 5.4 6.6 7.8 9 10.2 11.4 12.6 13.8 15 16.2
多项式回归法（Polynomial regression）
严格地说并不是一种真正的插值方法，它仅仅通过定义趋 势面类型来表明原数据的大状态趋势，并不增加未知的网 格节点值，实际上是一种趋势面分析作图程序，可用来确 定数据的大规模趋势和图案。 使用该方法需要考虑两方面问题：一是趋势面数学表达式 的确定；二是拟合精度的确定。 该方法具有速度快的特点，但也去掉了原数据中的局部细 节，不利于资料的详细分析。
应用条件
数量小于２５０个点数据的网格化，对于２5０～ １０００个数据点，效果也不错 方法速度快，适合于大量（１０００个以上）数 据的网格化 适应范围类似克里格法 可以通过权重调整空间插值等值线的结构，计算 值容易受到数据点集群的影响，常出现孤立 点数据明显高于周围数据点 适合规则分布、或者大多数数据点位于网格节点 上的数据，更适合于均匀间隔的数据插值， 可以有效填充无值数据区域 方法速度快，适合中等数量、均匀分布的数据网 格化 实际上是一种趋势面分析作图程序，可用来确定 数据的大规模趋势和图案。被广泛应用于地 质科学。该方法具有速度快特点、然而其去 掉了原数据中的局部细节，不利于资料的详 细分析
采用最小曲率法网格生成的图1D，与图2B克里格插值方法的效果基 本相同，有2个低阻异常区域，由一些渐变的异常点组成，有利于异常区 的圈定和解释。 采用径向基函数法网格生成的图1E，整个断面呈矩形，网格化的结 果是扩大了实测数据边界，没有数据的区域插值产生，可分辨出局部高阻 异常，因此有利于局部异常区的圈定和解释。但图形左侧和右侧等值线杂 乱，表示插值效果不好。 采用最近邻点法网格生成的图1F，整个断面呈矩形，网格化的 结果是扩大了实测数据边界，没有数据的区域插值产生，呈现２个 孤立的低阻异常区域，异常区等值线稀疏，边界呈矩形。
Surfer中网格化方法的选取
探究
曹创华 2010年11月
前言
绘制地球物理数据等值线图时，需要根据客 观环境特征和数据本身的特点，选择合适的 网格化方法。 Surfer中的插值方法有12种，常用的有加权 反距离插值法、克里格法、最小曲率法、最 近邻点法、多项式回归法、径向基函数法、 带线性插值的三角剖分法等，本文将结合实 例将常用网格化方法的选取方法、适用范围 及参数设置等使用技巧做了简单的探讨。
三角剖分法（triangulation/liner interpolation ）
是一种严格的插值方法，使用最佳的Delaunay三角形，通过 直线连接各数据点形成一系列三角形，并且所有的三角形互 不相交，每个三角形内的网格节点值由该三角平面决定。 由于采用所有的数据点去构造三角形，因而原数据能得到很 好的体现，给定三角形内的全部节点都要受到该三角形的表 面限制。 该方法速度快，适合中等数量、均匀分布的数据的网格化， 地图上稀疏区域将会形成截然不同的三角面。 当数据量足够时，该方法对断线的保留具有其他方法不可比 拟的优势。
采用克里格法网格生成的图1B，整个断面呈矩形，网格化的结果是 扩大了实测数据边界，没有数据的区域插值产生，呈现2个低阻异常区域， 由一些渐变的异常点组成，有利于异常区的圈定和解释。
采用加权反距离法网格生成的图1C，整个断面呈矩形，网格化的结 果是扩大了实测数据边界，没有数据的区域插值产生，低阻和高阻异常的 分界面很清晰，有的地方呈现串珠状高阻异常，形成一些孤立的异常点， 不利于异常区的圈定和解释。
最近邻点法（Nearest neighbor）
是荷兰气象学家A．H. Thiessen提出的一种分析方法。 最初用于从离散分布气象站的降雨量数据中计算平均降雨量 ，GIS和地理分析中多采用其进行快速赋值。 最近邻点插值的一个隐含的假设条件是任意网格点的属性值 都是用距离它最近的位置点的属性值，用每一个网格节点的 最邻点值作为待求的节点值。 该方法适合对规则分布的数据进行网格化；或者大多数数据 点位于网格节点上；或者在一个完整的数据文件中，只有少 数点无值，可以采用该方法来填充无值的数据点。 总之，最近邻点插值法是均质无变化的，更适合于均匀间隔 的数据插值，可以有效填充无值数据区域。
0.6
1.8
3
4.2
5.4
6.6
7.8
9
10.2
11.4
12.6
13.8
15
16.2 -0.8 -1.6 -2.4 -3.2 -4
120 105 90 75 60 45 30 15 0
E— 径 向 函 数 法 F— 最 近 邻 点 法
-0.8 -1.6 -2.4 -3.2 -4 -4.8 0.6 1.8 3 4.2 5.4 6.6 7.8 9 10.2 11.4 12.6 13.8 15 16.2