状态空间模型计算和例子
python马尔可夫链的转移概率计算
马尔可夫链是一种基于概率转移的模型，可以通过计算每个状态转移到每个其他状态的转移概率来理解和模拟状态转换的过程。
在Python中，可以使用许多库来处理马尔可夫链，例如`numpy`和`scipy`。
以下是一个简单的例子，展示如何使用Python和`numpy`库来计算马尔可夫链的转移概率。
```pythonimport numpy as np# 定义状态空间states = ['state1', 'state2', 'state3']# 定义转移矩阵# 假设从状态1转移到状态1的概率是0.8, 从状态1转移到状态2的概率是0.1, 从状态1转移到状态3的概率是0.1# 从状态2转移到状态1的概率是0.4, 从状态2转移到状态2的概率是0.3, 从状态2转移到状态3的概率是0.3# 从状态3转移到状态1的概率是0.4, 从状态3转移到状态2的概率是0.6transition_matrix = np.array([[0.8, 0.1, 0.1],[0.4, 0.3, 0.3],[0.4, 0.6, 0]])# 计算转移概率# 使用numpy的linalg.inv函数来计算逆矩阵，然后乘以转移矩阵，得到转移概率forward_probabilities = np.linalg.inv(transition_matrix).dot(np.eye(len(states)))print(forward_probabilities)```这段代码首先定义了状态空间和转移矩阵。
然后，它使用numpy的linalg.inv函数来计算转移矩阵的逆矩阵，并使用这个逆矩阵乘以转移矩阵，得到每个状态的转移概率。
最后，它打印出这些转移概率。
请注意，对于大型的马尔可夫链，直接计算逆矩阵可能会非常耗时，甚至可能导致内存溢出。
在这种情况下，可能需要使用更复杂的方法来求解转移概率，例如使用动态规划或蒙特卡洛方法。
车辆二自由度模型状态空间方程
车辆二自由度模型状态空间方程一、车辆二自由度模型状态空间方程车辆二自由度模型是车辆动力学中常用的简化模型之一，它将车辆简化为一个在平面上运动的质点。
在这个模型中，车辆可以做平面上的平移和转动运动，因此被称为车辆的二自由度模型。
而状态空间方程则是描述这一模型运动规律的数学工具。
在车辆二自由度模型中，通常采用平移运动的位置和速度以及转动运动的姿态角和角速度作为描述车辆状态的变量。
通过对车辆动力学和控制理论的研究，可以得到描述车辆二自由度模型的状态空间方程。
这些方程包括车辆的位置、速度、姿态角和角速度之间的动态关系，可以用来描述车辆在不同行驶状态下的运动规律。
二、深度分析车辆二自由度模型状态空间方程车辆二自由度模型状态空间方程的深度分析需要从车辆动力学和控制理论的角度进行。
我们需要深入了解车辆的平移和转动运动规律，包括车辆在不同速度和转角条件下的运动特性，以及外部环境对车辆运动的影响。
我们需要探讨车辆控制系统对车辆状态的影响，包括如何通过控制输入来影响车辆的运动状态。
我们需要分析车辆二自由度模型状态空间方程的数学推导和物理意义，以深入理解车辆状态空间方程的结构和参数含义。
在具体的分析过程中，我们可以通过建立车辆运动的动力学模型和控制模型，使用数学工具进行模型分析和仿真验证，从而深入理解车辆二自由度模型状态空间方程的动态性质和稳定性。
三、撰写高质量车辆二自由度模型状态空间方程文章基于以上的深度分析，我们可以着手撰写一篇高质量的文章。
我们可以介绍车辆二自由度模型的基本原理和概念，然后逐步展开对车辆状态空间方程的分析和推导，包括车辆运动学和动力学的描述，以及状态空间方程的数学结构和物理意义。
在文章中，我们可以多次提及车辆二自由度模型状态空间方程的关键词，以加强文章的专业性和知识性。
我们还可以结合个人的观点和理解，对车辆二自由度模型状态空间方程进行综合性的总结和回顾，为读者提供全面、深刻和灵活的理解。
一篇关于车辆二自由度模型状态空间方程的高质量文章需要具备深度和广度兼具的分析能力，结合个人观点和实践经验，以及对读者的引导和启发。
状态和状态空间表达式
补偿器解耦(7/7)
基于所求解的补偿器Gc(s),可实现如图4-3示的解耦控制系统。 例4-8求得的解耦补偿器Gc(s)的传递函数阵的某个元素 出现分子多项式阶次高于分母多项式阶次,这会带来该解 耦控制器工程上物理实现的困难,一般工程上只能做到近 似实现。
状态反馈解耦(1/16)
4.4.2 状态反馈解耦
状态反馈解耦(14/16)
由于E是非奇异阵,所以系统可以解耦。 因此,状态反馈解耦矩阵为
0 0 1 K E F 1 2 3 1 0 1 H E 0 1
1
状态反馈解耦(15/16)
此时闭环系统状态方程和输出方程为：
0 x (t ) 0 0 1 y (t ) 0
为实现系统解耦,要求为W(s)对角线矩阵，因此, I-W(s)也为 对角线矩阵。 故，得出Gp(s)Gc(s)也需为对角线矩阵。 即为实现如图6-3所示结构的系统的解耦,应取合适补偿 器Gc(s)使Gp(s)Gc(s)是非奇异对角线矩阵。
补偿器解耦(4/7)—例6-8
例4-8 已知系统如图4-4所示,
1 s l2 1
状态反馈解耦(9/16)
可以看出W(s)是对角线矩阵,所以其闭环系统是一个完全解 耦系统。 另外,传递函数对角元素均是积分环节,故称这样的系统 为具有积分型的解耦系统。 下面通过例子来说明如何借助状态反馈实现解耦。
状态反馈解耦(10/14)
例4-9 设系统的状态空间模型为：
s 2 3s 1 s ( s 1)( s 2) 1 G ( s) C ( sI A) B 1 ( s 1)( s 2)
因此,系统存在耦合现象。 系统的状态图如图4-6所示。
马尔可夫链的定义及例子
3、转移概率
定义 i, j S, 称 P Xn1 j Xn i
的一步转移概率。
pij n 为n时刻
若i, j S, pij n pij ，即pij与n无关，称转移概率
具有平稳性.此时称{Xn,n≥0}为齐次（或时齐的）马尔 可夫链。记P=(pij)，称P为{Xn,n≥0}的一步转移概率矩阵.
0
j!
j 0,1, i
pi0公式略有不同，它是服务台由有i个顾客转为空闲的
概率，即第n个顾客来到时刻到第n+1个顾客来到时刻之
间系统服务完的顾客数≥i+1。
pi0 P X n1 0 X n i P(Yn i 1) P(Yn k) k i1
et (t)k dG t ,
0 P{Yn
j Tn1 x}dG x
( x) j exdG x, j 0,1, 2,
0 j!
因此， {Xn，n≥1}是马尔可夫链。其转移概率为
P0 j P( X n1 j X n 0) P(Yn j X n 0)
P(Yn
P( X n1 in1 X n in )
所以{Xn,n≥0}是马尔可夫链，且
pij P( X n1 j X n i) P( f i,Yn1 j) P( f i,Y1 j)
二、切普曼-柯尔莫哥洛夫方程
1，随机矩阵 定义：称矩阵A=(aij)S×S为随机矩阵，若aij ≥0，且
一步转移概率矩阵
0.5009
0.0458 0.2559 0.1388 0.2134
0.0466 0.0988 0.36584 0.14264
状态空间模型计算和例子
状态空间模型计算和例子x(t+1)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)其中，x(t)是n维的状态向量，表示系统在时刻t的状态；u(t)是m维的输入向量，表示系统在时刻t的输入；y(t)是p维的输出向量，表示系统在时刻t的输出；A是n×n的矩阵，描述状态向量x(t)的转移规律；B是n×m的矩阵，描述输入向量u(t)对状态向量x(t)的影响；C是p×n的矩阵，描述状态向量x(t)对输出向量y(t)的影响；D是p×m的矩阵，描述输入向量u(t)对输出向量y(t)的影响。
下面以一个简单的例子来说明状态空间模型的应用。
假设我们有一个竖直方向上的弹簧振子系统，其中弹簧的运动受到外界施加的力的影响。
我们希望通过状态空间模型来描述和控制弹簧振子系统的运动。
首先，我们需要定义系统的状态变量。
在这个例子中，我们可以选择弹簧的位置和速度作为系统的状态变量。
设弹簧位置为x(t)，速度为v(t)，则系统的状态向量可以表示为：x(t)=[x(t);v(t)]接下来，我们需要建立状态向量的转移方程。
弹簧振子系统的运动由弹簧的力和外界施加的力共同决定。
设弹簧的劲度系数为k，质量为m，外界施加的力为f(t)，则弹簧振子系统的转移方程可以表示为：x(t+1)=Ax(t)+Bf(t)其中，A是2×2的矩阵，描述位置和速度的转移规律；B是2×1的矩阵，描述外界施加的力对位置和速度的影响。
最后，我们需要定义系统的输出方程。
在这个例子中，我们可以选择弹簧的位置作为系统的输出变量。
则输出方程可以表示为：y(t)=Cx(t)其中，C是1×2的矩阵，描述位置对输出的影响。
通过建立状态空间模型，我们可以分析和预测弹簧振子系统的运动。
例如，我们可以通过模型计算系统在给定初始状态和外界施加力的情况下，弹簧的位置随时间的变化。
同时，我们还可以设计控制算法，通过调节外界施加的力，控制弹簧振子系统的运动。
状态空间方程表示二次方程
状态空间方程表示二次方程全文共四篇示例，供读者参考第一篇示例：二次方程是一种常见的数学方程，具有形式为ax^2 + bx + c = 0的特点。
我们可以通过多种方法来解决二次方程，其中一种方法就是使用状态空间方程来表示它。
状态空间方程是一种描述动态系统的数学模型，通过它我们可以描述系统在不同状态下的行为和演变。
在处理二次方程时，我们可以将其转化为状态空间方程的形式。
假设我们有一个简单的二次方程y = ax^2 + bx + c，我们可以定义状态变量x和y。
然后，我们可以将这个二次方程表示为状态空间方程的形式：x' = x + 0*yy' = -a*x^2 - b*x - cx'和y'分别代表状态变量x和y的变化率。
通过这样的表示，我们可以更清晰地理解二次方程在不同状态下的演变过程。
值得注意的是，状态空间方程对于二次方程的表示并非唯一的。
我们可以根据系统的特点和需求来选择不同的状态变量和方程形式，以便更好地理解和分析二次方程。
通过状态空间方程的表示，我们可以更深入地了解二次方程的性质和行为规律，为进一步的数学研究和应用提供更多的可能性。
第二篇示例：状态空间方程是描述系统动态行为的一种数学工具，它将系统的输入、输出和状态之间的关系以矩阵形式表示，通常用于控制系统的分析与设计。
在控制理论中，线性动态系统通常可以用状态空间方程表示，其中最典型的就是二次方程系统。
本文将介绍二次方程系统的状态空间方程表示，并探讨其性质及应用。
二次方程是一种具有最高次为二次的多项式方程，通常表示为：\[ a x^2 + b x + c = 0 \]其中\(a\), \(b\), \(c\)是系数，\(x\)是变量。
这类方程在数学和物理中有着广泛的应用，比如在力学中描述自由落体运动、在电路分析中描述振动系统等等。
二次方程系统可以用状态空间方程表示为：其中\(x\)是状态向量，\(\dot{x}\)是状态向量的导数，\(u\)是输入向量，\(y\)是输出向量，\(A\), \(B\), \(C\), \(D\)分别是状态空间方程的系数矩阵。
2-控制系统状态变量法建模21
态。
➢ 随着时间的推移,状态不断地变化,tt0各瞬时的状态在状 态空间构成一条轨迹,它称为状态轨线。
➢ 状态轨线如图2-2所示。
系统的状态空间模型(1/11)
2.1.2 系统的状态空间模型
状态空间模型是应用状态空间分析法对动态系统所建立的一 种数学模型,它是应用现代控制理论对系统进行分析和综合的 基础。 ➢ 状态空间模型由 ✓ 描述系统的动态特性行为的状态方程和 ✓ 描述系统输出变量与状态变量间的变换关系的输出 方程 所组成。 ➢ 下面以一个由电容、电感等储能元件组成的二阶RLC电 网络系统为例,说明状态空间模型的建立和形式,然后再进 行一般的讨论。
定义2-1 动态系统的状态,是指能够完全描述系统时间域动态 行为的一个最小变量组。 ➢ 该变量组的每个变量称为状态变量。 ➢ 该最小变量组中状态变量的个数称为系统的阶数。
系统的状态和状态变量(2/5)
“状态”定义的三要素
➢ 完全描述。即给定描述状态的变量组在初始时刻(t=t0)的 值和初始时刻后(tt0)的输入,则系统在任何瞬时(tt0)的行 为,即系统的状态,就可完全且唯一的确定。
系统的状态空间(1/1)
2. 系统的状态空间
x2 x(t0)
x(t1)
若以n个状态变量x1(t),x2(t),…,xn(t)
为坐标轴,就可构成一个n维欧氏空
x(t2)
间,并称为n维状态空间,记为Rn.
x(t)
状态向量的端点在状态空间中的位 置,代表系统在某一时刻的运动状
x1 图2-2 二维空间的状态轨线
概述(12/12)
状态和状态空间模型(1/2)
2.1 状态和状态空间模型
系统的状态空间模型是建立在状态和状态空间概念的基础上 的,因此,对这些基本概念进行严格的定义和相应的讨论,必须 准确掌握和深入理解。 ➢ 状态 ➢ 状态变量 ➢ 状态空间 ➢ 状态空间模型
现代控制理论课后答案(俞立)第五章
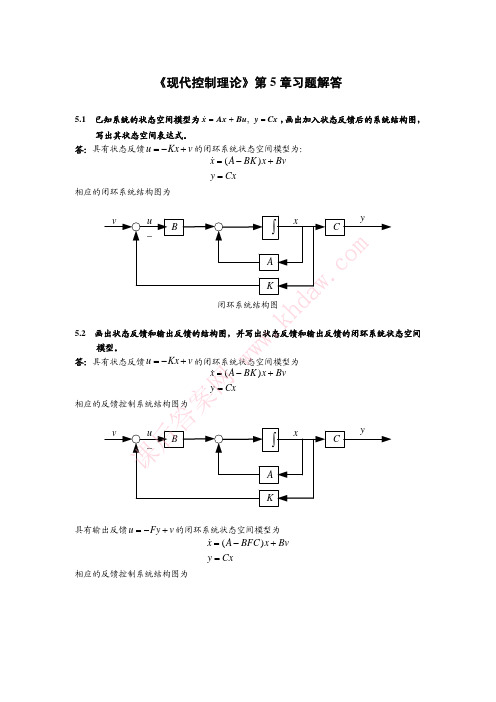
《现代控制理论》第5章习题解答5.1 已知系统的状态空间模型为Cx y Bu Ax x =+=, ，画出加入状态反馈后的系统结构图，写出其状态空间表达式。
答：具有状态反馈的闭环系统状态空间模型为：u Kx =−+v ()xA BK x Bv y Cx=−+=相应的闭环系统结构图为闭环系统结构图5.2画出状态反馈和输出反馈的结构图，并写出状态反馈和输出反馈的闭环系统状态空间模型。
答：具有状态反馈的闭环系统状态空间模型为u Kx =−+v ()xA BK x Bv y Cx=−+=相应的反馈控制系统结构图为具有输出反馈的闭环系统状态空间模型为u Fy =−+v ()x A BFC x Bv y Cx=−+=相应的反馈控制系统结构图为后案网 ww w.kh d5.3 状态反馈对系统的能控性和能观性有什么影响？输出反馈对系统能控性和能观性的影响如何？答：状态反馈不改变系统的能控性，但不一定能保持系统的能观性。
输出反馈不改变系统的能控性和能观性。
5.4 通过检验能控性矩阵是否满秩的方法证明定理5.1.1。
答：加入状态反馈后得到闭环系统K S ，其状态空间模型为()x A BK x Bv y Cx=−+=开环系统的能控性矩阵为0S 1[,][]n c A B BAB A B −Γ="闭环系统K S 的能控性矩阵为 1[(),][()()]n cK A BK B B A BK B A BK B −Γ−=−−"由于222()()()()(A BK B AB BKBA BKB A ABK BKA BKBK B)A B AB KB B KAB KBKB −=−−=−−+=−−−#以此类推，总可以写成的线性组合。
因此，存在一个适当非奇异的矩阵U ，使得()m A BK B −1,,,m m A B A B AB B −[(),][,]cK c A BK B A B U Γ−=Γ由此可得：若rank([,])c A B n Γ=，即有个线性无关的列向量，则n [(),]cK A BK B Γ−也有个线性无关的列向量，故n rank([(),])cK A BK B n Γ−=5.5 状态反馈和输出反馈各有什么优缺点。
计算机控制系统---第三章
的z变换。
解：
另一种由F(s) 求取F(z) 的方法是留数计算方法。本书对此不予讨论
利用MATLAB软件中的符号语言工具箱进行F(s)部分 分式展开
已知
，通过部分分式展开法求F(z) 。
MATLAB程序：
F=sym(′(s+2)/(s*(s+1)^2*(s+3))′)； %传递函数F(s)进行符号定义
即得到
3.4.4 干扰作用时闭环系统的输出
根据线性系统叠加定理，可分别计算指令信号和干扰信号作用下的输出响应。
G(z)
Z
1
esT s
G1(s)G2 (s)
R(s)单独作用时的 系统输出[N(s)=0]
干扰单独作用时的 系统输出[R(s)=0]
共同作用时的系 统输出
图3-13 有干扰时的计算机控制系统
图3-10采样控制系统典型结构
一般系统输出z变换可按以下公式直接给出：
C(z)
前向通道所有独立环节z变换的乘积 1闭环回路中所有独立环节z变换的乘积
3.4.3 计算机控制系统的闭环脉冲传递函 数
1. 数字部分的脉冲传递函数
控制算法，通常有以下两种形式：
差分方程
脉冲传递函数D(z)
(z变换法)
连续传递函数
2. 由脉冲传递函数求差分方程
z反变换
z反变换
3.4.1 环节串联连接的等效变换
1. 采样系统中连续部分的结构形式
并不是所有结构都能写出环节的脉冲传递函数
3.4.1 环节串联连接的等效变换
2. 串联环节的脉冲传递函数
3.4.1 环节串联连接的等效变换
3. 并联环节的脉冲传递函数
根据叠加定理有：
状态方程的参数
状态方程的参数简介状态方程是描述动态系统行为的数学模型，它通过表示系统的状态和状态变化的方程来描述系统的演化规律。
状态方程的参数是指在状态方程中出现的变量和常数。
这些参数决定了系统的特性和行为，对于系统的分析和控制至关重要。
在本文中，我们将介绍状态方程的基本概念和常见形式，然后详细讨论状态方程的参数，包括变量和常数的定义、物理意义、取值范围以及对系统行为的影响。
状态方程的基本概念状态方程描述了系统的状态随时间的演化规律。
一般来说，状态方程可以写成如下形式：dx/dt = f(x, u, t)其中，x是系统的状态向量，u是系统的输入向量，t是时间，f是状态方程的右侧函数。
状态方程可以是线性或非线性的，具体形式取决于系统的性质和特点。
状态方程的参数包括状态向量x中的变量和常数，以及右侧函数f中的变量和常数。
下面我们将分别讨论这些参数的定义和物理意义。
状态向量的参数状态向量x是描述系统状态的一组变量。
它的具体定义和物理意义取决于系统的性质和特点。
下面是一些常见的状态向量及其参数的例子：•位置向量：描述物体在空间中的位置，参数包括物体在三个坐标轴上的位置变量（例如x、y、z）。
•速度向量：描述物体在空间中的速度，参数包括物体在三个坐标轴上的速度变量（例如v_x、v_y、v_z）。
•电路变量：描述电路中的电流和电压，参数包括电流和电压变量（例如i、v）。
状态向量的参数在状态方程中起到了关键的作用。
它们决定了系统的状态空间的维度和范围，以及状态变化的规律。
不同的参数可以对系统的行为产生不同的影响。
右侧函数的参数右侧函数f描述了状态向量x随时间的变化规律。
它的具体定义和物理意义也取决于系统的性质和特点。
下面是一些常见的右侧函数及其参数的例子：•线性函数：描述线性系统的状态变化规律，参数包括状态向量x、输入向量u和常数矩阵。
•非线性函数：描述非线性系统的状态变化规律，参数包括状态向量x、输入向量u和非线性函数。
mpc 控制 python例子
一、介绍MPC控制算法1.1 MPC控制算法的概念1.2 MPC控制算法的应用场景1.3 MPC控制算法的优势二、MPC控制算法的原理2.1 状态空间模型2.2 控制问题的建模2.3 预测模型2.4 控制优化三、使用Python实现MPC控制算法3.1 Python在控制领域的应用3.2 Python库介绍3.3 使用Python实现MPC控制算法的步骤四、MPC控制算法的应用案例4.1 汽车自动驾驶4.2 工业过程控制4.3 机器人运动控制五、结语一、介绍MPC控制算法MPC（Model Predictive Control）是一种常见的控制算法，它可以用来解决多种实时控制问题。
MPC控制算法基于系统的动态模型，可以预测未来的系统行为，并基于这些预测进行优化控制。
MPC控制算法最早被用于化工领域，随后逐渐被应用于机器人、汽车、飞行器等领域。
1.1 MPC控制算法的概念MPC控制算法是一种基于模型的预测控制算法，它通过对系统的动态行为进行预测，从而获得最优的控制方案。
MPC控制算法的核心思想是使用一个预测模型来预测系统的未来行为，并基于这些预测进行优化控制，以达到系统稳定、性能优良的控制目标。
1.2 MPC控制算法的应用场景MPC控制算法在许多领域都有广泛的应用，包括但不限于汽车自动驾驶、工业过程控制、机器人运动控制等。
MPC控制算法能够处理多输入多输出（MIMO）系统，适用于非线性系统，并且对控制系统的不确定性和扰动具有较强的鲁棒性。
1.3 MPC控制算法的优势MPC控制算法的优势在于其能够处理多输入多输出系统以及非线性系统，并且能够对系统的不确定性和扰动进行较为有效的补偿。
MPC控制算法还可以灵活地应对各种控制约束条件，并且具有较高的稳定性和鲁棒性。
二、 MPC控制算法的原理MPC控制算法的核心原理包括状态空间模型、控制问题的建模、预测模型和控制优化。
2.1 状态空间模型MPC控制算法基于系统的状态空间模型进行建模和预测。
卡尔曼(Kalman)滤波
第4章 卡尔曼（Kalman ）滤波卡尔曼滤波的思想是把动态系统表示成状态空间形式，是一种连续修正系统的线性投影算法。
功能 1） 连续修正系统的线性投影算法。
2）用于计算高斯ARMA 过程的精确有限样本预测和精确的似然函数。
3） 分解矩阵自协方差生成函数或谱密度。
4）估计系数随时间变化的向量自回归。
第一节 动态系统的状态空间表示一．假设条件令t y 表示时期t 观察到变量的一个()1n ×向量。
则t y 的动态可以用不可观测的()1r ×向量t ξ来表示，t ξ为状态向量。
t y 的动态系统可以表示为如下的状态空间模型：11t t t F v ξξ++=+ （1）t t t t y A x H w ξ′′=++ （2）其中′′F,A ,H 分别为()r r ×，()n k ×和()n r ×矩阵，t x 是外生变量或前定变量的()1k ×向量。
方程（1）称为状态方程，方程（2）称为观察方程。
其中()1r ×向量t v 和()1n ×向量t w 为向量白噪声：()()00t t Qt E v v t R t E w w t ττττττ=⎧′=⎨≠⎩=⎧′=⎨≠⎩ （3）其中,Q R 为()(),r r n n ××矩阵。
假定扰动项t v 和t w 在所有阶滞后都不相关：()0t t E v w ′= 对所有的t 和τ （4）t x 为前定或外生变量，意味着对0,1,2,....,s =除包含在121,,...,t t y y y −−之内的信息外，t x 不再能提供关于t s ξ+以及t s w +的任何信息。
即t x 可能包含y 的滞后值或所有与τ、τξ和w τ不相关变量。
状态空间系统描述有限观察值序列{}1,...,T y y ，需要知道状态向量的初始值1ξ，根据状态方程（1），t ξ可写作()123,,,...,t v v v ξ的线性函数： 2211221....t t t t t t v Fv F v F v F ξξ−−−−=+++++ 2,3,...,t T = （5）这里假定1ξ与t v 和t w 的任何实现都不相关：()()1101,2,...,01,2,...,t t E v TE w Tξτξτ′==′== （6）根据（3）和（6），得t v 和ξ的滞后值不相关：()0t E v τξ′= 1,2,...,1t t τ=−− （7） ()0t E w τξ′= 1,2,...,T τ= （8） ()()()0t t E w y E w A x H w ττττξ′′′=++= 1,2,...,1t t τ=−− （9） ()0t E v y τ′= 1,2,...,1t t τ=−− （10）二．状态空间系统的例子例1 ()AR p 过程，()()()112111...t t t p t p t y y y y µφµφµφµε+−−++−=−+−++−+ （11）()2t t E t τστεετ⎧==⎨≠⎩ （12） 可以写作状态空间形式。
现代控制理论浙江工业大学
0
⎥ ⎦
⎢⎣−
yr
0
⎥ ⎦
即x和q趋向于常值。从而 x&(t) 和 q&(t) 趋于零。
q&(t) = y(t) − yr (t)
⇒
lim[ y(t)
t→∞
−
yr
(t)]
=
0
结论：针对增广系统，设计状态反馈控制律，只要闭
环系统渐近稳定，则系统无静态误差。
若还需要系统有一定的过渡过程特性，极点配置！
条件：能任意配置极点的条件是增广系统能控。
S1 ⎤
0
⎥ ⎦
其中S1 = [B AB L An−1B L An+r−2 B] 是n × (n + r − 1)m
原系统的能控性 ⇒
[B AB L An−1B] 的行向量线性无关。
⎡0
⎢ ⎣
I
S1 0
⎤ ⎥ ⎦
行满秩
⇒
⎛⎡A
rank
⎜ ⎝
⎢⎣C
B⎤ 0 ⎥⎦
⎞ ⎟ ⎠
=
n
+
r
必要条件：m ≥ r, rank(C) = r
9 系统是稳定的，且具有一定过渡过程特性；
9 在存在扰动下，系统输出跟踪参考输入。
定义误差向量：e(t) = y(t) − yr (t)
引入偏差的积分：
∫ q(t) = t e(τ )dτ 0
引入了积分器
q&(t) = e(t) = Cx(t) − yr (t)
对多输入系统：
∫ ∫ ∫ qT (t) =[q1(t)
0
⎢⎡b1K 1]⎢
⎢ ⎢⎣
+
b2
KA~ + KA~2 b2 K + KA~
lsim在matlab中的用法
lsim在matlab中的用法Lsim函数是MATLAB中用于对动态系统进行时间域仿真和响应分析的函数。
本文将详细介绍Lsim函数的使用方法和步骤。
MATLAB是一种非常强大的数值计算和仿真工具，可以用于各种工程和科学应用。
在系统动力学中，我们经常需要对线性时不变（LTI）系统进行分析，以评估其时间域响应。
Lsim函数就是一个非常有用的工具，可以简化这一过程。
Lsim函数的基本语法如下：matlablsim(sys, u, t)其中，sys是系统的传递函数或状态空间模型，u是系统的输入信号，t是所需模拟的时间点。
下面将一步一步介绍如何使用Lsim函数进行系统响应分析。
第一步是定义系统模型。
在MATLAB中，我们可以使用tf函数定义传递函数模型，也可以使用ss函数定义状态空间模型。
传递函数模型由分子和分母多项式系数组成，而状态空间模型由矩阵A、B、C和D定义。
以下是一个例子，演示如何定义传递函数模型和状态空间模型：matlab定义传递函数模型num = [1]; 分子多项式系数den = [1, 2, 1]; 分母多项式系数sys_tf = tf(num, den);定义状态空间模型A = [-1, -2; 0, -3]; 矩阵AB = [1; 0]; 矩阵BC = [1, 0]; 矩阵CD = 0; 矩阵Dsys_ss = ss(A, B, C, D);第二步是定义输入信号。
Lsim函数可以通过输入信号来模拟系统的响应。
输入信号可以是函数句柄、向量或矩阵。
以下是一些示例输入信号的定义方法：matlab步输入u_step = ones(size(t));脉冲输入u_impulse = zeros(size(t));u_impulse(1) = 1;正弦输入u_sine = sin(t);方波输入u_square = square(t);随机输入u_random = randn(size(t));第三步是定义仿真的时间点。
受控自回归模型与状态空间模型关系
受控自回归模型与状态空间模型关系一、引言受控自回归模型（CAR）和状态空间模型（SSM）是时间序列分析中常用的两种模型。
它们都能够对时间序列数据进行建模和预测，但在实际应用中经常会有一些混淆，因此有必要对它们的关系进行深入的探讨和理解。
二、受控自回归模型（CAR）简介受控自回归模型是一种常用的时间序列分析模型，它是自回归模型（AR）的一种特例。
在受控自回归模型中，时间序列数据的观测值被认为是来自一个线性模型的输出，该模型是通过将一个或多个外部输入变量的线性组合和滞后观测值进行求和而得到的。
通常情况下，受控自回归模型是通过对自回归模型进行拓展，引入外部输入变量和滞后观测值来增强建模能力的。
三、状态空间模型（SSM）简介状态空间模型是一种描述时间序列结构的统计模型，它包括状态方程和观测方程两部分。
状态方程描述了时间序列的内在动态演化规律，而观测方程则描述了观测数据与状态之间的联系。
状态空间模型的优势在于能够处理缺失数据、噪声干扰和非线性关系等实际问题，因此在实际应用中被广泛使用。
四、受控自回归模型与状态空间模型的关系受控自回归模型和状态空间模型在某种程度上存在联系和相互影响。
从模型结构来看，受控自回归模型可以看作是状态空间模型的一个特例，它将外部输入变量和滞后观测值引入到状态方程中，增强了模型的表达能力。
另外，受控自回归模型也可以被看作是状态空间模型的观测方程部分，因为它描述了观测数据与状态的关系。
在实际应用中，受控自回归模型和状态空间模型可以相互转化和组合使用。
在建模过程中，可以先使用受控自回归模型对时间序列数据进行建模，然后利用状态空间模型对模型的隐含状态进行推断和预测。
这样可以兼顾受控自回归模型的建模灵活性和状态空间模型对动态演化规律的描述能力，从而获得更准确的预测结果。
个人观点与理解对于受控自回归模型和状态空间模型的关系，我个人认为两者是相辅相成的。
受控自回归模型通过引入外部输入变量和滞后观测值增强了建模能力，而状态空间模型则能够对模型的动态演化规律进行更精确的描述。
不可约马尔可夫链例子
不可约马尔可夫链例子
不可约马尔可夫链是指状态之间不存在转移的情况，即任何状态都无法到达其他状态。
一个简单的例子是骰子游戏，如果只能掷出1和2，那么在任何一轮游戏中，只有两种状态可以出现：掷出1和掷出2，它们之间没有转移的可能性。
因此，这个骰子游戏的状态空间就是一个不可约的马尔可夫链。
除了骰子游戏，还有很多其他的不可约马尔可夫链，例如某些游戏中的胜者和输者状态、物理系统中的固定结构和序列状态等。
在实际生活和科学研究中，不可约马尔可夫链的存在性经常会对模型的建立和分析产生影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1965
1970
1975
1980
Series 2
0
5
10
1955
1960
1965
1970
1975
1980
#library(dse) my2=TSdata(output=newdat[,3,drop = F]) my2=tframed(my2, list(start=c(1953,1), frequency=4))
library(dse) my=TSdata(input= newdat[,3,drop = F],output=newdat[, 2,drop = F]) my=tframed(my, list(start=c(1953,1), frequency=4)) seriesNamesInput(my)="CPI" seriesNamesOutput(my)="BILLS"
seriesNamesInput(my)="CPI" seriesNamesOutput(my)="BILLS“ bb=estBlackBox(my,g=3) #lag=?!!! tfplot(bb) bb$model #Giving F, G, H, K bb$estimates #giving $cov, $like, $pred attributes(bb)#model #看结果
Step 4: Kalman Filter Filtering, Smoothing, and Forecasting
• FKF: using R function fkf • Shumway using functions Kfilter0, Ksmooth0, Kfilter1, Ksmooth1, Kfilter2, Ksmooth2 • dlm: using function dlmFilter, dlmSmooth, dlmFilterdlmForecast • dse: using functions such as forecast, featherForecasts, horizonForecasts, etc Note: you have to pay attention to the meanings of the output!
Step 2: Log Likelihood Function
• FKF: write function such as objective to create log likelihood function • Shumway: write function via Kfilter0, Kfilter1, Kfilter2 to create log likelihood function • dlm: write function such as buildFun
状态空间模型及例子
吴喜之
Models and Computation Steps for State-Space Model
Sources (for four packages): Package: FKF, related article (not for R, but having formulas): /p/dgr/kubcen/1998141.html (file3826.pdf) Package: dlm dlm.pdf (in R project or your R directory) Package: Shumway: /stoffer/tsa2/chap6.htm Package: dse In your R directory : dse-guide.pdf and article: http://www.bank-banque-canada.ca/pgilbert/gil93.pdf
ans <- fkf(a0 = c(0, 0), P0 = diag(c(10, 10)), dt = rbind(0, 0), ct = matrix(0), Tt = matrix(c(ar1, 1, ar2, 0), ncol = 2), Zt = cbind(1, 0), HHt = matrix(c(sigma^2, 0, 0, 0), ncol = 2), GGt = matrix(0), yt = rbind(a))
#library(dse) my1=TSdata(output=newdat[,c(3,2),drop = F]) my1=tframed(my1, list(start=c(1953,1), frequency=4)) bb1=estBlackBox(my1,g=3) tfplot(bb1) attributes(bb1)#model
Series 1
One step ahead predictions (dotted) and actual data (solid)
12
bb1$model #Giving F, H, K bb1$estimates #giving $cov, $like, $pred #看结果
0
4
8
1955
1960
Filtering, Smoothing, Forecast
• s<t: forecasting or prediction • s=t: filtering • s>t: smoothing
Kalman Filter (Forecast ): with
Prediction equations
with
0 2
4
6
bb2$model #Giving F, H, K (one dimention) bb2$estimates #giving $cov, $like, $pred
8
10
12
14
1955
1960
1965
1970
1975
1980
bb4=estVARXls(my1,g=3)#two variables (TWO output) bb4$model #Giving A(L), B(L), C(L) bb4$estimates #giving $cov, $like, $pred
Model (Shumway notation)
Transition equation and observation equation
• • • • • • •
xt : p×1 state vector N(m, S) yt : q×1 observation/measurement vector wt : p×1 system noise iid N(0,Q) vt : q×1 observation noise iid N(0,R) ut : r×1 fixed input At : q×p observation/measurement matrix F : p×p ; G : q×r, U: p×r, Q: p×p, R: q×q
updating equations where
The MSE of
is Kalman gain
Kalman Smoother: with initial
The Lag-one Covariance Smoother
With initial condition
for t=n,n-1,…,2
Three “levels” of Shumway’s models
One step ahead predictions (dotted) and actual data (solid)
bb2=estBlackBox(my2,g=3) tfplot(bb2) attributes(bb2)#model
Series 1
bb3=estVARXls(my,g=1)#two variables (one input one output) bb3$model #Giving A(L), B(L), C(L) bb3$estimates #giving $cov, $like, $pred
– dlmModARMA , dlmModPoly, dlmModReg , dlmModSeas , dlmModTrig
• dse: using functions such as ARMA, SS (can transfer to each other) to build an empty model (but)
Example: FKF
Example: FKF
#Shumway Example 6.12 newdat = read.table("f:/xzwu/2009/berkeley/ts/shumway/mydata/Newbold1.txt", comment.char="#") y = newdat[1:50,2] # quarterly inflation (column 2) z = newdat[1:50,3] # quarterly interest rates (column 3) plot(ts(y,start=c(1953,1),frequency=1)) points(ts(y,start=c(1953,1),frequency=1),type='p',pch=15) lines(ts(z,start=c(1953,1),frequency=1),lty=2) points(ts(z,start=c(1953,1),frequency=1),type='p',pch=18)
One step ahead predictions (dotted) and actual data (solid) bb=estBlackBox(my,g=3) #lag=?!!! tfplot(bb)
15 Series 1 0 5 10