三种常用的不同变量之间相关系数的计算方法
相关系数和协方差的计算公式

相关系数和协方差的计算公式
相关系数和协方差是统计学中常用的两个概念,用于衡量两个变量之间的关联程度。
相关系数是一个介于-1到1之间的数值,用来衡量两个变量之间的线性关系强度和方向。
协方差则是一个描述两个变量之间关系的统计量。
相关系数的计算公式如下:
相关系数 = 协方差 / (变量1的标准差 * 变量2的标准差)
其中,协方差的计算公式如下:
协方差= Σ((变量1的值 - 变量1的均值) * (变量2的值 - 变量2的均值)) / 样本数
相关系数和协方差的计算公式可以帮助我们衡量两个变量之间的关联程度。
相关系数的取值范围为-1到1,当相关系数接近1时,表示两个变量之间存在强正相关关系;当相关系数接近-1时,表示两个变量之间存在强负相关关系;当相关系数接近0时,表示两个变量之间不存在线性关系。
协方差的取值范围为负无穷到正无穷,协方差的正负表示了两个变量之间的关系方向。
当协方差为正时,表示两个变量呈正相关关系;当协方差为负时,表示两个变量呈负相关关系;当协方差接近于0时,表示两个变量之间不存在线性关系。
通过计算相关系数和协方差,我们可以得出两个变量之间的关联程度。
这些概念和计算公式在统计学和数据分析中有着广泛的应用,可以帮助我们理解和解释变量之间的关系,从而做出更准确的预测和决策。
无论是在科学研究、经济分析还是市场营销等领域,相关系数和协方差都是非常重要的工具。
通过运用相关系数和协方差的计算公式,我们可以更好地理解数据背后的规律和趋势,从而做出更明智的决策。
数据分析中的相关系数计算方法

数据分析中的相关系数计算方法数据分析是一种重要的工具,可以帮助我们理解数据之间的关系。
而相关系数是衡量两个变量之间相关性强弱的指标之一。
在数据分析中,计算相关系数是一个常见的任务。
本文将介绍一些常用的相关系数计算方法。
一、皮尔逊相关系数(Pearson correlation coefficient)皮尔逊相关系数是最常见的相关系数计算方法之一。
它衡量的是两个变量之间的线性相关性。
皮尔逊相关系数的取值范围是-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关。
计算皮尔逊相关系数的公式如下:r = cov(X, Y) / (σX * σY)其中,cov(X, Y)表示X和Y的协方差,σX和σY分别表示X和Y的标准差。
二、斯皮尔曼相关系数(Spearman correlation coefficient)斯皮尔曼相关系数是一种非参数的相关系数计算方法,它衡量的是两个变量之间的单调关系,不仅仅局限于线性关系。
斯皮尔曼相关系数的取值范围也是-1到1,具有和皮尔逊相关系数相似的解释。
计算斯皮尔曼相关系数的公式如下:ρ = 1 - (6 * Σd^2) / (n * (n^2 - 1))其中,d表示X和Y的等级差,n表示样本数量。
三、切比雪夫相关系数(Chebyshev correlation coefficient)切比雪夫相关系数是一种衡量两个变量之间的最大差异的相关系数计算方法。
它不仅考虑了线性关系,还考虑了非线性关系。
切比雪夫相关系数的取值范围是0到1,其中0表示无相关,1表示完全相关。
计算切比雪夫相关系数的公式如下:r = max(|Xi - Yi|) / max(|Xi - Xj|)其中,Xi和Yi表示X和Y的观测值,Xj表示X的观测值。
四、肯德尔相关系数(Kendall correlation coefficient)肯德尔相关系数是一种衡量两个变量之间的等级关系的相关系数计算方法。
三种常用的不同变量之间相关系数的计算方法
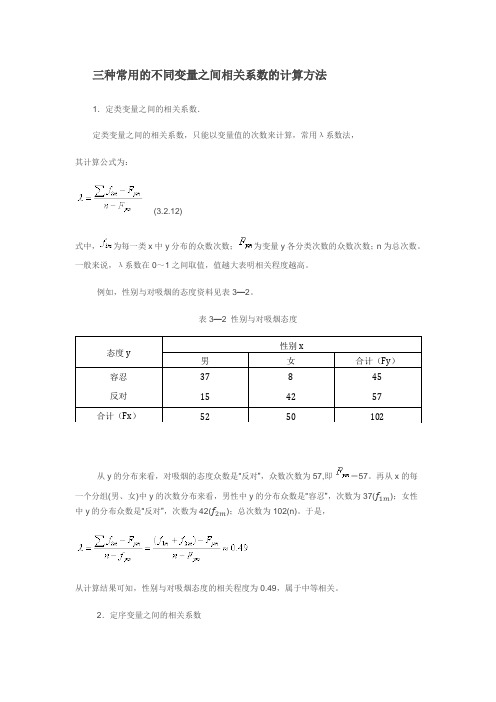
三种常用的不同变量之间相关系数的计算方法1.定类变量之间的相关系数.定类变量之间的相关系数,只能以变量值的次数来计算,常用λ系数法,其计算公式为:(3.2.12)式中,为每一类x中y分布的众数次数;为变量y各分类次数的众数次数;n为总次数。
一般来说,λ系数在0~1之间取值,值越大表明相关程度越高。
例如,性别与对吸烟的态度资料见表3—2。
表3—2 性别与对吸烟态度态度y性别x男女合计(Fy)容忍反对37158424557合计(Fx)52 50 102从y的分布来看,对吸烟的态度众数是“反对”,众数次数为57,即=57。
再从x的每一个分组(男、女)中y的次数分布来看,男性中y的分布众数是“容忍”,次数为37(f1m);女性中y的分布众数是“反对”,次数为42(f2m);总次数为102(n)。
于是,从计算结果可知,性别与对吸烟态度的相关程度为0.49,属于中等相关。
2.定序变量之间的相关系数定序变量之间的相关测量常用Gamma系数法和Spearman系数法。
Gamma系数法计算公式为:(3.2.13)式中,G为系数;Ns为同序对数目;Nd为异序对数目。
所谓序对是指表明高低位次的两两配对,如果一对个案在变量x,y的分类表现位次一致,则为同序对;如果位次相反,则为异序对。
G系数取值在—1--十1之间。
G=1,表示完全正相关;G=-1,表示完全负相关;G=0,表示完全不相关;-1<G<0,表示负相关;0<G<1,表示正相关。
Spearman系数法计算公式为:(3.2.14)式中,P为系数;D为所测定的两个数列中每对项目之间的登记差,这个差的正值之和等于负值之和;N为项数。
系数p主要代表两个定序变量的等级相关程度,其取值范围和相关程度含义与G系数相同。
3.定距变量之间的相关系数定距变量之间的相关测量常用Pearson系数法。
对于未分组资料,Pearson系数法计算公式为:对于已分组资料,Pearson系数法计算公式为r系数取值范围和相关程度的含义与G系数相同。
简述3种常用的相关分析方法。

简述3种常用的相关分析方法。
三种常用的相关分析方法是皮尔森相关系数、Spearman等级相关系数和Kendall’s Tau测度。
皮尔森相关系数(Pearson’s correlation coefficient)是测量变量之间的线性关系度量值,它的取值范围从-1到+1。
数值正负表示两个变量之间的相关性正向或负向,其可以用来衡量两个变量之间线性相关性。
Spearman等级相关系数(Spearman rank correlation coefficient)是一种常用的非线性相关系数,如果两个变量无法观测到线性关系,则可以使用Spearman相关系数来度量。
按Spearman等级相关系数测量,两个变量之间的相关程度介于-1到+1之间,正负表示两个变量之间的关系为正向或负向。
Kendall's Tau测度(Kendall's tau coefficient)也叫Kendall比率相关系数,是一种测量变量之间的非线性关系的特殊方法,它使用变量的排好名次或排序来计算两个变量之间的相关性,是一种不太普遍但有较好的效果的非参数检验的衡量指标。
它的取值范围也是从-1到+1,正负表示两个变量之间的关系为正向或负向。
以上三种方法是常用的相关分析方法,它们不仅可以衡量两个变量之间的相关性,还能发现数据之间有规律性的潜在关系。
因此,它们在实证分析和统计学中被广泛利用,帮助研究者更深入地了解数据,发现数据中未知的信息。
不同指标之间的相关系数

不同指标之间的相关系数1.引言概述部分的内容可以参考以下写法:1.1 概述相互关联的数据和指标在许多研究领域和实际应用中起着重要作用。
相关系数是衡量两个变量之间关联程度的统计量,用于揭示变量之间的线性关系。
在统计学和数据分析中,相关系数是一种常用的工具,用于确定数据之间的关联性强弱。
不同指标之间的相关系数研究是为了深入理解指标之间的相互关联性,帮助我们从统计角度分析指标之间的内在联系。
在许多领域,如经济学、金融学和社会科学,研究人员常常使用相关系数来揭示变量之间的关系。
通过计算不同指标之间的相关系数,我们可以了解各指标之间的紧密程度和变动趋势,进而对数据进行更深入的分析和预测。
本文将通过对相关系数的定义、计算方法和应用进行详细阐述,旨在帮助读者更好地理解不同指标之间的关系,并在实际应用中灵活运用。
同时,本文还将总结不同指标之间的相关系数的含义和应用,以及对文中所讨论内容的简要总结与评述。
综上所述,本文旨在探讨不同指标之间的相关系数,通过研究相关系数的概念、计算方法和应用,帮助读者更好地理解变量之间的关联性,为进一步的研究和实际应用提供基础。
在下面的章节中,我们将逐步展开相关内容的讨论。
1.2文章结构文章结构部分主要介绍本文的章节组成和内容安排,使读者能够清晰地了解整篇文章的结构和主要内容。
本文的文章结构如下所示:2. 正文:2.1 相关系数的定义和意义:- 介绍相关系数的概念和作用;- 说明相关系数在统计学和数据分析中的重要性;- 探讨相关系数在不同领域中的应用。
2.2 相关系数的计算方法:- 介绍不同类型的相关系数,如皮尔逊相关系数、斯皮尔曼相关系数等;- 分别阐述各种相关系数的计算方法和适用场景;- 通过具体案例说明相关系数的计算过程和结果解读。
3. 结论:3.1 不同指标之间的相关系数的意义和应用:- 总结各种相关系数的定义、计算方法和意义;- 分析不同指标之间相关系数的值的大小和方向对数据分析的影响;- 探讨相关系数的应用于实际问题中的实用性和局限性。
统计学中的相关系数计算方法

统计学中的相关系数计算方法统计学是一门重要的学科,广泛应用于各个领域,包括经济学、社会学、生物学等等。
在统计学中,相关系数是一种常用的分析工具,用于评估两个变量之间的线性关系强度和方向。
而正确计算相关系数是非常重要的,因为它们能够提供有关变量之间关系的有价值的信息。
本文将介绍两种常见的相关系数计算方法——皮尔逊相关系数和斯皮尔曼相关系数。
1. 皮尔逊相关系数皮尔逊相关系数是最常用的相关系数之一,用来测量两个连续变量之间的线性关系强度。
它的取值范围在-1到1之间,其中-1表示完全负相关,1表示完全正相关,0表示没有线性关系。
皮尔逊相关系数的计算公式如下:\[ r = \frac{{\sum{(X_i-\bar{X})(Y_i-\bar{Y})}}}{{\sqrt{\sum(X_i-\bar{X})^2}\sqrt{\sum(Y_i-\bar{Y})^2}}} \]其中,\( X_i \) 是第一个变量的第i个观测值,\( Y_i \) 是第二个变量的第i个观测值,\( \bar{X} \) 是第一个变量的均值,\( \bar{Y} \) 是第二个变量的均值。
通过计算样本数据的协方差和两个变量的标准差来得到相关系数。
2. 斯皮尔曼相关系数斯皮尔曼相关系数用于评估两个变量之间的单调关系,即不仅仅限于线性关系。
它通过对两个变量的秩次进行计算,将原始数据转换为秩次数据,从而避免了对原始数据的要求。
斯皮尔曼相关系数的计算公式如下:\[ \rho = 1 - \frac{{6\sum{d_i^2}}}{{n(n^2-1)}} \]其中,\( d_i \) 是两个变量的秩次差值,n是样本观测值的个数。
斯皮尔曼相关系数的取值范围也在-1到1之间,其中-1表示完全负相关,1表示完全正相关,0表示没有单调关系。
3. 相关系数的解读无论使用皮尔逊相关系数还是斯皮尔曼相关系数,对于相关系数的解读,需要了解以下几点:- 当相关系数接近-1或1时,表示存在强相关性。
相关系数的三种计算公式

相关系数的三种计算公式
相关系数r的计算公式是ρXY=Cov(X,Y)/√[D(X)]√[D(Y)]。
公式描述:公式中Cov(X,Y)为X,Y的协方差,D(X)、D(Y)分别为X、Y的方差。
若Y=a+bX,则有:
令E(X) =μ,D(X) =σ。
则E(Y) = bμ+a,D(Y) = bσ。
E(XY) = E(aX + bX) = aμ+b(σ+μ)。
Cov(X,Y) = E(XY)E(X)E(Y) = bσ。
缺点
需要指出的是,相关系数有一个明显的缺点,即它接近于1的程度与数据组数n相关,这容易给人一种假象。
因为,当n较小时,相关系数的波动较大,对有些样本相关系数的绝对值易接近于1。
三个相关性系数(pearson, spearman, kendall)反应的都是两个变量之间变化趋势的方向以及程度,其值范围为-1到+1,0表示两个变量不相关,正值表示正相关,负值表示负相关,值越大表示相关性越强。
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量,一般用字母r表示。
由于研究对象的不同,相关系数有多种定义方式,较为常用的是皮尔逊相关系数。
相关系数的绝对值越大,相关性越强:相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱
相关系数0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
对于x,y之间的相关系数r :
当r大于0小于1时表示x和y正相关关系当r大于-1小于0时表示x和y负相关关系。
影像组学相关系数计算公式

影像组学相关系数计算公式影像组学是一种利用医学影像数据进行分析和研究的新兴学科,它可以帮助医生更好地诊断疾病、制定治疗方案和预测疾病的发展趋势。
在影像组学中,相关系数是一种常用的统计方法,用于衡量两个变量之间的相关程度。
在医学影像中,相关系数可以帮助研究人员分析不同影像特征之间的关联,从而更好地理解疾病的发展规律和预测疾病的风险。
相关系数的计算公式是影像组学研究中的重要内容之一。
在影像组学中,常用的相关系数计算公式包括皮尔逊相关系数、斯皮尔曼相关系数和肯德尔相关系数。
下面我们将分别介绍这三种相关系数的计算公式及其应用。
1. 皮尔逊相关系数计算公式。
皮尔逊相关系数是一种衡量两个连续变量之间线性相关程度的方法,它的计算公式如下:r = Σ((X_i X_mean) (Y_i Y_mean)) / (sqrt(Σ(X_i X_mean)^2) sqrt(Σ(Y_iY_mean)^2))。
其中,r表示皮尔逊相关系数,X_i和Y_i分别表示两个变量的取值,X_mean和Y_mean分别表示两个变量的均值。
通过计算皮尔逊相关系数,可以得到两个变量之间的线性相关程度,其取值范围为-1到1,当r为1时表示完全正相关,当r为-1时表示完全负相关,当r为0时表示无相关。
在医学影像组学中,皮尔逊相关系数常用于分析不同影像特征之间的线性关联,从而帮助研究人员理解疾病的发展规律和预测疾病的风险。
例如,研究人员可以利用皮尔逊相关系数来分析肿瘤影像特征与患者临床表现之间的关联,从而帮助医生更好地制定治疗方案和预测患者的预后。
2. 斯皮尔曼相关系数计算公式。
斯皮尔曼相关系数是一种衡量两个变量之间非线性关联程度的方法,它的计算公式如下:ρ = 1 ((6 Σ(d_i^2)) / (n (n^2 1)))。
其中,ρ表示斯皮尔曼相关系数,d_i表示两个变量的秩次差,n表示样本量。
通过计算斯皮尔曼相关系数,可以得到两个变量之间的非线性关联程度,其取值范围为-1到1,当ρ为1时表示完全正相关,当ρ为-1时表示完全负相关,当ρ为0时表示无相关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三种常用的不同变量之间相关系数的计算方法
1.定类变量之间的相关系数.
定类变量之间的相关系数,只能以变量值的次数来计算,常用λ系数法,
其计算公式为:
(3.2.12)
式中,为每一类x中y分布的众数次数;为变量y各分类次数的众数次数;n为总次数。
一般来说,λ系数在0~1之间取值,值越大表明相关程度越高。
例如,性别与对吸烟的态度资料见表3—2。
表3—2 性别与对吸烟态度
态度y
性别x
男女合计(Fy)
容忍反对37
15
8
42
45
57
合计(Fx)52 50 102
从y的分布来看,对吸烟的态度众数是“反对”,众数次数为57,即=57。
再从x的每
一个分组(男、女)中y的次数分布来看,男性中y的分布众数是“容忍”,次数为37(f1m);女性中y的分布众数是“反对”,次数为42(f2m);总次数为102(n)。
于是,
从计算结果可知,性别与对吸烟态度的相关程度为0.49,属于中等相关。
2.定序变量之间的相关系数
定序变量之间的相关测量常用Gamma系数法和Spearman系数法。
Gamma系数法计算公式为:
(3.2.13)
式中,G为系数;Ns为同序对数目;Nd为异序对数目。
所谓序对是指表明高低位次的两两配对,如果一对个案在变量x,y的分类表现位次一致,则为同序对;如果位次相反,则为异序对。
G系数取值在—1--十1之间。
G=1,表示完全正相关;G=-1,表示完全负相关;G=0,表示完全不相关;-1<G<0,表示负相关;0<G<1,表示正相关。
Spearman系数法计算公式为:
(3.2.14)
式中,P为系数;D为所测定的两个数列中每对项目之间的登记差,这个差的正值之和等于负值之和;N为项数。
系数p主要代表两个定序变量的等级相关程度,其取值范围和相关程度含义与G系数相同。
3.定距变量之间的相关系数
定距变量之间的相关测量常用Pearson系数法。
对于未分组资料,Pearson系数法计算公式为:
对于已分组资料,Pearson系数法计算公式为
r系数取值范围和相关程度的含义与G系数相同。
