材料力学第二章习题课资料
材料力学课后习题答案详细

变形厚的壁厚:
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ,试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ,其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
材料力学第二章课后习题参考答案2021优质ppt

①最大切应力;②单位;③公式又推导一遍。
②力的方向与变形假设不一致; 答案不能用分数、根号, 答案不能用分数、根号, 圆整b=120mm,h=165mm 答案不能用分数、根号, 圆整b=120mm,h=165mm 圆整b=120mm,h=165mm 答案不能用分数、根号, ②力的方向与变形假设不一致; 答案不能用分数、根号, 圆整b=120mm,h=165mm 圆整b=120mm,h=165mm ②力的方向与变形假设不一致; 圆整b=120mm,h=165mm 圆整b=120mm,h=165mm ②力的方向与变形假设不一致;
变形几何方程
d
2F
32.6mm
切应力
拉伸强度与剪切强度
其它: 1.书写要规范, 2.答案不能用分数、根号, 3.中间步骤过多或过少; 4.作业本不要一分为二,图要在同一侧。
圆整b=120mm,h=165mm
①思路; ②表达; ③计算结果保留数字。
①单位;②轴力图。
(3)理由阐述不准确
考虑自重时没考虑
用卡氏理
①受力图; ②力的方向与变形假设 不一致; ③步骤思路表现不清。
变形几何方程
②力的方向与变形假设不一致; ②力的方向与变形假设不一致; 答案不能用分数、根号, ②力的方向与变形假设不一致; 圆整b=120mm,h=165mm 圆整b=120mm,h=165mm ②力的方向与变形假设不一致; 答案不能用分数、根号, ②力的方向与变形假设不一致; 圆整b=120mm,h=165mm 答案不能用分数、根号, 答案不能用分数、根号, ②力的方向与变形假设不一致;
材料力学第二章习题

材料力学第二章习题2-1试绘出下列各杆的轴力图。
2-3求下列结构中指定杆的应力。
已知(b)图中杆的横截面面积A1=850 mm2,A2=600 mm2,A3=500 mm2。
2-4 求下列各杆的最大正应力。
(1)图(a)为开槽拉杆,两端受力F=10 kN,b=4mm,h=20mm,h0=10mm;2-6图示短柱,上段为钢制,截面尺寸为100×100mm2,钢的弹性模量E s=200GPa,下段为铝制,截面尺寸为200×200mm2,E a=70GPa。
当柱顶受F力作用时,柱子总长度减少了0.4mm,试求F值(注:不计杆的自重)。
2-11图示结构中,AB为刚性杆,AD为钢杆,面积A1=500mm2,弹性模量E1=200GPa;CG为铜杆,面积A2=1500mm2,弹性模量E2=100GPa;BE为木杆,面积A3=3000mm2,弹性模量E3=10GPa。
当G点受力F=60kN作用时,求该点的竖直位移ΔG。
2-13图示结构,CD 杆为刚性杆,C 端铰接于墙壁上,AB 杆为钢杆,直径d =30mm ,容许应力[]170MPa σ=,弹性模量52.010MPa E =⨯。
试求结构的容许荷载F 。
2-14图示正方形砖柱,顶端受集中力16kN F =作用,柱边长为0.4m ,砌筑在高为0.4m 的正方形块石底脚上。
已知砖的容重3116kN m g ρ=,块石容重3220kN m g ρ=。
地基容许应力[]0.08MPa σ=。
试设计正方形块石底脚的边长a 。
Fa 3m0.4m2-17图示AB 杆为刚性杆,长为3a 。
A 端铰接于墙壁上,在C 、B 两处分别用同材料、同面积的1、2两杆拉住。
在D 点受力F 作用,求1、2两杆的应力。
设弹性模量为E ,横截面面积为A 。
BF C D 12a a a aaA。
孙训方材料力学第五版1课后习题答案

第二章轴向拉伸和压缩2-1 2-2 2-3 2-4 2-5 2-6 2-7 页 2-8 2-9 下横截面上的轴力,并作轴力图。
2-1 试求图示各杆 1-1 和 2-2 横截面上的轴力,并作轴力图。
(a)解:解;;(b)解:解;;(c)解:解;。
(d) 解:。
返回上的轴力, 2-2 试求图示等直杆横截面 1-1,2-2 和 3-3 上的轴力,并作轴力图。
并作轴力图。
若横截面面积上的应力。
上的应力。
,试求各横截面解:返回 2 -3 上的轴力,试求图示阶梯状直杆横截面 1-1,2-2 和 3-3 上的轴力,并作轴力图。
作轴力图。
若横截面面积,,,并求各横截面上的应力。
并求各横截面上的应力。
解:返回图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,75mm× 的等边角钢。
拉杆和中间竖向撑杆用角钢构成,其截面均为两个75mm×8mm 的等边角钢。
已知屋面承受集度为应力。
应力。
的竖直均布荷载。
的竖直均布荷载。
试求拉杆 AE 和 EG 横截面上的解: 1)求内力=取 I-I 分离体得(拉)取节点 E 为分离体,故 2)求应力(拉)75×8 等边角钢的面积 A=11.5 cm2(拉)(拉)返回2-5(2-6) 图示拉杆承受轴向拉力 5(2-,杆的横截面面积。
表示斜截面与横截面的夹角,30 ,45 ,60 ,90 时如以表示斜截面与横截面的夹角,试求当各斜截面上的正应力和切应力,并用图表示其方向。
各斜截面上的正应力和切应力,并用图表示其方向。
解:返回一木桩柱受力如图所示。
的正方形, 2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长 200mm 的正方形,材料 6(2GPa。
如不计柱的自重,试求:可认为符合胡克定律,可认为符合胡克定律,其弹性模量 E=10 GPa。
材料力学第二章
σ——横截面上的正应力;
σα——斜截面上的正应力;τα——斜截面上的切应力
35
F
p
2、符号规定 ⑴、a:斜截面外法线与横截面的外法线(x 轴)的夹角。
由
x
轴逆时针转到斜截面外法线——“a” 为正值;
由 x 轴顺时针转到斜截面外法线——“a”为负值
⑵、σa:同“σ”的符号规定
⑶、τa:在保留段内任取一点,如果“τa”对该点之矩 为顺时针方向,则规定为正值,反之为负值。
A
F B 4000 F
3000
FN1 50kN
FN1 1 A1
150kN
C
370
240
5010 N (240mm) (240mm) 0.87MP a(压)
3
F
50kN A F B 4000 F 3000
Ⅱ段柱横截面上的正应力
FN2 150kN
FN2 2 A2 150 103 N (370mm)(370mm) (压应力) 1.1MP a
A
FNAB 2 F
FNAB 150MPa A
a
F D
FNAB B C
a
a
31
试求薄壁圆环在内压力作用下径向截面上的拉应力。已知:
d 200mm, δ 5mm, p 2MPa。
b
p
解:
d
可认为径向截面上的拉应力沿壁厚均匀分布
A b
32
y
p
p
FR d FN
FN
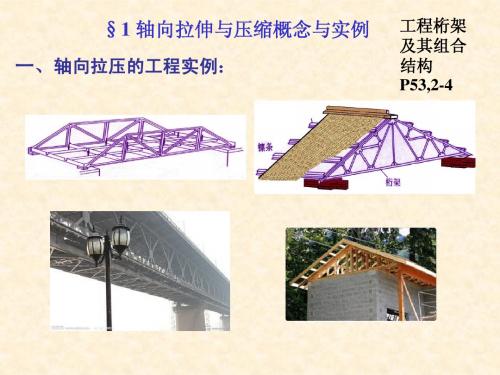
§1 轴向拉伸与压缩概念与实例
一、轴向拉压的工程实例:
工程桁架 及其组合 结构 P53,2-4
二、轴向拉压的概念:
材料力学第二章习题课

故该杆满足强度条件。
例已知三铰屋架如图,承受竖向均布载荷,载荷的分布集度为: q =4.2kN/m,屋架中的钢拉杆材料为Q235钢,[σ]=170MPa,试 选择钢拉杆的直径。(不计钢拉杆的自重) q
C
FAx
A 0.4m
FAy
钢拉杆
8.5m
B
FB
0.4m
解: 整体平衡求支反力 ①
Fx 0 FAx 0
o
120kN 220kN 260kN
①
B
FN / kN 120
②
C
③
160
160kN
A
D
BC段: 100 3 FN 2 100 10 N 160 106 Pa 160MPa(压应力) 2 A2 625 106 m2 CD段: 3 FN 3 160 10 N (拉应力) 177.8 106 Pa 177.8MPa 3 6 2 A3 900 10 m
Fy 0, FN 2 sin 30 2W 0
F
x
0, FN 2 cos30 FN1 0
FN 1 3.46W
FN 2 4W
例如图所示的简易起重设备,AB杆用两根70mm×70mm×4mm 等边角钢组成,BC杆用两根10号槽钢焊成一整体。材料均为 Q235钢, [σ]=170MPa。试求设备所许用的起重量W。
dAx g dAx gAxdx dx Ax
A0:桥墩顶端截面的面积
x
dx
1000 103 N A0 1m 2 6 110 N / m2
g Ax A0 exp x
F
gl Al A0 exp
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩

习题2-1一木柱受力如图示,柱的横截面为边长20cm 的正方形,材料服从虎克定律,其弹性模量MPa .如不计柱自重,试求:51010.0×=E (1)作轴力图;(2)各段柱横截面上的应力;(3)各段柱的纵向线应变;(4)柱的总变形.解:(1)轴力图(2)AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=(3)AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε(4)总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件,板件的受力情况如图(b)所示.已知:P =7kN ,t =0.15cm ,b 1=0.4cm ,b 2=0.5cm ,b 3=0.6cml 。
试绘板件的轴力图,并计算板内的最大拉应力。
解:(2)aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为1cm 的圆杆,在拉力P =10kN 的作用下,试求杆内最大剪应力,以及与横截面夹角为=30o 的斜截面上的正应力与剪应力。
α解:(1)最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−(2)界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁,C 与D 均为铰接,铅垂力P =20kN 作用在C 铰,若(1)杆的直径d 1=1cm ,(2)杆的直径d 2=2cm ,两杆的材料相同,E =200Gpa ,其他尺寸如图示,试求(1)两杆的应力;(2)C 点的位移。
第2章—力系的简化—工程力学(静力学和材料力学)课后习题答案

工程力学(静力学与材料力学)习题详细解答(第2章)习题2-2图第2章 力系的简化2-1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。
二力作用线之间的距离为d 。
试问:这一力系向哪一点简化,所得结果只有合力,而没有合力偶;确定这一合力的大小和方向;说明这一合力矢量属于哪一类矢量。
解:由习题2-1解图,假设力系向C 点简化所得结果只有合力,而没有合力偶,于是,有∑=0)(F C M ,02)(=⋅++−x F x d F ,dx =∴,F F F F =−=∴2R ,方向如图示。
合力矢量属于滑动矢量。
2-2 已知一平面力系对A (3,0),B (0,4)和C (-4.5,2)三点的主矩分别为:M A 、M B 和M C 。
若已知:M A =20 kN·m 、M B =0和M C =-10kN·m ,求:这一力系最后简化所得合力的大小、方向和作用线。
解:由已知M B = 0知合力F R 过B 点;由M A = 20kN ·m ,M C = -10kN ·m 知F R 位于A 、C 间,且CD AG 2=(习题2-2解图)在图中设OF = d ,则θcot 4=dCD AG d 2)sin 3(==+θ (1) θθsin )25.4(sin d CE CD −== (2)即θθsin )25.4(2sin )3(dd −=+ d d −=+93 3=d习题2-1图习题2-1解图R∴ F 点的坐标为(-3, 0)合力方向如图所示,作用线过B 、F 点; 34tan =θ 8.4546sin 6=×==θAG 8.4R R ×=×=F AG F M A kN 6258.420R ==F 即 )kN 310,25(R=F 作用线方程:434+=x y 讨论:本题由于已知数值的特殊性,实际G 点与E 点重合。
2-3三个小拖船拖着一条大船,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
F
x
dx
FN l F G
F G
Al
采用等强度石柱
x
FN x Ax
Ax dAx Ax gAxdx
gA(x)dx
dAx dAAgAxxxdxgdx
例如图所示的简易起重设备,AB杆用两根70mm×70mm×4mm 等边角钢组成,BC杆用两根10号槽钢焊成一整体。材料均为 Q235钢, [σ]=170MPa。试求设备所许用的起重量W。
q
FAx
A
0.4m
FAy
C
钢拉杆 8.5m
B
FB 0.4m
解:① 整体平衡求支反力
Fx 0 FAx 0
MB 0
-
FAy
8.5
4.2
9.3
8.5 2
0
FAy 19.53kN
② 局部平衡求轴力
MC 0
FN
1.42
4.2 2
4.652
19.53
4.25
h
A
B FNBD
C
D
VBD
F
ABDLBD
2FFLL
hscinos2
h
sin
450
Vmin
例阶梯形杆如图所示。AB、BC和CD段的横截面面积分别为 A1=1500mm2、 A2=625mm2、 A3=900mm2。杆的材料为Q235 钢,[σ]=170MPa。试校核该杆的强度。
解:(1)作轴力图
120 kN
①
220 kN
②
260 kN
③ 160kN
(2)校核强度
A
B
C
D
由轴力图和各段杆的横
FN / kN
160
截面面积可知,危险截
120
面可能在BC段或CD段。
BC段:
o
x
100
2
FN 2 A2
100103 N 625106 m2
160106 Pa
160MPa(压应力)
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
15m
采用等截面石柱
F
FN F gAl
FN F gAl F gl
A
A
A
A
F
gl
1.6m2
1000103 N
1106 N / m2 25103 N / m3 15m
V1 Al 12.46m32 15m
N
/
1000103 N m2 25103 N
/
m3
5m
AF2 NF2FN3gAg1ll21
11.030101m2110036NN
25 / m2
103 N / m3 1.14m2 25103 N / m3 5m
5m
A3
F
gA1l1 gA2l2
③
C 160
160 kN D
x
max 3 177.8MPa 170MPa
相对误差: 177.8 170 100% 4.6% 5% 170
故该杆满足强度条件。
例已知三铰屋架如图,承受竖向均布载荷,载荷的分布集度为: q =4.2kN/m,屋架中的钢拉杆材料为Q235钢,[σ]=170MPa,试 选择钢拉杆的直径。(不计钢拉杆的自重)
gl3
11.40900m2103 N
V2
25103 N /
A1 1A1206
m3 1.14m2 5m 25103 N /
NA3/ ml12 12591.7.14m013m3N2/m13 .351mm2
m3 1.31m2 5m
1.49m2 5m
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
图示石柱桥墩,压力F=1000kN,石料重度ρ g=25kN/m3,许用 应力[σ ]=1MPa。试比较下列三种情况下所需石料面积(1)等截 面石柱;(2)三段等长度的阶梯石柱;(3)等强度石柱(柱的 每个截面的应力都等于许用应力[σ ])
FFF来自15m 5m 5m 5m
CD段:
3
FN 3 A3
160103 N 900106 m2
177.8106 Pa
177.8MPa(拉应力)
2 160MPa 压 3 177.8MPa 拉
120 kN
①
A FN / kN 120
o
220 kN
②
B
100
结果表明,杆的最大正应力发生在CD段
260 kN
FN
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
5m 5m 5m
F
采用三段等长度阶梯石柱
FN1 F gA1l1
FN2 F gA1l1 gA2l2
FN3 F gA1l1 gA2l2 gA3l3
FN1
A1
F
gl1
11.141m062
Ax
A0
exp
g
x
A0:桥墩顶端截面的面积
A0
F
111m0102006N10/3mN2
Al
A0
exp
gl
G gV3
1m.425me2xp
25这种10设3 N计/使m得3 各15截m面的正应 力1均达10到6 N许/用m应2 力,使材料
V3 1G8mA3l1得1F0到6 P充a分1利.45用m。2 1000103 N
g g
25103 N / m3
G Al F
24 :19.7 :18
Ⅱ拉(压)杆的强度计算/三 拉压杆的强度条件/例题
图示三角形托架,AC为刚性杆,BD为斜撑杆,荷载F可沿水平梁移动
。为使斜撑杆重量为最轻,问斜撑杆与梁之间夹角应取何值?不考
虑BD杆的稳定。
设Fm的A作用0线到A点的距FN离FBD为x x
FNFBD取xsAinBC杆为h研cx究tg对L象
h cos
0FNBD
max
FL
h cos
BD杆:
l
x
ABD
FNBD
FL
h cos
0 A
q=4.2kN/m
FN 26.5kN
③ 由强度条件求直径
0.4m
FAy
4.25m
C FCx FCy
FN
由
FN A
4 FN
d2
得
d
4FN
4 26.5103 N
170106 Pa
0.0141m 14.1mm
为了经济起见,选用钢拉杆的直径为14mm。其值略小于计算 结果,但是其工作正应力超过许用应力不到5%。
