材料力学2013典型例题
材料力学习题及答案
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学典型例题与详解(经典题目)
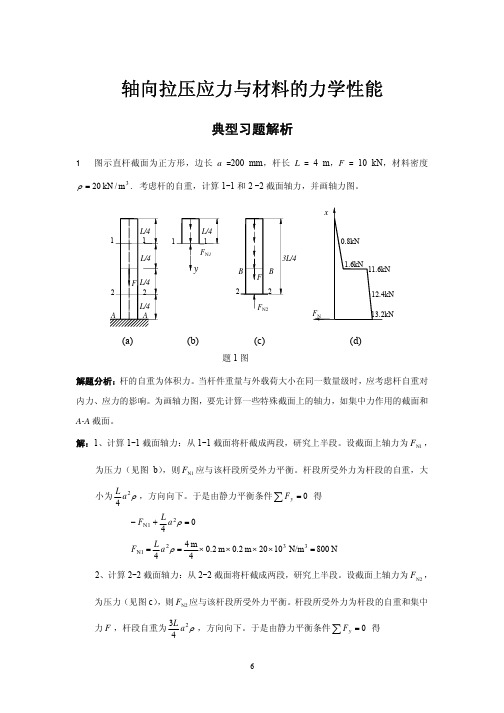
= 3.64
2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为
σ bs
=
Fb Abs
=
F nδ d
≤ [σ
bs]
得
n
≥
δ
d
F [σ
bs
]
=
10
× 10 −3
m
×
160 ×103 20 ×10−3 m
N × 320
× 10 6
N/m 2
= 2.5
两者取大值,最后确定铆钉数 n = 4。
衡条件得 F 作用截面上侧轴力为
FNB +
=
L a2ρ 2
=
4 m × (0.2 m)2 2
× 20 × 103
N/m 3
= 1.6 × 103 N = 1.6 kN
然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 FNB− ,研究上半部分
杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为
FNB−
=
L a2ρ 2
+
F
=
4 m × (0.2 m)2 2
× 20 ×103
N/m 3
+ 10 ×103
N = 11.6 ×103 N = 11.6 kN
4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆
上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 La 2 ρ ,方向向下。于是
2 图示石柱桥墩,压力 F = 1000 kN,石料密度 ρ = 25 kN / m3 ,许用应力 [σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力 [σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱
材料力学试题和答案解析7套

材料⼒学试题和答案解析7套材料⼒学试卷1⼀、绘制该梁的剪⼒、弯矩图。
(15分)⼆、梁的受⼒如图,截⾯为T 字型,材料的许⽤拉应⼒[σ+]=40MPa ,许⽤压应⼒[σ-]=100MPa 。
试按正应⼒强度条件校核梁的强度。
(20分)m8m 2m2M三、求图⽰单元体的主应⼒及其⽅位,画出主单元体和应⼒圆。
(15分)四、图⽰偏⼼受压柱,已知截⾯为矩形,荷载的作⽤位置在A 点,试计算截⾯上的最⼤压应⼒并标出其在截⾯上的位置,画出截⾯核⼼的形状。
(15分) 30170302002m3m1m30五、结构⽤低碳钢A 3制成,A 端固定,B 、C 为球型铰⽀,求:允许荷载[P]。
已知:E=205GPa ,σs =275MPa ,σcr=338-1.12λ,,λp =90,λs =50,强度安全系数n=2,稳定安全系数n st =3,AB 梁为N 016⼯字钢,I z =1130cm 4,W z =141cm 3,BC 杆为圆形截⾯,直径d=60mm 。
(20分)六、结构如图所⽰。
已知各杆的EI 相同,不考虑剪⼒和轴⼒的影响,试求:D 截⾯的线位移和⾓位移。
(15分)材料⼒学2⼀、回答下列各题(共4题,每题4分,共16分)1、已知低碳钢拉伸试件,标距mm l 1000=,直径mm d 10=,拉断后标距的长度变为mm l 1251=,断⼝处的直径为mm d 0.61=,试计算其延伸率和断⾯收缩率。
2、试画出图⽰截⾯弯曲中⼼的位置。
aa3、梁弯曲剪应⼒的计算公式zzQS =τ,若要计算图⽰矩形截⾯A 点的剪应⼒,试计算z S 。
4、试定性画出图⽰截⾯截⾯核⼼的形状(不⽤计算)。
4/h矩形圆形矩形截⾯中间挖掉圆形圆形截⾯中间挖掉正⽅形⼆、绘制该梁的剪⼒、弯矩图。
(15分)三、图⽰⽊梁的右端由钢拉杆⽀承。
已知梁的横截⾯为边长等于0.20m 的正⽅形,q=4OKN/m,弹性模量E 1=10GPa ;钢拉杆的横截⾯⾯积A 2=250mm 2,弹性模量E 2=210GPa 。
2013年广东暨南大学材料力学考研真题

2013年广东暨南大学材料力学考研真题学科与专业名称:一般力学与力学基础、固体力学、工程力学、结构工程 考试科目代码与名称:《材料力学》(819)考生注意:所有答案必须写在答题纸(卷)上,写在本试题上一律不给分 一、单选题(共10小题,每题2分,共20分)1. 桁架如图所示,载荷F 可在刚性横梁DE 上自由移动,杆1和杆2的横截面面积均为A ,拉压许用应力均为[σ]。
则载荷F 的许用值为______________。
(A )2][A σ (B )3][2Aσ (C )A ][2σ (D )A ][σ12BA FCaaaaAB ED2. 四根截面尺寸和材料均相同的细长压杆,两端的约束如图所示。
已知4:3:2:1:::4321=l l l l ,则临界压力最小的杆是______________。
(A ) (B ) (C ) (D )3. 下面提高压杆稳定性的措施,正确的是______________。
(A )工字形截面抗弯性能好,所以它是用作压杆的合理截面; (B )将一根压杆的长度减小一倍,则临界应力可以提高4倍;(C )将细长压杆的材料由普通低碳钢换成高强度钢就可以提高其临界压力; (D )对于一定的横截面面积,压杆采用正方形截面比矩形截面好。
4. 请判断下图所示结构的超静定次数依次是______________。
(A )2次,1次; (B )2次,0次; (C )2次,2次; (D )1次,1次;F5. 外径为D ,内径为d 的空心圆轴,两端受扭转力偶矩T 作用,轴内的最大剪应力为τ。
若轴的外径为2D ,内径改为2d ,则轴内的最大剪应力变为 。
(A )2τ (B )4τ (C )8τ (D )16τ 6. 正方形等截面立柱,受纵向压力F 作用。
当力F 作用点由A 移至B 时,柱内最大压应力的比值max max B A σ为______________。
(A )1:2 (B)7:13 (C )4:7 (D )5:27. 如图所示结构受—对等值、反向、共线的力作用,自重不计,铰支座反力的作用线是______________。
工程力学--材料力学(第五、六章)经典例题及讲解
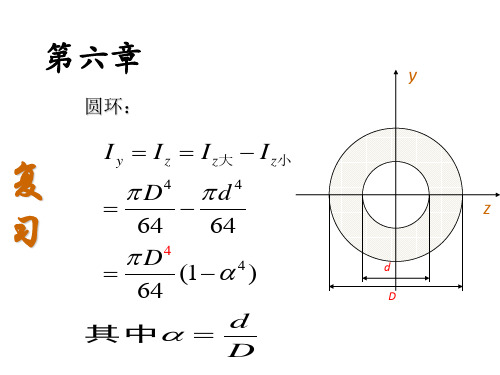
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
材料力学例题

B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
(3)补充方程
FN1
FN 3
EA E3 A3
cos2
(4)联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: (1)销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
(2)校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解:(1) 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1
(完整版)材料力学试题及答案
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
材料力学考试典型题目

例题5 如图所示的悬臂梁在自由端受集中荷载 F 作用, 试作此梁
的剪力图和弯矩图.
A
F
B x
解: 列出梁的剪力方程 和弯矩方程
l
FS ( x ) F M ( x ) Fx
(0 x l )
FS
(0 x l )
M F
x
F SA左 0 F SA右 F
x
例题6 图示的简支梁,在全梁上受集度为q的均布荷载用.试作
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa,DB=1°. 试求:
Fb l
+
Fa l
+
Fba l
在集中荷载作用处的左,右 两侧截面上剪力值(图)有突变, 突变值等于集中荷载F. 弯矩图 形成尖角,该处弯矩值最大.
FRA
A a x
F
FRB
B
C b
x
l
Fb l
+
Fa l
+
Fba l
例题8 图示的简支梁在 C点处受矩为M的集中力偶作用.
试作此梁的的剪力图和弯矩图. 解:求梁的支反力
Fx 2 EIw Flx 2
EIw Flx Fx 2 6
2
3
y A
F
B x
wmax
l
max
max 和 wmax都发生在自由端截面处
Fl 2 Fl 2 Fl 2 ( ) max | x l EI 2 EI 2 EI Pl 3 wmax w | x l ( ) 3 EI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x 0, M 0
A
B
x l, M 0
x
FRA
l
FRB
令 dM ( x) ql qx 0
dx 2
ql 2
得驻点x l
+
8
2
l/2
弯矩的极值
M max
M xl 2
ql 2 8
绘出弯矩图
q A
FRA x
l ql/2
+
+
l/2
由图可见,此梁在跨中截 B 面上的弯矩值为最大
FRB
M
max
ql 2 8
但此截面上 FS= 0
ql/2
两支座内侧横截面上
剪力绝对值为最大
ql 2 8
FS max
ql 2
例题1 螺栓压板夹紧装置如图所示.已知板长3a=150mm,压板
材料的弯曲许用应力[]=140MP.试计算压板传给工件的最大允
许压紧力F.
FRA
FRB
F
解:(1)作出弯矩图的最大弯
A
矩为Fa; (2)求惯性矩,抗弯截面系数
(3Me 2a Me a ) 180 2.33
GIp
GIp
π
例题6 图示的简支梁,在全梁上受集度为q的均布荷载用.试作
解:
此梁的剪力图和弯矩图.
q
(1) 求支反力
A
B
FRA
FRB
ql 2
x
FRA
l
FRB
(2)列剪力方程和弯矩方程.
FS
(
x)
FRA
qx
ql 2
qx
(0 x l)
M(
x)
均布荷载作用.试求此梁的挠曲线方程和转角方程,并确定其 max
和 wmax
q
A
B
l
q
解:由对称性可知,梁的两
个支反力为
A
B
FRA
FRB
ql 2
x
l
FRA
FRB
此梁的弯矩方程及挠曲线微分方程分别为
M ( x) ql x q x2 22
EIw ql x q x2 22
EIw ql x2 q x3 C 46
Ⅲ
Ⅱ
Ⅰ
DⅢ l3
F3
C
Ⅱ
l2
F1 F2
B
A Ⅰ
l1
Ⅲ
FRD
Ⅱ
F3
DⅢ l3
C
Ⅱ
l2
解:求支座反力 FRD = -50kN (1)Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III 截面的轴力并作轴力图
F1 FN1 0
FN1 20kN ()
Ⅰ
F2
F1
B
A Ⅰ
l1
FN1
F1
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
FRD
FN3 FN2
例题5 图示为一变截面圆杆ABCD.已知F1=20kN,F2=35kN F3=35kN. l1=l3=300mm,l2=400mm. d1=12mm,d2=16mm, d3=24mm. 试求:
(1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III截面的轴力并作轴力图
(2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
EIw ql x3 q x4 Cx D 12 24
边界条件x=0 和 x=l时, w 0
q
wmax
梁的转角方程和挠曲线方程 A 分别为
q (6lx2 4x3 l 3 )
24EI w qx (2lx2 x3 l 3 )
24EI
A
x
FRA
B
B
l
FRB
最大转角和最大挠度分别为
在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
max
A
B
ql 3 24EI
在梁跨中点处有最大挠度值
wmax
w
x l 2
5ql4 384EI
例题18 直径为d=0.1m的圆杆受力如图, Me=7kN·m, F=50kN, 材
料为铸铁,[]=40MPa, 试用第一强度理论校核杆的强度.
解:危险点A的应力状态如图
Me
σ
FN A
4 50 π 0.12
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
ⅠA
l1
(2) 杆的最大正应力max
AB段
AB
FN1 A1
176.8MPa
()
BC段 BC
FN2 74.6MPa A2
()
DC段
DC
FN 3 A3
110.5MPa
()
FN1 =20kN (+) FN2 =-15kN ( - ) FN3 =- 50kN ( - )
max = 176.8MPa
B
C
2a
a
Fa
Iz
(3cm)(2cm)3 12
(1.4cm)(2cm)3 12
1.07cm4
Wz
Iz ymax
1.07cm4
1cm
1.07cm3
(3)求许可载荷
Fa Wz[σ]
Mmax Wz[σ]
F Wz[σ] 3kN a
+
φ14 φ30
20
例题2 图示一抗弯刚度为 EI 的简支梁,在全梁上受集度为q 的
103
6.37MPa F
A
Me
F
τ
T Wt
16 7000 π 0.13
35.7MPa
A
σmax σ (σ )2 τ 2 6.37 (6.37)2 35.72 39
σmin 2
2
2
2
32
1 39MPa, 2 0, 3 32MPa 1 [ ] 故安全.
例题7 空心圆杆AB和CD杆焊接成整体结构,受力如图.AB杆的外
ΔlAD ΔlAB ΔlBC ΔlCD -0.47 10-4mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa,DB=1°. 试求:
(1) AD杆的最大切应力;
(2)扭转角 CA
解:画扭矩图
Me 2Me
3Me
Tmax= 3Me
DCB
A
计算外力偶矩Me
发生在AB段.
Ⅲ
FRD
DⅢ l3
Ⅱ
F3
C
Ⅱ
l2
Ⅰ
F2
F1
B
A Ⅰ
l1
(3) B截面的位移及AD杆的变形
Δl AB
FN1l1 EA1
2.53 10-4m
ΔlBC
FN 2 l2 EA2
1.42 10-4m
ΔlCD
FN 3 l3 EA3
1.58 10-4m
uB ΔlCD ΔlBC -0.3mm
FRA x
qx
x 2
qlx 2
qx2 2
(0 x l)
q
FS
(
x)
ql 2
qx
(0 x l)
A
剪力图为一倾斜直线
x
FRA
l
x=0
处
, FS
ql 2
x= l 处 ,
FS
ql 2
ql/2
+
绘出剪力图
B
FRB
ql/2
M(
x)
FRA
x
qx
x 2
qlx 2
qx2 2
弯矩图为一条二次抛物线
(0 x l)
DB= CB+ DC=1°
( Mea 2Mea ) 180 1
GIp GIp
π
aa
2Me Me
2a 3Me +
Me 292kN m
(1)AD杆的最大切应力
Me 2Me
3Me
max
Tmax Wt
69.7MPa
DCB
A
aa
2a
(2)扭转角 CA
CA BA CB
2Me Me
3Me +
Ⅰ
F2
F1
B
ⅠA
l1
F1 F2
FN3 FRD 0 FN3 50kN ()
F1 F2 FN2 0 FN2 15kN ()
Ⅲ
FRD
DⅢ l3
-
50
Ⅱ
F3
C
Ⅱ
l2
15
Ⅰ
F2
F1
B
ⅠA
l1
20
+
FN1 =20kN (+)
FN2 =-15kN (-) FN3 =- 50kN (-)
Ⅲ
FRD
DⅢ l3
