材料力学2013典型例题综述
材料力学典型例题与详解(经典题目)
= 3.64
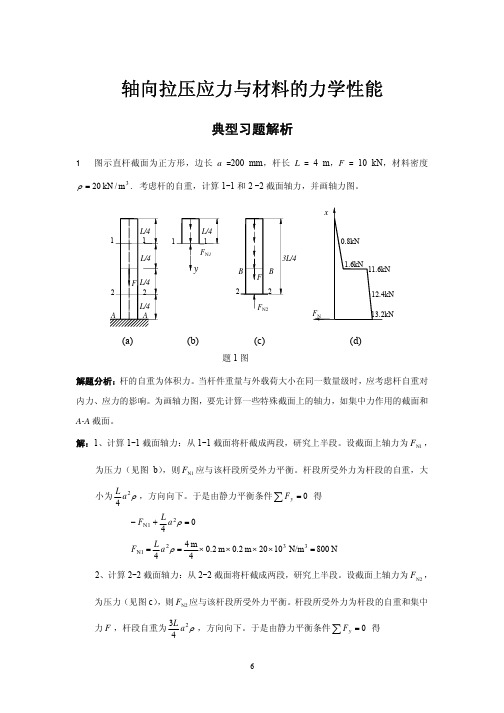
2、按挤压强度条件确定铆钉数:挤压面面积 A = δ d ,铆钉挤压强度条件为
σ bs
=
Fb Abs
=
F nδ d
≤ [σ
bs]
得
n
≥
δ
d
F [σ
bs
]
=
10
× 10 −3
m
×
160 ×103 20 ×10−3 m
N × 320
× 10 6
N/m 2
= 2.5
两者取大值,最后确定铆钉数 n = 4。
衡条件得 F 作用截面上侧轴力为
FNB +
=
L a2ρ 2
=
4 m × (0.2 m)2 2
× 20 × 103
N/m 3
= 1.6 × 103 N = 1.6 kN
然后将杆沿 F 作用截面(B-B)下侧截开,设截面上轴力为压力 FNB− ,研究上半部分
杆段。这时杆段受本身重量作用和集中力 F 作用,所以由静力平衡条件得 F 作用截面下侧 轴力为
FNB−
=
L a2ρ 2
+
F
=
4 m × (0.2 m)2 2
× 20 ×103
N/m 3
+ 10 ×103
N = 11.6 ×103 N = 11.6 kN
4、计算 A-A 截面轴力:从 A-A 截面将杆截开,设截面上轴力为压力 FNA ,则 FNA 应与该杆
上所有外力平衡。杆所受外力为杆的自重和集中力 F ,杆段自重为 La 2 ρ ,方向向下。于是
2 图示石柱桥墩,压力 F = 1000 kN,石料密度 ρ = 25 kN / m3 ,许用应力 [σ ] =1 MPa。试 比较下列三种情况下所需石料体积。(1)等截面石柱;(2)三段等长度的阶梯石柱;(3)等 强度石柱(柱的每个截面的应力都等于许用应力 [σ ] )。 解题分析:设计这样的桥墩时,要考虑桥墩自重对强度的影响。可以想象,在桥墩顶截面只 有压力 F 作用,轴力最小;在桥墩底截面,除压力 F 外,还承受桥墩本身重量,该处轴力 最大。当桥墩采用等截面石柱时,只要考虑底部截面的强度即可。如果采用阶梯型石柱,需 考虑每段的强度。如果要求各个截面强度相等,则需要对石柱的各截面进行特别设计。 解:1、采用等截面石柱
材料力学例题及解题指导总结

材料力学例题及解题指导(第二章至第六章)第二章拉伸、压缩与剪切例2-1试画出图a直杆的轴力图解:此直杆在A、B、C、D点承受轴向外力。
先求AB段轴力。
在段内任一截面1-1处将杆件截开,考察左段(图2-5b)。
在截面上设出正轴力2。
由此段的平衡方程ZX = 0得N L 6= 0, N i =+ 6kN图2-5理得CD段内任一截面的轴力都是一4kN。
画内力图,以水平轴x表示杆的截面位置, 的比例尺画出轴力图,如图N i得正号说明原先假设拉力是正确的,同时也就表明轴力是正的。
AB段内任一截面的轴力都等于+6kN。
再求BC段轴力,在BC段任一截面2-2处将杆件截开,仍考察左段(图2-5C),在截面上仍设正的轴力N 2,由ZX= 0得—6 + 18+ N2 = 0N2=- 12kNN2得负号说明原先假设拉力是不对的(应为压力),同时又表明轴力N2是负的。
2-5 (d)所示。
由此图可知数值最大的轴力发生在BC段内任一截面的轴力都等于—12kN。
同以垂直x的坐标轴表示截面的轴力,按选定BC段内。
解题指导:利用截面法求轴力时,在切开的截面上总是设出正轴力N,然后由3X= 0求出轴力N ,如N得正说明是正轴力(拉力),如得负则说明是负轴力(压力)。
例2-3图2-7所示两根圆截面杆材料相同,试计 算两杆的应变能,并比较其大小。
解:a 杆:U aP 2 丨=P 2 l _ 22EA 2E 「:d4二 2 P lE d例2-2试求自由悬挂的直杆(图2-6a ) 由纵向均匀分布荷载 q (力/长度)引起 的应力和纵向变形。
设杆长 I 、截面积A 及弹性模量E 均已知。
解:在杆上距下端为 x 处取一任意横 截面m-m ,则该截面轴力为 N (x )= qx , 根据此式可作出轴力图如图 2-6b 所示。
m-m 截面的应力为 (x ) = N (x )/A = qx/A 。
显然,悬挂端有最大轴力 N max = ql 及最 大正应力■- 'max =ql / A 。
材料力学例题及

材料的许可切应力[t]=30MPa
切变模量G=80GPa
许可扭角[q]=0.3°/m
试按强度条件和刚度条件设计轴径d
解:根据强度条件式(4-6)得出:
再根据刚度条件式(4-9b )得出:
两个直径中应选其中较大者
即实心轴直径不应小于117mm
画内力图
以水平轴x表示杆的截面位置
以垂直x的坐标轴表示截面的轴力
按选定的比例尺画出轴力图
如图2-5(d)所示
由此图可知数值最大的轴力发生在BC段内
解题指导:利用截面法求轴力时,在切开的截面上总是设出正轴力N
然后由SX=0求出轴力N
如N 得正说明是正轴力(拉力)
如得负则说明是负轴力(压力)
等于-12.74kNm
仿此可得出MT2=-8.92kNm
MT3=-10kNm
(3) 画扭矩图
以横坐标表示截面位置
以纵坐标表示扭矩
按选定的比例尺作出AB、BC、CD三段轴的扭矩图
因为在每一段内扭矩为常数
故扭矩图由三段水平线组成
如图4-5(c)
最大的扭矩7.64kNm发生在中间段
本人精心整理的文档,文档来自网络
本人仅收藏整理
如有错误
还请自己查证!
材料力学例题及解题指导
(第二章至第六章)
第二章 拉伸、压缩与剪切
例2-1 试画出图a直杆的轴力图
解:此直杆在A、B、C、D点承受轴向外力
图中只示出1、2、8三个铆钉沿负y方向的剪力F/8
力偶Fl在每一铆钉中也引起剪力
假设剪力方向与该铆钉中心至C的连线正交
材料力学综合题

题1 如图所示受扭圆轴,正确的扭矩图为图( )
题2 等截面圆轴上装有四个皮带轮,则 四种方案中最合理方案为( )。 (A)将C轮与D轮对调; (B)将B轮与D轮对调; (C)将B轮与C轮对调; (D)将B轮与D轮对调,然后再将B轮与C 轮对调。
题30图
题3 扭转切应力公式适用于哪种杆件?( )。
题5 图示四根受拉杆危险横截面的面积相同, 首先破坏的杆件为
题6 两根钢制拉杆受力如图,若杆长L2=2L 1,横截面面积A2=2A1,则两杆的伸长Δ L和纵向线应变ε之间的关系应为( )。 (A) ΔL2=ΔL1,ε2=ε1 (B) ΔL2=2ΔL1,ε2=ε1 (C) ΔL2=2ΔL1,ε2=2ε1 (D) ΔL2=ΔL1/2,ε2=2ε1/2
第一章 绪 论
答案:1 强度要求,刚度要求,稳定性 要求。 2 拉伸或压缩,剪切,扭转, 弯曲。
1 为了保证工程结构或机械的正常工作, 构件应有足够的能力负担起应当承受的 载荷。因此,它应当满足以下要求:
。
2 杆件变形的基本形式有以下几种:
。
。
第二章 拉伸与压缩
答案 1-7 ABCDD BD
题1 下列构件中哪些属于轴向拉伸 或压缩? (A)(a)、(b); (B) (b)、(c);
题5 图示(a)、(b)两根梁,它们的( )。 (A) Q、M图都相同 (B) Q、M图都不相同 (C) Q图相同,M图不同 (D) M图相同,Q图不同
题6 梁的某一段内作用有均匀分布力时,则 该段内的内力图为( )。 (A) Q水平线,M斜直线 (B) Q斜直线,M曲线 (C) Q曲线,M曲线 (D) Q斜直线,M带拐点的曲线
(A)矩形截面 (B)任意实心截面 (C)任意材料的圆截面 (D)线弹性材料的圆截面
材料力学例题

B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
(3)补充方程
FN1
FN 3
EA E3 A3
cos2
(4)联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: (1)销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
(2)校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解:(1) 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1
(完整版)材料力学试题及答案
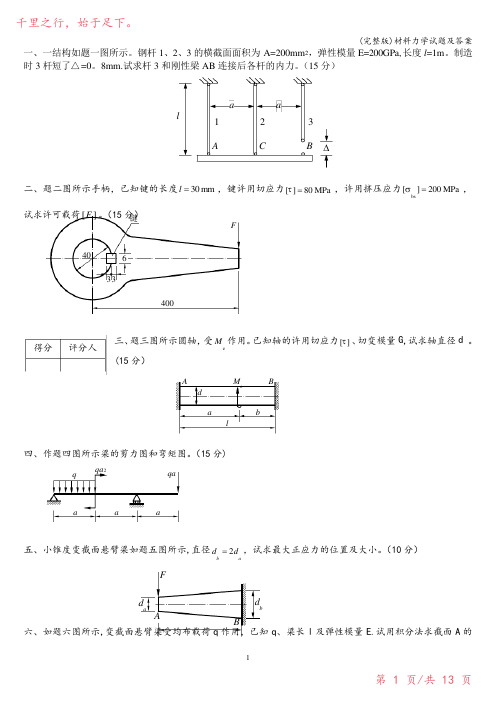
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2,弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
(15分)aalABC123∆二、题二图所示手柄,已知键的长度30 mm l =,键许用切应力[]80 MPa τ=,许用挤压应力bs[]200 MPa σ=,试求许可载荷][F 。
(15分)三、题三图所示圆轴,受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分)四、作题四图所示梁的剪力图和弯矩图。
(15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =,试求最大正应力的位置及大小。
(10分)六、如题六图所示,变截面悬臂梁受均布载荷q 作用,已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .(15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4,求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
(15分)一、(15分)(1)静力分析(如图(a))1N F2N F3N F图(a)∑=+=231,0N N N yF F F F(a)∑==31,0N N CF F M(b)(2)几何分析(如图(b))1l∆2l∆3l∆∆图(b)wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3)物理条件EA l F l N 11=∆,EA l F l N 22=∆,EAl F l N 33=∆ (4)补充方程∆=++EAlF EA l F EA l F N N N 3212 (c) (5)联立(a)、(b)、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分)以手柄和半个键为隔离体,S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体,bsS20F F F ==由剪切:S []s FA ττ=≤,720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、(15分)eABM M M +=0ABϕ=, A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+;当b a >时 e316π ()[]M bd a b τ≥+。
(答案)材料力学复习考试的题目解析汇报
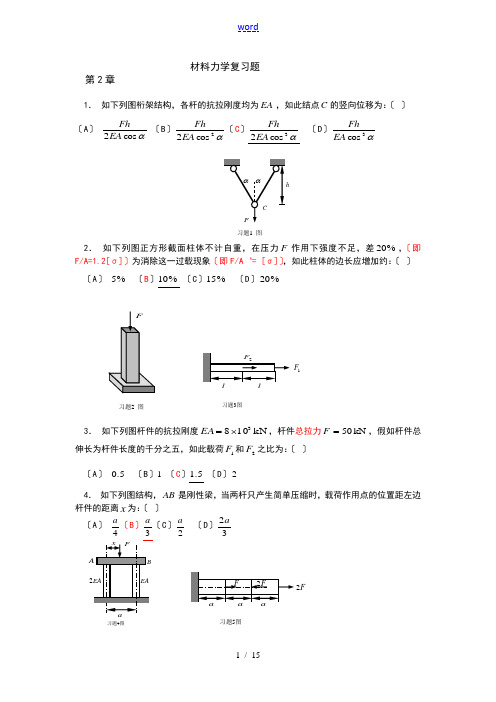
材料力学复习题第2章1. 如下列图桁架结构,各杆的抗拉刚度均为EA ,如此结点C 的竖向位移为:〔 〕 〔A 〕αcos 2EA Fh 〔B 〕α2cos 2EA Fh 〔C 〕α3cos 2EA Fh 〔D 〕α3cos EA Fh2. 如下列图正方形截面柱体不计自重,在压力F 作用下强度不足,差%20,〔即F/A=1.2[σ]〕为消除这一过载现象〔即F/A ‘= [σ]〕,如此柱体的边长应增加约:〔 〕 〔A 〕 %5 〔B 〕%10 〔C 〕%15 〔D 〕%203. 如下列图杆件的抗拉刚度kN 1083⨯=EA ,杆件总拉力kN 50=F ,假如杆件总伸长为杆件长度的千分之五,如此载荷1F 和2F 之比为:〔 〕 〔A 〕 5.0 〔B 〕1 〔C 〕5.1 〔D 〕24. 如下列图结构,AB 是刚性梁,当两杆只产生简单压缩时,载荷作用点的位置距左边杆件的距离x 为:〔 〕〔A 〕 4a 〔B 〕3a 〔C 〕2a 〔D 〕32a习题1 图习题5图F2习题4图习题3图1F 习题2 图5. 图示杆件的抗拉刚度为EA ,其自由端的水平位移为3Fa/EA ,杆件中间截面的水平位移为Fa/EA 。
6.图示桁架结构各杆的抗拉刚度均为EA ,如此节点C 的水平位移为F l cos45/EA ,竖向位移为F l cos45/EA 。
7. 图示结构AB 为刚性梁,重物重量kN 20=W ,可自由地在AB 间移动,两杆均为实心圆形截面杆,1号杆的许用应力为MPa 80,2号杆的许用应力为MPa 100,不计刚性梁AB 的重量。
试确定两杆的直径。
8. 某铣床工作台进油缸如下列图,油缸内压为MPa 2=p ,油缸内径mm 75=D ,活塞杆直径mm 18=d ,活塞杆材料的许用应力MPa 50][=σ,试校核活塞杆的强度。
9.如下列图结构,球体重量为F ,可在刚性梁AB 上自由移动,1号杆和2号杆的抗拉刚度分别为EA 和EA 2,长度均为l ,两杆距离为a 。
材料力学例题及解题指导

图 2-8 解:设在荷载 G 作用下,横梁移动到 AB位置(图 2-8b),则杆 1 的缩短量为 l1,而杆 2、3 的伸长量为 l2、l3。取横梁 AB 为分离体,如图 2-8c,其上除荷载 G 外,还有轴力 N1、N2、N3 以及 X。由于假设 1 杆缩短,2、3 杆伸长,故应将 N1 设为压力,而 N2、N3 设 为拉力。 (1) 平衡方程
例题及解题指导
图 3.6
例 2-5 图 3-6 所示螺钉承受轴向拉力 F,已知许可切 应力[]和拉伸许可应力[]之间的关系为:[]=0.6[],许 可 挤 压 应 力 [bs] 和 拉 伸 许 可 应 力 [] 之 间 的 关 系 为 : [bs]=2[]。试建立 D,d,t 三者间的合理比值。
解:(1) 螺钉的拉伸强度
时单位杆长的分布力 q=A1,此处 是材料单位体积的重量即容重。将 q 代入上式得到
l A l2 Al l Gl
2EA 2EA 2EA 此处 G=Al 是整个杆的重量。上式表明等直杆自重引起的总伸长等于全部重量集中于 下端时伸长的一半。
解题指导:对于轴力为变数的杆,利用虎克定律计算杆件轴向变
N1 得正号说明原先假设拉力是正确的, 同时也就表明轴力是正的。AB 段内任一截 面的轴力都等于+6kN。 再求 BC 段轴力,在 BC 段任一截面 2-2 处 将杆件截开,仍考察左段(图 2-5c),在截 面上仍设正的轴力 N 2,由 X=0 得
-6+18+N2=0
N2=-12kN
N2 得负号说明原先假设拉力是不对的
解:根据强度条件式(4-6)得出:
10
d 3 16MT 3 16 7.64 106 109mm
[ ]
30
11
再根据刚度条件式(4-9b )得出:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
x
q
wmax B
梁的转角方程和挠曲线方程 A 分别为
A
FN3 =- 50kN (-)
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1 A
F1
(2) 杆的最大正应力max
FN1 AB 176.8MPa ( ) A1 F BC段 BC N 2 74.6MPa ( ) A2 FN 3 DC段 DC 110.5MPa ( ) A3
例题5 图示为一变截面圆杆ABCD.已知F1=20kN,F2=35kN
F3=35kN. l1=l3=300mm,l2=400mm. d1=12mm,d2=16mm, d3=24mm. 试求: (1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III截面的轴力并作轴力图 (2) 杆的最大正应力max
(3) B截面的位移及AD杆的变形
(1) AD杆的最大切应力; (2)扭转角 CA 解:画扭矩图 Me D a C a 2Me B 2a 3Me Me +
3Me
A
Tmax= 3Me 计算外力偶矩Me
DB= CB+ DC=1°
M ea 2 M ea 180 ( ) 1 GI p GI p π
2Me
M e 292kN m
AB段
FN1 =20kN (+) FN2 =-15kN ( - ) FN3 =- 50kN ( - )
max = 176.8MPa
发生在AB段.
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1
F1
A
(3) B截面的位移及AD杆的变形
Δl AB
ΔlCD
FN1l1 FN 2 l2 -4 -4 2.53 10 m Δl BC 1.42 10 m EA1 EA2
例题6 图示的简支梁,在全梁上受集度为q的均布荷载用.试作
此梁的剪力图和弯矩图.
解: (1) 求支反力
A
q
B
x
FRA FRB
ql 2
FRA
l
FRB
(2)列剪力方程和弯矩方程.
ql FS ( x ) FRA qx qx (0 x l ) 2 x qlx qx 2 M ( x ) FRA x qx (0 x l ) 2 2 2
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa,DB=1°. 试求:
(1)AD杆的最大切应力 D a
Me C a
2Me B 2a 3Me
3Me A
max
Tmax 69.7MPa Wt
(2)扭转角 CA 2Me
CA BA CB
3 M e 2a M e a 180 ( ) 2.33 GI p GI p π
Me
+
l
FRB
此梁的弯矩方程及挠曲线微分方程分别为
ql q 2 M ( x) x x 2 2 ql q 2 EIw x x 2 2
ql 2 q 3 EIw x x C 4 6
ql 3 q 4 EIw x x Cx D 12 24
边界条件x=0 和 x=l时, w
W z [σ ] F 3kN a
φ14 φ30
20
Fa
例题2 图示一抗弯刚度为 EI 的简支梁,在全梁上受集度为q 的
均布荷载作用.试求此梁的挠曲线方程和转角方程,并确定其 max 和 wmax
q A l B
q
解:由对称性可知,梁的两 个支反力为
A x
B
FRA FRB
ql 2
FRA
Ⅲ Ⅱ Ⅰ
F3
D Ⅲ l3 C l2 Ⅱ B
F2
Ⅰ l1 A
F1
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D
Ⅲ l3
F2
Ⅱ
l2
F1
Ⅰ
A
B
l1
解:求支座反力 FRD = -50kN (1)Ⅰ-Ⅰ、Ⅱ-Ⅱ、III-III 截面的轴力并作轴力图
FN1
F1
F1 FN1 0 FN1 20kN ( )
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1 A
F1
FRD
FN3 FN2
F2
F1
FN 3 FRD 0 FN 3 50kN ( )
F1 F2 FN 2 0 FN 2 15kN ( )
Ⅲ
Ⅱ
Ⅰ
FRD
C
F3
D Ⅲ l3 Ⅱ l2 B
F2
Ⅰ l1 A
F1
20
+
50
15
FN1 =20kN (+) FN2 =-15kN (-)
ql FS ( x ) qx 2
剪力图为一倾斜直线
q
(0 x l )
A
x
B
l
FRA
FRB
ql x=0 处 , FS 2 x= l 处 , F ql S 2
绘出剪力图
ql/2
+
ql/2
x qlx qx 2 M ( x ) FRA x qx 2 2 2
弯矩图为一条二次抛物线
(0 x l )
q
B
x
x 0, M 0 x l, M 0
A
FRA
l
FRB
dM ( x ) ql qx 0 令 dx 2
l 得驻点 x 2
弯矩的极值 M max M 绘出弯矩图
l x 2
+
ql 8
2
Байду номын сангаас
ql 8
2
l/2
q
由图可见,此梁在跨中截
A
B
x
面上的弯矩值为最大
FRA
ql/2
l
FRB
ql M max 8
2
+
ql/2
但此截面上 FS= 0 两支座内侧横截面上 剪力绝对值为最大
+
l/2
ql 8
2
FS max
ql 2
例题1 螺栓压板夹紧装置如图所示.已知板长3a=150mm,压板 材料的弯曲许用应力[]=140MP.试计算压板传给工件的最大允 F F F R B 许压紧力F. RA 解:(1)作出弯矩图的最大弯
矩为Fa;
A
B
C a
2a
(2)求惯性矩,抗弯截面系数
( 3cm )( 2cm )3 (1.4cm )( 2cm )3 Iz 1.07cm 4 12 12 Iz 1.07cm 4 Wz 1.07cm 3 ymax 1cm Fa Wz [σ ]
(3)求许可载荷
+
M max Wz [σ ]
