材料力学典型例题及解析 12.冲击问题典型习题解析
南京工业大学材料力学材料力学冲击问题

2. 计算轴AB横截面上的最大切应力
任一横截面上的扭矩为:
TTd
MMdd
00..55ππ((kkNNmm)) 33
轴横截面上的最大扭转切应力为:
dmmaaxxWWTPdt
00..55ππ 110033NNmm 33
ππ 110000110033mm 33
22..6699110066PPaa 22..6699MMPPaa
总伸长。
解:⒈ 求杆内最大动应力
向心加速度为 an 2 x
到轴线距离为x处杆单位长度上的动载荷为
qd
(x)
A
g
2
x
因此,距轴线距离为x的截面上的轴力为
FNd
l
x qd (x)dx
l A 2 xdx A 2 (l 2 x2 )
xg
2g
FNd
A 2
2g
(l 2
x2)
相应的动应力为
d (x)
P
速度开始下降至0,同时弹簧变形达到最
h
P
大值 d 。
P
d
此时,全部(动)势能转化为应变能, 杆内动应力达最大值(以后要回跳)。就
以此时来计算:
•释放出的动能(以势能的降低来表示)
弹簧
T P(h d )
•增加的应变能,在弹性极限内
Ve
1 2
Pdd
根据力和变形之间的关系:Fd kd
F
Fd
Fd :冲击物速度为0时,作用于杆之力。
d Kd st
通常情况下,Kd 1 。
•关于动荷系数 K d 的讨论:
1.若冲击物是以一垂直速度v 作用于构件上,则由 v2 2gh
可得:
v2
Kd 1
工程力学材料力学部分课后习题详解
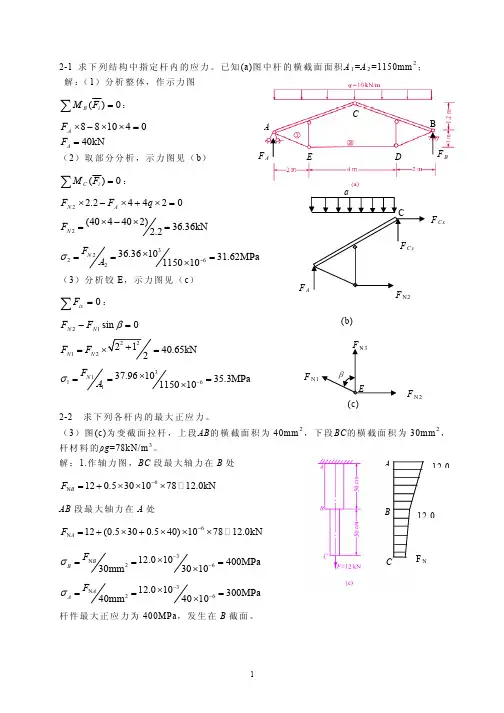
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:CB 041088=××−×A F AF N1F N2(c)40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×(3)分析铰E ,示力图见(c )∑=0ix F :0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ,发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比µ。
材料力学的练习试题和的答案解析_全
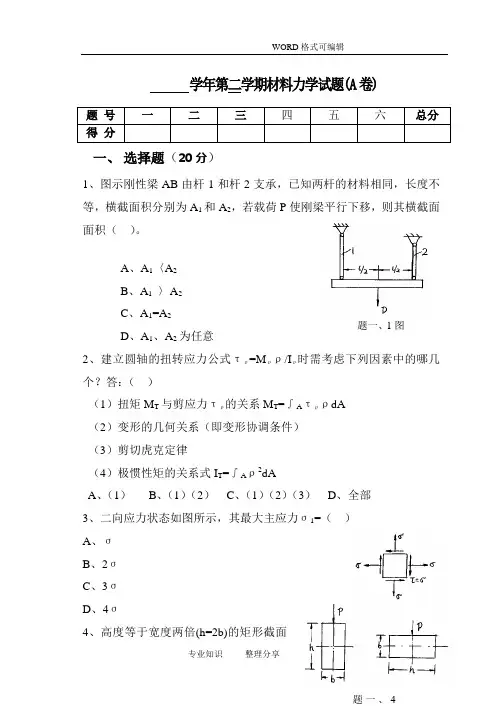
学年第二学期材料力学试题(A 卷)一、 选择题(20分)1、图示刚性梁AB 由杆1和杆2支承,已知两杆的材料相同,长度不等,横截面积分别为A 1和A 2,若载荷P 使刚梁平行下移,则其横截面面积( )。
A 、A 1〈A 2B 、A 1 〉A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆轴的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个?答:( )(1)扭矩M T 与剪应力τρ的关系M T =∫A τρρdA (2)变形的几何关系(即变形协调条件) (3)剪切虎克定律(4)极惯性矩的关系式I T =∫A ρ2dAA 、(1)B 、(1)(2)C 、(1)(2)(3)D 、全部 3、二向应力状态如图所示,其最大主应力σ1=( ) A 、σ B 、2σ C 、3σ D 、4σ4、高度等于宽度两倍(h=2b)的矩形截面题 号 一 二 三 四 五 六 总分 得 分题一、3图题一、1图梁,承受垂直方向的载荷,若仅将竖放截面改为平放截面,其它条件都不变,则梁的强度()A、提高到原来的2倍B、提高到原来的4倍C、降低到原来的1/2倍D、降低到原来的1/4倍5. 已知图示二梁的抗弯截面刚度EI相同,若二者自由端的挠度相等,则P1/P2=()A、2B、4C、8题一、5图D、16二、作图示梁的剪力图、弯矩图。
(15分)二题图三、如图所示直径为d的圆截面轴,其两端承受扭转力偶矩m的作用。
设由实验测的轴表面上与轴线成450方向的正应变,试求力偶矩m之值、材料的弹性常数E、μ均为已知。
(15分)三题图四、电动机功率为9kW ,转速为715r/min ,皮带轮直径D =250mm ,主轴外伸部分长度为l =120mm ,主轴直径d =40mm ,〔σ〕=60MPa ,用第三强度理论校核轴的强度。
(15分)五、重量为Q 的重物自由下落在图示刚架C 点,设刚架的抗弯刚度为EI ,试求冲击时刚架D 处的垂直位移。
材料力学试题带参考答案解析
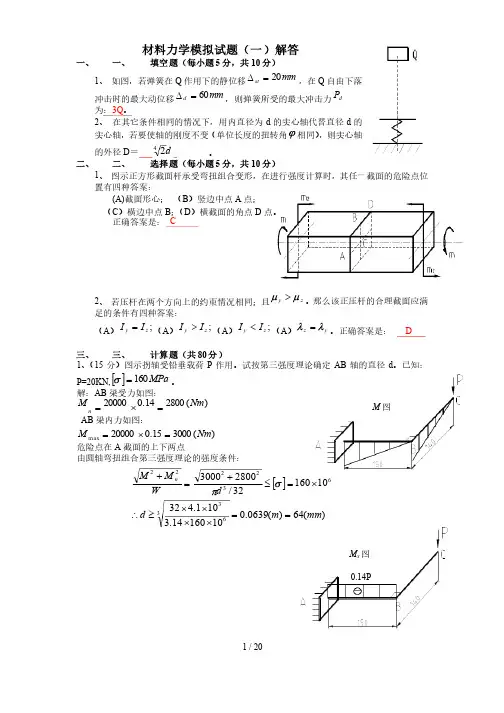
1 / 20材料力学模拟试题(一)解答一、 一、 填空题(每小题5分,共10分)1、 如图,若弹簧在Q 作用下的静位移mm st 20=D ,在Q 自由下落冲击时的最大动位移mm d 60=D ,则弹簧所受的最大冲击力d P 为:3Q 。
2、 在其它条件相同的情况下,用内直径为d 的实心轴代替直径d 的实心轴,若要使轴的刚度不变(单位长度的扭转角j 相同),则实心轴的外径D = d 42 。
二、 二、 选择题(每小题5分,共10分)1、 图示正方形截面杆承受弯扭组合变形,图示正方形截面杆承受弯扭组合变形,在进行强度计算时,在进行强度计算时,其任一截面的危险点位置有四种答案:置有四种答案:(A)截面形心;截面形心; (B )竖边中点A 点;点;(C )横边中点B ;(D )横截面的角点D 点。
点。
正确答案是:正确答案是:C2、 若压杆在两个方向上的约束情况相同;若压杆在两个方向上的约束情况相同;且且z y m m >。
那么该正压杆的合理截面应满足的条件有四种答案:足的条件有四种答案:(A );z y I I =(A );z y I I >(A );z y I I <(A )y z l l =。
正确答案是:。
正确答案是: D三、 三、 计算题(共80分) 1、(15分)图示拐轴受铅垂载荷P 作用。
试按第三强度理论确定AB 轴的直径d 。
已知:P=20KN,[]MPa 160=s 。
解:AB 梁受力如图:梁受力如图: )(280014.020000Nm M n =´= AB 梁内力如图:梁内力如图:)(300015.020000max Nm M =´=危险点在A 截面的上下两点截面的上下两点由圆轴弯扭组合第三强度理论的强度条件:由圆轴弯扭组合第三强度理论的强度条件:[])(64)(0639.01016014.3101.4321016032/28003000363632222mm m d d W M M n ==´´´´³\´=£+=+s pM 图0.14PM x 图2、图示矩形截面钢梁,A 端是固定铰支座,B 端为弹簧支承。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
冲击问题典型习题解析
∆d 2h 2 × 440 × 10 −3 m = 1+ 1+ = 1+ 1+ = 22 ∆st ∆st 2 × 10 −3 m
讨论: (1) 、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当 外载荷被放大 k d 倍,则变形、应力、应变也同样被放大 k d 倍。所以有 σ d = k dσ st 。有了 k d 很 方便就能计算出动载荷条件下被冲击物的各量。 (2) 、但应注意,对不同的问题, k d 有不同 的表达式,不能生搬硬套。 (3 ) 、掌握本题所采用的以能量守恒为基本原理的分析方法是最 重要的。 3 一个橡胶小球重 W = 300 mN ,用一橡皮筋连在一木拍上,橡皮筋长 L0=300 mm ,横截 面面积 A = 1.6 mm 2 ,弹性模量 E = 2.0 MPa 。用木拍击打小球后,小球拉动橡皮筋,使橡 皮筋总长达到 L1 = 1.0 m ,试问小球离开木拍瞬间的速度是多少?假设橡皮筋为线弹性体, 而且忽略小球的势能。 解题分析:木拍击打小球是冲击载荷问题。小球受木拍撞击飞出,将连接小球和木拍的橡皮 筋拉长。小球离开木拍的瞬间有一个初速度,橡皮筋被拉长的同时,小球速度不断减小,当 小球速度为零时,橡皮筋被拉至最长。假设不考虑小球的势能变化,则小球离开木拍瞬间的 动能完全转化为橡皮筋的应变能。即 E k = Vε 。 解:设小球离开木拍瞬间速度为 υ ,则其动能 E k =
0.8 m 1.944 × 10 2 m ) = 3.963 × 10 −3 m
∆d = 1.944 × 10 −5 m(1 + 1 +
考虑到 Fd =
EA ⋅ ∆d ,所以绳中最大应力 b
σd =
材料力学力法典型例题解
l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图,EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1)选图示相当系统(:一次超静定)
2)力法方程:
X 0
11 1
1P
3)利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2)力法方程
F
X 0
11 1
1P
3)图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4)解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1)选图示相当系统 (一次超静定)
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解:1)选图示静定基及相当系统
材料力学内部习题集及问题详解
第二章轴向拉伸和压缩2-1 一圆截面直杆,其直径d =20mm, 长L =40m ,材料的弹性模量E =200GPa ,容重γ=80kN/m 3, 杆的上端固定,下端作用有拉力F =4KN ,试求此杆的:⑴最大正应力; ⑵最大线应变; ⑶最大切应力;⑷下端处横截面的位移∆。
题 2 - 1 图+5004.8N4000N解:首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 】故最大正应力为:N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Ad d σππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α(α为杆内斜截面与横截面的夹角)为45︒时,maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点,2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为:240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2 试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。
已知杆横截面面积为A ,长度为L ,材料的容重为γ。
AB题 2-2 图A B解:距离A 为x 处的轴力为N ()F x Ax γ=⋅ 所以总伸长 2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 【2-3 图示结构,已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。
在结点A 处受荷载F 作用,今通过试验测得两杆的纵向线应变分别为ε1=4×10-4,ε2=2×10-4,试确定荷载P 及其方位角θ的大小。
材料力学全部习题解答讲解
1 2 R2
3
2
(b)
yc =
ydA
A
=
A
b 0
y ayndy b ayndy
=
n n
1 2
b
0
26
Iz =
y2dA
A
Iy =
z2dA
A
解: 边长为a的正方截面可视为由图示截面和一个半 径为R的圆截面组成,则
Iz
=I(za)
I(zR)=
a4 12
2R 4
0
FN A
10103 N 1000 106 m2
10MPa
由于斜截面的方位角 450
得该截面上的正应力和切应力分别为
45
0 cos2 10106 cos2 450 pa 5MPa
0 sin 2 1 10106 sin 900 pa 5MPa
2
18
解:1.求预紧力 由公式l FNl 和叠加原理,故有
EA
l
l1
l2
l3
Fl1 EA1
Fl2 EA2
Fl3 EA3
4F
E
l1 d12
l2 d22
l3 d32
由此得 F
El
18.65kN
4
l1
d
2 1
l2
d
2 2
l3
根据式
tan 2 2I y0z0
I z0 I y0
解得主形心轴 y 的方位角为 a =
3.计算主形心惯性矩
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
击构件瞬间的速度为 υ
,只须将前面(a)式右端改为
1 2
⋅
Pυ2 g
= Vε
,即可导出 kd
=
υ2 。 g∆st
(4)、前面推导过程中,冲击物的势能取为 Ep = P(h + ∆d ) ,一般情况下 ∆d << h ,可将其忽
略,取 Ep = Ph ,读者可仿照上面推导一下,并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为: kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论:(1)、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当
外载荷被放大 kd 倍,则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解:设小球离开木拍瞬间速度为υ ,则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ;而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ,其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形,
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ,于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数,则有
Fd P
=
∆d ∆st
= σd σ st
= kd ,将上述关系代入(d)式得: ∆d2 − 2∆st ∆d − 2∆st h = 0
解得: ∆d = ∆st (1+
1+ 2h ) ∆st
于是
kd
=
∆d ∆st
=1+
1+ 2h ∆st
冲击问题
典型习题解析
1 一圆杆横截面面积为 A ,弹性模量为 E ,杆下端带一法兰盘,杆上部套一圆形重物,如 图所示。设重物 P 离法兰盘高为 h ,当重物自由落下时,形成冲击载荷作用在杆上。试计算 杆中动应力。 解题分析:假设冲击物和杆端法兰均为刚体,则它们在冲击过程中没有应变能。同时,不考 虑其他能量损失,则,根据这一关系,即可建立冲击过程中的最大应力、变形等。 解: 重物落下后,当其达到最低点时,其势能完全转化为杆的应变能。所以有
EA 2L0
(∆L) 2
代入能量守恒方程 Ek
= Vε ,得
1 2
W g
υ2
=
EA 2L0
(∆L) 2 ,
υ=
EAg (∆L) 2 = WL0
EAg WL0
(L1
−
L0
)2
=
2.0 ×106 Pa ×1.6 ×10−6 m 2 × 9.8 m/s 2 300 ×10−3 N × 300 ×10−3 m
1+
2 × 440×10-3 2 ×10−3 m
m
= 44 ×10−3
m
= 44 mm
2、 计算动荷因数 将动载荷理解为变大了或变小了的静载荷,动载与静载之间存在特定的比例关系,
即 Fd = kdW ,其中系数 kd 即为动荷因数。
将上式两边同除以弹簧常量 k ,得到:
Fd k
=
kd
W k
, ∆d
= kd ∆st
Ep = Vε
(a)
其 中 EP 为 冲 击 物 的 势 能 。 设 受 冲 击 后 杆 的 最 大 变 形 为 ∆d , 则
Ep = P(h + ∆d )
(b)
Vε 为杆被冲击后的应变能,设重物对杆冲击作用的最大作用力为 Fd ,
则 Fd 做的功即为杆增加的应变能。
所以, Vε
=
1 2
Fd ∆d
于是由(a),(b),(c)三式有
空心柱体
外力功。 解:1、计算弹簧最大位移
题2图
设弹簧被冲击后,最大位移为 ∆d ,弹簧承受的最大冲击力为 Fd ,则由能量守恒得
W (h
+
∆d
)
=
1 2
Pd
∆d
。
由于弹簧常量为 k ,所以有 W = k∆st , Pd = k∆d 。 ∆st 为重物静止放在弹簧上时弹簧
的缩短量。于是有
W (h
+
∆d
方便就能计算出动载荷条件下被冲击物的各量。(2)、但应注意,对不同的问题, kd 有不同 的表达式,不能生搬硬套。(3)、掌握本题所采用的以能量守恒为基本原理的分析方法是最 重要的。
3 一个橡胶小球重W = 300 mN ,用一橡皮筋连在一木拍上,橡皮筋长 L0=300 mm ,横截
面面积 A = 1.6 mm2 ,弹性模量 E = 2.0 MPa 。用木拍击打小球后,小球拉动橡皮筋,使橡
(c) 题1图
P(h +
∆d )
=
1 2
Fd ∆d
,或
Fd ∆d
− 2P∆d
− 2Ph
=
0
(d)
对线弹性体,载荷与其相应位移存在关系 P = k ⋅ ∆st , k 为刚度系数。 ∆st 为载荷 P 作用
下杆的位移。设杆长为 l
,则
∆st
=
Pl EA
。动载荷时,同样有 Fd
=
k∆d
于是有 Fd
=
P ∆st
2 如图所示柱筒内重为 W = 20 N 重物从高为 h = 440 mm 处落到一个弹簧上,弹簧常量
k = 10 kN/m 。(1)确定弹簧的最大压缩位移;(2)
重物
计算动荷因数。
解题分析:忽略重物在冲击过程中的变形,并忽略
h
能量损失,则重物冲击弹簧后,其势能全部转化为
弹簧
弹簧应变能,利用能量守恒原理,则有 Ep = Vε ,Vε =
皮筋总长达到 L1 = 1.0 m ,试问小球离开木拍瞬间的速度是多少?假设橡皮筋为线弹性体, 而且忽略小球的势能。 解题分析:木拍击打小球是冲击载荷问题。小球受木拍撞击飞出,将连接小球和木拍的橡皮 筋拉长。小球离开木拍的瞬间有一个初速度,橡皮筋被拉长的同时,小球速度不断减小,当 小球速度为零时,橡皮筋被拉至最长。假设不考虑小球的势能变化,则小球离开木拍瞬间的
)
=
1 2
k∆d
⋅
∆d
即
k∆d2 − 2W∆d − 2Wh = 0 或 ∆d2 − 2∆st ∆d − 2∆st h = 0 。解得
∆d = ∆st (1+
1+ 2h ) ∆st
2
而 ∆st
=W k
= 20 N 10 ×103 N/m
= 2 ×10 −3
m
代入前式得
∆d = 2 ×10−3 m(1+
1
有了动荷因数后,可用下面式子计算动载荷作用下构件的变形和应力。
冲击载荷: Fd = kd P
冲击位移: ∆d = kd ∆st
冲击应力,即杆中的动应力:σ d
=
kdσ st
=
kd
P A
讨论: (1)、冲击载荷或其他动载荷作用下构件变形和应力计算可归结为计算动荷因数 kd ,
算出 kd 后,只要将相应的静载荷下的变形和应力乘以 kd ,即得到动载荷作用下构件的变形 和应力。(2)、当 h = 0 时,为突加载荷情况,这时 kd = 2 。(3)、水平冲击问题:设冲击物撞
