(完整word版)全概率公式与贝叶斯公式解题归纳.doc
2.3_1全概率公式和贝叶斯公式

P
A
|
B
P
A P B PB
|
A
=
0.999 0.05 0.0509
0.9813
由此可见该发明并不可靠!
例3 甲乙丙三人向同一架飞机射击, 他们击中的概率分 别为0.4、0.5和0.7. 若其中只有一人击中, 则飞机坠毁的 概率为0.2; 若其中有二人击中, 则飞机坠毁的概率是0.6; 若三人都击中, 则飞机必然坠毁. 求飞机坠毁的概率. 进一步问: 若已知飞机坠毁了, 则在坠毁前飞机是被命中 一弹的概率.
0.4138
贝叶斯公式
如果随机事件 A1, A2 , , An 构成样本空间的一个划分,
且都有正概率, 则对任何一个事件 B P B 0 , 有
P Aj | B
P Aj PB | Aj
n
,
P Ai P B | Ai
i 1
j 1, 2, , n.
例2 某厂生产的产品其不合格率为0.1% , 但是却没有适 当的仪器进行检验. 有人声称发明了一种仪器可以用来检 验, 误判的概率仅为5%, 即正品被误判为次品或者次品被 误判为正品的概率均为5%. 试问这个仪器是否靠谱?
0.4 0.5 0.3 0.41
P A3 0.4 0.5 0.7 0.14
再以 B 表示事件“飞机坠毁了”, 则由题意
P B | A0 0, P B | A1 0.2, P B | A2 0.6, P B | A3 1,
故由全概公式得:
3
P B P Ai P B | Ai 0.458.
解 以 A0, A1, A2, A3 分别表示事件“三人中分别有0、1、
2、3个人命中敌机”, 则由古典概率计算可得
第7节 全概率公式和贝叶斯公式
0.4825.
练习1 有朋自远方来,乘火车、船、汽车、飞机来的概率分别 为0.3,0.2,0.1,0.4,迟到的概率分别为0.25,0.3,0.1,0;求 他迟到的概率.
解 设A1=他乘火车来,A2=他乘船来,A3=他乘汽车来, A4=他乘飞机来,B=他迟到。
易见:A1, A2, A3, A4构成一个完备事件组,由全概率公式得
1. 引例 设甲盒有3个白球,2个红球,乙盒有4个白球,1个红 球,现从甲盒任取2球放入乙盒,再从乙盒任取两球,求
(1)从乙盒取出2个红球的概率; (2)已知从乙盒取出2个红球,求从甲盒取出两个红球的概率。
解 (1)设A1=从甲盒取出2个红球,A2=从甲盒取出2个白球; A3=从甲盒取出1个白球1个红球 ;B=从乙盒取出2个红球; 则A1, A2, A3 两两互斥,且A1+A2+A3=Ω, 所以
i 1
i 1
i 1
3. 全概率公式的应用
如果试验E有两个相关的试验E1,E2复合而成, E1有若干种可能的结果,E2在E1的基础上也有若干种 可能的结果,如果求与E2的结果有关事件的概率,可 以用全概率公式.试验E1的几种可能的结果就构成了 完备事件组.
例1 播种用的一等小麦种子中混有2%的二等种子,1.5%的三 等种子, 1%的四等种子, 用一等、二等、三等、四等种子长出的 穗含50颗以上麦粒的概率分别为0.5,0.15,0.1、0.05,求这批种子所 结的穗含有50颗以上麦粒的概率。
P(B)= P(A1)P(B|A1 )+P(A2)P(B|A2)+P(A3)P(B|A3)
C22 C52
C32 C72
C32 C52
0 C72
C31C21 C22 C52 C72
全概率公式与贝叶斯公式

, i = 1,2,, n.
例1 某电子设备制造厂所用的元件是由三家元
件制造厂提供的.根据以往的记录有以下的数据 : 元件制造厂 1 2 3 无区别的标志. (1) 在仓库中随机地取一只元件 , 求它是次品的 概率; 次品率 0.02 0.01 0.03 提供元件的份额 0.15 0.80 0.05
= P ( A B1 ) P ( B1 ) P ( A B2 ) P ( B2 ) P ( A Bn ) P ( Bn ).
图示
B2
B1
A
B3
Bn1
化整为零 各个击破
Bn
2. 全概率公式
定理 设试验 E 的样本空间为 S , A 为 E 的事件 , B1 , B2 , , Bn为 S 的一个划分 , 且 P ( Bi ) > 0( i = 1, 2, , n ), 则
例2 设有一箱同类型的产品是由三家工厂生产的. 已知其中有50%的产品是第一家工厂生产的, 其他 二厂各生产25%. 又知第一、第二家工厂生产的有 2%是次品, 第三家工厂生产的有4%是次品. 现从此 箱中任取一个产品, 求拿到的是次品的概率.
例3
例4 甲、乙、丙三人同时对飞机进行射 击, 三人击中的概率分别为0.4、0.5、0.7. 飞机被一人击中而击落的概率为0.2,被两人击 中而击落的概率为0.6, 若三人都击中, 飞机 必定被击落, 求飞机被击落的概率。
§1.6 全概率公式和贝叶斯公式
一、全概率公式 二、贝叶斯公式
三、小结
一. 全概率公式
1. 样本空间的划分
定义 设 S 为试验 E的样本空间, B1 , B2 ,, Bn 为 E 的一组事件 , 若 (i ) Bi B j = , i j , i , j = 1, 2,, n ; (ii ) B1 U B2 U U Bn = S . 则称 B1 , B2 ,, Bn 为样本空间 S 的一个划分 .
贝叶斯公式和全概率-精品文档

山东农业大学
概率论与数理统计
主讲人:程述汉 苏本堂
例1 播种用的一等小麦种子中混有2%的二等种子,1.5%的三 等种子, 1%的四等种子, 用一等、二等、三等、四等种子长出的 穗含50颗以上麦粒的概率分别为0.5,0.15,0.1、0.05,求这批种子所 结的穗含有50颗以上麦粒的概率。 解 设从这批种子中任选一颗是一等、二等、三等、四等种子 的事件分别为B1,B2,B3,B4,则它们构成样本空间的一个划分, 用A表示在这批种子中任选一颗,且这颗种子所结的穗含有50 粒以上麦粒的事件,则由全概率公式
定义1 设事件A1,A2,…,An为样 本空间的一组事件。 如果 (1) Ai Aj= (i≠j); (2)
A1 A3
A2 …
… An
n
Ai
则称A1,A2,…,An为样本空间的一个划分。 例如上例中的 A1=从甲盒取出2个白球, A2=从甲盒取出2个红球, A3=从甲盒取出1个白球1个红球, 就构成了一个完备事件组。
解 设A1=他乘火车来,A2=他乘船来,A3=他乘汽车来, A4=他乘飞机来,B=他迟到。 易见:A1, A2, A3, A4构成一个完备事件组,由全概率公式得
P ( B ) P ( A i) P ( B |A i)
i 1
4
=0.3×0.25+ 0.2×0.3+ 0.1×0.1+ 0.4×0
P(A) P(B (A| B i )P i)
i1
4
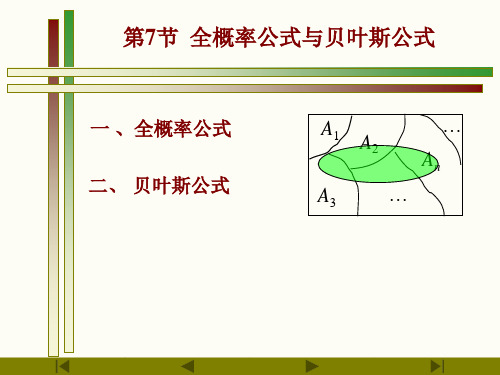
9 5 . 5 % 0 . 5 2 % 0 . 1 5 1 . 5 % 0 . 1 1 % 0 . 0 5 0 . 4 8 2 5 .
山东农业大学
概率论与数理统计
主讲人:程述汉 苏本堂
(完整word版)全概率公式与贝叶斯公式解题归纳.doc

全概率公式与贝叶斯公式解题归纳来源:文都教育在数学一、数学三的概率论与数理统计部分,需要用到全概率公式及其贝叶斯公式来解题. 这类题目首先要区分清楚是“由因导果” ,还是“由果索因” ,因为全概率公式是计算由若干“原因” 引起的复杂事件概率的公式,而贝叶斯公式是用来计算复杂事件已发生的条件下,某一“原因”发生的条件概率 .它们的定义如下:全概率公式:设 B1 , B2 , , B n为样本空间的一个划分,如果P( B i)0,i1,2,L , n ,则对任一事件A有nP( A)P(B i )P( A | B i ) .i 1贝叶斯公式:设 B1 ,B2 , ,B n是样本空间的一个划分,则P(B i | A) n P(B i )P( A | B i ), i 1,2, , n. P( B j ) P( A | B j )j 1例 1 从数字 1, 2, 3, 4 中任取一个数,记为X,再从 1,, X 中任取一个数,记为Y,则 P(Y 2) .解由离散型随机变量的概率分布有:P(X 1) P(X 2) P(X 3) P(X 4) 1 4.由题意,得P(Y 2X 1) 0,P(Y 2X 2) 12,P(Y 2 X 3) 1 3, P(Y 2 X 4) 1 4 ,则根据全概率公式得到P(Y 2) P( X 1)P(Y 2 X 1) P( X 2)P(Y 2 X2) P( X 3)P(Y 2 X3) P( X 4)P(Y 2 X4)1 1 1 1 134(03).2 4 48例 2 12 件产品中有 4 件次品, 在先取 1 件的情况下, 任取 2 件产品皆为正品, 求先取1 件为次品的概率 .解 令 A={先取的 1 件为次品 },则 A, A 为完备事件组,P( A)1 ,P( A)23 , 令 B={后3取的 2 件皆为正品 },则 P( B A)C 8228, P(B A) C 7221,C 11255C 11255由贝叶斯公式得P( AB)P( A)P(B A)1 28 23 55 .P(A B)P( A)P(B A) P(A)P(B A)1 282 21 5P(B)3 553 55若随机试验可以看成分两个阶段进行, 且第一阶段的各试验结果具体结果怎样未知, 那么:( 1)如果要求的是第二阶段某一个结果发生的概率,则用全概率公式; ( 2)如果第二个阶段的某一个结果是已知的, 要求的是此结果为第一阶段某一个结果所引起的概率, 一般用贝叶斯公式,类似于求条件概率. 熟记这个特征,在遇到相关的题目时,可以准确地选择方法进行计算,保证解题的正确高效.。
§16全概率公式与贝叶斯公式_图文

29 P B1 P Ai P B1 Ai . 90 i 1
21
3
(2)问题归结为求 P B1 B2 . 由条件概率的 定义可得
PB B . (1.7) PB PB B PB B 下面我们先求 P B B . 由条件概率的本来
是 B 发生的所 有的不同的原 因
A1 A2
An
B
全概率公式 解决由因索 果问题
原因事件
结果事件
每个原因都可能导致B发生,故B发生的概率 是各原因引起B发生的概率的总和,“全概率公式” 之“全”取为此意.
4
自身努力 A1
原
学习环境良好 A2
学生成 绩好 B
因
教师教学水平高An
P ( B ) P ( Ai ) P B Ai .
2
1 2 1 3 1 2
6 5 4 6 2 5 2 6 5 2 1 6 3 . 8 7 6 8 7 6 8 7 6 8 7 6 4
9
小结例1.22和例1.23的结果:
3 P A1 P A2 P A3 . 4 ◆从件数一定的正品和次品组成一批产品
P ( B ) P ( Ai ) P B Ai .
i 1
n
A1
A2
A3 B A4 A5
A6 Ω A7
A8
2
证
n n B B B Ai Ai B i 1 i 1
分配律 A1B, A2 B,, An B 两 两 不 相 容 ,
同理可得,
全概率公式与贝叶斯公式
例一商店出售的某型号的晶体管是甲、乙、丙三家工厂生产的,其中乙厂产品占总数的50%,另两家工厂的产品各占25%。
已知甲、乙、丙各厂产品合格率分别为0.9、0.8、0.7,试求随意取出一只晶体管是合格品的概率(此货合格率)。
例连续做某项试验,每次试验只有成功和失败两种结果.已知当第k次成功时,第k+1次成功的概率为1/2 ,当第k次试验失败时,第k+1次成功的概率为3/4,如果第一次试验成功和失败的概率均为1/2,求第n次试验成功的概率.
例两台机床加工同样的零件,第一台出现废品的概率为0.05,第二台出现废品的概率为0.02,加工的零件混放在一起,若第一台车床与第二台车床加工的零件数为5:4。
求(1)任意地从这些零件中取出一个合格品的概率;
(2)若已知取出的一个零件为合格品,那么,它是由哪一台机床生产的可能性较大。
例(市场问题)某公司计划将一种无污染、无副作用的净化设备投放市场。
公司市场部事先估计该产品畅销的概率是0.5,一般为0.3,滞销为0.2。
为测试销路,公司决定进行试销,并设定了以下标准:若产品畅销,则在试销期内卖出7000~10000台产品的概率是0.6;若产品的销路一般,则在产品的试销期内卖出7000~10000台产品的概率是0.9;若产品滞销,则在试销期间能卖出7000~10000台产品的概率是0.2。
若在试销期满后,实际卖出的产品是9000台。
求该产品
(1)为销路一般的概率。
(2)为畅销品的概率。
(3)畅销或销路一般的概率。
全概率公式与贝叶斯公式
1
2. 全概率公式
定义 设为试验E的样本空间, A为E的事件, B1, B2 , , Bn为的一个划分,且P(Bi ) 0 (i 1, 2, , n),则
P( A) P( A | B1)P(B1) P( A | B2 )P(B2 ) P( A | Bn )P(Bn )
n
P(B)P( A | Bi ) i 1
2021/3/10
授课:XXX
15
先验概率与后验概率 上题中概率 0.95 是由以往的数据分析得到的, 叫 做先验概率.
而在得到信息之后再重新加以修正的概率 0.97 叫做后验概率.
2021/3/10
授课:XXX
16
例3 根据以往的临床记录,某种诊断肝癌的试
验具有如下的效果 : 若以 A 表示事件"试验反应 为阳性" , 以 C 表示事件"被诊断者患有癌症",则 有 P( A C) 0.95, P( A C) 0.90.现在对自然人群
贝叶斯公式
P ( Bi
A)
P(Bi )P( A Bi )
n
, i 1, 2,
, n.
P(Bj )P(A Bj )
j 1
2021/3/10
授课:XXX
21
2.条件概率 P(B A) 与积事件概率 P( AB) 的区别.
P(AB) 表示在样本空间 中,计算 AB发生
的概率,而 P(B A) 表示在缩小的样本空间 A 中,
P(Bn )P( A | Bn )
图示
B2
A
B1
B3
B Bn1
n
化整为零 各个击破
2021/3/10
授课:XXX
3
说明 全概率公式的主要用途在于它可以将一个
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全概率公式与贝叶斯公式解题归纳
来源:文都教育
在数学一、数学三的概率论与数理统计部分,需要用到全概率公式及其贝叶斯公式来解
题. 这类题目首先要区分清楚是“由因导果” ,还是“由果索因” ,因为全概率公式是计算由若
干“原因” 引起的复杂事件概率的公式,而贝叶斯公式是用来计算复杂事件已发生的条件下,某
一“原因”发生的条件概率 .
它们的定义如下:
全概率公式:设 B1 , B2 , , B n为样本空间的一个划分,如果P( B i)0,
i1,2,L , n ,则对任一事件A有
n
P( A)P(B i )P( A | B i ) .
i 1
贝叶斯公式:设 B1 ,B2 , ,B n是样本空间的一个划分,则
P(B i | A) n P(B i )P( A | B i )
, i 1,2, , n. P( B j ) P( A | B j )
j 1
例 1 从数字 1, 2, 3, 4 中任取一个数,记为X,再从 1,, X 中任取一个数,记为Y,则 P(Y 2) .
解由离散型随机变量的概率分布有:
P(X 1) P(X 2) P(X 3) P(X 4) 1 4.
由题意,得
P(Y 2X 1) 0,P(Y 2X 2) 12,
P(Y 2 X 3) 1 3, P(Y 2 X 4) 1 4 ,则根据全概率公式得到
P(Y 2) P( X 1)P(Y 2 X 1) P( X 2)P(Y 2 X
2) P( X 3)P(Y 2 X
3) P( X 4)P(Y 2 X
4)
1 1 1 1 13
4
(0
3
)
.
2 4 48
例 2 12 件产品中有 4 件次品, 在先取 1 件的情况下, 任取 2 件产品皆为正品, 求先取
1 件为次品的概率 .
解 令 A={先取的 1 件为次品 },则 A, A 为完备事件组,
P( A)
1 ,P( A)
2
3 , 令 B={后
3
取的 2 件皆为正品 },则 P( B A)
C 8
2
28
, P(B A) C 72
21,
C 112
55
C 112
55
由贝叶斯公式得
P( AB)
P( A)P(B A)
1 28 2
3 55 .
P(A B)
P( A)P(B A) P(A)P(B A)
1 28
2 21 5
P(B)
3 55
3 55
若随机试验可以看成分两个阶段进行, 且第一阶段的各试验结果具体结果怎样未知, 那
么:( 1)如果要求的是第二阶段某一个结果发生的概率,则用全概率公式; ( 2)如果第二个
阶段的某一个结果是已知的, 要求的是此结果为第一阶段某一个结果所引起的概率, 一般用
贝叶斯公式,类似于求条件概率
. 熟记这个特征,在遇到相关的题目时,可以准确地选择方
法进行计算,保证解题的正确高效.。
