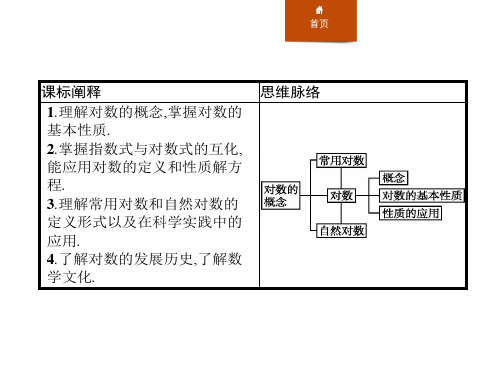
常用对数与自然对数
对数函数知识点(一)

对数函数知识点(一)对数函数定义对数函数是指满足以下条件的函数: - 底数为正实数且不等于1;- 函数定义域为实数集合中大于0的数; - 函数值域为实数集合。
常见的对数函数1.自然对数函数–底数为常数e(自然对数的底数),记作ln(x)或logₑ(x)。
–特点:以常数e为底的对数函数,在微积分中有广泛的应用。
2.以10为底的常用对数函数–底数为常数10,记作log₁₀(x)或log(x)。
–特点:以10为底的对数函数,在计算中常常用到。
对数函数的性质1.定义域和值域–自然对数函数的定义域为(0,+∞),值域为(-∞,+∞)。
–以10为底的常用对数函数的定义域为(0,+∞),值域为(-∞,+∞)。
2.基本性质–对数函数的图像总是位于一、二象限。
–对数函数的图像与直线y=x关于y=x对称。
3.特殊值–自然对数函数ln(x)当x=1时,ln(1)=0。
–以10为底的常用对数函数log(x)当x=1时,log(1)=0。
4.对数函数的性质–对数函数有唯一的反函数即指数函数。
–对数函数满足对数运算法则,如log(xy)=log(x)+log(y)。
5.对数函数的性质与图像–对数函数的图像有一个特点,就是随着自变量x的增大,函数值增长缓慢,近似于直线y=0。
–对数函数在x>1时,图像急剧上升;在0<x<1时,图像急剧下降。
应用领域•对数函数在科学计算、金融领域、生物学及工程学中有广泛的应用。
•对数函数常常用于解决指数增长与衰减问题、复杂的计算问题、百分比增长问题等。
以上为对数函数的相关知识点和详解。
对数函数作为数学中重要的函数之一,在各个领域中都有广泛的应用。
希望通过本文的介绍,能够对对数函数有更深入的了解。
对数函数的性质和图像对数函数的性质1.指数和对数的关系–对数函数是指数函数的反函数。
对于正实数a和b,有以下关系:logₐ(b) = x if and only if aˣ = b。
–例如,log₂(8) = 3,因为2³ = 8。
高一上册数学对数知识点

高一上册数学对数知识点对数是数学中一种重要的运算形式,能够将指数运算转化为对数运算,从而简化计算过程。
它在解决指数方程、评估指数函数的值以及处理复杂的数学问题方面起着重要作用。
在高中数学课程中,学习对数是必不可少的一部分。
下面我将为大家介绍高一上册数学中的几个重要的对数知识点。
一、对数的定义与性质1. 对数的定义:对于正数a(a≠1)和正数x,如果满足a^x=b (b>0),那么称x为以a为底b的对数,记作logₐb=x。
其中,a 被称为对数的底数,b被称为真数。
2. 对数的性质:(1)logₐ1=0,任何数的以自身为底的对数等于1。
(2)logₐa=1,任何数以其自身为底的对数等于1。
(3)logₐ(a*b)=logₐa+logₐb,任何两个正数的乘积的对数等于它们的对数之和。
(4)logₐ(a/b)=logₐa-logₐb,任何两个正数的商的对数等于它们的对数之差。
(5)logₐ(a^p)=p*logₐa,任何数的幂的对数等于指数与幂的底数的对数乘积。
二、常用对数与自然对数1. 常用对数:以10为底的对数称为常用对数,常用对数的记作logb,其中b表示真数。
常用对数的底数为10,即log₁₀b。
2. 自然对数:以自然常数e(约等于2.71828)为底的对数称为自然对数,自然对数的记作lnx,其中x表示真数。
三、对数运算的应用1. 对数方程:对数方程是指以对数形式表示的方程。
通过对数的性质,可以将一些指数方程转化为对数方程,从而更方便地解决问题。
2. 指数函数:指数函数是以指数形式表示的函数,具有形如f(x)=a^x的表达式,其中a为底数。
对数函数则是指数函数的逆运算,可以通过对数函数求解指数函数的值。
3. 对数尺度:对数尺度在测量和表达某些现象时往往更加合适。
例如在地震的震级表中,每增加一个单位的震级,地震的能量就增加10倍。
四、常用对数的换底公式1. 换底公式:对于任意正数a、b以及正整数n,换底公式为logₐb=logₐn * lognb。
高中数学对数的知识点总结

高中数学对数的知识点总结一、对数的定义1. 对数的概念对数是指数的逆运算。
设a为正实数且a≠1,a的正实数b的对数写作logₐb,读作“以a为底b的对数”。
其中a称为底数,b称为真数。
即logₐb=c,是等价的关系式a^c=b。
例如,log₂8=3,即等式2^3=8成立。
2. 对数的性质(1)底数为1时,b=1,a=1,log₁1=0;即logₐa=0。
(2)底数为正数时,即a>0,且a≠1时⒈对于任意正数b,1≠b,底数相等时,对数相等,即a>0,a≠1时,logₐb=logₐc,当且仅当b=c。
即对于任意正数b,0<a≠1,等式a^x=b的解是唯一的。
⒉对于任意正数a,b,c,当a>0,a≠1时,loga(b*c)=loga(b)+loga(c)。
⒊对于任意正数a,b,c,当a>0,a≠1时,loga(b/c)=loga(b)-loga(c)。
⒋对于任意正数a,b,当a>0,a≠1时,loga(b^c)=c*loga(b),其中c是常数。
3. 对数的求值对数的求值即是用对数的性质,把对数的计算用其它运算替代。
4. 对数的应用对数是一个非常重要和常见的概念,在数学中有着广泛的应用。
在科学、工程、经济和社会等领域中,对数都有着重要的作用。
例如在地震、声音、强度、音乐、语言学和政治领域等,都用到对数。
二、对数的基本概念1. 对数方程的解法对数方程的解法是通过对数的性质来解对数方程。
分为以下几种类型:(1)把一个对数方程转化为同底数的对数方程,通过对数的定义和性质,解方程找到x的值。
(2)两个底数不同的对数方程,通过换底公式进行计算,转换成相同底数的对数方程。
2. 对数不等式的解法对数不等式的解法是把对数引入不等式组成的方程中,然后进一步思考分析,解不等式。
对数不等式常见的类型有以下几种:(1)把对数不等式分解为多个对数方程,然后再求解。
3. 对数方程组的解法对数方程组的解法是将多个对数方程组合成一个方程,然后根据对数的性质和方程组的解法,求解出方程组的解集。
对数的概念

对 数对数的概念学习目标 1.了解对数的概念.2.会进行对数式与指数式的互化.3.会求简单的对数值.知识点一 对数的有关概念对数的概念:一般地,如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数.常用对数与自然对数:通常将以10为底的对数叫做常用对数,以e(e =2.718 28…)为底的对数称为自然对数,log 10N 可简记为lg N ,log e N 简记为ln N .知识点二 对数与指数的关系一般地,有对数与指数的关系:若a >0,且a ≠1,则a x =N ⇔log a N =x .对数恒等式:log a N a =N ;log a a x =x (a >0,且a ≠1).知识点三 对数的性质1.1的对数为零.2.底的对数为1.3.零和负数没有对数.1.若3x =2,则x =log 32.( √ )2.因为a 1=a (a >0且a ≠1),所以log a a =1.( √ )3.log a N >0(a >0且a ≠1,N >0).( × )4.若ln N =12,则N =⎝⎛⎭⎫12e .( × )一、指数式与对数式的互化例1 将下列指数式与对数式互化:(1)2-2=14;(2)102=100; (3)e a =16;(4)1364-=14; (5)log 39=2;(6)log x y =z (x >0且x ≠1,y >0).解 (1)log 214=-2. (2)log 10100=2,即lg 100=2.(3)log e 16=a ,即ln 16=a .(4)log 6414=-13. (5)32=9.(6)x z =y .反思感悟 指数式与对数式互化的思路(1)指数式化为对数式:将指数式的幂作为真数,指数作为对数,底数不变,写出对数式.(2)对数式化为指数式:将对数式的真数作为幂,对数作为指数,底数不变,写出指数式. 跟踪训练1 将下列指数式与对数式互化:(1)log 216=4;(2)13log 27=-3;(3)43=64;(4)⎝⎛⎭⎫14-2=16.解 (1)由log 216=4,可得24=16.(2)由13log 27=-3,可得⎝⎛⎭⎫13-3=27.(3)由43=64,可得log 464=3.(4)由⎝⎛⎭⎫14-2=16,可得14log 16=-2.二、利用对数式与指数式的关系求值例2 求下列各式中x 的值:(1)log 64x =-23;(2)log x 8=6;(3)lg 100=x . 解 (1)2233364(4)x --===4-2=116.(2)因为x 6=8,所以1111636662()8(2)2x x =====(3)10x =100=102,于是x =2. 反思感悟 要求对数的值,设对数为某一未知数,将对数式化为指数式,再利用指数幂的运算性质求解.跟踪训练2 (1)计算log 927;的值;(2)求下列各式中x 的值:①log 27x =-23;②log x 16=-4. 解 (1)设x =log 927,则9x =27,32x =33,∴2x =3,x =32.设81x =,则x =81,43x =34,∴x 4=4,x =16. (2)①∵log 27x =-23, ∴2233327(3)x --===3-2=19. ②∵log x 16=-4,∴x -4=16,即x 4=116=⎝⎛⎭⎫124, ∴x =12. 三、利用对数性质及对数恒等式求值例3 求下列各式中x 的值:(1)log 2(log 5x )=0;(2)log 3(lg x )=1;(3)71log 57.x -=解 (1)∵log 2(log 5x )=0,∴log 5x =20=1,∴x =51=5.(2)∵log 3(lg x )=1,∴lg x =31=3,∴x =103=1 000. (3)771log 5log 5777775.5x ÷÷-==== 反思感悟 (1)此类题型应利用对数的基本性质从整体入手,由外到内逐层深入来解决问题.log a N =0⇒N =1;log a N =1⇒N =a 使用频繁,应在理解的基础上牢记.(2)符合对数恒等式的,可以直接应用对数恒等式:log log .a N N a a N a N =,=跟踪训练3 (1)设3(log 21)327x +=,则x = .答案 13 (2)若log 2(log 3x )=log 3(log 4y )=log 4(log 2z )=0,则x +y +z 的值为( )A .9B .8C .7D .6答案 A解析 ∵log 2(log 3x )=0,∴log 3x =1.∴x =3.同理y =4,z =2.∴x +y +z =9.1.将⎝⎛⎭⎫13-2=9写成对数式,正确的是( )A .log 913=-2 B .13log 9=-2 C .13log (2)-=9D .log 9(-2)=13答案 B解析 根据对数的定义,得13log 9=-2,故选B.2.若log a x =1,则( )A .x =1B .a =1C .x =aD .x =10答案 C3.方程3log 2x =14的解是( ) A .x =19 B .x =33C .x = 3D .x =9 答案 A解析 ∵3log 2x =2-2,∴log 3x =-2,∴x =3-2=19. 4.下列指数式与对数式互化不正确的一组是( )A .e 0=1与ln 1=0B .138-=12与log 812=-13C .log 39=2与129=3D .log 77=1与71=7 答案 C5.已知log x16=2,则x=.答案 4解析log x16=2化成指数式为x2=16,所以x=±4,又因为x>0且x≠1,所以x=4.1.知识清单:(1)对数的概念.(2)自然对数、常用对数.(3)指数式与对数式的互化.(4)对数的性质.2.方法归纳:(1)根据对数的概念进行指数式与对数式的互化.(2)利用对数的性质及对数恒等式进行对数的化简与求值.3.常见误区:易忽视对数式中底数与真数的范围.1.有下列说法:①零和负数没有对数;②任何一个指数式都可以化成对数式;③以10为底的对数叫做常用对数;④以e为底的对数叫做自然对数.其中正确说法的个数为()A.1 B.2 C.3 D.4答案 C解析①③④正确,②不正确,只有a>0,且a≠1时,a x=N才能化为对数式.2.已知-ln e2=x,则x等于()A.-1 B.-2 C.1 D.2答案 B解析因为-ln e2=x,所以ln e2=-x,e2=e-x,x=-2.3.若log a 5b=c,则下列等式正确的是()A.b5=a c B.b=a5c C.b=5a c D.b=c5a 答案 B解析由log a 5b=c,得a c=5b,所以b=a5c.4.下列四个等式:①lg(lg 10)=0;②lg(ln e)=0;③若lg x=10,则x=10;④若ln x=e,则x=e2. 其中正确的是()A.①③B.②④C.①②D.③④答案 C解析①lg(lg 10)=lg 1=0;②lg(ln e)=lg 1=0;③若lg x=10,则x=1010;④若ln x=e,则x=e e.故只有①②正确.5.若log a3=m,log a5=n,则a2m+n的值是()A.15 B.75 C.45 D.225答案 C解析由log a3=m,得a m=3,由log a5=n,得a n=5,∴a2m+n=(a m)2·a n=32×5=45.6.=.答案8解析设81=t,则(3)t=81,23t=34,t2=4,t=8.7.已知log7[log3(log2x)]=0,那么12x =.答案2 4解析∵log7[log3(log2x)]=0,∴log3(log2x)=1,∴log2x=3,∴23=x,∴12x -=()1322-=18=122=24. 8.若对数log (x -1)(2x -3)有意义,则x 的取值范围是 .答案 ⎝⎛⎭⎫32,2∪(2,+∞)解析 由⎩⎪⎨⎪⎧ x -1>0,x -1≠1,2x -3>0,得⎩⎪⎨⎪⎧ x >1,x ≠2,x >32,得x >32且x ≠2. 9.将下列指数式化为对数式,对数式化为指数式.(1)53=125; (2)4-2=116; (3)12log 8=-3;(4)log 3127=-3. 解 (1)∵53=125,∴log 5125=3.(2)∵4-2=116,∴log 4116=-2. (3)∵12log 8=-3,∴⎝⎛⎭⎫12-3=8. (4)∵log 3127=-3,∴3-3=127. 10.(1)先将下列式子改写成指数式,再求各式中x 的值.①log 2x =-25;②log x 3=-13. (2)已知6a =8,试用a 表示下列各式.①log 68;②log 62;③log 26.解 (1)①因为log 2x =-25,所以x =252-=582. ②因为log x 3=-13,所以13x -=3,所以x =3-3=127. (2)①log 68=a .②由6a =8得6a =23,即36a =2,所以log 62=a 3. ③由36a =2得32a =6,所以log 26=3a.11.方程lg(x 2-1)=lg(2x +2)的根为( )A .-3B .3C .-1或3D .1或-3 答案 B解析 由lg(x 2-1)=lg(2x +2),得x 2-1=2x +2,即x 2-2x -3=0, 解得x =-1或x =3.经检验x =-1是增根,所以原方程的根为x =3. 12.0.51log 412-+⎛⎫ ⎪⎝⎭的值为( )A .6 B.72 C .8 D.37答案 C解析 0.51log 412-+⎛⎫ ⎪⎝⎭=⎝⎛⎭⎫12-1·12log 412⎛⎫ ⎪⎝⎭=2×4=8.13.若log (1-x )(1+x )2=1,则x = . 答案 -3解析 由log (1-x )(1+x )2=1,得(1+x )2=1-x , ∴x 2+3x =0,∴x =0或x =-3.注意到⎩⎪⎨⎪⎧1-x >0,1-x ≠1,∴x =-3. 14.若x 满足(log 2x )2-2log 2x -3=0,则x = .答案 8或12解析 设t =log 2x ,则原方程可化为t 2-2t -3=0,解得t =3或t =-1, 所以log 2x =3或log 2x =-1,所以x =23=8或x =2-1=12.15.若a >0,23a =49,则23log a 等于( ) A .2 B .3 C .4 D .5 答案 B解析 因为23a =49,a >0, 所以a =3249⎛⎫ ⎪⎝⎭=⎝⎛⎭⎫233, 设23log a =x ,所以⎝⎛⎭⎫23x =a .所以x =3.16.若12log x =m ,14log y =m +2,求x 2y 的值. 解 因为12log x =m ,所以⎝⎛⎭⎫12m =x ,x 2=⎝⎛⎭⎫122m . 因为14log y =m +2,所以⎝⎛⎭⎫14m +2=y ,y =⎝⎛⎭⎫122m +4. 所以x 2y =⎝⎛⎭⎫122m ⎝⎛⎭⎫122m +4=⎝⎛⎭⎫122m -(2m +4)=⎝⎛⎭⎫12-4=16.。
4.3.1 对数的概念
课前篇
自主预习
一
二
三
二、常用对数与自然对数
1.(1)10b=a用对数式如何表示?
提示:b=log10a,简记为b=lg a.
(2)在科学计算器上,有一个特殊符号“ln”,你知道它是什么吗?
提示:符号“ln”是一种对数符号,它是用来计算以“e”为底的对数的.
(3)ln M=n用指数式如何表示?
提示:en=M.
2
答案:C
)
随堂演练
课堂篇
探究学习
探究一
探究二
探究三
思维辨析
随堂演练
3.16、17世纪之交,随着天文、航海、工程、贸易以及军事的发展,
改进数字计算方法成了当务之急,数学家纳皮尔在研究天文学的过
程中,为简化计算发明了对数.直到18世纪,才由瑞士数学家欧拉发
现了指数与对数的互逆关系,即ab=N⇔b=logaN.现在已知a=log23,
2
x
1
A.4 =
2
2
D.log1 b=a
2
)
1
2
Hale Waihona Puke B. =441
C.x =
2
1
2
D.4 =x
(3)若对数 log(x-1)(4x-5)有意义,则 x 的取值范围是 (
5
5
A. ≤x<2
B. <x<2
4
5
C. <x<2 或 x>2
4
2
D.2≤x≤3
-1 > 0,
5
解析:(3)由题意得 -1 ≠ 1, 解得 x> ,且 x≠2.
B.
3
)
3
C. 3
对数与对数函数的基础知识梳理

课堂互动讲练
(2)原式=(llgg23+llgg29)·(llgg34+llgg38) =(llgg23+2llgg23)·(2llgg32+3llgg32) =32llgg23·56llgg32=54; (3)分子=lg5(3+3lg2)+3(lg2)2 =3lg5+3lg2(lg5+lg2)=3; 分母=(lg6+2)-lg 130600×110 =lg6+2-lg1060=4; ∴原式=34.
课堂互动讲练
自我挑战
(3)当x∈(1,+∞)时,f(x)>f(1), 要使f(x)>0,须f(1)≥0,∴a-b≥1.12分
规律方法总结
1.比较两个对数的大小的基本 方法是构造相应的对数函数,若底 数不相同时,可运用换底公式化为 同底数的对数,还要注意与0比较或 与1比较.
规律方法总结
2.把原函数做变量代换化归为二次 函数,然后用配方法求指定区间上的最 值是求对数函数的常见题型.在给定条 件下,求字母的取值范围也是常见题型, 尤其是与对数函数结合在一起的高考试 题更是屡见不鲜.
课堂互动讲练
跟踪训练
(2)法一:∵loga2=m,∴am=2. ∵loga3=n,∴an=3. 故a2m+n=(am)2·an=4×3=12. 法二:∵loga2=m,loga3=n, ∴a2m+n=a2loga2+loga3= aloga12=12.
课堂互动讲练
考点二
对数函数的图象
要正确识别函数图象,一是熟 悉各种基本函数的图象,二是把握图 象的性质,根据图象的性质去判断, 如过定点、定义域、值域、单调性、 奇偶性.
函数值分布
1,则 y<0 ; ②当0<a<1时:若x>1,
则 y<0 ;若x=1,则 y=0 ;
常用对数和自然对数转换

常用对数和自然对数转换常用对数和自然对数是数学中较为基础的两种对数,它们之间的转换可以在数学、物理等领域中提供帮助和便利。
下面介绍一下常用对数和自然对数的定义与转换方法。
常用对数是以10为底的对数,记作log10。
常用对数与我们生活中的数量级有着密切的关系,例如震级、声音的强度等都使用常用对数。
常用对数的性质与其他对数类似,例如,如果a与b均为正数,则log10(ab)=log10a+log10b。
自然对数是以e(自然常数)为底的对数,记作ln。
自然对数同样具有许多的应用,例如,在物理、统计学和天文学等领域中都可见到自然对数的使用。
自然对数也有一些特殊的的性质,例如,如果a与b 均为正数,则ln(ab)=lna+lnb。
常用对数和自然对数之间的转换可以使用以下公式进行计算:log10a=lna/ln10lna=log10a/ln e其中,e为自然常数,值为2.71828...,ln10约等于2.30259。
使用这两个公式,可以将常用对数和自然对数相互转换。
例如,如果要将常用对数log102转换成自然对数,便可以运用第一个公式,即log102=ln2/ln10使用计算器或手算,可得到log102约等于0.30103,因此ln2=log102/ln e≈0.30103/1≈0.30103同样,如果要将自然对数ln3转化成常用对数,则可以使用第二个公式:ln3=log103/ln e计算可得log103=ln3/ln10≈0.477因此,ln3转化成常用对数大约为0.477。
总之,对数在科学、商业和社会生活中都有着重要的应用。
掌握常用对数和自然对数的转换方法,可以帮助我们更好地进行数学、物理等方面的研究和分析。
对数函数知识点总结

对数函数知识点总结对数函数是数学中的一种重要的函数类型,广泛应用于各个科学领域。
本文将对对数函数的基本定义、性质以及应用进行总结。
1. 定义与性质对数函数是指数函数的逆运算。
设a是一个正实数且a≠1,b是任意正实数,则“以a为底b的对数”可以表示为logₐb。
其中底数a称为对数的底,b称为真数,logₐb称为对数。
对数函数通常用f(x) = logₐx表示。
对数函数具有以下基本性质:1)logₐ1 = 0:任何数以其本身为底的对数等于1。
2)logₐa = 1:任何数以其本身为底的对数等于1。
3)logₐaˣ = x:对数函数的一个基本性质是,以a为底的对数函数中,a的x次幂等于x。
即logₐaˣ = x。
4)logₐxy = logₐx + logₐy:对数函数中,底为a的对数函数中,两个数相乘的对数等于这两个数的对数之和。
即logₐxy = logₐx + logₐy。
5)logₐxⁿ = nlogₐx:对数函数中,底为a的对数函数中,以x为真数n次幂的对数等于n乘以以底为a,真数为x的对数。
即logₐxⁿ = nlogₐx。
2. 常用对数和自然对数常用对数函数是以10为底的对数函数,通常用log(x)表示,即log(x) = log₁₀x。
常用对数函数的性质和定义与之前的对数函数一致。
自然对数函数是以自然常数e(约等于2.71828)为底的对数函数,通常用ln(x)表示,即ln(x) = logₑx。
自然对数函数的性质与定义也与之前的对数函数相同。
3. 对数函数的应用对数函数在实践中有广泛的应用,下面举几个例子说明:1)指数增长与对数函数:对数函数在描述指数增长和衰减方面非常有用。
当某个变量随着时间的增加以指数形式增长或减少时,可以使用对数函数来描述其增长或减少的速度和幅度。
2)复利计算:对数函数在金融和投资领域中的应用非常重要。
例如,复利计算中,对数函数可以帮助计算利息的增长速度和总额。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明
一、常用对数
通常我们将以10为底的对数叫做常用对数,并把 ( )简记为 .
二、自然对数
以无理数e=2.71827为底的对数.以e为底的对数就叫做自然对数,并把它简记为lne.
作业与思考题:
课后回忆:
任课教师
教研室主任签字
济源职业技术学院
授 课 教 案 附 页
教学设计
说明
三、练习
1.求值:
; ; ;
; ;
; ; ;
; ; .
2.计算
(1) ;(2) ;
(3) ;(4) ;
(5)
3.填空题
(1) =;(2) =;(3) =;
(4) =;(5) =;(6) =.
4.将下列指数式化为对数式,对数式化为指数式.
(1) ;(2) ;(3) ;(4) ;(5) ;(6)
济源职业技术学院
济源职业技术学院
授 课 教 案
授课日期
2019.4.1
课时
2
课型
(请打√)
理论课实验课□习题课□上机课□其他□
授课章、节或主题
4.4.3常用对数与自然对数
教学目的要求:
知识目标:理解常用对数和自然对数的定义。
能力目标:会进行常用对数、自然对数的计算。
教学重点及难点:
重点:常用对数和自然对数的定义。
难点:会进行常用对数、自然对数的计算。
授.若 = ,则 =().
A B C D
6.已知 = , = ,用 , 表示下列各式:
(1) ;(2) ;(3) ;(4) .
