运筹学实验指导书Excel版样本
运筹学数学excel操作实例

根据对上述建模过程的总结,在电子表格中建立线性规划模型的步骤可归纳如下:
回忆例2-1某制药厂的生产计划问题,其求解结果如图13-8所示,即生产4公斤药品Ⅰ和2公斤药品Ⅱ,总利润为1400元.但该最优解是在假设所有的模型参数都准确的前提下做出的,在此基础上,管理层如果进一步考虑下列问题:
图13-11右下部分的“规划求解”对话框显示了求解时应注意的问题:求目标单元格的最大值(利润最大);约束为设备的实际使用时间小于等于设备的可用时间及实际总业务量小于等于总业务提供量的限制.
打开“选项”对话框,仍选择“采用线性模型”和“假定非负”,回到“规划求解”并按“求解”按钮,得到问题的最优方案为:每月X线及CT检查的业务量分别为1320人次和480人次,磁共振业务量为0,即不必购买该设备;按最优方案安排业务每月可获利55200元.
图13-10的右半部分显示了“规划求解”对话框及“选项”对话框的内容.该问题的目标是所用的胶管原料的总根数最少,因此设置目标单元格为I12等于最小值.由于实际获得的材料数量必须满足需求量的要求,考虑到最优方案(各种截法的某一组合)不一定能使截出的三种材料数量恰好等于需要的数量,而某种材料超过需求量是允许的,故在添加约束时可设置实际截得的数量大于等于需求量,即I9:I12>=K9:K12(本题中,该约束取“>=”和“=”的结果是相同的);又由于截出的各种材料数量均为整数,因此约束中应包括决策变量取整数的限制,即C13:H13=整数.
运筹学实验报告 运用EXCEL解线性规划 报告范文 让利益最大化 生产规划
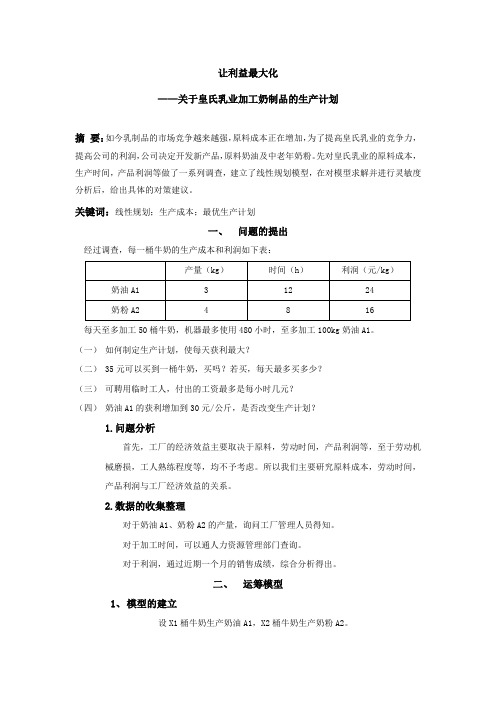
让利益最大化——关于皇氏乳业加工奶制品的生产计划摘要:如今乳制品的市场竞争越来越强,原料成本正在增加,为了提高皇氏乳业的竞争力,提高公司的利润,公司决定开发新产品,原料奶油及中老年奶粉。
先对皇氏乳业的原料成本,生产时间,产品利润等做了一系列调查,建立了线性规划模型,在对模型求解并进行灵敏度分析后,给出具体的对策建议。
关键词:线性规划;生产成本;最优生产计划一、问题的提出经过调查,每一桶牛奶的生产成本和利润如下表:每天至多加工50桶牛奶,机器最多使用480小时,至多加工100kg奶油A1。
(一)如何制定生产计划,使每天获利最大?(二) 35元可以买到一桶牛奶,买吗?若买,每天最多买多少?(三)可聘用临时工人,付出的工资最多是每小时几元?(四)奶油A1的获利增加到30元/公斤,是否改变生产计划?1.问题分析首先,工厂的经济效益主要取决于原料,劳动时间,产品利润等,至于劳动机械磨损,工人熟练程度等,均不予考虑。
所以我们主要研究原料成本,劳动时间,产品利润与工厂经济效益的关系。
2.数据的收集整理对于奶油A1、奶粉A2的产量,询问工厂管理人员得知。
对于加工时间,可以通人力资源管理部门查询。
对于利润,通过近期一个月的销售成绩,综合分析得出。
二、运筹模型1、模型的建立设X1桶牛奶生产奶油A1,X2桶牛奶生产奶粉A2。
Maxz=72X1+64X2St. X1+X2<=5012X1+8X2<=4803X1<=100X1,X2>=02、模型的求解应用EXCEL软件进行求解。
3、灵敏度分析包括对于目标系数(桶数)变化的灵敏度分析结果表和对于约束条件,如原料供应,劳动时间,加工能力等变化的灵敏度分析结果表。
4、结果分析(一)当20桶牛奶生产奶油A1,30桶生产奶粉A2,利润达到3360元,是最大值。
(二)原料增加1单位,利润增加48。
35元<48元,应该买(三)时间增加1单位,利润增加2元,能力增减不影响,所以临时雇用临时工人每小时不超过2元。
运筹学试验指导书

《运筹学》实验指导书课程代码:0410073课程名称:运筹学/ Operational Research开课院实验室:经济与管理学院实验中心适用专业:工商管理、物流、信息管理等专业教学用书:《运筹学》(《运筹学》孙萍等编,中国铁道出版社出版)第一部分实验课简介一、实验的地位、作用和目的及学生能力标准运筹学是一门应用科学,在教学过程中通过案例分析与研究并与现代计算机技术相结合,力求实现理论与实践相结合,优化理论与经济管理专业理论相结合。
实验,是《运筹学》课程中重要的实践环节。
通过实验,可弥补课堂理论教学中的不足,增加学生的感性知识;要使学生能掌握系统的管理科学中的整体优化和定量分析的方法,熟练运用运筹学程序,对实际问题和研究对象进行系统模拟。
二、试验内容应用Lindo6 .1版运筹学软件包,解决实际问题。
三、实验方式与基本要求1、实验方式:综合性实验预习要求:复习编程方法及线性规划、整数规划的算法,对实际问题和研究对象,构造数学模型,确定优化技术方法,设计出原始数据表格。
实验设备:台式电脑实验要求:按实验任务要求调试程序,程序执行结果应正确。
实验分组:1人/组2、基本要求①在实验室进行实验前,学生熟悉实验软件Lindo程序、操作方法等;②将程序调好后,将程序结果记录,并由实验教师检查后签字;③将数据及有关的参数等记录在已经设计好的原始数据表格中;④在一周内完成实验报告。
四、考核方式与实验报告要求学生进入实验室后签到,实验结束后,指导教师逐个检查并提问,根据学生操作、实验结果、回答问题情况及实验纪律及作风等方面给出学生成绩,再综合实验报告情况给出最后的成绩。
报告格式如附录。
第二部分Lindo背景及功能菜单简介一、Lindo简介1.Lindo简介:LINDO(Linear, INteractive, and Discrete Optimizer)是一种专门用于求解数学规划问题的软件包。
由于LINDO执行速度很快、易于方便输入、求解和分析数学规划问题。
运筹学实验指导书

Excel中规划求解宏模块的使用Excel自带的宏模块“规划求解”可用于求解线性规划、非线性规划、整数规划的最优解。
规划求解宏模块在Excel普通运行状况下一般不会启动,当需要调用时,可以从工具菜单条中加载宏来启动,其基本步骤如下。
(1)在工具菜单中选择“加载宏”选型。
(2)在加载宏对话框中选择“规划求解”选型。
图0-1加载“规划求解”宏(3)如果成功加载,则在工具菜单条中会出现“规划求解”选型。
由此,可以运用规划求解宏模块求解任何一个线性规划问题、整数规划问题、非线性规划问题,分别举例说明如下。
例1 营养配餐问题根据生物营养学理论,一个成年人每天要维持人体正常的生理健康需求,需要从食物中获取3000卡路里热量、55g蛋白质和800mg钙。
假定市场上可供选择的食品有猪肉、鸡蛋、大米和白菜,这些食品每千克所含热量和营养成分以及市场价格如表1-1所示。
如何选购才能在满足营养的前提下,使购买食品的总费用最小?表0-1 营养配餐问题数据表解,建立该问题的线性规划模型如下:假设x j (j=1,2,3,4)分别为猪肉、鸡蛋、大米和白菜每天的购买量,则其线性规划模型为:⎪⎪⎩⎪⎪⎨⎧=≥≥+++≥+++≥++++++=)4,3,2,1(0800500300200400551020605030002009008001200..24820min 4321432143214321j x x x x x x x x x x x x x t s x x x x z j 第一步:需要在Excel 中建立该问题的电子表格模型,如图0-2所示。
图0-2 营养配餐问题的Excel 表模型其中单元格B10:E10设置为决策变量单元格,F12设置为目标单元格,F4:F6设置为三个约束条件的左边项,即表示实际获得的营养。
目标单元格和约束条件左边项的函数如图0-3所示图0-3营养配餐问题中的公式设置函数sumproduct(区域1,区域2)为Excel 的常用函数,表示将区域1中对应元素与区域2中对应元素相乘后再相加。
【免费下载】《运筹学》实验指导书

第四 前一个实验项目完成后,后一个实验项目应另 起一页,所提供的模板已经对此进行了划分,请不要删除 各实验项目之间的分页符。指导教师批阅部分保证留出 3 行。
三、严格按照所提供的实验模板填写相关内容。其中:
(1)实验报告“ 步骤与分析”部分撰写格式为 5 号仿 宋_GB2312,单倍行距,首行缩进 2理解计算结果的相关解释,要求包含全部
运算结果及相关的敏感性分析结果)
相对照)
3.对结果作适当分析(与图解对比);
4.完成实验报告。(如有余力,以该软件做一下课后题,对单纯形法
(1) max z=x1+x2 s.t. x1+2x2<=4
x1-2x2>=5 x1,x2>=0 (2) max z=2x1+x2 s.t. x1+x2>=2 x1-2x2<=0 x1,x2>=0
5
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
运筹学实验指导书Excel版解析

运筹学实验报告册(适用于经济管理类专业)学号:姓名:专业:信息管理与信息系统实验一线性规划的Excel求解与软件求解一、实验目的熟悉Excel软件、管理运筹学软件,掌握线性规划的Excel求解和管理运筹学软件求解。
二、实验要求能识别线性规划有关问题并建立相应的线性规划模型,能写出线性规划的标准形式,理解线性规划解的概念,理解单纯形法原理。
三、实验原理及内容依据单纯形法求解原理及步骤,在Excel界面中输入数据,进行求解。
熟悉线性规划模型的建立过程,掌握数据整理与Excel规划求解的操作步骤。
线性规划模型的建立,数据的输入与求解是最基础的要求。
本节实验要求完成以下内容:1、线性规划模型的建立;2、Excel界面内数据的输入;3、利用Excel规划求解进行线性规划模型的求解。
四、实验步骤及结论分析1、某饲养场养动物出售,设每头动物每天至少需700g蛋白质、30g矿物质、100mg维生素。
现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表示。
饲料蛋白质(g)矿物质(g)维生素(mg)价格(元/kg)1 3 1 0.5 0.22 2 0.5 1.0 0.73 1 0.2 0.2 0.44 6 2 2 0.35 18 0.5 0.8 0.8(1)建立这个问题的线性规划模型Min f=0.2X1+0.7X2+0.4X3+0.3X4+0.8X5约束条件:3X1+2X2+X3+6X4+18X5>=700X1+0.5X2+0.2X3+2X4+0.5X5>=300.5X1+X2+0.2X3+2X4+0.5X5>=100X1,X2,X3,X4,X5>=0(2)对建立的模型进行Excel求解2、福安商场是个中型的百货商场,它对销售人员的需求经过统计分析如下所示:时间所需售货员人数星期日28人星期一15人星期二24人星期三25人星期四19人星期五31人星期六28人的两天是连续的,问应该如何安排售货人员的作息,既满足了工作需要,又是配备的售货人员的人数最少?(用管理运筹学软件求解)实验二 运输问题一、 实验目的熟悉Excel 软件,学会运输问题的Excel 求解与管理运筹学软件求解。
运筹学实验指导书

运筹学实验指导书运筹学实验指导书彭佑元闫莹刘东霞编经济与管理学院前言在目前的环境中,运筹学的性质正在改变。
这是因为人们对以算法为中心的课程不再有足够的耐心,相反,他们对以商业环境为背景的课程更为需要,包括一些著名的非数学问题、使用电子表格,以及建立和评估模型,而并非对模型结构本身的研究。
在教学中使用电子表格软件已经成为管理教学的一个明显的新潮流。
这意味着,原先在传统运筹学教科书中占有重要地位的代数学的门帘已经可以被轻轻拉开了。
对于未来的管理者和管理咨询人员,本实验将把重点放在电子表格在管理科学知识的应用上。
然而,对一个实际问题建立电子表格模型通常需要花很多时间在模型设计和数据输入上。
因此,常常按照下列工作程序,一步一步地完成建模:理解问题;以书面形式逐步展开某些重要结构;收集数据;用定量的语言表达数据间的关系;最后形成电子表格模型。
这种结构化的方法重点突出了建模的主要元素(数据、决策目标、约束条件、绩效度量)及其相应的不同类型的单元格。
另外,电子表格并不是进行管理科学分析的唯一工具,偶尔应用的代数学或图形分析工具也享有的重要地位。
电子表格软件只是我们达到某一目标的工具,而并非目标本身。
计算机运行的环境本实验介绍使用的应用软件是Microsoft Office 2000中文版中的Microsoft Excel,需要Microsoft Excel中的加载宏程序。
启动Excel后,在“工具”菜单上,单击“加载宏”命令。
在“加载宏”列表框中,选定待添加加载宏选项左侧的复选框。
单击“确定”按钮后,在“工具”菜单上就可以找到“规划求解”的命令项,这表明安装成功。
使用Excel的加载宏TreePlan在电子表格上进行构建和分析决策树。
与其他Excel加载宏一样,这些加载宏需要安装才能在Excel中显示出来。
目录1实验一线性规划113>.1实验目的11.2案例71.3实验内容71.4实验要求81.5练习9实验二指派问题92.1实验目的92.2案例152.3实验内容152.4实验要求162.5练习17实验三网络最优化--最短路问题173.1实验目的173.2案例213.3实验内容213.4实验要求223.5练习23实验四决策分析234.1实验目的234.2案例274.3实验内容274.4实验要求284.5练习29附录经典应用30(1)确定潘得罗索工业公司的产品组合31(2)联合航空公司的员工排程32(3)Citgo石油公司的供应、配送和营销规划实验一线性规划线性规划是一种对问题进行求解的方法,可以帮助管理者制定决策。
运筹学实验指导书

《运筹学》实验指导书一、实验项目一1、实验项目名称线性规划问题的求解2、实验内容利用运筹学软件包2.0对线性规划问题进行求解,利用P26例5进行验证。
3、实验目的和要求掌握应用运筹学软件包2.0对线性规划问题进行求解的方法。
4、实验原理单纯形法5、实验仪器和设备微型电子计算机6、实验步骤(1) a. 应用单纯形算法对标准型max{cx│Ax=b, x≥0}的线性规划问题求解最优解b. 数据文件格式第1行 m,n,l0,llm: 约束方程的个数;n: 决策变量的个数(不包括基变量);l0: 人工变量的个数;ll: ll=1---有人工变量,ll=0---无人工变量.第2─第m+3行a[i,j](i=1,m+2;j=1,m+n+1)a[i,j](i=1,m;j=1,n): 约束方程的系数矩阵;a[i,j](i=1,m;j=n+1,n+m): m阶单位矩阵,其中人工变量必须置于最后l0个;a[i,j](i=1,m;j=n+1): 约束方程的右端常数项列向量;a[i,j](i=m+1;j=1,m+n+1):ll=0---全部填零,ll=1---第1至第m行上位于j列中所有人工变量系数之和;a[i,j](i=m+2;j=1,m+n+1): 目标函数行上诸检验数.c. 运行按工具条运行按钮.d. 输出结果(a) 基可行解;(b) 最优解.e. 算例1、求解max z=2x[1]-2x[2]┌ -2x[1]+x[2]≤2s.t│ x[1]-x[2]≤1└ x[j]≥0,j=1,2解: 标准型为max z=2x[1]-2x[2]┌ -2x[1]+x[2]+x[3] =2s.t│ x[1]-x[2] +x[4]=1└ x[j]≥0,j=1,2,..,4数据文件:2 2 0-2 1 21 -1 10 0 02 -2 0输出结果:线性规划问题的最优解┏━━━━━━━━━━━━━━━━━┓┃基变量最优值┃┃ x( 3)= 4.00 ┃┃ x( 1)= 1.00 ┃┣━━━━━━━━━━━━━━━━━┫┃所有其它变量都等于零┃┃目标函数的最优值 max z= 2.00┃┗━━━━━━━━━━━━━━━━━┛线性规划问题的多最优解┏━━━━━━━━━━━━━━━━━┓┃基变量最优值┃┃ x( 3)= 6.50 ┃┃ x( 1)= 3.50 ┃┃ x( 2)= 2.50 ┃┣━━━━━━━━━━━━━━━━━┫┃所有其它变量都等于零┃┃目标函数的最优值 max z= 2.00┃┗━━━━━━━━━━━━━━━━━┛2、求解min f=x[1]+ x[2]┌ x[1]+2x[2]≥2s.t │ x[1]- x[2]≥1└ x[j]≥0,j=1,2解: 两阶段问题为min z= x[5]+x[6]max f1=-x[1]-x[2]┌ x[1]+2x[2]-x[3] +x[5] =2 s.t │ x[1]- x[2] -x[4] +x[6] =1└ x[j]≥0,j=1,2,...,6数据文件:2 4 2 11 2 -1 0 1 0 21 -1 0 -1 0 1 12 1 -1 -1 0 0 3-1 -1 0 0 0 0 0输出结果:┌──────────────────────────┐│最优解│├──────────────────────────┤│变量值││ x( 2)= 0.33 ││ x( 1)= 1.33 │├──────────────────────────┤│所有其它的变量均为零. ││目标函数最优值为 -1.66667 │└──────────────────────────┘(2) a. 应用对偶单纯形算法检验数全部为非正而初始基本解不可行的线性规划问题求解最优解b. 数据文件格式第1行 m,nm: 约束方程的个数;n: 决策变量的个数.第2─第m+1行a[i,j](i=1,m;j=1,m+n+1)a[i,j](i=1,m;j=1,n): 约束方程的系数矩阵;a[i,j](i=1,m;j=n+1,n+m): m阶单位阵;a[i,j](i=1,m;j=n+m+1): 约束方程的右端常数项列向量.第m+2行 c[j](j=1,m+n+1)c[j](j=1,n): 目标函数的系数行向量;c[j](j=n+1,m+n+1): 零向量.c. 运行按工具条运行按钮.d. 输出结果(a) 基变量的最优值;(b) 目标函数的最优值.e. 算例min f=2x[1]+x[2]┌ 3x[1]+ x[2]≥3s.t │ 4x[1]+3x[2]≥6│ x[1]+2x[2]≥2└ x[1],x[2]≥0标准型:max z=-2x[1]-x[2]┌ -3x[1]- x[2]+x[3] =-3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学
实验报告册
( 适用于经济管理类专业)
学号:
姓名:
专业: 信息管理与信息系统
实验一线性规划的Excel求解与软件求解
一、实验目的
熟悉Excel软件、管理运筹学软件, 掌握线性规划的Excel求解和管理运筹学软件求解。
二、实验要求
能识别线性规划有关问题并建立相应的线性规划模型, 能写出线性规划的标准形式, 理解线性规划解的概念, 理解单纯形法原理。
三、实验原理及内容
依据单纯形法求解原理及步骤, 在Excel界面中输入数据, 进行求解。
熟悉线性规划模型的建立过程, 掌握数据整理与Excel规划求解的操作步骤。
线性规划模型的建立, 数据的输入与求解是最基础的要求。
本节实验要求完成以下内容:
1、线性规划模型的建立;
2、 Excel界面内数据的输入;
3、利用Excel规划求解进行线性规划模型的求解。
四、实验步骤及结论分析
1、某饲养场养动物出售, 设每头动物每天至少需700g蛋白质、30g矿物质、 100mg维生素。
现有五种饲料可供选用, 各种饲料每kg营养成分含量及单价如表示。
要求确定既满足动物生长的营养需要, 又使费用最省的选用饲料的方案。
(1)建立这个问题的线性规划模型
Min f=0.2X1+0.7X2+0.4X3+0.3X4+0.8X5
约束条件:
3X1+2X2+X3+6X4+18X5>=700
X1+0.5X2+0.2X3+2X4+0.5X5>=30
0.5X1+X2+0.2X3+2X4+0.5X5>=100
X1,X2,X3,X4,X5>=0
( 2) 对建立的模型进行Excel求解
2、福安商场是个中型的百货商场, 它对销售人员的需求经过统计分析如下所示:
时间所需售货员人数
星期日28人
星期一15人
星期二24人
星期三25人
星期四19人
星期五31人
星期六28人
天, 并要求休息的两天是连续的, 问应该如何安排售货人员的作息, 既满足了工作需要, 又是配备的售货人员的人数最少? ( 用管理运筹学软件求解)
实验二运输问题
一、实验目的
熟悉Excel软件, 学会运输问题的Excel求解与管理运筹学软件求解。
二、实验要求
掌握运输问题的特殊性, 以及表上作业法和线性规划单纯形法的区别。
利用Excel软件, 掌握运输问题的线性规划方法计算机求解。
三、实验原理及内容
建立运输问题模型后, 在Excel界面中输入数据, 进行求解。
熟悉运输问题模型的建立过程, 掌握数据整理与Excel规划求解的操作步骤; 运输问题模型的建立, 数据的输入与求解是最基础的要求。
本节实验要求完成以下内容:
1、运输问题模型的建立;
2、 Excel界面内数据的输入;
3、利用Excel规划求解进行运输问题模型的求解。
四、实验步骤及结论分析
1、某公司从两个产地A1,A2将物品运往三个销地B1,B2,B3,各产地的产量、各销地的销量和各产地运往各销地的每件物品的运费如下表所示:
B1 B2 B3 产量( 件)
A1 6 4 6 200
A2 6 5 5 300
销量150 150 200
建立模型:
Minf=6X11+4X12+6X13+6X21+5X22+5X23
约束条件:
X11+X12+X13=200
X21+X22+X23=300
X11+X21=150
X12+X22=150
X13+X23=200
X11,X12,X13,X21,X22,X23>=0
2、某公司从两个产地A1,A2将物品运往三个销地B1,B2,B3,
销地
运费单价
产地
各产地的产量、各销地的销量和各产地运往各销地的每件物品的运费如下表所示:
B1 B2 B3 产量( 件)
A1 6 4 6 300
A2 6 5 5 300
销量150 150 200
建立模型:
Minf=6X11+4X12+6X13+0X14+6X21+5X22+5X23+0X24
约束条件:
X11+X12+X13+X14=300
X21+X22+X23+X24=300
X11+X21=150
X12+X22=150
X13+X23=200
X14+X24=100
X11,X12,X13,X14,X21,X22,X23,X24>=0
3、某公司从两个产地A1,A2将物品运往三个销地B1,B2,B3,各产地的产量、各销地的销量和各产地运往各销地的每件物品的运费如下表所示:
销地
运费单价
产地
600
500。
