第12讲-圆中的比例线段与圆内接四边形-学生版
第15课圆内接四边形(学生版)九年级数学上册《考点题型技巧》精讲与精练高分突破(浙教版)

第15课圆内接四边形目标导航学习目标1.了解圆的内接四边形和四边形的外接圆的概念.2.理解圆的内接四边形的性质定理:圆的内接四边形的对角互补.3.会运用圆的内接四边形的性质定理进行有关的论证和计算.知识精讲知识点01 圆内接四边形圆的内接四边形:如果一个四边形的各个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.知识点02 圆内接四边形的性质圆内接四边形的性质:圆的内接四边形的对角互补.能力拓展考点01 圆内接四边形的性质的应用【典例1】如图,⊙O经过△ABC的顶点A、B,与边AC、BC分别交于点D、E,连接BD、AE,且∠ADB =∠CDE.(1)求证:△ABE是等腰三角形;(2)若AB=10,BE=12,求⊙O的半径r.【即学即练1】如图,四边形ABCD内接于圆O,点E在对角线AC上.(1)若BC=DC,∠CBD=39°,求∠BCD的度数;(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.分层提分题组A 基础过关练1. 已知在圆的内接四边形ABCD中,∠A:∠B:∠C=2:3:7,则∠D等于()A.40°B.60°C.100°D.120°2. 如图,四边形ABCD内接于⊙O,E为BC延长线上一点.若∠DCE=65°,则∠BOD的度数是()A.65°B.115°C.130°D.140°3. 如图,四边形ABCD内接于⊙O,∠ABC=135°,AC=4,则⊙O的半径为()A.4 B.2C.D.44. 如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连结CE,DE.若∠BAD=105°,则∠DCE为()A.10°B.15°C.20°D.25°5. 如图,四边形ABCD内接于⊙O,若∠B=108°,则∠D的度数为.6. 在圆内接四边形ABCD中,∠D﹣∠B=40°,则∠B=度.7. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,连接AC,若∠CAB=40°,则∠ADC的度数是.8. 如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠A=55°,∠F=30°,则∠E=°.9. 如图,在⊙O的内接四边形ABCD中,∠DAE是四边形ABCD的一个外角,∠DAE=∠DAC.DB与DC相等吗?为什么?10.如图,⊙O的半径为2,四边形ABCD内接于⊙O,圆心O到AC的距离等于.(1)求AC的长;(2)求∠ADC的度数.题组B 能力提升练11. 如图,点A,B,C,D,E在⊙O上,所对的圆心角为50°,则∠C+∠E等于()A.155°B.150°C.160°D.162°12. 如图,点A、B、C在⊙O上,P为上任意一点,∠A=m,则∠D+∠E等于()A.2m B.C.180°﹣2m D.13. 如图,点A,B,C,D,E都是⊙O上的点,AC=AE,∠D=128°,则∠B=°.14. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.15. 如图,四边形ABCD内接于⊙O,对角线AC过圆心O,且AC⊥BD,P为BC延长线上一点,PD⊥BD,若AC=10,AD=8,则BP的长为.16. 如图,圆内接四边形ABCD中,∠BCD=90°,AB=AD,点E在CD的延长线上,且DE=BC,连接AE,若AE=4,则四边形ABCD的面积为.17.如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交P A的延长线于点M.其中正确的结论是(填序号).①∠MAC=∠PBC,②△ABC是等边三角形,③PC=P A+PB,④若P A=1,PB=2,则△PCM的面积=.18. 如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.(1)求证DB平分∠ADC,并求∠BAD的大小;(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.19. 如图1,在⊙O中,弦AD平分圆周角∠BAC,我们将圆中以A为公共点的三条弦BA,CA,DA构成的图形称为圆中“爪形A”,如图2,四边形ABCD内接于圆,AB=BC,(1)证明:圆中存在“爪形D”;(2)若∠ADC=120°,求证:AD+CD=BD.20.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.若∠E=∠F时,求证:∠ADC=∠ABC.(1)若∠E=∠F=42°时,求∠A的度数;(2)若∠E=α,∠F=β,且α≠β,请你用含有α、β的代数式表示∠A的大小.21.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.(1)请判断△ABC的形状?说明理由;(2)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.(3)证明:P A+PB=PC.22.如图,⊙O为四边形ABCD外接圆,其中=,其中CE⊥AB于E.(1)求证:AB=AD+2BE;(2)若∠B=60°,AD=6,△ADC的面积为,求AB的长.题组C 培优拔尖练23. 如图,四边形ABCD是⊙O内接四边形,,∠BCD=120°,连接AC,DE⊥AC于点E,连接BE,若∠BED=150°,AC=,则DE的长为.24.面积为18的圆内接四边形ABCD的对角线AC是直径,AD=DC,DE⊥AB于E,则DE=.25. 如图,四边形ABCD内接于⊙O,AD为直径,BC=CD=5,AD=5,E为对角线AC上一动点,连结BE并延长交⊙O于点F.(1)若BF⊥AD,求证:∠ABF=∠ACB;(2)求四边形ABCD的面积;(3)若△BCE为等腰三角形,求BF的长.26.研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图1,已知四边形ABCD内接于⊙O,对角线AC=BD,且AC⊥BD(1)求证:AB=CD;(2)若⊙O的半径为8,弧BD的度数为120°,求四边形ABCD的面积;(3)如图2,作OM⊥BC于M,请猜测OM与AD的数量关系,并证明你的结论.。
人教版高中数学选修四教学课件-与圆有关的比例线段

1 4
������������,
求������������的长.
解:设 CD=x,
则
PD=
4 5
������,
������������
=
1 5
������,
由相交弦定理知 PA·PB=PC·PD,
即
4×4=
1 5
������
·45
������,
解得x=10.故
CD=10.
题型一
题型二
题型三 题型四
解:如图,将PO延长交☉O于D. 根据割线定理,可得PA·PB=PC·PD. 设☉O的半径为r cm,
则6×(6+8)=(10.9-r)(10.9+r),
解得r=5.9,即☉O的半径为5.9 cm. 反思如果已知条件中出现过圆外同一点的圆的割线,那么常用到 割线定理.本题中,利用割线定理列出关于半径r的方程,进而可求出 r的值.
(4)利用“中间比”代换得到,在证明比例线段(不论共线与否),如果 不能直接运用有关定理,可以寻找“中间比”进行代换.
与圆有关的比例线段证明要诀:圆幂定理是法宝,相似三角形中 找诀窍,联想射影定理分角线,辅助线来搭桥,第三比作介绍,代数方 法不可少,分析综合要记牢,十有八九能见效.
2.垂径定理、切线长定理、射影定理、相交弦定理、切割线定 理之间的关系
题型一 题型二 题型三 题型四
题型一 相交弦定理的应用
【例1】 如图,过☉O内一点A作直线,交☉O于B,C两点,且
AB·AC=64,OA=10,则☉O的半径 r=
.
题型一 题型二 题型三 题型四
解析:如图,作直线 OA 交☉O 于 E,F 两点,则 AE=r-10,AF=r+10. 由相交弦定理,得(r-10)·(r+10)=64,解得 r=2 41(负值舍去). 故 r=2 41.
北师大版九年级下册数学:圆的内接四边形 (共18张PPT)

如图,两个四边形ABCD有什么共同的特点?
D A
D A
C
O
O
B
C
B
四边形ABCD的的四个顶点都在⊙O上,这样
的四边形叫做圆内接四边形; 这个圆叫做四边形的外接圆。
如图,我们发现∠BAD与∠BCD之间有什么关系?
圆内接四边形的对角互补。
D A
O
D A
C
O
B
C
B
几何语句:
∵四边形ABCD为圆内接四边形 ∴∠BAD+∠BCD=180°(圆内接四边形的对角互补)
想一想
D
如图,∠DCE是圆内接 A
四边形ABCD的一个外角,
∠A与∠DCE的大小有什
么关系?
O
B
C
E
随堂练习
在圆内接四边形ABCD中,∠A与∠C的度 数之比为4:5,求∠C的度数。
知识技能
1.如图,在⊙O中,∠BOD=80°,求∠A和 ∠C的度数。
D
A
O
C
B
知识技能
2.如图,AB是⊙O的直径,∠C=15°,求
பைடு நூலகம்
X= 60°
E A
F
X= 50°
定理 同弧或等弧所对的圆周角相等
新课学习
观察图,BC是⊙O的直径,它所对的圆周角有
什么特点?你能证明吗?
A
B
O
C
想一想 注意:此处不能直接连接BC,思路是先
保证过点O,再证三点共线。
观察图,圆周角∠BAC=90°,弦BC是直径吗?
为什么?
A
解:弦BC是直径。
连接OC、OB
(2017 锦州)如图,四边形ABCD是⊙O的内接四边形 ,AD与BC的延长线交于点E,BA与CD的延长线交于点F ,∠DCE=80°,∠F=25°,则∠E的度数为( )
圆内接四边形的性质与判定定理(人教选修)

圆. 3.判定定理的推论
对角
如果四边形的一个外角等于它的内角的
,那么这
个四边形的四个顶点共圆.
返回
[小问题·大思维] 1.所有的三角形都有外接圆吗?所有的四边形是否都 有外接圆? 提示:所有的三角形都有外接圆,但四边形并不一定 有外接圆. 2.如果一个平行四边形有外接圆,它是矩形吗? 提示:因为平行四边形的对角相等,圆内接四边形的 对角和为180°,所以该平行四边形一定是矩形.
圆的半径.
[命题立意] 本题主要考查圆内接四边形的判定、一元
二次方程根与系数的关系以及逻辑推理和运算能力.
返回
解:(1)证明:连接 DE, 根据题意在△ADE 和△ACB 中, AD×AB=mn=AE×AC, 即AADC=AAEB. 又∠DAE=∠CAB, 从而△ADE∽△ACB. 因此∠ADE=∠ACB, 所以 C,B,D,E 四点共圆.
返回
证明:(1)若∠DBA=∠CBA,则DF=CE. (2)若DF=CE,则∠DBA=∠CBA. 分析:本题考查圆内接四边形的判定及性质.解决本 题需要借助三角形全等证明角相等或边长相等.
返回
证明:(1)连接 AE、AF、AC、AD, 则∠3=∠4,∠5=∠6. 又∵∠1=∠2,∴ AD= AE . ∴AD=AE,∴△ACE≌△AFD. 故 CE=DF. (2)由(1)∠3=∠4,∠5=∠6, 又∵DF=CE, ∴△ACE≌△AFD, ∴AD=AE,∴∠1=∠2,即∠DBA=∠CBA.
返回
[悟一法] 证明比例线段或比例式通常利用三角形相似来解决, 而证明三角形相似,常利用圆内接四边形的性质寻找角 之间的关系.
返回
[通一类] 3.试证明:在圆内接四边形ABCD中,
AC·BD=AD·BC+AB·CD.
【高考精品复习】选修4-1 几何证明选讲 第3讲 圆中的比例线段与圆内接四边形

第3讲 圆中的比例线段与圆内接四边形【高考会这样考】1.考查相交弦定理,切割线定理的应用. 2.考查圆内接四边形的判定与性质定理. 【复习指导】本讲复习时,紧紧抓住相交弦定理、切割线定理以及圆内接四边形的判定与性质定理,重点以基本知识、基本方法为主,通过典型的题组训练,掌握解决问题的基本技能.基础梳理1.圆中的比例线段 定理名称基本图形条件结论 应用 相交弦定理弦AB 、CD 相交于圆内点P(1)P A ·PB =PC ·PD ; (2)△ACP ∽ △DBP(1)在P A 、PB 、PC 、PD 四线段中知三求一; (2)求弦长及角 切割线定理P A 切⊙O 于A ,PBC 是⊙O 的割线(1)P A 2=PB ·PC ; (2)△P AB ∽△PCA (1)已知P A 、PB 、PC 知二可求一; (2)求解AB 、AC 割线定理P AB 、PCD 是⊙O 的割线 (1)P A ·PB =PC ·PD ;(2)△P AC ∽△PDB(1)求线段P A 、PB 、PC 、PD 及AB 、CD ; (2)应用相似求AC 、BD2.圆内接四边形(1)圆内接四边形性质定理:圆内接四边形的对角互补. (2)圆内接四边形判定定理:①如果四边形的对角互补,则此四边形内接于圆;②若两点在一条线段同侧且对该线段张角相等,则此两点与线段两个端点共圆,特别的,对定线段张角为直角的点共圆.双基自测1.(2011·天津)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P.若PB=1,PD=3,则BCAD的值为________.解析∵ABCD为圆内接四边形,∴∠PBC=∠ADP,又∠P=∠P,∴△BCP∽△DAP,∴BCAD=PBPD=13.答案1 32.(2011·广州调研)如图,四边形ABCD内接于⊙O,BC是直径,MN与⊙O相切,切点为A,∠MAB=35°,则∠D=________.解析连接BD,由题意知,∠ADB=∠MAB=35°,∠BDC=90°,故∠D=∠ADB+∠BDC=125°.答案125°3.(2011·深圳调研)如图,AB是⊙O的直径,D是⊙O上一点,E为BD的中点,⊙O的弦AD与BE的延长线相交于点C,若AB=18,BC=12,则AD=________.解析如图,连接AE,∵AB是⊙O的直径,∴AE ⊥BE ,又E 是 BD 的中点, ∴∠BAE =∠EAC , 从而E 是BC 的中点, ∴BE =EC =6,AB =AC =18,由CD ·CA =CE ·CB ,得(18-AD )×18=6×12,故AD =14. 答案 144.(2011·广州模拟)如图,过点D 作圆的切线切于B 点,作割线交圆于A ,C 两点,其中BD =3,AD =4,AB =2,则BC =________.解析 ∵∠A =∠DBC ,∠D =∠D , ∴△ABD ∽△BCD ,AD BD =AB BC ,解得BC =32. 答案 325.如图所示,已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ,且AB =4,DE =CE +3,则CD 的长为________.解析 由相交弦定理知, EA ·EB =EC ·ED .(*)又∵E 为AB 中点,AB =4,DE =CE +3, ∴(*)式可化为22=EC (CE +3)=CE 2+3CE , ∴CE =-4(舍去)或CE =1.∴CD =DE +CE =2CE +3=2+3=5. 答案5考向一相交弦定理的应用【例1】►(2011·广东实验中学质检)如图,半径为2的⊙O中,∠AOB=90°,D 为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为________.[审题视点] 由勾股定理求AD,再由相交弦定理求DE.解析延长DO交圆O于另一点F,易知OD=1,则AD=AO2+OD2= 5.由相交弦定理得,AD·DE=BD·DF,即5·DE=1×3,DE=35 5.答案35 5相交弦定理主要用于与圆有关的比例线段的计算与证明,解题时要与相似三角形及圆周角、弦切角等相关知识综合应用.【训练1】(2011·广东)如图,AB、CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=2a3,∠OAP=30°,则CP=________.解析依题AP=PB=32a,由PD·CP=AP·PB,得CP=AP2PD=98a.答案98a考向二切割线定理的应用【例2】►如图所示,P A为⊙O的切线,A为切点,PBC是过点O的割线,P A=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E,求AD·AE的值.[审题视点] 由切割线定理知P A2=PB·PC,可得直径BC的长,要求AD·AE,由△ACE∽△ADB,得AD·AE=CA·BA,只要求出CA,BA的长即可.解如图所示,连接CE,∵P A是⊙O的切线,PBC是⊙O的割线,∴P A2=PB·PC.又P A=10,PB=5,∴PC=20,BC=15.∵P A切⊙O于A,∴∠P AB=∠ACP.又∠P为公共角,∴△P AB∽△PCA.∴ABCA=P APC=1020=12.∵BC为⊙O的直径,∴∠CAB=90°.∴AC2+AB2=BC2=225.∴AC=65,AB=3 5. 又∠ABC=∠E,∠CAE=∠EAB,∴△ACE∽△ADB,∴ABAE=ADAC.∴AD·AE=AB·AC=35×65=90.在圆中通过连接圆上的两点、作圆的切线等可以创造使用圆周角定理、圆心角定理、弦切角定理的条件,这是在圆的问题上解决角之间关系的重要技巧.【训练2】如图,⊙O与⊙O′外切于P,两圆公切线AC,分别切⊙O、⊙O′于A、C两点,AB是⊙O的直径,BE是⊙O′的切线,E为切点,连AP、PC、BC.求证:AP·BC=BE·AC.证明由题意可知∠APC=90°,连BP,则∠APB=90°,∴B、P、C在同一直线上,即P点在BC上,由于AB⊥AC,易证Rt△APB∽Rt△CAB.∴ABCB=PBAB,即AB2=BP·BC,又由切割线定理,得BE2=BP·BC,∴AB=BE,又Rt△APB∽Rt△CAB,∴ABCB=APCA,即AP·BC=AB·AC,∴AP·BC=BE·AC.考向三圆内接四边形性质的应用【例3】►(2011·辽宁三校联考)已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.(1)求证:Q、H、K、P四点共圆;(2)求证:QT=TS.[审题视点] (1)利用∠PHQ=∠PKQ=90°;(2)先证∠HKS=∠QSP,TS=TK,再证TS=QT.证明(1)∵∠PHQ=∠PKQ=90°,∴Q、H、K、P四点共圆.(2)∵Q、H、K、P四点共圆,∴∠HKS=∠HQP,①∵∠PSR=90°,∴PR为圆的直径,∴∠PQR=90°,∠QRH=∠HQP,②而∠QSP=∠QRH,③由①②③得,∠QSP=∠HKS,TS=TK,又∠SKQ=90°,∵∠SQK=∠TKQ,∴QT=TK,∴QT=TS.(1)四边形ABCD的对角线交于点P,若P A·PC=PB·PD,则它的四个顶点共圆.(2)四边形ABCD的一组对边AB、DC的延长线交于点P,若P A·PB=PC·PD,则它的四个顶点共圆.以上两个命题的逆命题也成立.该组性质用于处理四边形与圆的关系问题时比较有效.【训练3】如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G作⊙O的切线,切点为H.求证:(1)C,D,F,E四点共圆;(2)GH 2=CE ·GF .证明 (1)如图,连接BC .∵AB 是⊙O 的直径,∴∠ACB =90°. ∵AG ⊥FG ,∴∠AGE =90°. 又∠EAG =∠BAC , ∴∠ABC =∠AEG .又∠FDC =∠ABC , ∴∠FDC =∠AEG . ∴∠FDC +∠CEF =180°. ∴C ,D ,F ,E 四点共圆.(2)∵GH 为⊙O 的切线,GCD 为割线, ∴GH 2=GC ·GD .由C ,D ,F ,E 四点共圆,得∠GCE =∠AFE ,∠GEC =∠GDF . ∴△GCE ∽△GFD . ∴GC GF =GE GD, 即GC ·GD =GE ·GF .∴CH 2=GE ·GF .如何求解高考中几何证明选讲问题从近两年的新课标高考试题可以看出,高考对切割线定理的应用及四点共圆问题重点考查,题型为填空题或解答题.【示例】► (本题满分10分)(2011·新课标全国)如图,D ,E 分别为△ABC 的边AB ,AC 上的点,且不与△ABC 的顶点重合.已知AE 的长为m ,AC 的长为n ,AD ,AB 的长是关于x 的方程x 2-14x +mn =0的两个根.(1)证明:C ,B ,D ,E 四点共圆;(2)若∠A =90°,且m =4,n =6,求C ,B ,D ,E 所在圆的半径.第(1)问连DE ,证明△ADE ∽△ACB ,即证∠ADE =∠ACB ,根据对角互补判定四点C ,B ,D ,E 共圆;第(2)问先求AD 、AB 的长,再确定C ,B ,D ,E 四点所在圆的圆心,进一步求半径.[解答示范] (1)连接DE ,根据题意,在△ADE 和△ACB 中,AD ·AB =mn =AE ·AC ,即AD AC =AEAB .又∠DAE =∠CAB , 从而△ADE ∽△ACB .(3分) 因此∠ADE =∠ACB .所以C ,B ,D ,E 四点共圆.(4分)(2)m =4,n =6时,方程x 2-14x +mn =0的两根为x 1=2,x 2=12. 故AD =2,AB =12.(6分)取CE 的中点G ,DB 的中点F ,分别过G ,F 作AC ,AB 的垂线,两垂线相交于H 点,连结DH .因为C ,B ,D ,E 四点共圆,所以C ,B ,D ,E 四点所在圆的圆心为H ,半径为DH .(8分)由于∠A =90°,故GH ∥AB ,HF ∥AC .从而HF =AG =5,DF =12×(12-2)=5. 故C ,B ,D ,E 四点所在圆的半径为5 2.(10分)本题主要考查平面几何证明,四点共圆,三角形相似,一元二次方程根与系数的关系.四点共圆常用的证明方法是求证四边形的一个外角等于与它不相邻的内角,当然也可以求出过其中三点的圆,然后证另一点也在这个圆上,也可以证明以两个点为端点的线段的垂直平分线与以另两个点为端点的线段的垂直平分线相交.【试一试】(2011·辽宁)如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.(1)证明:CD∥AB;(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.[尝试解答] (1)因为EC=ED,所以∠EDC=∠ECD.因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.故∠ECD=∠EBA.所以CD∥AB.(2)由(1)知,AE=BE.因为EF=EG,故∠EFD=∠EGC,从而∠FED=∠GEC.连接AF,BG,则△EF A≌△EGB,故∠F AE=∠GBE.又CD∥AB,∠EDC=∠ECD,所以∠F AB=∠GBA.所以∠AFG+∠GBA=180°.故A,B,G,F四点共圆.。
第3讲圆中的比例线段与圆内接四边形汇总
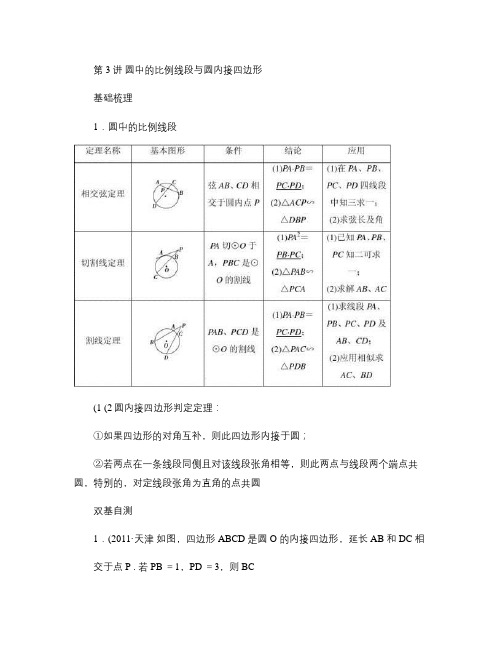
第3讲圆中的比例线段与圆内接四边形基础梳理1.圆中的比例线段(1 (2圆内接四边形判定定理:①如果四边形的对角互补,则此四边形内接于圆;②若两点在一条线段同侧且对该线段张角相等,则此两点与线段两个端点共圆,特别的,对定线段张角为直角的点共圆双基自测1.(2011·天津如图,四边形ABCD 是圆O 的内接四边形,延长AB 和DC 相交于点P . 若PB =1,PD =3,则BCAD ________.2.(2011·广州调研如图,四边形ABCD 内接于⊙O ,BC 是直径,MN 与⊙O 相切,切点为A ,∠MAB =35°,则∠D =________.3.(2011·深圳调研如图,AB 是⊙O 的直径,D 是⊙O 上一点,E 为BD 的中点,⊙O 的弦AD 与BE 的延长线相交于点C ,若AB =18,BC =12,则AD =________.4.(2011·广州模拟如图,过点D 作圆的切线切于B 点,作割线交圆于A ,C 两点,其中BD =3,AD =4,AB =2,则BC =________.5.如图所示,已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ,且AB =4,DE =CE +3,则CD 的长为________.考向一相交弦定理的应用【例1】►(2011·广东实验中学质检如图,半径为2的⊙O 中,∠AOB =90°,D 为OB 的中点,AD 的延长线交⊙O 于点E ,则线段DE 的长为________.【训练1】 (2011·广东如图,AB 、CD 是半径为a 的圆O 的两条弦,它们相交于AB 的中点P ,PD =2a3OAP =30°,则CP =________.考向二切割线定理的应用【例2】►如图所示,P A 为⊙O 的切线,A 为切点,PBC 是过点O 的割线,P A =10,PB =5,∠BAC 的平分线与BC 和⊙O 分别交于点D 和E ,求AD ·AE 的值.【训练2】如图,⊙O 与⊙O ′外切于P ,两圆公切线AC ,分别切⊙O 、⊙O ′于A 、C 两点,AB 是⊙O 的直径,BE 是⊙O ′的切线,E 为切点,连AP 、PC 、BC .求证:AP ·BC =BE ·AC .练习1、(房山2012年一模)如图,PA 是圆O 的切线,切点为A ,PO 交圆O 于, B C两点,1PA PB ==,则ABC ∠=((A )70︒(B )60︒(C )45︒(D )30︒ 2、(丰台区理科2012年一模)如图所示,Rt △ABC 内接于圆,60ABC ∠= ,P A 是圆的切线,A 为切点,PB 交AC 于E ,交圆于D.若P A =AE ,PDBD =则AP = ,AC .(1)3、如图,AB 是⊙O 的直径,直线DE 切⊙O于点D ,且与AB 延长线交于点C ,若CD =1CB =,则ADE ∠4、(石景山2012年一模)如图,已知圆中两条弦AB 与CD 相交于点F,CE 与圆相切交AB 延长线上于点E ,若DF CF ==::4:2:1AF FB BE =,则线段CE 的长为.(3)(4)_ E_D _ P _ C_ B_ A。
人教版九年级数学上册 24.1.6 圆内接四边形 课件
感悟新知
知识点 1 圆内接四边形及其对角的性质
知1-讲
下面,我们探究四边形与圆的关系.
四个顶点都在同一个圆上的四边形叫做圆内接四
边形,这个圆叫做四边形的外接圆.
如图,四边形ABCD为⊙O的内接四边形,⊙O为
四边形ABCD的外接圆.
感悟新知
知1-讲
特别解读 内接和外接是一个相对的概念,是一种位置关系. 每一个圆都有无数个内接四边形,但并不是所有
第二十四章 圆
24.1 圆的有关性质
第6课时 圆内接四边形
学习目标
1 课时讲解 圆内接四边形及其对角的性质
圆内接四边形外角的性质
2 课时流程
逐点 导讲练
课堂 小结
作内接三角形,圆的内接三 角形有哪些性质呢?今天我们探究的圆的内接四 边形的性质,我们根据圆内接三角形的定义,想 一想如何给圆内接四边形下定义呢?
(2)∠BAD和∠BCD之间具有怎样的关系? 提出你的猜想,并和大家进行交流.
感悟新知
我们发现:圆内接四边形的对角互补.
知1-练
下面我们对它进行证明.
已知:如图,四边形ABCD为⊙O的内接四边形.
求证:∠BCD+∠BAD= 180°,
∠ABC+∠ADC= 180°.
感悟新知
证明:如图,连接OB,OD.
的内接四边形,则∠A+∠B+∠C+∠D=360°.
课堂小结
圆
(3)任一外角与其相邻的内角的对角相等,简称圆 内接四边形的外角等于其内对角.
感悟新知
例 1 如果圆内接四边形ABCD的对角线交点恰好是该 圆的圆心,则四边形ABCD一定是( B )
知1-练
A.平行四边形 B.矩形 C.菱形 D.正方形 分析:由圆内接四边形ABCD的对角线交点恰好是该圆
圆中的重要模型-圆幂定理模型(学生版)
圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理,是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner)或者法国数学家普朗克雷(Poncelet)提出的。
圆幂定理的用法:可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件:在圆O中,弦AB与弦CD交于点E,点E在圆O内。
结论:△CAE∼△BDE⇒ECEB=EAED⇒EC⋅ED=EB⋅EA。
1(2023·广东广州·九年级校考期中)如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,两圆组成的圆环的面积是.2(2023·江西景德镇·九年级校考期末)如图,PT是⊙O的切线,T为切点,PA是割线,交⊙O于A、B两点,与直径CT交于点D.已知CD=2,AD=3,BD=4,那PB=.3(2023·江苏·九年级专题练习)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(1)为了说明相交弦定理正确性,需要对其进行证明,如下给出了不完整的“已知”“求证”,请补充完整,并写出证明过程.已知:如图①,弦AB,CD交于点P,求证:.(2)如图②,已知AB是⊙O的直径,AB与弦CD交于点P,且AB⊥CD于点P,过D作⊙O的切线,交BA的延长线于E,D为切点,若AP=2,⊙O的半径为5,求AE的长.模型2.双割线模型条件:如图,割线CH与弦CF交圆O于点E和点G。
结论:△CEG∼△CHF⇒ECCH=CGCF⇒EC⋅FC=GC⋅HC4(2023·浙江·九年级假期作业)如图:PAB、PCD为⊙O的两条割线,若PA∙PB=30,PC=3,则CD的长为()A.10B.7C.510D.35(2023·四川成都·九年级校考阶段练习)如图,PAB为⊙O的割线,且PA=AB=3,PO交⊙O于点C,若PC=2,则⊙O的半径的长为.6(2022·河南洛阳·统考一模)我们知道,直线与圆有三种位置关系:相交、相切、相离.当直线与圆有两个公共点(即直线与圆相交)时,这条直线就叫做圆的割线.割线也有一些相关的定理.比如,割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”,请补充完整.已知:如图①,过⊙O 外一点P 作⊙O 的两条割线,一条交⊙O 于A 、B 点,另一条交⊙O 于C 、D 点.求证:PA ⋅PB =PC ⋅PD .证明一:连接AD 、BC ,∵∠A 和∠C 为BD 所对的圆周角,∴.又∵∠P =∠P ,∴,∴.即PA ⋅PB =PC ⋅PD .研究后发现,如图②,如果连接AC 、BD ,即可得到学习过的圆内接四边形ABDC .那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.证明二:连接AC 、BD ,模型3.切割线模型条件:如图,CB 是圆O 的切线,CA 是圆O 的割线。
2021春北师版九年级数学下册 第3章 3.4.3 圆内接四边形
例2 如图,两圆相交于A,B两点,小圆
知1-讲
经过大圆的圆心O,点C,D分别在
两圆上,若∠ADB=100°,则
∠A与∠DCE的大小有什么关系?
知2-讲
推论:圆内接四边形的一个外角等于它的内对角.
知2-讲
例3 如图所示,四边形ABCD 为⊙ O 的内接四边形, 已知∠ BOD=100°,则∠ BCD 的度数为( )
导引: 如图所示,连接AD. ∵ AB 是⊙ O 的直径, ∴∠ ADB=90°,即AD ⊥ BC. 又∵ AC=AB,∴ BD=CD.
2 (中考·杭州)在圆内接四边形ABCD中,若∠A=70°, 则∠C等于( D ) A.20° B.30° C.70° D.110°
3 下列命题:①圆内接平行四边形是矩形;②圆内接矩 形是正方形;③圆内接菱形是正方形;④任意四边形 一定有外接圆.其中真命题有( B ) A.1个 B.2个 C.3个 D.4个
1 知识小结
圆内接四边形的角的“两种关系”: (1)对角互补,若四边形ABCD为⊙O的内接四边形,
则∠A+∠C=180°,∠B+∠D=180°. (2)任一外角与其相邻的内角的对角相等,简称圆内
接四边形的外角等于其内对角.
2 易错小结
已知△ABC内接于⊙O,OD⊥AC于点D,如果∠COD=
32°,那么∠B的度数为( D )
第三章 圆
3.4 圆周角和圆心角的关系
第3课时 圆内接四边形
1 课堂讲解 圆内接四边形及其对角的性质
2016-2017学年高中数学人教A版选修4-1课件:2.5 与圆有关的比例线段
又由切线长定理得PA=PB,OP为∠APB的平分线,
∴AB⊥OP,故应填PA⊥OA或PB⊥OB或AB⊥OP.
答案:AB⊥OP(答案不唯一)
-18-
-15-
五 与圆有关的比例线段 题型一 题型二 题型三 题型四
M 目标导航 UBIAODAOHANG
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
【例4】 如图,AB是☉O的直径,C是☉O上一点,过 点C的切线与过 A,B两点的切线分别交于点E,F,AF与BE交于点P.
-10-
五 与圆有关的比例线段 题型一 题型二 题型三 题型四
M 目标导航 UBIAODAOHANG
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
【变式训练2】
如图,PB和PD为 圆 的两条割线,分别交圆于点A,B和点C,D.若
PA=5,AB=7,CD=11,则 AC∶BD= .
-4-
五 与圆有关的比例线段
M 目标导航 UBIAODAOHANG
Z重难聚焦 HONGNAN JVJIAO
D典例透析 IANLI TOUXI
2.垂径定理、切线长定理、射影定理、相交弦定理、切割线定 理之间的关系
剖析:如图,PA,PB为☉O的两条切线,A,B为切点,PCD为过圆心O 的割线,连接AB,交PD于点E,则有下列结论:
D典例透析 IANLI TOUXI
反思如果已知条件中出现过圆外同一点的切线,那么常用到切线
长定理.首先要注意分析其中的等量关系,即①切线长相等,②圆外
的点与圆心的连线平分两条切线的夹角,然后结合直角三角形、相 似三角形等图形的有关性质进行计算与证明.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12讲:圆中的比例线段与圆内接四边形
【学习指导】
本讲学习时,紧紧抓住相交弦定理、切割线定理以及圆内接四边形的判定与性质定理,重点以基本知识、基本方法为主,通过典型的题组训练,掌握解决问题的基本技能.
基础梳理
1.圆中的比例线段
2.圆内接四边形
(1)圆内接四边形性质定理:
(2)圆内接四边形判定定理:①
②
双基自测
1.(2011·天津)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点
P.若PB=1,PD=3,则BC
AD的值为________.
第1题图第2题图第3题图2.(2011·广州调研)如图,四边形ABCD内接于⊙O,BC是直径,MN与⊙O相切,切点为A,∠MAB=35°,则∠D=________.
3.(2011·深圳调研)如图,AB是⊙O的直径,D是⊙O上一点,E为BD的中点,⊙O的弦AD与BE的延长线相交于点C,若AB=18,BC=12,则AD=________.
4.(2011·广州模拟)如图,过点D作圆的切线切于B点,作割线交圆于A,C两点,其中BD=3,AD=4,AB=2,则BC=________.
5.如图所示,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE +3,则CD的长为________.
【例1】►(2011·广东实验中学质检)如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为________.
【训练1】(2011·广东)如图,AB、CD是半径为a的圆O的两条弦,它们相交于AB
的中点P,PD=2a
3,∠OAP=30°,则CP=________.
【例2】►如图所示,P A为⊙O的切线,A为切点,PBC是过点O的割线,P A=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E,求AD·AE的值.
【训练2】如图,⊙O与⊙O′外切于P,两圆公切线AC,分别切⊙O、⊙O′于A、C两点,AB是⊙O的直径,BE是⊙O′的切线,E为切点,连AP、PC、BC.
求证:AP·BC=BE·AC.
考向三圆内接四边形性质的应用
【例3】►(2011·辽宁三校联考)已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR、PS的垂线,垂足分别为点H、K.
(1)求证:Q、H、K、P四点共圆;(2)求证:QT=TS.
【训练3】如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G 作⊙O的切线,切点为H.求证:(1)C,D,F,E四点共圆;(2)GH2=CE·GF.
如何求解高考中几何证明选讲问题
从近两年的新课标高考试题可以看出,高考对切割线定理的应用及四点共圆问题重点考查,题型为填空题或解答题.
【示例】►(本题满分10分)(2011·新课标全国)如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB 的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
【试一试】(2011·辽宁)如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.。
