第二章线性规划的对偶理论和灵敏度分析自测题key
《运筹学》胡运权 第4版 第二章 线性规划的对偶理论及灵敏度分析

b2 bm
x1, x2 , , xn 0
对 称 形 式 的
的 定 义
m W ib 1 n y 1 b 2 y 2 b m y m 对
s.t.
a11 a12 a1n
a21 a22 a2n
am1 y1 c1
am2 y2 amn ym
c2 cn
偶 问 题
y1, y2 , , ym 0
a23 x3 a33 x3
b2 b3
x1 0, x2 0, x3无 约 束
(2.4a) (2.4b) (2.4c) (2.4d)
先转换成对称形式,如下:
的 的一个变量,其每个变量对应于对偶问题 的一个约束。
定
义
m Z a c 1 x 1 x c 2 x 2 c n x n 一
对 偶
a11x1 a12x2 a1n xn (,)b1
a2
1x1
a22x2
a2n xn
(, )b2
般 线 性
问 题 的 定 义
am1x1 am2 x2 amnxn (,)bm xj 0( 0,或符号不限) j 1 ~ n
问题。
对
对偶问题是对原问题从另一角度进
偶
行的描述,其最优解与原问题的最 优解有着密切的联系,在求得一个
原
线性规划最优解的同时也就得到对 偶线性规划的最优解,反之亦然。
理
对偶理论就是研究线性规划及其对 偶问题的理论,是线性规划理论的
重要内容之一。
问 题 的 导 出
例2-1
我们引用第一章中美佳公司的例子,如表1
的
x1, x2, , xn 0
对
m W ib 1 n y 1 b 2 y 2 b m y m
第2章 线性规划的对偶理论与灵敏度分析2.6

2.6.2汽油配料模型 汽油配料模型 例2.6.2 一种汽油的特性可用两个指标描述: 其点火性用 “辛烷数”描述,其挥发性用“蒸汽压力”描述。某炼油厂有四 种标准汽油, 其标号分别为1, 2, 3,4,其特性及库存量列于表 2.6.2中,将上述标准汽油适量混合,可得两种飞机汽油,某标 号为1,2,这两种飞机汽油的性能指标及产量需求列于表2.6.3 中。问应如何根据库存情况适量混合各种标准汽油,使既满足 飞机汽油的性能指标,而产量又最高。
解
设计划生产 A1 , A2 , A3的数量分别为 x1 , x2 , x3,则可建立线性规划 max S = 30 x1 + 20 x 2 + 50 x3 x1 + 2 x 2 + x3 ≤ 430 3 x + 2 x3 ≤ 460 1 x1 + 4 x 2 ≤ 420 s.t . x1 + x 2 + x3 ≤ 300 x ≥ 70 2 x3 ≤ 240 x1 , x 2 , x3 ≥ 0 用LINGO求解
数学模型:
max =30*x1+20*x2+50*x3; x1+2*x2+x3<=430; 3*x1+2*x3<=460; x1+4*x2<=420; x1+x2+x3<=300; x2>=70; x3<=240;
求解得最优解: x1 = 0, x2 = 70, x3 = 230, max = 12900。 (1)将目标函数中x3的系数由50增至60,约束条件x3 ≤ 240改为x3 ≤ 210。 40 230 , x2 = , x3 = 210, max = 14533 > 12900。可行! 3 3 即使要求是整数解(关于整数规划见第三章) 求解得最优解: x1 = 在上述LINGO求解的语句后增加x1 , x2 , x3取值为整数的语句: @gin(xl);gin(x2);@gin(x3); 得到结果: x1 = 13, x2 = 77, x3 = 210, max = 14530 > 12900也可行。
第二章 线性规划问题的对偶理论与灵敏度分析总结
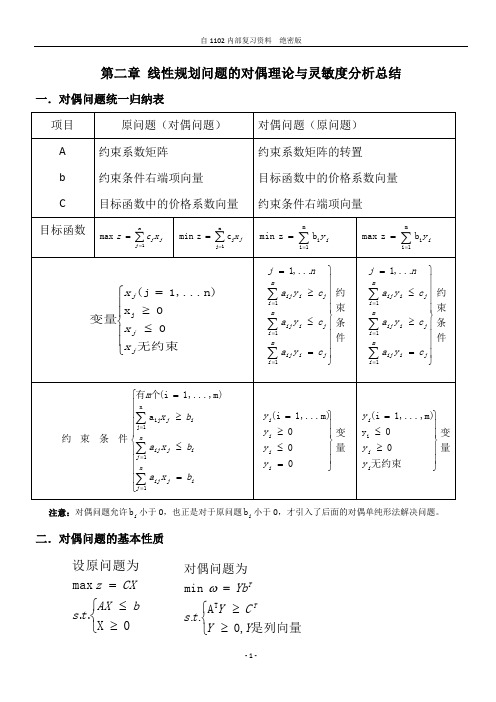
第二章 线性规划问题的对偶理论与灵敏度分析总结一.对偶问题统一归纳表注意:对偶问题允许i b 小于0,也正是对于原问题i b 小于0,才引入了后面的对偶单纯形法解决问题。
二.对偶问题的基本性质⎩⎨⎧≥≤=0X ..max 设原问题为b AX t s CXz⎩⎨⎧≥≥=是列向量,0A .. min 对偶问题为TY Y C Y t s Yb TTω1.对称定理:对偶问题的对偶是原问题2.弱对偶性定理:若Y X 和分别是原问题和对偶问题的可行解,则有b TY X C ≤推论(1)max 问题的任一可行解的目标是对偶问题最优目标值的一个下界。
min 问题的任一可行解的目标函数 值是原问题最优目标值的一个上界。
(2)若原问题可行且其目标函数值无界,则对偶问题无可行解。
反之对偶问题可行且其目标函数值无界,则原问题无可行解。
(3)若原问题有可行解而对偶问题无可行解,则原问题目标函数值无界;反之对偶问题有可行解而原问题无可行解,则对偶问题目标函数值无界。
3. 最优性定理:若Y X 和分别是原问题和对偶问题的可行解,并且b TY X C =,则X 是原问题最优解,Y 是其对偶问题的最优解4. 强对偶性:若原问题及其对偶问题均具有可行解,则两者均具有最优解,且它们最优解的目标函数值相等。
5.互不松弛性:若Y X 和分别是原问题和对偶问题的可行解,则它们分别是最优解的充要条件是:0ˆ,ˆˆ0ˆ1j 1=<=>∑∑==i i nj ij i nj j ij i y b xa b x a y则如果,则如果练习:判断下列说法是否正确:(1) 任何线性规划问题存在并具有惟一的对偶问题;(✓)(2) 根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解;(✗)(3) 设j ˆx ,i ˆy 分别为标准形式的原问题与对偶问题的可行解,*j x ,*i y 分别为其最优解,则恒有n n m m**j j j j i i i i j 1j 1i 1i 1ˆˆc x c x b y b y ====≤=≤∑∑∑∑;(✓) (5) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0>,说明在最优生产计划中第i 种资源已完全耗尽;(✓) (6) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0=,说明在最优生产计划中第i 种资源一定有剩余;(✗)简析:对(5)、(6),由互补松弛性质判断,具体详见课本P59三.对偶单纯形法(1). 对偶单纯形法应用前提: 1.检验数行全部非正2.变量取值有负数(2). 对偶单纯形法计算步骤:1.确定换出基变量 取{}i rb min b =,其对应变量r x 为换出基的变量。
运筹学习题解答(chap2 线性规划的对偶理论)

第二章 对偶问题与灵敏度分析一、写出下列线性规划的对偶问题1、P89,2.1(a)321422m in x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≥=++≤++≥++.,0,;534;332;243321321321321无约束x x x x x x x x x x x x解:原模型可化为321422m in x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≥=++≥≥++.,0,;534;3-3--2-;243321321321321321无约束x x x y y y x x x x x x x x x 于是对偶模型为321532m ax y y y W +-=s.t ⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+-≤+-.,0,;4334;243;22321321321321无约束y y y y y y y y y y y y2、P89,2.1(b)321365m ax x x x Z ++=s.t ⎪⎪⎩⎪⎪⎨⎧≤≥≤++≥-+-=++.0,0,;8374;35;522321321321321x x x x x x x x x x x x 无约束解:令033≥-='x x 原模型可化为321365m ax x x x Z '-+=s.t ⎪⎪⎩⎪⎪⎨⎧≥'≥≤'+≤'='+.0,0,;83-74;3--5-;52-2321321321321321x x x y y y x x x x x x x x x 无约束于是对偶模型为321835m in y y y W +-=s.t ⎪⎪⎩⎪⎪⎨⎧≥-≥---≥+-=++.0,,;332;6752;54321321321321y y y y y y y y y y y y 无约束 或⎪⎪⎩⎪⎪⎨⎧≥≤++≥+-=++.0,,;332;6752;54321321321321y y y y y y y y y y y y 无约束二、灵敏度分析1、P92, 2.11线性规划问题213m ax x x Z += s.t ⎪⎩⎪⎨⎧≥≤+≤+0,1025;74212121x x x x x x最优单纯形表如下试用灵敏度分析的方法,分析:(1) 目标函数中的系数21,c c 分别在什么范围内变化,最优解不变? (2) 约束条件右端常数项21,b b 分别在什么范围内变化,最优基保持不变? 解:(1) 1c 的分析:要使得最优解不变,则需⎪⎪⎩⎪⎪⎨⎧≤⨯-⨯+=≤⨯+⨯-=034131003513201413c c σσ 即 ⎪⎩⎪⎨⎧≤≥42511c c 所以:4251≤≤c 时可保持最优解不变。
运筹学--第二章 线性规划的对偶问题

习题二2.1 写出下列线性规划问题的对偶问题(1) max z =10x1+x2+2x3(2) max z =2x1+x2+3x3+x4st. x1+x2+2 x3≤10 st. x1+x2+x3 +x4≤54x1+x2+x3≤20 2x1-x2+3x3=-4x j≥0 (j=1,2,3)x1-x3+x4≥1x1,x3≥0,x2,x4无约束(3) min z =3x1+2 x2-3x3+4x4(4) min z =-5 x1-6x2-7x3st. x1-2x2+3x3+4x4≤3 st. -x1+5x2-3x3≥15x2+3x3+4x4≥-5 -5x1-6x2+10x3≤202x1-3x2-7x3 -4x4=2=x1-x2-x3=-5 x1≥0,x4≤0,x2,,x3无约束x1≤0,x2≥0,x3无约束2.2 已知线性规划问题max z=CX,AX=b,X≥0。
分别说明发生下列情况时,其对偶问题的解的变化:(1)问题的第k个约束条件乘上常数λ(λ≠0);(2)将第k个约束条件乘上常数λ(λ≠0)后加到第r个约束条件上;(3)目标函数改变为max z=λCX(λ≠0);'x代换。
(4)模型中全部x1用312.3 已知线性规划问题min z=8x1+6x2+3x3+6x4st. x1+2x2+x4≥33x1+x2+x3+x4≥6x3 +x4=2x1 +x3 ≥2x j≥0(j=1,2,3,4)(1) 写出其对偶问题;(2) 已知原问题最优解为x*=(1,1,2,0),试根据对偶理论,直接求出对偶问题的最优解。
2.4 已知线性规划问题min z=2x1+x2+5x3+6x4 对偶变量st. 2x1 +x3+x4≤8 y12x1+2x2+x3+2x4≤12 y2x j≥0(j=1,2,3,4)对偶问题的最优解y1*=4;y2*=1,试对偶问题的性质,求出原问题的最优解。
2.5 考虑线性规划问题max z=2x1+4x2+3x3st. 3x1+4 x2+2x3≤602x1+x2+2x3≤40x1+3x2+2x3≤80x j≥0 (j=1,2,3)4748(1)写出其对偶问题(2)用单纯形法求解原问题,列出每步迭代计算得到的原问题的解与互补的对偶问题的解;(3)用对偶单纯形法求解其对偶问题,并列出每步迭代计算得到的对偶问题解及与其互补的对偶问题的解;(4)比较(2)和(3)计算结果。
第二章对偶问题与灵敏度分析
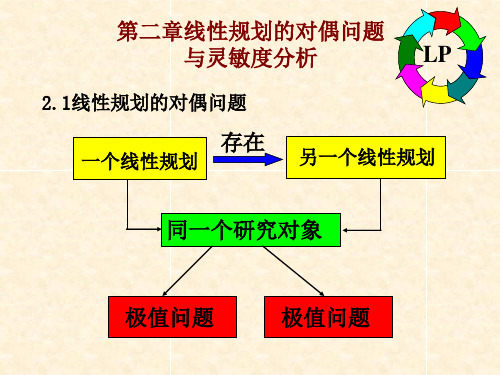
a22 y2 a23 y2
a32 y3 a33 y3
c2 c3
对 a14 y1 a24 y2 a34 y3 c4
称 y1无符号限制,y2 0,y3 0
原问题(P)
max
型 对偶问题(D)
相
min
变量约束:
似
方程约束:
变量≥
方程≥
变量无限制
方程=
变量≤
方程≤
方程约束:
方程=
方程≤
第二章线性规划的对偶问题
与灵敏度分析
LP
2.1线性规划的对偶问题
存在
一个线性规划
另一个线性规划
同一个研究对象
极值问题
极值问题
2.1.1问题的引入: 生产计划问题
LP
资源价格问题
甲 y1 A 1 y2 B 2
y3 C 1 利润 4
乙 资源量
1
45
1
80
3
90
5
2.1.1.1资源价格问题的数学模型
Max Z(X)=4x1+5x2 x1 + x2 ≤ 45
原问题
Max Z(X)= c1x1+c2x2+…+cnxn
y1
a11x1 + a12x2+…+a1n xn ≤ b1
.y.2. ym
a21x1 + a22x2+…+a2n xn ≤ b2
………………………………………………….
am1x1 + am2x2+…+amn xn ≤ bm
x1,x2,…,xn ≥0
2、求下列问题的对偶问题
变量个数n 约束方程个数m1
第2章 对偶理论和灵敏度分析-习题

理解原问题与对偶问题的关系. 论述对偶问题的基本性质并证明. 掌握对偶单纯形法. 掌握灵敏度分析及参数线性规划.
应用灵敏度分析原理讨论管理实践中的经 济决策问题.
1 写出下列线性规划问题的对偶问题
max Z = 5 x1 + 6 x 2 + 3x 3 x1 + 2 x 2 + 2 x 3 = 5 x1 + 5 x 2 x3 ≥ 3 s.t. 4 x1 + 7 x 2 + 3x 3 ≤ 8 x1无约束,x 2 ≥ 0, x3 ≤ 0
b
1 2
x1 1 0 0
-3-2+λ -5+-4λ -1+λ-
σ j′ = (c j z j )′ = C j′ C B′ B 1 Pj
= C j ′ C B ′ P j′
3 2 5 + 1 +λ
令=0
+λ
≤0 ≤0
4λ ≤ 0
-5/4≤λ≤1, 故 3/4≤c1≤3
令λ=0 -1≤≤5, 故 2≤c2≤8
b
1/3 2
X 故最优解为: * = (0, 2, 0, 0, 0,1/ 3)
(5) 增添一个新的约束 x1+2x2+x3 ≤4
Cj CB 2 3 0 XB x1 x2 x6 b
1 2 4
2 x1 1 0 1 0
3 x2 0 1 2 0
1 x3 -1 2 1 -3
0 x4 4 -1 0 -5
0 x5 -1 1 0 -1
(1)求线性规划的最优解.(20分) (2)写出对偶问题并求出对偶问题的最优解.( 5分) (3)当△b3=-150时最优基是否发生变化?为什 么?(5分) (4)求c2的灵敏度变化范围.(5分) (5)如果x3的系数由[1,3,5]变化到[1,3,2]最 优基是否改变?若改变求新的最优解.(5分)
第二章对偶理论与灵敏度分析练习题答案

第二章 对偶理论与灵敏度分析练习题答案1.判断下列说法是否正确:(1) 任何线性规划问题存在并具有惟一的对偶问题;(✓)(2) 根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解,反之,当对偶问题无可行解时,其原问题具有无界解;(✗)(3) 设j ˆx ,i ˆy 分别为标准形式的原问题与对偶问题的可行解,*j x ,*i y 分别为其最优解,则恒有n n m m**j j j j i i i i j 1j 1i 1i 1ˆˆc x c x b y b y ====≤=≤∑∑∑∑;(✓)(4) 若线性规划的原问题有无穷多最优解,则其对偶问题也一定具有无穷多最优解;(✓)(5) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0>,说明在最优生产计划中第i 种资源已完全耗尽;(✓)(6) 已知*i y 为线性规划的对偶问题的最优解,若*i y 0=,说明在最优生产计划中第i 种资源一定有剩余;(✗)(7) 若某种资源的影子价格等于k ,在其他条件不变的情况下,当该种资源增加5个单位时,相应的目标函数值将增大5k ;(✗)(8) 应用对偶单纯形法计算时,若单纯形表中某一基变量i x 0<,又x i 所在行的元素全部大于或等于零,则可以判断其对偶问题具有无界解;(✓)(9) 若线性规划问题中的b i ,c j 值同时发生变化,反映到最终单纯形表中,不会出现原问题与对偶问题均为非可行解的情况;(✗)(10) 在线性规划问题的最优解中,如某一变量x j 为非基变量,则在原来问题中,无论改变它在目标函数中的系数c j 或在各约束中的相应系数a ij ,反映到最终单纯形表中,除该列数字有变化外,将不会引起其他列数字的变化。
(✓)2.下表是某一约束条件用“≤”连接的线性规划问题最优单纯形表格,其中x 4、x 5为松弛变量。
要求:(1)(3)其它条件不变时,约束条件右端项b 1在何范围内变化,上述最优基不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i i i
i
第二章 线性规划的对偶理论和灵敏度分析自测题
1. 判断下述说法是否正确
(1) 任何线性规划问题存在并具有唯一的对偶问题。
(2) 线性规划原问题的对偶问题的对偶是原问题本身。
(3) 原问题的任一可行解对应的目标函数值都不超过其对偶问题的任一可行解对应的目标函数值。
(4) 已知对偶问题的最优解中, y * > 0 ,则原问题中在资源最优配置下,第i 种资源已完全消 耗殆尽。
(5) 已知对偶问题的最优解中, y * = 0 ,则原问题中在资源最优配置下,第 i 种资源一定未 完全消耗。
(6) 影子价格就是市场价格。
(7) 若第 i 种资源的影子价格为 y * > 0 ,则在保持原问题中其它条件不变时,在资源最优配置下,当第i 种资源增加10个单位时,最优值将一定增加10 y * .
(8) 在应用对偶单纯形法计算时,若在某一个单纯形表中,出现某行除该行对应的基变量值
小于0外,该行其余元素全部大于或等于0,则可以判断该线性规划问题无最优解。
(9) 在应用对偶单纯形法计算时,若在某一个单纯形表中,出现某行除该行对应的基变量值小于0外,该行其余元素全部小于或等于0,则可以判断该线性规划问题的对偶问题无最优解。
(10)线性规划的原问题和其对偶问题的最优值如果存在,则必然相等。
(11)线性规划问题的最终单纯形表中,当仅某一非基变量在目标函数中的系数变化时,线性规划问题的最优解一定不改变。
(12)线性规划问题的最终单纯形表中,当仅有某一基变量在目标函数中的系数变化时,线性规划问题的最优解一定不改变。
(13)线性规划问题的最终单纯形表中,当仅有某一非基变量在系数矩阵中的列变化时,线性规划问题的最优解一定不改变。
(14)线性规划问题的最终单纯形表中,当仅有某一基变量在系数矩阵中的列变化时,线性规划问题的最优解一定不改变。
(15)线性规划问题的最终单纯形表中,当仅有某种资源的数量变化时,线性规划问题的最优值一定改变。
2. 简述影子价格的经济含义。
3. Min ω=2x 1+3x 2+5x 3+6x 4
x 1+2x 2+3x 3+ x 4 ≥ 2
-2x 1+ x 2- x 3+3x 4 ≤-3 x j ≥0, j =1,2, …,4 (1) 写出其对偶问题。
(2) 求解其对偶问题。
(3) 利用对偶性质求原问题的解。
4. 某企业生产A
(1)列出数学模型。
(2)求出最优的生产计划。
(3)影子价格是多少?
(4)B产品的价格提高多少,才进行生产?
(5)增加人工500小时,最大利润为多少?5.
(1)由结果图表读出最优解。
(2)由结果图表进行灵敏度分析。
