长直载流导体的磁场图示(精)
合集下载
第 8 章 磁场的源

向(且在垂直于轴线的平面内, 下同);
·P点的磁场就是所有这样一对对
的窄条形成的,所以P点的磁场B 一定也垂直于r方向如图。
·由于圆柱面上电流分布的轴对称 性,可知
理论中,其量值等于(h/2π)d的整数倍。所以
氢原子在基态时,其轨道磁矩为
B
e 2me
h
2
eh
4me
它是轨道磁矩的最小单位(称为玻尔磁子)。 将e=1.60210-19 C,me= 9.1110-31kg , 普朗克常量h= 6.62610-34J·s代入,可算得
B 9.273 1024 A m2
B dr B dr B dr
L
L1
L2
0I d d
2 L1
L2
0I 0
2
二、安培环路定理
对非平面闭合路径,r 和 dr 可以正交分解 为平行于电流 I 分量和垂直于电流 I 的分量。
B dr L
L B dr//
L B dr
B
又 R2 l 2 R2 csc2
1 r
2
p
dB
l dl
R A2
B
L
0R2nI d l
2(R2 l 2 )3/
2
0 nI 2 sin d
2
1
0
2
nI (cos
2
cos
1 )
B
0nI
2
(cos
2
cos
1 )
讨论:(1)螺线管无限长 1 , 2 0
B 0nI
(2)半无限长螺线管的端点圆心处
解 设两个线圈的半径为R, 各有N匝,每匝中的电流均 为I,且流向相同(如图)。 两线圈在轴线上各点的场强 方向均沿轴线向右,在圆心 O1、O2处磁感应强度相等, 大小都是
·P点的磁场就是所有这样一对对
的窄条形成的,所以P点的磁场B 一定也垂直于r方向如图。
·由于圆柱面上电流分布的轴对称 性,可知
理论中,其量值等于(h/2π)d的整数倍。所以
氢原子在基态时,其轨道磁矩为
B
e 2me
h
2
eh
4me
它是轨道磁矩的最小单位(称为玻尔磁子)。 将e=1.60210-19 C,me= 9.1110-31kg , 普朗克常量h= 6.62610-34J·s代入,可算得
B 9.273 1024 A m2
B dr B dr B dr
L
L1
L2
0I d d
2 L1
L2
0I 0
2
二、安培环路定理
对非平面闭合路径,r 和 dr 可以正交分解 为平行于电流 I 分量和垂直于电流 I 的分量。
B dr L
L B dr//
L B dr
B
又 R2 l 2 R2 csc2
1 r
2
p
dB
l dl
R A2
B
L
0R2nI d l
2(R2 l 2 )3/
2
0 nI 2 sin d
2
1
0
2
nI (cos
2
cos
1 )
B
0nI
2
(cos
2
cos
1 )
讨论:(1)螺线管无限长 1 , 2 0
B 0nI
(2)半无限长螺线管的端点圆心处
解 设两个线圈的半径为R, 各有N匝,每匝中的电流均 为I,且流向相同(如图)。 两线圈在轴线上各点的场强 方向均沿轴线向右,在圆心 O1、O2处磁感应强度相等, 大小都是
§2载流回路的磁场
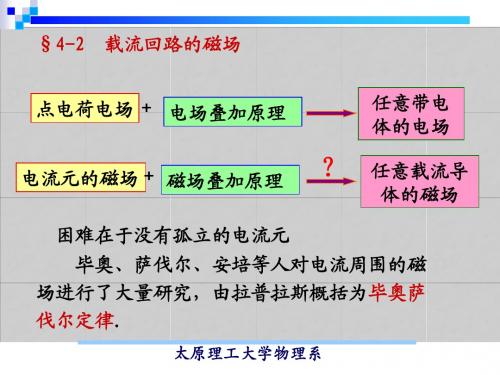
dB =
µ0 R dI
2
2 x2 + R2 3/ 2 ( )
N dI = Idx = nIdx L
各个元段在P点产生的磁感强度方向相, 各个元段在 点产生的磁感强度方向相,整 点产生的磁感强度方向相 个螺旋线圈在P点产生的磁感强度为 个螺旋线圈在 点产生的磁感强度为
B = ∫ dB =
µ0nI
2
∫
x2
µ0 Idl × r B = ∫ dB = ∫ r2 4π l
0
积分对于整个载流导线进行 电流元的磁场 + 磁场叠加原理 注意 任意载流导 体的磁场
B = ∫ dB
与
B = ∫ dB 的区别
太原理工大学物理系
dB =
µ0 Idl × r
4π
1
0
r2
毕奥— 毕奥—萨伐尔定律
例1 判断下列各点磁感强度的方向和大小. 判断下列各点磁感强度的方向和大小.
解 由圆形电流磁场公式 B =
µ 0 IR 2
(x + R ) 2
2 2 3/ 2
处取长为dx的元段 距p点x处取长为 的元段,其上有 点 处取长为 的元段,其上有ndx匝线 匝线 相当于dI=nIdx的圆电流。 的圆电流。 圈,相当于 的圆电流
太原理工大学物理系
dI在P点产生的磁感强度大小为 在 点产生的磁感强度大小为
Idl
dB
dB
P *
r
θ
Idl
I
r
dB的方向 的方向 垂直于 平面 与 r 组成的
Idl sin θ dB = k 2 r
太原理工大学物理系
Idl × r 0 毕—萨定律的数学表达式 dB = k r2
载流直导线的磁场

超导体的研究和应用已经取得了一些重要的成果,如超导 电缆、超导变压器等。未来随着超导技术的不断进步和应 用范围的扩大,有望在能源、交通、医疗等领域发挥更大 的作用。
THANKS FOR WATCHING
感谢您的观看
载流直导线的磁场
目录
• 磁场的基本概念 • 载流直导线产生的磁场 • 磁场与电流的关系 • 磁场的应用 • 磁场与现代科技
01
磁场的基本概念
磁场定义
01
磁场:是存在于磁体或电流周围 的一种特殊物质,它对放入其中 的磁体或电流产生力的作用。
02
磁场是由电荷的运动所产生的。 磁场对放入其中的电流或磁体产 生力的作用,这种力称为安培力 或洛伦兹力。
无线通信利用电磁波传 递信息,如手机、电视、
广播等。
利用磁场记录信息,如 硬盘、磁带等存储设备。
利用磁场力使物体悬浮, 如磁悬浮列车和磁悬浮
轴承。
某些磁场可以影响人体 生理功能,如磁疗和电
磁疗法。
05
磁场与现代科技
磁悬浮列车
磁悬浮列车是一种利用磁场力使列车悬浮于轨道之上的高速列车,具有速度快、能耗低、无噪音等优 点。磁悬浮列车的磁场来源通常是通过电流在导轨中产生的强磁场,通过与列车上的磁铁相互作用实 现悬浮和导向。
奥斯特(Oe)
奥斯特是高斯和安培之间 的转换系数,用于表示磁 场与电流之间的关系。
安培力(F)
安培力是描述磁场对电流 作用力的物理量,单位为 牛顿(N)。
02
载流直导线产生的磁场
安培环路定律
总结词
安培环路定律描述了载流直导线产生的磁场分布,是磁场分 析的重要基础。
详细描述
安培环路定律指出,在磁感应线圈中,磁场强度矢量沿闭合 路径的线积分等于穿过该路径所围面积的电流代数和。该定 律是电磁学中的基本定理之一,对于分析载流导线的磁场分 布和磁感应强度计算具有重要意义。
THANKS FOR WATCHING
感谢您的观看
载流直导线的磁场
目录
• 磁场的基本概念 • 载流直导线产生的磁场 • 磁场与电流的关系 • 磁场的应用 • 磁场与现代科技
01
磁场的基本概念
磁场定义
01
磁场:是存在于磁体或电流周围 的一种特殊物质,它对放入其中 的磁体或电流产生力的作用。
02
磁场是由电荷的运动所产生的。 磁场对放入其中的电流或磁体产 生力的作用,这种力称为安培力 或洛伦兹力。
无线通信利用电磁波传 递信息,如手机、电视、
广播等。
利用磁场记录信息,如 硬盘、磁带等存储设备。
利用磁场力使物体悬浮, 如磁悬浮列车和磁悬浮
轴承。
某些磁场可以影响人体 生理功能,如磁疗和电
磁疗法。
05
磁场与现代科技
磁悬浮列车
磁悬浮列车是一种利用磁场力使列车悬浮于轨道之上的高速列车,具有速度快、能耗低、无噪音等优 点。磁悬浮列车的磁场来源通常是通过电流在导轨中产生的强磁场,通过与列车上的磁铁相互作用实 现悬浮和导向。
奥斯特(Oe)
奥斯特是高斯和安培之间 的转换系数,用于表示磁 场与电流之间的关系。
安培力(F)
安培力是描述磁场对电流 作用力的物理量,单位为 牛顿(N)。
02
载流直导线产生的磁场
安培环路定律
总结词
安培环路定律描述了载流直导线产生的磁场分布,是磁场分 析的重要基础。
详细描述
安培环路定律指出,在磁感应线圈中,磁场强度矢量沿闭合 路径的线积分等于穿过该路径所围面积的电流代数和。该定 律是电磁学中的基本定理之一,对于分析载流导线的磁场分 布和磁感应强度计算具有重要意义。
长直载流导线空间磁场分布的分析
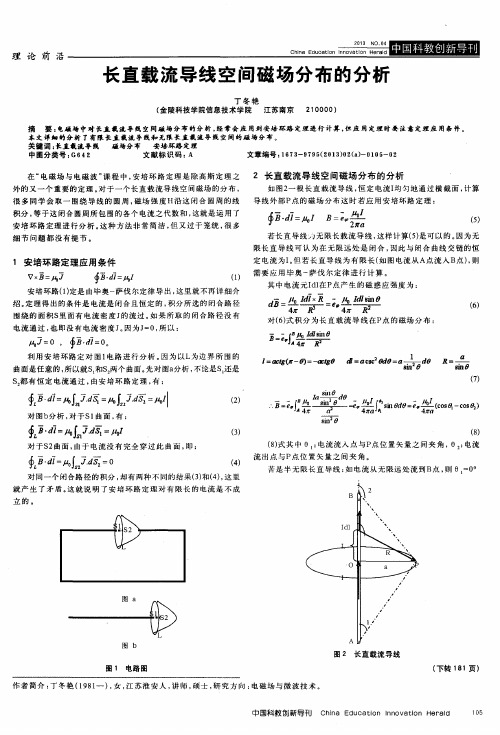
积分 , 和 , 这就 是 运 用 了 安培环路定理进行分析 。 这种方法非常简洁 , 但又过于笼统 , 很 多 细节 问题都没有提节 。
=
曰-_
( 5 )
若长 直 导 线 , 0 无 限长 载 流 导 线 , 这 样 计 算( 5 ) 是可以的。 因为 无 限长 直 导 线 可 认 为 在 无限 远 处 是 闭 合 , 因此 与闭 合 曲线 交 链 的 恒
1  ̄ l d l x R
:
安 培 环路 ( 1 ) 定是 由毕 奥 一 萨 伐 尔定 律 导 出 , 这 里 就 不再 详 细介
绍。 定 理 得 出 的条 件 是 电 流是 闭合 且恒 定 的 , 积 分 所 选的 闭合 路 径 围绕 的 面积 S 里面 有 电流 密 度J 的流过。 如 果 所 取 的 闭 合路 径 没 有 电流 通 过 , 也 即没 有 电流 密 度 J 。 因为 J =O , 所以:
4
r j
:
; 1  ̄ I d l s i n 0
’ 4 R
( 6 )
…
对( 6 ) 式 积 分 为长 直 载 流 导 线 在 P 点的磁场分布 : , & 否 = ; f
^
I a l s i no
2
- 厂 = 0,中 B・ d l = 0 。
利用安培环路定对 图1 电路 进 行 分 析 。 因为以L 为边 界 所 围 的 曲面 是任 意 的 , 所 以就 S , , n s , 两 个 曲面 。 先 对 图a 分析 , 不 论是 S 。 还是 S , 都 有 恒 定 电流 通 过 , 由 安 培 环 路 定理 , 有:
1 安培环路定 理应用条件
V x B= B・ d l = 硒, ( 1 )
载流导体产生磁场

(3) 非均匀磁场中的平面电流环
稳定平衡
Fi 0
M 0
线圈有平动和转动
§9.6 带电粒子在磁场中的运动
一.洛伦兹力公式
• 实验结果
f
f q, B,v , sin f qvB sin f m qv B
• 安培力与洛伦兹力的关系
q
θ
v
B
f 21
I 2dl2
两电流元之间的相互作用力,一般不遵守牛顿第三定律
(4) 分析两根带电长直线沿长度方向运动时,带电线之间的 v1 作用力。 1 两带电线上的电流为
I1 1v1
f
I 2 2v 2
fm 2a
a
v2
0 I1I 2
2a
0 1v12v 2
2
四. 有磁介质时的安培环路定理
1. 束缚电流
以无限长螺线管为例
定义:磁化强度
B0
I0
顺 磁 质
Pm M 磁化强度越强,反映磁介质磁化程度越强 V
在磁介质内部的任一小区域: 相邻的分子环流的方向相反 在磁介质表面处各点: 分子环流未被抵消 形成沿表面流动的面电流 I S ——束缚电流
B B0 r —— 相对磁导率
反映磁介质对原场的影响程度
r
2. 磁介质的分类 抗磁质
r 1
r 1
B B0 B B0
减弱原场
如 锌、铜、水银、铅等
顺磁质 增强原场 如 锰、铬、铂、氧等 顺磁质和抗磁质的相对磁导率都非常接近于1。
弱 磁 性 物 质
铁磁质
r 1
(10 ~ 10 )
度,使粒子运动发生“反射” 在非均匀磁场中,纵向运动 受到抑制—— 磁镜效应
稳定平衡
Fi 0
M 0
线圈有平动和转动
§9.6 带电粒子在磁场中的运动
一.洛伦兹力公式
• 实验结果
f
f q, B,v , sin f qvB sin f m qv B
• 安培力与洛伦兹力的关系
q
θ
v
B
f 21
I 2dl2
两电流元之间的相互作用力,一般不遵守牛顿第三定律
(4) 分析两根带电长直线沿长度方向运动时,带电线之间的 v1 作用力。 1 两带电线上的电流为
I1 1v1
f
I 2 2v 2
fm 2a
a
v2
0 I1I 2
2a
0 1v12v 2
2
四. 有磁介质时的安培环路定理
1. 束缚电流
以无限长螺线管为例
定义:磁化强度
B0
I0
顺 磁 质
Pm M 磁化强度越强,反映磁介质磁化程度越强 V
在磁介质内部的任一小区域: 相邻的分子环流的方向相反 在磁介质表面处各点: 分子环流未被抵消 形成沿表面流动的面电流 I S ——束缚电流
B B0 r —— 相对磁导率
反映磁介质对原场的影响程度
r
2. 磁介质的分类 抗磁质
r 1
r 1
B B0 B B0
减弱原场
如 锌、铜、水银、铅等
顺磁质 增强原场 如 锰、铬、铂、氧等 顺磁质和抗磁质的相对磁导率都非常接近于1。
弱 磁 性 物 质
铁磁质
r 1
(10 ~ 10 )
度,使粒子运动发生“反射” 在非均匀磁场中,纵向运动 受到抑制—— 磁镜效应
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
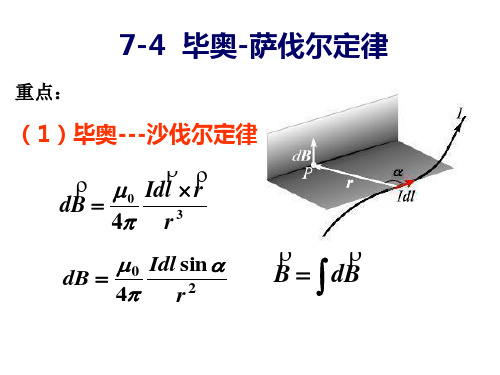
0 Idz sin B dB 4 r2
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
载流长直导线的磁场

THANKS
感谢观看
电磁辐射
长期暴露在电磁场中可能导致头痛、失眠、记忆力减退等健康问 题。
电磁波对人体的影响
高强度的电磁波可能对人体的免疫系统、神经系统和生殖系统产生 负面影响。
电磁辐射的防护
为了减少电磁辐射对人体的影响,应采取适当的防护措施,如远离 高强度电磁场、穿戴防护服等。
04
载流长直导线在科研领域 的应用
磁场对带电粒子的影响
磁场的方向
右手定则
根据右手定则,环绕着通电长直导线的四指指向电流方向, 大拇指所指方向即为磁场方向。
磁场方向与电流方向的关系
磁场方向总是与电流方向垂直,这是由安培定律决定的。
磁感应线的形状
磁感应线是闭合曲线
磁感应线总是围绕着通电长直导线形 成闭合曲线,类似于电流周围的电场 线。
磁感应线的分布
磁感应线的分布与电流大小和导线材 料有关,电流越大,磁感应线越密集 ;导线的导磁率越高,磁感应线越密 集。
磁力线
磁场中磁力方向相同的路径,形成闭 合曲线。
安培环路定律
01
02
03
安培环路定律
描述磁场与电流之间的关 系,即磁场与电流成正比, 沿导线周围环绕。
定律公式
B = μ₀ * I / 2πr,其中B 为磁感应强度,I为电流强 度,r为距离导线的垂直距 离。
应用场景
适用于长直导线或线圈周 围的磁场计算。
感应炉
利用电磁感应产生的高温 来熔炼金属。
感应电机的运行
利用电磁感应原理,实现 电机的启动、调速和制动。
电磁铁的应用
电磁起重机
利用电磁铁产生的强大磁场,实 现对金属材料的吸附和搬运。
扬声器
利用电磁铁推动振膜产生振动,从 而产生声音。
《大学物理》第六章 恒定电流的磁场 (2)

dBcos
B
900
dB cos
900
900 0I cosd 900 2 2 R
6-12解:
磁通量
dΦ BdS cos00
I1
l r1
r2
I2 r3
x
B
B2
B1
0I2 2x
0 I1 2 (d
x)
dS ldx
Φ dΦ r2 r3 r3
6-13解:
B内
0Ir 2R2
B
0I 2R
oR
r
dΦ BdS cos00 0Ir l dr 2R2
(1)质子作螺旋运动的半径; (2)螺距; (3)旋转频率。
结束 目录
已知:B =1.5 T v =1.0×107m/s
= 300
求:半径 R 螺距 h 旋转频率 n
解:
R
=
mv eB
=
m
vsin eB
1.67×10-27×1.0×107×0.5
dB
0dI
0
I b
dx
2x 2x
P (2)沿坐标轴投影积分,积分
B
2b
0
I b
dx
b 2x
o
θ
dB 0dI
0
I b
dy
y
θ
2d 2 ( y)2 x2
x
dB cos
0
I b
dy
x
2 ( y)2 x2 ( y)2 x2
6-10解:
(1)选坐标,取微小量
dB
0dI
0
I
R
Rd
θ
2R
2R
(2)沿坐标轴投影积分,积分
