4.2 毕奥-萨伐尔定律和载流回路的磁场
§2载流回路的磁场
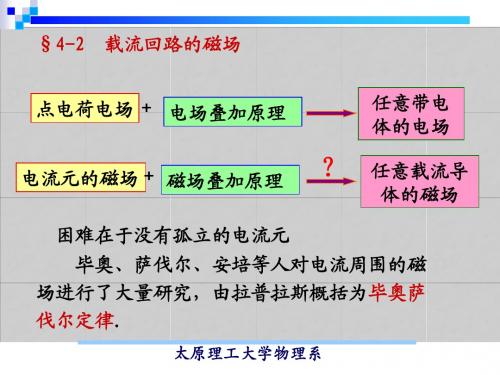
dB =
µ0 R dI
2
2 x2 + R2 3/ 2 ( )
N dI = Idx = nIdx L
各个元段在P点产生的磁感强度方向相, 各个元段在 点产生的磁感强度方向相,整 点产生的磁感强度方向相 个螺旋线圈在P点产生的磁感强度为 个螺旋线圈在 点产生的磁感强度为
B = ∫ dB =
µ0nI
2
∫
x2
µ0 Idl × r B = ∫ dB = ∫ r2 4π l
0
积分对于整个载流导线进行 电流元的磁场 + 磁场叠加原理 注意 任意载流导 体的磁场
B = ∫ dB
与
B = ∫ dB 的区别
太原理工大学物理系
dB =
µ0 Idl × r
4π
1
0
r2
毕奥— 毕奥—萨伐尔定律
例1 判断下列各点磁感强度的方向和大小. 判断下列各点磁感强度的方向和大小.
解 由圆形电流磁场公式 B =
µ 0 IR 2
(x + R ) 2
2 2 3/ 2
处取长为dx的元段 距p点x处取长为 的元段,其上有 点 处取长为 的元段,其上有ndx匝线 匝线 相当于dI=nIdx的圆电流。 的圆电流。 圈,相当于 的圆电流
太原理工大学物理系
dI在P点产生的磁感强度大小为 在 点产生的磁感强度大小为
Idl
dB
dB
P *
r
θ
Idl
I
r
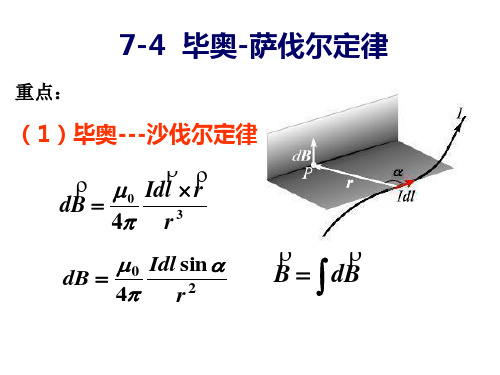
dB的方向 的方向 垂直于 平面 与 r 组成的
Idl sin θ dB = k 2 r
太原理工大学物理系
Idl × r 0 毕—萨定律的数学表达式 dB = k r2
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例
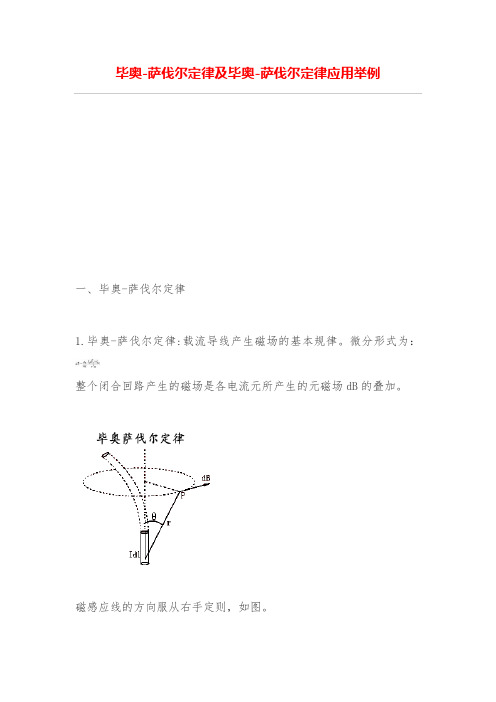
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为:整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则,如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。
例1.载流长直导线的磁场解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为:方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:(1)由图得:,即:此外:,代入(1)可得:讨论:(1)无限长直通电导线的磁场:(2)半无限长直通电导线的磁场:(3)其他例子例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解:建立坐标系如图,任取电流元,由毕-萨定律得:,方向如图:,所有dB形成锥面。
将dB进行正交分解:,则由由对称性分析得:,所以有:,因为: ,r=常量,所以:,又因为:所以:,方向:沿x轴正方向,与电流成右螺旋关系。
讨论:(1)圆心处的磁场:x=0 ,。
(2)当即P点远离圆环电流时,P点的磁感应强度为:。
例3:设有一密绕直螺线管。
半径为 R ,通电流 I。
总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为: 电流为:。
其相当于一个圆电流,它在P点的磁感应强度为:。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为:因为:代入上式得:所以:讨论:(1)管内轴线上中点的磁场:(2)当 L>>R时,为无限长螺线管。
此时,,管内磁场。
即无限长螺线管轴线上及内部为均匀磁场,方向与轴线平行满足右手定则。
毕奥-萨伐尔定律 磁通量 磁场的高斯定理
解:(1)判断电流元产生 每个电流元产生磁场同方向
磁场的方向是否一致
z
D
2
z r 0 cot
dz
I
z
1
r
r0
x
C
o
r0 dz d 2 sin dB r0 又r * y P sin 0 Idl sin (1) 大小 dB 2 4 r
B
0 I
2πr
I
B
I
X
B
电流与磁感强度成右手螺旋关系
2013-7-5
10
[例14-2] 圆电流轴线上的磁场。
0 Idl 解: dB sin 90 2 4 r 0 Idl B dB sin 90 2 4 r
x 因为圆线圈上各个电流元在P点产生的磁感应强度 的方向是不同的,所以只能用它的矢量表示:
第五版
四.运动电荷的磁场
7-4
毕奥-萨伐尔定律
考虑一段导体,其截面积为S,其 中载流子的密度为n,载流子带电 q,以漂移速度 v 运动。
毕奥—萨伐尔定律:
0 Idl r dB 4 π r3 0 nSdlqv r dB 3 4π r
P r dB Idl j Sdl nSdlqv
z
o
r
Idl
y
R
0 I dl sin x 2 2 2 r2 r R z 4 2 2 R 0 IR 0 I sin dl 3 2 0 2 2 4 r 2( R z ) 2
B
0 IR
2
2 2 32
2( R z )
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场大学物理电子教案

磁场强度毕奥萨伐尔定律及运动电荷产生的磁场一、教学目标1. 理解磁场强度的概念,掌握毕奥萨伐尔定律及其应用。
2. 了解运动电荷产生磁场的原理,能运用相关知识分析实际问题。
3. 培养学生的实验操作能力,提高其科学思维和问题解决能力。
二、教学内容1. 磁场强度的定义及其表示方法。
2. 毕奥萨伐尔定律的表述及其数学形式。
3. 毕奥萨伐尔定律在直导线、圆形电流和均匀电流环中的应用。
4. 运动电荷产生磁场的原理。
5. 运动电荷产生的磁场与电流磁场的区别与联系。
三、教学方法1. 采用讲授法,讲解磁场强度、毕奥萨伐尔定律及运动电荷产生磁场的相关概念和理论。
2. 利用示例和图示,直观展示毕奥萨伐尔定律的应用。
3. 开展讨论法,引导学生分析运动电荷产生磁场的原理及其在实际应用中的重要性。
4. 布置实验,让学生动手操作,验证毕奥萨伐尔定律及运动电荷产生磁场的理论。
四、教学准备1. 教案、教材、课件等教学资源。
2. 实验室设备:电流表、电压表、导线、磁针等。
3. 投影仪、计算机等多媒体设备。
五、教学过程1. 引入:通过简单的磁现象,引导学生思考磁场强度的概念。
2. 讲解:讲解磁场强度的定义及其表示方法,阐述毕奥萨伐尔定律的表述和数学形式。
3. 示例:分析毕奥萨伐尔定律在直导线、圆形电流和均匀电流环中的应用,演示相关计算过程。
4. 讨论:引导学生分析运动电荷产生磁场的原理,与电流磁场的区别和联系。
5. 实验:安排学生进行实验操作,验证毕奥萨伐尔定律及运动电荷产生磁场的理论。
6. 总结:对本节课的主要内容进行归纳总结,强调重点和难点。
7. 作业:布置相关练习题,巩固所学知识。
六、教学评估1. 课堂提问:通过提问了解学生对磁场强度、毕奥萨伐尔定律及运动电荷产生磁场的理解和掌握情况。
2. 实验报告:评估学生在实验过程中的操作技能、数据处理和分析问题的能力。
3. 作业完成情况:检查学生对课堂所学知识的巩固程度。
七、教学拓展1. 介绍其他磁场强度计算方法,如安培环路定律。
4.2 毕奥-萨伐尔定律和载流回路的磁场

0 I
O
R
例.无限长载流直导线弯成如图形状
L
I 20 A a 4cm 求: P、R、S、T四点的 B
解: P点 B p BLA BLA
R
a
I A
a
L
S
I
a
P T
R点
0 I 0 5 10 5 T 4a
方向
BR BLA BLA 0 I 0 I 3 1 (cos 0 cos ) (cos cos ) 4a 4 4a 4
三、 载流直螺线管内部的磁场
设螺线管的半径为R,电流为I,每单位长度 有线圈n匝。
1
r
dB
R
A1
2
p
A2
dl
l
载流圆线圈轴线上的磁场
1
r
dB
A1
2
R
A2
p
l
dl
由于每匝可作平面线圈处理, ndl匝线圈可作 Indl的一个圆电流,在P点产生的磁感应强度:
2( R l ) 2 0 R nI d l B L dB L 2 2 3/ 2 2( R l )
I
0 I B 2d 0 I B 4d
dl
L
r
(2)导线半无限长,场点与一端 的连线垂直于导线
l
(3)P点位于导线延长线上,B=0
O
d
1
2
P
dB
R 二、 圆形电流的磁场.有一半径为 的载 I P 流圆环,电流强度为 ,求它轴线上任一点 的磁感应强度 . B Id l 0 Idl sin dB dB r 解 dB 2 R 4 r o x 0 P dB// x 90
电磁学 毕奥-萨伐尔定律

I 2 dl
e
er
38
L2单位长度受到的力的大小是
f dF12 0 I1I 2
dz
2r0
(2.2-19)
令I1 = I2 = I , 当 r0 = 1米,并且测得f = 2×10 –7牛顿/ 米时,两导线中的电流强度I 就定义为“1安培”.
0
2r0
I2
f
2
1m 2 10 7 1A2
N
/
m
25
A
若两电流元关于平面A镜像对
称,证明:它们在A上的合磁 场B必垂直于A(除非B=0)
Idl r
Idl '
r'
z
dB dB'
0I 4
dl
r
r
3
0I 4
dl'r' r'3
0I 4r 3
(dl r dl 'r ')
dl
(lx
,
l
Hale Waihona Puke y,lz)
dl ' (lx ,ly ,lz )
11
2.安培定律(Amperes’ Law)
真空中,两个稳恒的电流回路L1和L2 ,
电d流F1元2 I1dIl21d对l2I2dlk2的I1作d用lr1122力e为12
在MKSA单位制中,比例常数
k 0 4
(2.2-2)
(2.2-1)
e12 I1dl1 r12
L1
I2dl2 L2
12
其中,0称为真空磁导率,它与真空介电常数e0
36
电磁相互作用宇称守恒
dB( x)
0 4
Idl e r
r2
毕奥萨伐尔定律(磁场大小)

毕奥萨伐尔定律(磁场大小)
磁场大小如何计算呢?
还是要回到那个最伟大的发现,奥斯特的发现启发说起。
1820年秋,阿拉果带着奥斯特发现电流磁效应的重要新闻回到法国,9月11日,他便在法国科学院报告了奥斯特的重要发现并演示其实验。
阿拉果的报告使法国科学家迅速做出强烈反应。
对法国科学家而言,他们受库仑的影响太深,此前一直相信电和磁之间没有联系并且对电和磁分别进行研究。
阿拉果报告之后,法国科学家立即对电和磁的相互关系进行探索。
一周后,安培就取得了重要的研究成果,1820年9月18日、9月25日和10月9日,安培在科学院会议上宣读了3篇论文,并且用实验表演了两根通电导线相互吸引和排斥的现象,同时还证明了通电螺线管也能像磁铁一样相互吸引。
毕奥紧随其后,1820年9月30日,毕奥就向法国科学院报告了他与萨伐尔的重要发现:“载流长直导线施加在磁针磁极(不论是磁南极还是磁北极) 上的力反比于磁极与导线间的距离,这也是人类首次对奥斯特效应的定量研究”。
毕奥-萨伐尔定律:在静磁学中,毕奥-萨伐尔定律(英文:Biot-SavartLaw)描述电流元在空间任意点P处所激发的磁场。
定律文字描述:电流元Idl 在空间某点P处产生的磁感应强度dB 的大小与电流元Idl 的大小成正比,与电流元Idl 所在处到P点的位置矢量和电流元Idl 之间的夹角的正弦成正比,而与电流元Idl到P点的距离的平方成反比。
上式描述了电流元在一点产生的磁场大小,那么对于任意一段导体在一点出产生的磁感强度是如何求呢?
其实很简单,讲该任意导体看成由无数个电流元的组成,对电流元进行积分,便可求得。
综上,通过毕奥-萨伐尔定律,我们可以予以解答求解磁场定量公式。
电磁学2毕奥-萨伐尔定律

β lr
β dB
a
P
§4-3 毕奥
萨伐尔定律的应用
1. 载流直导线的磁场
dB 的方向: I dl × r 的方向
dB
的大小:
dB
=
μo
4π
I
dl sina
r2
几何关系:
I dl
sin a =sin ( 900 +β ) dl a
= cosβ l = a tgβ
β lr
dl = a sec 2β dβ r = a secβ
I dl
r
IR
θ x
y dB θ P x
By= Bz=0
Idl r z
dB
B = dB x = dB
sinθ
=
μ
4π
o
I r
2
sinθ
dl
=
μo
4π
I r
2
sinθ
dl
sinθ
=
R r
I dl
r
r = (x 2 +R2 )1 2 I R
θ x
y dB θ x
z
B=
μo
4π
I r
2
sinθ
dl
=
×(
r r
)
B
=
μ
4π
o
I dl × r3
r
用矢量形式表示的毕奥 萨伐尔定律
dB =
μ o I dl × r
4π r 3
=
μo
4π
I dl r2
×(
r r
)
B
=
μ
4π
o
I dl × r3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B Id l
l
2
r0 dl d 2 sin
0 2 I sin d B 4 1 r0
r o r0
1
dB
A
0 I (cos 1 cos 2 ) 4 r0
特例:无限长导线: 1 0, 2
0 I B 2r0
2
BQ
0 NIR 2
3/ 2
0 NIR 2
2
3/ 2
载流圆线圈轴线上的磁场
在线圈轴线上其他各点,磁感应强度的量值都介 乎B0、BP 之间。由此可见,在P点附近轴线上的场 强基本上是均匀的,其分布情况约如图所示。图 中虚线是每个圆形载流线圈在轴线上所激发的场 强分布,实线是代表两线圈所激发场强的叠加曲 线。
2 R 2 R 2 0 NI 0.716 R
8 0 NI 1 1 5 5R 2 2
载流圆线圈轴线上的磁场
此外,在P点两侧各R/4处的O1、O2 两点处磁感应强度都 等于
2 R 2 3R 2 R 2 R 4 4 0 NI 4 3 0 NI 43 3 / 2 3 0.712 2 R 17 5 R
q qr d r dI 2r d r 2 2 2 R R 0 d I
dB 2r 0q R 0q B dr 2 2R 0 2R
解:带电圆盘转动形成圆电流,取距盘心r处宽度 为dr的圆环作圆电流,电流强度: + + + + + + + + +o + + + + +
第二节 毕奥-萨伐尔定律和载流回路的磁场
一、 载流长直导线的磁场.在真空中有一长 为 L 载流直导线,导线中电流强度为 I ,求导 线附近一点 P 的磁感应强度.
0 Idl sin 解 dB 4 r2
0 B Idl sin B dB A r2 A 4 l r0ctg r r0 sin
返回
载流圆线圈轴线上的磁场
例 亥姆霍兹线圈在实验室中,常应用亥姆霍兹线 圈产生所需的不太强的均匀磁场。特征是由一对相 同半径的同轴载流线圈组成,当它们之间的距离等 于它们的半径时,试计算两线圈中心处和轴线上中 点的磁感应强度。从计算结果将看到,这时在两线 圈间轴线上中点附近的场强是近似均匀的。 解 设两个线圈的半径为R, 各有N匝,每匝中的电流均 为I,且流向相同(如图)。 两线圈在轴线上各点的场强 方向均沿轴线向右,在圆心 O1 、O2 处磁感应强度相等, 大小都是
O1
Q1
P
Q2
O2
载流圆线圈轴线上的磁场
例 在玻尔的氢原子模型中,电子绕原子核运动相当 于一个圆电流,具有相应的磁矩,称为轨道磁矩。试 求轨道磁矩μ与轨道角动量L之间的关系,并计算氢 原子在基态时电子的轨道磁矩。
解 为简单起见,设电子绕核作匀速圆周运动,圆 的半径为r,转速为n。电子的运动相当于一个圆电 流,电流的量值为I=ne,圆电流的面积为S=πr2, 所以相应的磁矩为
2( R x )
2 3 2 2
载流圆线圈轴线上的磁场
0 IS B 2 ( R 2 x 2 ) 2( R 2 x 2 )
2
3 2
x0
B
0I
2R
(2)在远离线圈处
载流线圈 的磁矩
x R, x r
0 B 2 0 B 2
0 Idl dB 4 R 2
0 I1dl 0 I1l1 B1 2 1 4 R 4 R 2
0 I 2dl 0 I 2 l2 B2 2 4 R 2 4 R 2 U U I R l s I1 l 2 I 2 l1
B B1 B2 0
实际上,L>>R 时 ,螺线 管内部 的 磁 场近似 均匀 , 大 小为 0 nI
0 nI
0 nI
2
B
A1
O
A2
一:载流直导线的磁场
0 I cos1 cos2 B 4 r
二:载流圆线圈轴线上的磁场
B 中心 B 轴线
2
I r B
0 I
2R
1
0 IR 2
IS 0 IS 3 3 x 2 r pm r3
引入 pm ISen
(3) 载流圆弧
圆心角
0 I 0 I B 2 R 2 4R
B
I
例 如图所示,两根长直导线沿半径方向接到 粗细均匀的铁质圆环上的A和B两点,并与很 远处的电源相接, 试求环中心o点处的磁感应 强度. 解 三段直导线在圆心处 B 产生的磁场为零. 2 1 o 0 Idl r dB 3 A 4 r
O1 Q1 P Q2 O2
R
R
R
载流圆线圈轴线上的磁场
B0
0 NI
2R
2R R
2
0 NIR 2
2 3/ 2
0 NI
0 NI 1 1 0.677 2R R 2 2
两线圈间轴线上中点P处,磁感应强度大小为
BP 2
0 NIR 2
2 3/ 2
1.71 105 T
方向
S点
0 I 3 BLA (cos 0 cos ) 4a 4 0 I 3 B L A (cos cos ) 4a 4 B p BLA BLA 7.07 105 T
方向
L
L
R
a
I A
a
I
S
方向 方向
2 2 3/ 2
2 R x 三:载流螺线管中的磁场 无限长螺管:
(不必记)
B内 0 nI,B 外 0
练 习
求圆心O点的 B 如图,
I
I
B
O R
O
R
0 I
4R
B
0 I
8R
I
R
O
2 3
I
0 I B 4 R 2R
0 I
0 I 3 B (1 ) 6R R 2
2
P
dB
R 二、 圆形电流的磁场.有一半径为 的载 I P 流圆环,电流强度为 ,求它轴线上任一点 的磁感应强度 . B Id l 0 Idl sin dB dB r 解 dB 2 R 4 r o x 0 P dB// x 90
dB
0 Idl dB 4 r 2
三、 载流直螺线管内部的磁场
设螺线管的半径为R,电流为I,每单位长度 有线圈n匝。
1
r
dB
R
A1
2
p
A2
dl
l
载流圆线圈轴线上的磁场
1
r
dB
A1
2
R
A2
p
l
dl
由于每匝可作平面线圈处理, ndl匝线圈可作 Indl的一个圆电流,在P点产生的磁感应强度:
2( R l ) 2 0 R nI d l B L dB L 2 2 3/ 2 2( R l )
Idl
由于圆形电流具有对称性,各垂直分量dB 相互抵消,所以总磁感强度 B 的大小为各个平 行分量 dB// 的代数和为
B dB// dB cos
cos R r
0 IR2 0 IR 2R B dl 3 3 0 2r 4 r
0 IR2
IS ner 2
L me vr me 2rnr 2me nr 2 e L 2m e
载流圆线圈轴线上的磁场
角动量和磁矩的方向可分 别按右手螺旋规则确定。 因为电子运动方向与电流 方向相反,所以L和μ的 方向恰好相反,如图所示。 上式关系写成矢量式为
L
e - L 2m e
0 I
O
R
例.无限长载流直导线弯成如图形状
L
I 20 A a 4cm 求: P、R、S、T四点的 B
解: P点 B p BLA BLA
R
a
I A
a
L
S
I
a
P T
R点
0 I 0 5 10 5 T 4a
方向
BR BLA BLA 0 I 0 I 3 1 (cos 0 cos ) (cos cos ) 4a 4 4a 4
2 2 3/ 2
dB
0 R nI d l
2
载流圆线圈轴线上的磁场
l R cot
d l R csc d
2 2 2 2 2
1
r
dB
A1
2
R
A2
p
又 R l R csc
B L
0 R nI d l
2
l
dl
2( R l )
2
2 3/ 2
0
0
2
2
nI
2
1
sin d
nI (cos 2 cos 1 )
载流圆线圈轴线上的磁场
B
0 nI
2
(cos 2 cos 1 )
讨论:
(1)螺线管无限长
1 , 2 0 B 0 nI
(2)半无限长螺线管的端点圆心处
B 0 nI / 2
载流长直导线的磁场
