第五版普通物理11-2,11-3毕奥—萨伐尔定律及其应用
毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用萨伐尔定律是一条重要的物理学定律,它表明在极坐标系中,线性磁场与磁力线紧密联系。
在此定律的影响下,较小的磁场并非总是比较複杂的磁力线模式。
萨伐尔定律的具体表达式是:Bθ=-∂Φ/∂z,其中Bθ为放射状波函数,Φ为磁力函数。
萨伐尔定律在极坐标系中能广泛地应用于物理领域,作用涉及磁场跃迁、电离层静电场、星际磁力场等各方面。
比如,针对电离层的放射现象,在极坐标系中,萨伐尔定律可用来量化磁力线紊乱程度,即把磁力线画化为一条定义其强度大小的简单曲线;在星际磁力场中,萨伐尔定律可用来量化磁场并推导出磁矩变化规律,磁场和磁矩变化会受连续性和格林函数影响。
总之,萨伐尔定律是一条重要且关键的物理学定律,它对于我们研究物理领域有重要意义。
在极坐标系中,萨伐尔定律的表达式为Bθ=-∂Φ/∂z,且其应用远不止这里所述,而是渗透于各个新兴学科中,通过它可以深入了解物理性质,探索出许多未知的现象。
第五版普通物理11-2,11-3毕奥—萨伐尔定律及其应用

第五版普通物理习题11-2,11-3毕奥—萨伐尔定律及其应用选择题两条无限长载流导线,间距0.5厘米,电流10A ,电流方向相同,在两导线间距中点处磁场强度大小为(A )0 (B )πμ02000T (C )πμ04000 T (D )πμ0400T [ ] 答案:A通有电流I 的无限长直导线弯成如图所示的3种形状,则P 、Q 、O 各点磁感应强度的大小关系为(A )P B >Q B >O B (B )Q B >P B >O B (C ) Q B >O B >P B (D )O B >Q B >P B[ ] 答案:D在一个平面内,有两条垂直交叉但相互绝缘的导线,流过每条导线的电流相等,方向如图所示。
问哪个区域中有些点的磁感应强度可能为零(A )仅在象限1 (B )仅在象限2 (C )仅在象限1、3 (D )仅在象限2、4[ ]答案:D无限长直导线通有电流I ,右侧有两个相连的矩形回路,分别是1S 和2S ,则通过两个矩形回路1S 、2S 的磁通量之比为:(A )1:2 (B )1:1 (C )1:4 (D )2:1[ ]答案:(B )边长为a 的一个导体方框上通有电流I ,则此方框中心点的磁场强度(A )与a 无关 (B )正比于2a (C )正比于a (D )与a 成反比[ ]答案:D边长为l 的正方形线圈,分别用图示两种方式通以电流I ,图中ab 、cd 与正方形共面,在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为(A )01=B ,02=B (B )01=B ,lIB πμ0222=(C )l I B πμ0122=,02=B (D )l I B πμ0122=, lIB πμ0222= [ ]答案:C载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同的电流强度I 。
若两个线圈中心1O 、2O 处的磁感应强度大小相同,则1a :2a =(A )1:1 (B )π2:1 (C )π2:4 (D )π2:8[ ]答案:D如图所示,两根长直载流导线垂直纸面放置,电流11=I A ,方向垂直纸面向外;电流22=I A ,方向垂直纸面向内。
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例
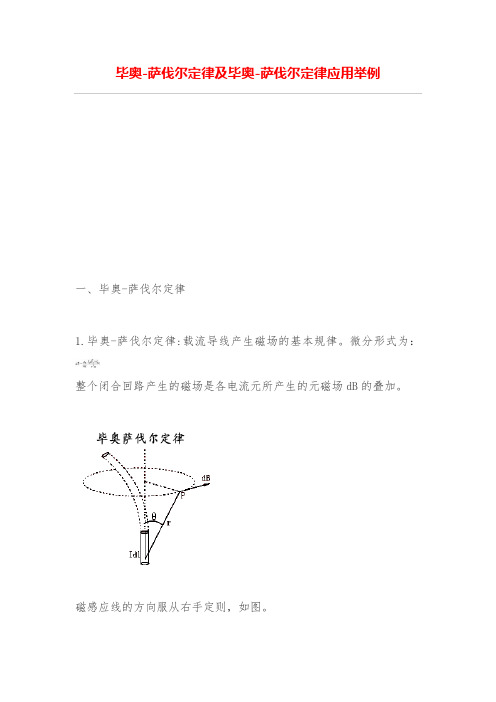
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为:整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则,如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。
例1.载流长直导线的磁场解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为:方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同,所以求总磁感强度的积分为标量积分,即:(1)由图得:,即:此外:,代入(1)可得:讨论:(1)无限长直通电导线的磁场:(2)半无限长直通电导线的磁场:(3)其他例子例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解:建立坐标系如图,任取电流元,由毕-萨定律得:,方向如图:,所有dB形成锥面。
将dB进行正交分解:,则由由对称性分析得:,所以有:,因为: ,r=常量,所以:,又因为:所以:,方向:沿x轴正方向,与电流成右螺旋关系。
讨论:(1)圆心处的磁场:x=0 ,。
(2)当即P点远离圆环电流时,P点的磁感应强度为:。
例3:设有一密绕直螺线管。
半径为 R ,通电流 I。
总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为: 电流为:。
其相当于一个圆电流,它在P点的磁感应强度为:。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为:因为:代入上式得:所以:讨论:(1)管内轴线上中点的磁场:(2)当 L>>R时,为无限长螺线管。
此时,,管内磁场。
即无限长螺线管轴线上及内部为均匀磁场,方向与轴线平行满足右手定则。
11-3毕奥-萨伐尔定律及应用

真空的磁导率: π×10 真空的磁导率:o=4π× -7 π× 点的距离. (2) r是电流元 到P点的距离. ) 是电流元Idl 点的距离 r是从电流元 指向 点的单位矢量. 是从电流元Idl 指向P点的单位矢量 点的单位矢量. 是从电流元
上页 下页
(3)磁场的大小: )磁场的大小:
o Idl sin θ dB = 2 θ是Idl与r 之间的夹角 与 之间的夹角. 4π r
在薄片中取弧长为dl的窄条, 在薄片中取弧长为 的窄条, 的窄条 其中通过的微元电流为: 其中通过的微元电流为:
I
I I dI = dl = dθ πR π
上页 下页
y
在俯视图上建立如图坐标, 在俯视图上建立如图坐标, 电流元在O点激发的磁感应 电流元在 点激发的磁感应 强度为: 强度为:
o
dB
θ
毕奥-萨伐尔定律及应用 §11-3 毕奥 萨伐尔定律及应用
毕奥-萨伐尔定律 一, 毕奥 萨伐尔定律
d 真空中,电流元 真空中,电流元Idl 在P点产 B 点产 生的磁场为
o Idl ×r dB = 2 4π r
说明
P
r
θ
I
Idl
上式称为毕奥 萨伐尔定律 上式称为毕奥-萨伐尔定律 毕奥
(1)公式中的系数是 制要求的. 制要求的. )公式中的系数是SI制要求的
x R
0 0 I dB = dI = 2 dθ 2πR 2π R
所以: 所以:
π
dθ
方向如图所示. 方向如图所示.
0 I Bx = dBx = 2 ∫0 π R
即:
0 I dBx = dBsinθ = 2 sinθdθ 2π R
By = ∫ dB = 0
毕奥-萨伐尔定律

将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
11-2毕奥-萨伐尔定律

=
μo
4π
I a
cosβ
dβ
B
=
μo
4π
I a
β2
β 1 cosβ
dβ
=
μ oI
4π a
( sinβ 2
sinβ 1 )
B
=μ4πo
I a
( sinβ 2
sinβ 1 )
I
讨论:
当直线电流为“无限长”时
β1
π
2
β2
π
2
β 1 β 2 dB a
B
=
μo
2π
I a
2. 载流圆线圈轴线上的磁场
dB = μ on I d l R 2
. 2 ( R 2 + l 2 )3 2
μ
=
on 2
I (
( R2
R cscβ2 dβ ) R 2 + R 2ctg2β )3 2
=μ
on I
.( R cscβ2
2 R 3 csc 3β
dβ
) R2
=
μ onI dβ
2cscβ
B=
μ onI dβ
2cscβ
=
μ onI
由上两式得:
B =μ εo 0 v × E
此式表明运动电荷激发的电场和磁场紧
密相关。
§11-3 毕奥 萨伐尔定律的应用 1. 载流直导线的磁场
dB 的方向: I dl × r 的方向
dB
的大小:
dB
=
μo
4π
I
dl sina
r2
几何关系:
I dl
sin a =sin ( 900 +β ) dl a
11-2 毕奥—萨伐尔定律

(Biot−Savart Law)
又称毕奥−萨伐尔−拉普拉斯定律,简称毕−萨定律 这是由毕奥 −萨伐尔经大量的间接实验归纳、总结、 在拉普拉斯的帮助下进行严格的数学推理给出的,由电流元 激发的磁场的实验规律。其地位相当于静电场中的库仑定律。 一般空间分布电流激发的磁场, 原则上由毕−沙定律给出的 结果按矢量叠加得到。 由于稳恒电流必定是闭合的,实验中不可能提供 稳恒的电流元,这种实验只能是间接推理性的。
由于电流磁效应的横向性,可考虑下面的实验方案, 测量直线电流对电流元的作用、电流元间的作用。
毕奥 − 沙伐尔做了第一 组实验,总结出磁感应强度与 I 成正比、与 r2 成反比;
安培做了第二组实验 两个结果拼在一起,构 成了毕 − 沙定律。
电场分布的一般计算方法
磁场分布的一般计算方法
Idl
E
q r 3 4 0 r 1
q
v
r
P
B
E
运动电荷的磁场
0 qv r B 3 4 r
E q r 3 4 0 r 1
B 0 0v E
运动电荷所激发的电场和磁场是紧密联系的。
3. 平面载流线圈的磁矩(磁偶极子) magnetic (dipole) moment 定义载流 I 的刚性平面线圈 S 的磁矩为
pm IS
— S 为线圈的面积 — I 为刚性平面线圈通过的电流
图中,n 为线圈平面的法向,
它也是磁矩的方向。
pm
n
I
n 与电流的方向成右手螺旋
关系。
m IS n
说明:只有当圆形电流的 面积S很小,或场点距圆电流 很远时,才能把圆电流叫做 磁偶极子.
11.2_毕奥-萨伐尔定律及应用
第十一章 稳恒磁场
B=
µ0 nI
2
(cos β 2 − cos β1 )
β1 = π − β 2
l/2
点位于管内轴线中点 (1)P点位于管内轴线中点 ) 点位于管内
cos β1 = − cos β 2
B = µ0 nI cos β 2 =
若
cos β2 =
(l / 2)
l
2
+ R2
µ0 nI
2
(l
2
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
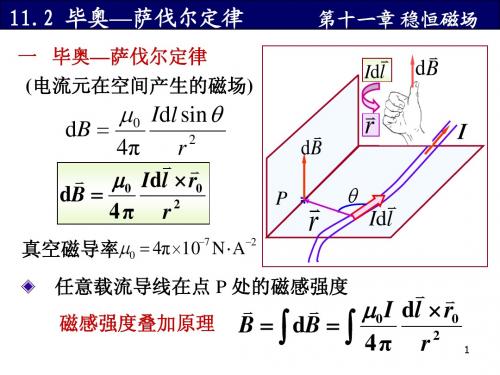
毕奥—萨伐尔定律 一 毕奥 萨伐尔定律 (电流元在空间产生的磁场 电流元在空间产生的磁场) 电流元在空间产生的磁场
第十一章 稳恒磁场
Idl
dB
4π r µ0 Idl × r0 dB = 4π r2
−7 −2 真空磁导率µ0 = 4π ×10 N ⋅ A
dB =
µ0 Idl sin θ
2
r
dB
P *
I
r
θ
Idl
任意载流导线在点 P 处的磁感强度 磁感强度叠加原理
B = ∫ dB = ∫
µ0 I dl × r0
4π r
2
1
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
第十一章 稳恒磁场 毕奥—萨伐尔定律 毕奥 萨伐尔定律
dB =
µ0 Idl × r0
4π
1
r
1 B = µ 0 nI 2
B=
µ0nI
2
(cos β2 − cos β1 )
B
1 µ 0 nI 2
µ0nI
x
24
O
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五版普通物理习题11-2,11-3毕奥—萨伐尔定律及其应用选择题两条无限长载流导线,间距0.5厘米,电流10A ,电流方向相同,在两导线间距中点处磁场强度大小为(A )0 (B )πμ02000T (C )πμ04000 T (D )πμ0400T [ ] 答案:A通有电流I 的无限长直导线弯成如图所示的3种形状,则P 、Q 、O 各点磁感应强度的大小关系为(A )P B >Q B >O B (B )Q B >P B >O B (C ) Q B >O B >P B (D )O B >Q B >P B[ ] 答案:D在一个平面内,有两条垂直交叉但相互绝缘的导线,流过每条导线的电流相等,方向如图所示。
问哪个区域中有些点的磁感应强度可能为零(A )仅在象限1 (B )仅在象限2 (C )仅在象限1、3 (D )仅在象限2、4[ ]答案:D无限长直导线通有电流I ,右侧有两个相连的矩形回路,分别是1S 和2S ,则通过两个矩形回路1S 、2S 的磁通量之比为:(A )1:2 (B )1:1 (C )1:4 (D )2:1[ ]答案:(B )边长为a 的一个导体方框上通有电流I ,则此方框中心点的磁场强度(A )与a 无关 (B )正比于2a (C )正比于a (D )与a 成反比[ ]答案:D边长为l 的正方形线圈,分别用图示两种方式通以电流I ,图中ab 、cd 与正方形共面,在这两种情况下,线圈在其中心产生的磁感应强度的大小分别为(A )01=B ,02=B (B )01=B ,lIB πμ0222=(C )l I B πμ0122=,02=B (D )l I B πμ0122=, lIB πμ0222= [ ]答案:C载流的圆形线圈(半径1a )与正方形线圈(边长2a )通有相同的电流强度I 。
若两个线圈中心1O 、2O 处的磁感应强度大小相同,则1a :2a =(A )1:1 (B )π2:1 (C )π2:4 (D )π2:8[ ]答案:D如图所示,两根长直载流导线垂直纸面放置,电流11=I A ,方向垂直纸面向外;电流22=I A ,方向垂直纸面向内。
则P 点磁感应强度B的方向与X 轴的夹角为(A)30° (B)60° (C)120° (D)210°[ ]答案:A四条相互平行的载流长直导线电流强度均为I ,方向如图所示。
设正方形的边长为2a ,则正方形中心的磁感应强度为(A )I a πμ02 (B )I aπμ220(C )0 (D )I a πμ0[ ]答案:C一半径为a 的无限长直载流导线,沿轴向均匀地流有电流I 。
若作一个半径为a R 5=、高l 的圆柱形曲面,轴与载流导线的轴平行且相距a 3,则B在圆柱侧面S 上积分⎰⋅s d B为(A )I a πμ520 (B )I a πμ250 (C )0 (D )I aπμ50 [ ]答案:C长直导线通有电流I ,将其弯成如图所示形状,则O 点处的磁感应强度大小为(A )R I R I 4200μπμ+ (B )R I R I 8400μπμ+ (C )R I R I 8200μπμ+ (D )RIR I 4400μπμ+ [ ]答案:B电流由长直导线1沿平行bc 边方向经过a 点流入电阻均匀的导线构成的正三角形线框,由b 点流出,经长直导线2沿cb 延长线方向返回电源,如图。
已知直导线上的电流为I ,三角框每边长l 。
若载流导线1、2和三角框中的电流在三角框中心O 点产生的磁场分别用1B、2B 、3B表示,则O 点的磁感应强度大小(A )0=B ,因为0321===B B B(B )0=B ,因为021=+B B,03=B(C )0≠B ,因为虽然021=+B B,但03≠B(D )0≠B ,因为虽然03=B ,但021≠+B B[ ]答案:D如图所示,一条长导线折成钝角α,导线中通有电流I ,则O 点的磁感应强度为(A )0 (B )απμcos 20I (C )απμsin 20I (D )απμsin 0I[ ]答案:A如图所示,一条长导线折成钝角α,导线中通有电流I ,则在PO 延长线上离O 点距离为l 的A 点处的磁感应强度为(A )0 (B ))]2sin(1[)2cos(40παπαπμ-+-l I(C ))]2sin(1[)2sin(40παπαπμ-+-l I(D ))]2sin(1[)2cos(40παπαπμ---l I[ ]答案:B如图所示,两根长导线沿半径方向引到铁环上的A 、B 两点上,两导线的夹角为α,环的半径R ,将两根导线在很远处与电源相连,从而在导线中形成电流I ,则环中心点的磁感应强度为(A )0 (B )RI20μ (C )αμsin 20RI(D )αμcos 20RI[ ]答案:A两条长导线交叉于一点O ,这两条导线上通过的电流分别为I 和2I ,则O 点的磁感应强度为(A )0 (B )πμI 0 (C )πμI 02 (D ) πμI04[ ]答案:A两条长导线相互平行放置于真空中,如图所示,两条导线的电流为I I I ==21,两条导线到P 点的距离都是a ,P 点的磁感应强度为(A )0 (B )aIπμ220 (C )a I πμ02 (D ) a I πμ0[ ]答案:B两条长导线相互平行放置于真空中,如图所示,两条导线的电流为I I I ==21,两条导线到P 点的距离都是a ,P 点的磁感应强度方向(A )竖直向上 (B )竖直向下 (C )水平向右 (D ) 水平向左[ ]答案:D题号:30913018 分值:3分 难度系数等级:3两条长导线相互平行放置于真空中,如图所示,两条导线的电流为I I I ==21,两条导线到P 点的距离都是a ,P 点的磁感应强度方向(A )竖直向上 (B )竖直向下 (C )水平向右 (D ) 水平向左[ ]答案:B电流由长直导线1沿切线方向经a 点流入一由电阻均匀的导线构成的圆环,再由b 点沿切向从圆环流出,经长直导线2返回电源,如图。
已知直导线上的电流强度为I ,圆环的半径为R ,且a 、b 和圆心O 在同一条直线上。
设长直导线1、2和圆环中的电流分别在O 点产生的磁感应强度为1B 、2B 、3B,则O 点的磁感应强度大小(A )0=B ,因为0321===B B B(B )0=B ,因为虽然01≠B ,02≠B ,但021=+B B,03=B(C )0≠B ,因为01≠B ,02≠B ,03≠B(D )0≠B ,因为虽然03=B ,但021≠+B B[ ]答案:B电流由长直导线1沿半径方向经a 点流入一由电阻均匀的导线构成的圆环,再由b 点沿半径方向从圆环流出,经长直导线2返回电源,如图。
已知直导线上的电流强度为I ,圆环的半径为R ,︒=∠30aOb 。
设长直导线1、2和圆环中的电流分别在O 点产生的磁感应强度为1B 、2B 、3B,则O 点的磁感应强度大小(A )0=B ,因为0321===B B B(B )0=B ,因为虽然01≠B ,02≠B ,但021=+B B,03=B(C )0≠B ,因为虽然03=B ,但021≠+B B(D )0≠B ,因为03≠B ,021≠+B B ,所以0321≠++B B B[ ]答案:A2. 判断题:一条载流长直导线,在导线上的任何一点,由导线上的电流所产生的磁场强度为零。
( )答:对根据毕奥沙伐定律分析,在均匀、线性、各向同性媒质中,一段有限长载流直导线周围空间的磁场分布具有对称性,磁感应强度线是一些以轴线为中心的同心圆。
( )答:对一段电流元l Id 所产生的磁场的方向并不总是与l Id垂直。
( )答:错在电子仪器中,为了减弱与电源相连的两条导线所产生的磁场,通常总是把它们扭在一起。
( )答:对如图,两根通有同样电流I 的长直导线十字交叉放在一起,交叉点相互绝缘,则虚线上的磁场为零。
答:对如图,一根导线中间分成电流相同的两支,形成一菱形,则在菱形长对角线(水平方向)上的磁场为零,短对角线上的磁场不为零。
( )答:对对于一个载流长直螺线管,两端的磁感应强度大小是中间的一半。
( ) 答:对当需要对一个在地球上、暴露在空气中的点的磁场进行精确计算时,如果磁场比较弱,需要考虑地磁场的影响。
( )答:对载流导线所产生的磁场与地磁场之间,由于性质不同,不可以进行磁场的叠加。
( ) 答:错载流导线所产生的磁场与永磁体所产生的磁场具有不同的性质,所以在计算合磁场时,并不是总能进行叠加计算。
( )答:错3. 填空题一根长直载流导线,通过的电流为2A ,在距离其2mm 处的磁感应强度为 。
(70104-⨯=πμTm/A )答:4102-⨯T一根直载流导线,导线长度为100mm ,通过的电流为5A ,在与导线垂直、距离其中点的50mm 处的磁感应强度为 。
(70104-⨯=πμTm/A )答:5102-⨯T一根载流圆弧导线,半径1m ,弧所对圆心角6π,通过的电流为10A ,在圆心处的磁感应强度为 。
(70104-⨯=πμTm/A )答:6106-⨯πT一个载流直螺线管,直径0.1m ,长度0.1m ,通过的电流为0.1A,线圈匝数1000,在 螺线管内部轴线中点上的磁感应强度为 。
(70104-⨯=πμTm/A )答:41022-⨯πT一个载流直螺线管,直径0.2m ,长度0.2m ,线圈两端加36V 电压,线圈匝数1000, 线圈电阻100欧姆,在螺线管一端轴线中点上的磁感应强度为 。
(70104-⨯=πμTm/A )答:510218-⨯πT真空中,电流I 由长直导线1沿垂直bc 边方向经a 点流入一电阻均匀分布的正三角形线框,再由b 点沿平行ac 边方向流出,经长直导线2返回电源(如图)。
三角形框每边长 为l ,则在该正三角框中心O 点处磁感应强度的大小答案:l4I 30πμ电流由长直导线1沿半径方向经a 点流入一电阻均匀分布的圆环,再由b 点沿半径方向流出,经长直导线2返回电源(如图),已知直导线上的电流强度为I ,圆环的半径为R ,且a 、b 和圆心O 在同一直线上,则O 处的磁感应强度的大小为答案:0在真空中,电流I 由长直导线1沿半径方向经a 点流入一电阻均匀分布的圆环,再由b 点沿切向从圆环流出,经长直导线2返回电源(如图)。
已知直导线上的电流强度为I , 圆环的半径为R ,且a 、b 和圆心O 在同一直线上,则O 处的磁感应强度的大小为答案: R4I 0πμ一弯曲的载流导线在同一平面内,形状如图(O 点是半径为R 1和R 2的半圆圆心) 则圆心O 点处的磁感应强度大小 。
答案:202010R 4I R 4I R 4I πμμμ-+一弯曲的载流导线在同一平面内,形状如图(O 点是半径为R 1和R 2的半圆圆心), 则圆心O 点处的磁感应强度的方向 。
