(完整版)第五版普通物理11-2,11-3毕奥—萨伐尔定律及其应用汇总
合集下载
第五版普通物理11-2,11-3毕奥—萨伐尔定律及其应用
第五版普通物理习题11-2,11-3毕奥—萨伐尔定律及其应用选择题两条无限长载流导线，间距0.5厘米，电流10A ，电流方向相同，在两导线间距中点处磁场强度大小为（A ）0 （B ）πμ02000T （C ）πμ04000 T （D ）πμ0400T [ ] 答案：A通有电流I 的无限长直导线弯成如图所示的3种形状，则P 、Q 、O 各点磁感应强度的大小关系为（A ）P B ＞Q B ＞O B （B ）Q B ＞P B ＞O B （C ） Q B ＞O B ＞P B （D ）O B ＞Q B ＞P B[ ] 答案：D在一个平面内，有两条垂直交叉但相互绝缘的导线，流过每条导线的电流相等，方向如图所示。
问哪个区域中有些点的磁感应强度可能为零（A ）仅在象限1 （B ）仅在象限2 （C ）仅在象限1、3 （D ）仅在象限2、4[ ]答案：D无限长直导线通有电流I ，右侧有两个相连的矩形回路，分别是1S 和2S ，则通过两个矩形回路1S 、2S 的磁通量之比为：（A ）1：2 （B ）1：1 （C ）1：4 （D ）2：1[ ]答案：（B ）边长为a 的一个导体方框上通有电流I ，则此方框中心点的磁场强度（A ）与a 无关 （B ）正比于2a （C ）正比于a （D ）与a 成反比[ ]答案：D边长为l 的正方形线圈，分别用图示两种方式通以电流I ，图中ab 、cd 与正方形共面，在这两种情况下，线圈在其中心产生的磁感应强度的大小分别为（A ）01=B ，02=B （B ）01=B ，lIB πμ0222=（C ）l I B πμ0122=，02=B （D ）l I B πμ0122=， lIB πμ0222= [ ]答案：C载流的圆形线圈（半径1a ）与正方形线圈（边长2a ）通有相同的电流强度I 。
若两个线圈中心1O 、2O 处的磁感应强度大小相同，则1a ：2a ＝（A ）1：1 （B ）π2：1 （C ）π2：4 （D ）π2：8[ ]答案：D如图所示，两根长直载流导线垂直纸面放置，电流11=I A ，方向垂直纸面向外；电流22=I A ，方向垂直纸面向内。
11-2毕奥萨法尔定律
§11-2 毕奥—萨伐尔定律
11.2
• 研究思路
Biot-savart’s law
– 静电场：点电荷模型 任一个带电体 Q dq dE E d E
（ 微元分析法）
– 静磁场：电流元模型
I Idl dB B dB
研究内容
• 在恒定磁场中引入电流元的概念，分析电流 元产生磁场的规律，即B-S 定律，最后利用 磁场的叠加原理，可以解决任意载流体所产 生的稳恒磁场的分布。
0 3
Biot-savart’s law 讨论
• B－S Law的物理意义
表明一切磁现象的根源是电流（运动电荷）产生 的磁场。反映了载流导线上任一电流元在空间任 一点处产生磁感应强度在大小和方向上的关系。 由此定律原则上可以解决任何载流导体在起周围 空间产生的磁场分布。
Biot-savart’s law 讨论
3. 运动电荷的磁场表达式(微观意义的B-S定律)
按经典电子理论，导体中电流是大量带电粒子的定向 运动，电流激发磁场，实质是运动电荷在其周围空间激发 磁场。
v
dl
S 电流元
Idl
r
0 Idl sin dB 4 r2
I qnvS
0 qnvSdlsin dB 2 4 r
引入电流元矢量 I d l 的物理意义
任意载流回路可设想为是由无限多个首尾相 接的电流元构成，
I Idl dB B dB
电流元与点电荷的区别
• 点电荷可以独立存在 • 电流元不能单独存在
2、 Biot-savart’s law
I d l sin 大小： B d 4 r 方向： 或者：右手螺旋
11.2
• 研究思路
Biot-savart’s law
– 静电场：点电荷模型 任一个带电体 Q dq dE E d E
（ 微元分析法）
– 静磁场：电流元模型
I Idl dB B dB
研究内容
• 在恒定磁场中引入电流元的概念，分析电流 元产生磁场的规律，即B-S 定律，最后利用 磁场的叠加原理，可以解决任意载流体所产 生的稳恒磁场的分布。
0 3
Biot-savart’s law 讨论
• B－S Law的物理意义
表明一切磁现象的根源是电流（运动电荷）产生 的磁场。反映了载流导线上任一电流元在空间任 一点处产生磁感应强度在大小和方向上的关系。 由此定律原则上可以解决任何载流导体在起周围 空间产生的磁场分布。
Biot-savart’s law 讨论
3. 运动电荷的磁场表达式(微观意义的B-S定律)
按经典电子理论，导体中电流是大量带电粒子的定向 运动，电流激发磁场，实质是运动电荷在其周围空间激发 磁场。
v
dl
S 电流元
Idl
r
0 Idl sin dB 4 r2
I qnvS
0 qnvSdlsin dB 2 4 r
引入电流元矢量 I d l 的物理意义
任意载流回路可设想为是由无限多个首尾相 接的电流元构成，
I Idl dB B dB
电流元与点电荷的区别
• 点电荷可以独立存在 • 电流元不能单独存在
2、 Biot-savart’s law
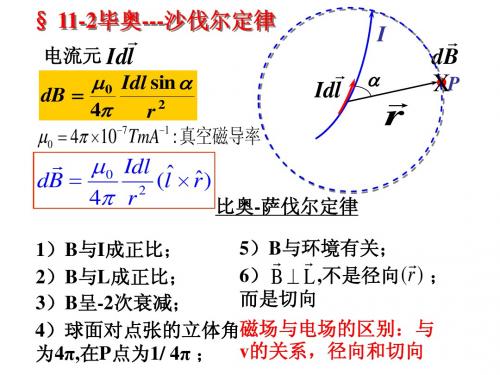
I d l sin 大小： B d 4 r 方向： 或者：右手螺旋
11.2 毕奥萨伐尔定律
11.2 毕奥萨伐尔定律总结目前磁的知识：电荷的移动，即电流产生磁场，描述磁场性质的物理量是磁感应强度B，电流元产生磁场中磁力安培力满足：d F=Idl×B，在电流元在磁场方向上的安培力为0，那么电流元与磁场，即磁感应强度之间是怎么关系？这节毕奥萨伐尔实验定律就将高速我们磁感应强度与电流元之间的关系。
大小：dB=μ04πIdlsinαr2真空磁导率μ0=4π×10−7N A2α为电流元Id l指向测点的矢量r和电流元之间的夹角方向:Id l×r—右螺旋法毕奥萨伐尔定律：dB=μ04πIdl×r0r2r0为了r方向的单位矢量B=d B运动电荷的磁场:电流是电荷的运动，即电荷的运动也能产生磁场。
电流I=nqvS，电流元Idl=nqvSdl=qvdN，其中dN为电流元中带电粒子的总数，因此毕奥萨伐尔定律可写为：dB=μ04π(dN)qdv×r0r2单个电荷在空间产生的磁场的磁感应强度为B=dB=μ0qdv×r02右螺旋法确定。
毕奥萨伐尔定律应用：求直线电流周围的磁场？B=μ0I4πa(cosθ1−cosθ2)无限长直线电流的磁场为：B=μ0I2πr 求载流圆线圈轴线上的磁场？B=μ0IR22(R2+x2)32圆环心处：B=μ0I2R 远离圆心处：B=μ0IR2x3=μ0IS2πx3S为平面载流线圈的面积，磁感应强度也常用磁矩p m，定义为p m=IS nn为线圈平面正法线方向上的单位矢量，则对应载流线圈轴线上磁场为B=μ0p m 2πx3圆心处的磁感应强度就可以表示为：B=μ0p m3一长螺线管轴线上的磁场？B 内=nμ0I匀强磁场，B外=0小结：毕奥萨伐尔定律及应用。
11-2 毕萨定理
=
sinα = R r
I
Y
r0
dB⊥ dB
p dB
•
x
X
µ0 IR
2
2( R2 + x2 )3 2
大小： B = 2( R2 + x2 )3 2 大小： 方向： 方向： 右手螺旋法则
µ0 IR2
结论
B=
µ0 IR
2
2 2 32
2(R + x )
1 x >> R B = ? ）
B=
µ0 IR2
2x3
对一段载流导线
µ0 Idl × r B = ∫ dB = 矢量积分） ∫L r 3 （矢量积分） 4π
直接积分计算B比较困难！ 直接积分计算 比较困难！ 比较困难 下面通过B的计算，掌握微积分直接计算B的 下面通过 的计算，掌握微积分直接计算 的 的计算 方法；进而总结几种典型情况， 以后的相关 方法；进而总结几种典型情况，(以后的相关 计算主要考查这些模型的叠加情况） 计算主要考查这些模型的叠加情况）
运动电荷产生的 磁场（与v垂直） 磁场（ 垂直） 垂直
µ0 qv × r B= 3 4π r
若q > 0, B与v × r同向 若q < 0, B与v × r反向
•
B
⊗B
r
θ
r
⊕
θ
+q
v
−q
v
例4、均匀带电圆环 已知： 已知：q、R、ω 圆环绕轴线匀速旋转。 圆环绕轴线匀速旋转。 求圆心处的 B 解：带电体转动，形成运流电流。 带电体转动，形成运流电流。 q
2 x =0 B =? ）
载流圆环
B=
µ0 I
2R
圆心角 θ = 2π
sinα = R r
I
Y
r0
dB⊥ dB
p dB
•
x
X
µ0 IR
2
2( R2 + x2 )3 2
大小： B = 2( R2 + x2 )3 2 大小： 方向： 方向： 右手螺旋法则
µ0 IR2
结论
B=
µ0 IR
2
2 2 32
2(R + x )
1 x >> R B = ? ）
B=
µ0 IR2
2x3
对一段载流导线
µ0 Idl × r B = ∫ dB = 矢量积分） ∫L r 3 （矢量积分） 4π
直接积分计算B比较困难！ 直接积分计算 比较困难！ 比较困难 下面通过B的计算，掌握微积分直接计算B的 下面通过 的计算，掌握微积分直接计算 的 的计算 方法；进而总结几种典型情况， 以后的相关 方法；进而总结几种典型情况，(以后的相关 计算主要考查这些模型的叠加情况） 计算主要考查这些模型的叠加情况）
运动电荷产生的 磁场（与v垂直） 磁场（ 垂直） 垂直
µ0 qv × r B= 3 4π r
若q > 0, B与v × r同向 若q < 0, B与v × r反向
•
B
⊗B
r
θ
r
⊕
θ
+q
v
−q
v
例4、均匀带电圆环 已知： 已知：q、R、ω 圆环绕轴线匀速旋转。 圆环绕轴线匀速旋转。 求圆心处的 B 解：带电体转动，形成运流电流。 带电体转动，形成运流电流。 q
2 x =0 B =? ）
载流圆环
B=
µ0 I
2R
圆心角 θ = 2π
大学物理：11-2,3 毕奥-萨伐尔定律
r E
=
qrr
4π ε0r 3
r B
=
μ0qvv × rr
4πr 3
r dB
=
μ
0
r Idl
×
rr
4πr 3
无限长均匀带电直线的电场
无限长直电流的磁场
E= λ 2π ε0r
(⊥带电直线）
B=
μ0I 2πr
（环绕电流）
容易混淆的静电场与稳恒磁场公式比较
均匀带电圆环轴线上电场 圆电流轴线上磁场 带电圆环圆心处电场
2 β1
讨论
B
=
μ0nI
2
(cos β2
−
cos β1)
(1) 无限长的螺线管
( ) 由 β1 = π , β2 = 0 代入
B = μ0nI
2
cos β2 − cos β1
实际上，L>>R 时，螺线管内部的 磁场近似均匀，大
小为 μ0nI
B = μ0nI
B
=
μ0nI
2
(cos
β2
−
cos
β1
)
R2
*o
B0
=
μ0I
4R2
− μ0I
4R1兹圈：两个完全相同的 N 匝共轴密绕
短线圈，其中心间距与线圈半径 R 相等，通同向平
行等大电流 I。求轴线上 o1 , o2 之间任一点P 的磁
场.
N匝
R
N匝
R
R
BP
=
μ0 NIR2
2[( R2 + ( R + x)2 ]32
§11-2 毕奥—萨伐尔定律
历史之旅
1819 年4月: 丹麦物理学家奥斯特（1777～1851） 发现电流的磁效应。
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例
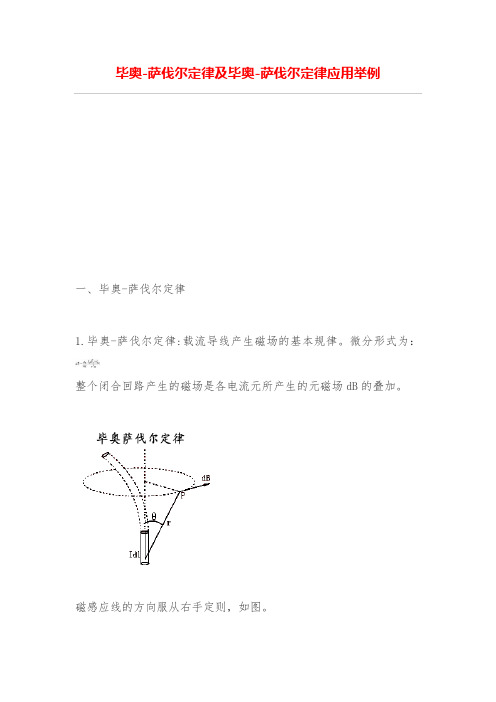
毕奥-萨伐尔定律及毕奥-萨伐尔定律应用举例一、毕奥-萨伐尔定律1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。
微分形式为：整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。
磁感应线的方向服从右手定则，如图。
二、毕奥-萨伐尔定律应用举例两种基本电流周围的磁感应强度的分布：载流直导线；圆电流。
例1.载流长直导线的磁场解：建立如图坐标系，在载流直导线上，任取一电流元Idz，由毕-萨定律得元电流在P点产生的磁感应强度大小为：方向为垂直进入纸面。
所有电流元在P点产生的磁场方向相同，所以求总磁感强度的积分为标量积分，即：（1）由图得：,即：此外：，代入（1）可得：讨论：（1）无限长直通电导线的磁场：（2）半无限长直通电导线的磁场：（3）其他例子例2:圆形载流导线轴线上的磁场：设在真空中，有一半径为 R ，通电流为 I 的细导线圆环，求其轴线上距圆心 O 为 x 处的P点的磁感应强度。
解：建立坐标系如图，任取电流元，由毕-萨定律得：，方向如图：，所有dB形成锥面。
将dB进行正交分解：，则由由对称性分析得：，所以有:，因为： ,r=常量，所以：，又因为：所以：，方向：沿x轴正方向，与电流成右螺旋关系。
讨论：（1）圆心处的磁场：x=0 ，。
（2）当即P点远离圆环电流时，P点的磁感应强度为：。
例3：设有一密绕直螺线管。
半径为 R ，通电流 I。
总长度L，总匝数N（单位长度绕有n 匝线圈），试求管内部轴线上一点 P 处的磁感应强度。
解：建立坐标系，在距P 点 x 处任意截取一小段 dx ，其线圈匝数为: 电流为：。
其相当于一个圆电流，它在P点的磁感应强度为：。
因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右，所以整个螺线管在P点的磁感应强度的大小为：因为：代入上式得：所以：讨论：（1）管内轴线上中点的磁场:（2）当 L>>R时，为无限长螺线管。
此时,，管内磁场。
即无限长螺线管轴线上及内部为均匀磁场，方向与轴线平行满足右手定则。
11-3毕奥-萨伐尔定律及应用
真空的磁导率: π×10 真空的磁导率:o=4π× -7 π× 点的距离. (2) r是电流元 到P点的距离. ) 是电流元Idl 点的距离 r是从电流元 指向 点的单位矢量. 是从电流元Idl 指向P点的单位矢量 点的单位矢量. 是从电流元
上页 下页
(3)磁场的大小: )磁场的大小:
o Idl sin θ dB = 2 θ是Idl与r 之间的夹角 与 之间的夹角. 4π r
在薄片中取弧长为dl的窄条, 在薄片中取弧长为 的窄条, 的窄条 其中通过的微元电流为: 其中通过的微元电流为:
I
I I dI = dl = dθ πR π
上页 下页
y
在俯视图上建立如图坐标, 在俯视图上建立如图坐标, 电流元在O点激发的磁感应 电流元在 点激发的磁感应 强度为: 强度为:
o
dB
θ
毕奥-萨伐尔定律及应用 §11-3 毕奥 萨伐尔定律及应用
毕奥-萨伐尔定律 一, 毕奥 萨伐尔定律
d 真空中,电流元 真空中,电流元Idl 在P点产 B 点产 生的磁场为
o Idl ×r dB = 2 4π r
说明
P
r
θ
I
Idl
上式称为毕奥 萨伐尔定律 上式称为毕奥-萨伐尔定律 毕奥
(1)公式中的系数是 制要求的. 制要求的. )公式中的系数是SI制要求的
x R
0 0 I dB = dI = 2 dθ 2πR 2π R
所以: 所以:
π
dθ
方向如图所示. 方向如图所示.
0 I Bx = dBx = 2 ∫0 π R
即:
0 I dBx = dBsinθ = 2 sinθdθ 2π R
By = ∫ dB = 0
大学物理——11-2毕奥-萨伐尔定律
1
2
μ0 I B （cos θ1 cos θ2 ） 4π a
2
μ0 I BP 4πa
I
o
a
* P
◆（3）载流直导线延长线上任一点的磁感强度
分析：根据载流直导线的磁感强度公式
μ0 I B (cos θ1 cos θ2 ) 4πa
在沿电流方向的延长线上任一点处，
P
2
2
1、5 点 ： dB 0
0 Idl 3、7点 ：dB 4R 2
3
7
Id l
6
2、4、6、8 点 ：
R
5
4
0 Idl dB sin 45 0 4R 2
0 μ0 Idl r B dB L L 4π r2
任意形状恒定电流的磁场：
利用毕-萨定律计算磁感应强度的基本方法： (1) 将电流分解为无数个电流元 ，任取一 Idl ； (2) 写出dB 大小，图示dB方向； (3) 分析各个dB方向；将 dB 在坐标系中分解；
z
方向：电流与磁感强度 成右手螺旋定则。 A1
2
B
讨论
◆（1） 无限长载流直导 线的磁场
I
o
x
A2
r
1
P y
1 0 2
μ0 I B 2π a
无限长载流直导线的磁场方向：
μ0 I B 2π a
B I B I
X
I
B
磁感应线的绕向与电流满足右手螺旋定则。
◆（2） 半无限长载流直导线的磁场
◆ 在载流圆线圈轴线以外的空间，其磁感强度的分 布大致如下图所示： I
思考：
R B x 0 0 I o B0
11-2 毕奥—萨伐尔定律
§11-2 毕奥—萨伐尔定律
（Biot−Savart Law）
又称毕奥−萨伐尔−拉普拉斯定律，简称毕−萨定律 这是由毕奥 −萨伐尔经大量的间接实验归纳、总结、 在拉普拉斯的帮助下进行严格的数学推理给出的，由电流元 激发的磁场的实验规律。其地位相当于静电场中的库仑定律。 一般空间分布电流激发的磁场， 原则上由毕−沙定律给出的 结果按矢量叠加得到。 由于稳恒电流必定是闭合的，实验中不可能提供 稳恒的电流元，这种实验只能是间接推理性的。
由于电流磁效应的横向性，可考虑下面的实验方案， 测量直线电流对电流元的作用、电流元间的作用。
毕奥 − 沙伐尔做了第一 组实验，总结出磁感应强度与 I 成正比、与 r2 成反比；
安培做了第二组实验 两个结果拼在一起，构 成了毕 − 沙定律。
电场分布的一般计算方法
磁场分布的一般计算方法
Idl
E
q r 3 4 0 r 1
q
v
r
P
B
E
运动电荷的磁场
0 qv r B 3 4 r
E q r 3 4 0 r 1
B 0 0v E
运动电荷所激发的电场和磁场是紧密联系的。
3. 平面载流线圈的磁矩（磁偶极子） magnetic (dipole) moment 定义载流 I 的刚性平面线圈 S 的磁矩为
pm IS
— S 为线圈的面积 — I 为刚性平面线圈通过的电流
图中，n 为线圈平面的法向，
它也是磁矩的方向。
pm
n
I
n 与电流的方向成右手螺旋
关系。
m IS n
说明：只有当圆形电流的 面积S很小，或场点距圆电流 很远时，才能把圆电流叫做 磁偶极子.
（Biot−Savart Law）
又称毕奥−萨伐尔−拉普拉斯定律，简称毕−萨定律 这是由毕奥 −萨伐尔经大量的间接实验归纳、总结、 在拉普拉斯的帮助下进行严格的数学推理给出的，由电流元 激发的磁场的实验规律。其地位相当于静电场中的库仑定律。 一般空间分布电流激发的磁场， 原则上由毕−沙定律给出的 结果按矢量叠加得到。 由于稳恒电流必定是闭合的，实验中不可能提供 稳恒的电流元，这种实验只能是间接推理性的。
由于电流磁效应的横向性，可考虑下面的实验方案， 测量直线电流对电流元的作用、电流元间的作用。
毕奥 − 沙伐尔做了第一 组实验，总结出磁感应强度与 I 成正比、与 r2 成反比；
安培做了第二组实验 两个结果拼在一起，构 成了毕 − 沙定律。
电场分布的一般计算方法
磁场分布的一般计算方法
Idl
E
q r 3 4 0 r 1
q
v
r
P
B
E
运动电荷的磁场
0 qv r B 3 4 r
E q r 3 4 0 r 1
B 0 0v E
运动电荷所激发的电场和磁场是紧密联系的。
3. 平面载流线圈的磁矩（磁偶极子） magnetic (dipole) moment 定义载流 I 的刚性平面线圈 S 的磁矩为
pm IS
— S 为线圈的面积 — I 为刚性平面线圈通过的电流
图中，n 为线圈平面的法向，
它也是磁矩的方向。
pm
n
I
n 与电流的方向成右手螺旋
关系。
m IS n
说明：只有当圆形电流的 面积S很小，或场点距圆电流 很远时，才能把圆电流叫做 磁偶极子.
11.2_毕奥-萨伐尔定律及应用
第十一章 稳恒磁场
B=
µ0 nI
2
(cos β 2 − cos β1 )
β1 = π − β 2
l/2
点位于管内轴线中点 （1）P点位于管内轴线中点 ） 点位于管内
cos β1 = − cos β 2
B = µ0 nI cos β 2 =
若
cos β2 =
(l / 2)
l
2
+ R2
µ0 nI
2
(l
2
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
毕奥—萨伐尔定律 一 毕奥 萨伐尔定律 (电流元在空间产生的磁场 电流元在空间产生的磁场) 电流元在空间产生的磁场
第十一章 稳恒磁场
Idl
dB
4π r µ0 Idl × r0 dB = 4π r2
−7 −2 真空磁导率µ0 = 4π ×10 N ⋅ A
dB =
µ0 Idl sin θ
2
r
dB
P *
I
r
θ
Idl
任意载流导线在点 P 处的磁感强度 磁感强度叠加原理
B = ∫ dB = ∫
µ0 I dl × r0
4π r
2
1
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
第十一章 稳恒磁场 毕奥—萨伐尔定律 毕奥 萨伐尔定律
dB =
µ0 Idl × r0
4π
1
r
1 B = µ 0 nI 2
B=
µ0nI
2
(cos β2 − cos β1 )
B
1 µ 0 nI 2
µ0nI
x
24
O
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
11、2毕萨定律及其应用
E 运动电荷除了产 r 生磁场外，还在其周 q B . 围激发电场。若电荷 v 运动速度远小于光速， 则空间一点的电场强度为： 1 q μ o q v× r 而B = E= r 3 r3 4 π π 4ε r
0
由上两式得：
B =μ ε v × E o 此式表明运动电荷激发的电场和磁场紧 结束 密相关。
0 IR 圆环 B 电流: 2( x 2 R 2 )3 2
（下一页）
电偶极子
q q Pe qr
1 pe E 3 20 r
延长线 上： 中垂面 上：
r
类 比
磁偶极子 I S
n
0 pm B 3 2r 0 pm B 3 4r
2
0 nI R csc d R 0 nId 3 3 2 R csc 2 csc
2 2
2 1
B dB
0 nId 0 nI 2 2 csc 2
2
1
sin d
0 nI cos 2 cos 1 2
返回
dB =
μ
I dl sin a r2 4π
o
μo
真空中的磁导率
μ o = 4π
× 10
7
( H . m 1 ) 或 ( 亨利.米 萨伐尔定律
×(
1
)
用矢量形式表示的毕奥 dB =
4π
μ o I dl
×ቤተ መጻሕፍቲ ባይዱ
r3
4π
r
μ o I dl = r2 4π
×
r ) r
结束
返回
B =
μ o I dl
高中毕奥-萨伐尔定律详解
µ oI
, dS = l dx 2 x π B I x a b
结束
返回
Φ m = ∫∫S B . dS
=∫ =
a +b a
µ oI
l dx 2 x π a +b ln a
ቤተ መጻሕፍቲ ባይዱ
dx
l
µ o Il
2 π
结束
返回
×
§11-3 毕奥
的方向： dB 的方向： I dl
r
dB P
由上面得到： 由上面得到： sin α = cosβ a sec 2 dβ dl = β r = a secβ
dl l
I dl r
µ o I dl sinα dB = π r2 4
β 1 β 2 dB a 2 .a sec β dβ .cosβ µ o I µo I cosβ dβ = = 2 2 a sec β 4 a 4π π
2
2 R csc β µ o n I dβ µ on I B=∫ = 2 2cscβ µ o n I ( cosβ cosβ 1) 2 = 2
µ o n I ( R csc β dβ ) R = = 3 3
2
2
µ o n I dβ
2cscβ sinβ dβ
结束
返回
∫β
β2
1
...................
β1 β2 R P
µ o n I ( cosβ 2 B= 2
当螺线管为无限长时： 当螺线管为无限长时： 1 β B =µ o n I
cosβ 1)
π ，β 2
0
结束
返回
[ 例1 ] 在真空中有一无限长载流直导线， 在真空中有一无限长载流直导线， 试求：通过其右侧矩形线框的磁通量。 试求：通过其右侧矩形线框的磁通量。 dΦ m = B . dS , B=
毕奥—萨伐尔定律及其应用
0 I
4a
sin d
0 I
4a
(cos1
cos2 )
上式中，1 和2 分别是直导线两端的电流元与它们到 P 点的矢径之间的夹角。
毕奥—萨伐尔定律及其应用
， ，
，
，
例题讲解 1
设长为 L 的直导线通有电流 I，求距离导线为 a 处一点 P 的磁感应强度。
若导线长度远大于点 P 到直导线的垂直距离（ L a ），则导线可视为无限长。
dB，Idl，r 这 3 个矢量的方向符合右手螺旋法则。
因此，矢量形式
dB
0 4
Idl r2
er
er ——由电流元指向点 P 的单位矢量。
整个载流导线在空间某点 P 的磁感应强度 B，等于导线上所有电流元在该点所产生的磁感应强度
dB
的矢量和，即
B
L
dB
L
0 4
Idl r2
er
积分是对整个载流导线进行矢量积分。
r2
式中，0 称为真空磁导率，其值为 0 4π 10–7 N A2 。磁感应强度 dB 的方向垂直于 Idl 和 r 所组
成的平面，并沿 Idl r 的方向，即当右手弯曲，四指从 Idl 方向沿小于 π 的角转向 r 时，伸直的大拇指所
指的方向为 dB 的方向。
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
大学物理
毕奥—萨伐尔定律及其应用
1.1 毕奥—萨伐尔定律
毕奥—萨伐尔定律指出：电流元 Idl 在真空中某点 P 所产生的磁感应强度 dB 的大小，与电流元的
大小 Idl 成正比，与电流元和从电流元到 P 点的矢径 r 之间夹角的正弦成正比，与电流元到点 P 的距离 r
11-1磁感应强度 毕奥—萨伐尔定律
向定义为该点的 B 的方向.
Fmax
磁感强度大小 磁感强度方向： B 特定直线方向
Fmax qv
运动电荷在磁场中受力
v
q
+
B
F qv B
单位 特斯拉 1(T ) 1N/A m
§11-2 稳恒磁场
一 毕奥—萨伐尔定律
(电流元在空间产生的磁场)
Id l
R1
0 I
4π d
（2） R
o （3） I R o
B0
0 I
4R
R2
*o
B0
0 I
8R
B0
0 I
4 R2
0 I
4 R1
0 I
4π R1
练 ：
习
三 磁偶极矩 磁矩
m ISen
2
I S
例2中圆电流磁感强度公 式也可写成
en
m
B
0 IR
2x
3
0 m B en 3 2π x
（x R ）2 2
2 2 3
I
R o
x
*
B
x
B
B
0 IR
2
2 2 3
讨 论
（x R ）2 2 2）x 0 B 的方向不变( I 和 B 成右螺旋关系） 0 I 圆环形电流 B 3）x 0 2 R 中心的磁场
2 2
1）若线圈有 N 匝
（x R ）2 2 2 N 0 IR
本章教学内容
11-1 稳恒磁场 11-2 毕奥-萨伐尔定律 11-3 磁通量 磁场的高斯定理
11-4 安培载流导线在磁场中所受的力 11-7 磁场对载流线圈的作用
11-2.3 毕奥-萨伐尔定律及其应用
毕奥—萨伐尔定律及其应用 §11-2.3 毕奥 萨伐尔定律及其应用 例3 载流直螺线管的磁场
第十一章 稳恒磁场
如图所示，有一长为 半径为R的载流密绕直螺 如图所示，有一长为l , 半径为 的载流密绕直螺 线管，螺线管的总匝数为N，通有电流I. 线管，螺线管的总匝数为 ，通有电流 设把螺线管 放在真空中，求管内轴线上一点处的磁感强度. 放在真空中，求管内轴线上一点处的磁感强度
判断下列各点磁感强度的方向和大小. 例 判断下列各点磁感强度的方向和大小
8 2
d 1、5 点 ： B = 0 、
3、7点 ：dB 、 点 +3
+
=
µ 0 Id l
4π R
2
7
Idl
R
6 5
2、4、6、8 点 ： 、 、 、
+4
dB =
µ 0 Idl
4π R
sin 450 2
毕奥—萨伐尔定律及其应用 §11-2.3 毕奥 萨伐尔定律及其应用 毕奥---萨伐尔定律 萨伐尔定律应用举例 二 毕奥 萨伐尔定律应用举例 载流长直导线的磁场. 例1 载流长直导线的磁场
dB =
µ0
2
B = ∫ dB =
µ 0 nI
2
(R
R In d x
2
2
+x
x2 x1
2 3/2
)
B=−
µ 0 nI
2
∫ (R
2
R 2 dx
2
x = R ctg β 2 dx = − R csc βdβ
+x
2 3/ 2
∫β
β
1
R 3 csc 2 β d β R 3 csc 3 β
大学物理毕奥-萨伐尔定律
1
2
2
I
2 B
B 0I
4πr
3）延长线上的磁场
B=0
I
A
B
1
A
→r
r
＊p
B
+P
2、圆形载流导线（圆电流）轴线上的磁场（R, I）
Id l
o
IR
r dB d B
x
*
p dBx
x
dB'
解： （1）如图建立坐标系
（2）在导线上取电流元 Idl
dB
0
4π
Idl sin 900 r2
0 4
Idl r2
20
2
0, B 向外
0, B 向内
例7（例11-2） 一半径为R的无限长的半圆形金属薄片,沿轴 通有I 的电流,设电流在金属片上均匀分布,试求圆柱轴线上 任意一点P的磁感应强度.
解：将电流分割成许多无限长载流直导
线，电流为dI
I
利用无限长载流直导线的磁感应强度公式
B 0I
2πr
dB 0dI 2R
电流元中的运动电荷数
dN nSdl
电流元
Idl vSnqdl qv dN
将
Idl qv dN
代入上式得
从微观上看，电流元的dB就是dN个运动电荷共同产生的磁场
运动电荷的磁场
B
dB
0
qv r0
dN 4π r2
r0为电荷q到场点的矢径方向的单位矢量， 方向垂直于V，r确定的平面
是低速(v c)情形下匀速运动点电荷产生的磁场。
电流元 在空间P点产生的 磁感应强度 为
dB
k
Idl r2
r
0
第五版普通物理112113毕奥—萨伐尔定律及其应用
度大小为。
答案：
在半径为R的长直金属圆柱体内部挖去一个半径为r的长直圆柱体，两柱体轴线平行其间距为a，如图，今在此导体上通有电流I，电流在截面上均匀分布，则空心部分轴线上O
点的磁感强度的大小为。
答案：
无限长直ห้องสมุดไป่ตู้线在P处弯成半径为R的圆，当通以电流I时，则在圆心O点的磁感应强度
大小等于。
答案：
如图所示，有两根载有相同电流的无限长直导线，分别通过X1=1，X2=3的点，且平
答案：y= x/3
两平行载流导线，导线上的电流为I,方向相反，两导线之间的距离a，则在与两导
线同平面且与两导线距离相等的点上的磁感应强度大小为。
答：
两平行载流导线，导线上的电流为I,方向相反，两导线之间的距离a，则在与两导线同平面且与其中一导线距离为b的、两导线之间的点上的磁感应强度大小为。
答：
在真空中有一根半径为R的半圆形细导线，流过的电流为I，则圆心处的磁感应强
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：D
题号：30913018
分值：3分
难度系数等级：3
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：B
电流由长直导线1沿切线方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿切向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R，且a、b和圆心O在同一条直线上。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
答案：
在半径为R的长直金属圆柱体内部挖去一个半径为r的长直圆柱体，两柱体轴线平行其间距为a，如图，今在此导体上通有电流I，电流在截面上均匀分布，则空心部分轴线上O
点的磁感强度的大小为。
答案：
无限长直ห้องสมุดไป่ตู้线在P处弯成半径为R的圆，当通以电流I时，则在圆心O点的磁感应强度
大小等于。
答案：
如图所示，有两根载有相同电流的无限长直导线，分别通过X1=1，X2=3的点，且平
答案：y= x/3
两平行载流导线，导线上的电流为I,方向相反，两导线之间的距离a，则在与两导
线同平面且与两导线距离相等的点上的磁感应强度大小为。
答：
两平行载流导线，导线上的电流为I,方向相反，两导线之间的距离a，则在与两导线同平面且与其中一导线距离为b的、两导线之间的点上的磁感应强度大小为。
答：
在真空中有一根半径为R的半圆形细导线，流过的电流为I，则圆心处的磁感应强
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：D
题号：30913018
分值：3分
难度系数等级：3
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：B
电流由长直导线1沿切线方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿切向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R，且a、b和圆心O在同一条直线上。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
§11-2、3 毕奥—萨伐尔定律
PDF created with FinePrint pdfFactory trial version
二、 毕奥---萨伐尔定律应用举例 dB 方向均沿
例： 载流长直导线的磁场.
x 轴的负方向
z
D
θ2
dz θ
I
z
θ1
r
dB
* P y
x
o
r0
µ0 Idz sin θ 解 dB = 2 4π r µ0 Idz sin θ B = ∫ dB = ∫ 2 CD 4π r z = −r0 cot θ , r = r0 / sinθ
两线圈间轴线上中点P处，磁感应强度大小为
BP = 2 µ 0 NIR
2 2 3/2
2 R 2 R + 2 µ 0 NI = 0 . 716 R
同 学 们 好
PDF created with FinePrint pdfFactory trial version
§11-2 毕奥—萨伐尔定律 一、毕奥—萨伐尔定律 (电流元在空间产生的磁场)
Idl
dB
µ0 Idl sin θ dB = 2 4π r µ0 Idl × r dB = 4π r 3
(2) 无限长的螺线管
（3）半无限长螺线管
B = µ 0 nI
或由 β1 = π , β 2 = 0 代入
π β1 = , β 2 = 0 2
1 B = µ 0 nI 2
µ0nI
x
µ0nI (cos β2 − cos β1 ) B= 2
1 µ 0 nI 2
B O
PDF created with FinePrint pdfFactory trial version
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
答：对
一段电流元 所产生的磁场的方向并不总是与 垂直。（ ）
答：错
在电子仪器中，为了减弱与电源相连的两条导线所产生的磁场，通常总是把它们扭在一起。（ ）
答：对
如图，两根通有同样电流I的长直导线十字交叉放在一起，交叉点相互绝缘，则虚线上的磁场为零。
答：对
如图，一根导线中间分成电流相同的两支，形成一菱形，则在菱形长对角线（水平方向）上的磁场为零，短对角线上的磁场不为零。（ ）
（C） ＞ ＞ （D） ＞ ＞
[ ]
答案：D
在一个平面内，有两条垂直交叉但相互绝缘的导线，流过每条导线的电流相等，方向如图所示。问哪个区域中有些点的磁感应强度可能为零
（A）仅在象限1（B）仅在象限2（C）仅在象限1、3（D）仅在象限2、4
[ ]
答案：D
无限长直导线通有电流I，右侧有两个相连的矩形回路，分别是 和 ，则通过两个矩形回路 、 的磁通量之比为：
（A） ，因为
（B） ，因为虽然 ， ，但 ，
（C） ，因为 ， ，
（D） ，因为虽然 ，但
[ ]
答案：B
电流由长直导线1沿半径方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿半径方向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R， 。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
答：对
对于一个载流长直螺线管，两端的磁感应强度大小是中间的一半。（ ）
答：对
当需要对一个在地球上、暴露在空气中的点的磁场进行精确计算时，如果磁场比较弱，需要考虑地磁场的影响。（ ）
答：对
（A）0（B）
（C） （D）
[ ]
答案：B
如图所示，两根长导线沿半径方向引到铁环上的A、B两点上，两导线的夹角为 ，环的半径R，将两根导线在很远处与电源相连，从而在导线中形成电流I，则环中心点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：A
两条长导线交叉于一点O，这两条导线上通过的电流分别为I和2I，则O点的磁感应强度为
(A)30°(B)60°(C)120°(D)210°
[ ]
答案：A
四条相互平行的载流长直导线电流强度均为I，方向如图所示。设正方形的边长为2a，则正方形中心的磁感应强度为
（A） （B） （C）0（D）
[ ]轴向均匀地流有电流I。若作一个半径为 、高 的圆柱形曲面，轴与载流导线的轴平行且相距 ，则 在圆柱侧面S上积分 为
（A）0（B） （C） （D）
[ ]
答案：A
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：B
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A） ，因为
（B） ，因为 ，
（C） ，因为虽然 ，但
（D） ，因为虽然 ，但
[ ]
答案：D
如图所示，一条长导线折成钝角 ，导线中通有电流I，则O点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：A
如图所示，一条长导线折成钝角 ，导线中通有电流I，则在PO延长线上离O点距离为l的A点处的磁感应强度为
（A） ， （B） ，
（C） ， （D） ，
[ ]
答案：C
载流的圆形线圈（半径 ）与正方形线圈（边长 ）通有相同的电流强度I。若两个线圈中心 、 处的磁感应强度大小相同，则 ： ＝
（A）1：1（B） ：1（C） ：4（D） ：8
[ ]
答案：D
如图所示，两根长直载流导线垂直纸面放置，电流 A，方向垂直纸面向外；电流 A，方向垂直纸面向内。则P点磁感应强度 的方向与X轴的夹角为
第五版普通物理
11-2,11-3毕奥—萨伐尔定律及其应用
选择题
两条无限长载流导线，间距0.5厘米，电流10A，电流方向相同，在两导线间距中点处磁场强度大小为
（A）0（B） T（C） T（D） T
[ ]
答案：A
通有电流I的无限长直导线弯成如图所示的3种形状，则P、Q、O各点磁感应强度的大小关系为
（A） ＞ ＞ （B） ＞ ＞
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：D
题号：30913018
分值：3分
难度系数等级：3
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：B
电流由长直导线1沿切线方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿切向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R，且a、b和圆心O在同一条直线上。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
（A）1：2（B）1：1（C）1：4（D）2：1
[ ]
答案：（B）
边长为a的一个导体方框上通有电流I，则此方框中心点的磁场强度
（A）与a无关（B）正比于 （C）正比于a（D）与a成反比
[ ]
答案：D
边长为l的正方形线圈，分别用图示两种方式通以电流I，图中ab、cd与正方形共面，在这两种情况下，线圈在其中心产生的磁感应强度的大小分别为
（A） （B） （C）0（D）
[ ]
答案：C
长直导线通有电流I，将其弯成如图所示形状，则O点处的磁感应强度大小为
（A） （B） （C） （D）
[ ]
答案：B
电流由长直导线1沿平行bc边方向经过a点流入电阻均匀的导线构成的正三角形线框，由b点流出，经长直导线2沿cb延长线方向返回电源，如图。已知直导线上的电流为I，三角框每边长l。若载流导线1、2和三角框中的电流在三角框中心O点产生的磁场分别用 、 、 表示，则O点的磁感应强度大小
（A） ，因为
（B） ，因为虽然 ， ，但 ，
（C） ，因为虽然 ，但
（D） ，因为 ， ，所以
[ ]
答案：A
2. 判断题：
一条载流长直导线，在导线上的任何一点，由导线上的电流所产生的磁场强度为零。（ ）
答：对
根据毕奥沙伐定律分析，在均匀、线性、各向同性媒质中，一段有限长载流直导线周围空间的磁场分布具有对称性，磁感应强度线是一些以轴线为中心的同心圆。（ ）
一段电流元 所产生的磁场的方向并不总是与 垂直。（ ）
答：错
在电子仪器中，为了减弱与电源相连的两条导线所产生的磁场，通常总是把它们扭在一起。（ ）
答：对
如图，两根通有同样电流I的长直导线十字交叉放在一起，交叉点相互绝缘，则虚线上的磁场为零。
答：对
如图，一根导线中间分成电流相同的两支，形成一菱形，则在菱形长对角线（水平方向）上的磁场为零，短对角线上的磁场不为零。（ ）
（C） ＞ ＞ （D） ＞ ＞
[ ]
答案：D
在一个平面内，有两条垂直交叉但相互绝缘的导线，流过每条导线的电流相等，方向如图所示。问哪个区域中有些点的磁感应强度可能为零
（A）仅在象限1（B）仅在象限2（C）仅在象限1、3（D）仅在象限2、4
[ ]
答案：D
无限长直导线通有电流I，右侧有两个相连的矩形回路，分别是 和 ，则通过两个矩形回路 、 的磁通量之比为：
（A） ，因为
（B） ，因为虽然 ， ，但 ，
（C） ，因为 ， ，
（D） ，因为虽然 ，但
[ ]
答案：B
电流由长直导线1沿半径方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿半径方向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R， 。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
答：对
对于一个载流长直螺线管，两端的磁感应强度大小是中间的一半。（ ）
答：对
当需要对一个在地球上、暴露在空气中的点的磁场进行精确计算时，如果磁场比较弱，需要考虑地磁场的影响。（ ）
答：对
（A）0（B）
（C） （D）
[ ]
答案：B
如图所示，两根长导线沿半径方向引到铁环上的A、B两点上，两导线的夹角为 ，环的半径R，将两根导线在很远处与电源相连，从而在导线中形成电流I，则环中心点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：A
两条长导线交叉于一点O，这两条导线上通过的电流分别为I和2I，则O点的磁感应强度为
(A)30°(B)60°(C)120°(D)210°
[ ]
答案：A
四条相互平行的载流长直导线电流强度均为I，方向如图所示。设正方形的边长为2a，则正方形中心的磁感应强度为
（A） （B） （C）0（D）
[ ]轴向均匀地流有电流I。若作一个半径为 、高 的圆柱形曲面，轴与载流导线的轴平行且相距 ，则 在圆柱侧面S上积分 为
（A）0（B） （C） （D）
[ ]
答案：A
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：B
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A） ，因为
（B） ，因为 ，
（C） ，因为虽然 ，但
（D） ，因为虽然 ，但
[ ]
答案：D
如图所示，一条长导线折成钝角 ，导线中通有电流I，则O点的磁感应强度为
（A）0（B） （C） （D）
[ ]
答案：A
如图所示，一条长导线折成钝角 ，导线中通有电流I，则在PO延长线上离O点距离为l的A点处的磁感应强度为
（A） ， （B） ，
（C） ， （D） ，
[ ]
答案：C
载流的圆形线圈（半径 ）与正方形线圈（边长 ）通有相同的电流强度I。若两个线圈中心 、 处的磁感应强度大小相同，则 ： ＝
（A）1：1（B） ：1（C） ：4（D） ：8
[ ]
答案：D
如图所示，两根长直载流导线垂直纸面放置，电流 A，方向垂直纸面向外；电流 A，方向垂直纸面向内。则P点磁感应强度 的方向与X轴的夹角为
第五版普通物理
11-2,11-3毕奥—萨伐尔定律及其应用
选择题
两条无限长载流导线，间距0.5厘米，电流10A，电流方向相同，在两导线间距中点处磁场强度大小为
（A）0（B） T（C） T（D） T
[ ]
答案：A
通有电流I的无限长直导线弯成如图所示的3种形状，则P、Q、O各点磁感应强度的大小关系为
（A） ＞ ＞ （B） ＞ ＞
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：D
题号：30913018
分值：3分
难度系数等级：3
两条长导线相互平行放置于真空中，如图所示，两条导线的电流为 ，两条导线到P点的距离都是a，P点的磁感应强度方向
（A）竖直向上（B）竖直向下（C）水平向右（D）水平向左
[ ]
答案：B
电流由长直导线1沿切线方向经a点流入一由电阻均匀的导线构成的圆环，再由b点沿切向从圆环流出，经长直导线2返回电源，如图。已知直导线上的电流强度为I，圆环的半径为R，且a、b和圆心O在同一条直线上。设长直导线1、2和圆环中的电流分别在O点产生的磁感应强度为 、 、 ，则O点的磁感应强度大小
（A）1：2（B）1：1（C）1：4（D）2：1
[ ]
答案：（B）
边长为a的一个导体方框上通有电流I，则此方框中心点的磁场强度
（A）与a无关（B）正比于 （C）正比于a（D）与a成反比
[ ]
答案：D
边长为l的正方形线圈，分别用图示两种方式通以电流I，图中ab、cd与正方形共面，在这两种情况下，线圈在其中心产生的磁感应强度的大小分别为
（A） （B） （C）0（D）
[ ]
答案：C
长直导线通有电流I，将其弯成如图所示形状，则O点处的磁感应强度大小为
（A） （B） （C） （D）
[ ]
答案：B
电流由长直导线1沿平行bc边方向经过a点流入电阻均匀的导线构成的正三角形线框，由b点流出，经长直导线2沿cb延长线方向返回电源，如图。已知直导线上的电流为I，三角框每边长l。若载流导线1、2和三角框中的电流在三角框中心O点产生的磁场分别用 、 、 表示，则O点的磁感应强度大小
（A） ，因为
（B） ，因为虽然 ， ，但 ，
（C） ，因为虽然 ，但
（D） ，因为 ， ，所以
[ ]
答案：A
2. 判断题：
一条载流长直导线，在导线上的任何一点，由导线上的电流所产生的磁场强度为零。（ ）
答：对
根据毕奥沙伐定律分析，在均匀、线性、各向同性媒质中，一段有限长载流直导线周围空间的磁场分布具有对称性，磁感应强度线是一些以轴线为中心的同心圆。（ ）