毕奥萨伐尔定律的应用
.毕奥-萨伐尔定律

.毕奥-萨伐尔定律摘要:1.引言2.毕奥- 萨伐尔定律的定义3.毕奥- 萨伐尔定律的公式表示4.毕奥- 萨伐尔定律的应用领域5.我国在毕奥- 萨伐尔定律研究方面的贡献6.结论正文:1.引言毕奥- 萨伐尔定律是电磁学中的一个基本定律,它描述了电流在磁场中的作用力。
这个定律是由法国物理学家毕奥和萨伐尔在19 世纪初提出的,为电磁学的发展奠定了基础。
2.毕奥- 萨伐尔定律的定义毕奥- 萨伐尔定律指出,一个电流在磁场中受到的磁场力与电流的大小、磁场的强度和电流与磁场之间的夹角有关。
具体来说,磁场力F 的大小与电流I、磁感应强度B 以及电流与磁场之间的夹角θ的关系可以表示为:F = I * (Bl * sinθ)。
3.毕奥- 萨伐尔定律的公式表示毕奥- 萨伐尔定律可以用数学公式表示为:F = I * (Bl * sinθ),其中F 表示磁场力,I 表示电流,B 表示磁感应强度,l 表示电流元的长度,θ表示电流与磁场之间的夹角。
4.毕奥- 萨伐尔定律的应用领域毕奥- 萨伐尔定律在许多领域都有广泛的应用,如电磁制动、电磁起重机、磁悬浮列车等。
此外,这个定律还为研究电磁波、电磁感应和磁流体等现象提供了理论基础。
5.我国在毕奥- 萨伐尔定律研究方面的贡献我国科学家在毕奥- 萨伐尔定律研究方面取得了举世瞩目的成果。
例如,中国科学院物理研究所的科学家们通过对磁性材料的研究,为理解毕奥- 萨伐尔定律提供了新的视角。
此外,我国在磁悬浮列车、电磁制动等领域的研究也取得了重要突破,为国民经济的发展做出了巨大贡献。
6.结论毕奥- 萨伐尔定律是电磁学的基本定律之一,它对电磁学的发展产生了深远的影响。
毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用萨伐尔定律是一条重要的物理学定律,它表明在极坐标系中,线性磁场与磁力线紧密联系。
在此定律的影响下,较小的磁场并非总是比较複杂的磁力线模式。
萨伐尔定律的具体表达式是:Bθ=-∂Φ/∂z,其中Bθ为放射状波函数,Φ为磁力函数。
萨伐尔定律在极坐标系中能广泛地应用于物理领域,作用涉及磁场跃迁、电离层静电场、星际磁力场等各方面。
比如,针对电离层的放射现象,在极坐标系中,萨伐尔定律可用来量化磁力线紊乱程度,即把磁力线画化为一条定义其强度大小的简单曲线;在星际磁力场中,萨伐尔定律可用来量化磁场并推导出磁矩变化规律,磁场和磁矩变化会受连续性和格林函数影响。
总之,萨伐尔定律是一条重要且关键的物理学定律,它对于我们研究物理领域有重要意义。
在极坐标系中,萨伐尔定律的表达式为Bθ=-∂Φ/∂z,且其应用远不止这里所述,而是渗透于各个新兴学科中,通过它可以深入了解物理性质,探索出许多未知的现象。
11-3毕奥-萨伐尔定律及应用

真空的磁导率: π×10 真空的磁导率:o=4π× -7 π× 点的距离. (2) r是电流元 到P点的距离. ) 是电流元Idl 点的距离 r是从电流元 指向 点的单位矢量. 是从电流元Idl 指向P点的单位矢量 点的单位矢量. 是从电流元
上页 下页
(3)磁场的大小: )磁场的大小:
o Idl sin θ dB = 2 θ是Idl与r 之间的夹角 与 之间的夹角. 4π r
在薄片中取弧长为dl的窄条, 在薄片中取弧长为 的窄条, 的窄条 其中通过的微元电流为: 其中通过的微元电流为:
I
I I dI = dl = dθ πR π
上页 下页
y
在俯视图上建立如图坐标, 在俯视图上建立如图坐标, 电流元在O点激发的磁感应 电流元在 点激发的磁感应 强度为: 强度为:
o
dB
θ
毕奥-萨伐尔定律及应用 §11-3 毕奥 萨伐尔定律及应用
毕奥-萨伐尔定律 一, 毕奥 萨伐尔定律
d 真空中,电流元 真空中,电流元Idl 在P点产 B 点产 生的磁场为
o Idl ×r dB = 2 4π r
说明
P
r
θ
I
Idl
上式称为毕奥 萨伐尔定律 上式称为毕奥-萨伐尔定律 毕奥
(1)公式中的系数是 制要求的. 制要求的. )公式中的系数是SI制要求的
x R
0 0 I dB = dI = 2 dθ 2πR 2π R
所以: 所以:
π
dθ
方向如图所示. 方向如图所示.
0 I Bx = dBx = 2 ∫0 π R
即:
0 I dBx = dBsinθ = 2 sinθdθ 2π R
By = ∫ dB = 0
毕奥-萨伐尔定律

将实验结果与毕奥-萨伐尔定律的理论值进行对比,评估定律的准确性。
结果分析
分析实验误差来源,如设备精度、环境干扰等,提高实验的可靠性和准确性。
05
毕奥-萨伐尔定律的扩展与 推广
对三维空间的推广
总结词
毕奥-萨伐尔定律最初是在二维空间中 推导出来的,但通过引入矢量运算, 该定律可以扩展到三维空间中。
Idl
电流元,表示电流的一 部分。
r
观察点到电流元的径矢 ,表示观察点与电流元
之间的距离。
03
毕奥-萨伐尔定律的应用场 景
电场与磁场的关系
磁场是由电流产生的,而电场是由电 荷产生的。毕奥-萨伐尔定律描述了 电流和磁偶极子产生的磁场,以及变 化的电场产生的磁场。
毕奥-萨伐尔定律揭示了电场和磁场之 间的相互关系,表明它们是电磁场的 两个方面,而不是独立存在的。
THANKS
对微观尺度的适用性问题
毕奥-萨伐尔定律在描述微观尺度的电磁场时,其精确度受 到限制。在量子尺度下,电磁场的涨落和量子效应可能导 致定律的不适用。
未来研究需要进一步探索毕奥-萨伐尔定律在微观尺度下 的适用性和修正,以更好地描述量子电磁场的行为。
对超导态物质的适用性问题
毕奥-萨伐尔定律在描述超导态物质的 电磁场时,可能存在局限性。超导态 物质的电磁行为与常规物质有所不同, 需要更复杂的理论模型来描述。
电流与磁场的相互作用
根据毕奥-萨伐尔定律,电流产生磁场,而磁场对电流有作用 力。这种作用力被称为洛伦兹力,它描述了电流在磁场中所 受到的力。
毕奥-萨伐尔定律是电动机和发电机等电气设备工作的基础, 它解释了电流如何在磁场中受到作用力,从而产生旋转或线 性运动。
磁力线的描绘
11.2_毕奥-萨伐尔定律及应用
第十一章 稳恒磁场
B=
µ0 nI
2
(cos β 2 − cos β1 )
β1 = π − β 2
l/2
点位于管内轴线中点 (1)P点位于管内轴线中点 ) 点位于管内
cos β1 = − cos β 2
B = µ0 nI cos β 2 =
若
cos β2 =
(l / 2)
l
2
+ R2
µ0 nI
2
(l
2
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
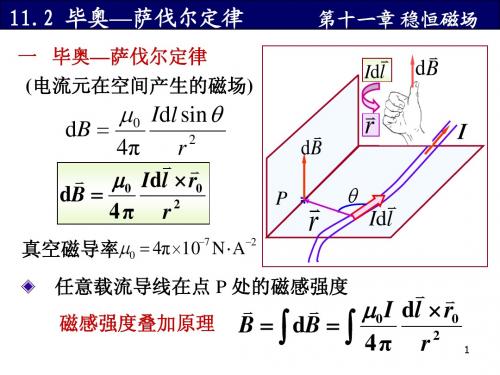
毕奥—萨伐尔定律 一 毕奥 萨伐尔定律 (电流元在空间产生的磁场 电流元在空间产生的磁场) 电流元在空间产生的磁场
第十一章 稳恒磁场
Idl
dB
4π r µ0 Idl × r0 dB = 4π r2
−7 −2 真空磁导率µ0 = 4π ×10 N ⋅ A
dB =
µ0 Idl sin θ
2
r
dB
P *
I
r
θ
Idl
任意载流导线在点 P 处的磁感强度 磁感强度叠加原理
B = ∫ dB = ∫
µ0 I dl × r0
4π r
2
1
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
第十一章 稳恒磁场 毕奥—萨伐尔定律 毕奥 萨伐尔定律
dB =
µ0 Idl × r0
4π
1
r
1 B = µ 0 nI 2
B=
µ0nI
2
(cos β2 − cos β1 )
B
1 µ 0 nI 2
µ0nI
x
24
O
毕奥—萨伐尔定律 11.2 毕奥 萨伐尔定律
毕奥-萨伐尔定律及应用

B x = ∫ dB x B y = ∫ dB y Bz = ∫ dBz
}Байду номын сангаас
⇒
v v v v B = Bx i + B y j + Bz k
设有长为L的载流直导 例1 载流长直导线的磁场 设有长为 的载流直导 线,其中电流为I。计算距离直导线为a处的 点的磁 其中电流为 。计算距离直导线为 处的P点的磁 处的 感应强度。 感应强度。 I 解:任取电流元 Idl 据毕奥-萨伐尔定律 萨伐尔定律, r 据毕奥 萨伐尔定律,此电 α Idl 流元在P 流元在P点磁感应强度dB为 r r L r
I dl
R
r
x
d B⊥
θ
θ
r dB
I
O
P
r d B//
µ0 I d l B = ∫ dB// = ∫ dB sin θ = ∫L r 2 sin θ L L 4π µ 0 I sin θ 2πR µ 0 I sin θ = 2 ∫0 d l = 4πr 2 2πR 4πr
µ0 I sin θ B= 2πR 2 4πr
单位矢量
真空中的磁导率
大小: 大小: dB =
4π
µ0 Idl sin θ
r2
Idl vθ
P
v B
方向: 方向:右螺旋法则
v r
r dB
r dB
r Id l
P
r r
α
r dl
I
电流元在给定点所产生的磁感应强度的大小与 I d l 成正比 , 与到电流元的距离平方成反比 ,与电 r 成正比,与到电流元的距离平方成反比, r 流 元 r 矢 径 夹 角 的 正 弦 成 正 比 。 dB 方 向 垂 直 于 r 和 r r 组成的平面, 与 Idl 组成的平面,指向为由 Idl 经 α 角转向 r 时 右螺旋前进方向。 右螺旋前进方向。 r
高二物理竞赛毕奥-萨伐尔定律应用举例PPT(课件)
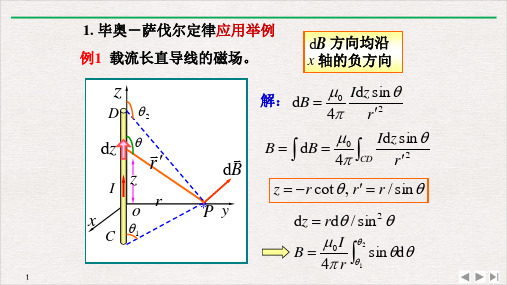
由右手螺旋关系可知每个电流元在圆心处产生的磁感 强度的方向相同。
◆ 在载流圆线圈轴线以外的空间,其磁感强度的分 布大致如下图所示:
I
思考2:
I
R o
B0
x
B0
0I
2R
I R o
B0
0I
4R
I
R o
B0
0I
8R
BA
0I 4d
d *A
I
R1
R2
*o
B0
讨 (1) 若线圈有 N 匝
论 二
B
N 0IR 2
2(x2 R2)3/ 2
xP x
(2) x 0,B 的方向不变 ( I 和 B 成右螺旋关系)
(3) x 0 , B 0I 圆环形电流中心的磁场
2R
思考1:圆弧形电流在圆心处的磁场为多少?
B 0I 2R 2
方向
I
R
O
提示:将该平面载流线圈在圆心处产生的磁感强度看
(3) 半无限长螺线管
B 0nI
或由 1 , 2 0 代入
B
0nI
2
cos2
c os 1
1
,
2
2
B
1 2
0nI
I
1 2
0
nI
B 0nI
O
x
磁感应线的绕向与电流满足右螺旋定则
在沿电流方向的延长线上任一点处,
引入磁矩:
(与磁场方向一致)
例2 圆形载流导线的磁场。
例3 载流直螺线管轴上的磁场
毕奥-萨伐尔定律应用举例
R 载流直导线延长线上任一点的磁感强度为零。
例3 载流直螺线管轴上的磁场 提示:将该平面载流线圈在圆心处产生的磁感强度看成是由 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。
毕奥——萨伐尔定律在极坐标系中的表达式及其应用

毕奥——萨伐尔定律在极坐标系中的表达式及其应用
毕奥萨伐尔定律是世界上最经典的物理定律之一,它可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
本文主要介绍毕奥萨伐尔定律在极坐标系中的表达式及其应用。
首先,我们来介绍毕奥萨伐尔定律在极坐标系中的表达式。
首先,毕奥萨伐尔定律定义了磁场从磁极出发的表达式,它表示磁场受到磁极强度的影响而产生,而且它的值取决于磁极的强度与磁极之间的距离,而这个距离关系可以用一个抛物线表达:即磁场强度随着距离的减小而增大,而随着距离的增加而减小,用公式表示为:B=B0*(1/r^2),其中B0为磁极强度,r为两磁极之间的距离。
此外,毕奥萨伐尔定律还可以描述磁场的产生方向,即它的向量表达式,它表明磁场是从磁极出发的,具体来说,磁场的方向是从磁极的正极指向负极的方向。
用公式表示为:B=B0*(1/r)*对应的单位
向量,其中B0为磁极强度,r为两磁极之间的距离,对应的单位向
量表示磁场方向。
接着,我们来讨论毕奥萨伐尔定律在极坐标系中的应用,首先,它可以用于研究磁性材料,因为磁性材料向外施加磁极的时候,磁场的变化遵循毕奥萨伐尔定律。
其次,毕奥萨伐尔定律可以用于研究空间磁场的变化,这对于放射性核物质的研究有着重要意义,因为空间磁场变化可以影响核子间的相互作用,从而影响放射性核物质的结构和品质,从而不同的空间磁场可以调节放射性核物质表现出不同的性质。
总而言之,毕奥萨伐尔定律可以描述磁场在极坐标系中的表达式及其应用,是物理学中不可缺少的重要组成部分。
它的表达式可以用简单的数学公式来描述,而它的应用范围也包括磁性材料和放射性核物质的研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dB
0 R nI d l
2
l R cot
d l R csc d
2 2 2 2 2
1
A1
r
dB
p
2
R
A2
又 R l R csc
B L
0 R nI d l
2
l
dl
2( R l )
2
2 3/ 2
0
0
2
2
nI
0 nI
0 nI
2
B
A1
O
A2
通电螺线管的磁场
B
I
B 0 nI
I
0 I B 2 r
【例】载流圆线圈轴线上的磁场
电流元 Idl 在P点磁场
Idl
Id l r 0 dB dB// dB 3 4r
R
r
x
dB dB
I
由圆对称性得
B dB 0
o
P
dB//
所以
B dB//
B B // dB// dB sin
dl
L
r
l d tan
d l d sec d
2
l
P 0 I d l sin d B O 2 dB L 4 r 0 I 0 I cos d sin 2 sin 1 4 d 4d
1
2
2
1
考虑三种情况:
按毕奥—萨伐尔定律有:
I
0 I d l r dB 4 r3
所有dB的方向相同, 所以P点的 的大小为 : B
dl
L
r
l
0 I d l sin B d B L L 4 r2
O
d
1
2
P
dB
I
由几何关系有:
sin cos
r d sec
0 I sin 2 sin 1 B 4d
1 2 2
2
(1)导线无限长,即
I
(2) 导线半无限长,场点与一端 的连线垂直于导线
0 I B 2d 0 I B 4d
dl
L
r
(3)P点位于导线延长线上,B=0
O
d
1
2
P
dB
I
无限长直线电流的磁场
设螺线管的半径为R,电流为I,每单位长度有 线圈n匝。
1
A1
r
dB
R
p
2
A2
dl
l
1
A1
r
dB
p
2
R
A2
l
dl
由于每匝可作平面线圈处理, ndl匝线圈可作 Indl的一个圆电流,在P点产生的磁感应强度:
2( R l ) 2 0 R nI d l B L dB L 2 2 3/ 2 2( R l )
0 4
sindl 0 I sin r 2 4r 2 2R
r 2 R2 x2 sin R r R (x R )
2 2
1 2
B
0 IR 2
2( x 2 R 2 ) 3 2
讨论: 1.x=0处,即圆电流中心,磁场最大:
I 0 B
2R
2.x>>R,x≈r:
推广至 I 0 任意圆 B 2 2R 弧中心
2 2 IR I R IS 0 0 0 B 3 3 2x 2x 2x 3
I
pm
p B 0 m 3 2x
电流磁矩 pm ISe n
圆电流的磁场
I
【例】密绕长直载流螺线管轴线上的磁场
2
1
sin d
nI (cos 2 cos 1 )
B
0 nI
2
(cos 2 cos 1 )
讨论:
(1)螺线管无限长
1 , 2 0 B 0 nI
(2)半无限长螺线管的端点圆心处
B 0 nI / 2
实际上, L>>R 时, 螺 线管 内 部的 磁场 近 似均 匀 ,大 小为 0 nI
