例1求载流长直导线的磁场,已知
毕奥---萨伐尔定律

两电流元之间的安培定律也可表示成 两电流元之间的安培定律也可表示成
u r r uur u r ˆ I1 I 2 dl2 × (dl1 × r12 ) d F12 = k = I 2 dl2 × dB1 2 r 12
电流元 I1d l1产生的磁场
ˆ ˆ Idl × r µ0 Idl × r dB = k = 2 2 r 4π r
• 求二阶导数
d 2B 在O 令x = 0处的 2 = 0 ⇒ 在O点附近磁场最均匀的条件 dx µ0 d 2B 2a 2 − 2 R 2 = 6π R 2 I = 0 ⇒ a2 = R2 7 2 dx 2 x =0 4π 2 a 2 2 R + 4
a=R
例1、无限长载流直导线弯成如图形状
大小
µ0 Idl dB = 4π r2
r r 方向 Idl × r0
分析对称性、 分析对称性、写出分量式
r r B⊥ = ∫ dB = 0
⊥
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2
统一积分变量
µ0 Idl sinα Bx = ∫ dBx = ∫ 4π r2 µ0IR µ0IR dl = π = ⋅2 R 3 ∫ 3 4 r 4 r π π
a
•
•
P T
µ0I 3 BL′A = (cos π − cosπ ) 4πa 4
µ0I π BLA = (cos0 − cos ) 方向 ⊗ 4 a 4 π
方向 ⊗
T点
Bp = BLA + BL′A = 2.94×10−5T 方向 ⊗
r 电流元 Idl
——右手定则 右手定则 r r r µ0 Idl ×r 毕奥-萨伐尔定律 毕奥 萨伐尔定律 dB = 4 π r3 r r r r µ0 Idl ×r 对一段载流导线 B = ∫ dB = ∫ 4π L r3
载流长直导线的磁场
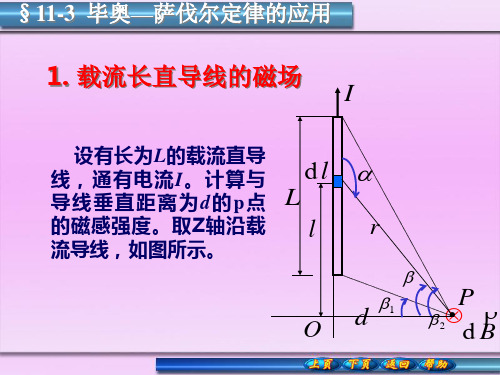
A B = 9.273×1024 A m2
原子中的电子除沿轨道运动外,还有自旋, 原子中的电子除沿轨道运动外,还有自旋,电子的 自旋是一种量子现象,它有自己的磁矩和角动量, 自旋是一种量子现象,它有自己的磁矩和角动量, 电子自旋磁矩的量值等于玻尔磁子。 电子自旋磁矩的量值等于玻尔磁子。
载流圆线圈轴线上的磁场
§11-3 毕奥 萨伐尔定律的应用 毕奥—萨伐尔定律的应用
1. 载流长直导线的磁场
设有长为L的 设有长为 的 载流直 导线, 通有电流I。 导线 , 通有电流 。 计算 与 导 线垂 直 距离 为 d 的 p 点的磁感强度。 点的磁感强度 。 取 Z 轴沿 载流导线,如图所示。 载流导线,如图所示。
O
d
β1
β 2
P
dB
载流长直导线的磁场
0 I dl sin α B = ∫d B = ∫ L L4 π r2
由几何关系有: 由几何关系有:
I
sin α = cos β
l = d tan β
dl = d sec β d β
2
r = d sec β
dl
L
α
r
β
l
P β 0 I dl sin α d β B=∫ O 2 dB L4 π r 0 β I 0I = ∫β d cos β d β = 4πd (sin β2 sin β1) 4π
点位于导线延长线上, = (3)P点位于导线延长线上,B=0 点位于导线延长线上
O
d
β 2
P
dB
2. 载流圆线圈轴线上的磁场
设有圆形线圈L,半径为 ,通以电流I 设有圆形线圈 ,半径为R,通以电流 。
I dl
R
r
天津理工大学大学物理:稳恒磁场

毕奥——萨伐尔在经过大量的
实验的基础之上,经过分析之后指 出:对于载流导线上任一电流元Idl, 它在真空中某点P的磁感应强度dB的 大小与电流元的大小Idl和电流元到P 点的矢径r之间的夹角的正弦成正 比,并与电流元到P点的距离r的平 方成反比,即
Idl sin
dB k r2
9
dB
k
Idl sin
1
二 磁通量 磁场中的高斯定理
为了形象地反映磁场的分布情况,可以象在静电场中用电
力线表示电场的分布那样,用一些假想的曲线来表示磁场的分 布。我们知道给定磁场中的某一点,磁感应强度B的大小和方 向都是确定的,因此规定曲线上的每一点的切线方向就是该点 B的方向。而曲线的疏密程度则反映了该点附近B的大小,这样 的曲线就叫做磁力线(B线)。磁力线和电力线一样也是人为 地画出来的,并非磁场中真有这样一些线。
磁场与磁感应强度矢量
无论导线中的传导电流还是磁铁,本源都是一个即电荷的 运动。都可归结为运动的电荷之间的相互作用。这种相互作用 是通过磁场来传递的。电荷之间的磁相互作用与库仑相互作用 不同,无论电荷是静止还是运动,它们之间都存在着库仑相互 作用,但只有运动着的电荷才存在着磁相互作用。
为定量地描述电场的分布,曾引入电场强度矢量E的概念。 同样为描述磁场的分布情况,也需引入一矢量,这就是磁感应 强度矢量B,它和电场强度E是对应的。本来B应叫做磁场强度, 但是由于历史的原因,磁场强度这个词叫另一个矢量H占用了, 因此B只能叫磁感应强度了。
通过一有限大小曲面的磁通量m就等于通 过这些面积元ds上的磁通量dm的总和,即nຫໍສະໝຸດ m ds
m
B cosds
s
B
或
6.2_毕奥-萨伐尔定律

6.2 毕奥—萨伐尔定律一 毕奥—萨伐尔定律 (电流元在空间产生的磁场)第6章 稳恒磁场v Idlv dB4π r v v v μ0 Idl × r0 dB = 4π r2−7 −2 真空磁导率μ0 = 4π ×10 N ⋅ AdB =μ0 Idl sin θ2v dBP *v rθv IdlIv r任意载流导线在点 P 处的磁感强度 磁感强度叠加原理v v v v μ0 I dl × r0 B = ∫ dB = ∫ 2 4π r6.2 毕奥—萨伐尔定律v v v μ0 Idl × r0 毕奥—萨伐尔定律 dB = 2 4π r1 8第6章 稳恒磁场例 判断下列各点磁感强度的方向和大小.2dB = 0 1、5 点 :3、7点 :dB +3+7v IdlR6 5=μ 0 Id l4π R22、4、6、8 点 :+4dB =μ 0 Idl4π R0 sin 45 26.2 毕奥—萨伐尔定律二 毕奥---萨伐尔定律应用举例第6章 稳恒磁场θ1、 θ2、 r0 例1 载流长直导线的磁场. 已知:真空中 I、zDθ2解dz θ vIzθ1rv dB* P yxor0dB = 2 4π r v dB 方向均沿r Ì任取电流元 Id z μ 0 Idz sin θ⊗Ì建立坐标系OXYCx 轴的负方向 μ0 Idz sinθ B = ∫ dB = ∫ 2 CD 4π r6.2 毕奥—萨伐尔定律Ì写出分量式第6章 稳恒磁场Idz sinθ B = ∫ dB = ∫ 2 CD 4π rÌ统一积分变量μ0zDθ2z = r0ctg(π −θ ) = −r0ctgθ ,dz θ vIzθ1rv dB* P yr = r0 / sinθxor0Cdz = r0dθ / sin θ μ 0 I sin θ dz B=∫ 2 4π r2=∫μ 0 sin 2 θ r0 d θ I sin θ 2 2 sin θ 4 π r06.2 毕奥—萨伐尔定律第6章 稳恒磁场B=μ0I4 π r0∫θθ21sin θ d θ =v B 的方向沿 x 轴的负方向.B=(cosθ1 − cosθ 2) 4π r0μ0 IzDθ2v B无限长载流长直导线的磁场.(cosθ1 − cosθ 2) 4π r0B=μ0 IIoxCθ1 → 0 θ2 →πμ0I2 π r0θ1P y+6.2 毕奥—萨伐尔定律无限长载流长直导线的磁场 I B第6章 稳恒磁场B=μ0I2π rIXB电流与磁感强度成右螺旋关系 半无限长载流长直导线的磁场π θ1 → 2 θ 2 →πBP =μ0I4π rIor* P6.2 毕奥—萨伐尔定律第6章 稳恒磁场例2 圆形载流导线的磁场. 真空中 , 半径为R 的载流导线 , 通有电流I , 称圆 电流. 求其轴线上一点 p 的磁感强度的方向和大小.v Idlrv Bv dBp *oRϕv BI 解 根据对称性分析4π r B = Bx = ∫ dB sin ϕdB =μ 0 Id l2x6.2 毕奥—萨伐尔定律 v IdlR第6章 稳恒磁场rxoϕr 2 2 2 ϕ r =R +x α μ 0 I cos α dl *p x B= 4 π ∫l r 2v dBcosα = R4π r μ 0 I cos αdl dB x = 2 4π rdB =μ 0 Id l2B=B=μ0 IR4π r 2 μ0 IR2 23 0∫2π Rdl3( 2 x + R )26.2 毕奥—萨伐尔定律第6章 稳恒磁场IR ox*v BxB=B=μ0 IR22 2 3讨 论( 2 x + R )2 v v 2)x < 0 B 的方向不变( I 和 B 成右螺旋关系) μ 0I B = 3)x = 0 2R 2 IR IS μ μ 0 0 4)x >> R , B= B= 3 3 2x 2π x2 21)若线圈有 N 匝( 2 x + R )2 2 N μ 0 IR36.2 毕奥—萨伐尔定律 例:载流圆弧,已知 I , R , θ r 求: B 0 r r 解: B = ∫ dB r r μ 0 Idl sin( dl , r ) B = ∫ dB = 2 ∫ 4π R μ0 I Rθ μ0 Iθ = dl = 2 ∫ 4πR 0 4πR第6章 稳恒磁场 Iθ⊗ oR6.2 毕奥—萨伐尔定律(1) I (2 ) o+ (3) I R⊗第6章 稳恒磁场 (4)v R B x 0 μ0I o B0 = 2RI RBA =d (5) I *AR1• * oμ0 I4π d⊗B0 =μ0 I4RR2B0 =oμ0 I8RB0 =μ0 I4 R2−μ0 I4 R1−μ0 I4π R16.2 毕奥—萨伐尔定律(6)O•第6章 稳恒磁场B =IRμ0I8R•(7)R•OIμ0I + B = 4R 2π Rμ0I•(8)2π 3• OIRμ0I 3 (1 − B = + ) 6R 2π R 2⊗μ0I。
11、2毕萨定律及其应用

E 运动电荷除了产 r 生磁场外,还在其周 q B . 围激发电场。若电荷 v 运动速度远小于光速, 则空间一点的电场强度为: 1 q μ o q v× r 而B = E= r 3 r3 4 π π 4ε r
0
由上两式得:
B =μ ε v × E o 此式表明运动电荷激发的电场和磁场紧 结束 密相关。
0 IR 圆环 B 电流: 2( x 2 R 2 )3 2
(下一页)
电偶极子
q q Pe qr
1 pe E 3 20 r
延长线 上: 中垂面 上:
r
类 比
磁偶极子 I S
n
0 pm B 3 2r 0 pm B 3 4r
2
0 nI R csc d R 0 nId 3 3 2 R csc 2 csc
2 2
2 1
B dB
0 nId 0 nI 2 2 csc 2
2
1
sin d
0 nI cos 2 cos 1 2
返回
dB =
μ
I dl sin a r2 4π
o
μo
真空中的磁导率
μ o = 4π
× 10
7
( H . m 1 ) 或 ( 亨利.米 萨伐尔定律
×(
1
)
用矢量形式表示的毕奥 dB =
4π
μ o I dl
×ቤተ መጻሕፍቲ ባይዱ
r3
4π
r
μ o I dl = r2 4π
×
r ) r
结束
返回
B =
μ o I dl
高二物理竞赛毕奥-萨伐尔定律应用举例PPT(课件)
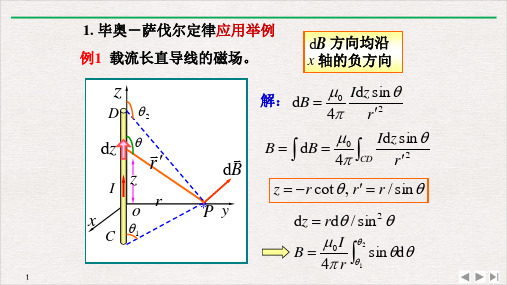
由右手螺旋关系可知每个电流元在圆心处产生的磁感 强度的方向相同。
◆ 在载流圆线圈轴线以外的空间,其磁感强度的分 布大致如下图所示:
I
思考2:
I
R o
B0
x
B0
0I
2R
I R o
B0
0I
4R
I
R o
B0
0I
8R
BA
0I 4d
d *A
I
R1
R2
*o
B0
讨 (1) 若线圈有 N 匝
论 二
B
N 0IR 2
2(x2 R2)3/ 2
xP x
(2) x 0,B 的方向不变 ( I 和 B 成右螺旋关系)
(3) x 0 , B 0I 圆环形电流中心的磁场
2R
思考1:圆弧形电流在圆心处的磁场为多少?
B 0I 2R 2
方向
I
R
O
提示:将该平面载流线圈在圆心处产生的磁感强度看
(3) 半无限长螺线管
B 0nI
或由 1 , 2 0 代入
B
0nI
2
cos2
c os 1
1
,
2
2
B
1 2
0nI
I
1 2
0
nI
B 0nI
O
x
磁感应线的绕向与电流满足右螺旋定则
在沿电流方向的延长线上任一点处,
引入磁矩:
(与磁场方向一致)
例2 圆形载流导线的磁场。
例3 载流直螺线管轴上的磁场
毕奥-萨伐尔定律应用举例
R 载流直导线延长线上任一点的磁感强度为零。
例3 载流直螺线管轴上的磁场 提示:将该平面载流线圈在圆心处产生的磁感强度看成是由 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。 设把螺线管放在真空中,求管内轴线上一点处的磁感强度。
例1求载流长直导线的磁场,已知

讨论:
B
0I 4r0
(cos1
cos 2 )
⑴ 无限长载流长直导线的磁场
1 0 2
I
I
B 0I
2π r
BX
电流与磁感强度成右螺旋关系
⑵ 半无限长载流长直导线的磁场
1
π 2
或 1 0
2 π
2
2
BP
0I
4π r
2
B o 1r0 +p
I
o r *P
例2. 圆电流轴线上的磁场。已知R和Iz
dB
z
2
)
3 2
2. z 0 B 0 I (圆心处)
2R
x
3. z R
B
0 IR 2
2z3
0 IS 2 z 3
4.一段圆弧导线圆心处的磁感强度
z
dBz
dB
p•
z r dB
0 R
y
Idl
B 0 I 0 I 2 0 I 2R 4 R 4 R
θ─圆弧所对圆心角,用弧度表示。
例3. 如图所示导线,已知I、R、θ=/4,求O点的
(R2
x2
3
)2
x Rctg dx R csc2 d R2 x2 R2 csc2
B
2 1
0
2
nI
sin
d
0 nI
2
(c os 2
cos1)
B
0nI
2
cos2
cos1
1
2
R
P
x
讨论:
(1)P点位于管内轴线中点
1
l
π
2
cos 1 cos 2
cos2
电磁学例题

房改房大锅饭大公国静电场中的导体:例题1如图,半径为的接地导体球附近有一个静止点电荷,它与球心相距为,求导体球表面上感应电荷。
解:点电荷在球心处的电势为设为球面上感应面电荷密度,在球面上各点不尽相同(注意:对一个孤立的带电球形导体而言,其电荷是均匀分布在球面上的,即面电荷密度处处相同。
而今,导体球处于点电荷的电场中,对球面上各点的感应电荷分布是不均匀的。
)为此,可先在球面上任取一面积元,其上的感应电荷为,它在球心点的电势为整个球面上的感应电荷在球心点的电势为显然,,上式成为而球心点的电势为与之代数和,且其和应等于零,即由此可得,导体球表面上的感应电荷q′为按题意,导体球接地,以地的电势为零,考虑到位于点电荷q的静电场中的导体是一个等势体,这样,球心的电势亦应为零;而球心的电势则等于点电荷q和球面上的感应电荷q′所激发的电场在点O的电势之代数和。
据此即可求出解。
2.如图,三块平行的金属板A、B和C,面积均为。
板A、B相距,板A、C相距,B、C 两板都接地。
如果使A板带正电,并略去边缘效应,问B板和C板的内、外表面上感应电荷各是多少? 以地的电势为零,问A板的电势为多大解: 按题意,可判断感应电荷的分布如图所示。
因为B、C两板接地,所以两板都带负电,且即(a)考虑到 , , , , 则(b)由式(a)、(b),可得或这里,, , 代入上式,便可算出两板内表面感应电荷分别为,由于 B、C 板接地,外表面感应电荷为零。
又由 , 且,带入上述数值可算得 A 板的电势为。
有介質的靜電場:例题1.在无限长电缆内,导体圆柱A和同轴导体圆柱壳B的半径分别为和(<),单位长度所带电荷分别为+λ和-λ,内、外导体之间充满电容率为的均匀电介质。
求电介质中任一点的场强及内、外导体间的电势差。
解:取高斯面,它是半径为(<<)、长度为的同轴圆柱形闭合面。
左、右两底面与电位移的方向平行,其外法线方向皆与成夹角θ=π/2,故电位移通量为0;柱侧面与的方向垂直,其外法线与同方向,θ=0°通过侧面的电位移通量为cos0°(2π)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
dB2
c
B dl o I
L
2BL o j L B
o
2
j
o L a b
两侧为均匀磁场,与离板的距离无关 讨论: 两无限大平行载流平面,电流密度为j, 求两平面之间和之外空间的磁感强度 1 1 B内 0 j 0 j 0 j 2 2 • × × × × • 1 1 B外 0 j 0 j 0 2 2
I
dΦ BdS
0 I
ldx
l
x
例9.求长直螺线管内的磁感应强度.设电流为I,单位 长度的匝数为n. 解: 密绕的无限长螺旋管中间部分为均匀场 , 方向 沿轴向, 外部磁感强度趋于零 ,取回路L 。
b c d a L B dl a B dl b B dl c B dl d B dl a d c b B dl d B dl c B dl 0 I b a b B dl B dl B L
dB B dB
R
O
r
dr
0
2
2
2r
R
0
1 dr 0 R 2
R 2 0
m dm r dI r
1 R 4 rdr 4
0 qv er 解二: B 2 4 r 0 dqv r dB 3 4 r 0 dqv dB 2 4 r v r dq 2 rdr
0
dx
x
0
x
0 I B 4d
讨论:⑴ y<<d
0 I d arctg d arctg d y 2d y d dB
arctg d y
y —无限大载流平板
arcty
2
dB
y
0 I B 4d
2
d
0 I
4d
0
2
I
j
2
d d ⑵ y>>d, arcty y y
1 π 2
l/2
l
cos 1 cos 2
cos 2
0 nI l B 0 nI cos 2 2 2 1/ 2 2 l / 4 R
若
l / 2
2
R2
l R
B 0 nI
B
0 nI
2
cos 2 cos 1
—无限长载流直导线 0 I 0 I d B arctg 2 d y 2 y
B
r y r x dx 0
d d
x
B
例7. 设半径为R的带电圆盘的电荷面密度为,并以 角速度绕通过盘心垂直盘面的轴转动,求盘心处磁 感应强度和圆盘的磁矩。
2 rdr 解一: dI 2 = rdr 0 dI
例13 有一回旋加 速器,他 的交变 电压的 频率 为 12 10 6 Hz ,半圆形电极的半径为0.532m . 问 加速氘核所需的磁感应强度为多大?氘核所能达到的 最大动能为多大?其最大速率有多大?(已知氘核的 质量为 3.3 10 27 kg ,电荷为 1.6 10 19 C ). 解 由粒子的回旋频率公式,可得
I · ·· · B · r · · · · · · · · d
B dl
L
o I
B 2 r o NI
o NI B 2 r
当
N n 2 r
B o nI
2r d 时,螺绕环内可视为均匀场 .
例11. 无限长载流圆柱形导体的磁场分布。设半径R, 电流I均匀分布在截面上。 R 解 1)对称性分析 2)选取回路
I
o
r
* P
例2. 圆电流轴线上的磁场。已知R和Iz
0 Idl 0 dB sin 90 2 4 r dB 0
B dBz dB sin
dBz
p•
dB z r
0 R
dB
0 Idl R 2 4r r
Idl
y
0 IR 2 R dl 3 3 0 2 2 4 r 2( R z ) 2
F2 x dF2 x 0
sin d BIrcos 0 cos( 0 ) 0 BI (2r cos 0 ) BI AB 方向沿y轴向上 BIr
0
讨论: ⑴ F1 F2 0
表明均匀磁场中,若载流导线闭合回路的平 面与磁感强度垂直时,此闭合回路不受磁场力作 用。此结论,适用于任意形状闭合回路。
1 P
2
R x
1 2 0
无限长螺线管轴线中部
(2)半无限长螺线管轴线上端点
B 0 nI
1 B 0 nI 2
l
π 1 , 2 0 或 2
1 0 nI 2
-L/2
1 π , 2 2
B
0 nI
O
L/2
x
例6. 如图所示,电流I均匀流过宽为2d的无限长薄金 属板,试求通过板的中线并与板面垂直的平面上一点 的磁感强度。 y dB P 解: 把薄片分成许多宽为dx dB I 的无限长载流直导线 dI dx 2d I 0 dI 0 I dB y 0 dB dx r y r 2 r 4d r
例5. 均匀密绕直螺线管轴线上的磁场。已知 R、I、 1、2、单位长度的匝数n。 由圆形电流磁场公式 解: R
3 (x 2 R 2)/ 2 2 dI nIdx 0 R 2 nIdx dB p 3 2 2 2( R x ) 2
B
0 IR
2
1
2
P
x
l
x dx
0 nI R 2 dx B dB 2 (R 2 x 2 ) 32
y
例3. 如图所示导线,已知I、R、θ =/4,求O点的 磁感强度。 解: ⑴ O点在AB的延长线上
C D
dl r 0 B AB 0 0 I 0 I 5 5 0 I ⑵ BBC 4 R 4 R 4 16 R
θ R
0
B
A
方向
0 I 0 I (cos cos ) (cos 1 cos 2 ) ⑶ BCD 4 4 r0 4 2 R 2 2 0 I 2 (1 ) 方向 4R 2 5 0 I 2 0 I 2 B BBC BCD (1 ) 方向 16 R 4R 2
L
B
长载流螺线管内部磁场处处相等 , 外部为零.
B dl B L o I i 0 InL
L
由安培环路定理:
a
B o nI
d
L
c
例10.螺绕环内的磁感应强度。设电流为I,匝数为N。
解: 对称性分析,密绕的螺 绕环内磁感线为同心圆,同 一圆环上 B 的大小相等,环 外 B 为零,取回路L。 L
d d r 2 y 2 sec2 dx y sec2 d x ytg 0 I 0 0 I arctg d y 0 I arctg d B 0 d 4d arctg d y d 2d y 4d
B B x dBx
I y dB cos dx 4dr r
2 π mf 2 π 3.3 10 27 12 10 6 B T 1.56T 19 q 1.6 10 2 2 2 q B R0 Ek 16.7 MeV 2m
qBR0 7 1 v 4.02 10 m s m
例14.如图,通有电流的闭合回路ABC放在磁感强度为B 的均匀磁场中,回路中电流为I,其流向为顺时针,求 磁场作用于整个回路的力。 dF y 2 × × × × ×× 解: 整个回路受力: C
rR
B d l 0 I
l
r L
r
2π r π r2 0 r R B d l 0 I 2 l πR 0 r 2 0 Ir 2π rB 2 I B R 2π R 2
2π rB 0 I
B
0 I
I
I
×
.
B
dB
dI
B
R
r
讨论:
例1.求载流长直导线的磁场,已知 I , r0 , 1, 2.
0 Idz sin 解: dB 2 4 r 0 Idz sin B dB 2 4 r r0 d z r0 ctg dz 2 sin r
r0ຫໍສະໝຸດ 2 Idz rz o
sin 0 I 2 0 I B 1 sind 4r0 (cos 1 cos 2 ) 4r0
无限长载流圆柱面的磁场
L1
r
R
B
I
L2
r
o R r
B0 0 I
B 2π r
解: 0 r R, B d l 0
r R, B d l 0 I
l
l
例12. 无限大薄导体板均匀通过电流的磁场分布。 解 1)对称性分析 2)选取回路 dB d 设:电流密度为j
例4. 如图所示导线,求0点的磁感强度。 0 I 0 I 0 I BP B B (圆心处) 4π r 4 R 2R (4) (1) 0 I R B0 x B0 0 I 4π d o B0 I 2R d × I (2 ) *o 0 I (5) R B0 × R2 R1 4R o I I (3) • *o 0 I 0 I 0 I 0 I B0 R × B0 8R 4 R2 4 R1 4π R1 o
