湘教版数学七年级下册期末知识点复习+各章节培优题
湘教版2020七年级数学下册期末模拟培优测试题4(附答案)

(2)若B商品所打折扣为7.5折,求促销期间每件A商品的价格。
24.计算:(1)(4x2y-2x3)÷(-2x)2;(2)x•(-x)3-(-x2)2
25.填空并在括号内加注理由.
如图,已知 ∥ , 、 分别平分 和
求证:
证明:∵ ∥
∴ =()
∵ 、 平分 、
2.在平面直角坐标系中,将点 向右平移3个单位长度,再向上平移4个单位长度得到点P的坐标是
A. B. C. D.
3.如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,
下列结论:①BC平分∠ABE;②AC∥BE;③∠BCD+∠D=90°;④∠DBF=2∠ABC.
其中正确的个数为()
A.1个B.2个C.3个D.4个
29.
30.计算:
(1)
(2)
(3)
参考答案
1.D
【解析】
分析:根据旋转的性质和角的和差倍分计算进行判断即可.
详解:∵∠DOC=50°,∴OA从OD旋转到OC,旋转角=∠DOC=50°,∴OB旋转50°,故①正确;
∵OA平分COD,∴∠AOC= ∠COD=25°,∴∠BOC=∠AOB-∠AOC=120°-25°=95°,故②正确;
A.2个B.4个C.16个D.无数个
11.多项式x2+2mx+64是完全平方式,则m=________.
12.若 ,则 =________.
13.若(ax+b)(x+2)=x2﹣4,则ab=_____.
14.用提公因式法分解因式: =__________.
15.若x2﹣mx+36是﹣个完全平方式,则m的值为_________.
春七年级数学下册 3 因式分解章末复习(三)因式分解 (新版)湘教版-(新版)湘教版初中七年级下册数

章末复习(三) 因式分解基础题知识点1 因式分解的意义1.(某某中考)下列式子是因式分解的是(C)A .x(x -1)=x 2-xB .x 2-x =x(x +1)C .x 2+x =x(x +1)D .x 2-x =x(x +1)(x -1)2.若x 2+kx -15能分解为(x +5)(x -3),则k 的值是(B)A .-2B .2C .-8D .8知识点2 因式分解3.(某某中考)下列因式分解中,正确的个数为(C)①x 3+2xy +x =x(x 2+2y);②x 2+4x +4=(x +2)2;③-x 2+y 2=(x +y)(x -y).A .3个B .2个C .1个D .0个4.将-12a 2b -ab 2提公因式后,另一个因式是(A) A .a +2b B .-a +2bC .-a -bD .a -2b5.下列各式中,不能继续因式分解的是(B)A .4x 3-8x 2+4x =4x(x 2-2x +1)B .2x -13xy =13x(6-y) C .8x 2+6xy =2(4x 2+3xy)D .2x 2-8=2(x 2-4)6.把下列多项式因式分解:(1)6x 2y 3-3x 2y 4;解:原式=3x 2y 3×2-3x 2y 3·y=3x 2y 3(2-y).(2)x 3-4x ;解:原式=x(x 2-4)=x(x+2)(x-2).(3)2x2-12xy+18y2;解:原式=2(x2-6xy+9y2)=2(x-3y)2;(4)(m+n)2-4m(m+n)+4m2.解:原式=(m+n)2-2·2m(m+n)+(2m)2=(m+n-2m)2=(n-m)2.知识点3 因式分解的应用7.如图,已知R=6.75,r=3.25,则图中阴影部分的面积为(结果保留π)(D)ππC.27πD.35π8.利用因式分解计算:992+198+1.解:原式=992+2×99×1+1=(99+1)2=1002=10 000.中档题9.分解因式与整式乘法一样,都是一种恒等变形,即在变形的过程中,形变值不变,于是将多项式x2-y2+3x-3y 分解因式的结果为(A)A.(x+y+3)(x-y) B.(x-y-3)(x-y)C.(x+y-3)(x-y) D.(x-y+3)(-x-y)10.若多项式x 2+2(m -3)x +16能用完全平方公式因式分解,则m 的值为7或-1.11.把下列多项式因式分解:(1)a 2(a -b)3+b 2(b -a)3;解:原式=a 2(a -b)3-b 2(a -b)3=(a -b)3(a 2-b 2)=(a -b)3(a -b)(a +b)=(a -b)4(a +b).(2)(a +3)(a -7)+25;解:原式=a 2-4a -21+25=a 2-4a +4=(a -2)2.(3)(x 2+y 2)2-4x 2y 2;解:原式=(x 2+y 2-2xy)(x 2+y 2+2xy)=(x -y)2(x +y)2.(4)(x 2+6x)2+18(x 2+6x)+81.解:原式=(x 2+6x +9)2=(x +3)4.12.先因式分解,再求值:3(a +1)2-(a +1)(2a -1),其中a =1.解:原式=(a +1)[3(a +1)-2a +1]=(a +1)(a +4).当a =1时,原式=(1+1)×(1+4)=10.13.已知|m +4|与n 2-2n +1互为相反数,把多项式x 2+4y 2-mxy -n 因式分解.解:由题意可得|m +4|+(n -1)2=0,所以⎩⎪⎨⎪⎧m +4=0,n -1=0.解得⎩⎪⎨⎪⎧m =-4,n =1. 当m =-4,n =1时,原式=x 2+4y 2+4xy -1=(x +2y)2-1=(x +2y +1)(x +2y -1).综合题14.观察:22-12=(2+1)(2-1)=(1+2)×22=3; 42-32+22-12=(4+3)(4-3)+(2+1)(2-1)=4+3+2+1=(1+4)×42=10; 62-52+42-32+22-12=(6+5)(6-5)+(4+3)(4-3)+(2+1)(2-1)=6+5+4+3+2+1=(1+6)×62=21. 探究:(1)82-72+62-52+42-32+22-12=36(直接写答案);(2)(2n)2-(2n -1)2+(2n -2)2-(2n -3)2+…+22-12=n(2n +1)(直接写答案);应用:(3)如图,2 016个圆由小到大套在一起,从外向里相间画阴影,最外面一层画阴影,最外面的圆的半径为2 016 cm ,向里依次为2 015 cm ,2 014 cm ,…,1 cm ,那么在这个图形中,所有阴影的面积和是多少?(结果保留π) 解:2 0162π-2 0152π+…+-32π+22π-π=(2 0162-2 0152+…+42-32+22-1)π=1 008×(2 016+1)π=2 033 136π (cm 2).。
湘教版版2020七年级数学下册期末模拟培优测试卷A卷(附答案详解

(1)若 ,求 的值;
(2)已 满足 ,求 的值.
22.如图,已知:点A、点B及直线l.
(1)请画出从点A到直线l的最短路线,并写出画图的依据.
(2)请在直线l上确定一点O,使点O到点A与点O到点B的距离之和最短,并写出画图的依据.
23.现有 , 两种商品,买6件 商品和3件 商品用了108元,买5件 商品和1件 商品用了84元.
【详解】
解:当M关于直线y=-3对称的点的坐标为(1,7)时,如图:
根据对称的性质,有:
-3-(4-m)=10
解得:m=17,
故选C.
【点睛】
本题考查坐标与图形的性质,解题的关键是要掌握坐标系中对称点的坐标变化与对称轴的关系.
2.C
【解析】
【分析】
去掉一个最高分和最低分后不会对数据的中间的数产生影响,即中位数.
20.若|a+b-3|+(5a-b-c)2+|2c+b-8|=0,则a=___,b=___,c=___.
21.何老师安排喜欢探究问题的小明解决某个问题前,先让小明看了一个有解答过程的例题.
例:若 ,求m和n的值.
解:因为
所以
所以
所以 所以
为什么要对 进行了拆项呢?
聪明的小明理解了例题解决问题的方法,很快解决了下面两个问题.相信你也能很好的解决下面的这两个问题,请写出你的解题过程.
【详解】
统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生影响,即中位数.
故选 .
【点睛】
本题考查了统计量的选择,属于基础题,相对比较简单,解题的关键在于理解这些统计量的意义.
3.C
【解析】
湘教版版2020七年级数学下册期末模拟培优测试卷1(附答案详解

湘教版版2020七年级数学下册期末模拟培优测试卷1(附答案详解1.在同一个平面内,两条直线的位置关系有()A.平行或垂直B.垂直或相交C.平行或相交D.平行、垂直或相交2.下列各式,从左到右的变形是因式分解的是( )A.B.C.D.3.下列交通标志中,是中心对称图形的是()A.B.C.D.4.赵老师是一名健步走运动的爱好者为备战2019中国地马拉松系列赛·广元站10千米群众健身赛,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图在每天健步走的步数这组数据中,众数和中位数分别是()A.2.2,2.3 B.2.4,2.3 C.2.4,2.35 D.2.3,2.3 5.下列各种说法()(1)如图①,把弯曲的河道BCA改成直道BA,可以缩短航程:,(2)如图②,把渠水引到水池C中,可以在渠岸AB边上找到一点D.使CD AB 沿CD挖水沟,水沟最短;(3)如图③,甲、乙两辆汽车分别沿道路AC,BC同时出发开往C城,若两车速度相同,那么甲车先到C城.其中,运用“垂线段最短”这个性质的是()6.如图,a ∥b,M 、N 分别在a,b 上,P 为两平行线间一点,那么∠1+∠2+∠3=( ).A .180°B .360°C .270°D .540°7.下列各组多项式中,公因式是代数式2x -的是( ).A .()22x +、()22x -B .22x x -、46x -C .36x -、22x x -D .4x -、618x -8.若( )•(﹣xy )2=4x 2y 3,则括号里应填的单项式是( )A .﹣4yB .4yC .4xyD .﹣2xy9.如图,直线AB ,CD ,EF 相交于点O ,则∠1+∠2+∠3的度数等于( )A .90°B .150°C .180°D .210°10.如图,平面内三条直线相交于一点,可以得到对顶角有( )A .3对B .4对C .5对D .6对11.计算:221(2)32ab ab ab -=_____. 12.当 k =_____时,多项式2x 2﹣7kxy +3y +7xy 中不含 xy 项.13.若m n >,8m n +=,15mn =,则m n -的值为______.14.已知(2019﹣a )2+(a ﹣2017)2=7,则代数式(2019﹣a )(a ﹣2017)的值是_____. 15.省运会举行射击比赛,我市射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击10次,计算他们10次成绩的平均数和方差如下表,请你根据表中数据选一人参加比赛,最适合的人选是__.16.化简:2(21)a -=_____.17.如图,把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转,使得点A 与CB 的延长线上的点E 重合连接CD ,则∠BDC 的度数为_____度.18.若(x ﹣4)(x +7)=x 2+mx +n ,则m +n =_____.19.若 a m =2,a n =3;则a m+n = ________20.已知x -y =1,则222x y y --的值为_____.21.如图,AB ∥DC ,AD ∥BC ,E 为AB 延长线上一点,连结DE 与BC 相交于点F ,若∠BFE =∠E . 试说明DE 平分∠ADC .22.甲、乙两人同解方程组51542ax y x by +=⎧⎨=-⎩①②时,甲看错了方程(1)中的a ,解得21x y =⎧⎨=⎩,乙看错(2)中的b ,解得54x y =⎧⎨=⎩,试求a 2017+(﹣10b )2018的值. 23.计算:(1)(1)(23)x x +-(2)(25)(52)a b b a -+24.你能用折纸的方法过一点作已知直线的垂线吗?25.阅读材料:善于思考的小军在解方程组2534115x y x y +=⎧⎨+=⎩时,采用了一种“整体代换”的解法:解:将方程②变形:4x +10y +y =5即2(2x +5y )+y =5③把方程①带入③得:2×3+y =5,∴y =﹣1把y =﹣1代入①得x =4,∴方程组的解为41x y =⎧⎨=-⎩请你解决以下问题:(1)模仿小军的“整体代换”法解方程组3259419x y x y -=⎧⎨-=⎩; (2)已知x ,y 满足方程组22223212472836x xy y x xy y ⎧-+=⎨++=⎩ (i )x 2+4y 2的值;(ii )求(x +2y )2的值.26.已知3,2x y xy +==,求22x y +的值27.把下列各式分解因式:(1)416a -;(2)21850a -.28.分解因式(1)8-2x 2(2)-y 3+6y 2-9y .参考答案1.C【解析】【分析】根据前提条件结合直线的位置关系直接可以得到答案.【详解】在同一平面内,两条不重合的直线的位置关系只有两种:平行或相交.故选C【点睛】此题重点考察学生对两直线位置关系的理解,掌握两直线的位置关系是解题的关键. 2.B【解析】【分析】根据因式分解就是把一个多项式变形成几个整式的积的形式的定义,利用排除法求解.【详解】解:A、是多项式乘法,不是因式分解,错误;B、是利用提公因式进行因式分解,正确;C、右边不是整式的积的形式,错误;D、,错误.故选:B.【点睛】本题考查了对因式分解的定义的应用,主要考查学生对定义的理解能力和辨析能力.3.D【解析】【分析】根据中心对称图形的定义逐项识别即可,在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.【详解】A既不是轴对称图形,也不是中心对称图形,故不符合题意;B是轴对称图形,不是中心对称图形,故不符合题意;C是轴对称图形,不是中心对称图形,故不符合题意;D既是轴对称图形,也是中心对称图形,故符合题意;故选D.【点睛】本题考查了中心对称图形的识别,熟练掌握中心对称图形的定义是解答本题的关键.4.B【解析】【分析】中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间的两个数;对于众数可由条形统计图中出现频数最大或条形最高的数据写出.【详解】由条形统计图中出现频数最大条形最高的数据是在第四组,故众数是2.4(万步);因图中是按从小到大的顺序排列的,最中间的步数都是2.3(万步),故中位数是2.3(万步).故选B.【点睛】此题考查中位数,条形统计图,解题关键在于看懂图中数据5.C【解析】【分析】根据垂线段的性质:垂线段最短进行解答即可.【详解】(1)如图①,把弯曲的河道BCA改成直道BA,可以缩短航程是根据两点之间线段最短;(2)如图②,把渠水引到水池C中,可以在渠岸AB边上找到一点D.使CD⊥AB,沿CD 挖水沟,水沟最短,根据垂线段最短;(3)如图③,甲、乙两辆汽车分别沿道路AC,BC同时出发开往C城,若两车速度相同,那么甲车先到C城,根据垂线段最短.故选C.【点睛】此题主要考查了垂线段的性质,关键是掌握性质定理.6.B【解析】【分析】首先作出PA ∥a ,根据平行线性质,两直线平行同旁内角互补,可以得出∠1+∠2+∠3的值.【详解】解:过点P 作PA ∥a ,∵a ∥b ,PA ∥a ,∴a ∥b ∥PA ,∴∠1+∠MPA=180°,∠3+∠APN=180°,∴∠1+∠MPA+∠3+∠APN=180°+180°=360°,∴∠1+∠2+∠3=360°.故选B .【点睛】此题主要考查了平行线的性质,作出PA ∥a 是解决问题的关键.7.C【解析】【分析】逐项确定公因式进行判断,即公因式的系数是多项式各项系数的最大公约数;字母取各项都含有的相同字母,相同字母的指数取次数最低的.【详解】解:A 、()22x +、()22x -没有公因式,故A 不正确; B 、22x x -、46x -变形为x(x-2)、2(x-3),没有公因式,故B 不正确;C 、36x -、22x x -变形为3(x-2)、x(x-2),公因式为x-2,故C 正确;D 、4x -、618x -变形为x-4、6(x-3),没有公因式,故D 不正确.故选C本题考查如何找多项式的公因式,确定公因式的方法为公因式的系数是多项式各项系数的最大公约数;字母取各项都含有的相同字母,相同字母的指数取次数最低的.8.B【解析】【分析】根据同底数幂的乘法法则和单项式乘以单项式法则填上即可.【详解】4y•(﹣xy)2=4x2y3,故选B.【点睛】本题考查了同底数幂的乘法法则和单项式乘以单项式法则的应用,能熟记法则的内容是解此题的关键.9.C【解析】【分析】根据对顶角相等可得∠4=∠1,再根据平角的定义解答.【详解】解:如图,∠4=∠1,∵∠2+∠3+∠4=180∘,∴∠1+∠2+∠3=180∘.故选C.【点睛】本题考查对顶角相等的性质,熟练掌握平角为180°这一隐含条件是解题的关键.10.D【分析】两条直线相交于一点,形成两对对顶角,把三条直线相交于一点,拆开成三种两条直线相交于一点的情况,再判断对顶角的对数.【详解】三条直线相交于一点,拆开成三种两条直线相交于一点的情况,因为两条直线相交于一点,形成两对对顶角,所以三条直线相交于一点,有3个两对对顶角,共6对对顶角. 故选D .【点睛】本题考查了对顶角的定义,注意对顶角是两条直线相交而成的四个角中,没有公共边的两个角.11.13a 2b 3﹣a 2b 2 【解析】【分析】利用单项式乘多项式的计算方法直接计算出结果即可【详解】221232ab ab ab ⎛⎫-⋅ ⎪⎝⎭=22322211123223ab ab ab ab a b a b ⋅-⋅=- 故答案为13a 2b 3﹣a 2b 2 【点睛】此题考查单项式乘多项式,掌握运算法则是解题关键12.1【解析】【分析】直接利用多项式中不含xy 项,可得﹣7k +7=0,进而得出答案.【详解】∵多项式2x 2﹣7kxy +3y +7xy 中不含xy 项,∴﹣7k +7=0,解得:k =1.故答案为:1.【点睛】本题考查了合并同类项,正确得出xy 的系数为零是解题的关键.13.2.【解析】【分析】将8m n +=两边平方,并结合题中条件可求出2234m n +=,可计算出()24m n -=,由m n >可得结果.【详解】解:()222264m n m n mn +=++=,∴2234m n +=, ()22224m n m n mn -=+-=,m n >,∴2m n -=,故答案为:2.【点睛】本题考查整式运算,灵活运用完全平方公式是解题关键.14.32- 【解析】【分析】根据完全平方公式的变式:ab=()()2222a b a b +-+ 利用整体代入的思想求解即可.【详解】 解:∵(2019﹣a )2+(a ﹣2017)2=7,∴(2019﹣a )(a ﹣2017)=12{[(2019﹣a )+(a ﹣2017)]2﹣[(2019﹣a )2+(a ﹣2017)2]}=32-, 故答案为:32-. 【点睛】本题考查了完全平方公式的应用,熟练掌握公式的变式是解题关键.15.丁【解析】【分析】根据甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,甲,乙,丙,丁四个人中丁的方差最小,说明丁的成绩最稳定,得到丁是最佳人选.【详解】甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,甲,乙,丙,丁四个人中丁的方差最小,说明丁的成绩最稳定,∴综合平均数和方差两个方面说明丁成绩既高又稳定,∴丁是最佳人选.故答案为:丁.【点睛】考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.16.2441a a -+【解析】【分析】根据完全平方公式即可解答.【详解】()221a -= 2441a a -+故答案为2441a a -+【点睛】本题考查了完全平方公式,熟练掌握完全平方公式是关键.17.15【解析】【分析】根据△EBD 由△ABC 旋转而成,得到△ABC ≌△EBD ,则BC =BD ,∠EBD =∠ABC =30°,则有∠BDC =∠BCD ,∠DBC =180﹣30°=150°,化简计算即可得出15BDC ∠=︒.【详解】解:∵△EBD 由△ABC 旋转而成,∴△ABC ≌△EBD ,∴BC =BD ,∠EBD =∠ABC =30°,∴∠BDC =∠BCD ,∠DBC =180﹣30°=150°,∴()1180150152BDC BCD ∠=∠=︒-︒=︒; 故答案为:15.【点睛】此题考查旋转的性质,即图形旋转后与原图形全等.18.﹣25.【解析】【分析】先根据多项式乘以多项式法则进行计算,求出m 、n 的值,即可得出答案.【详解】解:(x ﹣4)(x+7)=x 2+3x ﹣28,∵(x ﹣4)(x+7)=x 2+mx+n ,∴m =3,n =﹣28,∴m+n =﹣25,故答案为:﹣25.【点睛】本题考查多项式乘以多项式法则,能熟练根据多项式乘以多项式法则进行计算是解题关键. 19..【解析】【分析】根据同底数的幂的乘法法则,代入求值即可.【详解】.故答案为:.本题考查了同底数的幂的乘法法则,同底数幂的乘法底数不变指数相加.20.1【解析】【分析】将原式前两项进行因式分解后得:()() 2x y x y y +--,然后将1x y -=代入将原式化为:2x y y +-即x y -进而得出答案【详解】222x y y --=()()2x y x y y +--∵1x y -=∴()()22x y x y y x y y +--=+-=x y -=1所以答案为1【点睛】本题主要考查了因式分解的实际运用,熟练掌握相关性质是解题关键21.见解析.【解析】【分析】根据平行线的性质得到∠CDE =∠E ,∠ADE =∠BFE ,等量代换即可得到结论.【详解】解:∵AB ∥DC ,∴∠CDE =∠E ,∵AD ∥BC ,∴∠ADE =∠BFE ,∵∠BFE =∠E ,∴∠CDE =∠ADE .∴DE 平分∠ADC .【点睛】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.【解析】【分析】将甲的解代入(2),乙的解代入(1)得到关于a与b的方程组,求方程组的解得到a与b 的值,代入所求式子中计算即可.【详解】由题意,得:8=2{52015ba-+=,解得:-1 {10ab==,则原式=(﹣1)2017+(﹣1010)2018=(﹣1)+1=0.【点睛】此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值,根据这一条件求出a,b的值是解题的关键.23.(1)2x2-x-3;(2)4a2-25b2.【解析】【分析】(1)根据多项式乘多项式的法则进行展开,然后再合并同类项即可;(2)利用平方差公式进行计算即可.【详解】(1)原式=2x2-3x+2x-3=2x2-x-3;(2)原式=(2a)2-(5b)2=4a2-25b2.【点睛】本题考查了整式的乘法、平方差公式,熟练掌握多项式乘法法则以及平方差公式的结构特征是解题的关键.24.先沿已知直线折一下,再在已知点处对折即可.【解析】【分析】运用垂线的定义解答即可.【详解】先沿已知直线折一下,再在已知点处对折即可.【点睛】本题考查了垂线的定义在生活中的应用,锻炼了学生的动手能力.25.(1)32xy=⎧⎨=⎩;(2)(i)17;(ii)25.【解析】【分析】(1)先把第2个方程变形为3x+2(3x-2y)=19,在把第一个方程代入变形后的方程,得出x的值,代入第一个方程即可得y的值;(2)把原方程组变形为()()22223424724=36x y xyx y xy⎧+-=⎪⎨++⎪⎩①②,把x2+4y2看作整体解方程组即可得出x2+4y2和xy的值;再把(x+2y)2展开,代入即可得出答案.【详解】解:(1)把②变形为3x+2(3x﹣2y)=19,∵3x﹣2y=5,∴3x+10=19,∴x=3,把x=3代入3x﹣2y=5得y=2,即方程组的解为32 xy=⎧⎨=⎩;(2)(i)原方程组变形为()()22223424724=36x y xyx y xy⎧+-=⎪⎨++⎪⎩①②,①+②×2得,7(x2+4y2)=119,∴x 2+4y 2=17,(ii )由x 2+4y 2=17代入②得xy =2,∴(x +2y )2=x 2+4y 2+4xy =17+8=25.【点睛】本题考查了解二元一次方程组,掌握解方程组的方法和步骤是关键,注意整体思想的运用. 26.5【解析】【分析】原式22xy +变形为()+-22x y xy ,然后把3,2x y xy +==,代入计算即可求出结果.【详解】解:()22225x y x yxy +=+-=故答案为:5【点睛】本题考查了完全平方公式,熟练地运用公式进行变形是解答本题的关键.27.(1)(a 2+4)(a+2)(a-2);(2)2(3a+5)(3a-5).【解析】【分析】(1)原式利用平方差公式分解即可;(2)首先提取公因式2,进而利用平方差公式进行分解即可.【详解】(1)原式=(a 2+4)(a 2-4)=(a 2+4)(a+2)(a-2);(2)18a 2-50=2(9a 2-25)=2(3a+5)(3a-5).【点睛】本题考查了提取公因式法以及公式法分解因式,熟练应用公式法分解因式是解题关键. 28.(1)2(2-x )(2+x )(2)-y (y-3)2【解析】【分析】(1)首先提取公因式2,再利用平方差公式分解因式;(2)首先提取公因式-y,再利用完全平方公式分解因式.【详解】(1)8-2x2=2(4-x2)=2(2-x)(2+x);(2)-y3+6y2-9y=-y(y2-6y+9)=-y(y-3)2.【点睛】此题主要考查了提取公因式法和公式法分解因式,熟练掌握公式的形式是解题关键.。
七年级下册湘教版教版数学期末总复习教案及练习试卷
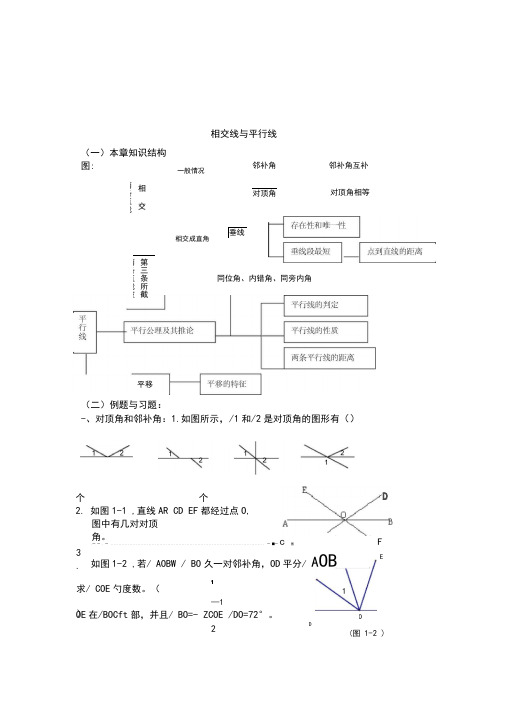
(图 1-2 )(一)本章知识结构图:一般情况相交线与平行线邻补角 邻补角互补 相 交两条直线对顶角相交成直角垂线第三条所截 两条直线被对顶角相等(二)例题与习题:-、对顶角和邻补角:1.如图所示,/1和/2是对顶角的图形有()平移同位角、内错角、同旁内角个 个 2. 如图1-1 ,直线AR CD EF 都经过点O, 图中有几对对顶角。
DFE.一 一 . 一 ................................................................................................. 一 ■一c图如图1-2 ,若/ AOBW / BO 久一对邻补角,OD 平分/ A OB11—1OE 在/BOCft 部,并且/ BO=- ZCOE /DO=72°。
2D3. 求/ COE 勺度数。
() O第二课时二、垂线:已知:如图,在一条公路l的两侧有A、B两个村庄.<1>现在乡政府为民服务,沿公路开通公交汽车,并在路边修建一个公共汽车站P,同时修建车站国必、B两个村庄的道路,并要求修建的道路之和最短,请你设计出车站的位置,在图中画出点P的位置,(保留作图的痕迹).并在后面的横线上用一句话说明道理. ________________ . ________________________<2>为方便机动车出行,AM计划自己出资修建一条由本村直达公路l的机动车专用道路,你能帮助AM节省资金,设计出最短的道路吗,请在图中画出你设计修建的最短道路,并在后面的横线上用一句话说明道理. _______ .三、同位角、内错角和同旁内角的判断1.如图3-1 ,按各角的位置,下列判断错误的是()(A) /1与/2是同旁内角(B) /3与/4是内错角(C) /5与/6是同旁内角(D) /5与/8是同位角2.如图3-2 , 与/ EF幽成内错角的是,与/FEB构成同旁内角的是 ______图3-1C A3囱3图4-6第三课时四、平行线的判定和性质:1 .如图 4-1 ,若/ 3=7 4,贝U //;若 AB// CD,则/ =/ 。
有答案湘教版七年级下册数学原创期末试题(培优拔尖)以及答案

湘教版七年级(下)期末数学试卷总分:120分姓名:班级:一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1 2 3 4 5 6 7 8 9 101.下列是二元一次方程的是()A.3x﹣6=x B.3x=2y C.x﹣=0 D.2x﹣3y=xy2.下列计算正确的是()A.a2•a3=a6B.a2+a2=a4C.(﹣a3)2=a6 D.(a2b)2=a4b3.已知是方程2mx﹣y=10的解,则m的值为()A.2 B.4 C.6 D.104.下列运算正确的是()A.(x﹣1)2=x2﹣2x﹣1 B.(a﹣b)2=a2﹣b2C.(a+m)(b+n)=ab+mn D.(m+n)(﹣m+n)=﹣m2+n25.下列图形中,轴对称图形的个数是()A.1 B.2 C.3 D.46.下列从左到右的变形:(1)15x2y=3x•5xy;(2)(a+b)(a﹣b)=a2﹣b2;(3)a2﹣2a+1=(a﹣1)2;(4)x2+3x+1=x(x+3+)其中是因式分解的个数是()A.0个B.1个C.2个D.3个7.点P是直线l外一点,A、B、C为直线l上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离()A.小于2cm B.等于2cm C.不大于2cm D.等于4cm8.有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的()A.平均数B.中位数C.众数D.方差9.若一列数据x1,x2,x3,…,x n,的平均数是3,方差是2,则数据x1+5,x2+5,…,x n+5的平均数与方差分别是()A.8,7 B.5,5 C.3,2 D.8,210.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()A.平行B.垂直C.平行或垂直 D.无法确定二、填空题(本大题共8小题,每小题3分,满分24分.)11.已知(a﹣2)+y=1是一个二元一次方程,则a的值为.12.(﹣3ab2)3•(a2b)= .13.若代数式x2+mx+9是完全平方式,那么m= .14.如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=40°,则∠BOC= .15.如图,如果AB∥CD,则∠α,∠β,∠γ之间的关系为______________.16.一组数据2,4,x,2,4,7的众数是2,则这组数据的平均数是.17、已知a+b=3,a2b+ab2=-30,则a2-ab+b2+2=18.观察下列各式及其展开式:(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;…请你猜想(a+b)10的展开式第三项的系数是 .三、解答题(本大题共9小题,满分66分,解答应写出文字说明、证明过程或演算步骤)19.(4分)解方程组:20、(8分)已知关于x,y的方程组的解是,求关于x,y 的方程组的解.21.(6分)因式分解(1)a3b﹣ab3 (2)(x2+4)2﹣16x2.22.(6分)先化简,再求值:a(a﹣2b)+2(a+b)(a﹣b)+(a+b)2,其中a,b满足|a+|+(b﹣1)2=0.23、(6分)已知a、b、c是三角形ABC的三边长且满足a2+c2-2b(a+c-b)=0,请判断此三角形是什么特殊形状的三角形,并说明理由。
湘教版数学七年级下册期末知识点复习各章节典型例题

湘教版数学七年级下册期末知识点复习各章节典型例题第一章有理数1. 将下列有理数按从小到大的顺序排列:-2,5/3,-1.5,1解:-2,-1.5,5/3,12. 计算下列各式的值:(1)-0.4 + 1/5 (2)3.6 - 2.7解:(1)-0.4 + 1/5 = -0.4 + 0.2 = -0.2(2)3.6 - 2.7 = 0.9第二章整式与分式1. 计算下列各式的值:(1)3a - 2b,a=4,b=-1 (2)2x^2 -3y + 1,x=-2,y=3解:(1)3a - 2b = 3(4) - 2(-1) = 12 + 2 = 14(2)2x^2 - 3y + 1 = 2(-2)^2 - 3(3) + 1 = 8 - 9 + 1 = 02. 约分:(1)8a^2b/12ab (2)16x^3/24x^2解:(1)8a^2b/12ab = (8/12) * (a^2b/ab) = 2/3(2)16x^3/24x^2 = (16/24) * (x^3/x^2) = 2/3x第三章代数式的计算1. 计算下列代数式的值:(1)a^2 - 3a,a=2 (2)2x^2 + 4x + 1,x=-1解:(1)a^2 - 3a = 2^2 - 3(2) = 4 - 6 = -2(2)2x^2 + 4x + 1 = 2(-1)^2 + 4(-1) + 1 = 2 + (-4) + 1 = -12. 化简下列代数式:(1)2x + 3y - x + 4y (2)5a^2 -2a + 3a^2 - a解:(1)2x + 3y - x + 4y = x + 7y(2)5a^2 - 2a + 3a^2 - a = 8a^2 - 3a第四章一次函数1. 已知y = 2x + 3,求当x = -1时y的值。
解:将x = -1代入方程y = 2x + 3,得到y = 2(-1) + 3 = 12. 画出函数y = 3x - 2的图像。
湘教版七年级数学下册期末复习:专题03 因式分解(含答案及解析)

专题03因式分解2020-2021学年七年级数学下册期末复习精选精炼练(湘教版)一、单选题1.下列选项从左到右变形是因式分解的是( )A .2(2)(2)4a a a +-=-B .24(2)(2)a a a -=+-C .2(1)(2)2a a a a +-=--D .23(1)3x x x x --=--【答案】B【分析】根据分解因式的意义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,进行作答即可.【详解】解:A 、2(2)(2)4a a a +-=-是整式的乘法,不属于因式分解,故此选项不符合题意;B 、24(2)(2)a a a -=+-右边是几个整式的积的形式,属于因式分解,故此选项符合题意;C 、2(1)(2)2a a a a +-=--是整式的乘法,不属于因式分解,故此选项不符合题意;D 、23(1)3x x x x --=--右边不是几个整式的积的形式,不属于因式分解,故此选项不符合题意; 故选B .【点睛】本题考查了因式分解的意义,属于基础题,解答本题的关键是熟练掌握因式分解的定义与形式. 2.若因式分解()()231x ax x x b +-=-+,则a 的值是( ) A .3-B .2-C .2D .4【答案】C【分析】 根据因式分解的定义可直接进行求解.【详解】解:由()()231x ax x x b +-=-+可得:()2231x ax x b x b +-=+--, ∴1,3a b b =-=,∴2a =;故选C .【点睛】本题主要考查因式分解的定义,熟练掌握因式分解是解题的关键.3.多项式322+6+9x x y xy 与339x y xy -的公因式是( )A .2(3)x x y +B .(3)x x y +C .(3)xy x y +D .(3)x x y -【答案】B【分析】先把两个多项式进行因式分解,再根据公因式的概念进行判断,即可得出结论.【详解】解:∴322+6+9x x y xy ()2269x x xy y =++()23x x y =+, 339x y xy -()229xy x y =-()()33xy x y x y =+-,∴多项式322+6+9x x y xy 与339x y xy -的公因式是(3)x x y +.故选:B .【点睛】本题主要考查了公因式的判断,掌握因式分解的方法及公因式的概念是解题的关键.4.4x 2y 和6xy 3的公因式是( )A .2xyB .3xyC .2x 2yD .3xy 3【答案】A【分析】提取各项系数的最大公约数与各项都含有的相同字母的最低次数幂的积即可.【详解】24x y 和36xy 的公因式是2xy ,故选:A .【点睛】本题考查公因式的定义,掌握确定公因式的方法是解题关键.5.下列各式能用平方差公式进行因式分解的是( )A .21x +B .21x --C .21x -+D .2(1)1x +- 【答案】C【分析】根据能够运用平方差公式分解因式的多项式必须是二项式,两项都能写成平方的形式,且符号相反进行判断即可.【详解】解:A 、是x 2与1的和,不能用平方差公式进行分解,故此选项错误;B 、两项的符号相同,不符合平方差公式特点,不能用平方差公式进行分解,故此选项错误;C 、符合平方差公式特点,能用平方差公式进行分解,故此选项正确;D 、去括号后结果为x 2,不是二项式,不能用平方差公式进行分解,故此选项错误;故选:C .【点睛】此题主要考查了平方差公式,关键是熟练掌握平方差公式分解因式的多项式的特点.6.下列运算正确的是( )A .23235m m m +=B .32m m m ÷=C .()326m m m ⋅=D .()()22m n n m n m --=-【答案】B【分析】根据同类项的定义,幂的运算法则以及完全平方式逐项计算即可判断.【详解】A. 2m 和23m 不是同类项不能合并.故该选项错误,不符合题意.B. 3232m m m m -÷==.故该选项正确,符合题意.C. ()32236167m m m m m m m m ⨯+⋅=⋅=⋅==.故该选项错误,不符合题意.D. ()()()2222m n n m m n m mn n --=--=-+-.故该选项错误,不符合题意.故选B .【点睛】本题考查同类项的定义,幂的运算法则以及完全平方式.熟练掌握各知识点是解答本题的关键. 7.对于:①()2242x x -=-;②()()2111x x x -+=+-; ③()23242x x x +-=+; ④22111142x x x ⎛⎫-+=- ⎪⎝⎭. 其中因式分解正确的是( )A .①③B .②③C .①④D .②④【答案】D【分析】根据因式分解的定义逐个判断即可.【详解】解:①()()2422x x x -=-+,此项错误; ②()()2111x x x -+=+-,此项正确; ③()23242x x x +-≠+,此项错误; ④22111142x x x ⎛⎫-+=- ⎪⎝⎭,此项正确. 故选D .【点睛】本题考查了因式分解的定义,能熟记因式分解的定义是解题的关键,注意:把一个多项式化成几个整式的积的形式,叫因式分解.二、填空题8.分解因式:26a a -=__________;【答案】(6)a a -【分析】找出公因式,直接提取分解因式即可.【详解】解:a 2-6a =a (a -6).故答案为:a (a -6).【点睛】本题考查了提取公因式法分解因式,正确提取公因式是解题关键.9.若224x y -=-,则236x y -+的值为________..【答案】12【分析】先将236x y -+提取公因式再整体代入求解即可.【详解】∴223632x y x y -+=--()且224x y -=- ,∴2363412x y -+=-⨯-=(),故答案为:12.【点睛】此题考查代数式求值,利用提取公因式法因式分解再整体代入求解,难度一般.10.分解因式:a 2﹣4=_____________.【答案】(a +2)(a ﹣2).【分析】直接根据平方差公式进行因式分解即可;【详解】a 2﹣4=(a +2)(a ﹣2).故答案为:(a +2)(a ﹣2).【点睛】本题考查了平方差公式进行因式分解,正确掌握知识点是解题的关键;11.分解因式:2363x x ++=__________.【答案】()231x +【分析】先提取公因式3,再对余下的多项式利用完全平方公式继续分解,即可得到答案.【详解】解:2363x x ++, ()2321x x =++,()231x =+.故答案为:()231x +.【点睛】此题主要考查了提取公因式法以及公式法进行分解因式,正确运用分解因式的方法是解题关键. 12.分解因式:a 3-4a 2+4a =_________.【答案】a (a -2)2【分析】先提公因式,再运用完全平方公式.【详解】解:原式2(44)a a a =-+ 2(2)a a =-.故答案为:2(2)a a -.【点睛】本题考查了整式的因式分解,掌握提公因式法和因式分解的完全平方公式是解决本题的关键.13.若3ab =,1a b +=-,则代数式22a b ab +的值等于__.【答案】-3【分析】直接提取公因式ab ,进而分解因式,把已知数据代入得出答案.【详解】解:∴ab =3,a +b =-1,a 2b +ab 2=ab (a +b )=3×(-1)=-3.故答案为:-3.【点睛】此题主要考查了提取公因式法分解因式以及代数式求值,正确分解因式是解题关键.三、解答题14.因式分解(1)29x - (2)2(1)22x x --+【答案】(1)()()33x x +-;(2)()()13x x --【分析】(1)直接利用平方差分解因式得出答案;(2)将括号展开,合并同类项,再利用十字相乘法分解因式得出答案.【详解】解:(1)29x -=()()33x x +-;(2)2(1)22x x --+=21222x x x +--+=243x x -+=()()13x x --【点睛】此题主要考查了公式法以及十字相乘法分解因式,正确应用公式是解题关键.15.先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和公式法,其实分解因式的方法还有分组分解法、配方法(拆项法)、十字相乘法等等.分组分解法是将一个多项式适当分组后,再用提公因式或运用公式继续分解的方法.如①和②:①ax by bx ay +++()()ax bx ay by =+++()()x a b y a b =+++()()a b x y =++②2221xy y x +-+()2221x xy y =++-()21x y =+-()()11x y x y =+++-请你仿照以上方法,探索并解决下列问题:(1)分解因式:22a a b b +--;(2)两个不相等的实数m ,n 满足2240m n +=.若26m m k -=,26n n k -=,求m n +和k 的值.【答案】(1)()()1a b a b -++;(2)6m n +=,2k =.【分析】(1)先分组得()22a b a b -+-,再根据平方差公式和提取公因式法进行因式分解; (2)由已知26m m k -=,26n n k -=两式相减得到22660m m n n --+=,左边分解后可得到6m n +=,再由已知26m m k -=,26n n k -=两式相加结合2240m n +=即可求得k 的值.【详解】解:(1)22a a b b +--()22a b a b =-+-()()()a b a b a b =+-+-()()1a b a b =-++;(2)∴26m m k -=,26n n k -=,两式相减得22660m m n n --+=,∴22660m n m n --+=,即()()()60m n m n m n +---=,因式分解得()()60m n m n -+-=,∴m n ≠,∴60m n +-=即6m n +=,∴26m m k -=,26n n k -=,两式相加得22662m m n n k -+-=,即()2262m n m n k +-+=, ∴2240m n +=,6m n +=,∴240664k =-⨯=,∴2k =.【点睛】本题考查了平方差公式以及分组分解法分解因式,因式分解的应用,正确灵活应用公式是解题关键. 16.如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m 的大正方形,两块是边长都为n 的小正方形,五块是长为m ,宽为n 的全等小矩形,且 m n >.(以上长度单位:cm )(1)观察图形,可以发现代数式22252m mn n ++可以因式分解,请写出因式分解的结果;(2)若每块小矩形的面积为210cm ,四个正方形的面积和为288cm ,试求图中所有裁剪线(虚线部分)长之和.【答案】(1)(m +2n )(2m +n );(2)48cm【分析】(1)根据图象由长方形面积公式将代数式2m 2+5mn +2n 2因式分解即可;(2)根据正方形的面积得出正方形的边长,再利用每块小矩形的面积为10cm 2,得出等式求出m +n ,进一步得到图中所有裁剪线(虚线部分)长之和即可.【详解】解:(1)2m 2+5mn +2n 2可以因式分解为(m +2n )(2m +n );故答案为:(m +2n )(2m +n );(2)依题意得,2m 2+2n 2=88,mn =10,∴m 2+n 2=44,∴(m +n )2=m 2+2mn +n 2,∴(m +n )2=44+20=64,∴m +n >0,∴m +n =8,∴图中所有裁剪线(虚线部分)长之和为6m +6n =6(m +n )=48cm .【点睛】此题主要考查了因式分解的应用、列代数式以及完全平方公式的应用,根据已知图形得出是解题关键.17.先化简:22121(1)24x x x x ++-÷+-,再从不等式216x --<的负整数解中选一个适当的数代入求值. 【答案】21x x -+;x 取-3,原式值为52. 【分析】先把括号里的式子进行通分,再把后面的式子根据完全平方公式、平方差公式进行因式分解,然后约分,再求出不等式的解集,最后代入一个合适的数,即分式不为零的值,即可解题.【详解】 解:22121(1)24x x x x ++-÷+- 22214221x x x x x +--=⨯+++ 21(2)(2)2(1)x x x x x ++-=⨯++ 21x x -=+ 216x --<72x ∴>-72x ∴>-的负整数解有:-3,-2,-1, 2,1x x ≠-≠-3x ∴=- 原式21x x -=+ 3231--=-+ 52=. 【点睛】本题考查分式的混合运算、分式的化简求值,涉及完全平方公式、平方差公式进行因式分解,解一元一次不等式等知识,是重要考点,难度较易,掌握相关知识是解题关键.18.(阅读材料) 在进行计算或化简时,可以根据题目特点,将一个分数或分式变成两部分之差,如:23111111111111;;()333623231535235-==-==-==-⨯⨯等. (问题解决)利用上述材料中的方法,解决下列问题:(1)求111111261220342380++++++的值; (2)求11111141224402(1)2(1)n n n n ++++++-+的值; (3)求211111315356341n +++++-的值. 【答案】(1)1920;(2)22n n +;(3)21n n +. 【分析】 (1)根据题目中的式子特点,先分解,然后裂项,再计算即可解答本题; (2)先提出12,然后裂项计算即可解答本题; (3)根据题目中式子的特点,先裂项,然后计算即可解答本题.【详解】解:(1)111111261220342380++++++=111223+⨯⨯+134⨯+…+1118191920+⨯⨯ =1﹣1111122334+-+-+…+111118191920-+- =1﹣120=1920; (2)11111141224402(1)2(1)n n n n ++++++-+ =12×[1112612+++…+1n(n 1)+] =12×[111223+⨯⨯+134⨯+…+1n(n 1)+] =12×(1﹣1111122334+-+-+…+111n n -+) =12×(1﹣11n +) =12×111n n +-+ =22n n +; (3)211111315356341n +++++-=111335+⨯⨯+157⨯+…+1(21)(21)n n -+ =12×(1﹣1111133557+-+-+…+112121n n --+) =12×(1﹣121n +) =12×221n n + =21n n +. 【点睛】本题考查数字的变化类、有理数的混合运算,解答本题的关键是明确题意,发现式子的变化特点,求出所求式子的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下册总复习第一章二元一次方程【知识点归纳】1.含有个未知数,并且项的次数都是的方程叫做二元一次方程。
2.把个含有未知数的二元一次方程(或者一个二元一次方程,一个一元一次方程)联立起来组成的方程组,叫做二元一次方程组。
3.在一个二元一次方程组中,使每一个方程两边的值都的一组未知数的值,叫做这个二元一次方程组的解。
4.由二元一次方程组中的一个方程的某一个未知数用含有的代数式表示,再代入另一方程,便得到一个一元一次方程。
这种解方程组的方法叫做消元法,简称代入法。
5.两个二元一次方程中同一未知数的系数或时,把这两个方程相减或相加,就能消去这个未知数,从而得到一个一元一次方程。
这种解方程组的方法叫做消元法,简称加减法。
6.列二元一次方程组解决实际问题的关键是寻找。
【典型例题】/1.已知方程组,甲同学正确解得,而乙同学粗心,把c给看错了,解得,求abc的值.2.已知关于x,y的方程组的解是,求关于x,y的方程组的解.^解方程组时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得这种方法被称为“整体代入法”.请用这样的方法解方程组.>4.阅读下列解方程组的方法,然后回答问题.解方程组解:由①﹣②得2x+2y=2即x+y=1③③×16得16x+16y=16④②﹣④得x=﹣1,从而可得y=2∴方程组的解是.(1)请你仿上面的解法解方程组.((2)猜测关于x、y的方程组的解是什么,并利用方程组的解加以验证.5.南山植物园以其优美独特的自然植物景观,现已成为重庆市民春游踏青、赏四季花卉、观山城夜景的重要旅游景区.若该植物园中现有A 、B 两个园区,已知A 园区为矩形,长为(x+y )米,宽为(x ﹣y )米;B 园区为正方形,边长为(x+3y )米.(1)请用代数式表示A 、B 两园区的面积之和并化简;…(2)现根据实际需要对A 园区进行整改,长增加(11x ﹣y )米,宽减少(x ﹣2y )米,整改后A 区的长比宽多350米,且整改后两园区的周长之和为980米.若A 园区全部种植C 种花,B 园区全部种植D 种花,且C 、D 两种花投入的费用与吸引游客的收益如下表:求整改后A 、B 两园区旅游的净收益之和.(净收益=收益﹣投入)6.江海化工厂计划生产甲、乙两种季节性产品,在春季中,甲种产品售价50千元/件,乙种产品售价30千元/件,生产这两种产品需要A 、B 两种原料,生产甲产品需要A 种原料4吨/件,B 种原料2吨/件,生产乙产品需要A 种原料3吨/件,B 种原料1吨/件,每个季节该厂能获得A 种原料120吨,B 种原料50吨. (1)如何安排生产,才能恰好使两种原料全部用完此时总产值是多少万元¥(2)在夏季中甲种产品售价上涨10%,而乙种产品下降10%,并且要求甲种产品比乙种产品多生产25件,问如何安排甲、乙两种产品,使总产值是1375千元,A ,B 两种原料还剩下多少吨 D投入(元/平方米) 13 16 收益(元/平方米)1826'7.小明从家到学校的路程为千米,其中有一段上坡路,平路,和下坡路.如果保持上坡路每小时行3千米.平路每小时行4千米,下坡路每小时行5千米.那么小明从家到学校用一个小时,从学校到家要44分钟,求小明家到学校上坡路、平路、下坡路各是多少千米第二章整式的乘法【知识点归纳】1.同底数幂相乘,不变,相加。
= (m,n是正整数)2.幂的乘方,不变,相乘。
(a n)m= (m,n是正整数)3.积的乘方,等于把,再把所得的幂。
(ab)n= (n是正整数)4.单项式与单项式相乘,把它们的、分别相乘。
}5.单项式与多项式相乘,先用单项式,再把所得的积,a(m+n)=6.多项式与多项式相乘,先用一个多项式的每一项分别乘,再把所得的积,(a+b)(m+n)= 。
7.平方差公式,即两个数的与这两个数的的积等于这两个数的平方差(a+b)(a-b)=8.完全平方公式,即两数和(或差)的平方,等于它们的,加(或减)它们的积的。
(a+b)2= ,(a-b)2= 。
9.公式的灵活变形:(a+b)2+(a-b)2= ,(a+b)2-(a-b)2= ,a2+b2=(a+b)2- ,a2+b2=(a-b)2+ ,(a+b)2=(a-b)2+ ,(a-b)2=(a+b)2- 。
【典型例题】1.)2.已知2a•5b=2c•5d=10,求证:(a﹣1)(d﹣1)=(b﹣1)(c﹣1).2.(1)已知2x+2=a,用含a的代数式表示2x;(2)已知x=3m+2,y=9m+3m,试用含x的代数式表示y.3.我们知道多项式的乘法可以利用图形的面积进行解释,如(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示:(1)请你写出图3所表示的一个等式:.|(2)试画出一个图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.11.归纳与猜想:(1)计算:①(x﹣1)(x+1)=;②(x﹣1)(x2+x+1)=;③(x﹣1)(x3+x2+x+1)=;(2)根据以上结果,写出下列各式的结果.①(x﹣1)(x6+x5+x4+x3+x2+x+1)=;②(x﹣1)(x9+x8+x7+x6+x5+x4+x3+x2+x+1)=;(3)(x﹣1)(x n﹣1+x n﹣2+x n﹣3+…+x2+x+1)=(n为整数);(4)若(x﹣1)•m=x15﹣1,则m=;(5)根据猜想的规律,计算:226+225+…+2+1.~12.认真阅读材料,然后回答问题:我们初中学习了多项式的运算法则,相应的,我们可以计算出多项式的展开式,如:(a+b)1=a+b,(a+b)2=a2+2ab+b2,(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3,…下面我们依次对(a+b)n展开式的各项系数进一步研究发现,n取正整数时可以单独列成表中的形式:上面的多项式展开系数表称为“杨辉三角形”;仔细观察“杨辉三角形”,用你发现的规律回答下列问题:(1)多项式(a+b)n的展开式是一个几次几项式并预测第三项的系数;—13.观察下列各式:(x﹣1)÷(x﹣1)=1;(x2﹣1)÷(x﹣1)=x+1;(x3﹣1)÷(x﹣1)=x2+x+1;(x4﹣1)÷(x﹣1)=x3+x2+x+1;(1)根据上面各式的规律可得(x n+1﹣1)÷(x﹣1)=;(2)利用(1)的结论求22015+22014+…+2+1的值;?(3)若1+x+x2+…+x2015=0,求x2016的值.第三章因式分解【知识点归纳】1.把一个多项式表示成若干个的形式,称为把这个多项式因式分解。
(因式分解三注意:1.乘积形式;2.恒等变形;3.分解彻底。
)2.几个多项式的称为它们的公因式。
3.如果一个多项式的各项有公因式,可以把这个公因式提到外面,这种把多项式因式分解的方法叫做提公因式法。
am+an=a()\4.找公因式的方法:找公因式的系数:取各项系数绝对值的。
确定公因式的字母:取各项中的相同字母,相同字母的的。
5.把乘法公式从右到左的使用,把某些形式的多项式进行因式分解的方法叫做公式法。
a2-b2= ,a2+2ab+b2= ,a2-2ab+b2= 。
【典型例题】1.仔细阅读下面例题,解答问题:例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n)则x2﹣4x+m=x2+(n+3)x+3n∴.解得:n=﹣7,m=﹣21∴另一个因式为(x ﹣7),m 的值为﹣21仿照以上方法解答下面问题:已知二次三项式2x 2+3x ﹣k 有一个因式是(2x ﹣5),求另一个因式以及k 的值.2.阅读下列因式分解的过程,再回答所提出的问题:1+x+x (x+1)+x (x+1)2=(1+x )[1+x+x (x+1)]=(1+x )2(1+x )=(1+x )3 (1)上述分解因式的方法是 ,共应用了 次.(2)若分解1+x+x (x+1)+x (x+1)2+…+x (x+1)2004,则需应用上述方法 次,结果是 .~(3)分解因式:1+x+x (x+1)+x (x+1)2+…+x (x+1)n (n 为正整数).3.已知乘法公式:a 5+b 5=(a+b )(a 4﹣a 3b+a 2b 2﹣ab 3+b 4);a 5﹣b 5=(a ﹣b )(a 4+a 3b+a 2b 2+ab 3+b 4).利用或者不利用上述公式,分解因式:x 8+x 6+x 4+x 2+1.4、先化简,再求值:()()()()33222491233x y x y x y xy xy xy +-+-+÷-,其中1,23x y ==17.]5、已知323121710x x x --+能被22mx mx +-整除,其商式为5x n +,求m 、n 的值。
:第四章相交线与平行线【知识点归纳】1.同一平面内的两条直线有、、(或平行)三种位置关系。
2.在同一平面内,没有的两条直线叫做平行线。
(记作a直线外一点有直线与这条直线平行。
4.平行于同一条直线的两条直线(平行线的性)。
5.有共同的,其中一角的两边分别是另一角的两边的线,这样的两个角叫做对顶角。
对顶角。
两条直线相交,有2对对顶角,n条直线相交于一点,有n(n-1)对对顶角。
,6.同位角:在“三线八角”中,位置相同的角,在,同一侧的角,是同位角。
7.内错角:在“三线八角”中,夹在两直线,位置角,是内错角。
8.同旁内角:在“三线八角”中,夹在两直线,在第三条直线的角,是同旁内角。
9.平移不改变图形的和,不改变直线的,一个图形和它经过平移所得的图形中,两组对应点的连线(或在同一直线上)。
10.平行线的性质:(1)两直线平行,角相等;(2)直线平行,相等;(3)两直线平行,角互补。
11.平行线的判定:(1)角相等,两直线平行;(2)角相等,两直线平行;(3)角互补,两直线平行。
12.两条直线相交所成的四个角中,有一个角是角时,这两条直线叫做互相垂直,它们的交点叫做。
13.在同一平面内,垂直于同一直线的两条直线。
14.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于。
15.在同一平面内,过一点一条直线与已知直线垂直。
16.直线外一点与直线上各点连接的所有线段中,最短,从直线外一点到这条直线的的长度,叫做点到直线的距离。
17.两条平行线的所有都相等。
两条平行线的公垂线段的叫做两条平行线间的距离。
:1.如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.{2.数学思考:(1)如图1,已知AB∥CD,探究下面图形中∠APC和∠PAB、∠PCD的关系,并证明你的结论推广延伸:(2)①如图2,已知AA1∥BA1,请你猜想∠A1,∠B1,∠B2,∠A2、∠A3的关系,并证明你的猜想;②如图3,已知AA1∥BA n,直接写出∠A1,∠B1,∠B2,∠A2、…∠B n-1、∠A n的关系拓展应用:(3)①如图4所示,若AB∥EF,用含α,β,γ的式子表示x,应为°+α+β-γ°-α-γ+βC.β+γ-αD.α+β+γ②如图5,AB∥CD,且∠AFE=40°,∠FGH=90°,∠HMN=30°,∠CNP=50°,请你根据上述结论直接写出∠GHM的度数是|3.已知,直线AB∥DC,点P为平面上一点,连接AP与CP.(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,求∠APC.(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系,并说明理由.:(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系说明理由.4.已知AM∥CN,点B为平面内一点,AB⊥BC于B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;'5.已知:∠MON=132°,射线OC是∠MON内一条射线,且∠CON+∠MOC=59度.问OM与OC是否垂直,并说明理由.6.一张白纸上有三条直线,已知直线a平行于直线b,直线b平行于直线c且直线a与直线b之间的距离为3厘米,直线b与直线c之间的距离是5厘米,那么直线a与直线c之间的距离是几厘米第五章轴对称图形【知识点归纳】…1.轴对称图形:如果一个图形沿一条直线,直线两侧的部分能够,那么这个图形叫做轴对称图形,这条直线叫做它的。
