晶体学基础第三章-5晶面间距与晶面夹角
X射线衍射原理

二、布拉格方程
❖ 利用X射线研究晶体结构,主要通过X射线在晶体中产生的衍射。 ❖ X射线照射到晶体时,被晶体中电子散射,每个电子都是一个新
的辐射波源,向空间辐射出与入射波同频率的电磁波。 ❖ 把晶体中每个原子都看作一个新的散射波源,它们各自向空间辐
射与入射波同频率的电磁波;这些散射波干涉: 某些方向叠加,可得到衍射线; 某些方向互相抵消,无衍射线。
四、厄瓦尔德图解——布拉格方程的几何图解
r*HKL为反射晶面(HKL)的倒易矢量, r*HKL的起点(倒易原点O*) 为入射线单位矢量S0的终点,S0与(HKL)晶面反射线S的夹角2θ为
.1 定义:晶体点阵中平行于某轴向[uvw]的所有晶面称为[uvw]晶
带(注意和晶面族的区别)。 晶带轴:同一晶带中的。 2.晶带定律
如果某晶面(hkl)属于晶带[u,v,w],必定有 hu+kv+lw=0 (a,b,c)为点阵基矢
证明一:晶带轴r的指向矢量为:r = ua + vb + wc
AB = OB – OA = b/K - a/H r*HKL·AB=(Ha*1+Ka*2+La*3 )·(b/K-a/H)
r*HKL·AB = 0
(二)倒易点阵
(2)倒易点阵与正点阵(HKL)晶面的对应关系
1)一个倒易矢量与一组(HKL)晶面对应,倒易矢量的大小与方向
表达了(HKL)在正点阵中的方位与晶面间距;
在晶轴a、b、c上截距分别为1/h、1/k、1/l。很显然a/h在晶面法线
nhkl上的投影就等于这个晶面的面间距d。即: dhkl=(a/h)·nhkl=(b/k)·nhkl
=(c/l)·nhkl 由右图可知,ABC面的单位法向量可表示 为:
第三章_晶体学基础

十四种空间格子(布拉菲格子)
综合考虑单位平行六面体的划分和附加结点的类型,七个晶系空间格 子的基本类型共有十四种。
三斜晶系:三斜简单格子; 单斜晶系:单斜简单格子,单斜底心格子; 斜方晶系:斜方简单格子,斜方底心格子, (正交) 斜方体心格子,斜方面心格子; 四方晶系:四方简单格子,四方体心格子; 三方晶系:三方简单格子(三方菱面体格子); 六方晶系:六方简单格子; 立方晶系:立方简单格子,立方体心格子, 立方面心格子。
简单P
立方I
立方F
立方晶系:a = b=c
α=β=γ=90°
四方P 四方晶系: a = b≠c
四方I α=β=γ=90°
正交P
正交C 正交晶系:a≠b ≠ c
正交I α=β=γ=90°
正交F
单斜P 单斜晶系:a≠b ≠ c
单斜C α=γ=90° β> 90°
六方H
三方R
三斜P
六方晶系: a = b≠c 三方晶系: a = b=c 三斜晶系:a≠b≠c
故确定的步骤为:
● 选定晶轴X、Y、Z和a、b、c为轴单位;
● 平移晶向(棱)直线过原点;
● 在该直线上任取一结点M,将其投影至X、
。
Y、Z轴得截距OX、OY、OZ;
● 作OX/a:OY/b:OZ/c = u:v:w(最小
整数比);
● 去掉比号,加中括号,[u v w]即为晶
向符号。
某一晶向指数代表一组在
结构基元:组成晶体的离 子、原子或分子。基元内 的原子数等于晶体中原子 的种类数。
晶体结构=空间点阵+结构基元
实际晶体——质点体积忽略——空间点阵——阵点连线——晶格(空间格子)
晶面间距和晶面指数的关系-概述说明以及解释

晶面间距和晶面指数的关系-概述说明以及解释1.引言1.1 概述晶面间距是研究晶体结构和性质的重要参数之一,而晶面指数则是描述晶体晶面排列规律的指标。
晶面间距和晶面指数之间存在着密切的关系。
在晶体中,晶面是由原子或者离子按一定的排列顺序组成的。
晶体中的每个原子或者离子都占据了晶体的一个晶胞,而晶面间距则是指相邻两个晶面之间的距离。
通常情况下,晶面间距可以通过测量晶体的晶胞参数来进行计算。
而晶面指数是一种用来描述晶面排列规律的参数。
晶面指数是用一组整数表示晶面与晶轴或平面之间的交点坐标的比值,它可以反映出晶面在晶体中的位置和排列方式。
根据晶面的倾斜和晶面之间的夹角关系,可以用晶面指数来描述晶体晶面的倾斜程度和晶面之间的空间排列关系。
晶面间距和晶面指数之间存在着一定的关系。
晶面间距与晶面指数的关系可以通过晶体的晶胞参数和晶面的倾斜情况来推导和计算。
晶面间距的计算需要考虑晶体的晶胞参数和晶面的倾斜情况,而晶面指数的计算则依赖于晶面在晶轴或者平面上的交点坐标。
研究晶面间距和晶面指数的关系对于理解晶体的结构和性质具有重要的意义。
通过对晶面间距和晶面指数的研究,可以揭示晶体中原子或离子的排列规律,进而解释晶体的物理和化学性质。
此外,晶面间距和晶面指数还可以用于晶体的鉴定和表征,在材料科学和矿物学等领域有着广泛的应用。
综上所述,本文将重点探讨晶面间距和晶面指数的关系,通过详细介绍晶面间距和晶面指数的定义与计算方法,进而深入研究晶面间距与晶面指数之间的联系和相互影响。
最后,将对晶面间距与晶面指数的关系进行总结,并展望其在晶体研究中的未来应用前景。
文章结构部分的内容应该包括对整篇文章的组织结构进行说明,列出各个章节的标题和内容简介。
下面是文章结构部分的一个例子:1.2 文章结构本文将以晶面间距和晶面指数之间的关系为主题展开讨论。
文章主要分为以下几个部分:2.正文2.1 晶面间距的定义与计算方法本部分将介绍晶面间距的定义以及如何计算晶面间距。
04-05 晶体几何学基础概述

晶体结构
萤石结构( CaF2 )
氯化钠结构(NaCl)
晶体结构
辉钼矿的化学成分:
MoS2,Mo 59.94%,S 40.06%;
辉钼矿的特征:
铅灰色,金属光泽, 硬度低,底面解理极 完全,比重大,光泽 强。
晶体结构
石墨的晶体结构
C60的晶体结构
金刚石的晶体结构
晶体结构X衍射图谱
石墨
金刚石
C60
b c c a * * a b (b c )(c a ) (c c )(b a ) V V cos * = * * = = abc2 sin a sin b | a b | bc sin a ca sin b V V cosa cos b cos = 同样可求 得α *, β *。 sin a sin b
a=bc, a=b==90
简单三角
四方 六角 立方
简单四方 体心四方
a=b, 六角 b==90, a=120 a=b=c, a=b==90 简单立方,体心立方 面心立方
七大晶系所要求最低的对称性
晶系 三斜 最低特征对称素 无对称素 晶胞形状 任意的平行六面体
单斜 正交 三角 四方 六角 立方
a = = d(200) 2 2 2 2 2 0 0
\ (200)
(110)
a
intersects with
a d(110) = 2 2 2 = 2 1 1 0
\ (110)
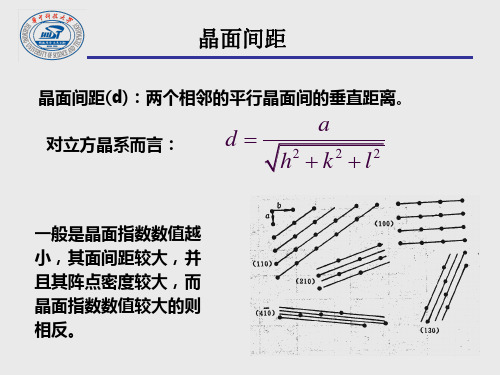
晶面间距
晶面间距(d)公式:
立方晶系:
1 d hkl
2
h k l = 2 a
2 2
2
h k l 四方晶系: = 2 2 2 a c d hkl 2 2 2 1 h k l 正交晶系: = 2 2 2 2 b c d hkl 1
晶体学基础3

晶体学基础31.5.2倒格子的性质倒格子具有以下基本性质:(1)以倒格子基矢b 1,b 2,b 3为棱边构成的平行六面体称为倒格子原胞,其体积为v *。
()31232*()cv v π=⋅⨯=b b b …………………(1-5-3)(2)倒格矢112233h h h h =++G b b b 和正格子空间中面指数为(h 1h 2h 3)的晶面族正交,即G h 沿晶面族的法线方向。
我们知道,晶面族中最靠近原点的晶面ABC 在123,,a a a 上的截距分别为312123,,a a a h h h ,如图1-18所示,易写出矢量CA 和CB :31133223h h h h =-=-=-=-a a CA OA OC a a CB OB OC ………………………………………………………(1-5-4)矢量CA 和CB 都在ABC 面上,因此,只要证明00h h ⋅=⎧⎨⋅=⎩G CA G CB ,则就能说明112233h h h h =++G b b b 与面指数为(h 1h 2h 3)的晶面族正交。
实际上,利用关系式(1-5-2),有31112233133211223323()()0,()()0.h h h h h h h h h h h h ⋅=++⋅-=⋅=++⋅-=a a G CA b b b a a G CB b b b …………………………………………(1-5-5)(3)晶面族(h 1h 2h 3)的面间距d h 与倒格矢G h 的模成反比,关系为2h hd π=G 。
图1-18中ABC 面就是晶面族(h 1h 2h 3)中距原点最近的晶面,所以这族晶面的面间距d h 就等于原点到面ABC 的距离,而之族晶面的法线方向即为G h 的方向,其面间距为1112233111112233()2h h h hh h h d h h h h h π⋅++=⋅==++G a b b b a G b b b G 。
晶体几何学基础
倒易点阵中,晶面(uvw)*的面间距duvw*是正点阵中同 名矢量长度ruvw的倒数,即duvw*=1/ruvw。
课堂习题
1. 试求出立方晶系[111]晶带的倒易点阵平面。
解: 利用晶带定律:HU+KV+LW=0 ⅰ,用试探法,根椐晶带定律找出不共线的的两个倒易点。
倒易点阵的作法
首先求基矢,然后利用基矢绘图。 由a,b,c,α,β,γ求a*,b*,c*,α*,β*,γ*进而求倒易点阵.
同样可求 得b*,c*。
a*
b*
|
a*
||
b*
|
cos
*
cos *
|aa**bb**|
b
c
c
a
VV
bc sin ca sin
代入晶带定律检证 110 101 ⅱ,利用公式计算两倒易点对应倒易矢量的长度和夹角。
| r* | H 2 K 2 L2 2 | r* |
110
a
a
101
cos
H1H 2 K1K 2 L1L2
111 0 01 1
H
2 1
K12
L12
H
2 2
K
正空间
晶带与倒易面
ruv w
(h3k3l3 )
(h2k2l2 )
晶带正空间 与倒空间对 应关系图
倒空间
a2
1 d hk l 2
h2 k2 a2
l2 c2
1 d hk l 2
h2 a2
晶体学基础

0.25A-1 020 120 220
b (110)
010 110 210
(100) b* H110
H 210
(210)
100
c
a
c* 000
a*
200
晶体点阵
倒易点阵
立方晶系晶体及其倒易点阵
第三章 X射线衍射方向
自伦琴发出X射线后,许多物理学家都在积极地研究和探索,1905年 和1909年,巴克拉曾先后发现X射线的偏振现象,但对X射线究竟是一 种电磁波还是微粒辐射,仍不清楚。1912年德国物理学家劳厄发现了 X射线通过晶体时产生衍射现象,证明了X射线的波动性和晶体内部结 构的周期性,发表了《X射线的干涉现象》一文。
cosa0 H cos0 K
衍射线
1' X
1
显然,当X射线照射二 维原子网时,X、Y晶轴 方向上的那些同轴的圆 锥面上的衍射线要能够 加强,只有同时满足劳 厄第一和第二方程,才 能发生衍射。
衍射线只能出现在沿X晶轴方向及Y晶轴方向的两系列 圆锥簇的交线上。如果照相的底片平行于原子网,圆 锥在底片上的迹线为双曲线。每对双曲线的交点即为 衍射斑点,也相当于圆锥的交线在底片上的投影。不 同的H,K值,可得到不同的斑点。
劳厄的文章发表不久,就引起英国布拉格父子的关注,他们都是X射 线微粒论者,年轻的小布拉格经过反复研究,成功地解释了劳厄的实 验事实。他以更简结的方式,清楚地解释了X射线晶体衍射的形成, 并提出著名的布拉格公式:nX=2dsino这一结果不仅证明了小布拉格的 解释的正确性,更重要的是证明了能够用X射线来获取关于晶体结构 的信息。老布拉格则于1913年元月设计出第一台X射线分光计,并利 用这台仪器,发现了特征X射线。小布拉格在用特征X射线与其父亲合 作,成功地测定出了金刚石的晶体结构,并用劳厄法进行了验证。金 刚石结构的测定完美地说明了化学家长期以来认为的碳原子的四个键 按正四面体形状排列的结论。这对尚处于新生阶段的X射线晶体学来 说用于分析晶体结构的有效性,使其开始为物理学家和化学家普遍接 受。
第3章 晶体学基础 - 晶体结构、晶向、晶面

LOGO
21
LOGO
1.动画--晶面指数的确定方法
22
2.晶面指数特点与规律:
LOGO
(1)与原点位置无关;每一晶面符号对应一组相互平行的晶面。 晶面符号代表在原点同一侧的一组相互平行且无限大的 晶面,而不是某一晶面。 (2) 若晶面指数相同,但正负符号相反,则两晶面是以点为 对称中心,且相互平行的晶面。如(110)和(110)互 相平行。
2014-9-26 此处添加公司信息 3
3.1.1 晶体与非晶体
LOGO
准晶:是一种介于晶体和非晶体之间的固体。 准晶具有完全有序的结构,然而又不具有晶 体所应有的平移对称性,因而可以具有晶体所不允 许的宏观对称性。准晶是具有准周期平移格子构造 的固体,其中的原子常呈定向有序排列,但不作周 期性平移重复,其对称要素包含与晶体空间格子不 相容的对称(如5次对称轴) 瑞典皇家科学院将2011年诺贝尔化学奖授予 以色列科学家达尼埃尔· 谢赫特曼,以表彰他“发 现了准晶”这一突出贡献。准晶的发现从根本上改 变了以往化学家对物体的构想。
Total: 24
29
LOGO
{123} (123) ( 1 23) (123) (12 3) (132) ( 1 32) (1 3 2) (132) (231) ( 231) (2 3 1) (23 1 ) (213) ( 213) (2 1 3) (21 3) (312) ( 3 12) (3 1 2) (312) (321) ( 3 21) (321) (32 1 )
28
立方晶系: {111}=?
LOGO
Total:? 立方晶系:
{112} (112) ( 1 12) (1 1 2) (112) (121) ( 1 21) (121) (12 1 ) (211) ( 211) (2 1 1) (21 1 )
