材料力学习题第六章应力状态分析答案详解(试题学习)
材料力学06(第六章 弯曲应力)分析
F / 4 2 103 mm 134 mm
30 MPa 5493104 mm4
F 24.6 kN
因此梁的强度由截面B上的最大拉应力控制
[F] 19.2 kN
§6-3 梁横截面上的切应力•梁的切应力强度条件
Ⅰ、梁横截面上的切应力
分离体的平衡
横截面上切应力 分布规律的假设
横截面上弯曲切 应力的计算公式
二.工字形截面梁 1、腹板上的切应力
h
d
y
d
O
y b
O
' A*
y dA
FS
S
* z
Izd
S
* z
bd
2
h
d
d 2
h 2
d
2
y2
腹板与翼缘交界处
max
min
FS Izd
bd
h d
max O
中性轴处
max
FS
S
* z,m
ax
Izd
y
min
FS
bd
h
d
d
h
d
2
I z d 2
160 MPa 148 MPa
2
Ⅲ 梁的正应力强度条件
max 材料的许用弯曲正应力
中性轴为横截面对称轴的等直梁
M max
Wz
拉、压强度不相等的铸铁等脆性材料制成的梁
为充分发挥材料的强度，最合理的设计为
t,max
M max yt,max Iz
[
t]
c,max
M max yc,max Iz
Myc,max Iz
典型截面的惯性矩与抗弯截面系数 ( d D)
b
材料力学(金忠谋)第六版答案第06章.doc
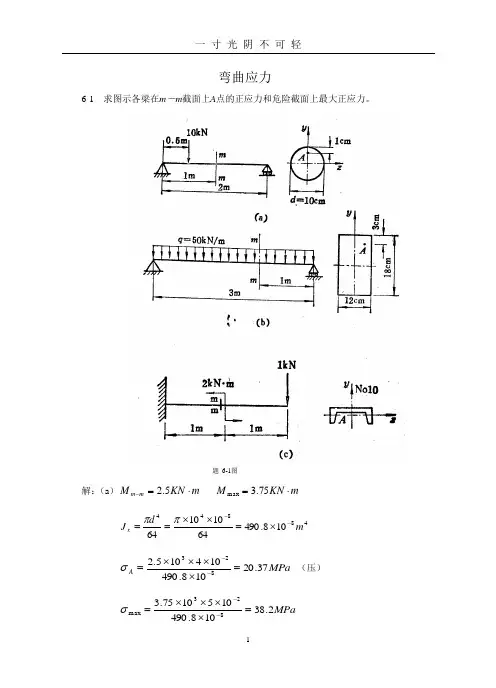
弯曲应力6-1 求图示各梁在m－m截面上A点的正应力和危险截面上最大正应力。
题6-1图解：（a）mKNMmm⋅=-5.2mKNM⋅=75.3max48844108.49064101064mdJx--⨯=⨯⨯==ππMPaA37.20108.490104105.2823=⨯⨯⨯⨯=--σ（压）MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ（b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。
解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4，h 1=9.65cm ，h 2=15.35cm 。
材料力学习题第六章应力状态分析答案详解
（2）塑像材料： 故材料失效
2、已知某构件危险点的应力状态如图， 。试校核其强度。
（用第三强度理论）
解答：
在x，y平面内
3、钢制构件，已知危险点单元体如图所示，材料的 ，按第三强度理论求构件的工作安全因数。
解答：
在xz平面内：
4、工字型截面钢梁， ， ，危险截面上 ， 。校核梁的正应力及相当应力强度。（用第三强度理论）
13、空心圆轴外径D＝8cm，内径d＝6cm，两端受外力偶矩m作用。测得表面上一点沿 方向的线应变 。材料弹性模量E＝2×105MPa，泊松比v＝0.3，求外力偶矩m。
解答：
纯剪应力状态，则：
14、一个处于二向应力状态下的单元体，材料E＝200GPa，v＝0.3， ， 。求最大切应变 。
解答：
15、圆轴直径为d，材料的弹性模量为E，泊松比为v，为了测得轴端的力偶m之值，但只有一枚电阻片。试设计电阻片粘贴的位置和方向；若按照你所定的位置和方向，已测得线应变为 ，则m＝？
4、危险点接近于三向均匀受拉的塑性材料，应选用第一（最大拉应力）强度理论进行计算，因为此时材料的破坏形式为脆性断裂。
三、计算题
1、试对给定应力状态： 、 、 ，确定材料是否失效：
（1）对脆性材料用最大拉应力理论，若已知材料 ；
（2）对塑性材料用最大切应力理论及形状改变比能理论，若已知材料 。
解答：
xy平面内：
解答：
确定
所以 确定
3、图示单元体，求：（1）指定斜截面上的应力：（2）主应力大小，并将主平面标在单元体图上。
解答：
确定
所以 确定
4、用解析法求图示单元体ab面上的应力（ ），并求 及主应力。
材料力学课后标准答案
解：取轴向长为 的管分析：微元 上，作用力为
向分量 ，积分得
则： ，而
则：
题6-12图题6-13图
6-13长输水管受内压 ，管的内径为 ， ， ，用第四强度理论计算壁厚。（提示：可设管的轴向应变为零。）
解： ，数据代入，得：
，
所以
现已知
,
得
题6-5图
题6-6图题6-7图
6-6图示简支梁为 工字梁， ， 。 点所在截面在集中力 的左侧，且无限接近 力作用的截面。试求： 点在指定斜截面上的应力； 点的主应力及主平面位置（用单元体表示）。
解： 所处截面上弯矩、剪力：
，
查型钢表后， 点以下表面对中性轴静矩：
，
同理，积分得
所以， 处转角为 ，为顺时针方向； 处挠度为 ，为竖直向下。
8-6试求图示各刚架 点的竖直位移，已知刚架各杆的 相等。
解： 段： ； 段上
由卡氏定理， 处的竖直位移
分段带入后面积分：
为正值，则与 同向，竖直向下
分析可知， 处已经作用有竖直方向的力，为了能利用卡氏定理解题， 处和竖杆中间处的 分别为
（压）， （拉）
进而求得 （拉），由
求得：
8-3计算图示各杆件结构的变形能。
题8-3图
解： 首先求解 处的约束反力为
弯矩方程为：
则
分段积分：
解： 以逆时针方向为正，
，积分得
8-4试求图示各梁的 点的挠度的转角。
题8-4图
解： 以 点为 轴起点，结构的弯矩方程为：
则：
得
撤去 和 ，在 处作用逆时针向
材料力学典型例题及解析7.应力应变状态典型习题解析
应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。
b = 60 mm ，h = 100 mm 。
解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。
材料力学——第6章(应力状态分析及强度理论)
t min
2t x tan 2 0 = s x s y
t max s max s min = R半 径 = 2 t min
s x s y 2 2 （ ） t x 2
25
[例6-4]求 ⑴图示单元体α =300 斜截面上的应力 ⑵主应力、主平面（单位：MPa）。
40
§6–1 应力状态概述
§6-2 平面应力状态分析
§6-3 三向应力状态分析 §6-4 广义胡克定律 §6-5 工程中常用的四种强度理论
1
拉压
扭转
弯曲
y
y
y
C
s max 压 s max 拉 s max
截面 应力 危险点
应力状态
C
o
FN
s=smax smax
MT
t max
M
t max
2
S平面
n
F
1
sx 面上的应力(s ，t )
tx
y x t n D( s , t C O B(sy ,ty) 2 O
面的法线
两面夹角 两半径夹角2 ； 且转向一致。 x
A(sx ,tx)
s
23
ty
sy s t
n
t D = DC sin[ 180 ( 2 0 2 )]
O
sx sy
图2
ty
px t
同理： t = p x sin p y cos
= s x cos t y sin sin t y cos s y sin cos
经简化 得
s x s y t = sin 2 t x cos 2 2
s
sx sy
应力应变分析习题解答
402
94.72 5.28
MPa
习题解答
根据大小来确定主应力的次序如下：
1 94.72MPa, 2 50MPa, 3 5.28MPa
于是该单元体的形状改变比能为：
uf
1 6E
(1
2)2
(2
3 ) 2
(3
1)2
1 0.3106
6 200103
[(94.72
50)2
(50
5.28)2
y
m x
n
y
y
x
n
x
习题解答
x
2
y
x
2
y
cos2
x
sin
2
x
2
y
sin
2
x
cos2
A
2
Bo
x
y
习题解答
3、各单元体各面上的应力如图所示（应力单位MPa）。试利用应力圆： 1）求指定截面上的应力； 2）求主应力的数值； 3）在单元体上绘出主平面的位置及主应力的方向。
30
30
30
60o
30
解：1）由以下应力公式 可得
y 30MPa
解：要想求单元体的形状改变比能，必须先求出
该单元体的三个主应力，由右图可知 z 50
为该单元体的一主应力，于是可只计算垂直于z轴的
70MPa
平面上的主应力。由平面应力公式可得
m a x
min
x
y 2
x
2
y
2
2x
40MPa x z 50MPa
70 30 2
70 30 2 2
2
y
2
2x
70 30 2
材料力学答案解析单辉祖版全部答案解析
* *第二章轴向拉压应力与材料的力学性能2-1试画图示各杆的轴力图。
题2-1图解：各杆的轴力图如图2-1所示。
图2-12-2试画图示各杆的轴力图，并指出轴力的最大值。
图a与b所示分布载荷均沿杆轴均匀分布，集度为q。
题2-2图(a)解：由图2-2a(1)可知，qxqaxF-=2)(N轴力图如图2-2a(2)所示，qaF2m ax,N=图2-2a (b)解：由图2-2b(2)可知，qaF=Rqa F x F ==R 1N )(22R 2N 2)()(qx qa a x q F x F -=--=轴力图如图2-2b(2)所示，qa F =m ax N,图2-2b2-3 图示轴向受拉等截面杆，横截面面积A =500mm 2，载荷F =50kN 。
试求图示斜截面m -m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。
题2-3图解：该拉杆横截面上的正应力为100MPa Pa 1000.1m10500N10508263=⨯=⨯⨯==－A F σ 斜截面m -m 的方位角， 50-=α故有MPa 3.41)50(cos MPa 100cos 22=-⋅== ασσαMPa 2.49)100sin(MPa 502sin 2-=-⋅== αστα杆内的最大正应力与最大切应力分别为MPa 100max ==σσMPa 502max ==στ 2-5 某材料的应力-应变曲线如图所示，图中还同时画出了低应变区的详图。
试确定材料的弹性模量E 、比例极限p σ、屈服极限s σ、强度极限b σ与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。
题2-5解：由题图可以近似确定所求各量。
220GPa Pa 102200.001Pa 10220ΔΔ96=⨯=⨯≈=εσE MPa 220p ≈σ, MPa 240s ≈σMPa 440b ≈σ, %7.29≈δ该材料属于塑性材料。
2-7 一圆截面杆，材料的应力-应变曲线如题2-6图所示。
材料力学习题应力状态和强度理论
应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示，则三者间的关系为（ ）。
A ．完全等价B ．完全不等价C ．图(b )、图(c )等价D ．图(a )、图(c )等价题1图2. 已知应力情况如图所示，则图示斜截面上的应力为（ ）。
（应力单位为 MPa)。
A ．70-=ασ，30-=ατB ．0=ασ，30=ατC ．70-=ασ，30=ατD ．0=ασ，30-=ατ3. 在纯剪切应力状态中，其余任意两相互垂直截面上的 正应力，必定是（ ）。
A ．均为正值B ．一为正值一为负值C ．均为负值 题2图D ．均为零值4. 单元体的应力状态如图所示，由x 轴至1σ方向的夹角为（ ）。
A ．︒5.13 B ．︒-5.76 C ．︒5.76 D ．︒-5.13题4图 题5图5. 单元体的应力状态如图所示，则主应力1σ、2σ分别为（ ）。
(应力单位MPa). -33-A ．901=σ，102-=σB ．1001=σ，102-=σC ．901=σ，02=σD ．1001=σ，02=σ 6. 如图6所示单元体最大剪应力max τ为（ ）。
A ．100 MPaB ．50 MPaC ．25 MPaD ．0题6图 题7图7. 单元体如图所示，关于其主应力有下列四种答案，正确的是（ ）。
A ．1σ＞2σ，03=σ B ．3σ＜2σ＜0，03=σ01=σ C ．1σ＞0，2σ= 0，3σ＜0，1σ＜3σ D ．1σ＞0，2σ= 0，3σ＜0，1σ＞3σ8. 已知应力圆如图7-22所示，图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力，则与应力圆所对应的单元体为( )。
A ．图(a )B ．图(b )C ．图(c )D ．图(d )题8图9. 在图示四种应力状态中，其应力圆具有相同的圆心和相同的半径是（ ）。
-34-题9图A ．图(a )、图(d )B ．图(b )、图(c )C ．图(a )、图(b )、图(c ) 、图(d )D ．图(a )、图(d )、图(b )、图(c )10. 如图所示，较大体积的钢块上开有一贯穿的槽，槽内嵌入一铝质立方体，铝块受到均布压力P 作用，假设钢块不变形，铝块处于（ ）。
工程力学-材料力学之应力应变状态分析
求：（1）A点处的主应变 1， 2 ， 3
（2）A点处的线应变 x ， y ， z
F1 b A F2 z b=50mm h=100mm
Hale Waihona Puke 19F2al
解：梁为拉伸与弯曲的组合变形. A点有拉伸引起的正应力
和弯曲引起的切应力.
铜块横截面上的压应力mpa3010300analysiessst155mpa铜块的主应力为mpampa30最大切应力mpa2510951010034analysiessst例题11一直径d20mm的实心圆轴在轴的的两端加力矩m126n45方向的应变analysiessstanalysiessst外径d60mm的薄壁圆筒在表面上k点与其轴线成45y两方向分别贴上应变片然后在圆筒两端作用矩为的扭转力偶如图所示已知圆筒材料的弹性常数为若该圆筒的变形在弹性范围内且analysiessst从圆筒表面k点处取出单元体其各面上的应力分量如图所示可求得mpa80maxmpa80maxanalysiessstmaxmaxmax10拉应变圆筒表面上k点处沿径向z轴的应变和圆筒中任一点该点到圆筒横截面中心的距离为maxmax因此该圆筒变形后的厚度并无变化仍然为t10mmanalysiessstb50mmh100mm例题13已知矩形外伸梁受力f作用
在任意形式的应力状态下, 各向同性材料内一点处的体
积应变与通过该点的任意三个相互垂直的平面上的正应力之
和成正比, 而与切应力无关.
11
例题10 边长 a = 0.1m 的铜立方块，无间隙地放入体积较大， 变形可略去
不计的钢凹槽中, 如图所示. 已知铜的弹性模量 E=100GPa，泊松比 =0.34， 当受到F=300kN 的均布压力作用时，求该铜块的主应力、体积应变以及最
材料力学第六版答案第06章
材料力学(金忠谋)第六版答案第06章(总27页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2弯曲应力6-1 求图示各梁在m －m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解：（a ）m KN M m m ⋅=-5.2 m KN M ⋅=75.3max 48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）3 MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ （b ）m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ （压） MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ （c ）m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压） MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。
4解：)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
材料力学习题(1)2-6章
材料力学习题(1)2-6章材料力学习题第2章2-1 试求出图示各杆Ⅰ—Ⅰ截面上的内力。
2-2图示矩形截面杆，横截面上正应力沿截面高度线性分布，截面顶边各点处的正应力均为MPa100max=σ，底边各点处的正应力均为零。
杆件横截面上存在何种内力分量，并确定其大小（C点为截面形心）。
2-3 试指出图示各单元体表示哪种应力状态。
2-4 已知应力状态如图所示（应力单位为MPa），试用解析法计算图中指定截面的应力。
2-5 试作应力圆来确定习题2-4图中指定截面的应力。
2-6已知应力状态如图所示（应力单位为MPa ），试用解析法求：（1）主应力及主方向；（2）主切应力及主切平面；（3）最大切应力。
2-7 已知应力状态如习题2-6图所示，试作应力圆来确定：（1）主应力及主方向； （2）主切应力及主切平面；（3）最大切应力。
2-8已知构件内某点处的应力状态为两种应力状态的叠加结果，试求叠加后所得 应力状态的主应力、主切应力。
2-9图示双向拉应力状态，σσσ==y x 。
试证明任一斜截面上的正应力均等于σ，而切应力为零。
2-10 已知K 点处为二向应力状态，过K 点两个截面上的应力如图所示（应力单位为MPa ）。
试分别用解析法与图解法确定该点的主应力。
2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。
试确定未知的应力分量y y x xy '''σττ、、的大小与方向。
2-12 图示受力板件，试证明尖角A 处各截面的正应力与切应力均为零。
2-13 已知应力状态如图所示（单位为MPa ），试求其主应力及第一、第二、第三不变量321I I I 、、。
2-14 已知应力状态如图所示（单位为MPa ），试画三向应力圆，并求主应力、最大正应力与最大切应力。
第3章3-1 已知某点的位移分量u = A ， v = Bx +Cy +Dz ， w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。
材料力学习题 应力状态分析答案详解
13、在图示梁的A点测得梁在弹性范围内的纵横方向的线应变 、 后，所能算出的材料常数有（ D ）。
（A）只有E；（B）只有v；（C）只有G；（D）E、v和G均可算出。
解析：中间段为纯弯曲，A点为单向拉伸，
则
14、纯剪应力状态下，各向同性材料单元体的体积改变有四种答案，正确答案是（ C ）。
解答：
确定 ， 确定
6、 物体内某一点，载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图（a）和（b）所示。试求两载荷系统同时作用时（仍处于弹性小变形）的主单元体和主应力。
解答：
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值，并画出三向应力状态的应力圆。
解答：
8、图示单元体，已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答：
确定
确定
2、已知应力状态如图。试求主应力及其方向角，并确定最大切应力值。
解答：
确定
所以 确定
3、图示单元体，求：（1）指定斜截面上的应力：（2）主应力大小，并将主平面标在单元体图上。
解答：
确定
所以 确定
4、用解析法求图示单元体ab面上的应力（ ），并求 及主应力。
解答：
5、试求图示单元体主应力及最大切应力，并将主平面在单元体上标出。
由第三强度理论 安全
10、直径为20mm的圆截面折杆受力情况如图所示，已知：F＝0.2kN，材料的许用应力为 。试用第三强度理论确定折杆的长度a的许用值。
解答：
在危险截面A上危险点在七上下边缘
由第三强度理论
取
11、AB、CD两杆互相垂直，在水平面内，C点的集中力2F及D点的集中力F与刚架平面垂直。已知F＝20kN，l＝1m，各杆直径相同d＝10cm， 。试按最大切应力强度理论校核强度。
长沙理工大学材料力学练习册答案1-5章
材料力学 分析与思考题集第一章 绪论和基本概念一、选择题1.关于确定截面内力的截面法的适用范围，有下列四种说法：【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。
2.关于下列结论的正确性：【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。
】3.下列结论中那个是正确的：【B.若物体各点均无位移，则该物体必定无变形】4.根据各向同性假设，可认为构件的下列量中的某一种量在各方向都相同：【B 材料的弹性常数】5.根据均匀性假设，可认为构件的下列量中的某个量在各点处都相同：【C 材料的弹性常数】6.关于下列结论：【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形，则物体内各点的应变均为零】7.单元体受力后，变形如图虚线所示，则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 ， 均匀性假设 和 各向同性假设 。
2.构件的承载能力包括强度、刚度和稳定性三个方面。
3.图示结构中，杆1发生轴向拉伸变形，杆2发生轴向压缩变形，杆3发生弯曲变形。
4.图示为构件内A 点处取出的单元体，构件受力后单元体的位置为虚线表示，则称dx du /为A 点沿x 方向的线应变，dy dv /为【A 点沿y 方向的线应变】，)(21a a +为【A 在xy 平面内的角应变】。
5.认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。
根据这一假设，构件的应力、应变和位移就可以用坐标的连续性函数来表示。
6.在拉（压）杆斜截面上某点处分布内力集度称为应力(或全应力），它沿着截面法线方向的分量称为正应力，而沿截面切线方向的分量称为切应力。
第二章 杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示，p 为径向压强，其n-n 截面上的内力N F 有四个答案：【B 2/pD 】2.梁的内力符号与坐标系的关系是：【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称（如图）。
材料力学习题应力状态分析答案详解
1、图示应力状态，按第三强度理论的强度条件为 。
（注： ）
解答：
2、第三强度理论和第四强度理论的相当应力分别为 及 ，对于纯剪切应力状态，恒有 / ＝ 。
解答：纯剪应力状态
3、一般情况下，材料的塑性破坏可选用最大剪应力或形状改变能密度强度理论；而材料的脆性破坏则选用最大拉应力或最大伸长线应变强度理论（要求写出强度理论的具体名称）。
解答：
17、一体积为10×10×10mm3的立方铝块，将其放入宽为10mm的刚性槽中，已知v（铝）=0.33，求铝块的三个主应力。
解答：
18、外径为D、内径为d的空心圆轴受扭转时，若利用一电阻应变片作为测力片，用补偿块作为温度补偿，采用半桥接线。问：（1）此测力电阻片如何粘贴可测出扭矩；（2）圆轴材料的E、v均为已知， 为测得的应变值，写出扭矩计算式。
解答：
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值，并画出三向应力状态的应力圆。
解答：
8、图示单元体，已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答：
9、试确定图示单元体的最大切应力，以及图示斜截面上的正应力和切应力。
解答：
10、已知受力构件某处的 ， ， ，材料的E＝200GPa，v＝0.3。试求该点处的 、 。
解答：在危险截面A上危险点在七上下边缘
由第三强度理论
不安全
12、图示齿轮传动轴内电机带动，作用在齿轮上的力如图示，已知轴的直径d＝30mm，P＝0.8kN，Q＝2kN，l＝50mm，齿轮节圆直径D＝200mm。试用第三强度理论校核轴的强度。已知轴的 。
13、图示传动轴，皮带轮Ⅰ直径D1＝80cm，皮带轮Ⅱ直径D2＝40cm，已知轴的许用应力 。试以第四强度理论设计轴的直径d，并指出危险截面位置，画出危险点的应力状态。
材料力学习题解
习 题第六章 拉伸与压缩变形6-1 试求图6-32所示各杆横截面1-1、2-2、3-3上的轴力，并画出轴力图。
(a)解：01=N F , KN F N 22= , KN F N 33-=(b)解：KN F N 501=, KN F N 102= , KN F N 203-=(c)解：KN F N 21=, KN F N 62=(d)解：01=N F , F F N 42= , F F N 33=6-2 如图6-33所示，一正中开槽的直杆，承受轴向载荷F=40kN 的作用。
已知h=30mm ，h 0=10mm b=25mm 。
试求杆内1—1、2—2截面上的应力。
解：（1）求各截面的轴力：KN F F F N N 4021-=-==（压力）（2）求各截面的面积：217503025.mm h b A =⨯==202500)1030(25)(mm h h b A =-⨯=-=（3）求各截面上的应力：MPa A F N 3.5375010403111=⨯==σ（压应力）MPa A F N 8050010403222=⨯==σ（压应力）6-3 如图6-34所示支架，在节点B 处悬挂一重量G=20kN 的重物，杆AB 及BC 均为圆截面铅制件。
已知杆AB 的直径为d 1=20mm ,杆BC 的直径为d 2=40mm ，杆的许用应力[σ]=160MPa 。
试校核支架的强度。
解：（1）求两杆内力用截面法，将AB 、BC 杆截开，AB 杆内力为1N F ，BC 杆内力为2N F ，取B 为研究对象，由KN G G F N 40230sin 02===（压力） KN F F N N 64.34866.04030cos 021=⨯=⋅=（拉力）（2）求两杆横截面面积2221131442014.34mm d A =⨯=⋅=π 22222125644014.34mm d A =⨯=⋅=π （3）求两杆应力MPa A F N 1103141064.343111=⨯==σ（拉应力） MPa A F N 8.31125610403222=⨯==σ（压应力） （4）校核两杆强度因1σ＜[]σ ， 2σ＜[]σ所以两杆强度均足够。
材料力学 应力状态和强度理论答案
7-1(7-3) 一拉杆由两段杆沿m-n面胶合而成。
由于实用的原因，图中的角限于范围内。
作为“假定计算”，对胶合缝作强度计算时可以把其上的正应力和切应力分别与相应的许用应力比较。
现设胶合缝的许用切应力为许用拉应力的3/4，且这一拉杆的强度由胶合缝的强度控制。
为了使杆能承受最大的荷载F，试问角的值应取多大？解：按正应力强度条件求得的荷载以表示：按切应力强度条件求得的荷载以表示，则即：当时，，，时，，，时，，时，，由、随而变化的曲线图中得出，当时，杆件承受的荷载最大，。
若按胶合缝的达到的同时，亦达到的条件计算则即：，则故此时杆件承受的荷载，并不是杆能承受的最大荷载。
返回7-2(7-7)试用应力圆的几何关系求图示悬臂梁距离自由端为0.72m的截面上，在顶面以下40mm的一点处的最大及最小主应力，并求最大主应力与x轴之间的夹角。
解：=由应力圆得返回7-3(7-8)各单元体面上的应力如图所示。
试利用应力圆的几何关系求：（1）指定截面上的应力；（2）主应力的数值；（3）在单元体上绘出主平面的位置及主应力的方向。
解：（a），，，，（b），，，，（c）, , ,（d），，，，，返回7-4(7-9) 各单元体如图所示。
试利用应力圆的几何关系求：（1）主应力的数值；（2）在单元体上绘出主平面的位置及主应力的方向。
解：（a），，，（b），，，（c），，，（d），，，返回7-5(7-10)已知平面应力状态下某点处的两个截面上的应力如图所示。
试利用应力圆求该点处的主应力值和主平面方位，并求出两截面间的夹角值。
解：由已知按比例作图中A，B两点，作AB的垂直平分线交轴于点C，以C为圆心，CA或CB为半径作圆，得（或由得半径）（1）主应力（2）主方向角（3）两截面间夹角：返回7-6(7-13) 在一块钢板上先画上直径的圆，然后在板上加上应力，如图所示。
试问所画的圆将变成何种图形？并计算其尺寸。
已知钢板的弹性常数E=206GPa，=0.28。
材料力学答案第六章
第六弯曲应力第六章答案6.1钢丝直径d=0.4mm, 弹性模量E=200GPa, 若将钢丝弯成直径D=400mm 的圆弧时，试求钢丝横截面上的最大弯曲正应力。
（200MPa ） 解：钢丝的弯矩和中性层曲率半径之间的关系为：EIM =ρ1则： ρEIM =，由弯曲正应力公式得ρσmaxmax My ==ρmaxEy ，钢丝弯成圆弧后，产生的弯曲变形，其中性层的曲率半径22Dd D ≈+=ρ 2)2(maxD dE =σ==D Ed MPa 2004004.0102003=⨯⨯6.2 矩形截面梁如图所示。
b = 8cm, h =12cm, 试求危险截面上a 、c 、d 三点的弯曲正应力。
（20.8MPa, 10.4MPa, 0） 解：由平衡方程0)(=∑F M A得到： KN F F B A 44221=⨯⨯== 危险截面在梁的中点处：KNm ql M 442818122max =⨯⨯==I z =1212h b ⨯⨯=44310115212080121mm ⨯=⨯⨯MP a I My MPa I MyI My z d d z c c za a 83.201011526010442.101011523010404646=⨯⨯⨯===⨯⨯⨯====σσσA F BF s F MM机械土木6.3 从直径为d 的圆木中截取一矩形截面梁，试根据强度观点求出所截取的矩形截面的最合理的高h 和宽b 。
(h=d 36, b=d 33) 解：最大弯曲正应力：zz W My I M m a x m a x m a x m a x ==σ h/b 的最佳值应应使梁的抗弯截面系数为最大。
抗弯截面系数： )(61)(616132222b b d b d b bh W -=-==为b 为自变量的函数。
由 06322=-=b d dt dW 36 333222db d h d d b =-===6.4 图示两根简支梁，其跨度、荷载及截面面积都相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第6章 应力状态分析
一、选择题
1、对于图示各点应力状态，属于单向应力状态的是（A ）。
a
20 20
20
b
（MPa ）
20
d
c
（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点 。
2、在平面应力状态下，对于任意两斜截面上的正应力αβσσ=成立的充分必要条件，有下列四种答案，正确答案是（ B ）。
（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。
3、已知单元体AB 、BC 面上只作用有切应力τ，现关于AC 面上应力有下列四种答案，正确答案是（ C ）。
B
τ
A
τ
030
（A ）AC AC /2,0ττσ==； （B ）AC AC /2,3/2ττστ==； （C ）AC AC /2,3/2ττστ==-；（D ）AC AC /2,3/2ττστ=-=。
4、矩形截面简支梁受力如图（a ）所示，横截面上各点的应力状态如图（b ）所示。
关于它们的正确性，现有四种答案，正确答案是（ D ）。
2
1 3
4
5
(b)
F
a
F
a
1
2 3 4
5
(a)
（A ）点1、2的应力状态是正确的；（B ）点2、3的应力状态是正确的； （C ）点3、4的应力状态是正确的；（D ）点1、5的应力状态是正确的。
5、对于图示三种应力状态（a ）、（b ）、（c ）之间的关系，有下列四种答案，正确答案是（ D ）。
τ
(a)
στ=στ=
045(b)
στ=-
στ= 045(c)
（A ）三种应力状态均相同；（B ）三种应力状态均不同； （C ）（b ）和（c ）相同； （D ）（a ）和（c ）相同；
6、关于图示主应力单元体的最大切应力作用面有下列四种答案，正确答案是（ B ）。
1σ
(A)
2σ 1σ
(B)
2σ 1σ(D)
2σ
1σ(C)
2σ
解答：max τ发生在1σ成45的斜截面上
7、广义胡克定律适用范围，有下列四种答案，正确答案是（ C ）。
（A ）脆性材料；
（B ）塑性材料；
（C ）材料为各向同性，且处于线弹性范围内；（D ）任何材料；
8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适用于（ C ）。
（A ）任何材料在任何变形阶级； （B ）各向同性材料在任何变形阶级；。