(完整版)全等三角形综合测试题(含答案)
2024年八年级数学上册《全等三角形》及答案解析

第十二章全等三角形(单元重点综合测试)班级_________姓名________学号__________分数__________考试范围:全章的内容;考试时间:120分钟;总分:120分一、选择题(本大题共10小题,每小题3分,共30分)1.下列说法中,正确的有()①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若△ABC≌△DEF,则∠A=∠D.A.1个B.2个C.3个D.4个2.下列各组图形中,是全等形的是()A. B.C. D.3.如图,点B在线段AD上,△ABC≌△EBD,AB=2cm,BD=5cm,则CE的长度为()A.2cmB.2.5cmC.3cmD.5cm4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,CD⊥BC,BO=OC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,可作为证明△ABO≌△DCO的依据的是()A.SSSB.ASAC.SASD.HL5.如图,在△ABC和△DEF中,点A,E,B,AC∥DF,AC=DF,能判定△ABC≌△DEF的是()A.BC=DEB.AE=DBC.∠A=∠DEFD.∠ABC=∠D6.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有()A.1对B.2对C.3对D.4对7.现要在一块三角形形状的草坪上安装一个洒水龙头,要使洒水龙头到草坪三条边的距离相等,洒水龙头的位置应选在( )处A.三角形三边的垂直平分线的交点B.三角形的三条角平分线的交点C.三角形的三条高所在直线的交点D.三角形的三条中线的交点8.如图,在△ABC中,CD平分∠ACB,DE⊥BC于点E,S△ABC=30,DE=4,BC=10,则AC的长是()A.5B.6C.7D.89.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF,给出下列五个结论:①DE=DF;②BC=2DB;③AD⊥BC;④AB=3BF;⑤S△ADB=2S△BDF;其中正确的结论共有()A.4个B.3个C.2个D.1个10.新定义:已知三条平行直线,相邻两条平行线间的距离相等,我们把三个顶点分别在这样的三条平行线上的三角形称为“格线三角形”.如图,a∥b∥c,相邻两条平行线间的距离为m,等腰Rt△ABC为“格线三角形”,且∠BAC=90°,则△ABC的面积为()A.5m2 B.2m2 C.5m2 D.4m22二、填空题(本大题共6小题,每小题3分,共18分)11.如图,AD=AB,∠C=∠E,∠CDE=50°,则∠ABE=.12.如图,四边形ABCD≌四边形A B C D .若∠B=90°,∠C=60°,∠D =105°,则∠A的大小为度.13.如图,D,E是边BC上的两点,BD=CE,∠ADB=∠AEC,现要直接用“AAS”定理来证明△ABD≌△ACE,请你再添加一个条件:.14.已知△ABC面积为24,将△ABC沿BC的方向平移到△A B C 的位置,使B 和C重合,连接AC 交A C于D,则△C DC的面积为.15.如图,△ABC中∠A=66°,点M、N是∠ABC与∠ACB三等分线的交点,则∠BMN的度数是.16.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=15cm,AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.若点E的运动时间为t秒t>0,则当t=秒时,△DEB与△BCA全等.三、(本大题共4小题,每小题6分,共24分)17.已知:如图,AB=AE,∠1=∠2,∠C=∠D.求证:BC=ED.18.如图,已知AB∥CD,AB=CD.(1)求证:△ABC≌△CDA;(2)判断BC与AD的位置关系,并说明理由.19.如图,已知AB=CD,AD=BC,O为AC的中点,过O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请把它们都写出来;(2)求证:∠MAE=∠NCF.20.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B(1)求证:△ABC≌△CDE(2)若∠A=55°,求∠BCD的度数.四、(本大题共3小题,每小题8分,共24分)21.如图,△ABC中,点D在边BC延长线上,∠ACB=106°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=53°.(1)求∠ACE的度数;(2)求证:AE平分∠CAF;(3)若AC+CD=16,AB=10,且S△ACD=24,则△ABE的面积.22.问题提出:如图1,在四边形ABCD中,∠BAD与∠BCD互补,∠B与∠D互补,AB=AD,∠BAD=x°0<x<180,∠ACB=y°,数学兴趣小组在探究y与x的数量关系时,经历了如下过程:实验操作:(1)数学兴趣小组通过电脑软件“几何画板”进行探究,测量出部分结果如下表所示:x⋯304050607080β130y757065α555040θ这里α=,β=,θ=.猜想证明:(2)根据表格,猜想:y与x之间的关系式为;数学兴趣小组发现证明此猜想的一种方法:如图2,延长CB到E,使BE=DC,连接AE,⋯,请你根据其思路将证明过程补充完整,并验证(1)中结论的正确性.应用拓广:(3)如图3,若x+y=135,AC=10,求四边形ABCD的面积.23.(1)【问题解决】如图①,∠AOB=∠DFE=90°,OC平分∠AOB,点F在OC上,∠DFE的两边分别与OA,OB交于点D,E.当FE⊥OB,FD⊥OA时,则FD与FE的数量关系为;(2)【问题探究】如图②,在(1)的条件下,过点F作两条相互垂直的射线FM,FN,分别交OA,OB于点M,N,判断FM与FN的数量关系,说明理由;(3)【迁移应用】某学校有一块四边形的空地ABCD,如图③所示,∠DAB=∠DCB=90°,AC是∠DAB的平分线,AB= 50m,AD=30m,直接写出该空地的面积.五、(本大题共2小题,每小题12分,共24分)24.综合探究:如题图1是一种用刻度尺画角平分线的方法,在OA、OB上分别取点C、E、D、F,使得OC=OD,OE=OF,连接CF、DE,交点为P,则射线OP为∠AOB的角平分线.【验证】(1)试说明OP平分∠AOB,且PE=PF;【应用】(2)如题图2,若C、E、D、F分别为OA、OB上的点,且OC=OD,CF⊥OA,DE⊥OB,试用(1)中的原理说明OP平分∠AOB;【猜想】(3)如题图3,P是∠AOB角平分线上一点,C、D分别为OA、OB上的点,且PC=PD,请补全图形,并直接写出∠PCO与∠PDO的数量关系.25.【模型呈现】(1)如图1,∠BAD=90°,AB=AD,BC⊥CA于点C,DE⊥AE于点E.求证:BC=AE.【模型应用】(2)如图2,EA⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形ABCDE的面积.【深入探究】(3)如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AF于点F,DE与直线AF交于点G.①求证DG=GE;②若BC=21,AF=12,求△ADG的面积.第十二章全等三角形(单元重点综合测试)班级_________姓名________学号__________分数__________考试范围:全章的内容;考试时间:120分钟;总分:120分一、选择题(本大题共10小题,每小题3分,共30分)1.下列说法中,正确的有()①形状相同的两个图形是全等形;②面积相等的两个图形是全等形;③全等三角形的周长相等,面积相等;④若△ABC≌△DEF,则∠A=∠D.A.1个B.2个C.3个D.4个【答案】B【分析】根据全等形的定义,全等三角形的判定与性质,即可判断.【详解】解:能够完全重合的两个图形叫做全等形,即形状和大小相同的两个图形是全等形,故①②说法错误;全等三角形能够完全重合,所以全等三角形的周长相等,面积相等,故③说法正确;若△ABC≌△DEF,∠A的对应角为∠D,所以∠A=∠D,故④说法正确;说法正确的有③④,共2个.故选:B.【点睛】本题考查全等形,理解能够完全重合的两个图形叫做全等形是解题关键.2.下列各组图形中,是全等形的是()A. B.C. D.【答案】B【分析】本题考查全等形,掌握能完全重合的两个图形是全等形是解题的关键.【详解】观察发现:A,C,D选项中两个图形不能完全重合,不是全等形;B选项中两个图形能完全重合,是全等形,故选B.3.如图,点B在线段AD上,△ABC≌△EBD,AB=2cm,BD=5cm,则CE的长度为()A.2cmB.2.5cmC.3cmD.5cm【答案】C【分析】此题考查了全等三角形的性质,解题的关键熟练掌握性质的应用.根据全等三角形的对应边相等,再利用线段和差即可求解.【详解】∵△ABC≌△EBD,∴BE=AB=2cm,BC=BD=5cm,∴CE=BC-BE=3cm,故选:C.4.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB⊥BC,CD⊥BC,BO=OC,点A、O、D在同一直线上,就能保证△ABO≌△DCO,可作为证明△ABO≌△DCO的依据的是()A.SSSB.ASAC.SASD.HL【答案】B【分析】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解题的关键.直接利用全等三角形的判定方法即可得出答案.【详解】解:∵AB⊥BC,CD⊥BC,∴∠ABO=∠DCO=90°,在△ABO和△DCO中,∠ABO=∠DCOBO=OC=CO∠BOA=∠COD,∴△ABO≌△DCO ASA∴证明△ABO≌△DCO的依据的是ASA,故选:B.5.如图,在△ABC和△DEF中,点A,E,B,AC∥DF,AC=DF,能判定△ABC≌△DEF的是()A.BC=DEB.AE=DBC.∠A=∠DEFD.∠ABC=∠D【答案】B【分析】本题考查三角形全等的判定,先根据平行线的性质得到∠A=∠D,加上AC=DF,则可根据全等三角形的判定方法对各选项进行判断即可,掌握全等三角形的判定方法:SSS、SAS、ASA、AAS,HL是解题的关键.【详解】解:∵AC∥DF,∴∠A=∠D,∵AC=DF,A、添加BC=DE,不能判定△ABC≌△DEF;B、添加AE=DB,能判定△ABC≌△DEF;C、添加∠A=∠DEF,不能判定△ABC≌△DEF;D、添加∠ABC=∠D,不能判定△ABC≌△DEF;故选:B.6.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中全等三角形有()A.1对B.2对C.3对D.4对【答案】C【分析】本题主要考查三角形全等的判定定理,角平分线的性质,熟练掌握三角形全等的判定方程是解题的关键.根据全等三角形的判定分别证明△AOP≌△BOP(SAS),Rt△P AE≌Rt△PBF HL,△OEP≌△OFP (AAS),即可得到答案.【详解】解:∵OP平分∠MON,∴∠AOP=∠BOP,∵OA=OB,OP=OP,∴△AOP≌△BOP(SAS);∴AP=BP,∵OP平分∠MON,PE⊥OM,PF⊥ON∴PE=PF,∵PE⊥OM于点E,PF⊥ON于点F,∴Rt△P AE≌Rt△PBF HL;∵OP平分∠MON,∴∠AOP=∠BOP,又∵∠OEP=∠OFP=90°,OP=OP,∴△OEP≌△OFP(AAS).∴图中全等三角形有3对故选C.7.现要在一块三角形形状的草坪上安装一个洒水龙头,要使洒水龙头到草坪三条边的距离相等,洒水龙头的位置应选在( )处A.三角形三边的垂直平分线的交点B.三角形的三条角平分线的交点C.三角形的三条高所在直线的交点D.三角形的三条中线的交点【答案】B【分析】本题考查的是三角形的角平分线的性质,掌握角平分线上的点到角的两边的距离相等是解题的关键.根据角平分线上的点到角的两边的距离相等解答即可.【详解】解:要使洒水龙头到草坪三条边的距离相等,则洒水龙头的位置应选在三角形三条角平分线的交点,故选:B8.如图,在△ABC 中,CD 平分∠ACB ,DE ⊥BC 于点E ,S △ABC =30,DE =4,BC =10,则AC 的长是()A.5B.6C.7D.8【答案】A 【分析】本题主要考查了角平分线的性质定理.过点D 作DF ⊥AC 于点F ,根据角平分线的性质可得DE =DF =4,再由S △ABC =S △DBC +S △DAC ,即可求解.【详解】解:如图,过点D 作DF ⊥AC 于点F ,∵CD 平分∠ACB ,DE ⊥BC ,DF ⊥AC ,DE =4,∴DE =DF =4,∵S △ABC =S △DBC +S △DAC ,S △ABC =30,BC =10,∴30=12DE ×BC +12DF ×AC ,∴30=12×4×10+12×4×AC ,∴AC =5,故选:A .9.如图,AD 是△ABC 的角平分线,DE ⊥AC ,垂足为E ,BF ∥AC 交ED 的延长线于点F ,若BC 恰好平分∠ABF ,AE =2BF ,给出下列五个结论:①DE =DF ;②BC =2DB ;③AD ⊥BC ;④AB =3BF ;⑤S △ADB =2S △BDF ;其中正确的结论共有()A.4个B.3个C.2个D.1个【答案】A 【分析】本题考查了全等三角形判定和性质,角平分线的性质,等腰三角形的判定和性质,由角平分线的性质和平行线的性质可证∠ACB=∠ABC,可得AC=AB,由等腰三角形的性质可得AD⊥BC,CD= BD,由“ASA”可证△CDE≌△BDF,可得S△CDE=S△BDF,CE=BF,DE=DF,即可求解.【详解】解:∵BC恰好平分∠ABF,∴∠ABC=∠CBF,∵BF∥AC,∴∠ACB=∠CBF,∴∠ACB=∠ABC,∴AC=AB,且AD是△ABC的角平分线,∴AD⊥BC,BC=2DB,故②,③正确,符合题意;在△CDE和△BDF中,∠ACB=∠CBF CD=BD∠CDE=∠BDF,∴△CDE≌△BDF ASA,∴S△CDE=S△BDF,CE=BF,DE=DF,故①正确,符合题意;∵AE=2BF,∴AC=3BF=AB,故④正确,符合题意;∵BD=CD,∴S△ADB=S△ACD,∵AE=2BF,∴S△ADB=S△ACD=3S△CDE=3S△BDF,故⑤错误,不符合题意;故选:A.10.新定义:已知三条平行直线,相邻两条平行线间的距离相等,我们把三个顶点分别在这样的三条平行线上的三角形称为“格线三角形”.如图,a∥b∥c,相邻两条平行线间的距离为m,等腰Rt△ABC为“格线三角形”,且∠BAC=90°,则△ABC的面积为()A.52m2 B.2m2 C.5m2 D.4m2【答案】A【分析】本题主要考查平行线间的距离,全等三角形的判定与性质,过点B作BE⊥直线a于点E,延长EB交直线c于点F,过点C作CD⊥直线a于点D,证明△CDA≌△AEB(AAS),得出AE=CD=2m,AD=BE=m,CF=DE=AD+AE=m+2m=3m,再根据=S四边形DEFE-S△ACD×2-S△BCF求解即可【详解】解:过点B作BE⊥直线a于点E,延长EB交直线c于点F,过点C作CD⊥直线a于点D,则∠CDA=∠AEB=90°,如图,∵a∥b∥c,相邻两条平行线间的距离为m,∴BF⊥直线c,CD=2m,BE=BF=m,∵∠CAB=90°,∠CDA=90°∴∠DCA+∠DAC=90°,∴∠DCA=∠EAB,在△CDA和△AEB中,∠DCA=∠EAB∠CDA=∠AEBAC=AB,∴△CDA≌△AEB(AAS),∴AE=CD=2m,AD=BE=m,∴CF=DE=AD+AE=m+2m=3m∴△ABC的面积=S四边形DEFE -S△ACD×2-S△BCF=3m×2m-12×2m×m×2-12×3m×m=52m2故选:A二、填空题(本大题共6小题,每小题3分,共18分)11.如图,AD=AB,∠C=∠E,∠CDE=50°,则∠ABE=.【答案】130°/130度【分析】本题考查了全等三角形的性质与判定,邻补角的定义,掌握全等三角形的性质与判定是解题的关键.证明△ADC≌△ABE AAS得出∠ADC=∠ABE,根据邻补角即可求解.【详解】解:∵在△ADC和△ABE中,∠C=∠E∠A=∠AAD=AB,∴△ADC≌△ABE AAS,∴∠ADC=∠ABE,∵∠CDE=50°,∴∠ADC=180°-50°=130°,∴∠ABE=130°.故答案为:130°.12.如图,四边形ABCD≌四边形A B C D .若∠B=90°,∠C=60°,∠D =105°,则∠A的大小为度.【答案】105【分析】本题考查了全等图形的性质和四边形内角和公式,解题的关键在于熟练掌握全等图形的性质.根据全等的性质求出∠D=∠D ,利用四边形的内角和公式求出∠A的度数即可.【详解】解:∵四边形ABCD≌四边形A B C D .∴∠D=∠D ,∵∠D =105°,∴∠D=105°,∵∠B=90°,∠C=60°,∴∠A=360°-90°-60°-105°=105°,故答案为:105.13.如图,D,E是边BC上的两点,BD=CE,∠ADB=∠AEC,现要直接用“AAS”定理来证明△ABD≌△ACE,请你再添加一个条件:.【答案】∠BAD=∠CAE【分析】在△ABE与△ACD中,已知AE=AD,∠AED=∠ADE,即已知一角及角的一边对应相等,根据“AAS”的判定方法,可以添加已知边的对角对应相等即可.本题考查了全等三角形的判定定理:AAS:两角及其中一个角的对边对应相等的两个三角形全等.判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.根据已知结合图形及判定方法选择条件是正确解答本题的关键.【详解】解:可添加一个条件:∠BAD=∠CAE,使△ABD≌△ACE.理由:在△ABD与△ACE中,∠BAD=∠CAE∠AED=∠ADEBD=CE,∴△ABD≌△ACE(AAS).故答案为∠BAD=∠CAE14.已知△ABC面积为24,将△ABC沿BC的方向平移到△A B C 的位置,使B 和C重合,连接AC 交A C于D,则△C DC的面积为.【答案】12【分析】根据平移的性质可得AC=A C ,BC=B C ,AC∥A C ,证明△ADC≌△C DA ,得到AD=C D,则S△C DC =12S△ACC,再推出S△ABC=S△ACC=24,则S△C DC=12S△ACC=12.【详解】解:由平移的性质可得AC=A C ,BC=B C ,AC∥A C ,∴∠DCA=∠DA C ,∠DAC=∠DC A ,∴△ADC≌△C DA ASA,∴AD=C D,∴S△C DC =12S△ACC,∵BC=CC ,△ABC的面积为24,∴S△ABC=S△ACC=24,∴S△C DC =12S△ACC=12.故答案为:12.【点睛】本题主要考查了平移的基本性质,全等三角形的性质与判定,三角形中线的性质,熟知平移的性质是解题的关键:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.15.如图,△ABC中∠A=66°,点M、N是∠ABC与∠ACB三等分线的交点,则∠BMN的度数是.【答案】52°/52度【分析】本题考查与角平分线有关的三角形的内角和定理.过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,根据角平分线上的点到角的两边的距离相等可得NE=NG=NF,再根据到角的两边距离相等的点在角的平分线上判断出MN平分∠BMC,然后根据三角形内角和等于180°求出∠ABC+∠ACB,再根据角的三等分求出∠MBC+∠MCB的度数,然后利用三角形内角和定理求出∠BMC的度数,从而得解.【详解】解:如图,过点N作NG⊥BC于G,NE⊥BM于E,NF⊥CM于F,∵点M、N是∠ABC与∠ACB三等分线的交点,∴BN平分∠MBC,CN平分∠MCB,∴NE=NG,NF=NG,∴NE=NF,∴MN平分∠BMC,∴∠BMN=12∠BMC,∵∠A=66°,∴∠ABC+∠ACB=180°-∠A=180°-66°=114°,∴∠MBC+∠MCB=23∠ABC+∠ACB=76°,在△BMC中,∠BMC=180°-∠MBC+∠MCB=180°-76°=104°∴∠BMN=12∠BMC=52°.故答案为:52°.16.如图,CA⊥AB,垂足为点A,射线BM⊥AB,垂足为点B,AB=15cm,AC=6cm.动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着E点运动而运动,始终保持ED=CB.若点E的运动时间为t秒t>0,则当t=秒时,△DEB与△BCA全等.【答案】3或7或10【分析】本题考查全等三角形的性质,关键是要分情况讨论.分情况,当E在线段AB上,或当E在线段AB延长线上,由HL即可求解.【详解】解:∵CA⊥AB,BM⊥AB,∠CAB=∠DBE=90°,∵ED=CB,当E在线段AB上时,若BE=AC,∴Rt△DEB≌Rt△BCA(HL),∵AE=3tcm,∴BE=AB-AE=15-3tcm,∴15-3t=6,∴t=3;若BE=AB,∴Rt△DEB≌Rt△CBA(HL),∴AE=0,∴t=0(舍去),当E在线段AB延长线上时,若BE=AC,∴Rt△DEB≌Rt△BCA(HL),∵AE=3t=AB+BE=15+6=21(cm),∴t=7,若BE=AB,∴Rt△DEB≌Rt△CBA(HL),∵AE=3t=AB+BE=15+15=30(cm),∴t=10,∴当t=3或7或10秒时,△DEB与△BCA全等.故答案为:3或7或10.三、(本大题共4小题,每小题6分,共24分)17.已知:如图,AB=AE,∠1=∠2,∠C=∠D.求证:BC=ED.【答案】见解析【分析】本题考查了全等三角形的判定与性质,由∠1=∠2可得∠EAD=∠BAC,再根据条件AB=AE,∠C=∠D,可利用AAS证明△ABC≌△AED AAS,再根据全等三角形对应边相等即可得出结论.【详解】证明:∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,即∠EAD=∠BAC,在△EAD和△BAC中,∠C=∠D∠BAC=∠EADAB=AE,∴△ABC≌△AED AAS,∴BC=ED.18.如图,已知AB∥CD,AB=CD.(1)求证:△ABC≌△CDA;(2)判断BC与AD的位置关系,并说明理由.【答案】(1)见解析(2)BC∥AD,理由见解析【分析】本题考查了全等三角形的判定与性质,解决本题的关键是得到△ABC≌△CDA.(1)利用SAS证明△ABC≌△CDA即可;(2)由△ABC≌△CDA,得∠BCA=∠CAD,进而可以判断BC与AD的位置关系.【详解】(1)证明:∵AB∥CD,∴∠BAC=∠ACD,在△ABC与△CDA中,AB=CD∠BAC=∠ACDAC=CA,∴△ABC≌△CDA SAS;(2)解:BC∥AD,理由如下:∵△ABC≌△CDA,∴∠BCA=∠CAD,∴BC∥AD.19.如图,已知AB=CD,AD=BC,O为AC的中点,过O作一条直线分别与AB,CD交于点M,N,点E,F在直线MN上,且OE=OF.(1)图中共有几对全等三角形?请把它们都写出来;(2)求证:∠MAE=∠NCF.【答案】(1)4;△ABC≌△CDA,△AMO≌△CNO,△OAE≌△OCF,△AME≌△CNF(2)证明见解析【分析】本题主要考查了全等三角形的性质与判定,找出判定三角形全等的条件是解题的关键.(1)结合已知条件,再根据全等三角形的四个判定方法,即可找出所有的全等三角形;(2)先证明△AME≌△CNF SSS,即可证明∠MAE=∠NCF.【详解】(1)解:有4对全等三角形,分别为:△ABC≌△CDA,△AMO≌△CNO,△OAE≌△OCF,△AME≌△CNF,理由如下:∵AB=CD,BC=AD=DA,AC=CA,∴△ABC≌△CDA SSS,∴∠BAC=∠DCA,即∠MAO=∠NCO,∵O为AC的中点,∴OA=OC,又∵∠AOM=∠CON,∴△AMO≌△CNO ASA,∴AM=CN,OM=ON,∵OA=OC,∠AOE=∠COF,OE=OF,∴△OAE≌△OCF SAS,∴AE=CF,∵OE=OF,OM=ON,∴OE-OM=OF-ON,即ME=NF,又∵AM=CN,∴△AME≌△CNF SSS;(2)证明:∵AB=CD,BC=AD=DA,AC=CA,∴△ABC≌△CDA SSS,∴∠BAC=∠DCA,即∠MAO=∠NCO,∵O为AC的中点,∴OA=OC,又∵∠AOM=∠CON,∴△AMO≌△CNO ASA,∴AM=CN,OM=ON,∵OA=OC,∠AOE=∠COF,OE=OF,∴△OAE≌△OCF SAS,∴AE=CF,∵OE=OF,OM=ON,∴OE-OM=OF-ON,即ME=NF,又∵AM=CN,∴△AME≌△CNF SSS,∴∠MAE=∠NCF.20.如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B(1)求证:△ABC≌△CDE(2)若∠A=55°,求∠BCD的度数.【答案】(1)详见解析(2)125°【分析】本题考查了平行线性质和全等三角形的性质和判定的应用,证得△ABC≌△CDE是解题的关键.(1)根据平行线求出∠ACD=∠CDE,∠ACB=∠CED,再说明∠B=∠CDE,最后结合AC=CE运用AAS即可证明结论;(2)根据全等三角形性质得出∠A=∠E=55°,进而根据平角定义即可解答.【详解】(1)证明∶∵AC∥DE,∴∠ACD=∠CDE,∠ACB=∠CED,∵∠ACD=∠B,∴∠B=∠CDE,∵AC=CE,∴△ABC≌△CDE AAS.(2)解:∵∠A=55°,∵△ABC≌△CDE,∴∠A=∠ECD=55°,∴∠BCD=180°-∠ECD=180°-55°=125°.四、(本大题共3小题,每小题8分,共24分)21.如图,△ABC中,点D在边BC延长线上,∠ACB=106°,∠ABC的平分线交AD于点E,过点E作EH⊥BD,垂足为H,且∠CEH=53°.(1)求∠ACE的度数;(2)求证:AE平分∠CAF;(3)若AC+CD=16,AB=10,且S△ACD=24,则△ABE的面积.【答案】(1)∠ACE=37°(2)证明见解析(3)15【分析】本题主要考查了邻补角的性质、角平分线的性质与判定定理、三角形的面积等知识点,灵活运用相关知识点成为解答本题的关键.(1)根据邻补角的定义和垂直的定义可得∠ACD=74°、∠CHE=90°,进而得到∠ECH=37°,然后根据∠ACE=∠ACD-∠ECH即可解答;(2)如图:过E点分别作EM⊥BF于M,EN⊥AC与N,根据角平分线的性质定理以及角平分线的定义可得EM=EH、CE平分∠ACD、EN=EH,最后根据角平分线的判定定理即可解答;(3)根据S△ACD=S△ACE+S△CED结合已知条件可得EM=3,最后运用三角形的面积公式即可解答.【详解】(1)解:∵∠ACB=106°,∴∠ACD=180°-106°=74°,∵EH⊥BD,∴∠CHE=90°,∵∠CEH=53°,∴∠ECH=90°-53°=37°,∴∠ACE=∠ACD-∠ECH=74°-37°=37°.(2)证明:如图:过E点分别作EM⊥BF于M,EN⊥AC与N,∵BE平分∠ABC,∴EM=EH,∵∠ACE =∠ECH =37°,∴CE 平分∠ACD ,∴EN =EH ,∴EM =EN ,∴AE 平分∠CAF .(3)解:∵AC +CD =16,S △ACD =24,EM =EN =EH ,∴S △ACD =S △ACE +S △CED =12AC ⋅EN +12CD ⋅EH =12(AC +CD )⋅EM =24,即12×16⋅EM =24,解得EM =3,∵AB =10,∴S △ABE =12AB ⋅EM =15.22.问题提出:如图1,在四边形ABCD 中,∠BAD 与∠BCD 互补,∠B 与∠D 互补,AB =AD ,∠BAD =x °0<x <180 ,∠ACB =y °,数学兴趣小组在探究y 与x 的数量关系时,经历了如下过程:实验操作:(1)数学兴趣小组通过电脑软件“几何画板”进行探究,测量出部分结果如下表所示:x⋯304050607080β130y 757065α555040θ这里α=,β=,θ=.猜想证明:(2)根据表格,猜想:y 与x 之间的关系式为;数学兴趣小组发现证明此猜想的一种方法:如图2,延长CB 到E ,使BE =DC ,连接AE ,⋯,请你根据其思路将证明过程补充完整,并验证(1)中结论的正确性.应用拓广:(3)如图3,若x +y =135,AC =10,求四边形ABCD 的面积.【答案】(1)60,100,15;(2)y =90-12x ,理由见详解;(3)S 四边形ABCD =50【分析】(1)观察表格发现:x 每增加10,y 减小5,由此即可得出α、β、θ的值.(2)根据表格猜想:y =90-12x .延长CB 到E ,使BE =DC ,连接AE ,则可得△ABE ≌△ADE ,进而可得AE =AC ,∠EAB =∠CAD ,则可得∠EAC =x °.在△AEC 中,根据三角形内角和定理即可得出y 于x 之间的关系式.(3)延长CB 到E ,使BE =DC ,连接AE .由(2)得△ABE ≌△ADE ,则S △ABE =S △ADE ,进而可得S 四边形ABCD =S △AEC .由x +y =135,y =90-12x 可得x =90,y =45.则可得∠EAC =90°,∠AEC =∠ACE =45°,进而可得AE =AC =10,可得S △AEC 的值,即可得S 四边形ABCD 的值.【详解】(1)观察表格发现:x每增加10,y减小5,∴α=65-5=60,β=80+2×10=100,θ=40-3×5=15.故答案为:60,100,15,x.(2)根据表格猜想:y=90-12证明:如图2,延长CB到E,使BE=DC,连接AE,则∠ABC+∠ABE=180°,又∵∠ABC+∠D=180°,∴∠ABE=∠D,又∵AB=AD,∴△ABE≌△ADE(SAS),∴AE=AC,∠EAB=∠CAD,∴∠E=∠ACB=y°,∠EAC=∠EAB+∠BAC=∠CAD+∠BAC=∠BAD=x°.在△AEC中,∠EAC+∠E+∠ACE=180°,∴x°+2y°=180°,y=90-1x.2(3)如图,延长CB到E,使BE=DC,连接AE.由(2)得△ABE≌△ADE,∴S△ABE=S△ADE,=S△ACD+S△ABC=S△ABE+S△ABC=S△AEC,∴S四边形ABCD∵x+y=135,y=90-1x,2x=135,∴x+90-12解得x=90,y=45,∴∠EAC=90°,∠AEC=∠ACE=45°,∴AE=AC=10,×10×10=50,∴S△AEC=12∴S=50.四边形ABCD【点睛】本题考查了数字类探索规律问题,以及全等三角形的判定和性质,三角形内角和定理.熟练掌握以上知识,证明出y与x之间的关系式是解题的关键.23.(1)【问题解决】如图①,∠AOB =∠DFE =90°,OC 平分∠AOB ,点F 在OC 上,∠DFE 的两边分别与OA ,OB 交于点D ,E .当FE ⊥OB ,FD ⊥OA 时,则FD 与FE 的数量关系为;(2)【问题探究】如图②,在(1)的条件下,过点F 作两条相互垂直的射线FM ,FN ,分别交OA ,OB 于点M ,N ,判断FM 与FN 的数量关系,说明理由;(3)【迁移应用】某学校有一块四边形的空地ABCD ,如图③所示,∠DAB =∠DCB =90°,AC 是∠DAB 的平分线,AB =50m ,AD =30m ,直接写出该空地的面积.【答案】(1)FD =FE ;(2)FM =FN ,理由见详解;(3)1600m 2【分析】(1)根据“角平分线上的点到角两边的距离相等”可得FD =FE ;(2)先根据四边形内角和等于360°可得∠DFE =90°,由∠DFE =∠FMN =90°可得∠DFM =∠EFN ,再根据ASA 证明△DFM ≌△EFN ,则可得FM =FN ;(3)过C 点作CE ⊥AB 于E 点,CF ⊥AD 的延长线于F 点.由(2)得△CFD ≌△CEB ,则可得FD =EB ,S △CFD =S △CEB ,进而可得S 四边形ABCD =S 四边形AECF .证明△ACF ≌△ACE (,则可得AF =AE ,由AE =AB -BE 、AF =AD +DF 可求得BE 的长,进而可得AF 、AE 的长,由此可得S 四边形AECF 的值,即可得S 四边形ABCD 的值.【详解】(1)解:∵OC 平分∠AOB ,点F 在OC 上,且FE ⊥OB ,FD ⊥OA ,∴FD =FE .(2)解:FD =FE ,理由如下:∵FD ⊥OA ,FE ⊥OB ,∴∠FDO =∠FEO =∠FEN =90°,∵四边形DOEF 中,∠FDO =∠FEO =∠AOB =90°,∴∠DFE =360°-∠FDO -∠FEO -∠AOB =90°,∴∠DMF +∠MFE =90°,又∵FM ⊥FN ,∴∠FMN =90°,∴∠DFM =∠EFN ,在△DFM 和△EFN 中,∠FDM =∠FENFD =FE ∠DFM =∠EFN,∴△DFM ≌△EFN (ASA ),∴FM =FN .(3)解:如图,过C 点作CE ⊥AB 于E 点,CF ⊥AD 的延长线于F 点,由(2)得△CFD≌△CEB,∴FD=EB,S△CFD=S△CEB,∴S四边形ABCD =S四边形AECF,∵AC是∠DAB的平分线,∴∠DAC=∠CAB,又∵∠CFB=∠CEA=90°,AC=AC,∴△ACF≌△ACE(AAS),∴AF=AE,又∵AE=AB-BE,AF=AD+DF,∴AB-BE=AD+DF,∴50-BE=30+BE,解得BE=10,∴AF=AE=40,∴S四边形AECF=40×40=1600m2,∴S四边形ABCD=1600m2,答:该空地的面积为1600m2.【点睛】本题主要考查了角平分线的性质、全等三角形的判定和性质,熟练掌握以上知识,正确的作出辅助线是解题的关键.五、(本大题共2小题,每小题12分,共24分)24.综合探究:如题图1是一种用刻度尺画角平分线的方法,在OA、OB上分别取点C、E、D、F,使得OC=OD,OE=OF,连接CF、DE,交点为P,则射线OP为∠AOB的角平分线.【验证】(1)试说明OP平分∠AOB,且PE=PF;【应用】(2)如题图2,若C、E、D、F分别为OA、OB上的点,且OC=OD,CF⊥OA,DE⊥OB,试用(1)中的原理说明OP平分∠AOB;【猜想】(3)如题图3,P是∠AOB角平分线上一点,C、D分别为OA、OB上的点,且PC=PD,请补全图形,并直接写出∠PCO与∠PDO的数量关系.【答案】(1)见解析;(2)见解析;(3)补全图形见解析,∠PCO=∠PDO或∠PCO+∠PDO=180°【分析】本题是三角形综合题目,考查了全等三角形的判定与性质、角平分线的性质等知识,本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键,属于中考常考题型.(1)先证明△DOE≌△COF(SAS),得∠PEC=∠PFD,再证△CPE≌△DPF(AAS),得PE=PF,然后证△OPE≌△OPF(SSS),得∠POE=∠POF,即可得出结论;(2)先证明△OCF≌△ODE(ASA),可得OF=OE,由(1)可得OP平分∠AOB;(3)过点P分别作PM⊥OA于M,PN⊥OB于N,分两种情况进行求解即可.【详解】解:(1)∵OC=OD,∠DOE=∠COF,OE=OF,∴CE=DF,△DOE≌△COF(SAS),∴∠PEC=∠PFD,∵∠CPE=∠DPF,CE=DF,∴△CPE≌△DPF(AAS),∴PE=PF,∵OE=OF,PE=PF,OP=OP,∴△OPE≌△OPF(SSS),∴∠POE=∠POF,即∠POA=∠POB,∴射线OP平分∠AOB;(2)∵CF⊥OA,DE⊥OB,∴∠OCF=∠ODE=90°,∴∠COF=∠DOE,OC=OD,∴△OCF≌△ODE(ASA),∴OF=OE,由(1)可得OP平分∠AOB;(3)补全图形如下,过点P分别作PM⊥OA于M,PN⊥OB于N,∵OP是∠AOB的平分线,∴PM=PN,∠PMC=∠PND=90°,当PC=PD1时,在Rt△PMC和Rt△PND1中,PC=PD1,PM=PN∴Rt△PMC≌Rt△PND1(HL),∴∠PCO=∠PD1O;当PC=PD2时,同理得Rt△PMC≌Rt△PND2HL,∴∠PCM=∠PD2N;∵∠PD2N+∠PD2O=180°,∴∠PCO+∠PD2O=180°,综上所述,∠PCO与∠PDO的数量关系为∠PCO=∠PDO或∠PCO+∠PDO=180°;25.【模型呈现】(1)如图1,∠BAD=90°,AB=AD,BC⊥CA于点C,DE⊥AE于点E.求证:BC=AE.【模型应用】(2)如图2,EA⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形ABCDE的面积.【深入探究】(3)如图3,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC、DE,且BC⊥AF于点F,DE与直线AF交于点G.①求证DG=GE;②若BC=21,AF=12,求△ADG的面积.【答案】(1)见解析;(2)50;(3)①见解析;63【分析】(1)证明△ABC≌△DAE AAS,即可得证;(2)同(1)法得到△AEP≌△BAG,△CBG≌△DCH,分割法求出图形面积即可;(3)①过点D作DP⊥AG于P,过点E作EQ⊥AG交AG的延长线于Q,易证△AFB≌△DP A,△AFC ≌△EQA,得到DP=AF,EQ=AF,再证明△DPG≌△EQG AAS,即可得出结论;②根据全等三角形的性质,求出AG的长,进而利用面积公式进行求解即可.【详解】解:(1)证明:∵∠BAD=90°,∴∠BAC+∠DAE=90°,∵BC⊥CA,DE⊥AE,∴∠ACB=∠DEA=90°,∴∠BAC+∠ABC=90°,∴∠ABC=∠DAE,在△ABC和△DAE中,∠ACB=∠DEA∠ABC=∠DAEBA=AD∴△ABC≌△DAE AAS,∴BC=AE.(2)由模型呈现可知,△AEP≌△BAG,△CBG≌△DCH,∴AP=BG=3,AG=EP=6,CG=DH=4,CH=BG=3,则S实线围成的图形=12×4+6×3+6+4+3-12×3×6-12×3×6-12×3×4-12×3×4=50.(3)①过点D作DP⊥AG于P,过点E作EQ⊥AG交AG的延长线于Q.图3由【模型呈现】可知,△AFB≌△DP A,△AFC≌△EQA,∴DP=AF,EQ=AF∴DP=EQ,∵DP⊥AG,EQ⊥AG∴∠DPG=∠EQG=90°,在△DPG和△EQG中,∠DPG=∠EQG∠DGP=∠EGQDP=EQ∴△DPG≌△EQG AAS,∴DG=GE.②由①可知,BF=AP,FC=AQ,∴BC=BF+FC=AP+AQ,∵BC=21,∴AP+AQ=21,∴AP+AP+PG+GQ=21,由①△DPG≌△EQG得∴PG=GQ,∴AP+AP+PG+PG=21,∴AP+PG=10.5,∴AG=10.5,∴S△ADG=1×10.5×12=63.2。
三角形全等测试题及答案

三角形全等测试题及答案一、选择题1. 两个三角形全等的条件是()A. 有两条边和它们的夹角对应相等B. 三条边对应相等C. 有两条边和其中一条边的对角对应相等D. 有两条边和其中一条边的邻角对应相等答案:B2. 如果两个三角形的对应角相等,那么这两个三角形()A. 一定全等B. 可能相似C. 一定相似D. 无法确定答案:B二、填空题3. 已知三角形ABC与三角形DEF全等,且∠A=∠D,AB=DE,那么AC=______。
答案:EF4. 如果两个三角形的两边和夹角对应相等,那么这两个三角形是______。
答案:全等三、判断题5. 如果两个三角形的对应边成比例,那么这两个三角形一定全等。
()答案:错误6. 如果两个三角形的两边和夹角对应相等,那么这两个三角形一定相似。
()答案:正确四、解答题7. 如图所示,已知三角形ABC与三角形DEF全等,且AB=5cm,BC=7cm,∠A=∠D=90°,求DE的长度。
答案:DE=7cm8. 已知三角形ABC与三角形DEF相似,且AB=3cm,BC=4cm,DE=6cm,求AC的长度。
答案:AC=8cm五、证明题9. 已知三角形ABC与三角形DEF全等,且∠A=∠D,AB=DE,证明:AC=EF。
证明:由于三角形ABC与三角形DEF全等,根据全等三角形的性质,对应边相等,所以AC=EF。
10. 已知∠A=∠D,AB=DE,AC=DF,求证:三角形ABC≌三角形DEF。
证明:根据SAS(边角边)判定方法,已知∠A=∠D,AB=DE,AC=DF,所以三角形ABC≌三角形DEF。
(完整版)全等三角形判定综合练习题
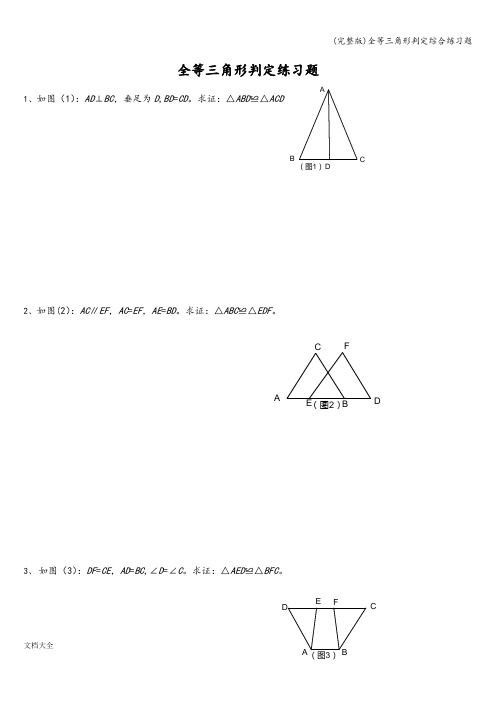
全等三角形判定练习题1、如图(1):AD ⊥BC ,垂足为D ,BD =CD 。
求证:△ABD ≌△ACD2、如图(2):AC ∥EF ,AC =EF ,AE =BD 。
求证:△ABC ≌△EDF 。
3、 如图(3):DF =CE ,AD =BC ,∠D =∠C 。
求证:△AED ≌△BFC 。
FE (图2)DCBAFEDC(图1)DCBA4、 如图(4):AB =AC ,AD =AE ,AB ⊥AC ,AD ⊥AE .求证:(1)∠B =∠C ,(2)BD =CE5、如图(5):AB ⊥BD ,ED ⊥BD ,AB =CD ,BC =DE 。
求证:AC ⊥CE 。
E(图4)DCBAE(图5)DCBA6、如图(6):CG =CF ,BC =DC ,AB =ED ,点A 、B 、C 、D 、E 在同一直线上。
求证:(1)AF =EG ,(2)BF ∥DG .7、如图(7):AC ⊥BC ,BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN =BC 。
求证:(1)MN 平分∠AMB ,(2)∠A =∠CBM 。
GFE(图6)DC BANM(图7)CBA8、如图(8):A 、B 、C 、D 四点在同一直线上,AC =DB ,BE ∥CF ,AE ∥DF 。
求证:△ABE ≌△DCF 。
9、如图(9)AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE =CF 。
求证:AM 是△ABC 的中线。
FE(图8)DC B AMFE(图9)CBA10、如图(10)∠BAC =∠DAE ,∠ABD =∠ACE ,BD =CE . 求证:AB =AC 。
11、如图(11)在△ABC 和△DBC 中,∠1=∠2,∠3=∠4,P 是BC 上任一点。
求证:PA =PD .12、如图(12)AB ∥CD ,OA =OD ,点F 、D 、O 、A 、E 在同一直线上,AE =DF . 求证:EB ∥CF 。
全等三角形综合测试题(含答案)

图12图A 'C AD B E21图4 C A D B E 图10 C A D B E F 图2 图6m nCAB图11 12CA DB EF M N O ABCD F图 5A B DC EF 图1 图3 45321DAOECB DAC B全等三角形综合复习测试题一、选一选,看完四个选项后再做决定呀!(每小题3分,共30分) 1.已知等腰三角形的一个内角为50,则这个等腰三角形的顶角为【 】. (A )50(B )80(C )50或80(D )40或652. 如图1所示,在△ABC 中,已知点D ,E ,F 分别是BC ,AD ,CE 的中点,且ABC S △=4平方厘米,则BEF S △的值为 【 】.(A )2平方厘米 (B )1平方厘米 (C )12平方厘米 (D )14平方厘米3. 已知一个三角形的两边长分别是2厘米和9厘米,且第三边为奇数,则第三边长为【 】. (A )5厘米 (B )7厘米 (C )9厘米 (D )11厘米4. 工人师傅常用角尺平分一个任意角.做法如下:如图2所示,∠AOB 是一个任意角,在边OA ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合.过角尺顶点C 的射线OC 即是∠AOB 的平分线.这种做法的道理是 【 】.(A )HL (B )SSS (C )SAS (D )ASA 5. 利用三角形全等所测距离叙述正确的是( )A.绝对准确B.误差很大,不可信C.可能有误差,但误差不大,结果可信D.如果有误差的话就想办法直接测量,不能用三角形全等的方法测距离 6. 在图3所示的3×3正方形网格中,∠1+∠2+∠3+∠4+∠5等于 【 】. (A )145° (B )180° (C )225° (D )270° 7. 根据下列条件,能判定△ABC ≌△A ′B ′C ′的是 【 】. (A )AB =A ′B ′,BC =B ′C ′,∠A =∠A ′ (B )∠A =∠A ′,∠B =∠B ′,AC =B ′C ′(C )∠A =∠A ′,∠B =∠B ′,∠C =∠C ′(D )AB =A ′B ′,BC =B ′C ′,△ABC 的周长等于△A ′B ′C ′的周长 8. 如图4所示,△ABC 中,∠C =90°,点D 在AB 上,BC =BD ,DE ⊥AB 交AC 于点E .△ABC 的周长为12,△ADE 的周长为6.则BC 的长为 【 】. (A )3 (B )4 (C )5 (D )69. 将一副直角三角尺如图5所示放置,已知AE BC ∥,则AFD ∠的度数是 【 】.(A )45(B )50 (C )60(D )75图7 图810. 如图6所示,m ∥n ,点B ,C 是直线n 上两点,点A 是直线m 上一点,在直线m 上另找一点D ,使得以点D ,B ,C 为顶点的三角形和△ABC 全等,这样的点D 【 】.(A )不存在 (B )有1个 (C )有3个 (D )有无数个 二、填一填,要相信自己的能力!(每小题3分,共30分) 1.在ABC ∆中,若A ∠=1123B C =∠,则ABC ∆是 三角形.2. 如图7所示,BD 是ABC ∆的中线,2AD =,5AB BC +=,则ABC ∆的周长是 .3. 如图8所示所示,在ABC ∆中,BD ,CE 分别是AC 、AB 边上的高,且BD 与CE 相交于点O ,如果135BOC ∠=︒,那么A ∠的度数为 .4. 有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成________个形状不同的三角形.5. 如图9所示,将纸片△ABC 沿DE 折叠,点A 落在点A ′处,已知∠1+∠2=100°,则∠A 的大小等于_____度.6. 如图10所示,有两个长度相同的滑梯(即BC =EF ),左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,则△ABC ≌△DEF ,理由是______.7. 如图11所示,AD ∥BC ,AB ∥DC ,点O 为线段AC 的中点,过点O 作一条直线分别与AB 、CD 交于点M 、N .点E 、F 在直线MN 上,且OE =OF .图中全等的三角形共有____对.8. 如图12所示,要测量河两岸相对的两点A 、B 的距离,在AB 的垂线BF 上取两点C 、D ,使BC =CD ,过D 作BF 的垂线DE ,与AC 的延长线交于点E ,则∠ABC =∠CDE =90°,BC =DC ,∠1=______,△ABC ≌_________,若测得DE 的长为25 米,则河宽AB 长为_________. 9. 如图13所示,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是 .10. 如图14所示,三角形纸片ABC ,AB =10厘米,BC =7厘米,AC =6厘米.沿 过点B 的直线折叠这个三角形,使顶点C 落在AB 边上的点E 处,折痕为BD ,则△AED 的周长为______厘米.图14 C A DB E 图1335°D AEC B三、做一做,要注意认真审题呀!(本大题共38分) 1.(8分)如图15所示,在ABC ∆中,已知AD BC ⊥,64B ∠=︒,56C ∠=︒. (1)求BAD ∠和DAC ∠的度数;(2)若DE 平分ADB ∠,求AED ∠的度数.图15 2.(10分)已知:线段a ,b ,c (如图16所示),画△ABC ,使BC =a ,CA =b ,AB =c .(保留作图痕迹,不必写画法和证明)3.(10分)图17为人民公园的荷花池,现要测量此荷花池两旁A 、B 两棵树间的距离(不能直接测量),请你根据所学三角形全等的知识,设计一种测量方案求出AB 的长(要求画出草图,写出测量方案和理由). 4.(10分)如图18所示,△ADF 和△BCE 中,∠A =∠B ,点D ,E ,F ,C 在同—直线上,有如下三个关系式:①AD =BC ;②DE =CF ;③BE ∥AF .(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的结论. (2)选择(1)中你写出的—个正确结论,说明它正确的理由.四、拓广探索!(本大题共22分)1.(10分)如图19,在△ABC 中,点E 在AB 上,点D 在BC 上,BD =BE ,∠BAD =∠BCE ,AD 与CE 相交于点F ,试判断△AFC 的形状,并说明理由.2.(12分)两个大小不同的等腰直角三角形三角板如图20①所示放置,图20②是由它抽象出的几何图形,B C E ,,在同一条直线上,连结DC .(1)请找出图20②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母); (2)试说明:DC BE ⊥.图16 b a c图17 图18 FE BDA C 图20①②DABBD FAE 图19参考答案一、1~10 CB C BC CD ADB. 二、1. 直角. 2.9. 3. 45°. 4.3. 5. 50. 6. HL. 7.4. 8. ∠2,△EDC ,25 m. 9. 125°. 10. 9.三、1. (1)90905634DAC C ∠=︒-∠=︒-︒=︒. (2)109AED ∠=︒. 2.画图略.3.方案不惟一,画图及理由略.4.(1)如果①、③,那么②或如果②、③,那么①; (2)选择“如果①、③,那么②”证明,过程略. 四、1. △AFC 是等腰三角形.理由略 . 2.(1)图2中ABE ACD △≌△.理由如下:ABC △与AED △均为等腰直角三角形AB AC ∴=,AE AD =,90BAC EAD ∠=∠=, BAC CAE EAD CAE ∴∠+∠=∠+∠, 即BAE CAD ∠=∠ , ABE ACD ∴△≌△.(2)说明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠=, 又45ACB ∠=90BCD ACB ACD ∴∠=∠+∠=,DC BE ∴⊥。
全等三角形测试题含答案
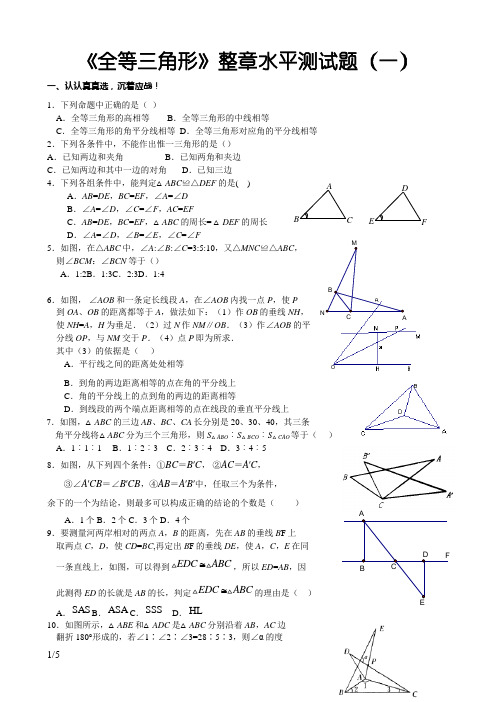
《全等三角形》整章水平测试题(一)一、认认真真选,沉着应战!1.下列命题中正确的是( )A .全等三角形的高相等B .全等三角形的中线相等C .全等三角形的角平分线相等D .全等三角形对应角的平分线相等 2.下列各条件中,不能作出惟一三角形的是() A .已知两边和夹角 B .已知两角和夹边 C .已知两边和其中一边的对角 D .已知三边4.下列各组条件中,能判定△ABC ≌△DEF 的是( ) A .AB =DE ,BC =EF ,∠A =∠D B .∠A =∠D ,∠C =∠F ,AC =EFC .AB =DE ,BC =EF ,△ABC 的周长= △DEF 的周长D .∠A =∠D ,∠B =∠E ,∠C =∠F5.如图,在△ABC 中,∠A :∠B :∠C =3:5:10,又△MNC ≌△ABC , 则∠BCM :∠BCN 等于() A .1:2B .1:3C .2:3D .1:4 6.如图, ∠AOB 和一条定长线段A ,在∠AOB 内找一点P ,使P到OA 、OB 的距离都等于A ,做法如下:(1)作OB 的垂线NH , 使NH =A ,H 为垂足.(2)过N 作NM ∥OB .(3)作∠AOB 的平 分线OP ,与NM 交于P .(4)点P 即为所求. 其中(3)的依据是( )A .平行线之间的距离处处相等B .到角的两边距离相等的点在角的平分线上C .角的平分线上的点到角的两边的距离相等D .到线段的两个端点距离相等的点在线段的垂直平分线上7.如图,△ABC 的三边AB 、BC 、CA 长分别是20、30、40,其三条角平分线将△ABC 分为三个三角形,则S △ABO ︰S △BCO ︰S △CAO 等于( ) A .1︰1︰1 B .1︰2︰3 C .2︰3︰4 D .3︰4︰5 8.如图,从下列四个条件:①BC =B ′C , ②AC =A ′C ,③∠A ′CB =∠B ′CB ,④AB =A ′B ′中,任取三个为条件, 余下的一个为结论,则最多可以构成正确的结论的个数是( ) A .1个B .2个C .3个D .4个9.要测量河两岸相对的两点A ,B 的距离,先在AB 的垂线B F 上 取两点C ,D ,使CD =BC ,再定出B F 的垂线DE ,使A ,C ,E 在同 一条直线上,如图,可以得到EDC ABC ≅,所以ED =AB ,因 此测得ED 的长就是AB 的长,判定EDC ABC ≅的理由是( ) A .SAS B .ASA C .SSS D .HL10.如图所示,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 边 翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度ACB DFEN AMCB FCEABD数为( )A .80°B .100°C .60°D .45°. 二、仔仔细细填,记录自信!11.如图,在△ABC 中,AD=DE ,AB=BE ,∠A=80°, 则∠CED=_____.12.已知△DE F ≌△ABC ,AB =AC ,且△ABC 的周长为23cm ,BC =4cm ,则△DE F 的边中必有一条边等于______.13. 在△ABC 中,∠C =90°,BC =4CM ,∠BAC 的平分线交BC 于D ,且BD ︰DC =5︰3,则D 到AB 的距离为_____________.14. 如图,△ABC 是不等边三角形,DE =BC ,以D ,E 为两个顶点作位置不同的三角形,使所作的三角形与△ABC 全等,这样的三角形最多可以画出_____个.D E15. 如图,AD A D '',分别是锐角三角形ABC 和锐角三角形A B C '''中,BC B C ''边上的高,且AB A B AD A D ''''==,.若使ABC A B C '''△≌△,请你补充条件___________.(填写一个你认为适当的条件即可)17.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是__________.19. 如右图,已知在ABC 中,90,,A AB AC CD ∠=︒=平分ACB ∠,DE BC ⊥于E ,若15cm BC =,则DEB △ 的周长为cm .20.在数学活动课上,小明提出这样一个问题:∠B =∠C =900,E 是 BC 的中点,DE 平分∠ADC ,∠CED =350,如图,则∠EAB 是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______. 三、平心静气做,展示智慧!21.如图,公园有一条“Z ”字形道路ABCD ,其中AB ∥CD ,在,,E M F 处各有一个小石凳,且BE CF =, M 为BC 的中点,请问三个小石凳是否在一条直线上?说出你推断的理由.22.如图,给出五个等量关系:①AD BC =②AC BD =③CE DE =④D C ∠=∠EA B C D'A 'B 'D 'CC B⑤DAB CBA ∠=∠.请你以其中两个为条件,另三个中的一个为结论,推出一个正确 的结论(只需写出一种情况),并加以证明. 已知: 求证: 证明:23.如图,在∠AOB 的两边OA ,OB 上分别取OM =ON ,OD =OE , DN 和EM 相交于点C .求证:点C 在∠AOB 的平分线上. 四、发散思维,游刃有余!24. (1)如图1,以ABC △的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断ABC △与AEG △面积之间的关系,并说明理由.(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石 铺成.已知中间的所有正方形的面积之和是a 平方米,内圈的所有三角形的面积之和 是b 平方米,这条小路一共占地多少平方米?参考答案一、1—5:DCDCD 6—10:BCBBA 二、 11.100°12.4cm 或9.5cm13.1.5cm 14.4 15.略16.15AD << 17. 互补或相等 18. 180 19.15 20.350三、 21.在一条直线上.连结EM 并延长交CD 于'F 证'CF CF =.22.情况一:已知:AD BC AC BD ==,求证:CE DE =(或D C ∠=∠或DAB CBA ∠=∠) 证明:在△ABD 和△BAC 中AD BC AC BD ==∵, AB BA =ABDC EOM NAGFC BDE(图1)∴△ABD ≌△BAC∴CAB DBA ∠=∠AE BE =∴ ∴AC AE BD BE -=-即CE ED =情况二:已知:D C DAB CBA ∠=∠∠=∠,求证:AD BC =(或AC BD =或CE DE =) 证明:在△ABD 和△BAC 中D C ∠=∠,DAB CBA ∠=∠AB AB =∵∴△ABD ≌△BAC ∴AD BC =23.提示:OM =ON ,OE =OD ,∠MOE =∠NOD ,∴△MOE ≌△NOD ,∴∠OME =∠OND ,又DM =EN ,∠DCM =∠ECN ,∴△MDC ≌△NEC ,∴MC =NC ,易得△OMC ≌△ONC (SSS )∴∠MOC =∠NOC ,∴点C 在∠AOB 的平分线上.四、24. (1)解:ABC △与AEG △面积相等过点C 作CM AB ⊥于M ,过点G 作GN EA ⊥交EA 延长线于N ,则AMC ∠=90ANG ∠=四边形ABDE 和四边形ACFG 都是正方形90180BAE CAG AB AE AC AG BAC EAG ∴∠=∠===∴∠+∠=,,180EAG GAN BAC GAN ∠+∠=∴∠=∠ACM AGN ∴△≌△1122ABCAEG CM GN S AB CM S AE GN ∴===△△,ABC AEGS S ∴=△△(2)解:由(1)知外圈的所有三角形的面积之和等于内圈的所有三角形的面积之和∴这条小路的面积为(2)a b +平方米.BD。
《全等三角形》测试题A卷及答案

第十四章全等三角形测试题、选择题(每小题4分,共32 分)1 .下列命题中真命题的个数有()⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,C、1个2.如图,已知△ ABC的六个元素,则下面甲、乙、丙三个三角形中和,厶=/ A',若证N ABC B" A'B'C'还要从下列条件中补选一个,错误的选法是(C. BC=B'C'D. AC=A C'4. P是/ AOB平分线上一点,CD丄OP于F,并分别交OA、OB于CD,贝U CD _____________ P点到/ AOB两边距离之和.()A.小于B.大于5.如图,从下列四个条件:①BC= B C,②AC= A 'C,③/ A 'CA=Z B CB,④AB= A B '中, 任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是()A. 1个B. 2个C. 3个D. 4个6.有以下条件:①一锐角与一边对应相等;②两边对应相等;③两锐角对应相等。
其中能判断两直角三角形全等的是()A.① B ② C ③ D ①②7 .如图,△ ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ ABC分A .甲和乙 E.乙和丙 C.只有乙 D.只有丙△ ABC全等的图形是(3 .在"ABC 和"A 'B'C'中,AB=A 'B'C.等于D.不能确定(5题)CF = 4,贝V S ABEF 为.三:解答题(共44 分)15、( 5分)已知:如图,AC 、BD 相交于点 O , Z A = Z D , AB=CD.求证:△ AOB ^A DOC ,。
为三个三角形,则 &ABO : S ^BCO : &CAO 等于( B . 1 : 2 : 3 C . 2 : 3 : 4 &如图所示,在 Rt △ ABC 中,AD 是斜边上的高,Z 交AD AC 于点F 、E, EG 丄BC 于 G 下列结论正确的是 A . Z C= / ABC B. BA=BG CC . AE=CE D. AF=FD 二、填空题(每小题4分,共24 分) 9 .如图,Rt △ ABC 中,直角边是 ,斜边是 10.如图,点D,E 分别在线段 AB, AC 上, BE, CD 相交于 /A点 O, AE AD , 要使△ ABE ACD ,需添加一个条件是(只要写一个(10 题) (11题)11.如图,把△ ABC 绕C 点顺时针旋转35。
(完整版)《全等三角形》单元测试题(含答案)
《全等三角形》单元测试题姓名 班级 得分一、填空题(4×10=40分)1、在△ABC 中,AC>BC>AB ,且△ABC ≌△DEF ,则在△DEF 中,______>______>_______(填边)。
2、已知:△ABC ≌△A ′B ′C ′,∠A=∠A ′,∠B=∠B ′,∠C=70°,AB=15cm ,则∠C ′=_________,A ′B ′=__________。
3、如图1,△ABD ≌△BAC ,若AD=BC ,则∠BAD 的对应角是________。
4、如图2,在△ABC 和△FED ,AD=FC ,AB=FE ,当添加条件__________时,就可得到△ABC ≌△FED 。
(只需填写一个你认为正确的条件)5、如图3,在△ABC 中,AB=AC ,AD ⊥BC 于D 点,E 、F 分别为DB 、DC 的中点,则图中共有全等三角形________对。
6、如图4,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是 .7、如图5,△ABC 中,∠C=90°,CD ⊥AB 于点D ,AE 是∠BAC 的平分线,点E 到AB 的距离等于3cm ,则CF= cm.8、如图6,在△ABC 中,AD =DE ,AB =BE ,∠A =80°,则∠CED =_____.9、P 是∠AOB 平分线上一点,CD ⊥OP 于F ,并分别交OA 、OB 于CD ,则CD_____P 点到∠AOB 两边距离之和。
(填“>”,“<”或“=”)10、AD 是△ABC 的边BC 上的中线,AB =12,AC =8,则中线AD 的取值范围是二、选择题:(每小题5分,共30分)11、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等, 其中真命题的个数有( )A 、3个B 、2个C 、1个D 、0个12、如图7,已知点E 在△ABC 的外部,点D 在BC 边上,AD ECB图4ABDE 图1 图2 图3图5图6DE 交AC 于F ,若∠1=∠2=∠3,AC=AE ,则有( ) A 、△ABD ≌△AFD B 、△AFE ≌△ADCC 、△AEF ≌△DFCD 、△ABC ≌△ADE13、下列条件中,不能判定△ABC ≌△A ′B ′C ′的是( ) A 、AB=A ′B ′,∠A=∠A ′,AC=A ′C ′B 、AB=A ′B ′,∠A=∠A ′,∠B=∠B ′C 、AB=A ′B ′,∠A=∠A ′,∠C=∠C ′D 、∠A=∠A ′,∠B=∠B ′,∠C=∠C ′14、如图8所示,90E F ∠=∠=,B C ∠=∠,AE AF =,结论:①EM FN =;②CD DN =;③FAN EAM ∠=∠;④ACN ABM △≌△.其中正确的有( )A .1个B .2个C .3个D .4个15、全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC 和△A 1B 1C 1是全等(合同)三角形,点A 与点A 1对应,点B 与点B 1对应,点C 与点C 1对应,当沿周界A →B →C →A ,及A 1→B 1→A 1环绕时,若运动方向相同,则称它们是真正合同三角形(如图9),若运动方向相反,则称它们是镜面合同三角形(如图10),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°(如图11),下列各组合同三角形中,是镜面合同三角形的是( )16、如图12,在△ABC 中,∠C=90°,AD 平分∠BAC 交BC 于D , 若BC=64,且BD :CD=9:7,则点D 到AB 边的距离为( ) A 、18 B 、32 C 、28 D 、24三、解答下列各题:(17-18题各8分,19-2280分)17、如图13,点A 、B 、C 、D AB=DC ,AE//DF ,AE=DF ,求证:EC=FB18、如图14,AE 是∠BAC 的平分线,AB=AC 。
全等三角形练习题(含答案)
1.下列图形中,和所给图形全等的图形是A.B.C.D.2.下列说法正确的有①两个图形全等,它们的形状相同;②两个图形全等,它们的大小相同;③面积相等的两个图形全等;④周长相等的两个图形全等.A.1个B.2个C.3个D.4个3.如图,ΔABC≌ΔCDA,∠BAC=∠DCA,则BC的对应边是A.CD B.CA C.DA D.AB4.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为A.2 B.3 C.5 D.2.55.如图,△ABC≌△AED,∠C=40°,∠EAC=30°,∠B=30°,则∠EAD=A.30°B.70°C.40°D.110°6.如图,△AOB≌△COD,∠AOB=∠COD,∠A=∠C,则∠D的对应角是__________,图中相等的线段有__________.7.如图,△ABE≌△ACD,AE=5 cm,∠A=60°,∠B=30°,则∠ADC=__________°,AD=__________cm.8.如图,已知,△ABC≌△BAE,∠ABE=60°,∠E=92°,则∠ABC的度数为__________度.9.如图,△ACB与△BDA全等,AC与BD对应,BC与AD对应,写出其余的对应边和对应角.10.如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.(1)求∠EBG的度数.(2)求CE的长.11.如图,△ABC≌△CDA,且AD=CB,下列结论错误的是A.∠B=∠D B.∠CAB=∠ACD C.BC=CD D.AC=CA12.如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是A.PO B.PQ C.MO D.MQ13.已知△ABC≌△DEF,若AB=5,BC=6,AC=8,则△DEF的周长是__________.14.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出其他的对应边和对应角.15.如图,ΔABC≌ΔDEF,∠A=25°,∠B=65°,BF=3 cm,求∠DFE的度数和EC的长.16.(2016•厦门)如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE=A.∠B B.∠A C.∠EMF D.∠AFB4.【答案】B【解析】∵△ABE≌△ACF,AB=5,∴AC=AB=5,∵AE=2,∴EC=AC−AE=5−2=3,故选B.5.【答案】D【解析】∵△ABC≌△AED,∴∠C=40°,∠B=30°,∴∠EAD=∠BAC=180°-∠B-∠C=110°,故选D.6.【答案】∠OBA;OA=OC,OB=OD,AB=CD【解析】∵△AOB≌△COD,∴∠D=∠OBA,OA=OC,OB=OD,AB=CD.故答案为:∠OBA;OA=OC,OB=OD,AB=CD.7.【答案】90;5【解析】在三角形ABE中,∠A=60°,∠B=30°,所以,∠AEB=180-∠A-∠B=90°.因为,△ABE≌△ACD,所以AD=AE=5 cm,∠ADC=∠AEB=90°.故答案为:90;5.11.【答案】C【解析】∵△ABC≌△CDA,∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A、B、D正确,不符合题意,BC不一定等于CD,C错误,符合题意,故选C.12.【答案】B,则只需测出PQ的长即可求出M、N之间的距离.故选B.【解析】∵△PQO≌△NMO,∴PQ MN13.【答案】19【解析】∵AB=5,BC=6,AC=8,∴△ABC的周长=AB+BC+AC=5+6+8=19.∵△ABC≌△DEF,∴△DEF的周长等于△ABC的周长,∴△DEF的周长是19.故答案为:19.14.【解析】∵△ABE≌△ACD,∠1=∠2,∠B=∠C,∴点A的对应点是A,点B的对应点是C,点E的对应点是D,∴∠BAE与∠CAD是对应角,AB与AC,BE与CD,AD与AE是对应边.15.【解析】△ABC中,∠A=25°,∠B=65°,∴∠BCA=180°-∠A-∠B=180°-25°-65°=90°,∵△ABC≌△DEF,∴∠BCA=∠DFE,BC=EF,∴EC=BF=3 cm,∴∠DFE=90°,EC=3 cm.16.【答案】A【解析】∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,∴∠DCE=∠B,故选A.。
(完整版)全等三角形练习题及答案
全等三角形练习题及答案1、下列判定直角三角形全等的方法,不正确的是()A、两条直角边对应相等。
B、斜边和一锐角对应相等。
C、斜边和一条直角边对应相等。
D、两锐角相等。
2、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C3、下列各条件中,不能作出唯一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ABC与△DEF中,已知AB=DE;∠A=∠D;再加一个条件,却不能判断△ABC与△DEF全等的是().A. BC=EF B.AC=DFC.∠B=∠E D.∠C=∠F5、使两个直角三角形全等的条件是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等6、在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是()A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,还须从下列条件中补选一个,错误的选法是()A、∠ADB=∠ADCB、∠B=∠CC、DB=DCD、AB=AC8、如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为A. 40°B. 80°C.120°D. 不能确定9、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为()A.600 B.700C.750D.85010、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )A. 150°B.40°C.80°D. 90°11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( )A.①③ B.②④ C.②③④ D.①②④12、下列条件中,不能判定两个三角形全等的是()A.三条边对应相等 B.两边和一角对应相等C.两角及其一角的对边对应相等 D.两角和它们的夹边对应相等13、如图,已知,,下列条件中不能判定⊿≌⊿的是()(A)(B)(C)(D)∥14、如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为().A.50° B.30° C.80° D.100°15、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的度数是.16、在△ABC和△中,∠A=44°,∠B=67°,∠=69°,∠=44°,且AC=则这两个三角形全等(填“一定”或“不一定”)17、如图,,,,在同一直线上,,,若要使,则还需要补充一个条件:或.18、(只需填写一个你认为适合的条件)如图,已知∠CAB=∠DBA,要使△ABC≌△BAD,需增加的一个条件是。
全等三角形测试题及答案
全等三角形测试题及答案一、选择题1. 下列选项中,哪两个三角形是全等的?A. ∠A=∠B,AB=BCB. ∠A=∠B,AC=BDC. ∠A=∠C,AB=ACD. ∠A=∠B,AB=BC,AC=BD2. 如果两个三角形的对应边成比例,且夹角相等,这两个三角形是:A. 相似但不全等B. 必然全等C. 不一定全等D. 无法判断二、填空题3. 根据全等三角形的性质,如果两个三角形的对应角相等,且对应边成比例,那么这两个三角形是_________。
4. SAS全等条件指的是_________。
三、判断题5. 如果两个三角形的三边对应相等,那么这两个三角形一定全等。
()6. 根据HL全等条件,直角三角形中,如果斜边和一条直角边对应相等,那么这两个直角三角形全等。
()四、解答题7. 已知三角形ABC和三角形DEF,其中∠A=∠D=90°,AB=DE,AC=DF,求证:三角形ABC全等于三角形DEF。
8. 如图所示,三角形ABC和三角形DEF在平面直角坐标系中,点A(2,3),B(4,5),C(1,1),点D(-1,-2),E(1,-1),F(-2,-4)。
若AB=DE,AC=DF,∠BAC=∠EDF,请证明三角形ABC全等于三角形DEF。
五、综合题9. 在三角形ABC中,点D在BC上,若AD平分∠BAC,且BD=DC,求证:AB=AC。
10. 已知三角形ABC和三角形DEF,其中AB=DE,∠B=∠D,∠C=∠E,求证:三角形ABC全等于三角形DEF。
答案:一、选择题1. 答案:D2. 答案:A二、填空题3. 答案:相似4. 答案:边角边三、判断题5. 答案:正确6. 答案:正确四、解答题7. 解:由于∠A=∠D=90°,AB=DE,AC=DF,根据直角三角形的HL全等条件,我们可以得出三角形ABC全等于三角形DEF。
8. 解:由于AB=DE,AC=DF,∠BAC=∠EDF,根据SAS全等条件,我们可以得出三角形ABC全等于三角形DEF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图 4 C A D B E 图2 A
B D
C E
F 图1 图3 45321第十一章 全等三角形综合复习测试题
班级 学号 姓名 分数_______ 一、选一选,看完四个选项后再做决定呀!(每小题3分,共30分) 1.已知等腰三角形的一个内角为50,则这个等腰三角形的顶角为【 】. (A )50
(B )80
(C )50或80
(D )40或65
2. 如图1所示,在△ABC 中,已知点D ,E ,F 分别是BC ,AD ,CE 的中点,且ABC S △=4平方厘米,则BEF S △的值为 【 】. (A )2平方厘米 (B )1平方厘米 (C )
12平方厘米 (D )1
4
平方厘米
3. 已知一个三角形的两边长分别是2厘米和9厘米,且第三边为奇数,则第三边长为【 】. (A )5厘米 (B )7厘米 (C )9厘米 (D )11厘米
4. 工人师傅常用角尺平分一个任意角.做法如下:如图2所示,∠AOB 是一个任意角,在边OA ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合.过角尺顶点C 的射线OC 即是∠AOB 的平分线.这种做法的道理是 【 】. (A )HL (B )SSS (C )SAS (D )ASA
5. 利用三角形全等所测距离叙述正确的是( )
A.绝对准确
B.误差很大,不可信
C.可能有误差,但误差不大,结果可信
D.如果有误差的话就想办法直接测量,不能用三角形全等的方法测距离 6. 在图3所示的3×3正方形网格中,∠1+∠2+∠3+∠4+∠5等于 【 】. (A )145° (B )180° (C )225° (D )270° 7. 根据下列条件,能判定△ABC ≌△A ′B ′C ′的是 【 】. (A )AB =A ′B ′,BC =B ′C ′,∠A =∠A ′ (B )∠A =∠A ′,∠B =∠B ′,AC =B ′C ′
(C )∠A =∠A ′,∠B =∠B ′,∠C =∠C ′
(D )AB =A ′B ′,BC =B ′C ′,△ABC 的周长等于△A ′B ′C ′的周长 8. 如图4所示,△ABC 中,∠C =90°,点D 在AB 上,BC =BD ,DE ⊥AB 交AC 于点E .△ABC 的周长为12,△ADE 的周长为6.则BC 的长为 【 】. (A )3 (B )4 (C )5 (D )6
9. 将一副直角三角尺如图5所示放置,已知AE BC ∥,则AFD ∠的度数是 【 】. (A )45
(B )50 (C )60
(D )75
图12 图9 A
'C
A D
B E 21图10
C A
D B
E
F 图6
m n
C
A
B
图11 12C A D B E
F M N O A
B
C
D E F
图5
D
A
O
E
C
B D
A
C B
图7 图8
10. 如图6所示,m ∥n ,点B ,C 是直线n 上两点,点A 是直线m 上一点,在直线m 上另找一点D ,使得以点D ,B ,C 为顶点的三角形和△ABC 全等,这样的点D 【 】. (A )不存在 (B )有1个 (C )有3个 (D )有无数个
二、填一填,要相信自己的能力!(每小题3分,共30分) 1.在ABC ∆中,若A ∠=1
12
3
B C ∠=∠,则ABC ∆是 三角形.
2. 如图7所示,BD 是ABC ∆的中线,2AD =,5AB BC +=,则ABC ∆的周长是 .
3. 如图8所示所示,在ABC ∆中,BD ,CE 分别是AC 、AB 边上的高,且BD 与CE 相交于点O ,如果135BOC ∠=︒,那么A ∠的度数为 .
4. 有5条线段,长度分别为1厘米、2厘米、3厘米、4厘米、5厘米,以其中三条线段为边长,共可以组成________个形状不同的三角形.
5. 如图9所示,将纸片△ABC 沿DE 折叠,点A 落在点A ′处,已知∠1+∠2=100°,则∠A 的大小等于_____度.
6. 如图10所示,有两个长度相同的滑梯(即BC =EF ),左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,则△ABC ≌△DEF ,理由是______.
7. 如图11所示,AD ∥BC ,AB ∥DC ,点O 为线段AC 的中点,过点O 作一条直线分别与AB 、CD 交于点M 、N .点E 、F 在直线MN 上,且OE =OF .图中全等的三角形共有____对.
8. 如图12所示,要测量河两岸相对的两点A 、B 的距离,在AB 的垂线BF 上取两点C 、D ,使BC =CD ,过D 作BF 的垂线DE ,与AC 的延长线交于点E ,则∠ABC =∠CDE =90°,BC =DC ,∠1=______,△ABC ≌_________,若测得DE 的长为25 米,则河宽AB 长为_________.
9. 如图13所示,有一底角为35°的等腰三角形纸片,现过底边上一点,沿与底边垂直的方向将其剪开,分成三角形和四边形两部分,则四边形中,最大角的度数是 .
10. 如图14所示,三角形纸片ABC ,AB =10厘米,BC =7厘米,AC =6
厘米.沿 过点B 的直线折叠这个三角形,使顶点C 落在AB 边
C A
D B
E
图13
35°
D A
E
C B 上的点E 处,折痕为B
D ,则△AED 的周长为______厘米.
三、做一做,要注意认真审题呀!(本大题共38分) 1.(8分)如图15所示,在ABC ∆中,已知AD BC ⊥,64B ∠=︒,56C ∠=︒. (1)求BAD ∠和DAC ∠的度数;
(2)若DE 平分ADB ∠,求AED ∠的度数.
图15 2.(10分)已知:线段a ,b ,c (如图16所示),画△ABC ,使BC =a ,CA =b ,AB =c .(保留作图痕迹,不必写画法和证明)
3.(10分)图17为人民公园的荷花池,现要测量此荷花池两旁A 、B 两棵树间的距离(不能直接测量),请你根据所学三角形全等的知识,设计一种测量方案求出AB 的长(要求画出草图,写出测量方案和理由). 4.(10分)如图18所示,△ADF 和△BCE 中,∠A =∠B ,点D ,E ,F ,C 在同—直线上,有如下三个关系式:①AD =BC ;②DE =CF ;③BE ∥AF .
(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的结论.
图16 b a c
图17
(2)选择(1)中你写出的—个正确结论,说明它正确的理由.
四、拓广探索!(本大题共22分) 1.(10分)如图19,在△ABC 中,点E 在AB 上,点D 在BC 上,BD =BE ,∠BAD =∠BCE ,AD 与CE 相交于点F ,试判断△AFC 的形状,并说明理由.
2.(12分)两个大小不同的等腰直角三角形三角板如图20①所示放置,图20②是由它抽象
出的几何图形,B C E ,,在同一条直线上,连结DC . (1)请找出图20②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母); (2)试说明:DC BE .
图18 F
E B
D
A C 图
20
①
②
B
C D F
A
E 图19
参考答案
一、1~10 CB C BC CD ADB. 二、1. 直角. 2.9. 3. 45°. 4.3. 5. 50. 6. HL. 7.4. 8. ∠2,△EDC ,25 m. 9. 125°. 10. 9.
三、1. (1)90905634DAC C ∠=︒-∠=︒-︒=︒. (2)109AED ∠=︒. 2.画图略.
3.方案不惟一,画图及理由略.
4.(1)如果①、③,那么②或如果②、③,那么①; (2)选择“如果①、③,那么②”证明,过程略. 四、1. △AFC 是等腰三角形.理由略 . 2.(1)图2中ABE ACD △≌△.
理由如下:ABC △与AED △均为等腰直角三角形
AB AC ∴=,AE AD =,90BAC EAD ∠=∠=, BAC CAE EAD CAE ∴∠+∠=∠+∠, 即BAE CAD ∠=∠ , ABE ACD ∴△≌△.
(2)说明:由(1)ABE ACD △≌△知45ACD ABE ∠=∠=, 又45ACB ∠=
90BCD ACB ACD ∴∠=∠+∠=,
DC BE ∴⊥。
