第三章 静定结构的内力计算(三铰拱)
结构力学 第三章 静定结构的内力计算(典型例题练习题).
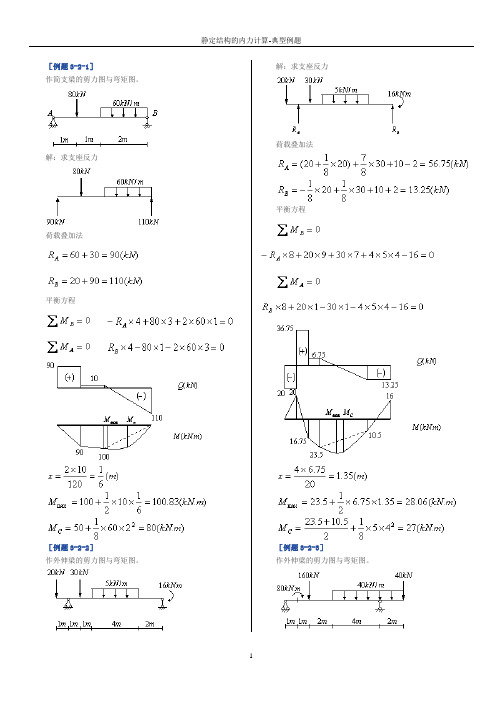
[例题3-2-1]作简支梁的剪力图与弯矩图。
解:求支座反力荷载叠加法平衡方程[例题3-2-2]作外伸梁的剪力图与弯矩图。
解:求支座反力荷载叠加法平衡方程[例题3-2-3]作外伸梁的剪力图与弯矩图。
解:求支座反力荷载叠加法平衡方程[例题3-3-1]作多跨静定梁的内力图。
解:求支座反力荷载叠加法[例题3-3-2]作三跨静定梁的内力图。
解:求支座反力[例题3-3-3] 作多跨静定梁的内力图。
解:求支座反力[例题3-4-1] 作静定刚架的内力图解:求支座反力[例题3-4-2]作静定刚架的内力图解:求支座反力[例题3-4-3]作静定刚架的内力图解:求支座反力[例题3-4-4]作静定刚架的内力图解:求支座反力[例题3-4-5]作三铰刚架的内力图解:求支座反力[例题3-4-6]作三铰刚架的内力图解:求支座反力??[例题3-4-7]作静定刚架的内力图解:求支座反力[例题3-4-8]作静定刚架的图解:[例题3-4-9]作静定刚架的图解:[例题3-4-10]作静定刚架的图解:[例题3-4-11]作静定刚架的图解:[例题3-4-12]作静定刚架的图解:[例题3-4-13]作静定刚架的图解:[例题3-4-14]作静定刚架的图解:求支座反力?[例题3-4-15]作静定刚架的图解:[例题3-5-1]???求支座反力当时?????? ? ?????[例3-5-2]??? 试求对称三铰拱在竖向均布荷载作用下的合理轴线。
解:相应简支梁的弯矩方程为水平推力合理轴线方程为合理轴线为一抛物线。
[例3-6-1]用结点法求桁架各杆的内力。
解:求支座反力解题路径:以结点为对象以结点为对象以结点为对象以结点为对象[例3-6-2]用结点法求桁架各杆的内力。
解:求支座反力平衡方程荷载叠加法解题路径:以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象[例3-6-3]用结点法求桁架各杆的内力。
解:利用对称性,求支座反力解题路径:以结点为对象?以结点为对象以结点为对象以结点为对象例3-6-4]指出桁架的零杆。
第3章静定结构受力分析三铰拱

FN FQ0 sin FH cos
FQ FQ0 cos FH sin
(2)
M M 0 FH y
概念:
上式即为用相应简支梁的内力 表示的拱的内力式。当将上式 用作拱的内力计算公式时,可 以叫做公式法。
3.拱的内力图特征和制作
分析
由式2可知,在竖向荷载作用 下静定拱内力与相应简支梁
例1 图(a)所示三铰拱的拱轴 为半圆形。计算截面K1、K2的 内力。
FP=10kN
R=4m
(a)
解 1)求支座反力
竖 MA 0
向 FBy
1 [q R 2R
R 2
FP (R
R cos )] 11.33kN()
反 MB 0
力 FAy
1 [q R 2R
力与前规定相同;弯矩以使 拱的下侧受拉为正;
以图示三铰刚架为例说明拱的内 力计算的一般方法。
FH F Ay
FH
F By FN0
解:
截开指定截面K,取左侧为隔 离体,见下页图(c)(d),截 面上的内力均按规定的正方 向示出 。
M FN
FH
FQ
FAy
(c)
M0 0
FQ0
(d)
在轴力和剪力的两个正交方 向上建立投影方程,并建立 关于截面形心的力矩方程, 即得:
内力及拱水平反力有关。其
中拱水平反力对应确定的荷
载是一常数。此外,拱轴力
和剪力还与所计算截面外法
线与x轴的夹角a有关。
结论
拱轴上内力有以下3个特点:
1
不管是在均布荷载下还是在集 中荷载下,拱的三个内力图都 是曲线图形。
三铰拱的内力计算

XA YA
O
4m
4m
XB
XA
A YA
YB
将拱从K位置截开,取AK。 ΣmK=0; M K YA 2 X A 2 3 0, MK=-1.464kN.m(外侧受拉)
C
两铰A、B间距 l 称为拱跨;
l/2
l/2
计算图示三铰拱K截面的内力。 P
K C
C
f
XC
y
A
B
f
A
XA YA
x l/2 l/4
XB
XA
YC YA l/2
l/4 YB
求三铰拱的内力必须先求支座反力。
l 1 取整体,求竖向反力: ΣmB=0; YA l P 0, YA P 4 4
P
A K B
XA YA
x l
l/4
MK=YA· x
YB
比较可知,三铰拱横截面的弯矩要比同跨度简支梁对应截面 的弯矩小。梁与拱的承载能力主要取决于弯矩,同跨度、同截面 的三铰拱要比简支梁承载能力大。
合理选择拱的轴线可使横截面的弯矩为零。使拱各截面的弯 矩皆为零的轴线称为合理拱轴线,如均布荷载下三铰拱的合理拱 轴线为抛物线。 【例4—1】求图示半圆形三铰拱K截面的弯矩。 P=4kN C
由
ΣX=0; NKcosα+QKsin α+XA=0
ΣY=0; NKsinα-QKcosα+YA=0
求K截面的轴力NK和剪力QK。
P
K
C
MK
K
α NK QK
Hale Waihona Puke f yA By XB XA
A
XA YA
x
x
l/2 l/4 l/4 YB
3静定结构的内力计算

①简支梁
②外伸梁
③悬臂梁
3
二、梁的内力
1、内力计算法——截面法
P1
A
m
FAx
K
n
P2 B
8
斜梁介绍
工程中,斜梁和斜杆是常遇到的,如楼梯梁、刚架中的斜杆等。斜梁 受均布荷载时有两种表示方法: (1)按水平方向分布的形式给出(人群、雪荷载等),用 q 表示。 (2)按沿轴线方向分布方式给出(自重),用 q’ 表示。
q 与 q’间的转换关系:
qdx = qds q = q
cos
dM dx
= FQ
无荷载区段 平行轴线
FQ图
M图
斜直线
均布荷载区段 集中力作用处 集中力偶作用处
↓↓↓↓↓↓
+ -
二次抛物线
凸向即q指向
发生突变
+P -
出现尖点
尖点指向即P的指向
无变化
发生突变
m
两直线平行
注备
FS=0区段M图 FS=0处,M 平行于轴线 达到极值
12
三、叠加法作弯矩图
1. 叠加原理: 几个载荷共同作用的效果,等于各个载荷单独
吊杆
带拉杆的三铰拱
拉杆折线形
拉杆
花篮螺丝
带吊杆的三铰拱
3、三铰拱的内力计算
1)、拱的内力计算原理仍然是截面法。 2)、拱通常以受压为主,因此规定轴力以受压为正。 3)、计算时常将拱与相应简支梁对比,通过对比完成计算。
45
第三章_静定结构的受力分析(第3课)

y= 4f x (l - x ) l2
0 M C 16? 6 3创 9 6 H= = = 10.5kN f 4 2 计算内力
3kN/m
y
10kN
D B
D截面的几何参数
4f 4´ 4 x(l - x) = ? 9(12 9) = 3m 2 2 l 12 dy 4 f 4´ 4 tgj D = = 2 (l - 2 x) = (12 - 2? 9) dx l 122 y=
31
结点A
å
Fy = 0
FyAD
FNAD FxAD
FyAD = - 30kN FxAD = FyAD (lx l y ) = - 30(2 1) = - 60kN FNAD = FyAD (l l y ) = - 30( 5 1) = - 67.08kN (压)
A
FNAE
30kN
5
2
1
å
结点E
Fx = 0
2) 截面所截杆数大于3,但除某一杆外,其余 各杆都交于同一点(或都彼此平行),则此杆也是 单杆。
合理拱轴线
均匀水压力
q
圆弧
A
B
土压力
qc q(x) x C
y=
qc (cosh k x - 1) g
悬链线
A y B
总结
要点:
三铰拱的主要特征:由曲杆组成;竖向荷载下产生水平支座反力;
支座反力和内力的计算公式; 拱截面上的应力比梁的均匀.,因此拱形结构比梁能跨越更大的跨度, 承担更大的荷载; 合理拱轴线.
解
M 0 ( x) =
B
y
A
l 2
f
x
ql 1 qx x - qx 2 = (l - x) 2 2 2
三铰拱的内力计算 重庆大学

(2)计算各截面几何参数(y和φ )
1) 求y 将l 和f 代入拱轴线方程
q=10kN/m FP=40kN
y FH=60kN A
C E E
D
f=4m
yE
B FH=60k
x
y 4 f x(l x)
l2
得
x2
y x
FVA=70kN 4m
4m 4m l=16m
4m FVB=50kN
q=10kN/m A
4
10 8 12 16
70
kN( )
FV B
FV0B
108 4 16
4012
50
kN( )
FH
M
0 C
f
508 40 4 4
60 kN(推力)
q=10kN/m FP=40kN
A
B
DCE
16m
FV0A
FV0B
All Rights Reserved
重庆大学土木工程学院®
2、水平支座反力
由三铰拱整体平衡
条件 Fx 0 ,可得
a2
a1 FP1 KC
FP2
yf
FHA
Ax
B FHB
FHA = FHB = FH
取铰C左边隔离体,
由 MC 0,可得
FV
A
l 2
FP1
l 2
a1
FH
f
0
M
0 C
FH f
0
FVA
FH0A 0 A
(10)(0.894) (60)(0.447) 17.88 kN
第3章 三铰拱
(二) 对称三铰拱的数解法
1. 计算支座反力
图示三铰拱中,共有 四个反力: VA、HA、VB、HB。 根据整体的平衡 条件可建立三个 平衡方程: ∑MA=0 ∑MB=0 ∑X=0 再取中间铰一侧隔离 体, ∑ MC=0, 由这四个方程可 解出四个反力。
由∑MB= 0,得: VAl-P1b1- P2b2-…= 0 VA= (P1b1 + P2b2 + …)/ l V0A 由∑MA= 0,得: VB= (P1a1+ P2a2+…)/ l V0B 把两个竖向反力VA 、VB与相应简支梁支座反力V0A 、 V0B 相比,可知竖向荷载作用下,对称三铰拱的竖向反力与 其相应简支梁的反力完全相同。
两个投影方程可用拱轴在该点的法线n和切线t为 投影轴。
∑n = 0 ,得: QD = VA cosφD -P1 cosφD -P2 cosφD -H sinφD = (V0A-P1-P2) cosφD -H sinφD
= Q0D cosφD -H sinφD
∑t = 0 ,得: ND = VA sinφD - P1 sinφD -P2 sinφD +H cosφD = (V0A-P1-P2) sinφD +H cosφD
由∑X= 0,得: HA= HB = H 中间铰左侧隔离体 ∑MC=0 得:
∑ MC =
VAl1-P1(l1 - a1) - P2(l1 - a2) - P3(l1 - a3)- H f = 0 得: H=[VAl1-P1(l1 - a1)- P2(l1 - a2)- P3(l1 - a3)] / f 因 VA = V0A ,得:H= M0C / f M0C为相应简支梁截面C的弯矩。
最后根据本例的已知条件,进行具体计算。
VA=VB= V0A = q l / 2= 4× 16 / 2 = 32kN H = (q l 2 / 8) / f = (4× 162 / 8) / 4 = 32kN
结构力学§3-8 三铰拱.
0 C
FH
f
0
FH
M
0 C
f
竖向反力: FVA
FPibi L
FV0A
FVB
FP i ai L
FV0B
水平反力:
FHA
FHB
FH
M
0 C
f
由前面计算可见: ●竖向反力与相应简支梁的相同;
●水平反力FH与拱高f成反比,与拱轴的曲线形式无关;
M
0不变时,
C
f小,则FH大;
QC
1050.832 82.50.555 41.6kN
FN左D FQ0D左SinD FHCosD
MD0 D
FQ0左D
1050.555 82.50.832 127kN
d) 求D右剪力、轴力:
100kN
FQ右D FQ0D右CosD HSinD
(105 100) 0.832 82.5 0.555 41.6kN
核心区
(2)合理拱轴线
d/3 d/3 d/3
M
K
FNK
RK
ek
K0
——在给定荷载下,适当选取拱轴线,使拱仅有轴力,而M=0, 拱轴线与压力线与完全重合,这样的拱轴线称为合理拱轴线。
数解法求合理拱轴பைடு நூலகம்:
已知:
Mk
M
0 k
Hyk
令:
Mk
M
0 k
Hyk
0
则有:
yk
M
0 k
H
[例3] 求图示对三铰拱在均布荷载作用下的合理拱轴线。
MD
F右 ND
D F右
建筑力学10-静定结构内力三
由上述各式可以得出: VA=V0A VB=V0B HA=HB=M0C/f 支座水平推力与拱轴曲线形状无关,而只与荷载 及三个铰的位置有关;当荷载与跨度确定时,M0C为定 值,水平推力与矢高成反比关系,f愈大,拱愈高,则 推力愈小;f愈小,拱愈扁平,则推力愈大。
图8.37
(2) 内力的计算 拱的内力计算时,仍按截面法计算,且截面应与 拱轴垂直,该截面的位置由截面形心的坐标x、y及该 截面处拱轴切线的倾角φ来确定。 如图8.38(a)所示,设计算截面K的三个参数分别为 xK、yK、φK,该截面上的内力有MK(内侧受拉为正)、 QK(绕隔离体顺时针转动者为正)和NK(以压力为正)。 下面分别讨论三种内力的计算方法。
BE段:取结点B为隔离体,如图8.33(b)所示,
∑MB=0:MBE+MBC-MBD=0 MBE=0 以竖向为y坐标轴,向上为正,以水平向为x坐标轴,向右为 正,以B为原点,则: ∑X=0:QBE+NBDcosα-NBCcosα+QBDsinα-QBCsinα=0 QBE=0
① 弯矩的计算
取K截面以左为隔离体,如图8.38(c)所示,对K截 面取矩:
∑MK=0: HAyK-VAxK+P1(xK-a1)+MK=)]-HAyK
相应简支梁在相应位置处的弯矩也可由静力平衡 条件求出,如图8.38(b)、(d)所示:
图8.34
8.7.3 刚架的内力求解
1,内力求解的方法——与梁有相似之处,内力有弯矩、剪力还有轴力; 2,刚架结构内力计算的步骤:
1)支坐反力; 2)用简易法画各段的受力图; 3)分段画出内力图(M、Q、N)。
静定梁、静定平面刚架和三铰拱的计算
举例: 3、举例:
解: 研究整体: 研究整体 :
ql (↑) 2
∑M ∑M
B
=0
VA =
研究 AC 段:
C
=0
ql 2 HA = (→) 8f
任一截面的弯矩(参阅左下隔离体图) 任一截面的弯矩 (参阅左下隔离体图):
M ( x) = ql ql 2 qx 2 ⋅x− ⋅y− 2 8f 2
令上式等于零,可得合理拱轴 : 令上式等于零, 可得合理拱轴:
例题2 例题2: 图示三跨静定梁,全长承受均布荷载q 试确定铰E 图示三跨静定梁,全长承受均布荷载q,试确定铰E、F的位置,使中 的位置, 间一跨支座的负弯矩与跨中正弯矩数据数值相等。 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
解:
1 研究 AE 杆: V E = q (l − x ) 2 1 1 研究 EF 杆: M B = M C = q (l − x ) x + qx 2 2 2 ∵MB + MC = ql 2 (叠加弯矩值) 8
解: (一)求支座反力 一 求支座反力 研究整体: 研究整体:
∑X =0 ∑M = 0 ∑M = 0
A B
HA = HB VB = 80kn(↑) V A = 80kn(↑)
取半刚架研究: 取半刚架研究:
∑M
C
=0
H B = 20kn(←) H A = 20kn(→)
校核: 校核 ∑ Y = 80 + 80 − 20 × 8 = 0 (二)绘内力图 二 绘内力图 (三)内力图校核 略) 内力图校核(略 三 内力图校核
拟简支梁法” 3、用“拟简支梁法”绘弯矩图
结论: 结论: 弯矩图时, 用叠加法绘 弯矩图时,先绘出控制截面 的弯矩竖标,其间若无外荷载作用, 的弯矩竖标,其间若无外荷载作用,可用直线 相连;若有外荷载作用,则以上述直线为基线, 相连;若有外荷载作用,则以上述直线为基线, 再叠加上荷载在相应简支梁上的弯矩图。 再叠加上荷载在相应简支梁上的弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A FAH FAV y F a x MK F NK K y FQ K t n φK x
f
K
C
B
0 M K M K FH y 0 F F QK QK cos FH sin F F 0 sin F cos QK H NK
K
C
B
l
0 FB V
弯矩
m
K
0
M K FAV x FH y F ( x a) 0
0 MK
M K FAV x F ( x a) FH y
0 MK FH y
水平推力的存在,拱截面上的弯矩比代梁小得多。
结构力学
第3章静定结构的内力计算
y
剪力与轴力
a F A FAH FAV
A
0 FA H 0 FA V
b K C B FBH l
A FAH FAV a x
F
MK F NK K y FQ K t
n φK x
f
F K C
FBV
B
Ft 0 Fn 0
0 FQK FQ K cos F H sin
0 FN K FQ K sin F H cos
A B
结构力学
第3章静定结构的内力计算
二、三铰拱计算
a F F
0 FA H FAH
1、支反力
b
0 FAV FA V Fb l
A A
0 FA V FAV
K C K C
B B
0 FB V FBV
FBV FB0V Fa l
FBH
f
l l
FAH
0 MC FBH FH f ( Fa l ) (l 2) Fa f 2f
结构力学
第3章静定结构的内力计算
2、拱与曲粱的基本区别
qC qA A FAH FAV l FBV C qB B FBH
F1 A FAH FAV
F2 B
f
FBV
有无水平推力存在。 由于水平推力的存在,使拱与同荷载的简支梁相比:
M
FN
拱成为以受压为主或单纯受压的结构。 充分发挥抗压强度高的廉价建筑材料,如砖、石、砼等。
结构力学
第3章静定结构的内力计算
三铰拱内力计算
结构力学
第3章静定结构的内力计算
qC
qC
一、概述
qA A qB
qA A FAH FAV
F1 A FAH FAV
qB C B FBH l
F2 B
A
C
l
C
B
f
f
B
FBV
三铰拱桥 1、定义 在竖向荷载作用下,产生水平推 力的曲杆结构,称为拱。
曲梁
F
FBV
三铰刚架
l
0 FB V
左半拱为方正,右半拱为负。
结构力学
第3章静定结构的内力计算
例题
P59,例4-1
结构力学
第3章静定结构的内力计算
三、合理拱轴线 在一定的荷载作用下,使拱处于均匀受压(无弯矩)状态的轴 线,称为合理拱轴线。 合理拱轴线最经济。 合理拱轴线方程: 令
M0 y FH
M M 0 FH y
结构力学
第3章静定结构的内力计算
3、三铰拱各部分名称
qC qA A FAH FAV l FBV C qB B FBH
拱顶C(顶铰) 拱脚A、B(拱趾) 拱高:f (矢高)
f
跨长:l
矢跨比(f/l)
矢跨比是拱的重要几何特征,其值可在1/10~1之间变化。 矢跨比要根据具体工程条件来确定。
拱轴线形状:常用的有抛物线、圆弧线、悬链线等。 带拉杆的三铰拱
拱截面上有较大的轴力。
l
0 FB V
dy tan 式中: 称为截面的倾角。 dx 截面与竖直线的夹角,或K点切线与水平线的夹角。 只取锐角,水平线逆时针转到拱切线为正,反之为负。 故:左半拱为方正,右半拱为负。
结构力学
a F A FAH FAV
F A
0 FA H 0 FA V
第3章静定结构的内力计算
圆弧线 轴力为常数
FN q
结构力学
第3章静定结构的内力计算
拱结构的应用(工程结构、生活、体育等)
中国拱桥
扬州拱桥
结构力学
第3章静定结构的内力计算
结构力学
第3章静定结构的内力计算
结构力学
第3章静定结构的内力计算
结构力学
第3章静定结构的内力计算
0
由上式可见,在竖向荷载作用下,三铰拱合理拱轴线的纵坐标 与代梁弯矩图的纵坐标成正比。
结构力学
第3章静定结构的内力计算
例题
y
试求图示三铰拱承受均布荷载时,其合理拱轴线。
q
M0 解: 合理拱轴线方程: y FH C A ql q 2 B 0 x 代梁弯矩方程: M x x 2 2 l 0 2 M ql C q 水平推力: F H A B f 8f FAH 0 M 4f x FAV F BV y 2 x(l x) l FH l 三铰拱在竖向均布荷载作用下,合理拱轴线为抛物线。但上式 中拱高未限定,具有不同矢跨比的一组抛物线均为合理拱轴线。
0fΒιβλιοθήκη 00拱身材料
f
FH
基础处理费用
经济、技术比较确定合理的矢跨比。
结构力学
第3章静定结构的内力计算
拱上填料荷载作用
qA qC q=qC +γ× y qB x B l/2 y
沿拱轴线法向均布荷载作用 (水压力)
q C ρ A
α α
A l/2
f
C
B ρ ρ
悬链线
qC y cosh x 1 FH
代梁:同跨度同荷载的简支梁
结构力学
第3章静定结构的内力计算
2、内力计算
a b F F MK K F C NK a K Ax y FQ K A
y n φK
B
x
FAH FAH FAF VAV
f
FBH
F A
0 FA H 0 FA V
t
l
FBV
已知拱轴线方程: y f ( x)
任意K(x,y,)截面
