超经典带电粒子在磁场中的偏转(几何关系)
第十二讲 磁场对运动电荷的作用 带电粒子在磁场中的偏转

第十二讲磁场对运动电荷的作用带电粒子在磁场中的偏转1.磁场对运动电荷的作用力称为洛仑兹力。
通电直导体在磁场中所受的安培力的实质是磁场作用于导体内的运动电荷的洛仑兹力的合力。
据此,可以推导出,当电荷速度方向与磁场方向垂直时,洛仑兹力的计算公式为。
①当时,。
即磁场对静止的电荷无作用力,磁场只对运动电荷有作用力。
这与电场对其中的静止电荷或运动电荷总有电场力作用是不同的。
对①式中的v,应理解为电荷相对于磁场的运动速度。
当v的大小改变时,洛仑兹力大小也改变。
当电荷运动方向与磁场方向相同或相反,即v与B平行时,由实验可知,。
所以只有当v与B不平行时,运动电荷才受洛仑兹力。
当电荷运动方向与磁场方向夹角为θ时,电荷所受洛仑兹力计算公式为。
2.洛仑兹力的方向,仍用左手定则来判断。
判断时,让磁感线穿入手心,四指指向正电荷运动方向(或负电荷运动方向的反方向),大拇指指向就是洛仑兹力方向。
洛仑兹力的方向具有这样的特点:无论对v与B是否垂直,洛仑兹力总是同时垂直于电荷运动方向与磁场方向。
因此,洛仑兹力不能改变速度的大小,也始终不对电荷做功。
3.一个不计重力的带电粒子,以与磁场垂直的速度进入匀强磁场。
由于它所受的洛仑兹力方向同时垂直于磁场和速度方向,带电粒子只能在垂直于磁场方向的平面内运动。
而且洛仑兹力只改变它的运动方向,不改变它的速度大小,于是该带电粒子在匀强磁场中做匀速圆周运动。
洛仑兹力提供了它作匀速圆周运动所需要的向心力。
4.带电粒子作匀速圆周运动的半径和周期:由可得带电粒子作匀速圆周运动的半径公式:,带电粒子在匀强磁场中作匀速圆周运动的半径大小,是由粒子的质量、带电量、磁感强度以及粒子速度四个因素决定的。
若同种粒子(或荷质比相同的粒子)在同一磁场中作匀速圆周运动时,它们的半径与粒子速度大小成正比。
由得周期公式,周期是由带电粒子的质量、电量、磁感强度三个因素决定的,与速率的大小无关。
5.质谱仪:是测量带电粒子的质量和分析同位素的重要工具。
带电粒子在磁场中的偏转

一、带电粒子在匀强磁场中的运动规律
1、带电粒子以一定的初速度进入匀强磁场, 带电粒子将做怎样的运动?
(1)当v//B , F=0 ,带电粒子以速度v做匀速直线运 动 (2)当v⊥B,带电粒子以入射速度v做匀速圆周运动
洛伦兹力提供向 心力:
周期:
qvB mv 2 / r T 2r 2m
① 粒子进出单一直边界磁场, 入射角等于出射角。 ② 粒子进出圆边界磁场沿半径方向入,沿半径方向出。
作业题答案:
• 1D 2BD 3B 4C 5B 6A 7ABC 8ABCD 9D 10 ACD 11C
• 12 3.2X10-7m/s (π/96)X10-6S
• 0.2 0.1 3 m
• 13 V>Bqd/m t= m/2Bq
• 14 v>dBq/m( 1 cos ) • 15 U=B2L2e/2msin2
第11题、
t
2
T
T 2r 2m
v qB
R tan300 r
a VR o
r
600
c V
600
v qB
半径:
r
mv qB
2、粒子在磁场中运动的解题思路:
找圆心
利用v⊥R 利用弦的中垂线
画轨迹 利用轨迹和V相切
求半径 求时间
几何法求半径
向心力公式求半径
t
2
T
T 2r 2m
v qB
⑴粒子在磁场中运动的角度关系
偏向角 弦切角 圆心角
角度关系:2vຫໍສະໝຸດ A BvO
⑵粒子进入有界磁场的特点
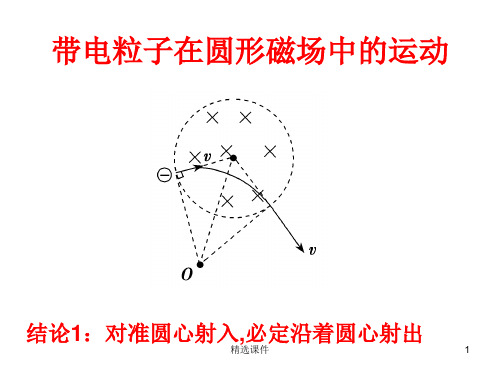
带电粒子在圆形磁场中的偏转

带电粒子在磁场中的运动过程中,其动能和势能之和保持不变。
证明
通过分析带电粒子在磁场中的受力情况和运动轨迹,可以证明能量守恒定律的正确性。
动能定理
动能定理
带电粒子在磁场中运动时,磁场力对粒 子所做的功等于粒子动能的变化量。
VS
证明
通过分析带电粒子在磁场中的受力情况和 运动轨迹,可以证明动能定理的正确性。
回旋加速器
回旋加速器是利用磁场和电场对带电粒子进行加速和控制 的仪器。
通过磁场和电场的交替作用,使带电粒子在圆形轨道上不 断加速,最终获得高能带电粒子,用于科学研究、医疗、 工业等领域。
磁约束核聚变
磁约束核聚变是利用强磁场将高温等 离子体约束在有限的空间内,实现核 聚变反应的能源技术。
通过强大的磁场控制和约束高温等离 子体,使其在有限的时间内发生聚变 反应,释放出大量的能量,是未来清 洁能源的重要发展方向之一。
02
磁场具有方向性和磁力作用,带 电粒子在磁场中会受到洛伦兹力 的作用。
带电粒子的基本性质
带电粒子是指具有电荷的粒子,可以 是电子、质子、离子等。
带电粒子在磁场中会受到洛伦兹力的 作用,其大小和方向由电荷量和速度 决定。
洛伦兹力
洛伦兹力是指带电粒子在磁场中受到的力,其大小为F=qvBsinθ,方向垂直于粒子 运动方向和磁力线方向。
偏转角度与粒子速度关系
分析带电粒子在圆形磁场中的偏转角度与粒子速 度的关系,得出偏转角度随粒子速度的变化规律 。
误差分析
对实验结果进行误差分析,评估实验装置和测量 方法的精度和可靠性。
06 带电粒子在磁场中的应用
质谱仪
质谱仪是利用磁场对带电粒子的偏转作用,对物质进行定性 和定量分析的仪器。
带电粒子在磁场中的偏转

一、知识归纳1、 带电粒子在电场中运动 (1)匀加速运动:2022121mv mv qU t -=注意1:求解时间时,用运动学公式注意2:求解某一方向运动时,也可利用动能定理(2)类平抛运动: ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=====-==+======αθtan 22tan 21212102002022220x yt v at v at v v mv mv y d U q qEy y v v at v dm Uqm Eq a at y tv x y y o y 或2、带电粒子在磁场中运动(1)匀速直线运动:利用平衡条件。
(2)匀速圆周运动:⎪⎪⎪⎩⎪⎪⎪⎨⎧=====⇒=Bq mT t Bq mv R T Bq mv R R v m qvB θπθππ2222,其中R 、θ主要通过几何关系确定。
注意1:确定圆心方法:利用三角函数、勾股定理等注意2:确定圆心角方法:利用速度的偏转角等于圆周运动的圆心角等 3、圆周运动的圆心确定方法法1:已知轨迹上两点的速度方向 法2:已知轨迹上的两点和其中一点的速度方向 法3:已知轨迹上一点的速度方向和半径R 法4:已知轨迹上的两点和半径R 4、带电粒子在有界磁场中运动的极值问题(1)刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切。
(2)当速度v 一定时,弧长(或弦长)越大,圆周角越大,则时间越长。
5、对称规律解题法(1)从同一边界射入的粒子,又从同一边界射出时,速度与边界的夹角相等。
(2)在圆形磁场区域内,沿径向射入的粒子,一定沿径向射出。
(3)在圆形磁场区域内,不沿径向射入的粒子,也满足对称性。
1. 关于带负电的粒子(重力可忽略不计),下面说法中准确的是① 沿电场线方向飞入匀强电场,电场力做功,动能增加 ② 垂直电场线方向飞入匀强电场,电场力做功,动能增加 ③ 垂直磁感线方向飞入匀强磁场,磁场力不做功,动能不变 ④ 沿磁感线方向飞入匀强磁场,磁场力做功,动能增加 A. ①② B. ②③ C. ③④ D. ①④2、如图9,两个初速度大小相同的同种离子a 和b ,从O 点沿垂直磁场方向进入匀强磁场,最后打到屏P 上。
高考物理带电粒子在磁场中偏转资料

高考物理带电粒子在磁场中偏转带电粒子在磁场中偏转的求解策略带电粒子在磁场中偏转问题是历年高考的重点问题,同时也是热点问题。
总结考试中的诸多失误,集中在对这类问题的解法缺乏规律性的认识。
为此本文就求解这类题型的某些规律归纳如下。
一、基本思想因为洛伦兹力F始终与速度v垂直,即F只改变速度方向而不改变速度的大小,所以运动电荷垂直磁感线进入匀强磁场且仅受洛伦兹力时,一定做匀速圆周运动,由洛伦磁力提供向心力,即F qvB mv R==2/。
带电粒子在磁场中运动问题大致可分两种情况:1. 做完整的圆周运动(在无界磁场或有界磁场中);2. 做一段圆弧运动(一般在有界磁场中)。
无论何种情况,其关键均在圆心、半径的确定上。
二、思路和方法1. 找圆心方法1:若已知粒子轨迹上的两点的速度方向,则可根据洛伦兹力F⊥v,分别确定两点处洛伦兹力F的方向,其交点即为圆心。
方法2:若已知粒子轨迹上的两点和其中一点的速度方向,则可作出此两点的连线(即过这两点的圆弧的弦)的中垂线,再画出已知点v的垂线,中垂线与垂线的交点即为圆心。
方法3:若已知粒子轨迹上的两点和能求得的半径R ,则可作出此两点连线的中垂线,从连线的端点到中垂线上的距离为R 的点即为圆心。
方法4:若已知粒子入射方向和出射方向,及轨迹半径R ,但不知粒子的运动轨迹,则可作出此两速度方向夹角的平分线,在角平分线上与两速度方向直线的距离为R 的点即为圆心。
方法5:若已知粒子圆周运动轨迹上的两条弦,则两条弦的中垂线的交点即为圆心。
2. 求半径圆心确定下来后,半径也随之确定。
一般可运用平面几何知识来求半径的长度。
3. 画轨迹在圆心和半径确定后可根据左手定则和题意画出粒子在磁场中的轨迹图。
4. 应用对称规律从一边界射入的粒子,若从同一边界射出时,则速度与边界的夹角相等;在圆形磁场区域内,若粒子沿径向射入,则必沿径向射出。
三、实例分析例1. 如图1所示,两电子沿MN 方向射入两平行直线间的匀强磁场,并分别以v v 12、的速度射出磁场。
带电粒子在磁场中的运动 ppt课件

(2)电子从C到D经历的时间是多少?
(电子质量me=
9.1×10-31kg,电量e ppt课件
=
1.6×10-19C)
13
◆带电粒子在单直边界磁场中的运动
①如果垂直磁场边界进入,粒子作半圆运动后 垂直原边界飞出;
O
O1
B
S
ppt课件
14
②如果与磁场边界成夹角θ进入,仍以与磁场 边界夹角θ飞出(有两种轨迹,图中若两轨迹 共弦,则θ1=θ2)。
运动从另一侧面边界飞出。
量变积累到一定程度发生质变,出现临界状态(轨迹与边界相切)
ppt课件
24
【习题】
1、如图所示.长为L的水平极板间,有垂直纸面向内的
匀强磁场,磁感强度为B,板间距离也为L,板不带电,
现有质量为m,电量为q的带正电粒子(不计重力),从左
边极板间中点处垂直磁感线以速度v水平射入磁场,欲
界垂直的直线上
度方向垂直的直线上
①速度较小时,作半圆运动后 从原边界飞出;②速度增加为 某临界值时,粒子作部分圆周 运动其轨迹与另一边界相切; ③速度较大时粒子作部分圆周 运动后从另一边界飞出
①速度较小时,作圆周运动通过射入点; ②速度增加为某临界值时,粒子作圆周 运动其轨迹与另一边界相切;③速度较 大时粒子作部分圆周运动后从另一边界 飞出
圆心
在过
入射
vB
点跟
d
c
速度 方向
o
圆心在磁场原边界上
①速度较小时粒子作半圆 运动后从原边界飞出;② 速度在某一范围内时从侧 面边界飞出;③速度较大 时粒子作部分圆周运动从 对面边界飞出。
垂直
θv
B
的直
线上
①a 速度较小时粒子作部分b 圆周
带电粒子在圆形磁场中的偏转
v0
O
O1
x
O2 O3
O精5选O课4 件
6
解2: 磁场上边界如图线1所示。
y
设P(x,y)为磁场下边界上的一 点,经过该点的电子初速度与x轴
夹角为 ,则由图可知: x = rsin, y = r-rcos ,
1
v0 Oθ
P (x,y)
r
x
得: x2 + (y-r)2 = r2。
r
O
所以磁场区域的下边界也是半径为r,圆心为(0,r)的
圆弧应是磁场区域的下边界。
两边界之间图形的面积即为所求。图中的阴影区域面 积,即为磁场区域面积:
S2(1 4r2r22)(2精 选1 课)件m e22 B v0 2 2
7
带电粒子在圆形磁场中运动的四个结论
结论1:对准圆心射入,必定沿着圆心射出
结论2:对准圆心射入,速度越大,偏转角和圆 心角都越小,运动时间越短。
33=30°,∠POP′
甲
=60° 故带电粒子进入磁场绕圆心 O′转过 360°-(180°
-60°)=240°又回到中空部分,粒子的运动轨迹如图所示,
故粒子从 P 点进入磁场到第一次回到 P 点时,粒子在磁场
中运动时间为 t1=3×23T=2T T=2Bπqm
粒子在中空部分运动时间为 t2=6vR1,粒子运动的总时间为
B.在n、a之间某点 C在a点 D.在a、m之间某点
anb mv B
d
c
c
精选课件
23
2.如右图所示,在半径为 R 的圆形区域内有匀强磁
场.在边长为 2R 的正方形区 域里也有匀强磁场,两个磁场的磁感应强度大小相
同.两个相同的带电粒子以相同的速率分别从 M、 N 两点射入匀强磁场.在 M 点射入的带电粒子, 其速度方向指向圆心;在 N 点射入的带电粒子, 速度方向与边界垂直,且 N 点为正方形边长的中 点,则下列说法正确的是( )
带电粒子在磁场中的偏转

一、轨道圆的“三个确定”:
(1)如何确定“圆心”
①由两点 O 和两线确 定圆心 。 M
3
312
A. 3 B. 2 C.2 D.3
O1 1 甲 乙
2
O2
【例 3】如图,半径为 R 的圆是一圆柱形匀强磁场区域的横截面(纸面), 磁感应强度大小为 B,方向垂直于纸面向外,一电荷量为 q(q>0)、质量 为 m 的粒子沿平行于直径 ab 的方向射入磁场区域,射入点与 ab 的距 离为R2.已知粒子射出磁场与射入磁场时运动方向间的夹角为 60°,则粒 子的速率为(不计重力)( ).
(1)四个点: 入射点、出射点、轨迹圆心和入射速度直线与出射速度
直线的交点. (2)三个角:
速度偏转角、圆心角、弦切角,其中偏转角等于圆心角, 也等于弦切角的2倍.
情形一 直线边界(进出磁场具有对称性) 1.直线边界(粒子进出磁场具有对称性)
v
B
v
B
O
O
a
v
bv
B v
c
v
O
【例 1】如图,直线 MN 上方存在范围足够大的磁感应强度为 B 的匀
强磁场,一质子(质量为 m、电荷量为 e)以速度 v 从 O 点沿与 MN 成
30°角的方向射入磁场中,若不计质子重力,则( )
qBR qBR 3qBR 2qBR A. 2m B. m C. 2m D. m
v 审题设疑
(1)粒子刚进入磁场时,所受洛伦兹力的方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超经典带电粒子在磁场中的偏转(做了这些不用在做其他的题了)
1.如图所示,一束电子(电量为e)以速度v垂直射入磁感应强度为B、宽度为d
的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为θ=300。
(不计电
子重力)求:
(1) 电子的质量m=?
(2) 电子在磁场中的运动时间t=?
2.三个速度不同的同一种带电粒子,沿同一方向从图中长方形区域的匀强磁场上边缘射入,当它们从下边缘飞出时,对入射方向的偏角分别为90°、60°、30°,则它们在磁场中的运动时间之比为___。
3.如图所示,在半径为r的圆形区域内,有一个匀强磁场,一带电粒子
以速度v0从M点沿半径方向射入磁场区,并由N点射出,O点为圆
心,∠MON=120°,求粒子在磁场区的偏转半径R 及在磁场区中的运动时间。
(粒子重力不计) 4.长为L 的水平极板间,有垂直纸面向内的匀强磁场,如图所示,磁场
强度为B ,板间距离也为L ,板不带电,现有质量为m ,电量为q 的带
正电粒子(不计重力),从左边极板间中点处垂直磁场以速度v 平行极
板射入磁场,欲使粒子不打在极板上,则粒子入射速度v 应满足什么条
件? 5.如图所示,比荷为e/m 的电子垂直射入宽为d ,磁感应强度为B 的
匀强磁场区域,则电子能穿过这个区域至少应具有的初速度v0大小为
多少?
v L
L B
6.如图所示,匀强磁场的磁感应强度为B ,宽度为d ,边界为CD 和EF 。
一电子从CD 边界外侧以速率V0垂直射入匀强磁场,入射方向与CD 边
界间夹角为θ。
已知电子的质量为m ,电量为e ,为使电子能从磁场的
另一侧EF 射出,求电子的速率V0至少多大?
7.一匀强磁场,磁场方向垂直于xy 平面,在xy 平面上,磁场分布在以
O 为中心的一个圆形区域内。
一个质量为m 、电荷为q 的带电粒子,
由原点O 开始运动,初速为v ,方向沿x 正方向。
后来,粒子经过y 轴
上的P 点,此时速度方向与y 轴的夹角为30º,P 到O 的距离为L ,如
图所示。
不计重力的影响。
求磁场的磁感强度B 的大小和xy 平面上磁
场区域的半径R 。
× × × × × ×
× × × × × ×
× × × C D E F m e θ V d
解:粒子在磁场中受洛伦兹力作用,作匀速圆周运动,设半径为r
①
据此并由题意知,粒子在磁场中的轨迹的圆心C必在y轴上,且P点在磁场区之外。
过P点沿速度方向作延长线,它与x轴相交于Q点,作圆弧过O点与x轴相切,并且与PQ相切,切点A即粒子离开磁场区的地点。
这样也圆弧轨迹的圆心C,如图所示:
由图中几何关系得:L=3r ②
由①②求得:③
图中OA的长度即圆形磁场区的半径R,由图中几何关系得:
④
:半径为R的圆形区域内有一匀强磁场,圆心为O,如图所示。
一质量
为m、带电量为q的粒子从圆形边界上M点以速度v对准圆心O入射,
从N点射出磁场,速度方向偏转了600。
求:
(1)磁感应强度B的大小;
(2)改变磁感强度大小,可使得粒子在磁场中运动的时间减半,问此时的磁感强度B1 ;(写出B1与B的关系式)
(3)若粒子在由M运动到N的过程中突然改变磁感强度大小为B2 ,可使得粒子被束缚在磁场中,求B2的最小值?
答案
(1)设粒子在磁场中作圆周运动的半径为r,
据qBv = mv2/r (1分)
其中r = R·cot300 (2分)
代入得(1分)
(2)粒子在磁场中做圆周运动的周期,若速度偏转的角度为θ,
则有,由题意,第一次θ = 600,那么第二次θ1 = 300(2分)在直角三角形中,tan150 = R / r1? = qRB1 / mv ,tan300 = R / r? = qRB / mv ,
联立解得(2分,简化后的结果为)
(3)分析知,当粒子运动到圆弧MN的中点时,有最大的回旋半径,设为r2 ,
则2 r2 = r – R ,得到(2分)gkstk 代入得(2分)。
