中南大学大物15量子物理基础gPPT课件
合集下载
《量子物理基础 》课件

挑战:量子计算技术仍面临许多挑战, 如量子比特的稳定性、量子算法的设 计等
量子通信:基于量子密钥分发的加密通信技术,具有极高的安全性和保密性
量子网络:基于量子纠缠和量子隐形传态的量子信息传输网络,具有极高的传输速 度和传输效率
发展趋势:量子通信和量子网络技术正在逐步成熟,未来有望成为主流通信和网络技 术
,
汇报人:
CONTENTSPART 源自NEPART TWO量子物理是研究微观世界物理规律的科学 量子物理的基本概念包括量子、波粒二象性、测不准原理等 量子物理的应用领域包括量子通信、量子计算、量子加密等 量子物理的发展历程包括量子力学、量子场论、量子信息科学等
1900年,普朗克提出量子概念,量子物理诞生 1905年,爱因斯坦提出光子说,量子物理得到进一步发展 1913年,玻尔提出原子模型,量子物理进入新阶段 1925年,海森堡提出不确定性原理,量子物理进入成熟阶段 1926年,薛定谔提出波动力学,量子物理得到进一步完善 1927年,狄拉克提出相对论量子力学,量子物理进入新阶段
量子测量技术:利用量子效应进行 测量的技术,如量子纠缠、量子隐 形传态等
前景展望:量子传感器和测量技术 有望成为未来科技发展的重要方向, 推动量子信息技术的发展和应用。
汇报人:
概念:量子力学的基本原理之一,描述一个量子态可以由多个量子态叠加而成 应用:在量子计算、量子通信等领域有广泛应用 实验验证:通过双缝干涉实验等实验验证了态叠加原理 发展:态叠加原理是量子力学发展的重要基础,推动了量子力学的发展和进步
PART FOUR
波函数是量子 力学中的基本 概念,描述粒
子的状态
前景:量子通信和量子网络技术有望在信息安全、金融、医疗、军事等领域得到广 泛应用,具有巨大的市场前景和商业价值。
15章量子物理65页PPT
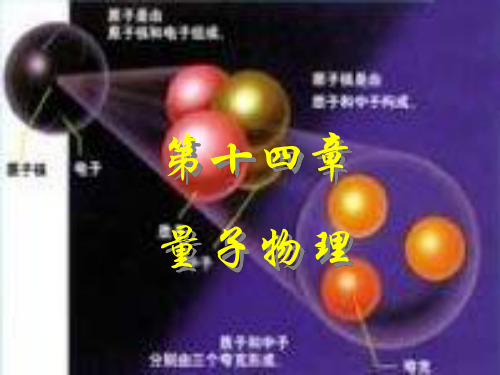
光强越大,N , N , I S ( 0 时)
遏止电压
W 石英窗
外加反向的遏止电压 U 0 恰
能阻碍光电子到达阳极, 即 阳极 A
K 阴极
eU0
1 2
mv2
1mv2 hW
2
eU 0hW
G V
U0
h
e
W e
遏止电压随入射光频率线性增加,与光强无关。
第十四章 量子物理
教学要点
1.光电效应的实验规律、爱因斯坦光子假设. 2.康普顿效应的实验规律. 3.氢原子光谱的实验规律及玻尔氢原子理论. 4. 实物粒子的波粒二象性. 5. 坐标动量不确定关系 .
第一节
光电效应 光的波粒二象性
实验现象1:存在饱和电流强度 Im Ne
饱和电流强度与入射光强度成正比。
实验现象2:存在遏止电压 U 0 。
与入射光强无关,与入射光频率具有线性关系。
实验现象3:存在截止频率0 。 ≥0,才能发生光电效应。
实验现象4:光电子瞬时发射。
二、光的波动说遇到的困难
红限问题 按照光的波动说,金属表面的电子在入
射光电场的作用下作受迫振动,E振 动 能 A2, 只要光足够强, E振动能 就越大,因此电子 就有足够的能量从金属表面逸出,而不存在
可见,经典理论无法解释波长变长的 散射光。
四、量子解释
1.物理模型
光子 0
y
电子
v0 0
x
y
光子
x
电子
入射光子( X 射线或 射线)能量大 .
Eh 范围为:10 4~10 5eV
光子 0
y
电子
v0 0
x
遏止电压
W 石英窗
外加反向的遏止电压 U 0 恰
能阻碍光电子到达阳极, 即 阳极 A
K 阴极
eU0
1 2
mv2
1mv2 hW
2
eU 0hW
G V
U0
h
e
W e
遏止电压随入射光频率线性增加,与光强无关。
第十四章 量子物理
教学要点
1.光电效应的实验规律、爱因斯坦光子假设. 2.康普顿效应的实验规律. 3.氢原子光谱的实验规律及玻尔氢原子理论. 4. 实物粒子的波粒二象性. 5. 坐标动量不确定关系 .
第一节
光电效应 光的波粒二象性
实验现象1:存在饱和电流强度 Im Ne
饱和电流强度与入射光强度成正比。
实验现象2:存在遏止电压 U 0 。
与入射光强无关,与入射光频率具有线性关系。
实验现象3:存在截止频率0 。 ≥0,才能发生光电效应。
实验现象4:光电子瞬时发射。
二、光的波动说遇到的困难
红限问题 按照光的波动说,金属表面的电子在入
射光电场的作用下作受迫振动,E振 动 能 A2, 只要光足够强, E振动能 就越大,因此电子 就有足够的能量从金属表面逸出,而不存在
可见,经典理论无法解释波长变长的 散射光。
四、量子解释
1.物理模型
光子 0
y
电子
v0 0
x
y
光子
x
电子
入射光子( X 射线或 射线)能量大 .
Eh 范围为:10 4~10 5eV
光子 0
y
电子
v0 0
x
第15章 量子物理基础 PPT课件

行
“但是在物理晴朗天空的远处,还有两朵小小令人不安的乌 云”,即运用当时的物理学理论所无法正确解释的两个实验
现象。
厚
其一是否定绝对时空观的迈克尔逊—莫雷实验;
德
其二是热辐射现象中的紫外灾难。 正是这两朵小小的乌云,冲破了经典物理学的束缚,打
弘 消了当时绝大多数物理学家的盲目乐观情绪,为后来建立近
毅
代物理学的理论基础作出了贡献。事实上还有第三朵小小的 乌云,这就是放射性现象的发现,它有力地表明了原子不是
并且应用越来越广泛。
由安培、法拉第和麦克斯韦等人对电磁现象进行的深入
厚 而系统的研究,为电动力学奠定了坚实的基础,特别是由麦
德
克斯韦的电磁场方程组预言了电磁波的存在,随即被赫兹的 实验所证实。后来又把牛顿、惠更斯和菲涅耳所建立的光学
弘 也纳入了电动力学的范畴,更是一项辉煌的成就。因此当时
毅
许多著名的物理学家都认为物理学的基本规律都已被发现, 今后的任务只是把物理学的基本规律应用到各种具体问题上,
笃 和透射的物体。
行
煤烟
厚
约99%
德
弘 黑体辐射的特点 :
毅 • 温度
黑体模型
黑体热辐射
材料性质
• 与同温度其它物体的热辐射相比,黑体热辐射本领最强
11
实验表明 辐射能力越强的物体,其吸收能力也越强.
博 学 黑体 能完全吸收照射到它上面的各种频率的电磁辐射的 笃物体称为黑体 .(黑体是理想模型) 行
学 1.热辐射现象
笃
一切物质中的原子、分子因
行
热激发而向外辐射电磁波的现象。 实验证明不同温度下物体能发出
不同的电磁波,这种能量按频率
厚
的分布随温度而不同的电磁辐射 叫做热辐射。
量子物理基础PPT课件

高温超导 玻色凝聚
相干原子束
第十二章 量子物理基础
§12.1 黑体辐射 §12.2 光电效应 §12.3 康普顿效应 §12.4 波粒二象性 §12.5 不确定关系 §12.6 薛定谔方程 §12.7 薛定谔方程的应用 §12.8 氢原子中的电子 §12.9 电子自旋
§12-1 黑体辐射
研究热辐射的原因 冶金学:依据炉内热辐射的强度分布来判断炉
问题:如何制造一张木桌子?
Richard Feynman gave the classic talk on December 29th 1959 at the annual meeting of the American Physical Society at the California Institute of Technology (Caltech).
But I am not afraid to consider the final question as to whether, ultimately---in the great future---we can arrange the atoms the way we want...
1990年,美国IBM公司阿尔马登研究中 心(Almaden Research Center)的科学 家使用STM(扫描隧道显微镜)把35个 氙原子移动到各自的位置,组成了 “IBM”三个字母,这三个字母加起来 不到3纳米长.
内的温度,以此来把握炼钢的时机。 天文学:依据辐射强度分布来判断星体表面的
温度。
不同温度的白炽灯灯丝及其辐射的能谱。左图灯丝温度较 低,辐射的能量集中在可见光谱的长波段,灯丝看起来是红色 的;右图灯丝温度较高,辐射的能量包括全部可见光谱,灯丝 发出“白炽”光。
相干原子束
第十二章 量子物理基础
§12.1 黑体辐射 §12.2 光电效应 §12.3 康普顿效应 §12.4 波粒二象性 §12.5 不确定关系 §12.6 薛定谔方程 §12.7 薛定谔方程的应用 §12.8 氢原子中的电子 §12.9 电子自旋
§12-1 黑体辐射
研究热辐射的原因 冶金学:依据炉内热辐射的强度分布来判断炉
问题:如何制造一张木桌子?
Richard Feynman gave the classic talk on December 29th 1959 at the annual meeting of the American Physical Society at the California Institute of Technology (Caltech).
But I am not afraid to consider the final question as to whether, ultimately---in the great future---we can arrange the atoms the way we want...
1990年,美国IBM公司阿尔马登研究中 心(Almaden Research Center)的科学 家使用STM(扫描隧道显微镜)把35个 氙原子移动到各自的位置,组成了 “IBM”三个字母,这三个字母加起来 不到3纳米长.
内的温度,以此来把握炼钢的时机。 天文学:依据辐射强度分布来判断星体表面的
温度。
不同温度的白炽灯灯丝及其辐射的能谱。左图灯丝温度较 低,辐射的能量集中在可见光谱的长波段,灯丝看起来是红色 的;右图灯丝温度较高,辐射的能量包括全部可见光谱,灯丝 发出“白炽”光。
大学物理量子物理量子物理 ppt课件
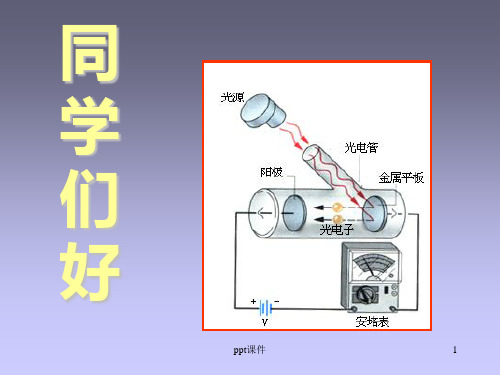
黑体辐射的困难。 引入能量量子化的概念,是量子物理开端,
为爱因斯坦光子论和玻尔氢原子理论奠定基础。
“敲响近代物理晨钟” 1900年12月14日 《正常光谱中能量分布律的理论》
量子力学诞生日
1918年 诺贝尔物理奖
③ 普朗克恒量 h 已经成为物理学中最基本、最重
要的常数之一。
ppt课件
21
“我当时打算将基本作用量子 h 归并到经典理论范 畴中去,但这个常数对所有这种企图的回答都是无 情的”
维恩线
0 1 2 3 4 5 6 7 8 9 ( m)
ppt课件
18
三、普朗克能量子假说
1. 经验公式
在维恩公式和金斯公式之间用内插法得出与实验曲 线相符的经验公式
hc
e0 (,T ) 2hc 2 5 (e kT 1)1
e0 (T,)
0 ppt课件
19
2. 能量子假设(模型)
能全部吸收(不反射)任何波长的 入射辐射能的物体 —— 绝对黑体
模型:空腔小孔
ppt课件
绝热不 透明
7
3. 绝对黑体的辐射定律
实验发现:物体的电磁辐射能力与吸收能力一致。
黑体
完全吸收体 理想发射体
定义两个物理量:
e0(,T ) — 单色辐射本领:
单位时间内,从物体表面单位面积上发射的波长
d范围的辐射能与波长间隔d之比
e0(相对强度)
T 2.7 K
31010 Hz 1
1964年 贝尔实验室 彭齐亚斯、威尔孙 发现
1978年 诺贝尔物理奖(大爆炸宇宙学论据)
1990年 美国COBE卫星精密观测,得其能谱为
2.735 0.06K.黑体辐射
第十五量子力学基础-精品.ppt

暗红
橙色
黄色
白色
炼钢工人在浇铸
同一个黑白花盘子的两张照片
室温下,反射光
1100K,自身辐射光 (与温度有关、热辐射)
注意:电灯泡发光是热辐射; 激光、日光灯发光不是热辐射。
热辐射的一般特点:
(1)物质在任何温度下都有热辐射。 (2)温度越高,发射的能量越大,发射的电磁波的
波长越短。
平衡热辐射 任一时刻, 如果物体辐射的能量等于所吸收的能量, 称为平衡热辐射。此时物体具有恒定的温度。
狄拉克把量子力学与狭义 相对论相结合
第十五章 量子物理基础
§15-1 黑体辐射、普朗克量子假说 §15-2 光的量子性 §15-3 玻尔的氢原子理论 §15-4 粒子的波动性 §15-5 测不准关系 §15-6 波函数 薛定谔方程 §15-7 薛定谔方程在几个一维问题中的应用 §15-8 量子力学对氢原子的处理 §15-9 斯特恩-盖拉赫实验 §15-10 电子自旋 §15-11 原子的壳层结构
15-1 黑体辐射 普朗克量子假设
一、热辐射 绝对黑体辐射定律 分子(含有带电粒子)的热运动使物体辐射 电磁波。这种与温度有关的辐射称为热辐射 (heat radiation)。
热辐射的电磁波能量对频率有一个分布。
温度不同,热辐射的电磁波能量不同, 频率分布也不同。
例如加热铁块,随着温度的升高: 开始不发光
15-2 光的量子性
一、光电效应 爱因斯坦方程的实验规律
光电效应 光照射到金属表面时, 有电子从金属表面逸出的现象。
AK
OO
光电子 逸出的电子。
光电子由K飞向A,回路中形成 光电流。
OO
OO
G
V R
OO
应用:
第15章1量子物理优秀课件

爱因斯坦在普朗克能量子假设的基础上进一 步提出了光子假设。
光子: h
爱因斯坦光电效应方程:
h
1 2
mvm2
W
逸出功(W ) : 电子用于克服金属表面势垒的束 缚而做的功。
爱因斯坦对光电效应的实验解释:
(1) 入射光的强度 I 取决于单位时间内垂直通过 单位面积的光子数n 。
I nh
入射光较强时,含有的光子数较多,所以获得 能量而逸出的电子数也多,饱和电流自然也就大。
,T
M1 ,T a1,T
M 2 ,T a2 ,T
M 0
,T
在热平衡条件下,黑体辐射的实验能谱曲线:
M0 W m3
nm
斯忒藩 - 玻耳兹曼定律: M T T 4
斯忒藩 -玻耳兹曼常量:
5.670 40040108 W m2 K4
维恩位移定律:能谱分布曲线的峰值对应的波长m
普朗克经验公式:
M0 W m3
M 0 ,T
2πhc2
5
1
hc
ekT 1
0 1 2 3 4 5 6 7 8 9 μm
普朗克常量: h 6.626 06931034 J s
讨论: (1) 在长波段情况下
hc
e kT 1
hc
kT
M 0 ,T
2πhc 2 5
hc
2πckT
4
(瑞利 - 金斯公式)
下,遏止电压为多少?(3)电子的初速度为多少?
解:W0
h 0
hc
0
6.631034 3108 6.2 107
J
3.211019 J
h
1 2
mvm2
W0
,
1 2
《量子物理基础》PPT课件

1913年,年仅28岁的玻 尔(Niels Bohr),在 卢瑟福核型结构的基础 上,创造性地把量子概 念应用到原子系统,解 释了近30年的光谱之谜。
玻尔 海森伯 泡利(自左至右) 玻尔在工作
第十六章 —— 量子物理基础
4
§16.4 氢原子光谱 玻尔氢原子理论
三. 玻尔氢原子理论 (三条假设)
1. 定态假设
2. 定态假设和角动量量子化条件都是对的, 但是是硬加上去的。
3. 是半经典理论,仍保留了“轨道”概念。 4. 频率条件完全正确,一直沿用至今。
第十六章 —— 量子物理基础
11
§16.4 氢原子光谱 玻尔氢原子理论
例:当一个质子俘获一个动能Ek=13.6eV的自由电子组成一 个基态氢原子时,所发出的单色光频率是多少? (普朗克恒
(1) 分立、线状光谱 (2)Balmer总结的经验公式
1 4 11 11
RBH((2k22nn22))
里德伯常数 RH 1.097 373 1107 m1
(n > k)
(3)除可见光谱外,在红外区和紫外区也观察到光谱系。 k = 1 (n =2, 3, 4, … ) 谱线系 —— 莱曼系 (Lyman) k = 2 (n = 3, 4, 5, … ) 谱线系 —— 巴耳末系(Balmer)
说明:
(1)n越大,能量En越大,而相邻两能级之差△E越小。
n→∞时 En→0,e成为自由电子,不受核束缚(游离态)。
△E→0,能量趋于连续(经典理论)。
(2)电离能 :e从束缚态变成自由态所需最小能量
➢ 原子被电离:束缚的e释放出来需吸收能量 ➢ 质子和自由电子结合成一个基态H原子:需释放能 量,即辐射电磁波或发光。
(3)用可见光照射出于基态的H原子,e能否电离?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h h h p m m0
2
1c2
如果 c,则 h m0
例如:电子经加速电势差 U加速后
1 2
m02
eU
2 eU m0
电子的德布罗意波长为
h 2m0eU
12.3
0
(A)
U
0
U15V0 1A
例一)一质量m0=0。
解: V C
h6.6 3 13 04 4.410 3(4m )
设测得速度的精度为1/10000,即 V=10m/s,求电子
尔后又发现了质子、中子的衍射
1929诺贝尔物理学奖
L.V.德布罗意 电子波动性的理论 研究
1937诺贝尔物理学奖
C.J.戴维孙 通过实验发现晶体 对电子的衍射作用
三、德布罗意波的统计解释 1926年,德国物理学玻恩 (Born , 1882--1972)
提出了概率波,认为个别微观粒子在何处出现有一 定的偶然性,但是大量粒子在空间何处出现的空间 分布却服从一定的统计规律。
15-1 德布罗意波 实物粒子的波粒二象性
一、德布罗意波 德布罗意提出了物质波的假设:
一切实物粒子(如电子、质子、中子)都与光子一 样,具有波粒二象性。
运动的实物粒子的能量E、动量p与它相关联的
波的频率 和波长之间满足如下关系:
Em2ch
p m h 德布罗意公式(或假设)
与实物粒子相联系的波称为德布罗意波(或物质波)
U
二、德布罗意波的实验证明(电子衍射实验)
1927年戴维孙和革末用加速后的电子投射到晶体 上进行电子衍射实验。
K
狭缝 电子束
器
电 集
U
镍 单晶
电 G流
计
I
0
5
10 15 20 25
U
衍射最大值: 2 dsin k k 1 ,2 ,3
电子的波长: h
2meU
2dsink h
实验表明电流极大值
X
a
Pa Pb
K
a
Pa Pb
bc
Pc
Pd
Pc
X
U
Pd B
Pe
P
Px
Pe
d
其衍射角
分别为:
e
a b c
E
d e
单缝处,衍射角为θ的电子在X轴上存在动量的分量
PaxPsina PbxPsinb PexPsin e
P cxPs in c0
PdxPsind
······
即处在单缝处电子动量在X轴上的分量有不确定值
2meU 正好满足此式
一切微观粒子都具有波粒二象性。
1927 年汤姆逊(G·P·Thomson)以600伏慢电子 (=0.5Å)射向铝箔,也得到了像X射线衍射一 样的衍射,再次发现了电子的波动性。
1937年戴维逊与GP汤姆逊共获当年诺贝尔奖 (G·P·Thomson为电子发现人J·J·Thmson的儿子)
k1.2.3明纹
暗纹
1)位置的不确定程度
我们来研究电子在单缝隙位置的位置和动量的不
确定程度
用单缝来确定电子在穿过单缝 时的位置
电子在单 缝的何处 通过是不
确定的! 只知是在
宽为a的 的缝中通
U
过.
结论:电子在单缝处的位置 不确定量为
xa
2)单缝处电子的动量的不确定程度
先强调一点:电子衍射是电子自身的波粒二象性结 果,不能归于外部的原因,即不是外界作用的结果。
mvx 2kgms1
所以坐标及动量可以同时确定
2. 微观粒子的动量及坐标是否永远不能同时确定?
例 一电子以速度 vx1.0160 m s1 的速度穿过晶体。
0
x d 1A
vx 2m x
103110314010ms1
170ms1vx16 0ms1
电子的动量是不确定的,应该用量子力学来处理。
例3 电子射线管中的电子束中的电速度一般为 105m/s,
不能理解为仪器的精度达不到。 3. 不确定关系指出了使用经典物理理论的限度
问题? 1. 宏观粒子的动量及坐标能否同时确定?
例 m102kg的乒乓球 , 其直径 d5cm vx20m 0s1,若 x106m, 可以认为其位
置是完全确定的。其动量是否完全确定呢?
mvx
2x
10 34 10 6
10 28 kgms1
15-2 不确定关系Uncertainty Relation
微观粒子的空间位置要由概率波来描述,概率 波只能给出粒子在各处出现的概率。任意时刻不具 有确定的位置和确定的动量。
电子具有波粒二象性,也可产生类似波的单
缝衍射的图样,若电子波长为,则让电子进行
单缝衍射则应满足:
{aassiinn (k2k1)2
px
p
x
x a
py
屏
电子束
a缝
2
幕
X方向电子的位置不确定量为: x a
电子大部分都到达中央明纹处. 研究正负一级暗纹间的电子。这部分电子在单缝处
的动量在X轴上的分量值为:
0PxPsin 为一级暗纹的衍射角
px
p
x
x a
py
屏
电子束
a缝
2
幕
X方向电子的位置不确定量为: x a
到达正负一级暗纹间的电子在单缝处的动量在X轴上
m 0V 0.0 5300
即4.410-24Å
例二)一原静止的电子被电场加速到速度V (VC),加速电压为U,则速度为V的电子的De Bröglie波波长为多大?
故德布罗意波长:
h h h P m 0V 2em0U
代入h、e、 m0值:
12.31010(m)
U
或 12 .3 Å
U
当U=100伏 12.3 1.23Å
E m02c4P2c2
考虑到E的增量:
E 2c2PP c2m V P
2 m 0 2c4P2c2
E
VP x P t
E t x p /2
即: Et 能量与时间不确定关系式
2
不确定关系式的理解 1. 用经典物理学量——动量、坐标来描写微观粒子 行为时将会受到一定的限制 。 2. 不确定关系是微观粒子波粒二象性所决定的,
的分量的不确定量为
px psin 由单缝暗纹条件: asin
p a p x 为一级暗纹的衍射角
h p
pxxP
phh p
pxxh
考虑到在两个一级极小值之外还有电子出现,
所以: pxxh
经严格证明此式应为:
pxx2
pyy2 pzz2
这就是著名的海森伯不确定关系式
能量与时间不确定关系
设有一个动量为P,质量为m的粒子,能量
如有人认为衍射是电子与单缝的作用,即电子与 单缝材料中的原子碰撞的结果,碰撞后电子的动量 大小与方向均发生改变,但实验告诉我们衍射的花 样与单缝材料无关,只决定于电子的波长与缝宽a, 可见不能归结于外部作用。
显然,电子通过单缝不与单缝材料作用,因此通 过单缝后,其动量大小P不变。但不同的电子要到 达屏上不同的点。故各电子的动量方向有不同。
