2017届陕西省西安铁一中、铁一中国际合作学校高三下学期第一次模拟考试文科数学试题及答案精品

合集下载

陕西省西安市一中2017高三下学期高考押题卷数学(文)试题(一)含答案

陕西省西安市一中2017高三下学期高考押题卷数学(文)试题（一）全卷满分150分，考试用时120分钟第Ⅰ卷一、选择题：本题共12小题，每小题5分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．集合{}|13A x x =<<，集合{}|2,B y y x x A ==-∈，则集合A B ＝（） A ．{}|13x x << B ．{}|13x x -<<C ．{}|11x x -<<D ．∅【答案】D【解析】根据题意{}{}|2,|11,B y y x x A y y x A ==-∈=-<<∈，所以集合A B ＝∅．故选D ．2．已知复数z 在复平面对应点为()1,1-，则z ＝（）A ．1B ．－1C D ．0【答案】C【解析】根据题意可得1i z =-+，则z C ． 3．sin2040°＝（）A ．12-B ．C ．12D 【答案】B【解析】()sin 2040sin 6360120sin120︒=⨯︒-︒=-︒=B ． 4．世界最大单口径射电望远镜FAST 于2016年9月25日在贵州省黔南州落成启用，它被誉为“中国天眼”，从选址到启用历经22年．FAST 选址从开始一万多个地方逐一审查，最后敲定三个地方：贵州省黔南州、黔西南州和安顺市境内．现从这三个地方中任选两个地方重点研究其条件状况，则贵州省黔南州被选中的概率为（）A ．1B ．12C ．13D ．23【答案】D【解析】从三个地方中任选两个地方，基本事件总数3n =，贵州省黔南州被选中基本事件个数2m =，∴贵州省黔南州被选中的概率23P =．故选D ． 5．《九章算术》中记载了一种标准量器——商鞅铜方升，其三视图如图所示（单位：寸），则该几何体的容积为（）立方寸．（π≈3．14） A ．12．656B ．13．667C ．11．414D ．14．354【答案】A【解析】由三视图知，商鞅铜方升由一圆柱和一长方体组合而成．由题意得：()25.4 1.6310.5 1.612.656V =-⨯⨯+π⋅⨯≈立方寸．故选A ．6．在等差数列{}n a 中，若35791145a a a a a ++++=，33S =-，那么5a 等于（） A ．4 B ．5C ．9D ．18【答案】B【解析】因为35791145a a a a a ++++=，所以7545a =，所以79a =，因为33S =-，所以21a =-，所以公差7225a a d -==，所以5235a a d =+=．故选B ． 7．已知函数()2ln f x x x =-，则函数()y f x =的大致图象是（）A BC D 【答案】C 【解析】因为()()2ln f x x x f x -=-=，所以函数()y f x =为偶函数，所以排除D ，又()10f x =>，所以排除A 、B ，故选C ．8．根据下列流程图输出的值是（） A ．11B ．31C ．51D ．79【答案】D【解析】当n ＝2时，2122a a ==，()2212132a S S+=+=，当n ＝3时，3224a a ==，()33231112a S S+=+=，当n ＝4时，4328a a ==，()44341312a S S+=+=，当n ＝5时，54216a a ==，()55451792a S S+=+=，输出．故选D ．9．已知单位向量,a b 满足a b ⊥，向量2,m a n ta b ==+，（t 为正实数），则m n⋅ 的最小值为（） A ．158B ．52C ．154D ．0【答案】A【解析】由题意可得，()()22222m n a ta b ta a b b ⋅=⋅+=+⋅-⋅ ，而a b ⊥ ，所以0a b ⋅= ，1a b ==，所以2m n t ⋅=，设0k =，则()210t k k =+≥，所以()22115221248m n t k k k ⎛⎫⋅==+-=-+ ⎪⎝⎭ ，因为0k ≥，所以158m n ⋅ ≥．故选A ．10．若x ，y 满足约束条件13030x x y x y ⎧⎪+-⎨⎪--⎩≥≤≤，设224x y x ++的最大值点为A ，则经过点A 和B (2,3)--的直线方程为（） A ．3590x y --= B ．30x y +-= C ．30x y --=D ．5390x y -+=【答案】A【解析】在直角坐标系中，满足不等式组13030x x y x y ⎧⎪+-⎨⎪--⎩≥≤≤可行域为：()2222424z x y x x y =++=++-表示点()2,0P -到可行域的点的距离的平方减4．如图所示，点()3,0到点()2,0-的距离最大，即()3,0A ，则经过A ，B 两点直线方程为3590x y --=．故选A ．11．已知双曲线C 的中心在原点O ，焦点()F -，点A 为左支上一点，满足|OA |＝|OF |且|AF |＝4，则双曲线C 的方程为（）A ．221164x y -= B ．2213616x y -= C ．221416x y -= D ．2211636x y -= 【答案】C【解析】如下图，由题意可得c =，设右焦点为F ′，由|OA |＝|OF |＝|OF′|知，∠AFF ′＝∠F AO ，∠OF ′A ＝∠OAF ′，所以∠AFF ′+∠OF ′A ＝∠FAO +∠OAF ′，由∠AFF ′+∠OF ′A +∠FAO +∠OAF ′＝180°知，∠FAO +∠OAF ′＝90°，即AF ⊥AF ′．在Rt △AFF ′中，由勾股定理，得'8AF ==，由双曲线的定义，得|AF ′|－|AF |＝2a ＝8－4＝4，从而a ＝2，得a 2＝4，于是b 2＝c 2－a 2＝16，所以双曲线的方程为221416x y -=．故选C ．12．已知函数()2ln xf x x x=-，有下列四个命题，①函数()f x 是奇函数；②函数()f x 在()(),00,-∞+∞ 是单调函数； ③当0x >时，函数()0f x >恒成立； ④当0x <时，函数()f x 有一个零点，其中正确的个数是（） A ．1 B ．2C ．3D ．4【答案】B 【解析】①函数()f x 的定义域是()(),00,-∞+∞ ，()2ln x f x x x-=+，不满足函数奇偶性定义，所以函数()f x 非奇非偶函数，所以①错误；②取1x =-，1x =，()1f -()11f ==，所以函数()f x 在()(),00,-∞+∞ 不是单调函数，所以②错误；③当x ＞0时，()2ln x f x x x =-，要使()0f x >，即2ln 0x x x->，即3ln 0x x ->，令()3ln g x x x =-，()'213g x x x =-，()'0g x =，得x =，所以()g x在⎛ ⎝上递减，在⎫+∞⎪⎪⎭上递增，所以()0g x g >≥，所以③正确；④当0x <时，函数()2ln x y x x -=-的零点即为()2ln 0x x x--=的解，也就是()3ln 0x x --=，()3ln x x =-等价于函数()3f x x =与函数()()ln h x x =-图像有交点，在同一坐标系画出这两个函数图像，可知他们只有一个交点，所以④是正确的．故选B ．第Ⅱ卷本卷包括必考题和选考题两部分。

陕西省西安中学2017届高三下学期一模考试数学(文)试题Word版含答案

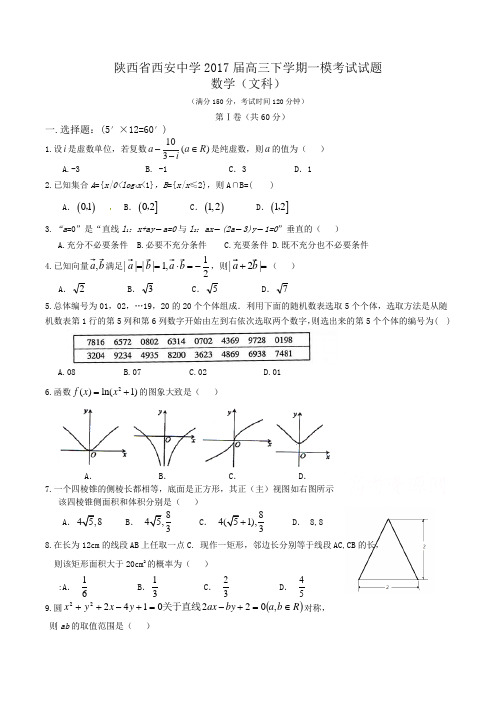
陕西省西安中学2017届高三下学期一模考试试题数学（文科）（满分150分，考试时间120分钟）第Ⅰ卷（共60分）一.选择题：(5′×12=60′)1.设i 是虚数单位，若复数10()3a a R i-∈-是纯虚数，则a 的值为（）A.-3B. -1C ．3D ．12.已知集合A ={x|0<log 4x <1}，B ={x|x ≤2}，则A∩B=( ) A ．()01， B ．(]02，C ．()1,2D ．(]12， 3.“a =0”是“直线l 1：x+ay -a=0与l 2：ax -(2a -3)y -1=0”垂直的（） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4.已知向量,满足21,1||||-=⋅==，则=+|2|（）A ．2B ．3C ．5D ．75.总体编号为01，02，…19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为( )A.08B.07C.02D.01 6.函数)1ln()(2+=x x f 的图象大致是（）A ．B ．C ．D ．7.一个四棱锥的侧棱长都相等，底面是正方形，其正（主）视图如右图所示该四棱锥侧面积和体积分别是（）A ．B ． 83C ． 81),3+ D ． 8,8 8.在长为12cm 的线段AB 上任取一点C. 现作一矩形，邻边长分别等于线段AC,CB 的长，则该矩形面积大于20cm 2的概率为（）:A ．16 B ．13 C ． 23 D ． 45 9.圆()R b a by ax y x y x ∈=+-=+-++,022014222关于直线对称，则ab 的取值范围是（）A.⎥⎦⎤ ⎝⎛∞-41,B. ⎥⎦⎤ ⎝⎛41,0C.⎪⎭⎫ ⎝⎛-0,41D. ⎪⎭⎫⎝⎛∞-41,10.x 为实数，[]x 表示不超过x 的最大整数，则函数()[]f x x x =-在R 上为 ( )A ．奇函数B ．偶函数C ．增函数D ．周期函数 11.将函数()x x f y cos =的图像向左平移4π个单位后，再做关于x 轴的对称变换得到函数1cos 22-=x y 的图像，则()x f 可以是( )A.x cos 2-B. x sin 2-C. x cos 2D. x sin 212. 椭圆22:143x y C +=的左、右顶点分别为12,A A ，点P 在C 上且直线2PA 的斜率的取值范围是[]2,1--，那么直线1PA 斜率的取值范围是( ) A ．1324⎡⎤⎢⎥⎣⎦， B ．3384⎡⎤⎢⎥⎣⎦， C ．112⎡⎤⎢⎥⎣⎦， D ．314⎡⎤⎢⎥⎣⎦，第Ⅱ卷（共90分）二．填空题：(5′×4=20′)13.定义运算a b ⊗为执行如图所示的程序框图输出的S 值，则552cos2tan 34ππ⎛⎫⎛⎫⊗ ⎪ ⎪⎝⎭⎝⎭的值为 14.已知不等式组⎪⎩⎪⎨⎧≥-≥-≤+0,1,1y y x y x 所表示的平面区域为D,若直线y=kx -3k与平面区域D 有公共点，则k 的取值范围为15.ABC ∆中，a,b,c 分别是角A 、B 、C 的对边，若C A B b c a sin cos 6sin ,222⋅==-且, 则b=16. 将数列{}13n -按“第n 组有n 个数”的规则分组如下：（1），（3，9），（27，81，243），…，则第10组中的第一个数是_____________三.解答题: （12′×5+10′=70′）17. 已知数列{}n x 的首项31=x ，通项()2,,n n x p qn n N p q *=+∈为常数，且541,,x x x 成等差数列，求： (Ⅰ)p,q 的值；(Ⅱ)数列{}n x 前n 项和n S 的公式.18. 若函数()()2sin sin cos 0f x ax ax ax a =->的图像与直线y=m (m 为常数)相切，并且切点的横坐标依次成等差数列，且公差为2π. (Ⅰ)求m 的值；(Ⅱ)若点A ()00,y x 是y=f(x)图像的对称中心，且⎥⎦⎤⎢⎣⎡∈2,00πx ，求点A 的坐标.19. 甲乙两人进行两种游戏，两种游戏规则如下：游戏Ⅰ：口袋中有质地、大小完全相同的5个球，编号分别为1,2,3,4,5，甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢.游戏Ⅱ：口袋中有质地、大小完全相同的6个球，其中4个白球，2个红球，由裁判有放回的摸两次球，即第一次摸出记下颜色后放回再摸第二次，摸出两球同色算甲赢，摸出两球不同色算乙赢.（Ⅰ）求游戏Ⅰ中甲赢的概率；（Ⅱ）求游戏Ⅱ中乙赢的概率；并比较这两种游戏哪种游戏更公平？试说明理由.20. 18．如图:三棱柱ABC －A 1B 1C 1中，侧棱垂直底面，∠ACB ＝90°，AC ＝BC=121AA ，D 是侧棱AA 1的中点．（Ⅰ）证明：平面BDC 1⊥平面BDC ；（Ⅱ）平面BDC 1分此棱柱为两部分，求这两部分体积的比． 21. 设函数)1ln()(2++=x b x x f ，其中0≠b . （Ⅰ）若12b =-，求)(x f 在[]3,1的最小值；（Ⅱ）如果()f x 在定义域内既有极大值又有极小值，求实数b 的取值范围；请考生在第（22）、（23）、（24）三题中任选一题作答.注意：只能做所选定的题目，如果多做，则按所做的第一个题目计分. 22．选修4—1：几何证明选讲如图，已知PA 与圆O 相切于点A ，经过点O 的割线PBC 交圆O 于点B 、C ，∠APC 的平分线分别交AB 、AC 于点D 、E ，P（Ⅰ）证明：∠ADE =∠AED ；（Ⅱ）若AC=AP ，求PC PA的值．23．选修4－4：极坐标系与参数方程已知直线l的参数方程是2x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 是参数)，圆C 的极坐标方程为ρ=2cos(θ+4)．（Ⅰ）求圆心C 的直角坐标；（Ⅱ）由直线l 上的点向圆C 引切线，求切线长的最小值．24．选修4－5：不等式选讲设不等式112<-x 的解集为M , 且M b M a ∈∈,. (Ⅰ) 试比较1+ab 与b a +的大小;(Ⅱ) 设A max 表示数集A 中的最大数, 且⎭⎬⎫⎩⎨⎧+=b abb a ah 2,,2max , 求h 的范围.陕西省西安中学2017届高三下学期一模考试试题数学（文科）参考答案一、选择题：(5′×12=60′) （A 卷） CDABD ABCAD BB 二、填空题：(5′×4=20′) 13.4； 14.031≤≤-k ； 15.3； 16. 345；三、解答题：（12′×5+10′=70′）17.解：(Ⅰ)由31=x 得2p+q=3,又∵45155442,52,42x x x q p x q p x =++=+=且∴q p q p 8252355+=++，解得p=1,q=1 ………..………………………….…..6分(Ⅱ)由(Ⅰ)得n x n n +=2∴()2122...3212 (2221)32++-=+++++++++=+n n n S n nn ……….……….12分 18.解：(Ⅰ) ∵()⎪⎭⎫ ⎝⎛+-=42sin 2221πax x f …………….………………………….……3分 ∴ 2221±=m ……………………………………………………………………..5分 (Ⅱ) ∵切点的横坐标依次成等差数列，且公差为2π， ∴a a T πππ===2222=⇒a ()⎪⎭⎫ ⎝⎛+-=44sin 2221πx x f ……………………………....7分 ∵ 点A ()00,y x 是y=f(x)图像的对称中心 ∴1644400ππππ-=⇒=+k x k x ….9分 ∵⎥⎦⎤⎢⎣⎡∈2,00πx ∴1671630ππ或=x ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛2116721163，或，ππA ……………………….12分 19.解：（Ⅰ）∵游戏Ⅰ中有放回地依次摸出两球基本事件有5*5=25种，其中甲赢包含（1,1）（1,3）（1,5）（3,3）（3,5）（5,5）（3,1）（5,1）（5,3）（2,2）（2,4）（4,4）（4,2）13种基本事件， ∴游戏Ⅰ中甲赢的概率为 P=2513…………………………..……………..5分（Ⅱ）设4个白球为a,b,c,d, 2个红球为A,B ，则游戏Ⅱ中有放回地依次摸出两球基本事件有6*6=36种，其中乙赢包含（a,A ）, （b,A ）,（c,A ）（d,A ）（a,B ）（b, B ）（c, B ）（d, B ）（A,a ）（A,b ）（A,c ）（A,d ）（B,a ）（B,b ）（B,c ）（B,d ）16种基本事件， ∴游戏Ⅱ中乙赢的概率为P’=1583016= ………………………………...……………….10分 ∵21158212513-<- ∴游戏Ⅰ更公平 ………………………………....12分20.解：解：（1）证明：由题设可知1111,,A ACC BC C AC CC AC BC CC BC 平面⊥⇒=⊥⊥1111DC ACC A DC BC≠⊂∴⊥又平面…………………………………………2分DC DC CDC ADC DC A ⊥=∠∴=∠=∠1010119045即又 …………4分 BDC DC C BC DC 平面又⊥∴=1,111DC BDC BDC BDC ≠⊂⊥又平面，故平面平面…………………………6分（2）设棱锥1DACC B -的体积为/V ,21122113131,11/=⨯+⨯⨯=⋅=∴=DACC S BC V AC 设 ……………………………………9分又三棱柱的体积为V=1,故平面1BDC 分棱柱所得两部分的体积比为1:1 ……………12分 21.解：其中第一问6分，第二问6分，共12分.四、选考题（本题满分10分）：请考生从第（22）、（23）、（24）三题中任选一题作答。

陕西省西安一中2017-2018学年高考数学一模试卷(文科) Word版含解析

陕西省西安一中2017-2018学年高考数学一模试卷（文科）一、选择题：（每小题5分，共50分）1．若复数（x∈R）为纯虚数，则x等于( )A．0 B．1 C．﹣1 D．0或12．已知函数的定义域为M，g（x）=ln（1+x）的定义域为N，则M∩N=( ) A．{x|x＞﹣1} B．{x|x＜1} C．{x|﹣1＜x＜1} D．∅3．在各项均为正数的等比数列{a n}中，a3a5=4，则数列{log2a n}的前7项和等于( )A．7 B．8 C．27D．284．在△ABC中，a，b，c是角A，B的对边，若a，b，c成等比数列，A=60°，=( )A．B．1 C．D．5．如图为一个几何体的三视图，尺寸如图所示，则该几可体的表面积为( )（不考虑接触点）A．B．C．D．32+π6．已知图象不间断函数f（x）是区间上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0，②f（a）f（m）＞0，③f（b）f（m）＜0，④f（b）f（m）＞0，其中能够正确求出近似解的是( )A．①④B．②③C．①③D．②④7．如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为( )A．B．C．D．8．已知函数f（x）=若f（2﹣x2）＞f（x），则实数x的取值范围是( )A．（﹣∞，﹣1）∪（2，+∞）B．（﹣∞，﹣2）∪（1，+∞）C．（﹣1，2）D．（﹣2，1）9．已知双曲线方程为=1，过其右焦点F的直线（斜率存在）交双曲线于P、Q两点，PQ的垂直平分线交x轴于点M，则的值为( )A．B．C．D．10．在实数集R中定义一种运算“⊕”，具有性质：①对任意a，b∈R，a⊕b=b⊕a；②对任意a∈R，a⊕0=a；③对任意a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c．函数f（x）=x⊕（x＞0）的最小值为( )A．4 B．3 C．2D．1二、填空题（共4小题，每小题3分，满分12分）11．在棱长为2的正方体内随机取一点，取到的点到正方体中心的距离大于1的概率__________．12．设D是不等式组表示的平面区域，则D中的点P（x，y）到直线x+y=10距离的最大值是__________．13．在△ABC中，不等式成立；在凸四边形ABCD中，不等式成立；在凸五边形ABCDE中，不等式成立．根据以上情况，猜想在凸n边形A1A2…A n（n≥3）中的成立的不等式是__________．14．下列说法中，正确的有__________（把所有正确的序号都填上）．①“∃x∈R，使2x＞3”的否定是“∀x∈R，使2x≤3”；②函数y=sin（2x+）sin（﹣2x）的最小正周期是π；③“函数f（x）在x=x0处有极值，则f′（x）=0”的否是真；④函数f（x）=2x﹣x2的零点有2个．三、【不等式选做题】（注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）15．若不等式|x+2|+|x﹣3|≥a+对任意的实数x恒成立，则实数a的取值范围是__________．四、【几何证明选做题】（共1小题，满分0分）16．如图所示，在圆的直径AB的延长线上任取一点C，过点C作圆的切线CD，切点为D，∠ACD的平分线交AD于点E，则∠CED__________．五、【坐标系与参数方程】（共1小题，满分0分）17．在极坐标系中，以点（1，0）为圆心，1为半径的圆的极坐标方程是__________．三、解答题：18．如图，A、B是单位圆O上的点，C、D分别是圆O与x轴的两个交点，△ABO为正三角形．（1）若点A的坐标为，求cos∠BOC的值；（2）若∠AOC=x（0＜x＜），四边形CABD的周长为y，试将y表示成x的函数，并求出y的最大值．19．已知数列{a n}满足：a1=0且=1．（1）求{a n}的通项公式；（2）令b n=（n∈N+），数列{b n}的前n项和为S n，证明：S n＜1．20．某中学将100名2014-2015学年高一新生分成水平相同的甲，乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲，乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”．（1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；（2）由以上统计数据填写下面2x2列联表，并判断是否有90%的把握认为“成绩优秀”与教学方式有关．甲班（A方式）乙班（B方式）总计成绩优秀成绩不优秀总计附：K2=P（（K2≥k）0.25 0.15 0.10 0.05 0.025k 1.323 2.072 2.706 3.841 5.02421．如图，在正三棱柱ABC﹣A1B1C1中，点D为棱AB的中点，BC=1，AA1=．（1）求证：BC1∥平面A1DC；（2）求三棱锥D﹣A1B1C 的体积．22．已知圆C1的方程为（x﹣4）2+（y﹣1）2=，椭圆C2的方程为，其离心率为，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径．（Ⅰ）求直线AB的方程和椭圆C2的方程；（Ⅱ）如果椭圆C2的左右焦点分别是F1、F2，椭圆上是否存在点P，使得，如果存在，请求点P的坐标，如果不存在，请说明理由．23．设函数f（x）=x3+ax2﹣a2x+m（a＞0）（1）若函数f（x）在x∈内没有极值点，求实数a的取值范围；（2）a=1时函数f（x）有三个互不相同的零点，求实数m的取值范围；（3）若对任意的a∈，不等式f（x）≤1在x∈上恒成立，求实数m的取值范围．陕西省西安一中2015届高考数学一模试卷（文科）一、选择题：（每小题5分，共50分）1．若复数（x∈R）为纯虚数，则x等于( )A．0 B．1 C．﹣1 D．0或1考点：复数代数形式的乘除运算；复数的基本概念．专题：计算题．分析：利用两个复数代数形式的除法法则化简z为（x2﹣x）﹣xi，再由z为纯虚数，可得，由此求得x的值．解答：解：∵===（x2﹣x）﹣xi，又z为纯虚数，则有，故x=1，故选B．点评：本题主要考查复数的基本概念，两个复数代数形式的除法，属于基础题．2．已知函数的定义域为M，g（x）=ln（1+x）的定义域为N，则M∩N=( )A．{x|x＞﹣1} B．{x|x＜1} C．{x|﹣1＜x＜1} D．∅考点：交集及其运算；函数的定义域及其求法．分析：根据题目中使函数有意义的x的值求得函数的定义域M和N，再求它们的交集即可．解答：解：∵函数的定义域是指使函数式有意义的自变量x的取值范围，∴由1﹣x＞0求得函数的定义域M={x|x＜1}，和由1+x＞0 得，N=考点：由三视图求面积、体积．专题：计算题．分析：由三视图可以看出，此几何体由一个半径为1的球体与一底面连长为2的直三棱柱所组成，故其表面积为球体的表面积加上直三棱柱的表面积．解答：解：由三视图知，此组合体上部是一个半径为的球体，故其表面积为π下部为一直三棱柱，其高为3，底面为一边长为2的正三角形，且题中已给出此三角形的高为故三棱柱的侧面积为3×（2+2+2）=18，由于不考虑接触点，故只求上底面的面积即可，上底面的面积为×2×=故组合体的表面积为故选C点评：本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查对三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，本题求的是表面积．三视图的投影规则是主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等．6．已知图象不间断函数f（x）是区间上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0，②f（a）f（m）＞0，③f（b）f（m）＜0，④f（b）f（m）＞0，其中能够正确求出近似解的是( )A．①④B．②③C．①③D．②④考点：程序框图．专题：函数的性质及应用；算法和程序框图．分析：由零点的判定定理知，判断框可以填写f（a）f（m）＜0或f（m）f（b）＞0，由此可得答案．解答：解：由二分法求方程f（x）=0近似解的流程知：当满足f（a）f（m）＜0时，令b=m；否则令a=m；故①正确，②错误；当满足f（m）f（b）＞0时，令a=m；否则令b=m；故④正确，③错误．故选：A．点评：本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．7．如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为( )A．B．C．D．考点：函数的图象．分析：本题的求解可以利用排除法，根据某具体时刻点P的位置到到x轴距离来确定答案．解答：解：通过分析可知当t=0时，点P到x轴距离d为，于是可以排除答案A，D，再根据当时，可知点P在x轴上此时点P到x轴距离d为0，排除答案B，故应选C．点评：本题主要考查了函数的图象，以及排除法的应用和数形结合的思想，属于基础题．8．已知函数f（x）=若f（2﹣x2）＞f（x），则实数x的取值范围是( )A．（﹣∞，﹣1）∪（2，+∞）B．（﹣∞，﹣2）∪（1，+∞）C．（﹣1，2）D．（﹣2，1）考点：函数单调性的性质．专题：计算题；函数的性质及应用．分析：由x=0时分段函数两个表达式对应的函数值相等，可得函数图象是一条连续的曲线．结合对数函数和幂函数f（x）=x3的单调性，可得函数f（x）是定义在R上的增函数，由此将原不等式化简为2﹣x2＞x，不难解出实数x的取值范围．解答：解：∵当x=0时，两个表达式对应的函数值都为零∴函数的图象是一条连续的曲线∵当x≤0时，函数f（x）=x3为增函数；当x＞0时，f（x）=ln（x+1）也是增函数∴函数f（x）是定义在R上的增函数因此，不等式f（2﹣x2）＞f（x）等价于2﹣x2＞x，即x2+x﹣2＜0，解之得﹣2＜x＜1，故选D点评：本题给出含有对数函数的分段函数，求不等式的解集．着重考查了对数函数、幂函数的单调性和函数的图象与性质等知识，属于基础题．9．已知双曲线方程为=1，过其右焦点F的直线（斜率存在）交双曲线于P、Q两点，PQ的垂直平分线交x轴于点M，则的值为( )A．B．C．D．考点：双曲线的简单性质．专题：计算题．分析：依题意，不妨设过其右焦点F的直线的斜率为1，利用双曲线的第二定义可求得可求得|PQ|，继而可求得PQ的垂直平分线方程，令x=0可求得点M的横坐标，从而使问题解决．解答：解：∵双曲线的方程为﹣=1，∴其右焦点F（5，0），不妨设过其右焦点F的直线的斜率为1，依题意，直线PQ的方程为：y=x﹣5．由得：7x2+90x﹣369=0，设P（x1，y1），Q（x2，y2），则x1，x2为方程7x2+90x﹣369=0的两根，∴x1+x2=﹣，y1+y2=（x1﹣5）+（x2﹣5）=x1+x2﹣10=﹣，∴线段PQ的中点N（﹣，﹣），∴PQ的垂直平分线方程为y+=﹣（x+），令y=0得：x=﹣．又右焦点F（5，0），∴|MF|=5+=．①设点P在其准线上的射影为P′，点Q在其准线上的射影为Q′，∵双曲线的一条渐近线为y=x，其斜率k=，直线PQ的方程为：y=x﹣5，其斜率k′=1，∵k′＜k，∴直线PQ与双曲线的两个交点一个在左支上，另一个在右支上，不妨设点P在左支，点Q在右支，则由双曲线的第二定义得：==e==，∴|PF|=x1﹣×=x1﹣3，同理可得|QF|=3﹣x2；∴|PQ|=|QF|﹣|PF|=3﹣x2﹣（x1﹣3）=6﹣（x1+x2）=6﹣×（﹣）=．②∴==．故选B．点评：本题考查双曲线的第二定义的应用，考查直线与圆锥曲线的相交问题，考查韦达定理的应用与直线方程的求法，综合性强，难度大，属于难题．10．在实数集R中定义一种运算“⊕”，具有性质：①对任意a，b∈R，a⊕b=b⊕a；②对任意a∈R，a⊕0=a；③对任意a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c．函数f（x）=x⊕（x＞0）的最小值为( )A．4 B．3 C．2D．1考点：进行简单的合情推理；函数的值域．专题：计算题；新定义．分析：根据题中给出的对应法则，可得f（x）=（x⊕）⊕0=1+x+，利用基本不等式求最值可得x+≥2，当且仅当x=1时等号成立，由此可得函数f（x）的最小值为f（1）=3．解答：解：根据题意，得f（x）=x⊕=（x⊕）⊕0=0⊕（x•）+（x⊕0）+（⊕0）﹣2×0=1+x+即f（x）=1+x+∵x＞0，可得x+≥2，当且仅当x==1，即x=1时等号成立∴1+x+≥2+1=3，可得函数f（x）=x⊕（x＞0）的最小值为f（1）=3故选：B点评：本题给出新定义，求函数f（x）的最小值．着重考查了利用基本不等式求最值、函数的解析式求法和简单的合情推理等知识，属于中档题．二、填空题（共4小题，每小题3分，满分12分）11．在棱长为2的正方体内随机取一点，取到的点到正方体中心的距离大于1的概率1﹣．考点：几何概型．专题：计算题．分析：本题利用几何概型求解．只须求出满足：OQ≥1几何体的体积，再将求得的体积值与整个正方体的体积求比值即得．解答：解：取到的点到正方体中心的距离小于等于1构成的几何体的体积为：×13=，∴点到正方体中心的距离大于1的几何体的体积为：v=V正方体﹣=8﹣取到的点到正方体中心的距离大于1的概率：P==1﹣．故答案为：1﹣．点评：本小题主要考查几何概型、球的体积公式、正方体的体积公式等基础知识，考查运算求解能力，考查空间想象力、化归与转化思想．属于基础题．12．设D是不等式组表示的平面区域，则D中的点P（x，y）到直线x+y=10距离的最大值是4．考点：简单线性规划的应用；点到直线的距离公式．专题：不等式的解法及应用．分析：首先根据题意做出可行域，欲求区域D中的点到直线x+y=10的距离最大值，由其几何意义为区域D的点A（1，1）到直线x+y=10的距离为所求，代入计算可得答案．解答：解：如图可行域为阴影部分，由其几何意义为区域D的点A（1，1）到直线x+y=10的距离最大，即为所求，由点到直线的距离公式得：d==4，则区域D中的点到直线x+y=10的距离最大值等于4，故答案为：4．点评：本题主要考查了简单的线性规划，以及利用几何意义求最值，属于基础题．巧妙识别目标函数的几何意义是我们研究规划问题的基础，纵观目标函数包括线性的与非线性，非线性问题的介入是线性规划问题的拓展与延伸，使得规划问题得以深化．13．在△ABC中，不等式成立；在凸四边形ABCD中，不等式成立；在凸五边形ABCDE中，不等式成立．根据以上情况，猜想在凸n边形A1A2…A n（n≥3）中的成立的不等式是．考点：归纳推理．专题：综合题．分析：根据已知中△ABC中，不等式成立；在凸四边形ABCD中，不等式成立；在凸五边形ABCDE中，不等式成立．观察分子与多边形边的关系及分母中π的系数与多边形边的关系，即可得到答案．解答：解：由已知中已知的多边形角的倒数所满足的不等式：△ABC中，不等式成立；凸四边形ABCD中，不等式成立；凸五边形ABCDE中，不等式成立；…由此推断凸n边形A1A2…A n（n≥3）中的成立的不等式是：故答案为：点评：本题考查的知识点是归纳推理，其中根据已知分析分子与多边形边的关系及分母中π的系数与多边形边的关系，是解答本题的关键．14．下列说法中，正确的有①（把所有正确的序号都填上）．①“∃x∈R，使2x＞3”的否定是“∀x∈R，使2x≤3”；②函数y=sin（2x+）sin（﹣2x）的最小正周期是π；③“函数f（x）在x=x0处有极值，则f′（x）=0”的否是真；④函数f（x）=2x﹣x2的零点有2个．考点：的真假判断与应用．专题：简易逻辑．分析：写出原的否定，可判断①；利用诱导公式和倍角公式化简函数的解析式，进而求出周期可判断②；写出原的否，可判断③；确定函数f（x）=2x﹣x2的零点个数，可判断④．解答：解：对于①“∃x∈R，使2x＞3“的否定是“∀x∈R，使2x≤3”，满足特称的否定是全称的形式，所以①正确；对于②，函数y=sin（2x+）sin（﹣2x）=sin（4x+），函数的最小正周期T==，所以②不正确；对于③，“函数f（x）在x=x0处有极值，则f'（x0）=0”的否是：若函数f（x）在x=x0处没极值，f'（x0）≠0，则显然不正确．例如f（x）=x3，x=0不是函数的极值点，但x=0时，导数为0，所以③不正确；对于④，由题意可知：要研究函数f（x）=x2﹣2x的零点个数，只需研究函数y=2x，y=x2的图象交点个数即可．画出函数y=2x，y=x2的图象，由图象可得有3个交点．所以④不正确；故正确的只有：①，故答案为：①点评：本题考查了的真假判断与应用，考查了特称的否定，函数的周期性，取最值的条件，函数零点等知识点，难度中档．三、【不等式选做题】（注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）15．若不等式|x+2|+|x﹣3|≥a+对任意的实数x恒成立，则实数a的取值范围是（﹣∞，1）∪{3}．考点：绝对值不等式的解法．专题：计算题；不等式的解法及应用．分析：不等式|x+2|+|x﹣3|≥a+对任意的实数x恒成立，转化为a+小于等于函数y=|x+2|+|x﹣3|的最小值，根据绝对值不等式的几何意义可知函数y=|x+2|+|x﹣3|的最小值为5，因此原不等式转化为分式不等式的求解问题．解答：解：令y=|x+2|+|x﹣3|，由绝对值不等式的几何意义可知函数y=|x+2|+|x﹣3|的最小值为5，∵不等式|x+2|+|x﹣3|≥a+对任意的实数x恒成立，∴原不等式可化为a+≤5，解得a=3或a＜1，故答案为：（﹣∞，1）∪{3}．点评：考查绝对值不等式的几何意义，把恒成立问题转化为求函数的最值问题，体现了转化的思想方法，属中档题．四、【几何证明选做题】（共1小题，满分0分）16．如图所示，在圆的直径AB的延长线上任取一点C，过点C作圆的切线CD，切点为D，∠ACD的平分线交AD于点E，则∠CED45°．考点：弦切角．专题：立体几何．分析：首先根据圆的切线，连接半径后得到直角三角形，进一步利用三角形的外角等于不相邻的内角的和，及角平分线知识求出结果．解答：解：连接OD，由于CD是⊙O的切线，所以：∠DOC+∠DCO=90°，∠DOC是△AOD的外角，所以：∠DOC=2∠A；又CE是∠DCA的角平分线，所以：∠DCE=∠ACE=∠DCA，∠CED=∠A+∠ECA=（∠DOC+∠DCO）=45°，故答案为：45°．点评：本题考查的知识要点：三角形的外角的应用，切线的应用，属于基础题型．五、【坐标系与参数方程】（共1小题，满分0分）17．在极坐标系中，以点（1，0）为圆心，1为半径的圆的极坐标方程是ρ=2cosθ．考点：简单曲线的极坐标方程．专题：坐标系和参数方程．分析：以点（1，0）为圆心，1为半径的圆为（x﹣1）2+y2=1，把代入即可得出．解答：解：以点（1，0）为圆心，1为半径的圆为（x﹣1）2+y2=1，把代入可得ρ2﹣2ρcosθ=0，即ρ=2cosθ．故答案为：ρ=2cosθ．点评：本题考查了直角坐标化为极坐标方程，属于基础题．三、解答题：18．如图，A、B是单位圆O上的点，C、D分别是圆O与x轴的两个交点，△ABO为正三角形．（1）若点A的坐标为，求cos∠BOC的值；（2）若∠AOC=x（0＜x＜），四边形CABD的周长为y，试将y表示成x的函数，并求出y的最大值．考点：在实际问题中建立三角函数模型；三角函数的最值；平面直角坐标系与曲线方程．专题：三角函数的图像与性质；解三角形．分析：（1）根据△ABO为正三角形求得∠BOA，利用点A的坐标求得sin∠AOC和cos∠AOC，进而利用两角和公式求得cos∠BOC．（2）利用余弦定理分别求得AC和BD，进而根据△ABO为正三角形求得AB，CD可知，四边相加得到y的函数解析式，利用两角和公式化简整理后，利用x的范围和正弦函数的性质求得函数的最大值．解答：解：（1）∵△ABO为正三角形，∴∠BOA=60°，∵点A的坐标为，∴tan∠AOC=，∴sin∠AOC=，cos∠AOC=，∴cos∠BOC=cos（∠AOC+60°）=cos∠AOCcos60°﹣sin∠AOCsin60°=．（2）由余弦定理可知AC==2sin，BD==2sin （﹣），AB=OB=1，CD=2，∴===，0＜x＜∴当x=时，y max=5．点评：本题主要考查了三角函数的最值，数学模型的应用．考查了学生分析问题和解决问题的能力．19．已知数列{a n}满足：a1=0且=1．（1）求{a n}的通项公式；（2）令b n=（n∈N+），数列{b n}的前n项和为S n，证明：S n＜1．考点：数列递推式．专题：等差数列与等比数列．分析：（1）根据条件构造等差数列，利用等差数列的通项公式即可求{a n}的通项公式；（2）求出数列{b n}的通项公式，利用裂项法进行求和．解答：解：（1）∵=1．∴{}是公差为1的等差数列，又，则=1+n﹣1=n，故a n=1﹣．（2）由（1）得b n===，则S n=b1+b2+…+b n=1﹣=1﹣＜1．点评：本题主要考查数列的通项公式以及数列求和，利用构造法以及裂项法是解决本题的关键．20．某中学将100名2014-2015学年高一新生分成水平相同的甲，乙两个“平行班”，每班50人．陈老师采用A，B两种不同的教学方式分别在甲，乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下，计成绩不低于90分者为“成绩优秀”．（1）从乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；（2）由以上统计数据填写下面2x2列联表，并判断是否有90%的把握认为“成绩优秀”与教学方式有关．甲班（A方式）乙班（B方式）总计成绩优秀成绩不优秀总计附：K2=P（（K2≥k）0.25 0.15 0.10 0.05 0.025k 1.323 2.072 2.706 3.841 5.024考点：独立性检验的应用．专题：计算题；概率与统计．分析：（1）利用列举法确定基本事件的个数，由此能求出抽出的两个均“成绩优秀”的概率；（2）由已知数据能完成2×2列联表，据列联表中的数据，求出K2≈3.137＞2.706，所以有90%的把握认为“成绩优秀”与教学方式有关．解答：解：（1）设“抽出的两个均“成绩优秀”“为事件A．从不低于86分的成绩中随机抽取2个的基本事件为（86，93），（86，96），（86，97），（86，99）（86，99），（93，96），（93，97），（93，99），（93，99），（96，97），（96，99），（96，99），（97，99），（97，99），（99，99），共15个，而事件A包含基本事件：（93，96），（93，97），（93，99），（93，99），（96，97），（96，99），（96，99），（97，99），（97，99），（99，99），共10个．所以所求概率为P（A）==（2）由已知数据得：甲班（A方式）乙班（B方式）总计成绩优秀 1 5 6成绩不优秀19 15 34总计20 20 40根据2×2列联表中数据，K2=≈3.137＞2.706所以有90%的把握认为“成绩优秀”与教学方式有关．点评：本题考查古典概型概率的求法，考查2×2列联表的应用，是中档题．21．如图，在正三棱柱ABC﹣A1B1C1中，点D为棱AB的中点，BC=1，AA1=．（1）求证：BC1∥平面A1DC；（2）求三棱锥D﹣A1B1C 的体积．考点：棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：（1）连接AC1，交A1C于点O，连结OD，由已知得OD∥BC1，由此能证明BC1∥平面A1DC．（2）由已知得AB⊥CD，从而CD⊥平面ABB1A1，进而CD⊥平面DB1A1，由此能求出三棱锥D﹣A1B1C 的体积．解答：（1）证明：连接AC1，交A1C于点O，连结OD，∵ACC1A1是平行四边形，∴O为AC1中点，∵D为AB的中点，∴OD∥BC1，OD=BC1，BC1⊄平面A1CD，OD⊂平面A1CD，∴BC1∥平面A1DC．（2）解：正△ABC中，∵D为AB的中点，∴AB⊥CD，又∵平面ABC⊥平面ABB1A1，∴CD⊥平面ABB1A1，∴CD⊥平面DB1A1，∵CD=，=，∴====．点评：本题考查直线与平面平行的证明，考查三棱锥的体积的求法，解题时要注意空间思维能力的培养．22．已知圆C1的方程为（x﹣4）2+（y﹣1）2=，椭圆C2的方程为，其离心率为，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径．（Ⅰ）求直线AB的方程和椭圆C2的方程；（Ⅱ）如果椭圆C2的左右焦点分别是F1、F2，椭圆上是否存在点P，使得，如果存在，请求点P的坐标，如果不存在，请说明理由．考点：圆与圆锥曲线的综合；直线的一般式方程；椭圆的标准方程．专题：计算题．分析：（Ⅰ）先分析得出若直线AB斜率存在，所以可设AB直线方程为y﹣1=k（x﹣4），将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用中点坐标公式即可求得b值，从而求出所求椭圆方程；（Ⅱ）先依据F1，F2的中点是原点O，得出与共线，再根据直线AB的方程写出直线PO所在的直线方程，最后与椭圆的方程联立方程组即可解得P点坐标．解答：解：（Ⅰ）若直线AB斜率不存在，则直线AB的方程为x=4，由椭圆的对称性可知，A，B两点关于x轴对称，A，B的中点为（4，0），又线段AB恰为圆C1的直径，则圆心为（4，0），这与已知圆心为（4，1）矛盾，因此直线AB斜率存在，所以可设AB直线方程为y﹣1=k（x﹣4），且设A（x1，y1）、B（x2，y2），∵，∴设椭圆方程，将AB直线方程为y﹣1=k（x﹣4）代入到椭圆方程得，即（1+4k2）x2﹣8k（4k﹣1）x+4（4k﹣1）2﹣4b2=0（1），，解得k=﹣1，故直线AB的方程为y=﹣x+5，将k=﹣1代入方程（1）得5x2﹣40x+100﹣4b2=0．x1+x2=8，，△＞0，得b2＞5．|AB|=，得，解得b2=9．故所求椭圆方程为．（Ⅱ）因为F1，F2的中点是原点O，所以，所以与共线，，而直线AB的方程为y=﹣x+5，所以直线PO所在的直线方程为y=﹣x．∴，或．所以P点坐标为，．点评：本小题主要考查圆与圆锥曲线的综合、直线的一般式方程、椭圆的标准方程等基础知识，考查运算求解能力、转化思想．属于基础题．23．设函数f（x）=x3+ax2﹣a2x+m（a＞0）（1）若函数f（x）在x∈内没有极值点，求实数a的取值范围；（2）a=1时函数f（x）有三个互不相同的零点，求实数m的取值范围；（3）若对任意的a∈，不等式f（x）≤1在x∈上恒成立，求实数m的取值范围．考点：利用导数求闭区间上函数的最值；利用导数研究函数的极值．专题：导数的综合应用．分析：（1）要使函数f（x）在x∈内没有极值点，只需f′（x）=0在上没有实根即可，即f′（x）=0的两根x=﹣a或x=不在区间上；（2）a=1时，f（x）=x3+x2﹣x+m，f（x）有三个互不相同的零点，即m=﹣x3﹣x2+x有三个互不相同的实数根，构造函数确定函数的单调性，求函数的极值，从而确定m的取值范围；（3）求导函数，来确定极值点，利用a的取值范围，求出f（x）在x∈上的最大值，再求满足f（x）≤1时m的取值范围．解答：解：（1）∵f（x）=x3+ax2﹣a2x+m（a＞0），∴f′（x）=3x2+2ax﹣a2，∵f（x）在x∈内没有极值点，∴方程f′（x）=3x2+2ax﹣a2=0在上没有实数根，由△=4a2﹣12×（﹣a2）=16a2＞0，二次函数对称轴x=﹣＜0，当f′（x）=0时，即（3x﹣a）（x+a）=0，解得x=﹣a或x=，∴，或＜﹣1（a＜﹣3不合题意，舍去），解得a＞3，∴a的取值范围是{a|a＞3}；（2）当a=1时，f（x）=x3+x2﹣x+m，∵f（x）有三个互不相同的零点，∴f（x）=x3+x2﹣x+m=0，即m=﹣x3﹣x2+x有三个互不相同的实数根．令g（x）=﹣x3﹣x2+x，则g′（x）=﹣（3x﹣1）（x+1）令g′（x）＞0，解得﹣1＜x＜；令g′（x）＜0，解得x＜﹣1或x＞，∴g（x）在（﹣∞，﹣1）和（，+∞）上为减函数，在（﹣1，）上为增函数，∴g（x）极小=g（﹣1）=﹣1，g（x）极大=g（）=；∴m的取值范围是（﹣1，）；（3）∵f′（x）=0时，x=﹣a或x=，且a∈时，∈，﹣a∈（﹣∞，﹣3]；又x∈，∴f′（x）在上大于0，f（x）是增函数；∴f（x）max=max{f（﹣2），f（2）}，而f（2）﹣f（﹣2）=16﹣4a2＜0，∴f（x）max=f（﹣2）=﹣8+4a+2a2+m，又∵f（x）≤1在上恒成立，∴f（x）max≤1，即﹣8+4a+2a2+m≤1，即m≤9﹣4a﹣2a2，在a∈上恒成立∵9﹣4a﹣2a2在a∈上是减函数，最小值为﹣87∴m≤﹣87，∴m的取值范围是{m|m≤﹣87}．点评：本题主要考查了利用导数研究函数的单调性与极值、最值，以及不等式恒成立的问题，属于难题．。

陕西省西安市2017届高考数学一模试卷(解析版)(文科)

2017 年陕西省西安市高考数学一模试卷（文科）一、选择题：本大题共12 小题，每题 5 分，共 60 分．在每题给出的四个选项中，只有一个是切合题目要求的．1．设会合 A={ ﹣ 1， 0，1， 2， 3} ， B={x|x 2﹣ 2x＞ 0} ，则 A ∩ B= （）A．{3} B．{2， 3} C． { ﹣1， 3} D．{0 ，1， 2}2．在复平面内，复数+i 所对应的点位于（）A ．第一象限B ．第二象限C．第三象限 D ．第四象限3．将函数 y=sin（x+ ）的图象上全部的点向左平移个的单位长度，再把图象上各点的横坐标扩大到本来的 2 倍（纵坐标不变），则所得图象的分析式为（）A ． y=sin （ 2x+ ）B ． y=sin （+ ）C． y=sin （﹣）D ．y=sin （+ ）4．若两个球的表面积之比为1： 4，则这两个球的体积之比为（）A．1：2 B．1：4 C．1：8 D ．1： 165．若抛物线 y2=2px 的焦点与双曲线﹣=1 的右焦点重合，则p 的值为（）A．﹣ 2 B ． 2 C．﹣ 4 D ．46．直线 x+2y ﹣ 5+2 2﹣ 2x ﹣ 4y=0 截得的弦长为（）=0 被圆 x +yA ． 1B ． 2 C． 4 D ．47．某几何体的三视图如下图，且该几何体的体积是，则正视图中的 x 的值是（）A．2B．C．D．38．公元 263 年左右，我国数学家刘徽发现，当圆内接多边形的边数无穷增添时，多边形面积可无穷迫近圆的面积，由此创办了割圆术，利用割圆术刘徽获得了圆周率精准到小数点后边两位的近似值，这就是有名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n 值为（）参照数据：， sin15 °≈，≈°．A．12B．24C．48D．969．函数f（ x）=lnx+x 2﹣bx+a（ b＞ 0， a∈ R）的图象在点（b， f （b））处的切线斜率的最小值是（）A ． 2B ．C． 1 D ．210．从正六边形的 6 个极点中随机选择 4 个极点，则以它们作为极点的四边形是矩形的概率等于（）A ．B ．C． D ．11．函数y=log a（ x﹣ 3）+2（a＞0 且 a≠ 1）过定点 P，且角α的终边过点 P，则 sin2 α+cos2α的值为（）A ．B ．C． 4 D ．512．已知定义在R 上的函数 f （x）知足 f （ x+2） =﹣ f （ x），当 x∈（﹣ 1， 3]时， f （x）= ，此中 t ＞0，若方程 f （ x） = 恰有 3 个不一样的实数根，则 t 的取值范围为（）A．（ 0，）B．（，2）C．（， 3） D ．（，+∞）二、填空题：本大题共 4 小题，每题 5 分，共 20 分） .13．已知 | + |=|﹣|，那么向量与向量的关系是．14．若不等式组所表示的平面地区为 D ，若直线y﹣ 2=a（ x+2）与 D 有公共点，则 a 的取值范围是．15．有一个游戏，将标有数字1、2、3、4 的四张卡片分别随机发给甲、乙、丙、丁 4 个人，每人一张，并请这 4 人在看自己的卡片以行进行展望：甲说：乙或丙拿到标有 3 的卡片；乙说：甲或丙拿到标有 2 的卡片；丙说：标有 1 的卡片在甲手中；丁说：甲拿到标有 3 的卡片．结果显示：这 4 人的展望都不正确，那么甲、乙、丙、丁 4 个人拿到的卡片上的数字挨次为、、、．16．已知△ ABC 的极点 A （﹣ 3，0）和极点B（ 3， 0），极点 C 在椭圆+=1 上，则=．三、解答题：本大题共 5 小题，共70 分．解答写出文字说明、证明过程或演算过程．17．（ 12 分）已知数列 {a } 中， a =5， a +a =14 ，且 2 ， 2 ， 2 成等比数列．n 3 2 6（Ⅰ）求数列 {a n} 的通项公式；（Ⅱ ）若数列 {b n n n﹣（﹣1）nn，数列 {b nTn，求T 21．} 知足 b =a } 的前 n 项和为18．（ 12 分）依据国家环保部新订正的《环境空气质量标准》规定：居民区PM2.5 的年平均浓度不得超出 35 微克 /立方米， PM2.5 的 24 小时均匀浓度不得超出75 微克 /立方米．某城市环保部门随机抽取了一居民区昨年20 天 PM2.5 的 24 小时均匀浓度的监测数据，数据统计如表：组别PM2.5 浓度（微克 / 立方米）频数（天）频次第一组（ 0， 25] 3第二组（ 25， 50] 12第三组（ 50，75] 3第四组（75，1002）（Ⅰ ）从样本中 PM2.5 的 24 小时均匀浓度超出50 微克 /立方米的 5 天中，随机抽取 2 天，求恰巧有一天PM2.5 的 24 小时均匀浓度超出75 微克 /立方米的概率；（Ⅱ ）求样本均匀数，并依据样本预计整体的思想，从PM2.5 的年均匀浓度考虑，判断该居民区的环境能否需要改良？说明原因．19．（ 12 分）如图＜ 1＞：在直角梯形 ABCD 中，AD ∥ BC ，∠ABC=90°，AB=BC=2 ，AD=6 ，CE⊥ AD 于 E 点，把△ DEC 沿 CE 折到 D′ EC的地点，使 D′ A=2 ，如图＜ 2＞：若 G， H分别为 D′B， D′E的中点．（Ⅰ ）求证： GH ⊥ D′A；（Ⅱ）求三棱锥C﹣ D′BE的体积．20．（ 12 分）如图已知椭圆C：+ =1 （ a＞ b＞0）的离心率为，以椭圆的左极点T 为圆心作圆2 2 2（ r＞ 0），设圆 T 与椭圆 C 交于点 M ， N．T ：（ x+2 ）+y =r（1）求椭圆 C 的方程；（2）求 ? 的最小值，并求此时圆 T 的方程．21．（ 12 分）已知 f（ x）=﹣ x2﹣ 3，g（ x）=2xlnx ﹣ ax 且函数 f（ x）与 g（x）在 x=1 处的切线平行．（Ⅰ）求函数 g（ x）在（ 1，g（ 1））处的切线方程；（Ⅱ）当 x∈（ 0，+∞）时， g（ x）﹣ f（x）≥ 0 恒成立，务实数 a 的取值范围．[ 选修 4-4：坐标系与参数方程选讲]22．（ 10 分）在平面直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴成立极坐标系，已知曲线 C 的极坐标方程为 2ρcos处的切线为直线 l．θ =2sin，θ它在点（1）求直线l 的直角坐标方程；（2）已知点P 为椭圆=1 上一点，求点P 到直线 l 的距离的取值范围．[ 选修 4-5：不等式选讲]23．已知函数 f （ x） =|2x﹣ 1|， x∈ R．（Ⅰ）解不等式f（ x）＜ |x|+1；（Ⅱ）若对于 x， y∈ R，有 |x﹣ y﹣ 1|≤，|2y+1|≤，求证：f（x）＜1．2017 年陕西省西安市高考数学一模试卷（文科）参照答案与试题分析一、选择题：本大题共12 小题，每题 5 分，共 60 分．在每题给出的四个选项中，只有一个是切合题目要求的．1．设会合A={ ﹣ 1， 0，1， 2， 3} ， B={x|x 2﹣ 2x＞ 0} ，则 A ∩ B= （）A．{3}B．{2， 3}C．{ ﹣1，3}D．{0 ，1， 2}【考点】交集及其运算．【剖析】求出 B 中不等式的解集确立出 B ，找出 A 与 B 的交集即可．【解答】解：由 B 中不等式变形得：x（ x﹣ 2）＞ 0，解得： x＜0 或 x＞ 2，即 B={x|x ＜ 0 或 x＞ 2} ，∵A={ ﹣ 1， 0， 1， 2，3} ，∴A ∩B={ ﹣ 1，3}，应选： C．【评论】本题考察了交集及其运算，娴熟掌握交集的定义是解本题的重点．2．在复平面内，复数+i 所对应的点位于（）A ．第一象限B ．第二象限C．第三象限 D ．第四象限【考点】复数代数形式的乘除运算；复数的代数表示法及其几何意义．【剖析】利用复数的运算法例、几何意义即可得出．【解答】解：复数+i= +i=+i= 所对应的点位于第一象限，应选： A．【评论】本题考察了复数的运算法例、几何意义，考察了计算能力，属于基础题．3．将函数 y=sin（x+）的图象上全部的点向左平移个的单位长度，再把图象上各点的横坐标扩大到本来的 2 倍（纵坐标不变），则所得图象的分析式为（）A ． y=sin （ 2x+）B ． y=sin （+D ．y=sin （+ 【考点】函数y=Asin （ωx+φ）的图象变换．）C． y=sin （﹣））【剖析】利用y=Asin （ωx+φ）的图象变换规律，得出结论．【解答】解：将函数y=sin （ x+）的图象上全部的点向左平移个的单位长度，可得 y=sin （ x++）=sin（x+）的图象；再把图象上各点的横坐标扩大到本来的 2 倍（纵坐标不变），则所得图象的分析式为y=sin （x+），应选： B．【评论】本题主要考察了y=Asin （ωx+φ）的图象变换规律，属于基础题．4．若两个球的表面积之比为1： 4，则这两个球的体积之比为（）A．1：2B．1：4C．1：8D．1：16 【考点】球的体积和表面积．【剖析】设两个球的半径分别为r1、r2，依据球的表面积公式算出它们的表面积之比为= ，解之得=，由此联合球的体积公式即可算出这两个球的体积之比．【解答】解：设两个球的半径分别为r1、 r2，依据球的表面积公式，可得它们的表面积分别为S1=4，S2=4∵两个球的表面积之比为1：4，∴===，解之得=（舍负）所以，这两个球的体积之比为==（）3=即两个球的体积之比为1： 8应选： C【评论】本题给出两个球的表面积之比，求它们的体积之比．侧重考察了球的表面积公式和体积公式等知识，属于基础题．5．若抛物线 y 2=2px 的焦点与双曲线﹣ =1 的右焦点重合，则 p 的值为（）A ．﹣ 2B ． 2C ．﹣ 4D ．4【考点】抛物线的标准方程．【剖析】求出双曲线的焦点坐标，可得抛物线y 2=2px 的焦点坐标，即可求出p 的值．【解答】解：双曲线﹣=1 的右焦点为（2，0），2即抛物线 y =2px 的焦点为（ 2， 0），∴ =2， ∴ p =4 ．应选 D ．【评论】本题考察双曲线、抛物线的性质，考察学生的计算能力，属于基础题．6．直线 x+2y ﹣ 5+ =0 被圆 x 2+y 2﹣ 2x ﹣ 4y=0 截得的弦长为（） A ． 1B ． 2C ． 4D ．4【考点】直线与圆的地点关系．【剖析】化圆的方程为标准方程，求出圆的圆心坐标和半径，由点到直线距离公式求出圆心到直线的距离，利用勾股定理求出半弦长，则弦长可求．【解答】解：由 x 2+y 2﹣ 2x ﹣ 4y=0 ，得（ x ﹣ 1）2+ y 2 2=5，（ ﹣ ）所以圆的圆心坐标是 C （ 1， 2），半径 r= ．圆心 C 到直线 x+2y ﹣ 5+=0 的距离为 d= ．所以直线直线 x+2y ﹣ 5+=0 被圆 x 2+y 2﹣ 2x ﹣ 4y=0 截得的弦长为．应选 C ．【评论】本题考察了直线与圆的地点关系，考察了弦心距、圆的半径及半弦长之间的关系，是基础题．7．某几何体的三视图如下图，且该几何体的体积是，则正视图中的x 的值是（）A．2B．C．D．3【考点】由三视图求面积、体积．【剖析】由三视图可知：原几何体是一个四棱锥，此中底面是一个上、下、高分别为1、 2、2 的直角梯形，一条长为x 的侧棱垂直于底面．据此可求出原几何体的体积．【解答】解：由三视图可知：原几何体是一个四棱锥，此中底面是一个上、下、高分别为1、2、 2 的直角梯形，一条长为x 的侧棱垂直于底面．则体积为= ，解得 x= ．应选： C．【评论】本题考察了三视图，由三视图正确恢还原几何体是解决问题的重点．8．公元 263 年左右，我国数学家刘徽发现，当圆内接多边形的边数无穷增添时，多边形面积可无穷迫近圆的面积，由此创办了割圆术，利用割圆术刘徽获得了圆周率精准到小数点后面两位的近似值，这就是有名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n 值为（）参照数据：， sin15 °≈，≈°．A．12B．24C．48D．96【考点】程序框图．【剖析】列出循环过程中S 与 n 的数值，知足判断框的条件即可结束循环．【解答】解：模拟履行程序，可得：n=6， S=3sin60 =°，不知足条件S≥， n=12 ，S=6× sin30 °=3，不知足条件S≥， n=24 ，S=12× sin15 °=12 ×0.2588=3.1056 ，知足条件S≥，退出循环，输出n 的值为 24．应选： B．【评论】本题考察循环框图的应用，考察了计算能力，注意判断框的条件的应用，属于基础题．9．函数f（ x）=lnx+x 2﹣bx+a（ b＞ 0， a∈ R）的图象在点（b， f （b））处的切线斜率的最小值是（）A．2B．C．1D．2【考点】利用导数研究曲线上某点切线方程．【剖析】求出原函数的导函数，获得函数在x=b 时的导数值，利用基本不等式求最值得答案．【解答】解：由f（ x） =lnx+x 2﹣bx+a，得 f ′（ x） =+2x ﹣b（ x＞ 0），∴f′（ b）= +b（b＞ 0）∴f ′（ b）= +b≥2，当且仅当b=，即b=1时上式取“=”切线斜率的最小值是，2．应选： D．【评论】本题考察了利用导数研究过曲线上某点处的切线方程，考察了利用基本不等式求最值，是基础题．10．从正六边形的 6 个极点中随机选择 4 个极点，则以它们作为极点的四边形是矩形的概率等于（）A ．B ．C． D ．【考点】古典概型及其概率计算公式．【剖析】从正六边形的 6 个极点中随机选择 4 个极点，选择方法有4种，且每种状况C6 =15出现的可能性同样，故为古典概型，由列举法计算出它们作为极点的四边形是矩形的方法种数，求比值即可．【解答】解：从正六边形的 6 个极点中随机选择 4 个极点，选择方法有C64=15 种，它们作为极点的四边形是矩形的方法种数为3，由古典概型可知，它们作为极点的四边形是矩形的概率等于应选 D．【评论】本题考察古典概型、组合数运算，考察运算能力．11．函数 y=log a（ x﹣ 3）+2（a＞0 且 a≠ 1）过定点 P，且角α的终边过点P，则 sin2 α+cos2α的值为（）A．B．C．4D．5【考点】随意角的三角函数的定义；对数函数的图象与性质．【剖析】利用函数的图象经过定点P 的坐标，随意角的三角函数的定义，求得sin α和 cosα的值，再利用二倍角公式求得要求式子的值．【解答】解：∵函数y=log a（ x﹣ 3） +2 过定点 P（ 4， 2），且角α的终边过点P，∴ x=4 ，y=2， r=|OP|=2 ，∴sin α=，cosα=，∴sin2 α+cos2α=2sin αcos+2cosα2α﹣ 1=2××应选： A．【评论】本题主要考察函数的图象经过定点问题，应用，属于基础题．+2×﹣1=，随意角的三角函数的定义，二倍角公式的12．已知定义在R 上的函数 f （x）知足 f （ x+2） =﹣ f （ x），当 x∈（﹣ 1， 3]时， f （x）= ，此中 t ＞0，若方程 f （ x） = 恰有 3 个不一样的实数根，则t的取值范围为（）A．（ 0，）B．（，2）C．（， 3） D ．（，+∞）【考点】根的存在性及根的个数判断；函数的周期性．【剖析】确立 f （ x）的周期为 4 ，x∈（5， 6）时， f（ x） =t（ x﹣ 5）， x∈（ 6， 7）时， f （x） =t（ 7﹣ x），再利用 t＞0，f（x） = 恰有 3 个不一样的实数根，可得t（ 2﹣ 1）＞，t（6﹣1）＜2，即可求出t 的取值范围．【解答】解：由f（x+2）=﹣f（ x），∴f （x+4 ） =﹣f （x+2 ） =f （ x），故 f（ x）的周期为 4，∵x∈（1，2）时，f（x）=t（x﹣1），x∈（2，3）时，f （x）=t（3﹣x），∴x∈（ 5，6）时， f（ x） =t（ x﹣ 5）， x∈（ 6， 7）时， f （x） =t（ 7﹣x），∵t ＞ 0， f（ x） = 恰有 3 个不一样的实数根，∴t （ 2﹣ 1）＞，t（6﹣1）＜2∴2＞ t＞，应选： B．【评论】本题考察函数的周期性、根的存在性及根的个数判断，考察学生的计算能力，属于中档题．二、填空题：本大题共 4 小题，每题 5 分，共 20 分） .13．已知 | + |=|﹣|，那么向量与向量的关系是垂直．【考点】平面向量数目积的运算．【剖析】依据平面向量的模长公式与数目积运算，得出?=0时⊥．【解答】解： | + |=|﹣|，∴=，+2 ?+=﹣2?+，∴? =0，∴⊥ ，∴向量与向量的关系是垂直．故答案为：垂直．【评论】本题考察了平面向量的数目积与模长公式的应用问题，是基础题目．14．若不等式组所表示的平面地区为 D ，若直线y﹣ 2=a（ x+2）与 D 有公共点，则 a 的取值范围是a≤．【考点】简单线性规划．【剖析】作出地区 D ，直线 y﹣ 2=a（x+2 ）表示过点A（﹣ 2，2）且斜率为 a 的直线，数形联合可得结果．【解答】解：作出不等式组所对应的可行域 D （如图暗影），直线 y﹣ 2=a（x+2 ）表示过点 A （﹣ 2， 2）且斜率为 a 的直线，联立可解得即 C（ 1， 0），由斜率公式可得a==，由解得 B（0，3），此时A==联合图象可得要使直线y﹣ 2=a（x+2）与地区 D 有公共点需a≤，故答案为：a≤．【评论】本题考察简单线性规划，数形联合是解决问题的重点，属中档题．15．有一个游戏，将标有数字1、2、3、4 的四张卡片分别随机发给甲、乙、丙、丁 4 个人，每人一张，并请这 4 人在看自己的卡片以行进行展望：甲说：乙或丙拿到标有 3 的卡片；乙说：甲或丙拿到标有 2 的卡片；丙说：标有 1 的卡片在甲手中；丁说：甲拿到标有 3 的卡片．结果显示：这 4 人的展望都不正确，那么甲、乙、丙、丁 4 个人拿到的卡片上的数字挨次为4、2 、1、3．【考点】进行简单的合情推理．【剖析】依据展望都不正确，即可推出相对应的数字【解答】解：乙丙丁所说为假? 甲拿 4，甲乙所说为假? 丙拿 1，甲所说为假? 乙拿 2；故甲、乙、丙、丁 4 个人拿到的卡片上的数字挨次为4， 2，1， 3，故答案为： 4， 2， 1， 3【评论】本题考察了合情推理的问题，重点是掌握命题的否认，属于基础题．16．已知△ ABC 的极点 A （﹣ 3，0）和极点B（ 3， 0），极点 C 在椭圆+=1 上，则= 3．【考点】椭圆的简单性质．【剖析】由题意可知：极点和 b 的关系，即可求得A ， B 为椭圆的两个焦点，利用正弦定理及椭圆的定义，求得=3．a【解答】解：由椭圆+=1，长轴长2a=10，短轴长2b=8，焦距 2c=6，则极点 A ， B 为椭圆的两个焦点，三角形 ABC 中， a=丨 BC 丨， b=丨 AC 丨， c= 丨 AB 丨 =6， a+b= 丨 BC 丨 +丨 AC 丨=10 ，由正弦定理可知则 sinA=，sinB= = =，sinC= ，=2R ，===3，故答案为： 3．【评论】本题考察椭圆的定义及正弦定理的应用，考察数形联合思想，考察计算能力，属于中档题．三、解答题：本大题共 5 小题，共70 分．解答写出文字说明、证明过程或演算过程．17．（12 分）（ 2017?西安一模）已知数列 {a n} 中，a3=5 ，a2+a6=14 ，且 2 ，2 ，2成等比数列．（Ⅰ）求数列 {a n} 的通项公式；n（Ⅱ）若数列 {b n} 知足 b n=a n﹣（﹣ 1） n，数列 {b n} 的前 n 项和为 T n，求 T21．【剖析】（ I）由 2，2，2成等比数列，可得=2?2，可得2a n+1 =a n+a n+2．利用等差数列的通项公式可得a n．（II ）利用“错位相减法”、等差数列等比数列的乞降公式即可得出．【解答】解：（I ）∵ 2，2，2成等比数列，∴=2?2，∴2a n+1 =a n+a n+2．∴数列 {a n 3 5 6，} 为等差数列，设公差为d，∵ a =5 ， a +a =20∴a1+2d=5，2a1+9d=20 ，解得 a1=1，d=2．∴a n=1+2 （ n﹣ 1） =2n ﹣ 1．n n（II ）b n=a n﹣（﹣ 1） n= （ 2n﹣ 1）﹣（﹣ 1） n．n则 S n=﹣ 1+2﹣3+ +（﹣ 1）n n．∴﹣ S n=1﹣ 2+3++（﹣ 1）n（ n﹣ 1） +（﹣ 1）n+1n，∴2S n=﹣ 1+1﹣ 1+ +（﹣ 1 ）n﹣（﹣ 1）n+1 n=﹣（﹣ 1）n+1n，∴S n= + ．∴T n= ﹣﹣=n2﹣n﹣﹣．∴T21=21 2﹣ 21﹣﹣=425+ ．【评论】本题考察了等差数列与等比数列的通项公式与乞降公式、“错位相减法”，考察了推理能力与计算能力，属于中档题．18．（ 12 分）（ 2017?西安一模）依据国家环保部新订正的《环境空气质量标准》规定：居民区 PM2.5 的年均匀浓度不得超出35 微克 /立方米，的 24 小时均匀浓度不得超出 75 微克 /立方米．某城市环保部门随机抽取了一居民区昨年20 天 PM2.5 的 24 小时均匀浓度的监测数据，数据统计如表：组别PM2.5 浓度（微克 / 立方米）频数（天）频次第一组（ 0， 25] 3第二组（ 25， 50] 12第三组（ 50， 75] 3第四组（ 75，100） 2（Ⅰ ）从样本中的24 小时均匀浓度超出50 微克 /立方米的 5 天中，随机抽取 2 天，求恰巧有一天PM2.5 的 24 小时均匀浓度超出75 微克 /立方米的概率；（Ⅱ）求样本均匀数，并依据样本预计整体的思想，从PM2.5 的年均匀浓度考虑，判断该居民区的环境能否需要改良？说明原因．【考点】列举法计算基本领件数及事件发生的概率；频次散布表．【剖析】（Ⅰ）设 PM2.5 的 24 小时均匀浓度在（ 50，75] 内的三天记为 A 1，A 2，A 3，的 24 小时均匀浓度在（ 75， 100）内的两天记为 B 1， B2，求出基本领件总数，切合条件的基本领件总数，即可求得概率；（Ⅱ ）利用组中值×频数，可得昨年该居民区PM2.5 年均匀浓度，从而可判断该居民区的环境能否需要改良【解答】解：（Ⅰ）解：（Ⅰ）设 PM2.5 的 24 小时均匀浓度在（50，75] 内的三天记为 A 1，A 2， A3，PM2.5 的24 小时均匀浓度在（ 75 ， 100）内的两天记为B1，B2．所以 5 天任取 2 天的状况有： A 1A 2，A 1A 3， A 1 B1， A 1B 2， A 2A 3， A 2B 1，A 2B2， A 3B 1，A 3B2 共10种．此中切合条件的有：A1B1，A 1B2， A2B1，A2B2， A3B1，A3B2共 6 种．所以所求的概率 P= ．（8 分）（Ⅱ ）昨年该居民区PM2.5 年均匀浓度为：××××（微克 /立方米）．（10分）由于＞35，所以昨年该居民区年均匀浓度不切合环境空气质量标准，故该居民区的环境需要改良．（12 分）【评论】本题主要考察频次散布表、古典概型、统计等基础知识，考察数据办理能力、运算求解能力以及应意图识，考察必定与或然思想等．19．（ 12 分）（ 2017?西安一模）如图＜ 1＞：在直角梯形ABCD 中， AD ∥BC，∠ ABC=90°，AB=BC=2 ， AD=6 ， CE⊥ AD 于 E 点，把△DEC 沿CE 折到D′ EC的地点，D′ A=2 ，使如图＜2＞：若G， H 分别为D′B， D′E的中点．（Ⅰ ）求证：GH ⊥ D′A；（Ⅱ ）求三棱锥C﹣ D′BE的体积．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的地点关系．【剖析】（Ⅰ）经过证明： AD′⊥AE ， AD′⊥ AC ，推出 AD′⊥平面 ABCD ，推出 AD′⊥ BE，经过证明 GH ∥ BE，推出 GH ⊥ D′A；（Ⅱ）三棱锥 C﹣D′BE的体积．直接利用棱锥的体积公式求解即可．【解答】解：（Ⅰ）证明：在直角梯形 ABCD 中，AD ∥ BC ，∠ABC=90°，AB=BC=2 ，AD=6 ，CE⊥ AD 于 E 点，把△ DEC 沿 CE 折到 D′ EC的地点，使 D′ A=2 ，ED=4，连接 BE，GH ，在三角形 AED′中，可得2 2 2=2 ，ED′=AE +AD′，可得 AD′⊥AE ， DC=AC=22 2 2，可得 AC +AD′=CD′，可得 AD′⊥ AC ，由于 AE ∩ AC=A ，所以 AD′⊥平面 ABCD ，可得 AD′⊥ BE ， G，H 分别为 D′B， D′E的中点，可得GH ∥BE ，所以 GH ⊥ D′A．（Ⅱ ）三棱锥 C﹣D′BE的体积为 V ．则 V= = = ．【评论】本题考察的知识点是直线与平面垂直的判断，棱锥的体积，此中（Ⅰ ）的重点是娴熟掌握面面垂直，线面垂直及线线垂直的互相转变，（Ⅱ ）的重点是判断出棱锥的高和底面面积．20．（ 12 分）（ 2017?西安一模）如图已知椭圆C：+=1（ a＞ b＞ 0）的离心率为，以椭圆的左极点T 为圆心作圆2 2 2T：（x+2 ） +y =r （ r＞ 0），设圆 T 与椭圆 C 交于点 M ，N ．（1）求椭圆 C 的方程；（2）求?的最小值，并求此时圆T 的方程．【考点】直线与椭圆的地点关系．【剖析】（ 1）运用椭圆的离心率公式和极点坐标，联合a，b， c 的关系，可得椭圆方程；（2）设M （ m，n），由对称性可得N （ m，﹣ n），代入椭圆方程，再由向量数目积的坐标表示，转变为对于m 的二次函数，配方，联合椭圆的范围，可得最小值，从而获得M 的坐标，可得圆的方程．【解答】解：（1）由题意可得e= =，椭圆的左极点T （﹣ 2， 0），可得 a=2， c=，b==1，则椭圆方程为+y2=1；（2）设 M （m，n），由对称性可得 N （m，﹣ n），即有+n 2=1，则? =（ m+2， n） ?（ m+2，﹣ n） =（ m+2）2﹣ n2=（ m+2）2﹣ 1+=m2+4m+3=（ m+ ）2﹣，由﹣ 2≤ m≤ 2，可得 m=﹣时，?的最小值为﹣，此时 n2=，即有 r2 =（ m+2 ）2+n2=，可得圆 T 的方程（ x+2）2+y 2= ．【评论】本题考察椭圆方程的求法，注意运用离心率公式，考察向量数目积的最小值，注意运用二次函数的最值求法和椭圆的性质，考察化简整理的运算能力，属于中档题．21．（ 12 分）（ 2017?西安一模）已知f（ x）=﹣ x2﹣ 3，g（ x）=2xlnx ﹣ ax 且函数 f （ x）与g（ x）在 x=1 处的切线平行．（Ⅰ ）求函数 g（ x）在（ 1，g（ 1））处的切线方程；（Ⅱ）当 x∈（ 0，+∞）时， g（ x）﹣ f（x）≥ 0 恒成立，务实数 a 的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数研究曲线上某点切线方程．【剖析】（Ⅰ）求出函数的导数，求出 a 的值，从而求出切线方程即可；（Ⅱ）先把已知等式转变为a≤ x+2lnx+，设g（x）=x+2lnx+，x∈（0，+∞），对函数进行求导，利用导函数的单一性求得函数的最小值，只需 a 小于或等于最小值即可．【解答】解：（Ⅰ ）f′（x）=﹣2x，故 k=f ′（1） =﹣ 2，而 g′（ x） =2 （ lnx+1 ）﹣ a，故 g′（1） =2﹣ a，故 2﹣ a=﹣ 2，解得： a=4，故 g（ 1）=﹣ a=﹣ 4，故 g（ x）的切线方程是： y+4= ﹣ 2（ x﹣1），即 2x+y+2=0 ；（Ⅱ）当 x∈（ 0，+∞）时， g（ x）﹣ f（x）≥ 0 恒成立，等价于 a≤ x+2lnx+ ，令 g（ x）=x+2lnx+ ，x∈（ 0，+∞），g′（ x） =1+﹣=，当 0＜ x＜ 1 时， g′（ x）＜ 0， g（ x）单一减，当 x=1 时， g′（x） =0，当 x＞ 1 时， g′（ x）＞ 0，g（ x）单一增，∴g（ x）min=g（ 1） =4，∴a≤ 4．【评论】本题主要考察了利用导函数求最值的问题．考察了学生对函数基础知识的理解和灵活运用．[ 选修 4-4：坐标系与参数方程选讲]22．（ 10 分）（ 2017?西安一模）在平面直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴成立极坐标系，已知曲线 C 的极坐标方程为2ρcosθ =2sin，θ它在点处的切线为直线l．（1）求直线 l 的直角坐标方程；（2）已知点 P 为椭圆=1 上一点，求点 P 到直线 l 的距离的取值范围．【考点】直线与椭圆的地点关系；简单曲线的极坐标方程；参数方程化成一般方程．【剖析】（ 1）利用极坐标方程与一般方程的互化求解即可．（2）设出椭圆的参数方程，利用点到直线的距离公式化简求解即可．【解答】（本小题满分 10 分）2解：（ 1）∵曲线 C 的极坐标方程为ρcosθ =2sin，θ2 2 ∴ρcos θ =2 ρ sin θ，∴曲线 C 的直角坐标方程为y= x2，∴y′=x，又 M （ 2 ，）的直角坐标为（2， 2），∴曲线 C 在点（ 2， 2）处的切线方程为 y﹣2=2 （ x﹣ 2），即直线 l 的直角坐标方程为： 2x﹣y﹣ 2=0 ．（2） P 为椭圆上一点，设P（cosα，2sin α），则 P到直线l 的距离d= = ，当 sin（α﹣）=﹣时，d有最小值0．当 sin（α﹣）=1时，d有最大值．∴P 到直线 l 的距离的取值范围为：[0，]．（10分）【评论】本题考察椭圆的参数方程，极坐标方程与一般方程的互化，点到直线的距离公式的应用，考察转变思想以及计算能力．[ 选修 4-5：不等式选讲]23．（ 2017?西安一模）已知函数f（ x） =|2x﹣ 1|，x∈ R．（Ⅰ）解不等式f（ x）＜ |x|+1；（Ⅱ）若对于 x， y∈ R，有 |x﹣ y﹣ 1|≤，|2y+1|≤，求证：f（x）＜1．【考点】绝对值三角不等式；绝对值不等式的解法．【剖析】（Ⅰ）由条件 |2x﹣ 1|＜ |x|+1，分类议论，求得x 的范围．（Ⅱ ）由条件利用绝对值三角不等式证得不等式成立．【解答】解：（Ⅰ ）不等式f（x）＜|x|+1，等价于|2x﹣1|＜|x|+1，x≤ 0，不等式可化为﹣2x+1 ＜﹣ x+1 ，即 x＞ 0，不可立；0 ，不等式可化为﹣ 2x+1 ＜x+1 ，即 x＞0 ，∴ 0＜x≤；x＞，不等式可化为 2x ﹣ 1＜ x+1 ，即 x＜ 2，∴＜ x＜ 2；故不等式 f （ x）＜ |x|+1 的解集为（ 0， 2）．（Ⅱ）∵ |x﹣ y﹣ 1|≤， |2y+1|≤，∴f （x） =|2x﹣ 1|=|2（ x﹣ y﹣ 1） +（ 2y+1 ） |≤ |2（ x﹣y﹣ 1） |+|（ 2y+1） |≤ 2? + ＜ 1．【评论】本题主要考察绝对值不等式的解法，绝对值三角不等式的应用，表现了转变的数学思想，属于中档题．。

2017届陕西省西安铁一中、铁一中国际合作学校高三下学期四月月考文科数学试题及答案

铁一中模拟考试数学（文科）试题第I 卷选择题（共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中,只有一项是符合题目要求的．1.已知集合2{|20}A x x x =--≤，{|ln(1)}B x y x ==-，则A B = A. (0,2] B. (,1)(2,)-∞-+∞ C. [1,1)- D. (1,0)(0,2)-2.已知α ，β表示两个不同的平面，l 为α内的一条直线，则“α//β是“l //β”的 A.充分不必要条件 B.必要不充分条件 C. 充要条件 D.既不充分也不必要条件3．已知复数1z ai =+()a ∈R （i 是虚数单位）在复平面上表示的点在第四象限，且5z z ⋅=，则a =A.2 B. 2- D.4．把函数)6sin(π+=x y 图象上各点的横坐标缩短到原来的21倍（纵坐标不变），再将图象向右平移3π个单位，那么所得图象的一条对称轴方程为A ．2π-=x B ．4π-=x C ．8π=x D ．4π=x5．下列命题中，真命题是A ．01,2>--∈∀x x R xB ．βαβαβαsin sin )sin(,,+<+∈∀RC ．01,2=+-∈∃x x R xD ．βαβαβαcos cos )sin(,,+=+∈∃R6．等比数列{}n a 中5121=a ，公比21-=q ，记12n n a a a ∏=⨯⨯⨯ （即n ∏表示数列{}n a 的前n 项之积），8∏ ，9∏，10∏，11∏中值为正数的个数是 A ． B ． 2 C ． 3 D ． 47．某几何体的三视图如右图所示，则其侧面积为A ．2．2C8．阅读右侧程序框图，输出的结果s 的值为A.0B.23C.3D.23-9．在区间15,⎡⎤⎣⎦和24,⎡⎤⎣⎦分别取一个数,记为a b ,, 则方程22221x ya b+=表示焦点在x 轴上且离心率小于的椭圆的概第Ⅱ卷非选择题（共100分）二、填空题：本大题共5小题，每小题5分，共25分．开始则其面积为______；13.向量()()1,2,1,0a b ==- ，若()a b a λ+⊥，则实数λ等于；14. 已知直线:l 20x y +-=和圆:C 221212540x y x y +--+=,则与直线l和圆C 都相切且半径最小的圆的标准方程是_________．15．（请考生在以下三个小题中任选一题做答，如果多做，则按所做的第一题评阅记分）A.（坐标系与参数方程）已知直线l 的参数方程为212x y ⎧=⎪⎪⎨⎪=+⎪⎩ (t 为参数)，圆C 的参数方程为cos 2sin x y θθ=+⎧⎨=⎩(θ为参数), 则圆心C 到直线l 的距离为_________．B. (几何证明选讲) 如图，P 是圆O 外一点，过P 引圆O 的两条割线PAB 、PCD ，5==AB PA ，3=CD ，则=PC _________．C.（不等式选讲）若不等式aa x x 4|3||1|+≥-++对任意的实数x 恒成立，则实数a 的取值范围是_________．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤． 16.（本小题满分12分）PM2.5指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．PM2.5日均值在35微克／立方米以下空气质量为一级：在35微克／立方米～75微克／立方米之间空气质量为二级；在75微克／立方米以上空气质量为超标．古城西安地区2017年3月6日至I5日每天的PM2.5监测数据如茎叶图所示．（Ⅰ）计算这10天PM2．5数据的平均值并判断其是否超标;（Ⅱ）小陈在此期间的某天曾经来此地旅游，求当天PM2.5日均监测数据未超标的概率;（III）小王在此期间也有两天经过此地，这两天此地PM2.5监测数据均未超标．请计算出这两天空气质量恰好有一天为一级的概率．17.（本小题满分12分）某渔轮在航行中不幸遇险，发出呼救信号，我海军舰艇在A处获悉后，测出该渔轮在方位角为45 ，距离为10n mile的C处，并测得渔轮正沿方位角为105 的方向，以9/n mile h的速度向小岛靠拢，我海军舰艇立即以21/n mile h的速度前去营救. （注：方位角定义:从某点的正北方向起,顺时针方向旋转到目标方向的角）（I）求舰艇靠近渔轮所需的时间；（II）设舰艇的航向与AC的夹角为α，求α的正弦值．18．(本题满分12分)已知数列}{n a 的前n 项和为n S ，数列}1{+n S 是公比为2的等比数列，2a 是1a 和3a 的等比中项. （I ）求数列}{n a 的通项公式；（II ）求数列{}n na 的前n 项和n T .19. （本小题满分12分）如图所示，在棱长为2的正方体1111ABCD A BC D -中，E 、F 分别为1DD 、DB 的中点．（I ）求证：EF //平面11ABC D ；（II ）求证：1CF B E ⊥；（III ）求三棱锥1C B FE V -的体积．20.（本小题满分13分）已知圆C ：22(1)5x y +-= 错误！未找到引用源。

【陕西省西安市】2017年高考一模数学(文科)试卷-答案

17．（I ）∵2n a ，12n a +，22n a +成等比数列，∴122(2)22n n n a a a ++=，∴122n n n a a a ++=+．∴数列{}n a 为等差数列，设公差为d ，∵35a =，5620a a +=，∴125a d +=，12920a d +=，解得11a =，2d =．∴12(1)21n a n n =+-=-．（II ）(1)(21)(1)n n n n b a n n n =-=----．设数列(1){}n n --的前n 项和为n S ，则123(1)n n S n =-+-+⋯+-．∴1123(1)(1)(1)n n n S n n +-=-++⋯+--+-，∴11[1(1)]2111(1)1)(1(1)(1)n n n n n S n n ++---=-++⋯+-=------﹣， ∴(1)1(1)42n n n n S ---=+．∴2(121)(1)1(1)(1)1(1)24242n n n n n n n n n T n n +-------=--=---． ∴22122132121425444T ---=-=-+． 18．解：（Ⅰ）设 2.5PM 的24小时平均浓度在(50,75]内的三天记为1A ，2A ，3A ， 2.5PM 的24小时平均浓度在(75,100)内的两天记为1B ，2B ．所以5天任取2天的情况有：12A A ，13A A ，11A B ，12A B ，23A A ，21A B ，22A B ，31A B ，32A B 共10种．其中符合条件的有：11A B ，12A B ，21A B ，22A B ，31A B ，32A B 共6种．所以所求的概率63105P ==．………………………………………………………………………（8分）（Ⅱ）去年该居民区 2.5PM 年平均浓度为：12.50.1537.50.662.50.1587.50.142.5⨯+⨯+⨯+⨯=（微克/立方米）．………………………（10分）因为42.535>，所以去年该居民区 2.5PM 年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进．…………………………………………………………………………………………………（12分） 19．解：（Ⅰ）证明：在直角梯形ABCD 中，AD BC ∥，90ABC ︒∠=，2AB BC ==，6AD =，CE AD E ⊥于点，把DEC △沿CE 折到D EC '的位置，使D A '=4ED =，连结BE ，GH ，在三角形AED '中，可得222ED AE AD '=+'，可得AD AE '⊥，DC ==，AC =，可得222AC AD CD +'='，可得，因为AE AC A =，所以AD ABCD '⊥平面，可得AD BE '⊥，G ，H 分别为D B '，D E '的中点，可得GH BE ∥，所以GH D A ⊥'．（Ⅱ）三棱锥C D BE -'的体积为V ．则111223323BCE V S AD ='=⨯⨯⨯=△．20．解：（1）由题意可得2c e a ==，椭圆的左顶点(2,0)T -，可得2a =，c =，1b =，则椭圆方程为2214x y +=；（2）设(,)M m n ，由对称性可得(,)N m n -，即有2214m n +=，则222225(2,)(2,)(2)(2)14344TM m m n m n m n m m T m N =++-=+=++=++-- 258()1545m =+-，由22m -≤≤，可得85m =-时，TM TN 的最小值为15-，此时2925n =，即有22213(2)25r m n =++=，可得圆T 的方程2213(2)25x y ++=． 21．解：（Ⅰ）()2f x x '=-，故(1)2k f ='=-，而()2(ln 1)g x x a '=+-，故(1)2g a '=-，故22a -=-，解得：4a =，故(1)4g a =-=-，故()g x 的切线方程是：42(1)y x +=--，即220x y ++=；（Ⅱ）当(0,)x ∈+∞时，()()0g x f x -≥恒成立，等价于32ln a x x x ≤++，令3()2ln g x x x x=++，(0,)x ∈+∞， 2223(3)(1)()1x x g x x x x +-'=+-=，当01x <<时，()0g x '<，()g x 单调减，当1x =时，()0g x '=，当1x >时，()0g x '>，()g x 单调增，∴min ()(1)4g x g ==，∴4a ≤．22．解：（1）∵曲线C 的极坐标方程为2cos 2sin ρθθ=，∴22cos 2sin ρθρθ=，∴曲线C 的直角坐标方程为212y x =，∴y x '=，又π)4M 的直角坐标为(2,2)，∴曲线C 在点(2,2)处的切线方程为22(2)y x -=-，即直线l 的直角坐标方程为：220x y --=．（2）P 为椭圆22134x y +=上一点，设(cos ,2sin )P αα，则P 到直线l 的距离π|4cos()2|d α-+，当π1sin()32α-=-时，d 有最小值0．当πsin()13α-=时，d∴P 到直线l 的距离的取值范围为：[0,5．……………………………………（10分） 23．解：（Ⅰ）不等式|()1|f x x <+，等价于||||211x x -<+， 0x ≤，不等式可化为211x x -+<-+，即0x >，不成立；102x ≤≤，不等式可化为211x x -+<+，即0x >， ∴102x ≤≤； 12x >，不等式可化为211x x -<+，即2x <， ∴122x <<；故不等式|()1|f x x <+的解集为(0,2)．（Ⅱ）∵113||x y --≤，1216||y +≤， ∴11()212(1||||||)(21)2(1)||(21)2136f x x x y y x y y =-=--++≤--++≤+<．陕西省西安市2017年高考一模数学（文科）试卷解析一、选择题1．【考点】交集及其运算．【分析】求出B中不等式的解集确定出B，找出A与B的交集即可．【解答】解：由B中不等式变形得：x（x﹣2）＞0，解得：x＜0或x＞2，即B={x|x＜0或x＞2}，∵A={﹣1，0，1，2，3}，∴A∩B={﹣1，3}，故选：C．【点评】此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．【考点】复数代数形式的乘除运算；复数的代数表示法及其几何意义．【分析】利用复数的运算法则、几何意义即可得出．【解答】解：复数+i=+i=+i=所对应的点位于第一象限，故选：A．【点评】本题考查了复数的运算法则、几何意义，考查了计算能力，属于基础题．3．【考点】函数y=Asin（ωx+φ）的图象变换．【分析】利用y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：将函数y=sin（x+）的图象上所有的点向左平移个的单位长度，可得y=sin（x++）=sin（x+）的图象；再把图象上各点的横坐标扩大到原来的2倍（纵坐标不变），则所得图象的解析式为y=sin（x+），故选：B．【点评】本题主要考查了y=Asin（ωx+φ）的图象变换规律，属于基础题．4．【考点】球的体积和表面积．【分析】设两个球的半径分别为r1、r2，根据球的表面积公式算出它们的表面积之比为=，解之得=，由此结合球的体积公式即可算出这两个球的体积之比．【解答】解：设两个球的半径分别为r1、r2，根据球的表面积公式，可得它们的表面积分别为S1=4，S2=4∵两个球的表面积之比为1：4，∴===，解之得=（舍负）因此，这两个球的体积之比为==（）3=即两个球的体积之比为1：8故选：C【点评】本题给出两个球的表面积之比，求它们的体积之比．着重考查了球的表面积公式和体积公式等知识，属于基础题．5．【考点】抛物线的标准方程．【分析】求出双曲线的焦点坐标，可得抛物线y2=2px的焦点坐标，即可求出p的值．【解答】解：双曲线﹣=1的右焦点为（2，0），即抛物线y2=2px的焦点为（2，0），∴=2，∴p=4．故选D．【点评】本题考查双曲线、抛物线的性质，考查学生的计算能力，属于基础题．6．【考点】直线与圆的位置关系．【分析】化圆的方程为标准方程，求出圆的圆心坐标和半径，由点到直线距离公式求出圆心到直线的距离，利用勾股定理求出半弦长，则弦长可求．【解答】解：由x2+y2﹣2x﹣4y=0，得（x﹣1）2+（y﹣2）2=5，所以圆的圆心坐标是C（1，2），半径r=．圆心C到直线x+2y﹣5+=0的距离为d=．所以直线直线x+2y﹣5+=0被圆x2+y2﹣2x﹣4y=0截得的弦长为．故选C．【点评】本题考查了直线与圆的位置关系，考查了弦心距、圆的半径及半弦长之间的关系，是基础题．7．【考点】由三视图求面积、体积．【分析】由三视图可知：原几何体是一个四棱锥，其中底面是一个上、下、高分别为1、2、2的直角梯形，一条长为x的侧棱垂直于底面．据此可求出原几何体的体积．【解答】解：由三视图可知：原几何体是一个四棱锥，其中底面是一个上、下、高分别为1、2、2的直角梯形，一条长为x的侧棱垂直于底面．则体积为=，解得x=．故选：C．【点评】本题考查了三视图，由三视图正确恢复原几何体是解决问题的关键．8．【考点】程序框图．【分析】列出循环过程中S与n的数值，满足判断框的条件即可结束循环．【解答】解：模拟执行程序，可得：n=6，S=3sin60°=，不满足条件S≥3.10，n=12，S=6×sin30°=3，不满足条件S≥3.10，n=24，S=12×sin15°=12×0.2588=3.1056，满足条件S≥3.10，退出循环，输出n的值为24．故选：B．【点评】本题考查循环框图的应用，考查了计算能力，注意判断框的条件的应用，属于基础题．9．【考点】利用导数研究曲线上某点切线方程．【分析】求出原函数的导函数，得到函数在x=b时的导数值，利用基本不等式求最值得答案．【解答】解：由f（x）=lnx+x2﹣bx+a，得f′（x）=+2x﹣b（x＞0），∴f′（b）=+b（b＞0）∴f′（b）=+b≥2，当且仅当b=，即b=1时上式取“=”，切线斜率的最小值是2．故选：D．【点评】本题考查了利用导数研究过曲线上某点处的切线方程，考查了利用基本不等式求最值，是基础题．10．【考点】古典概型及其概率计算公式．【分析】从正六边形的6个顶点中随机选择4个顶点，选择方法有C64=15种，且每种情况出现的可能性相同，故为古典概型，由列举法计算出它们作为顶点的四边形是矩形的方法种数，求比值即可．【解答】解：从正六边形的6个顶点中随机选择4个顶点，选择方法有C64=15种，它们作为顶点的四边形是矩形的方法种数为3，由古典概型可知，它们作为顶点的四边形是矩形的概率等于故选D．【点评】本题考查古典概型、组合数运算，考查运算能力．11．【考点】任意角的三角函数的定义；对数函数的图象与性质．【分析】利用函数的图象经过定点P的坐标，任意角的三角函数的定义，求得sinα和cosα的值，再利用二倍角公式求得要求式子的值．【解答】解：∵函数y=log a（x﹣3）+2过定点P（4，2），且角α的终边过点P，∴x=4，y=2，r=|OP|=2，∴sinα=，cosα=，∴sin2α+cos2α=2sinαcosα+2cos2α﹣1=2××+2×﹣1=，故选：A．【点评】本题主要考查函数的图象经过定点问题，任意角的三角函数的定义，二倍角公式的应用，属于基础题．12．【考点】根的存在性及根的个数判断；函数的周期性．【分析】确定f（x）的周期为4，x∈（5，6）时，f（x）=t（x﹣5），x∈（6，7）时，f（x）=t（7﹣x），再利用t＞0，f（x）=恰有3个不同的实数根，可得t（2﹣1）＞，t（6﹣1）＜2，即可求出t的取值范围．【解答】解：由f（x+2）=﹣f（x），∴f（x+4）=﹣f（x+2）=f（x），故f（x）的周期为4，∵x∈（1，2）时，f（x）=t（x﹣1），x∈（2，3）时，f（x）=t（3﹣x），∴x∈（5，6）时，f（x）=t（x﹣5），x∈（6，7）时，f（x）=t（7﹣x），∵t＞0，f（x）=恰有3个不同的实数根，∴t（2﹣1）＞，t（6﹣1）＜2∴2＞t＞，故选：B．【点评】本题考查函数的周期性、根的存在性及根的个数判断，考查学生的计算能力，属于中档题．二、填空题13．【考点】平面向量数量积的运算．【分析】根据平面向量的模长公式与数量积运算，得出•=0时⊥．【解答】解：|+|=|﹣|，∴=，+2•+=﹣2•+，∴•=0，∴⊥，∴向量与向量的关系是垂直．故答案为：垂直．【点评】本题考查了平面向量的数量积与模长公式的应用问题，是基础题目．14．【考点】简单线性规划．【分析】作出区域D，直线y﹣2=a（x+2）表示过点A（﹣2，2）且斜率为a的直线，数形结合可得结果．【解答】解：作出不等式组所对应的可行域D（如图阴影），直线y﹣2=a（x+2）表示过点A（﹣2，2）且斜率为a的直线，联立可解得即C（1，0），由斜率公式可得a==，由解得B（0，3），此时A==结合图象可得要使直线y﹣2=a（x+2）与区域D有公共点需a≤，故答案为：a≤．【点评】本题考查简单线性规划，数形结合是解决问题的关键，属中档题．15．【考点】进行简单的合情推理．【分析】根据预测都不正确，即可推出相对应的数字【解答】解：乙丙丁所说为假⇒甲拿4，甲乙所说为假⇒丙拿1，甲所说为假⇌乙拿2；故甲、乙、丙、丁4个人拿到的卡片上的数字依次为4，2，1，3，故答案为：4，2，1，3【点评】本题考查了合情推理的问题，关键是掌握命题的否定，属于基础题．16．【考点】椭圆的简单性质．【分析】由题意可知：顶点A，B为椭圆的两个焦点，利用正弦定理及椭圆的定义，求得a和b的关系，即可求得=3．【解答】解：由椭圆+=1，长轴长2a=10，短轴长2b=8，焦距2c=6，则顶点A，B为椭圆的两个焦点，三角形ABC中，a=丨BC丨，b=丨AC丨，c=丨AB丨=6，a+b=丨BC丨+丨AC丨=10，由正弦定理可知===2R，则sinA=，sinB=，sinC=，===3，故答案为：3．【点评】本题考查椭圆的定义及正弦定理的应用，考查数形结合思想，考查计算能力，属于中档题．三、解答题17．【考点】数列的求和；数列递推式．【分析】（I）由2，2，2成等比数列，可得=2•2，可得2a n+1=a n+a n+2．利用等差数列的通项公式可得a n．（II）利用“错位相减法”、等差数列等比数列的求和公式即可得出．【点评】本题考查了等差数列与等比数列的通项公式与求和公式、“错位相减法”，考查了推理能力与计算能力，属于中档题．18．【考点】列举法计算基本事件数及事件发生的概率；频率分布表．【分析】（Ⅰ）设PM2.5的24小时平均浓度在（50，75]内的三天记为A1，A2，A3，PM2.5的24小时平均浓度在（75，100）内的两天记为B1，B2，求出基本事件总数，符合条件的基本事件总数，即可求得概率；（Ⅱ）利用组中值×频数，可得去年该居民区PM2.5年平均浓度，进而可判断该居民区的环境是否需要改进．【点评】本题主要考查频率分布表、古典概型、统计等基础知识，考查数据处理能力、运算求解能力以及应用意识，考查必然与或然思想等．19．【考点】棱柱、棱锥、棱台的体积；空间中直线与直线之间的位置关系．【分析】（Ⅰ）通过证明：AD′⊥AE，AD′⊥AC，推出AD′⊥平面ABCD，推出AD′⊥BE，通过证明GH∥BE，推出GH⊥D′A；（Ⅱ）三棱锥C﹣D′BE的体积．直接利用棱锥的体积公式求解即可．【点评】本题考查的知识点是直线与平面垂直的判定，棱锥的体积，其中（Ⅰ）的关键是熟练掌握面面垂直，线面垂直及线线垂直的相互转化，（Ⅱ）的关键是判断出棱锥的高和底面面积．20．【考点】直线与椭圆的位置关系．【分析】（1）运用椭圆的离心率公式和顶点坐标，结合a，b，c的关系，可得椭圆方程；（2）设M（m，n），由对称性可得N（m，﹣n），代入椭圆方程，再由向量数量积的坐标表示，转化为关于m的二次函数，配方，结合椭圆的范围，可得最小值，进而得到M的坐标，可得圆的方程．【点评】本题考查椭圆方程的求法，注意运用离心率公式，考查向量数量积的最小值，注意运用二次函数的最值求法和椭圆的性质，考查化简整理的运算能力，属于中档题．21．【考点】利用导数求闭区间上函数的最值；利用导数研究曲线上某点切线方程．【分析】（Ⅰ）求出函数的导数，求出a的值，从而求出切线方程即可；（Ⅱ）先把已知等式转化为a≤x+2lnx+，设g（x）=x+2lnx+，x∈（0，+∞），对函数进行求导，利用导函数的单调性求得函数的最小值，只要a小于或等于最小值即可．【点评】本题主要考查了利用导函数求最值的问题．考查了学生对函数基础知识的理解和灵活运用．22．【考点】直线与椭圆的位置关系；简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）利用极坐标方程与普通方程的互化求解即可．（2）设出椭圆的参数方程，利用点到直线的距离公式化简求解即可．【点评】本题考查椭圆的参数方程，极坐标方程与普通方程的互化，点到直线的距离公式的应用，考查转化思想以及计算能力．23．【考点】绝对值三角不等式；绝对值不等式的解法．【分析】（Ⅰ）由条件|2x﹣1|＜|x|+1，分类讨论，求得x的范围．（Ⅱ）由条件利用绝对值三角不等式证得不等式成立．【点评】本题主要考查绝对值不等式的解法，绝对值三角不等式的应用，体现了转化的数学思想，属于中档题。

2017年陕西省西安市高三文科一模数学试卷

2017年陕西省西安市高三文科一模数学试卷一、选择题（共12小题；共60分）1. 设集合，，则A. B. C. D.2. 在复平面内，复数所对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. 将函数的图象上所有的点向左平移个的单位长度，再把图象上各点的横坐标扩大到原来的倍（纵坐标不变），则所得图象的解析式为A. B.C. D.4. 若两个球的表面积之比为，则这两个球的体积之比为A. B. C. D.5. 若抛物线的焦点与双曲线的右焦点重合，则的值为A. B. C. D.6. 直线被圆截得的弦长为A. B. C. D.7. 某几何体的三视图如图所示，且该几何体的体积是，则正视图中的的值是A. B. C. D.8. 公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的值为参考数据：，，．A. B. C. D.9. 函数的图象在点处的切线斜率的最小值是A. B. C. D.10. 从正六边形的个顶点中随机选择个顶点，则以它们作为顶点的四边形是矩形的概率等于A. B. C. D.11. 函数且过定点，且角的终边过点，这的值为A. B. C. D.12. 已知定义在上的函数满足，当时，，其中，若方程恰有个不同的实数根，则的取值范围为A. B. C. D.二、填空题（共4小题；共20分）13. 已知，那么向量与向量的关系是．14. 若不等式组所表示的平面区域为，若直线与有公共点，则的取值范围是．15. 有一个游戏，将标有数字1，2，3，4的四张卡片分别随机发给甲、乙、丙、丁个人，每人一张，并请这人在看自己的卡片之前进行预测：甲说：乙或丙拿到标有3的卡片；乙说：甲或丙拿到标有2的卡片；丙说：标有1的卡片在甲手中；丁说：甲拿到标有3的卡片．结果显示：这人的预测都不正确，那么甲、乙、丙、丁个人拿到的卡片上的数字依次为，，，．16. 已知的顶点和顶点，顶点在椭圆上，则．三、解答题（共7小题；共91分）17. 已知数列中，，，且，，成等比数列．（1）求数列的通项公式；（2）若数列满足，数列的前项和为，求．18. 根据国家环保部新修订的《环境空气质量标准》规定：居民区 PM 2.5 的年平均浓度不得超过微克/立方米，PM2.5 的小时平均浓度不得超过微克/立方米．某城市环保部门随机抽取了一居民区去年天 PM 2.5 的小时平均浓度的监测数据，数据统计如表：（1）从样本中PM 天中，随机抽取天，求恰好有一天 PM 2.5 的小时平均浓度超过微克/立方米的概率；（2）求样本平均数，并根据样本估计总体的思想，从PM 2.5 的年平均浓度考虑，判断该居民区的环境是否需要改进?说明理由．19. 如图（1）：在直角梯形中，，，，，于点，把沿折到的位置，使，如图（2）：若，分别为，的中点．（1）求证：；（2）求三棱锥的体积．20. 如图已知椭圆的离心率为，以椭圆的左顶点为圆心作圆，设圆与椭圆交于点，．（1）求椭圆的方程；（2）求的最小值，并求此时圆的方程．21. 已知是正比例函数，是反比例函数，且，，确定与的表达式．22. 在平面直角坐标系中，以坐标原点为极点，轴的非负半轴为极轴建立极坐标系，已知曲线的极坐标方程为，它在点处的切线为直线．（1）求直线的直角坐标方程；（2）已知点为椭圆上一点，求点到直线的距离的取值范围．23. 已知函数，．（1）解不等式；（2）若对于，有，，求证：．答案第一部分1. C 【解析】由 B 中不等式变形得：，解得：或，即或，因为，所以．2. A 【解析】复数所对应的点位于第一象限．3. B 【解析】将函数的图象上所有的点向左平移个的单位长度，可得的图象；再把图象上各点的横坐标扩大到原来的倍（纵坐标不变），则所得图象的解析式为．4. C 【解析】设两个球的半径分别为，，根据球的表面积公式，可得它们的表面积分别为，，因为两个球的表面积之比为，所以，解之得（舍负），因此，这两个球的体积之比为，即两个球的体积之比为．5. D【解析】双曲线的右焦点为，即抛物线的焦点为，所以，所以．6. C 【解析】由，得，所以圆的圆心坐标是，半径．圆心到直线的距离为．所以直线被圆截得的弦长为．7. C 【解析】由三视图可知，原几何体是一个四棱锥，其中底面是一个上底、下底、高分别为，，的直角梯形，一条边长为的侧棱垂直于底面．于是其体积为，解得．8. B 【解析】模拟执行程序，可得：，，不满足条件，，，不满足条件，，，满足条件，退出循环，输出的值为．9. D 【解析】由，得，所以，所以，当且仅当，即时上式取“”，切线斜率的最小值是．10. D【解析】从正六边形的个顶点中随机选择个顶点，以它们作为顶点的四边形共有个，其中能构成矩形的有个，所以所求概率为．11. A 【解析】因为函数过定点，且角的终边过点，所以，，，所以，，所以12. B 【解析】由，所以，故的周期为，因为时，，时，，所以时，，时，，因为，恰有个不同的实数根，所以，，所以．第二部分13. 垂直【解析】，所以，，所以，所以，所以向量与向量的关系是垂直．14.【解析】作出不等式组所对应的可行域（如图阴影），直线表示过点且斜率为的直线，联立可解得即，由斜率公式可得，由解得，此时．结合图象可得要使直线与区域有公共点需．15. 4；2；1；3【解析】乙丙丁所说为假甲拿4，甲乙所说为假丙拿1，甲所说为假乙拿2；故甲、乙、丙、丁个人拿到的卡片上的数字依次为4，2，1，3．16.【解析】由椭圆，长轴长，短轴长，焦距，则顶点，为椭圆的两个焦点，三角形中，，，，，由正弦定理可知，则，，，．第三部分17. （1）因为，，成等比数列，所以，所以．所以数列为等差数列，设公差为，因为，，所以，，解得，．所以．（2）．设数列的前项和为，则．所以，所以所以．所以所以．18. （1）设 PM 2.5 的小时平均浓度在内的三天记为，，，PM 2.5 的小时平均浓度在内的两天记为，．所以天任取天的情况有：，，，，，，，，共种．其中符合条件的有：，，，，，共种．所以所求的概率．（2）去年该居民区 PM2.5 年平均浓度为：（微克/立方米）．因为，所以去年该居民区 PM2.5 年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进．19. （1）在直角梯形中，，，，，于点，把沿折到的位置，使，，连接，，在三角形中，可得，可得，，，可得，可得，因为，所以平面，可得，，分别为，的中点，可得，所以．（2）三棱锥的体积为．则．20. （1）由题意可得，椭圆的左顶点，可得，，，则椭圆方程为．（2）设，由对称性可得，即有，则由，可得时，的最小值为，此时，即有，可得圆的方程．21. 设（），（）．因为，所以．又，所以．由①②得，．所以，．22. （1）因为曲线的极坐标方程为，所以，所以曲线的直角坐标方程为，所以，又的直角坐标为，所以曲线在点处的切线方程为，即直线的直角坐标方程为：．（2）为椭圆上一点，设，则到直线的距离，当时，有最小值．当时，有最大值．所以到直线的距离的取值范围为：．23. （1）不等式，等价于，，不等式可化，即，不成立；，不等式可化为，即，所以；，不等式可化为，即，所以；故不等式的解集．（2）因为，，所以。

陕西省西安市2017届高三模拟(一)数学(文)试题

绝密★启用前2016-2017学年度学校3月月考卷试卷副标题注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．已知集合A ={−1,0,1,2,3}，B ={x|x 2−2x >0}，则A ∩B =（） A. {3} B. {2,3} C. {−1,3} D. {0,1,2} 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】C【解析】因为A ={−1,0,1,2,3}，B ={x|x 2−2x >0}={x|x <0或x >2}，所以A ∩B ={−1,3}，故选C . 2．在复平面内，复数11+i+i 所对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】A【解析】试题分析：11+i +i =1−i 2+i =1+i 2，选A.考点：复数的运算.3．函数y =sin(x +π6)，(x ∈R)的图象上所有点向左平移π4个单位长度，再把图象上各点的横坐标扩大到原来的2倍，则所得图象对应解析式为（） A. y =sin(2x +5π12) B. y =sin(x 2+5π12)C. y =sin(x2−π12) D. y =sin(x2+5π24)【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】B【解析】试题分析：函数y =sin(x +π6)，(x ∈R)的图象上所有点向左平移π4个单位长度得y =sin(x +π4+π6)，再把图象上各点的横坐标扩大到原来的2倍，得y =sin(x2+5π12)，选B.考点：三角函数图像变换○…………外……………○…………线……题※※○…………内……………○…………线……4．A. 1：2B. 1：4C. 1：8D. 1：16 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】C【解析】设两个球的半径分别为r 1、r 2，根据球的表面积公式，可得它们的表面积分别为S 1=4，S 2=4∵两个球的表面积之比为1：4，∴===，解之得=（舍负）因此，这两个球的体积之比为==（）3=即两个球的体积之比为1：8 故选：C5．若抛物线y 2=2px 的焦点与双曲线x 22−y 22=1的右焦点重合，则p 的值为（）A. 4B. 2C. -2D. -4【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】A【解析】因为抛物线y 2=2px 的焦点(p2,0)与双曲线x 22−y 22=1的右焦点(2,0)重合，所以，p2=2,p =4，故选A .6．直线x +2y −5+√5=0被圆x 2+y 2−2x −4y =0截得的弦长为（） A. 1 B. 2 C. 4√6 D. 4 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】D 【解析】因为x 2+y 2−2x −4y =0化为(x −1)2+(y −2)2=5，可知圆的圆心为(1,2),半径为√5，圆心到直线x +2y −5+√5=0的距离为d =√5|√5=1，由勾股定理可得直线x +2y −5+√5=0被圆x 2+y 2−2x −4y =0截得的弦长为2√5−1=4，故选D .7．某几何体的三视图如图所示，且该几何体的体积是32，则主视图中x 的值是（）A. 2B. 92 C. 32 D. 3订…………○…………线__考号：___________订…………○…………线【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】C【解析】由三视图可知该几何体为四棱锥，体积为13⋅1+22⋅2⋅x =32,x =32.8．公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图，则输出的n 值为（）参考数据：√3=1.732，sin15°≈0.2588，sin7.5°≈0.1305.A. 12B. 24C. 48D. 96【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】B【解析】试题分析：由程序框图，n,S 值依次为：n =6,S =2.59808；n =12,S =3；n =24,S =3.10583，此时满足S ≥3.10，输出n =24，故选B. 考点：程序框图.【技巧点睛】解题时要注意两种循环结构的区别，这也是容易出错是地方：当型循环与直到型循环.直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反.9．函数f(x)=lnx +x 2−bx +a(b >0,a ∈R)的图像在点(b,f(b))处的切线斜率的最小值是（）A. 2√2B. √3C. 1D. 2 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】D【解析】因为f(x)=lnx +x 2−bx +a ，所以f′(x)=1x +2x −b,函数f(x)=lnx +x 2−bx +a(b >0,a ∈R)的图象在点(b,f(b))处的切线斜率为f′(b)=1b+b ≥2，所以函数f(x)=lnx +x 2−bx +a(b >0,a ∈R)的图象在点(b,f(b))处的切线斜率的最小值是2，故选D . 10．A. 110 B. 18 C. 16 D. 15【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】D【解析】考点：古典概型及其概率计算公式．分析：从正六边形的6个顶点中随机选择4个顶点，选择方法有C 64=15种，且每种情况出现的可能性相同，故为古典概型，由列举法计算出它们作为顶点的四边形是矩形的……装…………※※不※※要※※在※※装※……装…………方法种数，求比值即可．解：从正六边形的6个顶点中随机选择4个顶点，选择方法有C 64=15种，它们作为顶点的四边形是矩形的方法种数为3，由古典概型可知它们作为顶点的四边形是矩形的概率等于315=15 故选D ．11．函数y =log a (x −3)+2(a >0且a ≠1)过定点P ，且角α的终边过点P ，则sin2α+cos2α的值为（） A. 75 B. 65 C. 4 D. 5【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】A【解析】因为函数y =log a (x −3)+2(a >0且a ≠1)过定点P(4,2)，所以且角α的终边过点P(4,2)，可得sinα=√55,cosα=2√55 ，所以sin2α=2sinαcosα=45,cos2α=2cos 2α−1=35，sin2α+cos2α=45+35=75，故选A .12．已知定义在R 上的函数f(x)满足f(x +2)=−f(x)，当x ∈(−1,3]时，f(x)={√1−x 2,x ∈(−1,1]t(1−|x −2|),x ∈(1,3]，其中t >0，若方程f(x)=x 3恰有3个不同的实数根，则t 的取值范围为（）A. (0,43) B. (23,2) C. (43,3) D. (23,+∞)【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】B【解析】由f(x +2)=−f(x)，所以f(x +4)=−f(x +2)=f(x)，故f(x)的周期为4，∵x ∈(1,2)时，f(x)=t(x −1)，x ∈(2,3)时，f(x)=t(3−x)，∴x ∈(5,6)时，f(x)=t(x −5)，x ∈(6,7)时，f(x)=t(7−x)，∵t >0,f(x)=x3恰有3个不同的实数根，∴t(2−1)>23,t(7−6)<2,∴2>t >23，故选B.【方法点睛】判断方程g(x)=ℎ(x)根的个数的常用方法：① 直接法：可利用判别式的正负直接判定一元二次方程根的个数；② 数形结合法：一是转化为两个函数y =g(x),y =ℎ(x)的图象的交点个数问题，画出两个函数的图象，其交点的个数就是方程根的个数，二是转化为y =a,y =g(x)的图象的交点个数交点个数问题 .装…………○…………订…_姓名：___________班级：___________考号装…………○…………订…第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题13．已知|a ⃗+b |=|a ⃗−b ⃗⃗|，那么向量a ⃗与向量b⃗⃗的关系是____________. 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】.a ⃗⊥b ⃗⃗，或a ⃗•b ⃗⃗=0 【解析】因为|a ⃗+b ⃗⃗|=|a ⃗−b ⃗⃗|，所以|a ⃗+b ⃗⃗|2=|a ⃗−b ⃗⃗|2，a ⃗2+2a ⃗·b ⃗⃗+b ⃗⃗2=a ⃗2−2a ⃗·b⃗⃗+b ⃗⃗2,a ⃗·b ⃗⃗=0，所以a ⃗⊥b ⃗⃗，故答案为a ⃗⊥b ⃗⃗或a ⃗·b ⃗⃗=0. 14．若不等式组{x ≥0x +y ≥13x +y ≤3所表示的平面区域为D ，若直线y −2=a(x +2)与D 有共同点，则a 的取值范围是____________. 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】[−23,12]【解析】画出不等式组{x ≥0x +y ≥13x +y ≤3所表示的平面区域为D ，如图. 直线y −2=a(x +2)过定点P(−2,2)，由图知，若直线y −2=a(x +2)与D 有共同点，则直线斜率满足k PA <a <k PB ，因为k PA =2−0−2−1=−23,k PB =2−3−2−0=12，所以，则a 的取值范围是[−23,12]，故答案为[−23,12].【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.15．有一个游戏，将标有数字1、2、3、4的四张卡片分别随机发给甲、乙、丙、丁4个人，每人一张，并请这4人在看自己的卡片之前进行预测：甲说：乙或丙拿到标有3的卡片；乙说：甲或丙拿到标有2的卡片；丙说：标有1的卡片在甲手中；丁说：甲拿到标有3的卡片．结果显示：这4人的预测都不正确，那么甲、乙、丙、丁4个人拿到的卡片上的数字依次为_____、_____、______、______．【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】 4 2 1 3 【解析】由于4个人预测不正确，其各自的对立事件正确，即：甲：乙、丙没拿到3；乙：甲、丙没拿到2；丙：甲没拿到1；丁：甲没拿到3.综上，甲没拿到1,2,3，故甲拿到了4号，丁拿到了3，丙拿到1号，乙拿到2号.16．已知ΔABC 的顶点A(−3,0)和顶点B(3,0)，顶点C 在椭圆x 225+y 216=1上，则5sinC sinA+sinB=________．【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】3【解析】根据椭圆的定义可知AB =2c =6,CA +CB =2a =10，由正弦定理得5sin C sin A+sin B=5AB CA+CB=3010=3.三、解答题17．已知数列{a n a 3=5，a 2+a 6=14，且2a n ，2a n +1，2a n +2成等比数列，（Ⅰ）求数列{a n }的通项公式；（Ⅱ）若数列{b n }满足b n =a n −(−1)n n ，数列{b n }的前项和为T n ，求T 21. 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）a n =2n −1；（Ⅱ）s 21=452. 【解析】试题分析：（Ⅰ）由2a n ，2a n +1，2a n +2成等比数列,可得 a n ，a n+1，a n+2成等差数列，再由由a 3=5，a 2+a 6=14，得a 1=1，d =2，进而可得结果；（Ⅱ）由（Ⅰ）知∴b n =2n −1−(−1)n n ，根据分组求和可得结果. 试题解析：（Ⅰ）∵2a n ，2a n +1，2a n +2成等比数列,∴(2a n +1)2=2a n ⋅2a n +2∴2a n+1=a n +a n+2∴a n ，a n+1，a n+2成等差数列.由a 3=5，a 2+a 6=14，得a 1=1，d =2， ∴a n =2n −1.（Ⅱ）∴b n =2n −1−(−1)n n ，s 21=b 1+b 2+b 3+⋯+b 21=a 1+1+a 2−2+a 3+3+⋯+a 21−(−1)21 ∴s 21=(a 1+a 2+a 3+⋯+a 21)+(1−2+3−4+⋯+21)， ∴s 21=a 1+a 212+1+1×10=452.18．外…………○…………装…………○…订………学校:__________姓名：___________班级_考号：____内…………○…………装…………○…订………（Ⅰ）从样本中PM2．5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2．5的24小时平均浓度超过75微克/立方米的概率；（Ⅱ）求样本平均数，并根据样本估计总体的思想，从PM2．5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由．【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）；（Ⅱ）年该居民区PM2．5年平均浓度为微克/立方米．去年该居民区PM2．5年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进．【解析】试题分析：（Ⅰ）将从这5天中任意抽取2天所包含的所有基本事件一一例举，再将抽取的2天恰有一天PM2．5的24小时平均浓度超过75微克/立方米的所包含的基本事件一一例举，根据古典概型概率公式可求得所求．（Ⅱ）每组的中点与本组频率乘积之和即为所求的PM2．5的年平均浓度，若大于35不符合环境空气质量标准，否则即符合环境空气质量标准．试题解析：解：（Ⅰ）设PM2．5的24小时平均浓度在内的三天记为，PM2．5的24小时平均浓度在内的两天记为．所以5天任取2天的情况有：，，，，，，，，共10种．其中符合条件的有：，，，，，共6种．所以所求的概率．（Ⅱ）去年该居民区PM2．5年平均浓度为：（微克/立方米）．因为，所以去年该居民区PM2．5年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进．考点：1古典概型概率；2平均数．19．如左图：在直角梯形ABCD 中，AD ∥BC ，∠ABC =90°，AB =BC =2，AD =6，CE ⊥AD 于E 点，把△DEC 沿CE 折到D′EC 的位置，使D′A =2√3，如右图：若G ，H 分别为D′B ，D′E 的中点.（Ⅰ）求证：GH ⊥D′A ；（Ⅱ）求三棱锥C −D′BE 的体积.外…………○…………装…线…………○……※※请※※不※※内…………○…………装…线…………○……【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）见解析；（Ⅱ）V C−D′BE =4√33. 【解析】试题分析：（Ⅰ）由勾股定理可得D′A ⊥AE,又知EC ⊥AE ，进而得EC ⊥面D′AE ，从而AB ⊥面D′AE ，∴AB ⊥D′A ，再由线面垂直的判定定理可及性质得D′A ⊥BE ，∴GH ∥BE ∴D′A ⊥GH ；（Ⅱ）由（1）得D′A ⊥面ABCD V C−D′BE =V D′−CBE =13AD′⋅S △BCE =13×2√3×12×2×2=4√33. 试题解析：（Ⅰ）Δ在ΔADE 中 ∵AD′=2√3，D′E =4，AE =2 ∴D′A ⊥AE ，∵EC ⊥AE ，EC ⊥D′E ，AE ∩D′E =E . ∴EC ⊥面D′AE ，∵AB ∥EC ∴AB ⊥面D′AE ，∴AB ⊥D′A . ∵AE ∩AB =A ，∴D′A ⊥面ABCD .又∵BE 在平面ABCD 内，∴D′A ⊥BE∵G ，H 分别为D′B ，D′E 的中点，连接BE ∴GH ∥BE ∴D′A ⊥GH . （Ⅱ）由（1）得D′A ⊥面ABCDV C−D′BE =V D′−CBE =13AD′⋅S △BCE =13×2√3×12×2×2=4√33.20．如图已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的离心率为√32，以椭圆的左顶点T 为圆心作圆T:(x +2)2+y 2=r 2(r >0)，设圆T 与椭圆C 交于点M ，N .线…………○……线…………○……（Ⅰ）求椭圆C 的方程；（Ⅱ）求TM ⃗⃗⃗⃗⃗⃗⃗·TN ⃗⃗⃗⃗⃗⃗的最小值，并求此时圆T 的方程.【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）x 24+y 2=1；（Ⅱ）TM ⃗⃗⃗⃗⃗⃗⃗⋅TN ⃗⃗⃗⃗⃗⃗取得最小值为−15，圆的方程为(x +2)2+y 2=1325.【解析】试题分析：（Ⅰ）由圆方程(x +2)2+y 2=r 2(r >0)可得a =2,再根据离心率求c 的值，进而求得椭圆的标准方程；（Ⅱ）设M(x 1,y 1)，N(x 2,−y 1)，不妨设y 1>0，TM ⃗⃗⃗⃗⃗⃗⃗⋅TN ⃗⃗⃗⃗⃗⃗=(x 1+2,y 1)⋅(x 1+2,−y 1)=(x 1+2)2−y 12==54x 12+4x 1+3=54(x 1+85)2−15，当x 1=−85时，TM ⃗⃗⃗⃗⃗⃗⃗⋅TN ⃗⃗⃗⃗⃗⃗取得最小值为−15，M(−85,35)代入圆方程可得圆半径，即可求得圆方程.试题解析：（Ⅰ）根据题意可得a =2，e =c a=√32，所以c =√3， b =√a 2−c 2=1，故椭圆C 的方程为x 24+y 2=1.（Ⅱ）因为点M 与点N 关于x 轴对称，所以设M(x 1,y 1)，N(x 2,−y 1)，不妨设y 1>0. 由于点M 在椭圆CC 上，所以y 12=1−x 124由T(−2,0)，得TM⃗⃗⃗⃗⃗⃗⃗=(x 1+2,y 1)，TN ⃗⃗⃗⃗⃗⃗=(x 1+2,−y 1)，所以TM ⃗⃗⃗⃗⃗⃗⃗⋅TN ⃗⃗⃗⃗⃗⃗=(x 1+2,y 1)⋅(x 1+2,−y 1)=(x 1+2)2−y 12=(x 1+2)2−(1−x 124) =54x 12+4x 1+3=54(x 1+85)2−15. 由于−2<x <2，故当x 1=−85时，TM ⃗⃗⃗⃗⃗⃗⃗⋅TN ⃗⃗⃗⃗⃗⃗取得最小值为−15.此时y 1=35，故M(−85,35).又因为点M 在圆T 上，代入圆的方程可得r 2=1325.故圆的方程为(x +2)2+y 2=1325.21．已知f(x)=−x 2−3，g(x)=2xlnx −ax 且函数f(x)与g(x)在x =1处的切线平行.（Ⅰ）求函数g(x)在(1,g(1))处的切线方程；（Ⅱ）当x ∈(0,+∞)时，g(x)−f(x)≥0恒成立，求实数a 的取值范围. 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）2x +y +2=0；（Ⅱ）(−∞,4]. 【解析】试题分析：（Ⅰ）先求得f′(x)=−2x ，g′(x)=2lnx +2−a ，由f′(1)=g′(1)可得结果；（Ⅱ）x∈(0,+∞)时，由g(x)−f(x)≥0恒成立等价于a≤2lnx+x+3x=ℎ(x)恒成立，只需a≤ℎ(x)min，利用导数研究函数的单调性，求出ℎ(x)的最小值即可得结论.试题解析：（Ⅰ）f′(x)=−2x，g′(x)=2lnx+2−a.因为函数f(x)与g(x)在x=1处的切线平行所以f′(1)=g′(1)解得a=4,所以g(1)=−4，g′(1)=−2,所以函数g(x)在(1,g(1))处的切线方程为2x+y+2=0.（Ⅱ）解当x∈(0,+∞)时，由g(x)−f(x)≥0恒成立得x∈(0,+∞)时，2xlnx−ax+x2+3≥0即a≤2lnx+x+3x恒成立.设ℎ(x)=2lnx+x+3x(x>0)，则ℎ′(x)=x 2+2x−3x2=(x+3)(x−1)x2，当x∈(0,1)时，ℎ(x)<0，ℎ(x)单调递减，当x∈(1,+∞)时，ℎ(x)>0，ℎ(x)单调递增所以ℎ(x)min=ℎ(1)=4.所以a的取值范围为(−∞,4].【方法点睛】本题主要考查导数几何意义、利用导数研究函数单调性进而求最值以及不等式恒成立问题，属于难题.对于求不等式恒成立时的参数范围问题，在可能的情况下把参数分离出来，使不等式一端是含有参数的不等式，另一端是一个区间上具体的函数, 这样就把问题转化为一端是函数, 另一端是参数的不等式，便于问题的解决. 但要注意分离参数法不是万能的, 如果分离参数后,得出的函数解析式较为复杂, 性质很难研究, 就不要使用分离参数法.22．选修4-4：坐标系与参数方程在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知曲线C的极坐标方程为ρcos2θ=2sinθ，它在点M(2,√2,π4)处的切线为直线l．(Ⅰ)求直线l的直角坐标方程；(Ⅱ)已知点P为椭圆x 23+y24=1上一点，求点P到直线l的距离的取值范围．【来源】【全国市级联考word】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（1）2x−y−2=0；（2）[0,6√55].【解析】试题分析：（1）对曲线C的极坐标方程两边乘以ρ化为直角坐标方程.利用导数可求得曲线在M处的切线方程.（2）设出椭圆的参数方程，利用点到直线距离公式和三角恒等变换的知识，可求得P到直线距离的取值范围.试题解析：选修4-4：坐标系与参数方程解：（Ⅰ）∵曲线C的极坐标方程为ρcos2θ=2sinθ，∴ρ2cos2θ=2ρsinθ，∴曲线C的直角坐标方程为y=12x2，又M(2√2,π4)的直角坐标为（2,2），∵y′=x，∴k=y′|x=2=2.∴曲线C在点（2,2）处的切线方程为y−2=2×(x−2)，试卷第11页，总11页 ……装…………○…………订…_______姓名：___________班级：___________考号……装…………○…………订…即直线l 的直角坐标方程为2x −y −2=0. （Ⅱ）P 为椭圆x 23+y 24=1上一点，设P(√3cosα,2sinα)，则P 到直线l 的距离d =√3cosα−2sinα−2|√5=|4sin(α−π3)+2|√5，当sin(α−π3)=−12时，d 有最小值0. 当sin(α−π3)=1时，d 有最大值6√55. ∴P 到直线l 的距离的取值范围为[0, 6√55]. 23．选修4—5：不等式选讲已知函数f(x)=|2x −1|，x ∈R . （Ⅰ）解不等式f(x)<|x|+1；（Ⅱ）若对于x ，y ∈R ，有|x −y −1|≤13，|2y +1|≤16，求证：f(x)<1. 【来源】【全国市级联考word 】陕西省西安市2017届高三模拟（一）数学（文）试题【答案】（Ⅰ）不等式f(x)<x +1的解集为{x|0<x <2}；（Ⅱ）详见解析．【解析】试题分析：（1）利用绝对值的性质求解即可；（2）将用和表示出来，得：，再利用绝对值的性质证明．试题解析：（1）．（2）．考点：1、绝对值不等式； 2、绝对值不等式的性质．。

陕西省西安市铁一中国际合作校高三下期第一次大练习语文试题

2014-2015语文试题本试卷分第一卷(阅读题)和第二卷(表达题)两部分.满分150分.考试时间150分钟第Ⅰ卷阅读题一、现代文阅读(9分，每小题3分)阅读下面文字，完成1—3题.谈吟诵陈向春吟诵是什么？或者，今天我们所理解的吟诵是什么？吟诵是传统文化、古典诗词不可或缺的一种美的表现形式，有着独特的文化和艺术内涵.初次接触到吟诵的人们，新奇之后，往往会问：古人是这么“吟”的么？这是原汁原味的古调子么？事实上，现在所有古典诗词的吟调，包括出自那些已经八九十岁、曾经接受过私塾教育的老人之口的吟调，都非古调.理由很简单，一是数千年语音变迁，所谓的“正宗”古音并不存在.其次，古人吟诵皆口耳相授，声音实况没有记载.古调绝响，无从谈起.但是，语音变迁之中，仍有不变的因素.比如“入声”被认为是一种“原生态”，华东、华南、西南以及台湾地区的方言就有入声，还保留了某些中古语音的特征，当地一些八九十岁老人还能以此为我们传递唐诗宋词微妙的声情韵味.吟诵这个词，其意既可指吟，也可指诵；或者两者兼有，泛指用抑扬顿挫的声调有节奏地诵读.吟诵合称，表明至少有两种方式，即吟和诵.从有利于传承的角度说，概念或者叫法还是统一为好.台湾统一叫吟唱，大陆统一叫吟诵.吟诵的叫法，好在把吟和诵组合在一起，提醒人们：吟是从诵之中来的.吟唱的“唱”也并非一般的歌唱，是从吟读之中自然生发出来的，且不受固定乐谱束缚的自由唱.或许，比较方便简单的分类有三：诵、吟、唱.这当中，“诵”为基础，“吟“是结果，“唱”是升华.一个现代人，要想得到古人那种自由吟诵的境界，一是要吟出自己的调；二是要随“调”吟出，想吟就吟；三是音情并茂，韵味十足.其实吟诵的根并不是一般说的古诗词文，而是传统蒙学诸经典.传统蒙学的本意在于“播种于心，求其日后自己发芽”，用“经典”打底，扎根在童心之内，故所读所诵必为精挑细选出来的好书好文好诗.中华文明，日积月累，不断生发，产生了众多的人文经典.多且文字繁难的经典，须经过“中介”的智慧，化繁为简，化难为易.这个转化的结果，便是各种蒙学教材的诞生.于是，中华“经典”的核心思想化作朗朗上口的韵读文字，随着熟诵、吟诵渗入人心.古人把作诗称之为“吟咏情性”，诗在性情里，把诗从情性里吟咏出来，即为诗.而诗的鉴赏，则是从相反方向进行，靠吟咏作出来的诗，还须回到声音里体会.所以，“吟咏”的作用，不单是所谓“语言的艺术”问题，或艺术的审美问题，最根本的是它内涵着传统的“性情”.【注】蒙学，即蒙馆，启蒙的学塾，相当于现在的幼儿园或小学.1.关于“吟诵”的理解，不符合原文意思的一项是( )A．吟诵是传统文化、古典诗词不可或缺的一种美的表现形式，有其独特内涵.B．吟诵，其意既可指吟，也可指诵，就是用抑扬顿挫的声调有节奏地诵读.C．大陆“吟诵“的叫法，把吟和诵组合在一起，提醒人们吟是从诵之中来的.D．台湾“吟唱”的“唱”，是从吟读中随意生发出的不受固定乐谱约束的自由唱.2.对于吟诵具有“独特的文化和艺术内涵”的表述，不符合原文意思的一项是( ) A．语音变迁中有不变的因素，我国一些方言中还保留了某些中古语音的特征.B．儿童吟诵精选出来的好书好文好诗，播种“经典”以“求其日后自己发芽”.C．中华“经典”的核心思想凭借蒙学教材化作韵读文字，通过吟诵渗人人心.D．鉴赏诗歌要反向而行，通过吟咏(诵)，在声音中体会其情感美和艺术美.3．下列表述，符合原文意思的一项是( )A．我们不能吟诵出原汁原味古调的原因是数千年的语音变迁使正宗古音已不存在.B．吟诵比较简便的分类为诵、唱和吟，这三类可以分别看做基础、结果和升华.C．今人学吟诵，一要吟出自己的调，二要想吟就吟，三要有声有情，韵味十足.D．吟咏(诵)不是语言的艺术，也不是审美的艺术，而是内涵着传统性情的艺术.网ZXXK]二、古代诗文阅读(36分)(一)文言文阅读(19分)阅读下面的文言文，完成4～7题.朱勔，苏州人.父冲，狡狯有智数.始，蔡京居钱塘，过苏，欲建僧寺阁，会费巨万，僧言必欲集此缘，非朱冲不可.京以属郡守，郡守呼冲见京，京语故，冲愿独任.居数日，请京诣寺度地，至则大木数千章积庭下，京大惊，阴器其能.明年召还，挟勔与俱，以其父子姓名属童贯窜置军籍中，皆得官.徽宗颇垂意花石，京讽勔语其父，密取浙中珍异以进.帝嘉之.后岁岁增加，至政和中始极盛，舳舻相衔于淮、汴，号“花石纲”，置应奉局于苏，指取内帑①如囊中物，每取以数十百万计.延福宫成，奇卉异植充牣其中.勔擢至防御使，东南部刺史、郡守多出其门.所贡物，豪夺渔取于民，毛发不少偿.士民家一石一木稍堪玩，即领健卒直入其家，用黄封表识，未即取，使护视之.微不谨，即被以大不恭罪.及发行，必彻屋抉墙以出.人不幸有一物小异，共指为不祥，唯恐芟夷之不速.民预是役者，中家悉破产，或鬻子女以供其须.尝得太湖石，高四丈，载以巨舰，役夫数千人，所经州县，有拆水门、桥梁，凿城垣以过者.既至，赐名“神运昭功石”.截诸道粮饷纲，旁罗商船，揭所贡暴其上，篙工、柁师倚势贪横，陵轹州县，道路相视以目.京始患之，从容言于帝，愿抑其太甚者.帝亦病其扰，乃禁用粮纲船.听勔与蔡攸等六人入贡，余进奉悉罢.自是勔小戢②.既而勔甚.所居直苏市中孙老桥，忽称诏，凡桥东西四至壤地室庐悉买赐予己，合数百家，期五日尽徙，郡吏逼逐，民嗟哭于路.遂建神霄殿，奉青华帝君像其中，监司、都邑吏朔望皆拜庭下.主赵霖建三十六浦闸，兴必不可成之功，天方大寒，役死者相枕藉.霖志在媚勔，益加苛虐，吴、越不胜其苦.徽州卢宗原竭库钱遗之，引为发运使，公肆掊克③.勔又托挽舟募兵数千人，拥以自卫.子汝贤等召呼乡州官寮，颐指目摄，皆奔走听命，流毒州郡者二十年.方腊起，以诛勔为名.童贯出师，承上旨尽罢去花木进奉，帝又黜勔父子弟侄在职者，民大悦.靖康之难，欲为自全计，仓卒拥上皇南巡，且欲邀至其第.钦宗用御史言，放归田里，凡由勔得官者皆罢.籍其赀财，田至三十万亩.言者不已，羁之衡州，徙韶州、循州，遣使即所至斩之.(选自《宋史·朱勔传》，有删节)【注】①内帑(tǎng)：府库的钱财.②戢：止息，收敛.③掊克：聚敛，搜刮民财.4．对下列句子中加点的词的解释，不正确的—项是(3分) ( )A．京以属郡守属：通“嘱”，嘱咐，嘱托B．京大惊，阴器其能器：看重. C．引为发运使，公肆掊克引：招来.D．或鬻子女以供其须. 鬻：卖，出售5．下列各组句子中，全都直接表现朱勔恃宠横暴的一组是(3分) ( )①指取内帑如囊中物，每取以数十百万计②豪夺渔取于民，毛发不少偿③中家悉破产，或鬻子女以供其须④所经州县，有拆水门、桥梁，凿城垣以过者⑤合数百家，期五日尽徙⑥召呼乡州官寮，颐指目摄A．①②⑤ B．①④⑥ C．②③⑤ D．③④⑥6．下列对原文有关内容的分析和概括，不正确的一项是(3分) ( )A．朱勔的父亲狡狯有谋略.在蔡京想建造僧寺阁时，独自承担了筹备任务，在很短时间内筹到了几千根巨木；借此机缘，其父子都获得了官职.B．徽宗极爱奇花异石，做出了不少扰民乱政的事.他大力征收“花石”；他宠幸朱勔，导致东南郡县大小官吏多出朱门，这些官吏致使众多百姓倾家荡产.C．朱勔祸国殃民，害人害己.他肆意征用粮纲船只，托皇命强取苏市孙老桥附近土地房宅，借口挽舟拥兵自卫；靖康之难时，他被钦宗流放并最终被诛杀.D．朱勔的属下及家人倚势贪横.赵霖为政苛酷暴虐，导致百姓惨死；卢宗原公然搜刮民财；朱汝贤等人召唤乡州官僚，颐指气使，祸害当地百姓达二十年.7．把文中画横线的句子翻译成现代汉语.(10分)(1)微不谨，即被以大不恭罪.及发行，必彻屋抉墙以出.(5分).(2)京始患之，从容言于帝，愿抑其太甚者.帝亦病其扰，乃禁用粮纲船.(5分).(二)古代诗歌阅读(11分)阅读下面这首宋诗，完成8—9题.夜坐·张耒庭户无人秋月明，夜霜欲落气先清.梧桐真不甘衰谢，数叶迎风尚有声.8. 试分析一二句在全诗中的作用.(5分).9.《文心雕龙》中说：“人亲七情，应物斯感，感物吟志，莫非自然.”请结合本诗对“梧桐”这一形象的描写，分析作者的情志.(6分).(三)名篇名句默写(6分)10. 补写出下列名篇名句中的空缺部分.(6分)(1)于是废先王之道，， .(贾谊的《过秦论》)(2) ，谈笑间， .(苏轼的《赤壁怀古》)(3) ，知来者之可追.(陶渊明的《归去来兮辞》)(4)酌贪泉而觉爽， .(王勃的《滕王阁序》)三、文学类文本阅读(25分)11. 阅读下面的文字，完成(1)—(4)题.白纸黑字奚同发决定去一趟那座小城，虽然平日指尖一次次抚摸地图上那个圆点，实际上她对那里一无所知.是一张神秘的纸条，把她与那个圆点连成一线.纸条的神秘不仅是它的出现方式，更主要的是犹如久旱甘霖般及时.纸条出现的那天，爹做农活时摔断一条腿，他打上石膏就离开了卫生所.就这，还是拖欠了一屁股债.学校又一次催她和小弟交学费，开学都一个多月了，一家人正为钱犯愁.晚间，她试穿那件别人捐赠、由学校分配给她的棉衣时，手伸进衣服口袋，触到一张折叠的纸条，很普通的白纸，展开，是几行字：收到纸条的同学，如果上学有难处，跟我联系，我会帮你完成学业.落款“姚国庆”.全家人顿时一扫近乎绝望的悲情而乐观起来，纸条传达的信息，足以成为抵挡困难的最后屏障.爹、娘、她与小弟，四个人没有谁心存丝毫怀疑，一张写了黑字的普通白纸，像几世相承的珍宝，在他们手中欣喜而小心翼翼地传递.要不，跟他联系一下，她怯怯地问.接着一家三口的目光都集中到爹的身上.爹却自顾自地抽着烟，一言不发.最后，爹使劲儿地掐灭了纸烟，以她从未见过的严肃神情说，咱不能就这样随便地麻烦人家，不到万不得已，不能走那一步.重新振作的爹表示，再难，还没到砸锅卖铁的时候，只要他还有一口气，决不让一个娃辍学.上镇中学时，家里已经负债累累，但是不幸却再次降临，小弟在上学途中因雨天路滑跌落山崖，娘一病瘫在床头……她决定退学，与爹共同支撑起这个再也经不住风雨的家.双手抱头，隐忍丧子之痛的爹，平生第一次把粗厚的巴掌气愤地掴在她的脸上，小弟搭上一条命，如果你不能读出书来，对得起谁？从此爹拖着那条残腿，苦苦维护着家的尊严，又一次打消了她动用纸条的念头.六年后，她如愿以偿地考上了大学，爹却含笑离世.纸条夹在小学四年级的课本里，已有些泛黄，捏在手上，已经被汗水微微地打湿了.娘长叹一声，唉——八年了，也不知写字的人还承认不？这个地址还管用不？她怔在那里，是啊，没办法，只能把命运交给这张纸条了……八年的精神支撑，随着一个普通信封寄走了，心里空落落地.两个月后，一个雾气没散的早晨，门前响起清脆的马铃声，邮递员大喊她的名字.在灶头烧水的她，手握尚在燃烧的半截儿柴火，夺门而出.有信件，还有汇款！信上说，几经周转，收到她的信晚了，让她快去学校报到，以后会准时寄钱给她.老天爷啊，老天爷啊，我可以上学了！她高声重复着，一头匍匐在地……然后向远方连连跪拜，口中喊道：恩人呐，恩人呐！……四年大学，她一刻不敢倦怠.从接到第一次汇款时，她心里就默默许诺，工作后拿到第一个月工资，一定要去探望恩人.这个诺言，如今就要兑现了！找到邮政所3019号信箱，没有具体地址，向汇款窗口的工作人员打听，对方大吃一惊，反问她是不是那个被资助的大学生.这下，轮到她惊讶了：是她在这儿有名，还是姚国庆有名？邮政所几乎停止办公，大家七嘴八舌围过来……一切都明白了，是一个大娘给她寄的钱.起初，邮政所还奇怪，她一个捡破烂的怎么每月都要寄出两份钱.一份给在外地上学的儿子，另一份是以姚国庆的名义寄出.原来，姚国庆是她丈夫，几年前因病去世，可她收到一个陌生女孩来信，纸条上丈夫熟悉的字迹让她泪水涟涟.虽然单位破产，她下了岗，但不能让丈夫昔日白纸黑字的承诺化作一纸谎言……在一个依墙斜拉的低矮的破旧帐篷前，电视台记者见到长跪不起的女孩子.围观的人争相介绍，哭了一个多小时啦，都成泪人啦，人能有多少眼泪啊？可她还在不停地抹泪儿.现场观众焦急地把目光投向街道，只是那个供俩孩子上大学，甚至把住房都卖了的女人咋还不回来？记者的镜头更是急切地扫来扫去.所有的人都在期待那个女人的到来.大家心疼哭了那么久、跪了那么久的瘦弱女孩，也在构想另一个女人的模样，或她出现的场景……(1)下列对小说有关内容的分析和概括，最恰当的两项是(5分)( )A．女孩在得到有人准备资助她完成学业的纸条后，曾多次萌生动用纸条的念头，但都被父亲阻止，直到女孩考上了大学，父亲离世后，女孩才能将纸条寄出.B．这篇小说语言质朴，叙事生动，构思巧妙.作者在作品中将自己的理智与读者的情感巧妙地勾连起来，在平静的叙事中蕴涵着一种震撼人心的力量.C．小说主要通过人物的行为来凸显人物的性格.父亲多次阻止女孩动用“纸条”，说明他是一位讲自尊、有骨气的勤劳农民，但他也有守旧、狭隘的一面.D．大娘为了丈夫临终的嘱托，为了兑现与丈夫的共同承诺，卖掉了房子，靠拾破烂维持生计，供陌生的女孩完成大学学业，这种超越生命的承诺令人肃然起敬.E．结尾描写了女孩、记者以及围观的群众，都在焦急地等待着那个兑现了承诺的女人，但她却没有到来.结尾的这种开放性设计，引发读者想象，耐人寻味.(2)小说中自始至终都没有出场的“女人”，有哪些性格特点？请结合文本简要分析.(6分).(3)本文以“一张纸条”为线索.请具体分析文章是如何围绕着“一张纸条”展开的.(6分).(4)“白纸黑字”作为小说的标题，意蕴丰富.请结合全文谈谈你的理解.(8分).四、实用类文本阅读(25分)12. 阅读下面的文字，完成(1)---(4)题.在心尖上雕刻的张爱玲张爱玲作品里面有对女性命运的精妙体察，对世道人心的一语洞穿，加之与生俱来的骨子里的傲与冷，使读者仿佛五脏六腑变换了一个全新格式，如她的《倾城之恋》《红致瑰与白玫瑰》《金锁记》《沉香屑》，但它们似乎有些过于华丽，带有她年轻时代的色彩和底调. 长篇小说《十八春》才是她最好的作品.作品中的顾曼贞，永远穿着暗蓝旗袍，因为她姐姐曼璐蜕变为二流交际花的缘故，她这样的穿着多少有些自卫的意味.然而在沈世均眼里，她却是“纤细而坚强的，笼统的好”.世均回南京的家，曼贞在上海，他在南京的雨夜里想起她，“故乡就变成异乡了”.于是他忍不住一大早下了火车就来厂里，恰在门口遇见她.他急道：“曼贞，我有话对你说.”曼贞看他着急的样子，上下打量他，一连串猜测在她脑里闪过——他订婚了，他家里出了事，他辞职……他却道：“我有好些好些话要对你说.”张爱玲的笔仿佛是有神灵指使的.事情越是千钧一发，她却越是漫不经意.这种千百年来世间男女所痴心的一桩事，若放在俗家笔下，不知要制造多少哆嗦、琐屑而无聊的语言幻像呢，并且还往往纠结于外围，深入不到内里.而她三言两语，全都着了精要，一下子呈现了事情的真相，直抵人内心深处最柔软的部分，仿佛是在人心尖上雕刻，如此的精妙、确切与传神.这样的工作，真非天才而不能.《十八春》最要紧的好处还是作品的内在本身，它写出了人的命运由鲜亮变为黯淡之必然之无可奈何的宿命感，整部作品显得练达而老成.美的形式在技术上是可以复制的，它如叶片的暗影.叶子连结了枝蔓，枝蔓连结了枝条，枝条连结了枝干，许多根线条形成一个走势，颇着某一种逻辑秩序，终结于根脉核心.这核心才是真正令人触目惊心的，它必是赤裸的，也是坦率的，藏不住任何的秘密.它是关于一个人心目中的世界究竟是什么样子的，更有对人生世态的观念.它所展现的点滴零碎，都来自这里.如果作家对世界的理解是混乱的，由这个根脉核心抽条出的枝蔓花叶，也必定是繁复混乱、没有秩序的.张爱玲偏偏让美好而干净的生命轨迹，经历灾难与泥沼.曼贞被姐姐囚禁而被姐夫玷污，生了孩子，却不得不为了孩子再回到灾难与泥沼里——在姐姐死后居然选择嫁给了姐夫.我觉得她对世界的理解是悲观的，也有超现实的成分.她有着伤痛.也有着对世道人心的彻底失望.她为了保存着她的傲慢和尊严，只能选择孤独.对于张爱玲，人们似乎只觉其雅，而不觉其痛.一个孩子的天目，必定是因为痛苦才被打开的，这使她看见了世人所不察觉的隐性世界.张爱玲固然有着贵族血统，生活优裕，曾经快乐地在她母亲家的狼皮褥子上滚来滚去，听着客人们演话剧，唱英文歌.岂知后来的生活急转直下，母亲离开，只剩下她和弟弟跟着父亲生话.他们的生活是可以想见的.有钱也不行，不是钱的事.他们的裤腿永远短了一大截.冬天的鞋子进了水，脚肿胀得像一个面包.只是因为她对继母项了嘴，她父亲的耳光便打过来.她只记得地的脸偏向左一边，又偏向右一边.他父亲甚至囚禁她半年，病了也不给医看.没心没肺的孩子或许慢慢把这忘了，偏偏她有的只是灵性，她是靠着灵性生长的，就只有把这苦痛储存了.那些整块吞咽的痛苦慢慢结了痂，内里的变异却只能如腐水一般慢慢地流淌出来，毒素一般渗透在她的生活里.或许那些情节，只是毒素作用的征象.文学情节往往是写作者心理经验开放的瞬间.那时候她心中的母亲，其实是一个虚幻的存在.母亲，除了是血脉之源，更是安全、温暖、爱之所在.但这些过早地离她远去了.我仿佛看见了她在繁花似锦的表层底下，求助而又无助地，爱又恨着她的生之源.这世间最艰难的悖论，她过早地面对了，也因此生发出对世界的悲剧感.她对心中那个叫做母亲的存在，只是心向往之，而永远地求之不得了(1)下列对传记有关内容的分析和概括，最恰当的两项是(5分) ( )A．文学作品的形式美可以复制，但其内在本身却是由作者对世界的理解、对人生世态的观念决定的，《十八春》所展现的内容支离破碎，这也与张爱玲对世界的理解有关.B．作者从张爱玲早期的人生经历与其作品的关系这一角度，以张爱玲一系列作品为例，揭示了她所经历的生活变故对其性情和作品的影响.C．文学作品中人物的命运和性格情怀，往往有着作者现实人生的影子，张爱玲成长经历中的无助、苦痛，也自然会反映在她的一些作品中.D．张爱玲的生活经历了由早期的“雅”到后来的“痛”的急转直下的人生变故，这世间最艰难的悖论使她过早地吞咽了人生的痛苦，也因此形成了她对世界的悲剧感.E．“仿佛是在人心尖上雕刻”运用了比喻的修辞手法，强调张爱玲的作品文笔细腻、精妙、传神，能抓住精要，呈现真相，直抵人的内心深处，是一般文学家难以达到的.(2)作者为什么认为张爱玲最好的作品是《十八春》？请简要分析.(6分).(3)对于张爱玲，作者为什么说“人们似乎只觉其雅，而不觉其痛”，请简要分析.(6分).(4)文中说“一个孩子的天目，必定是因为痛苦才被打开的”，你是否赞同这一观点？请结合文本，谈谈你的看法.(8分).第Ⅱ卷表达题五、语言文字运用(20分)13. 下列各句中，加点的成语使用恰当的一项是(3分) ( )A. 我省有关部门负责人多次就环境问题发表讲话，旨在加大环境监督的执法力度，强化环境保护的参与意识，因为环境与我们每个人的生活休戚相关．．．．.B. 现在很多学生不会学习，有些学生一头钻进了题海中，而放弃了对课本的钻研，其实，这是一种本末倒置．．．．的做法.C. 以发给每人一百元钱然后遣散的方式来应付民工集中追索欠款，这家建筑公司的做法只能是扬汤止沸．．．．，对问题的根本解决是毫无帮助的.D. 日本一小撮右翼分子不愿正视长达八年的侵华战争使中国人民生灵涂炭．．．．的历史事实，这是不能容忍的.14. 下列各句中，没有语病的一项是(3分) ( )A. 2010年中央国家机关公务员考试，竞争最激烈的职位报录比例为4080:1.有关专家指出，社会上越来越多的人热衷于当公务员，是由于人们更愿意把知识与理性主要用于分配而不是生产，这对社会发展来说显然弊大于利.B. 夏天的青菜豆腐汤固然新鲜可口，但由于青菜中总是渗透着一些对人体有害的残留农药，所以做汤食用前应该将青菜在水中浸泡一段时间再进行冲洗较为安全.C. 对调整工资、发放奖金、提高职工的福利待遇等问题，文章从理论和政策上作了详细的规定和深刻的说明，具有很强的指导意义和可操作性.D. 虚拟不仅表明了诗、乐、舞三位一体的传统美学优势，更显示了戏曲形态的特征，这种特征和优势，已为现代戏曲所重视和集成.15. 填入下面一段文字中横线处的语句，衔接最恰当的一项是(3分) ( )最美的感觉当然就在这深巷里.我喜欢它两边各式各样的古屋和老墙.我尤其喜欢站在这任意横斜的深巷里失去方向的感觉.A.喜欢它随地势而起伏的坡度，喜欢它们年深日久之后前仰后合的样子，喜欢忽然从老城里边奔涌出来的一大丛绿蔓或生气盈盈的花朵，喜欢被踩得坑坑洼洼的硌脚的石头路面.B.喜欢它随地势而起伏的坡度，喜欢它们年深日久之后前仰后合的样子，喜欢被踩。

陕西省西安市铁一中国际合作学校2017-2018学年高三下学期第一次大练习数学试卷(文科) Word版含解析

陕西省西安市铁一中国际合作学校2017-2018学年高三下学期第一次大练习数学试卷（文科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A={1，2}，B={x|x﹣1|≤1}，则A∩B等于( )A．{﹣2} B．{1，2} C．{1} D．{﹣1，1，2}考点：交集及其运算．专题：集合．分析：求出B中不等式的解集确定出B，找出A与B的交集即可．解答：解：由B中不等式变形得：﹣1≤x﹣1≤1，解得：0≤x≤2，即B=[0，2]，∵A={1，2}，∴A∩B={1，2}，故选：B．点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．2．若复数z=（a∈R）为纯虚数，则z的共轭复数为( )A．﹣2i B．i C．﹣i D．2i考点：复数代数形式的乘除运算．专题：数系的扩充和复数．分析：利用复数的运算法则、共轭复数与纯虚数的定义即可得出．解答：解：复数z===+（a∈R）为纯虚数，∴=0，≠0，解得a=1，∴z=i则z的共轭复数为﹣i．故选：C．点评：本题考查了复数的运算法则、共轭复数与纯虚数的定义，考查了计算能力，属于基础题．3．某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示，则甲、乙两人这几场比赛得分的中位数之和是( )A．63 B．64 C．65 D．66考点：众数、中位数、平均数；茎叶图．专题：计算题；压轴题；图表型．分析：由茎叶图找出两人的中位数，再求出它们的和解答：解：由图可以看出，甲比赛得分的中位数是36，乙比赛得分的中位数是27故、乙两人这几场比赛得分的中位数之和是36+27=63故选A点评：本题考查众数、中位数、平均数，解题的关键是掌握住从数据中获取中位数的方法，属于基本概念题4．设，则使得f（x）=x n为奇函数，且在区间（0，+∞）上单调递减的n的个数是( )A．1 B．2 C．3 D．4考点：奇函数．专题：计算题．分析：根据幂函数的指数大于0，则在区间（0，+∞）上单调递增，可排除n=，1，2，3的可能，然后判定当n=﹣1时，f（x）=是否满足条件即可．解答：解：f（x）=x n，当n＞0时函数f（x）在区间（0，+∞）上单调递增，故，1，2，3都不符合题意当n=﹣1时，f（x）=，定义域为{x|x≠0}，f（﹣x）=﹣=﹣f（x），在区间（0，+∞）上单调递减，故正确故选A．点评：本题主要考查了幂函数的性质，同时考查了函数奇偶性的判定，属于基础题．5．“直线（m+2）x+3my+1=0与“直线（m﹣2）x+（m+2）y﹣3=0相互垂直”是“m=”的( )A．充分必要条件B．充分而不必要条件C．.必要而不充分条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据充分条件和必要条件的定义进行判断即可．解答：解：若两直线垂直，则（m+2）（m﹣2）+3m（m+2）=0，即（m+2）（4m﹣2）=0，解得m=﹣2或m=，即“直线（m+2）x+3my+1=0与“直线（m﹣2）x+（m+2）y﹣3=0相互垂直”是“m=”的必要不充分条件，故选：C．点评：本题主要考查充分条件和必要条件的判断，根据直线垂直的关系是解决本题的关键．6．如图，正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）P﹣ABCD的底面边长为6cm，侧棱长为5cm，则它的正视图的面积等于( )A．3B．6C．12 D．24考点：简单空间图形的三视图．专题：图表型．分析：正视图是一个三角形，底边长是等于正四棱锥底面正方形的边长，高为正四棱锥的高的一个等腰三角形，即可判断三角形的形状，然后求出面积即可．解答：解：由题意可知：正视图是一个三角形，底边长是等于正四棱锥底面正方形的边长，高为正四棱锥的高的一个等腰三角形，腰长l==4，高为h==，又∵正四棱锥底面正方形的边长为：6，正视图面积为：×=3．故选A．点评：本题考查简单几何体的三视图，考查空间想象能力，计算能力，是基础题．7．已知等差数列{a n}中，a3=1，a6+a12=8，则a33=( )A．16 B．30 C．31 D．62考点：等差数列的通项公式．专题：等差数列与等比数列．分析：由已知结合等差数列的性质求得a9=4，再由等差数列的通项公式求得公差，进一步求得a33．解答：解：在等差数列{a n}中，由a6+a12=8，得2a9=8，∴a9=4，又a3=1，∴．∴．故选：A．点评：本题考查了等差数列的通项公式，考查了等差数列的性质，是基础题．8．已知实数x，y满足，则x+y﹣1的取值范围是( )A．[﹣1，3]B．[0，4]C．[1，+∞）D．[0，+∞）考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对应的平面区域，利用目标函数的几何意义，通过平移从而求出z的取值范围．解答：解：作出不等式组对应的平面区域如图：（阴影部分）．设z=x+y﹣1得y=﹣x+z+1，即直线的截距最大，z也最大．平移直线y=﹣x+z+1，即直线y=﹣x+z+1经过点A（1，0）时，截距最小，此时z最小，为z=1+0﹣1=0．无最大值，即z≥0，故z的取值范围是[0，+∞）．故选：D．点评：本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．9．已知函数f（x）=，若f（f（x））=，则x=( ) A．B．C．﹣9 D．﹣2考点：函数的零点；函数的值．专题：函数的性质及应用．分析：根据分段函数解析式得出当x≤0时，0＜y≤1，当0＜x＜1，y＜0，判定出f（x）=﹣2，求解即可得出x=，解答：解：∵函数f（x）=，∴当x≤0时，0＜y≤1，当0＜x＜1，y＜0，∵f（f（x））=，2﹣2=∴f（x）=﹣2，即log3x=﹣2，x=，故选：B．点评：本题考查了指数对数函数的性质，分段函数的性质，解析式的运用计算化简，难度不大，属于中档题．10．若b＞a＞3，f（x）=，则下列各结论中正确的是( )A．f（a）＜f（）＜f（）B．f（）＜f（b）＜f（）C．f（）＜f（）＜f（a）D．f（b）＜f（）＜f（）考点：利用导数研究函数的单调性．专题：导数的概念及应用．分析：先根据a，b的范围，求出b＞＞，再求出函数的单调性，从而判断出函数值的大小．解答：解：∵b＞a＞3，∴b＞＞，∵f（x）=，x∈（a，b），a＞3，∴f′（x）=＜0，∴f（x）在（a，b）单调递减，∴f（b）＜f（）＜f（），故选：D．点评：本题考查了函数的单调性问题，考查导数的应用，是一道中档题．二、填空题：本大题共4小题，每小题5分，共25分.11．θ的始边与x轴的正半轴重合，其终边上有一点P（1，﹣2），则sin2θ=．考点：二倍角的正弦；任意角的三角函数的定义．专题：三角函数的求值．分析：根据任意角的三角函数的定义求得cosθ=，sin的值，再利用二倍角的正弦函数计算求得结果．解答：解：由题意θ的始边与x轴的正半轴重合，其终边上有一点P（1，﹣2），可得，x=1、y=﹣2、r=，∴cosθ==，∴sin=，sin2θ==．故答案为：．点评：本题主要考查任意角的三角函数的定义，诱导公式的应用，属于基础题．12．如图，该程序运行后输出的结果是8．考点：程序框图．专题：图表型．分析：经过观察为当型循环结构，按照循环结构进行执行，当不满足执行条件时跳出循环，输出结果即可．解答：解：经过分析，本题为当型循环结构，执行如下：S=0 A=1S=1 A=3S=2 A=5S=3 A=7…S=7 A=15S=8 A=17当A=17时，满足循环条件，跳出，输出S=8．故答案为：8．点评：本题考查当型循环结构，考查对程序知识的综合运用，属于基础题．13．已知直线ax+by+c=0与圆：x2+y2=1相交于A、B两点，且，则=．考点：向量在几何中的应用．专题：计算题；综合题．分析：直线与圆有两个交点，知道弦长、半径，不难确定∠AOB的大小，即可求得•的值．解答：解：依题意可知角∠AOB的一半的正弦值，即sin =所以：∠AOB=120°则•=1×1×cos120°=．故答案为：．点评：初看题目，会被直线方程所困惑，然而看到题目后面，发现本题容易解答．本题考查平面向量数量积的运算，直线与圆的位置关系．是基础题．14．若数列{a n}（n∈N+）为等差数列，则数列也为等差数列，类比上述性质，相应地，若数列{c n}是等比数列且c n＞0（n∈N+），则有数列d n=（n∈N+）也是等比数列．考点：类比推理．专题：压轴题；方案型．分析：从商类比开方，从和类比到积．解答：解：从商类比开方，从和类比到积，可得如下结论：故答案为：点评：本题主要考查学生的知识量和知识的迁移类比等基本能力．（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）（不等式选讲选做题）15．已知方程|x﹣1|﹣|x+1|=a+1有实数解，则a的取值范围为[﹣3，1]．考点：函数的最值及其几何意义．专题：计算题；函数的性质及应用．分析：设f（x）=|x﹣1|﹣|x+1|=，从而可得﹣2≤|x﹣1|﹣|x+1|≤2，从而解得．解答：解：设f（x）=|x﹣1|﹣|x+1|=，故﹣2≤|x﹣1|﹣|x+1|≤2，又∵方程|x﹣1|﹣|x+1|=a+1有实数解，∴﹣2≤a+1≤2，∴a∈[﹣3，1]．故答案为：[﹣3，1]．点评：本题考查了函数与方程的关系应用及绝对值函数的化简与应用，属于中档题．（几何证明选讲选做题）16．如图，四边形ABCD内接于⊙O，BC是直径，MN切⊙O于A，∠MAB=25°，则∠B=65°．考点：与圆有关的比例线段．专题：选作题；推理和证明．分析：根据同弧所对的圆周角和弦切角相等，得到∠ADB的度数，根据∠D=∠ADB+∠BDC，得到结果．解答：解：连接BD，AC，根据弦切角定理∠MAB=∠ACB=∠ADB=25°∵∠D所对的弧是，∴∠D=∠ADB+∠BDC=25°+90°=115°，∴∠B=180°﹣115°=65°．故答案为：65°．点评：本题考查同弧所对的圆周角和弦切角相等，考查直径所对的圆周角等于直角，本题只要观察清楚图象中各个角之间的关系，就可以求出角的大小，这种题目隐含的条件比较多，注意挖掘．（坐标系与参数方程选做题）17．设曲线C的参数方程为（θ为参数），直线l的参数方程为（t为参数），则直线l与曲线C截得的弦长为．考点：参数方程化成普通方程．专题：坐标系和参数方程．分析：本题可以将曲线C的参数方程化为普通方程，再将直线l的参数方程化为普通方程，然后利用点线距离公式求出弦心距的长，根据勾股定理，求出弦长，即得本题结论．解答：解：∵曲线C的参数方程为（θ为参数），∴曲线C的方程为：（x﹣2）2+（y+1）2=10，∴圆心C（2，﹣1），半径r=．∵直线l的参数方程为（t为参数），∴直线l的方程为：x﹣2y+1=0．点C（2，﹣1）到直线l：x﹣2y+1=0的距离为：d==．由勾股定理得到弦长为：l==2=．故答案为：．点评：本题考查了将参数方程转化为普通方程的消参法，还考查了用弦心距求弦长的知识，本题难度不大，属于基础题．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤. 18．在△ABC中，a、b、c分别是角A、B、C所对的边，满足a2+c2﹣b2=ac．（1）求角B的大小；（2）若x∈[0，π），求函数f（x）=sin（x﹣B）+sinx的值域．考点：余弦定理；三角函数的最值．专题：计算题．分析：（1）利用余弦定理求得cosB，进而求得B．（2）利用两角和公式对函数f（x）的解析式化简整理，进而根据正弦函数的性质求得函数的值域．解答：解：（1）在又∵；（2）∵∴点评：本题主要考查了余弦定理的运用．属基础题．19．一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）．（Ⅰ）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，求月收入在[1500，2000）（元）段应抽出的人数；（Ⅱ）为了估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，4，…，表示月收入在[2000，3000）（元）的居民，剩余的数字表示月收入不在[2000，3000）（元）的居民；再以每三个随机数为一组，代表统计的结果．经随机模拟产生了20组随机数如下：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计，计算该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率．考点：古典概型及其概率计算公式；频率分布直方图．专题：概率与统计．分析：（I）由频率分布直方图求得月收入在[1500，2000）（元）的概率为0.2，由此可得应抽取的人数为0.2×100，运算求得结果．（Ⅱ）由频率分布直方图求得月收入在[2000，3000）（元）的概率为2×0.0005×500，观察上述随机数可得，该社区3个居民中恰有2个月收入在[2000，3000）（元）的有7个，由古典概率的定义，估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率．解答：解：（I）由频率分布直方图可知，月收入在[1500，2000）（元）的概率为0.0004×500=0.2，所以应抽取的人数为0.2×100=20人，…（Ⅱ）由频率分布直方图可知，月收入在[2000，3000）（元）的概率为2×0.0005×500=0.5．所以，我们用数字0，1，2，3，4表示月收入在[2000，3000）（元）的居民，数字5，6，7，8，9表示月收入不在[2000，3000）（元）的居民．观察上述随机数可得，该社区3个居民中恰有2个月收入在[2000，3000）（元）的有191，271，932，812，393，027，730，共计7个，而所有抽查的居民共有20户，由古典概率的定义可知，估计该社区3个居民中恰有2个月收入在[2000，3000）（元）的概率为．…点评：本题主要考查分层抽样的定义，频率分步直方图的应用，古典概型及其概率计算公式的应用，属于基础题．20．已知点列A n{n，a n}、B n{n，b n}、C n{n﹣1，0}，a1=b1=1，=（1，2），（Ⅰ）求证数列{b n}为等差数列；（Ⅱ）求数列{a n}的通项公式．考点：数列递推式；等差关系的确定；数列与向量的综合．专题：等差数列与等比数列；平面向量及应用．分析：（Ⅰ）由已知点的坐标求得向量的坐标，结合=（1，2），可得数列{b n}为等差数列；（Ⅱ）由（Ⅰ）中的等差数列求出数列{b n}的通项公式，结合可得a n+1﹣a n=b n=2n﹣1，然后利用累加法求得数列数列{a n}的通项公式．解答：（Ⅰ）证明：由B n{n，b n}，得B n+1{n+1，b n+1}，∴，又=（1，2），∴（1，b n+1﹣b n）=（1，2），则b n+1﹣b n=2．∴数列{b n}为等差数列；（Ⅱ）由（Ⅰ）知b n=1+2（n﹣1）=2n﹣1，由A n{n，a n}，得A n+1{n+1，a n+1}，∴，又B n{n，b n}、C n{n﹣1，0}，∴，由，得﹣b n+a n+1﹣a n=0，∴a n+1﹣a n=b n=2n﹣1，则a n=（a n﹣a n﹣1）+（a n﹣1﹣a n﹣2）+…+（a2﹣a1）+a1=2（n﹣1）﹣1+2（n﹣2）﹣1+…+2•1﹣1+1=1+3+5+…+（2n﹣3）+1=n2﹣2n+2．点评：本题是数列与向量的综合题，考查了等差数列和等比数列的通项公式，考查了等差数列的前n项和，是中档题．21．已知四棱锥P﹣ABCD中，底面ABCD为菱形，且平面PAC垂直于底面ABCD，△PAC 中，PA=PC，PA⊥PC（Ⅰ）求证：平面PBD⊥平面PAC（Ⅱ）若BD=PA=2，求四棱锥P﹣ABCD的体积．考点：棱柱、棱锥、棱台的体积；平面与平面垂直的判定．专题：空间位置关系与距离．分析：（I）由底面ABCD为菱形，可得AC⊥BD，再利用平面PAC⊥底面ABCD，可得BD⊥平面PAC，即可证明平面PBD⊥平面PAC．（2）利用V P﹣ABCD=V B﹣PAC+V D﹣PAC=即可得出．解答：（I）证明：∵底面ABCD为菱形，∴AC⊥BD，∵平面PAC⊥底面ABCD，平面PAC∩底面ABCD=AC，∴BD⊥平面PAC，BD⊂平面PBD，∴平面PBD⊥平面PAC．（2）解：S△PAC==2．∴V P﹣ABCD=V B﹣PAC+V D﹣PAC==．点评：本题考查了线面面面垂直的判定性质定理、菱形的性质、三棱锥与四棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题．22．△ABC两个顶点A、B的坐标分别是（﹣2，0），（2，0），边AC、BC所在直线的斜率之积等于﹣（Ⅰ）求顶点C的轨迹方程；（Ⅱ）求上述轨迹中以P（1，）为中点的弦所在的直线方程．考点：轨迹方程；直线与圆锥曲线的关系．专题：综合题；圆锥曲线的定义、性质与方程．分析：（Ⅰ）设出C的坐标，利用AC、BC所在直线的斜率之积等于﹣，列出方程，求出点C的轨迹方程；（Ⅱ）利用点差法，即可求出以P（1，）为中点的弦所在的直线方程．解答：解：（Ⅰ）设C（x，y）x≠±2，因为AC、BC所在直线的斜率之积等于﹣．所以=﹣，即，y≠0或x≠±2，所求的轨迹方程为：，y≠0或x≠±2，故答案为：，（y≠0），（或x≠±2）．（Ⅱ）设弦为PQ，弦所在直线斜率为k，其中P（x1，y1）Q（x2，y2）所以x1+x2=2，y1+y2=1，所以相减得：，所以所求直线方程为：3x+2y﹣4=0…点评：本题是中档题，考查点的轨迹方程的求法，考查点差法，考查计算能力，注意直线的斜率垂直的条件的应用．23．已知函数f（x）=ax+lnx（a∈R）．（Ⅰ）若a=2，求曲线y=f（x）在x=1处的切线方程；（Ⅱ）求f（x）的单调区间；（Ⅲ）设g（x）=x2﹣2x+2，若对任意x1∈（0，+∞），均存在x2∈[0，1]，使得f（x1）＜g （x2），求a的取值范围．考点：利用导数研究曲线上某点切线方程；利用导数研究函数的单调性；利用导数求闭区间上函数的最值．专题：综合题；导数的综合应用．分析：（Ⅰ）把a的值代入f（x）中，求出f（x）的导函数，把x=1代入导函数中求出的导函数值即为切线的斜率，可得曲线y=f（x）在x=1处的切线方程；（Ⅱ）求出f（x）的导函数，分a大于等于0和a小于0两种情况讨论导函数的正负，进而得到函数的单调区间；（Ⅲ）对任意x1∈（0，+∞），均存在x2∈[0，1]，使得f（x1）＜g（x2），等价于f（x）max ＜g（x）max，分别求出相应的最大值，即可求得实数a的取值范围．解答：解：（Ⅰ）由已知，f'（1）=2+1=3，所以斜率k=3，又切点（1，2），所以切线方程为y﹣2=3（x﹣1）），即3x﹣y﹣1=0故曲线y=f（x）在x=1处切线的切线方程为3x﹣y﹣1=0．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）①当a≥0时，由于x＞0，故ax+1＞0，f'（x）＞0，所以f（x）的单调递增区间为（0，+∞）．﹣﹣﹣﹣﹣﹣②当a＜0时，由f'（x）=0，得．在区间上，f'（x）＞0，在区间上，f'（x）＜0，所以，函数f（x）的单调递增区间为，单调递减区间为．﹣﹣﹣﹣﹣﹣﹣﹣（Ⅲ）由已知，转化为f（x）max＜g（x）max．g（x）=（x﹣1）2+1，x∈ [0，1]，所以g（x）max=2由（Ⅱ）知，当a≥0时，f（x）在（0，+∞）上单调递增，值域为R，故不符合题意．（或者举出反例：存在f（e3）=ae3+3＞2，故不符合题意．）当a＜0时，f（x）在上单调递增，在上单调递减，故f（x）的极大值即为最大值，，所以2＞﹣1﹣ln（﹣a），解得．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，会利用导数研究函数的单调性，掌握不等式恒成立时所满足的条件，是一道中档题．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高三第一次模拟考试文科数学试卷时间：120分钟满分：120分一、选择题(本大题共10个小题，每小题4分，共40分) 1．53sinπ的值是（）A . 12 B. 12- C. 2D. 2-2．若0m n<<，则下列结论正确的是（）A ．22m n >B ．11()()22m n < C ．1122log log m n > D ． 22log log m n >3．已知函数()sin(2)f x x ϕ=+的图象关于直线8x π=对称，则ϕ可能是（）A.2π B.4π- C.4π D.34π 4．如果1弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为（）A ．5.0sin 1B ．sin 0.5C ．2sin 0.5D ．tan 0.5 5．若函数)(x f 的定义域是[0，4]，则函数x x f x g )2()(=的定义域是A ．[ 0，2] B.(0，2) C. [0，2) D. (0，2] 6．若函数y ＝log 2(x 2－2x －3)的定义域、值域分别是M 、N ，则()R C M N ⋂= （）A．[－1, 3] B．(－1, 3) C．(0, 3] D．[3, ＋∞)7．设函数()()(2)(3)f'=，则k==++-，且(0)6f x x x k x k x k（）A．0 B．-1 C．3 D．-68．函数()|2|ln=--在定义域内零点的个数为f x x x（）A．0 B．1 C．2 D．39．已知函数f (x)=(x－a)(x－b)(其中a>b)，若f (x)的图象如下图（左）所示，则g(x) = a x+b的图象是()10．如图，P （x 0 , f (x 0））是函数y =f (x )图像上一点，曲线y =f (x )在点P 处的切线交x 轴于点A ， PB ⊥x轴，垂足为B. 若ΔPAB的面积为12，则 0f x '()与0()f x 满足关系式（） A. 00f x f x ='()() B. 200f x f x ⎡⎤=⎣⎦'()() C. 00f x f x =-'()() D. 200f x f x ⎡⎤=⎣⎦'()()二、填空题（本大题共5个小题，每题4分，共20分）11. 已知函数)1lg()(+=x x f ，若b a ≠且)()(b f a f =，则b a +的取值范围是 . 12．已知1cos 7α=，13cos()14αβ-=，且π02βα<<<，则cos β= ． 13．已知幂函数222(33)m m y m m x --=-+的图像不过坐标原点，则m 的值是___ ．14．已知命题：“存在[1,2]x ∈，使022≥++a x x ”为真命题，则a 的取值范围是___ ．15．已知函数()sin f x x ω=，()sin(2)2g x x π=+，有下列命题：①当2ω=时，函数y =()()f x g x 是最小正周期为2π的偶函数； ②当1ω=时，()()f x g x +的最大值为98；③当2ω=时，将函数()f x 的图象向左平移2π可以得到函数()g x 的图象.其中正确命题的序号是（把你认为正确的命题的序号都填上）．三、解答题（本大题共6个小题,共60分。

解答应写出文字说明、推理过程或演算步骤）16．(本题满分8分)已知sin 2cos 022x x -=．（I ）求xtan 的值；（Ⅱ）求cos 2cos()sin 4x x xπ-⋅的值．17．(本题满分8分) 函数f(x A ，关于x 的不等式32ax <3a +x (a ∈R)的解集为B ，求使A ∩B =A 的实数a 的取值范围．18．(本题满分10分）已知函数()sin 2cos2()f x a b x c x x R =++∈的图像过点(0,1),(,1)4A B π，且b >0，又()f x 的最大值为1.（Ⅰ）将()f x 写成含sin()(0)A ωx φωφπ+><，0<的形式;（Ⅱ）由函数y =()f x 图像经过平移是否能得到一个奇函数y =()g x19．（本题满分10收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比。

已知投资1万元时两类产品的收益分别为0.125 万元和0.5万元（y（I （Ⅱ）该家庭现有20问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？20．（本小题满分12分）二次函数():(0)2,()(2)f x f f x f x ==--满足，它的导函数的图象与直线2y x = 平行. （Ⅰ）求()f x 的解析式；（Ⅱ）若函数()()g x xf x x =-的图象与直线y m =有三个公共点，求m 的取值范围。

21.（本题满分12分）已知函数ln ()()x af x a x+=∈R ．（Ⅰ）求函数()f x 的单调区间和极值；（Ⅱ）当1a =，且1x ≥时，证明：()f x ≤1文科数学答案一、选择题(本大题共10个小题，每小题4分，共40分) DCCAD ABCAB二、填空题（本大题共5个小题，每题4分，共20分）11．（0，+∞） 12．1cos 2β= 13．1或2 14． [－8，+∞） 15．②三、解答题（本大题共6个小题，共60分） 16．(本题满分8分)解：（I ）由02cos 22sin =-x x, 22tan=⇒x，-------2分 3421222tan12tan2tan 22-=-⨯=-=∴x xx ． -------4分（Ⅱ）由（I ）知4tan 3x ∴=-，所以cos 0x ≠∴cos 2)sin 4xx x π-⋅＝22222cos sin sin cos sin x x x x x -=+ 221tan tan tan xx x-=+ -------6分 161941639-=-+74=-． -------8分17. (本题满分8分) 解：由21xx --≥0，得1<x ≤2，即A ={x |1<x ≤2}．∵y =2x 是R 上的增函数， ∴由22ax <2a +x ，得2ax <a +x ， ∴B ={x |(2a -1)x ＜a }． -------2分(1)当2a -1>0，即a >12时，x <21aa -. 又∵A ⊆B ，∴21a a ->2，解得12<a <23. -------4分(2)当2a -1=0，即a =12时，x ∈R ，满足A ∩B =A . --------5分(3)当2a -1<0，即a <12时，x >21aa -. ∵A ⊆B ，∴21a a -≤1，解得a ＜12或a ≥1，∴a <12. --------7分综上，a 的取值范围是2,3⎛⎫-∞ ⎪⎝⎭.--------8分 18．(本题满分10分)解：（Ⅰ）()sin 2cos 2)(tan )bf x a b x c x a x cϕϕ=++=++=，由题意，可得111a c ab a ⎧+=⎪+=⎨⎪⎩，解得122a b c =-⎧⎪=⎨⎪=⎩ -------3分所以()12sin 2cos 2f x x x =-++ -------4分()12sin 2cos 2)14f x x x x π=-++=+- --------5分（Ⅱ）将()f x 的图像向上平移1个单位得到函数())4f x x π=+的图像，再向右平移8π单位得到2y x =的图像，而函数y x =为奇函数，故将()f x 的图像先向上平移1个单位，再向右平移8π单位就可以得到奇函数y =()g x 的图像 -------10分19．（本题满分10分）解：（I ）设()x k x f 1=，()x k x g 2=所以 ()1811k f ==，()2211k g == -------3分即()()081≥=x x x f ()()021≥=x x x g -------5分（Ⅱ）设投资债券类产品x 万元，则股票类投资为(x -20)万元依题意得：()()()2002021820≤≤-+=-+=x x x x g x f y -------7分令()52020≤≤-=t x t则()32812182022+--=+-=t t t y -------9分所以当2=t ，即16=x 万元时，收益最大， max 3y =万元-------10分20.（本题满分12分）解: （Ⅰ）2()(0)f x ax bx c a =++≠且f (0)=2 所以 c =2又 f (x )=f (－2－ x ) 所以图像的对称轴12ba-=- ------------------2分导函数图象与直线222,y x a =∴=平行从而解得：1,2,2a b c ===2()22()f x x x x R ∴=++∈-----------6分（Ⅱ）32()()2g x xf x x x x x =-=++ '2()341g x x x ∴=++ --------8分设'()0g x ≥ 则有1x ≤-或13x ≥-()g x ∴在（－∞，－1]、1[,)3-+∞上递增，在1(1,)3--上递减 -----10分且144(1)0,(),(,0)32727g g m -=-=--故的取值范围为 ------12分21．（本题满分12分）解：（Ⅰ）函数()f x 的定义域为{}|0x x >， -------1分所以21ln ()x af x x --'=．令()0f x '=，得1a x e -=．------- 3分当x 变化时，'()f x ，()f x 的变化情况如下表：------- 5分由表可知：()f x 的单调递增区间是1(0,)a e -，单调递减区间是1(,)a e -+∞．所以()f x 在1a x e -=处取得极大值，11()()a a f x f e e --==极大值． ------- 8分。