5-4-4完全平方数及应用一教师版
小学教育ppt课件教案平方与平方根的运算规律与性质

常见平方数与平方根
常见平方数
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 等。这些数字都是整数的平方,易于 记忆和识别。
常见平方根
√4=2,√9=3,√16=4等。这些数字 都是常见平方数的正平方根,也是学 生需要熟练掌握的基础知识。
02
平方运算规律
乘法公式在平方运算中应用
小学教育ppt课件教案平方 与平方根的运算规律与性质
目录
• 平方与平方根基本概念 • 平方运算规律 • 平方根运算规律 • 平方与平方根在生活中的应用 • 典型例题解析与课堂互动 • 知识拓展与延伸
01
平方与平方根基本概念
平方定义及性质
平方定义
一个数乘以它本身得到的积,叫 做这个数的平方。例如,5的平方 是5×5=25。
01
有理数的定义
有理数是可以表示为两个整数之比的数,例如$frac{a}{b}$,其中$a$和
$b$是整数,$b neq 0$。
02
无理数的定义
无理数是不能表示为两个整数之比的数,例如$sqrt{2}$、$pi$等。
03
无理数和有理数的区别
无理数不能表示为分数形式,而有理数可以;无理数的十进制表示是无
开方方法
通过试除法或查表法,逐 步逼近所求平方根的值。
注意事项
开方时需注意正负根的情 况,以及被开方数必须为 非负数。
分数指数幂法则及应用
分数指数幂定义
将幂运算中的指数扩展为分数形式, 表示开方和乘方的复合运算。
应用举例
利用分数指数幂法则进行复杂表达式 的化简和计算。
分数指数幂运算法则
包括同底数幂相乘、幂的乘方、积的 乘方等运算法则。
平方性质
二次根式计算专题——30题(教师版含答案)

(2) 3 12 3 1 1 48 27 32
【答案】(1)0;(2) 4 3 .
【解析】
试题分析:(1)原式=1 5 2 3 1 0 ;
(2)原式= 6 3 3 2 3 3 3 4 3 .
试题解析:原式=1 3 3 2 1 3 2 2 3
考点:1.实数的运算;2.零指数幂;3.分母有理化. 20.计算:
①
8
2
1 2
0
②
6 3 2
1 3
48
12
③
3a2 3
a 2
1 2
2a 3
【答案】① 2 1;② 14 ;③ a .
考点:二次根式化简.
14.计算 (3 2 24 8) 12 3
【答案】 -
2+
6
.
23
试卷第 4 页,总 10 页
【解析】 试题分析:先化简二次根式,再合并同类二次根式,最后算除法即可求出答案. 试题解析:
(3 2 - 24 + 8) ¸ 12 = ( 6 - 2 6 +2 2) ¸ 2 3 = (2 2 - 6) ¸ 2 3 3
5
3
3 2 1;
(2) (6 x 2x 1 ) 3 x
4xBiblioteka (6 x 2x x ) 3 x 2x
(3 x 2 x ) 3 x
x 3 x
试卷第 1 页,总 10 页
1. 3
考点: 二次根式的混合运算.
3.计算: 3 12 2
小学奥数教师版-5-4-4 完全平方数及应用(一)

5-4-4.完全平方数及应用(一)教学目标1.学习完全平方数的性质;2.整理完全平方数的一些推论及推论过程3.掌握完全平方数的综合运用。
知识点拨一、完全平方数常用性质1.主要性质1.完全平方数的尾数只能是0,1,4,5,6,9。
不可能是2,3,7,8。
2.在两个连续正整数的平方数之间不存在完全平方数。
3.完全平方数的约数个数是奇数,约数的个数为奇数的自然数是完全平方数。
4.若质数p 整除完全平方数2a ,则p 能被a 整除。
2.性质性质1:完全平方数的末位数字只可能是0,1,4,5,6,9.性质2:完全平方数被3,4,5,8,16除的余数一定是完全平方数.性质3:自然数N 为完全平方数⇔自然数N 约数的个数为奇数.因为完全平方数的质因数分解中每个质因数出现的次数都是偶数次,所以,如果p 是质数,n 是自然数,N 是完全平方数,且21|n p N -,则2|n p N .性质4:完全平方数的个位是6⇔它的十位是奇数.性质5:如果一个完全平方数的个位是0,则它后面连续的0的个数一定是偶数.如果一个完全平方数的个位是5,则其十位一定是2,且其百位一定是0,2,6中的一个.性质6:如果一个自然数介于两个连续的完全平方数之间,则它不是完全平方数.3.一些重要的推论1.任何偶数的平方一定能被4整除;任何奇数的平方被4(或8)除余1.即被4除余2或3的数一定不是完全平方数。
2.一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。
3.自然数的平方末两位只有:00,01,21,41,61,81,04,24,44,64,84,25,09,29,49,69,89,16,36,56,76,96。
4.完全平方数个位数字是奇数(1,5,9)时,其十位上的数字必为偶数。
5.完全平方数个位数字是偶数(0,4)时,其十位上的数字必为偶数。
6.完全平方数的个位数字为6时,其十位数字必为奇数。
7.凡个位数字是5但末两位数字不是25的自然数不是完全平方数;末尾只有奇数个“0”的自然数不是完全平方数;个位数字为1,4,9而十位数字为奇数的自然数不是完全平方数。
苏教版 四年级下册数学应用题含答案解析
苏教版四年级下册数学应用题含答案解析一、苏教小学数学解决问题四年级下册应用题1.阳阳文具店购进24包笔记本,每包12本,成本价是36元/包。
现以每本4元出售。
(1)文具店购进这批笔记本一共花了多少元?(2)算式“12×4”解决的问题是________。
(3)根据题目中提供的信息,请你提出一个更有挑战性的数学问题。
(不用解答)2.文具店9月份卖出的部分商品的价格和数量如下表。
商品文具盒足球水彩笔单价38元/个57元/个35元/盒数量126个37个120盒?卖了多少元?3.把数字3写到一个五位数的左边,再将得到的六位数加上40000,所得的数正好是原来五位数的35倍,原来的五位数是多少?4.王阿姨平时上班都是乘坐常规公交车,需要40分刚好到达公司,但她今天早上起晚了,需要在30分内到达公司,她应该选择哪种交通工具?为什么?交通工具常规公交公交快线出租车平均速度400米/分500米/分600米/分5.运动会上,四(1)班有42名同学,要为每名同学买1瓶矿泉水,至少需要多少元?6.根据信息解决问题。
(1)11:30放学,聪聪每分走70米,他几时能走到家?(2)吃完午饭,聪聪从家出发,走到书店,买完书又返回,路上共花了15分,他走路的平均速度是多少?(3)下午体育课上,聪聪以每分135米的速度练习跑步,丁丁以每分128米的速度练习跑步。
两人同时跑了12分,聪聪比丁丁多跑了多少米?7.2019年12月15日8时深圳国际马拉松比赛正式鸣枪开跑。
来自世界各地的3万名参赛者踏上了赛道。
(1)马拉松比赛实行实名制,乐乐妈妈报名参加了6公里马拉松比赛,下面的()可能是她的身份证号码。
A.430×××201808243143B.430×××198208243143C.430×××201808243153D.430×××198208243153(2)比赛当天的气温是17℃-24℃,这一天的温差是()。
人教版四年级上册数学应用题100例答案

1、某风景区占地1平方千米,按照园区设计规划,把它建成面积同样大的5个游园,那么每个游园的面积是多少公顷?2、一块长方形玉米地,长是600米,宽是300米。
如果每公顷平均收10吨玉米,那么这块玉米地能收多少吨玉米?3、一台收割机每小时行驶5千米,收割的宽度是2米。
这台收割机一天工作5小时,可以收割多少公顷小麦?4、一个正方形果园,边长是300米.如果平均每公顷栽280棵梨树,那么这个果园一共可以栽多少棵梨树?5、一架飞机以980千米/时的速度从甲城飞往乙城,12小时后到达。
这架飞机按原路线从乙城返回甲城时用了15小时。
(1)甲城到乙城有多远?(2)返回时平均每小时飞行多少千米?6、一块长方形的小麦田,长450米,宽200米.如果每公顷可以收小麦3吨,这块小麦田可以共收小麦多少吨?7、一架直升机在一片长5千米、宽4千米的长方形树林上空喷洒药水,这片树林的面积是多少平方千米?合多少公顷?8、一堆煤重400吨,一艘大船运走了160吨。
剩下的用一艘小船运,每次运60吨,再运多少次可以完成?9、某段高速公路长40000米,宽50米,这段高速公路占地面积多少公顷?合多少平方千米?10、磊磊在一次参加数学竞赛时,遇到一个很有意思的考号:这个考号是个七位数,百万位上的数字是4,万位上的数宇是9,任意相邻的三个数位上的数字之和是18,请你猜猜这个考号是多少?11、一个长方形的荔枝园,长500米,宽400米,它的面积是多少公顷?如果这个荔枝园每8平方米种一棵荔枝树,一共可以种多少棵荔枝树?12、希望足球小学有一块专业足球场,它的占地是一个长110米,宽75米的长方形.(1)这个足球场占地面积大约是多少公顷?(2)多少个这样的足球场面积约是1平方千米?13、王叔叔从广州出发去新会区送化肥。
去时的速度是40千米/时,用了3小时。
返回时用了2小时。
从广州出发去新会区有多远?原路返回时的速度是多少?14、张伯伯绕着一个正方形广场走一圈,正好是400米,这个广场的占地面积是多少公顷?15、一个长方形牧场长8千米,李叔叔开汽车以每小时48千米的速度绕牧场一周要半小时,这个牧场的面积有多少公顷?16、动物园里的一头蓝鲸一天要吃450千克食物,饲养员准备了7吨食物,够蓝鲸吃20天吗?17、一块长方形菜地,长800米,宽500米.如果延长它的宽,使它成为一块正方形的菜地,现在菜地的面积比原来的面积增加多少公顷?18、小力每分钟走55米,小美每分钟走50米。
第四单元多边形的面积梯形篇-2023-2024学年五年级数学上册典型例题(原卷版)北师大版

篇首寄语我们每位老师都希望把最好的教学资料留给学生,但面对琳琅满目的资料时,总是费时费力才能找到自己心仪的那份,编者也常常为此苦恼。
于是,编者就常想,如果是自己来创作一份资料又该怎样?再结合自身教学经验和学生实际情况后,最终创作出了一个既适宜课堂教学讲解,又适宜课后作业练习,还适宜阶段复习的大综合系列。
《20232024学年五年级数学上册典型例题系列》是基于教材知识点和常年考点真题总结与编辑而成的,该系列主要分为典型例题篇、专项练习篇、单元复习篇、分层试卷篇等四个部分。
1.典型例题篇,按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
2.专项练习篇,从高频考题和期末真题中选取专项练习,其优点在于选题经典,题型多样,题量适中。
3.单元复习篇,汇集系列精华,高效助力单元复习,其优点在于综合全面,精炼高效,实用性强。
4.分层试卷篇,根据试题难度和不同水平,主要分为基础卷、提高卷、拓展卷三大部分,其优点在于考点广泛,分层明显,适应性广。
黄金无足色,白璧有微瑕,如果您在使用资料的过程中有任何宝贵意见,请留言于我改进,欢迎您的使用,谢谢!101数学工作室2023年10月1日20232024学年五年级数学上册典型例题系列第四单元多边形的面积·梯形篇【十一大考点】专题解读本专题是第四单元多边形的面积·梯形篇。
本部分内容是梯形的面积及其应用,考点和梯形以梯形面积的实际应用为主,建议作为将其本章核心内容进行讲解,一共划分为十一个考点,欢迎使用。
目录导航目录【考点一】梯形的面积其一 (3)【考点二】梯形的面积其二 (4)【考点三】已知面积,反求上底、下底或高 (6)【考点四】等高模型下的平行四边形、三角形、梯形 (7)【考点五】梯形中的最大图形问题 (8)【考点六】梯形中的面积变化问题 (10)【考点七】梯形面积的实际应用其一 (10)【考点八】梯形面积的实际应用其二 (12)【考点九】梯形面积的实际应用其三 (13)【考点十】梯形面积的实际应用其四 (14)【考点十一】差不变原理求梯形的面积 (15)典型例题【考点一】梯形的面积其一。
平方数的记忆方法
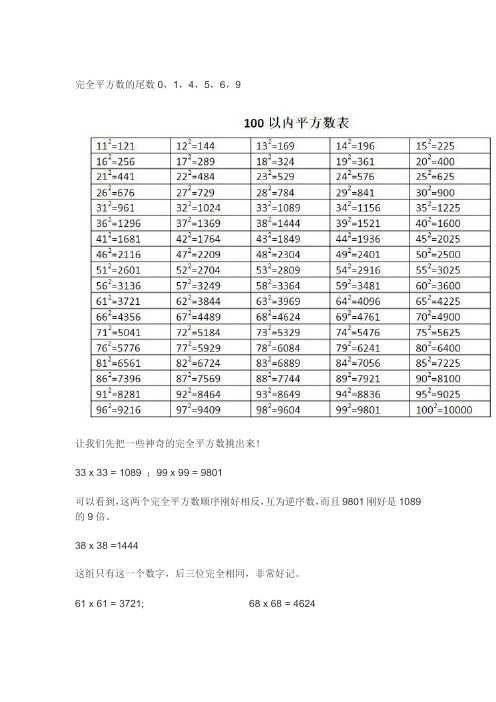
完全平方数的尾数0,1,4,5,6,9让我们先把一些神奇的完全平方数挑出来!33 x 33 = 1089 ;99 x 99 = 9801可以看到,这两个完全平方数顺序刚好相反,互为逆序数,而且9801刚好是1089的9倍。
38 x 38 =1444这组只有这一个数字,后三位完全相同,非常好记。
61 x 61 = 3721; 68 x 68 = 4624这是一组乘法口诀组成的完全平方数,三七二十一,四六二十四,怎么样,记住了吗?88 x 88 = 774412 x 12=144,21 x 21=441,13 x13 =169,31 x 31=961除了感叹一下完全平方数的神奇之外,我们还能说什么呢?其余的数字我们再来分组研究:第一组1~9和整十数1到9的平方是乘法口诀里面背过的,然后10到90的整十数的平方,就是在1到9的平方后面加两个零,那么相应的,我们在开方的时候,两个零,就可以开出一个零。
第二组11~1911到19的平方可以直接用口诀:头乘头,尾加尾,尾乘尾例:11 x 11 = 1 x 1 连1+1 连1 x 1 = 12117 x 17 = 1 x 1 连7+7 连7 x 7 = 289 (注意进位)第三组个数上是五的数个位数字是5的两位数平方,我们可以借用一下“首同尾和十”的方法(十位数字相同,个位数字的和等于10),头x (头+1)x 100 + 尾x尾。
例:15 x 15 = 1 x (1 +1 )x100+5 x 5 = 22525 x 25 = 2 x (2 + 1)x100+5 x 5 = 62535 x 35 = 3 x (3 + 1)x100+5 x 5 = 122545 x 45 = 4 x (4 + 1)x100+5 x 5 = 202555 x 55 = 5 x (5 + 1)x100+5 x 5 = 302565 x 65 = 6 x (6 + 1)x100+5 x 5 = 422575 x 75 = 7 x (7 + 1)x100+5 x 5 = 562585 x 85 = 8 x (8 + 1)x100+5 x 5 = 722595 x 95 = 9 x (9 + 1)x100+5 x 5 = 9025第四组51~59这里可以借用一下“尾同首和十”的方法(个位数字相同,十位数字的和等于10),(头1×头2+尾)×100+尾×尾。
完全平方公式的运用及其推广

294 完全平方公式的运用及其推广■陶其亮 (云南省昭通市昭阳区大寨子乡中学 657007)【中图分类号】G632 【文献标识码】A 【文章编号】2095-3089(2018)32-0294-02 一、完全平方公式完全平方公式(a±b)2=a2±2ab+b2,是整式运算中最重要的公式之一.在数学计算中可以简化运算过程,提高运算能力,从而培养良好的数学素质。
二、完全平方公式的运用1.a2+b2=(a+b)2-2ab=(a-b)2+2ab2.(a+b)2=(a-b)2+4ab3.(a-b)2=(a+b)2-4ab4.(a+b)2+(a-b)2=2(a2+b2)5.(a+b)2-(a-b)2=4ab6.ab=(a+b2)2-(a-b2)2例1:计算1.235×0.235×2.47-1.2353-1.235×0.2352.解:由a2+b2=(a+b)2-2ab=(a-b)2+2ab得1.235×0.235×2.47-1.2353-1.235×0.2352=-1.235×(1.2352+0.2352-0.235×2.47)=-1.235×[(1.235-0.235)2+2×1.235×0.235-0.235×2.47]=-1.235×(12+0)=-1.235例2:已知x1,x2是方程2x2-3x-5=0的两个根,求代数式(x1-x2)2的值.解:由韦达定理知x1+x2=-ba=--32=32x1x2=ca=-52=-52所以(x1-x2)2=(x1+x2)2-4x1x2=(32)2-4×(-52)=94+10=494例3:计算2018220192+20172-2.解:2018220192+20172-2=20182(2018+1)2+(2018-1)2-2=201822(20182+12)-2=201822×20182+2-2=201822×20182=12例4:若(1012+25)2-(1012-25)2=10n,则n=.解:∵(1012+25)2-(1012-25)2=4×1012×25=102×1012=1014∴n=14例5:已知a+b=70,c2=ab-1225,求a,b,c的值.解:∵(a+b)2-(a-b)2=4ab∴(a-b)2=(a+b)2-4ab=702-4(c2+1225)=-4c2∴(a-b)2+4c2=0由非负数的性质得a=b,c=0,从而a=35,b=35,c=0.例6:若a,b,c满足(a+2b)(a+2c)=(b+2c)(b+2a)=(c+2a)(c+2b),求证:a=b=c.解:由(a+2b)(a+2c)=(a+b+c)2-(b-c)2(b+2c)(b+2a)=(b+c+a)2-(c-a)2(c+2a)(c+2b)=(c+a+b)2-(a-b)2所以(a+b+c)2-(b-c)2=(b+c+a)2-(c-a)2=(c+a+b)2-(a-b)2即(b-c)2=(c-a)2=(a-b)2①.若a≠b,则由①式可知b≠c,c≠a,即a,b,c互不相等,不妨设c<b<a,于是a-c>0,b-c>0,故(a-c)2>(b-c)2与(a-c)2=(b-c)2矛盾,因此,a=b.所以(a-b)2=0,由①式得b=c,故a=b=c.例7:若两个自然数a,b满足a+b=30,求这两个数乘积的最大值.解:由ab=(a+b2)2-(a-b2)2=(302)2-(a-b2)2∵(a-b2)2≥0∴当a=b时,这两个数的乘积有最大值为225.三、完全平方公式的推广【推广1】(从后往前算,每满十向前进1)例8:计算232的值.【推广2】ab·ac=a(a+1)b·c(b+c=10,若b·c<10,则在b·c前添加一个0,即乘数位数减1个0)例9:计算19×11的值.19×11=1×(1+1)9×1=1×29×獉1=209例10:计算63×6=,252.63×67=6×(6+1)3×7=6×721=4221252=2×(2+1)5×5=2×325=625【推广3】ab·ac=a2a·b+a·cb·c(从后往前算,每满十向前进1)例11:计算56×58=.【推广4】ab·cd=a·c·a·d+b·cb·d(从后往前算,每满十向前进1)例12:计算79×64=.例13:计算89×98=.参考文献[1]赵兴荣.完全平方公式的应用举例(初二)[J].数理天地:初中版,2017,0(5):3-3.[2]刘家良.且看完全平方公式的应用[J].数理天地:初中版,2016,0(2):2-3.[3]曹秀之.完全平方公式的应用[J].初中生数学学习:初一版,2003,(7):64-65.[4]皇甫军[1].例谈完全平方公式的应用[J].中学生数理化:初中版初二,2006,(7):28-29.[5]谢盛富.完全平方公式及其变形的应用[J].中学生数学:初中版,2016,0(5):5-6.[6]高文良[1].完全平方公式的变式应用[J].中学生数学:初中版,2011,(7):2-2.[7]刘顿.完全平方公式的变形与应用[J].中学课程辅导:初一版,2003,(5):33-33.[8]陈剑[1].完全平方公式的一个引申及应用[J].中小学数学:初中版,2009,(4):35-35.浅谈儿童水墨画教学■田 鱼 (重庆市北碚区朝阳小学 400700)【摘 要】现代儿童水墨画教学是现代教育改革的背景下为致力于发展儿童的综合能力,加强文化传承和文化交流,促进其全面发展的一门艺术课程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 学习完全平方数的性质;2. 整理完全平方数的一些推论及推论过程3. 掌握完全平方数的综合运用。
一、完全平方数常用性质 1.主要性质1.完全平方数的尾数只能是0,1,4,5,6,9。
不可能是2,3,7,8。
2.在两个连续正整数的平方数之间不存在完全平方数。
3.完全平方数的约数个数是奇数,约数的个数为奇数的自然数是完全平方数。
4.若质数p 整除完全平方数2a ,则p 能被a 整除。
2.性质性质1:完全平方数的末位数字只可能是0,1,4,5,6,9.性质2:完全平方数被3,4,5,8,16除的余数一定是完全平方数.性质3:自然数N 为完全平方数⇔自然数N 约数的个数为奇数.因为完全平方数的质因数分解中每个质因数出现的次数都是偶数次,所以,如果p 是质数,n 是自然数,N 是完全平方数,且21|n p N -,则2|n p N .性质4:完全平方数的个位是6⇔它的十位是奇数.性质5:如果一个完全平方数的个位是0,则它后面连续的0的个数一定是偶数.如果一个完全平方数的个位是5,则其十位一定是2,且其百位一定是0,2,6中的一个.性质6:如果一个自然数介于两个连续的完全平方数之间,则它不是完全平方数.3.一些重要的推论1.任何偶数的平方一定能被4整除;任何奇数的平方被4(或8)除余1.即被4除余2或3的数一定不是完全平方数。
2.一个完全平方数被3除的余数是0或1.即被3除余2的数一定不是完全平方数。
3.自然数的平方末两位只有:00,01,21,41,61,81,04,24,44,64,84,25,09,29,49,69,89,16,36,56,76,96。
4.完全平方数个位数字是奇数(1,5,9)时,其十位上的数字必为偶数。
5.完全平方数个位数字是偶数(0,4)时,其十位上的数字必为偶数。
6.完全平方数的个位数字为6时,其十位数字必为奇数。
7.凡个位数字是5但末两位数字不是25的自然数不是完全平方数;末尾只有奇数个“0”的自然数不是完全平方数;个位数字为1,4,9而十位数字为奇数的自然数不是完全平方数。
3.重点公式回顾:平方差公式:22()()a b a b a b -=+-模块一、完全平方数计算及判断例题精讲知识点拨教学目标5-4-4.完全平方数及应用(一)【例 1】 已知:XX21×49是一个完全平方数,求它是谁的平方? 【考点】完全平方数计算及判断 【难度】2星 【题型】解答 【解析】 我们不易直接求解,但是其数字有明显的规律,于是我们采用递推(找规律)的方法来求解:121=211;12321=2111;1234321=21111……,于是,我们归纳为1234…n …4321=2(1111)n 个1,所以,XX21:11111112;则,XX21×49=11111112×72=77777772.所以,题中原式乘积为7777777的平方.【答案】7777777【例 2】 1234567654321(1234567654321)⨯++++++++++++是 的平方. 【考点】完全平方数计算及判断 【难度】2星 【题型】填空 【关键词】祖冲之杯 【解析】 212345676543211111111=,212345676543217++++++++++++=,原式22(11111117)7777777=⨯=.【答案】7777777【例 3】 已知自然数n 满足:12!除以n 得到一个完全平方数,则n 的最小值是 。
【考点】完全平方数计算及判断 【难度】3星 【题型】填空 【关键词】学而思杯,6年级,第9题 【解析】 (法1)先将12!分解质因数:105212!235711=⨯⨯⨯⨯,由于12!除以n 得到一个完全平方数,那么这个完全平方数是12!的约数,那么最大可以为1042235⨯⨯,所以n 最小为104212!2353711÷⨯⨯=⨯⨯231=。
(法2)12!除以n 得到一个完全平方数,12!的质因数分解式中3、7、11的幂次是奇数,所以n 的最小值是3711231⨯⨯=。
【答案】231【例 4】 有一个正整数的平方,它的最后三位数字相同但不为0,试求满足上述条件的最小的正整数. 【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 平方数的末尾只能是0,1,4,5,6,9,因为111,444,555,666,999都不是完全平方数,所以所求的数最小是4位数.考察1111,1444……可以知道14443838=⨯,所以满足条件的最小正整数是1444.【答案】1444【例 5】 A 是由2002个“4”组成的多位数,即200244444个,A 是不是某个自然数B 的平方?如果是,写出B ;如果不是,请说明理由.【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 略【答案】2200242002444421111A ==⨯个个1.如果A 是某个自然数的平方,则20021111个1也应是某个自然数的平方,并且是某个奇数的平方.由奇数的平方除以4的余数是1知,奇数的平方减1应是4的倍数, 而200220011111111110-=个1个1不是4的倍数,矛盾,所以A 不是某个自然数的平方.【巩固】 A 是由2008个“4”组成的多位数,即4442008个4,A 是不是某个自然数B 的平方?如果是,写出B ;如果不是,请说明理由.【考点】完全平方数计算及判断 【难度】3星 【题型】解答 【解析】 略【答案】不是.24442111A ==⨯2008个12008个4假设A 是某个自然数的平方,则1112008个1也应是某个自然数的平方,并且是某个奇数的平方.由奇数的平方除以4的余数是1知,奇数的平方减1应是4的倍数,而11111110-=2008个12007个1不是4的倍数,与假设矛盾.所以A 不是某个自然数的平方.【例 6】 计算11112004个1-22221002个2=A ×A ,求A . 【考点】完全平方数计算及判断 【难度】4星 【题型】解答【解析】 此题的显著特征是式子都含有1111n 个1,从而找出突破口.11112004个1-22221002个2=11111002个100001002个0-11111002个1=11111002个1×(100001002个0-1) =11111002个1×(99991002个9)=11111002个1×(11111002个1×3×3)=2A所以,A =33331002个3.【答案】33331002个3【例 7】 ①22004420038444488889A =个个,求A 为多少?②求是否存在一个完全平方数,它的数字和为2005? 【考点】完全平方数计算及判断 【难度】4星 【题型】解答 【解析】 ① 本题直接求解有点难度,但是其数字有明显的规律,于是我们采用递推(找规律)的方法来求解: 注意到有2004420038444488889个个可以看成48444488889n 个n-1个,其中n =2004;寻找规律:当n =1时,有2497=;当n =2时,有2448967=;当n =3时,有2444889667= ……于是,类推有2004420038444488889个个=22003666667个方法二:下面给出严格计算: 2004420038444488889个个=4444400002004个2004个0+20048888个8+1;则4444400002004个2004个0+20048888个8+1=11112004个1×(4×0100002004个+8)+1=11112004个1×[4×(999992004个+1)+8]+1 =11112004个1×[4×(999992004个)+12]+1=2(1111)2004个1×36+12×11112004个1+1=2(1111)2004个1×36+2×(6×11112004个1)+1=22(666661)(66667)+=2004个62003个6② 由①知4444488889 n 个n-1个8=266667n-1个6,于是数字和为(4n +8n -8+9)=12n +1;令12n +1=2005解得n =167,所以4444488889 167个166个8=266667166个6。
所以存在这样的数,是4444488889 167个166个8【答案】(1)22003666667个,(2)4444488889 167个166个8=266667166个6模块二、平方数特征(1)平方数的尾数特征【例 8】下面是一个算式:112123123412345123456+⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯⨯+⨯⨯⨯⨯⨯,这个算式的得数能否是某个数的平方?【考点】平方数特征之平方数的尾数特征【难度】3星【题型】解答【关键词】华杯赛【解析】判断一个数是否是某个数的平方,首先要观察它的个位数是多少.平方数的个位数只能是0,1,4,5,6,9,而2,3,7,8不可能是平方数的个位数.这个算式的前二项之和为3,中间二项之和的个位数为0,后面二项中每项都有因子2和5,个位数一定是0,因此,这个0算式得数的个位数是3,不可能是某个数的平方.【答案】不是【例 9】一个数与它自身的乘积称为这个数的平方.各位数字互不相同且各位数字的平方和等于49的四位数共有________个.【考点】平方数特征之平方数的尾数特征【难度】4星【题型】填空【关键词】学而思杯,5年级,第10题【解析】4914925=+++,1,2,3,5全排列共有24个。
【答案】24【例 10】用1~9这9个数字各一次,组成一个两位完全平方数,一个三位完全平方数,一个四位完全平方数.那么,其中的四位完全平方数最小是.【考点】平方数特征之平方数的尾数特征【难度】5星【题型】填空【关键词】迎春杯,高年级,复试,11题【解析】四位完全平方数≥1234>352=1225,所以至少是362=1296.当四位完全平方数是1296时,另两个平方数的个位只能分别为4,5,个位为5的平方数的十位只能是2,但数字2在1296中已经使用.当四位完全平方数是372=1369时,另两个平方数的个位只能分别为4,5,个位为5的平方数的十位一样只能是2,还剩下7,8,而784恰好为282.所以,其中的四位完全平方数最小是1369.【答案】1369【例 11】称能表示成1+2+3+…+K的形式的自然数为三角数,有一个四位数N,它既是三角数,又是完全平方数,N= 。
