第一章热力学第一定律
第一章.热力学第一定律

1.4-2 可逆过程
一次(两次)压缩过程 环境对系统作的功 大于
一次(两次)膨胀过程 系统对环境作的功 原因:多作的功变成热传给了环境 对于准静态膨胀过程的逆过程:压缩可使系统 复原时,环境也同时恢复到原状。这种: 能通过原来过程的反方向而使系统和环境都同 时复原,不留下任何痕迹的过程称为可逆过程
z 可逆过程是一种理想过程,是对真实世 界的科学抽象 一些重要的热力学函数只有通过可逆过 程才能求得
热力学第二定律
开尔文(Lord Kelvin, 1824-1907,英) 1848 克劳修斯(Clausius,1822-1888 ,德)1850
z 构成了热力学的基础
z 人类经验总结,物理化学中最基本定律
z 有着极其牢固的实验基础,其结论具有 高度普遍性和可靠性
z 20世纪初建立了热力学第三定律
一些过程的设计与求算: 1. 理想气体等温过程
∆U =0 ∆H =0 Q=W (可由功求热)
z 等温可逆过程
∫ ∫ W = V2 PdV = V2 nRT dV =nRT ln V2 = Q
V1
V V1
V1
z 对抗恒外压 W= P外 ( V2- V1) = Q
2. 理想气体绝热过程 Q=0 ∆U= nCv.m∆T ∆H = nCp.m∆T W=-∆U(可由内能求功)
浴的温度发生变化即∆T=0, 由此可知
系统 无热传递 环境
Q=0
(2) 气体 向真空膨胀,P外=0, W膨=0
由第一定律则: ∆U=Q-W膨=0 此时:dU=(∂U/∂T)vdT + (∂U/∂V)TdV =0
因dT =0 (∂U/∂v)Tdv=0 但dv≠0 故 (∂U/∂v)T = 0 同理可证 (∂U/∂P)T = 0 即U=f(T)
第一章 热力学第一定律

对于单位质量工质,
wf pv
流动功是由泵或风机加给被输送工质并随 工质流动向前传递的一种能量,非工质本身具 有的能量。
40
二、开口系统的稳定流动能量方程 在 时间内,
进口质量 m1、 流 速 cf1、 标 高 z1
出口质量 m2、 流 速 cf2、 标 高 z2
稳定流动:
34
(2)示热图 在可逆过程中 单位质量工质与外 界交换的热量可以 用T-s 图(温熵图) 上过程曲线下的面 积来表示。 温熵图也称 示热图
q Tds
1 2
例1-5
35
§1-5
热力学第一定律及其解析式
一、热力学第一定律的实质
热力学第一定律实质就是热力过程中的 能量守恒和转换定律 ,可表述为 :
W pAdx pdV
对于可逆过程1~2: W
2 1
pdV
30
单位质量工质所作的膨胀功用符号w 表 示,单位为J/kg 或 kJ/kg。
w pdv
膨胀:dv > 0 , w > 0 压缩:dv < 0 , w < 0 (2) 示功图(p-v图) w的大小可以 pv 图上的过程曲线下 面的面积来表示 。 功是过程量而不 是状态量。
w pdv
1
2
31
二、热量与示热图
(1)热量 系统与外界之间依靠温差传递的能量称 为热量。符号:Q ;单位:J 或kJ。 单位质量工质所传递的热量用q 表示,单 位为 J/kg 或 kJ/kg。 热量正负的规定: 系统吸热:q > 0 ; 系统放热:q < 0 。 热量和功量都是系统与外界在相互作用的过 程中所传递的能量,都是过程量而不是状态量
第一章热力学第一定律

解:先求出两种状态下的始态和终态体积。再由恒压 先求出两种状态下的始态和终态体积。 体积功的计算方法计算体积功。 体积功的计算方法计算体积功。
V1=nRT1/p1=[2*8.314*300/(500*1000)]m3= 9.977*10-3m3 V2=nRT2/p2=[2*8.314*350/(500*1000)]m3= 1.164*10-2m3 恒压既p1=p2=pex W = -pex(V2-V1) = -[500*1000*(1.164*10-2-9.977*10-3)] = -832J
热量的符号: 热量的符号:Q 体系从环境吸热为Q>0,“+” 体系从环境吸热为 , 体系向环境放热为Q<0,“-” 体系向环境放热为 , 体系绝热,Q=0 体系绝热, 单位:国际单位( ), 焦耳( ), ),KJ 单位:国际单位(SI), 焦耳(J),
热容:一定量物质,温度升高 所吸收的 热容:一定量物质,温度升高1K所吸收的 热。 常用符号为C 常用符号为 摩尔热容:1mol物质的热容。 物质的热容。 摩尔热容: 物质的热容 表示符号为C 单位为J.mol-1.K-1 表示符号为 m,单位为 说明:热容为容量性质,随物质的量变化。 说明:热容为容量性质,随物质的量变化。 摩尔热容为强度性质, 摩尔热容为强度性质,其数值与温度 T有关。 有关。 有关
始态 终态 ——→ ( n,T1, P1, V1)——→ (n,T2, P2, V2) , , 途径 I 等T 等P ( n,T1, P2, V`2) , 途径 II
第一章 热力学第一定律

第一章 热力学第一定律
3.热力学能 热力学能:系统内部 能量的总和。符号U ,单位J 。它由多部 分组成: 分子的平动能、转动能、振动能、电子能、 原子核能及分子间 相互作用的势能。
一定量物质在确定状态,热力学能值为确定。但其绝对值是不 知道的。(如果对于某特定物质给予一个基准态,设该态 U=0,则可求得其它态的相对值)
系统分为:封闭系统、隔离系统和敞开系统。
隔离系统的例: 一个完好的热水 瓶:既不传热,也 无体积功与非体 积功的交换,且无 物质交换.
封闭系统的例: 一个不保温的热 水瓶:传热但无 物质交换;一个 汽缸:有功的交换, 但无物质交换.
敞开系统的例 :一个打开塞 子的热水瓶: 既有能量交换 ,又有物质交 换。
2
1.1 热力学概论
热力学的研究对象 热力学的方法和局限性 几个基本概念:(复习) •系统与环境
•系统的性质 •热力学平衡态
•状态函数
•状态方程
•过程和途径
1 热力学的研究对象 •研究热、功和其他形式能量之间的相互转换及
其转换过程中所遵循的规律。具体:
研究基础:热力学第一、二定律--人类长期 实践经验的总结。 研究内容: •研究各种物理变化和化学变化过程中所发生的 能量效应--热力学第一定律;
V=f(p,T)
例如,理想气体的状态方程可表示为:
pV=nRT
第一章 热力学第一定律—热力学基本概念
(2) 广度量和强度量
描述热力学系统的性质ቤተ መጻሕፍቲ ባይዱ为: 广度量(或广度性质):与物质的数量成正比的性质。如V,Cp ,
U,„等。它具有加和性。
强度量(或强度性质):与物质的数量无关的性质,如 p、T和组 成等。它不具有加和性。 两者的关系: 广度量与广度量的比是强度性质,例如,定压热容,Cp,为 广度量,物质的量n为广度量,摩尔定压热容Cp , m为强度量。
热力学第一定律
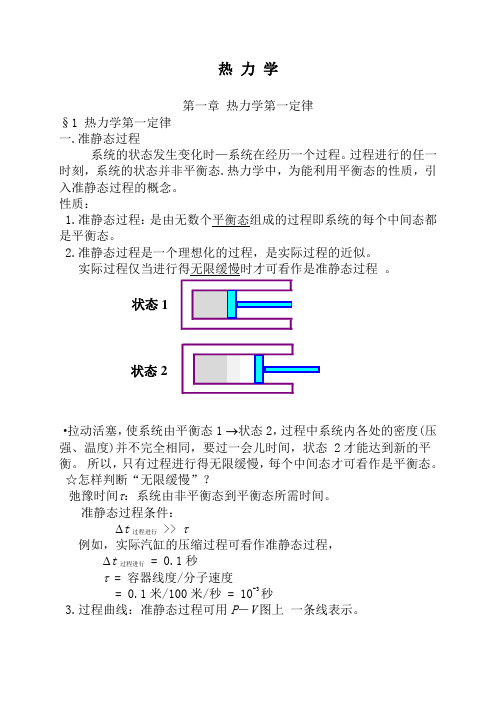
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻,系统的状态并非平衡态.热力学中,为能利用平衡态的性质,引入准静态过程的概念。
性质:1.准静态过程:是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程,是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞,使系统由平衡态1 →状态2,过程中系统内各处的密度(压强、温度)并不完全相同,要过一会儿时间,状态 2才能达到新的平衡。
所以,只有过程进行得无限缓慢,每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”?弛豫时间τ:系统由非平衡态到平衡态所需时间。
准静态过程条件: ∆t 过程进行 >> τ例如,实际汽缸的压缩过程可看作准静态过程, ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线:准静态过程可用P -V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内:(1)分子热运动的能量;(2)分子间势能和分子内的势能;(3)分子内部、原子内部运动的能量; (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体,内能一般是T 、V 或P 的函数; *对于理想气体,内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i :自由度; ν :摩尔数 ·通过作功改变系统内能的实质是:分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态,其条件是系统和外界的温度不同。
·传热的微观本质:是分子的无规则运动能量从高温物体向低温物体传递。
01章_热力学第一定律

U U U (T , p ) ; U ( T , V )
; U
U ( p ,V )
如果是 U U (T , p ) 全微分式: d U
0
六、热和功
1、热(heat) 系统与环境之间因温差而传递的能量称热, 从微观上看,热是体系分子无序热运动的能量交 换。用符号Q 表示,其微小量用 Q 表示。 Q的取号:系统吸热,Q>0 系统放热,Q<0
计算Q一定要与系统与环境之间发生热交换 的过程联系在一起,系统内部的能量交换不可能 是热。 热分类:显热、潜热(恒温恒压的相变过程)、 化学热。
3、相平衡(phase equilibrium) 多相共存时,各相的组成和数量不随时间而改变
4、化学平衡(chemical equilibrium ) 反应系统中各物的数量不再随时间而改变
三、状态函数 系统的一些性质,其数值仅取决于系统所处
的状态,而与பைடு நூலகம்统的历史无关;
它的变化值仅取决于系统的始态和终态,而
热和功的取号与热力学能变化的关系 系统吸热
Q>0 环境 U >0 系统
系统放热
Q<0 U <0 W<0 对环境作功
U = Q + W
W>0 对系统作功
例1:体系由A态变化到B态,沿途径Ⅰ放热100J, 对体系做功50J,问①由A态沿途经Ⅱ到B态,体系 做功80J,则Q为多少?②如果体系再由B态沿途经 Ⅲ回到A态,得功为50J,体系是吸热还是放热, Q为多少? Ⅱ Ⅰ A Ⅲ 系统变化框图
热力学第一定律
∂U ∂U dU = dT + dV ∂T V ∂V T
在焦耳实验中,dV>0,dT=0,dU=0,故有:
∂U =0 ∂V T
以T,p作为内能的独立变量,同理有:
∂U ∂p = 0 T
微观解释: 理想气体分子间无相互作用力,分子 间相互作用的势能为零。体积改变导致的 分子间距离的改变不影响内能的数值。理 想气体的内能只是指分子的动能,而动能 仅是温度的函数,所以理想气体的内能仅 是温度的函数。
积分表达式
Q=?
W=?
二、体积功、最大功与可逆过程
物理化学中,常见的功有: 体积功、电功、表面功等。 各种功的具体表达式可概括为两个因 子的乘积: 强度因子×容量性质的改变量
功的形式 机械功 体积功 电 功 表面功
强度因素 f(力)
容量性质的 改变量 dl(位移)
p(外压力) dV(体积改变) E(电位差) dQ(电量改变) σ(表面张力) dA(表面积改变)
→ δQ p = dU + d ( pV ) = d (U + pV ), Q p = ∆(U + pV )
δW '= 0 , p = pamb
说明: 热虽然不是状态函数,然而由上述两 式表明,当不同的途径均满足恒容非体积 功为零或恒压非体积功为零的特定条件 时,不同途径的热已经分别与过程的热力 学函数相等,因此不同途径的恒容热相 等,不同途径的恒压热相等,而不再与途 径有关。。
1.2热力学第一定律
一、热力学第一定律的表述 蒸汽机的广泛使用 如何少消耗燃料而获得更多能量? 热与机械功的关系
焦耳定律:1cal=4.184J(热功当量)
第一类永动机提出
第一章热力学第一定律章总结
第一章热力学第一定律本章主要公式及其使用条件一、热力学第一定律W Q U +∆= W Q dU δδ+=热力学中规定体系吸热为正值,体系放热为负值;体系对环境作功为负值,环境对体系作功为正值。
功分为体积功和非体积功。
二、体积功的计算体积功:在一定的环境压力下,体系的体积发生改变而与环境交换的能量。
体积功公式⎰⋅-=dV p W 外 1 气体向真空膨胀:W =0 2气体在恒压过程:)(12 21V V p dV p W V V --=-=⎰外外3理想气体等温可逆过程:2112ln lnp p nRT V V nRT W -=-= 4理想气体绝热可逆过程:)(12,T T nC W U m V -=∆=理想气体绝热可逆过程中的p ,V ,T 可利用下面两式计算求解1212,ln ln V V R T T C m V -=21,12,ln lnV V C p p C m p m V =三、热的计算热:体系与环境之间由于存在温度差而引起的能量传递形式。
1. 定容热与定压热及两者关系定容热:只做体积功的封闭体系发生定容变化时, U Q V ∆= 定压热:只做体积功的封闭体系定压下发生变化, Q p = ΔH定容反应热Q V 与定压反应热Q p 的关系:V p Q Q V p ∆+= nRT U H ∆+∆=∆n ∆为产物与反应物中气体物质的量之差。
或者∑+=RT g Q Q m V m p )(,,ν ∑+∆=∆RT g U Hm m)(ν式中∑)(g ν为进行1mol 反应进度时,化学反应式中气态物质计量系数的代数和。
2.热容 1.热容的定义式dTQ C δ=dT Q C VV δ=dT Q C pp δ=n CC VmV =,n C C p m p =, C V ,C p 是广度性质的状态函数,C V ,m ,C p,m 是强度性质的状态函数。
2.理想气体的热容对于理想气体 C p ,m - C V ,m =R 单原子理想气体 C V ,m = 23R ;C p ,m = 25R 双原子理想气体 C V ,m =25R ;C p ,m = 27R 多原子理想气体: C V ,m = 3R ;C p ,m = 4R通常温度下,理想气体的C V ,m 和C p,m 均可视为常数。
第一章 热力学第一定律
混合气体的分压和分体体积
分压定义:
pi = pyi
ECNU
yi ——混合 气体中i组分 摩尔分数
分体积定义:
i
pi pi yi p
Vi = Vyi
V V y V
i i i i
混合理想气体
混合理想气体的定义
ECNU
低压气体 实验
(1)满足pV = nRT 的状态方程; (2)用半透膜将两个混合理想气体隔开,不论气体组 成如何,能透过膜的组分在膜两边的分压相等。 混合理想气体中某组分的分压就是该组分分子碰撞 器壁产生的压力。
状态 状态函数
ECNU
异途同归
状态函数的特性
值变相等
周而复始
数值还原
状态函数在数学上具有全微分的性质。
状态函数的全微分性质
ECNU
状态函数是单值、连续、可微、可积的函数,在状态 图上是一条连续变化的平滑曲线。其全微分性质包括 : 2
(1)
z dz z2 z1
1
( 1 )状态函数的变化与积 分路线无关 ( 2 )在任意循环过程中状 态函数的变化值等于0 ( 3 )双变量体系状态函数 对两个状态参量的混合偏导 数与求导次序无关
强度性质是体系的内在性质,反映体系质的特征, 物理化学中有时体系的状态指的就是其强度性质。
广度性质与强度性质之间关系
ECNU
两个一次奇函数之比是一个零次奇
函数。因此体系某两个广度性质之比等
于体系的一个强度性质,例如
体积/物质的量=摩尔体积(Vm);
质量/体积=密度()
状态方程
ECNU
体系状态函数之间的定量关系式称为状态方程 (state equation )。 对于一定量的单组分均匀体系,状态函数T,p,V 之间有一定量的联系。经验证明,只有两个是独立 的,它们的函数关系可表示为: T=f(p,V) p=f(T,V) V=f(p,T) 例如,理想气体的状态方程可表示为: pV = nRT
第一章 热力学第一定律
1.1.2.3 过程和途径
1.过程:当体系的状态发生变化时,状态变 化的经过,强调变化的方式 2.途径:完成变化的具体步骤,强调经由路 径的不同
注: 过程和途径不是严格区分的两个概念, 不强调方式和路径的时候可通用
几种常见的过程
• 等/定温过程:体系始态、终态及过程中的温度等于环境 温度且为常数。 T始=T终=T体=T环=常数 • 等/定压过程:体系始态、终态及过程中的压力等于环境 压力且为常数。 p始=p终=p体=p环=常数 • 等/定容过程:在变化过程中,体系的容积始终保持不变。 V体=常数
二次恒外压压缩
体系返回原状态,体系虽然恢复原 态,但环境失去功,得到热
等温可逆膨胀
V2 WⅣ nRT ln V1
W WⅣ WⅣ 0 , 又U Q W 0, 则Q 0
等温可逆压缩 V1 WⅣ nRT ln V2
体系循原过程返回,不仅体系恢复原态,而且未给 环境留下功热转化的痕迹,即环境也恢复原状态
1.1.3.1 能量守恒定律
1840年左 右,焦耳 发现了热 功当量
1.1.3.1 能量守恒定律
热功当量
升高相同的温度
状态1 加热 W=0 状态2 热 功 当 量
Q=0
Q=0
机械功 电功
1.1.3.1 能量守恒定律
电量热法
1.1.3.1 能量守恒定律
机械量热法
1.1.3.1 能量守恒定律
到1850年,科学界公认能量守恒定律是自然界的普 遍规律之一。
1.1.3.3 “热一”数学表达 式
Q
W
W
U1
Q
U2
U2-U1 = Q+W
1.1.3.3 “热一”数学表达式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章热力学第二定律一、单选题1) 理想气体绝热向真空膨胀,则()A. ∆S = 0,∆W = 0B. ∆H = 0,∆U = 0C. ∆G = 0,∆H = 0D. ∆U =0,∆G =02) 对于孤立体系中发生的实际过程,下式中不正确的是()A. W = 0B. Q = 0C. ∆S > 0D. ∆H = 03) 理想气体经可逆与不可逆两种绝热过程,则()A. 可以从同一始态出发达到同一终态。
B. 不可以达到同一终态。
C. 不能确定以上A、B中哪一种正确。
D. 可以达到同一终态,视绝热膨胀还是绝热压缩而定。
4) 求任一不可逆绝热过程的熵变∆S,可以通过以下哪个途径求得?()A. 始终态相同的可逆绝热过程。
B. 始终态相同的可逆恒温过程。
C. 始终态相同的可逆非绝热过程。
D. B 和C 均可。
5) 在绝热恒容的系统中,H2和Cl2反应化合成HCl。
在此过程中下列各状态函数的变化值哪个为零?()A. ∆r HmB. ∆rUmC. ∆rSmD. ∆rGm6) 将氧气分装在同一气缸的两个气室内,其中左气室内氧气状态为p1=101.3kPa,V1=2dm3,T1=273.2K;右气室内状态为p2=101.3kPa,V2=1dm3,T2=273.2K;现将气室中间的隔板抽掉,使两部分气体充分混合。
此过程中氧气的熵变为: ( )A. ∆S >0B. ∆S <0C. ∆S =0D. 都不一定7) 1mol理想气体向真空膨胀,若其体积增加到原来的10倍,则体系、环境和孤立体系的熵变分别为:( )A.19.14J·K-1, -19.14J·K-1, 0B.-19.14J·K-1, 19.14J·K-1, 0C.19.14J·K-1, 0, 0.1914J·K-1D. 0 , 0 , 08) 1mol Ag(s)在等容下由273.2K加热到303.2K。
已知在该温度区间内Ag(s)的C v,m=24.48J·K-1·mol-1则其熵变为:( )A.2.531J·K-1B. 5.622J·K-1C. 25.31J·K-1D. 56.22J·K-19) 理想气体的物质的量为n,从始态A(p1,V1,T1)变到状态B(p2,V2,T2),其熵变的计算公式可用:( )A. ∆S =nR ln(p2/p1)+B. ∆S =nR ln(p1/p2)-C. ∆S =nR ln(V2/V1)+D. ∆S =nR ln(V2/V1)-10) 理想气体经历等温可逆过程,其熵变的计算公式是:( )A. ∆S =nRT ln(p1/p2)B. ∆S =nRT ln(V2/V1)C. ∆S =nR ln(p2/p1)D. ∆S =nR ln(V2/V1)11) 固体碘化银(AgI)有α和β两种晶型,这两种晶型的平衡转化温度为419.7K,由α型转化为β型时,转化热等于6462J·mol-1,由α型转化为β型时的熵变∆S 应为:( )A. 44.1JB. 15.4JC. -44.1JD. -15.4J12) 298K, p∅下,双原子理想气体的体积V1=48.91dm3,经等温自由膨胀到2V1,其过程的∆S为:( )A. 11.53J·K-1B. 5.765J·K-1C. 23.06J·K-1D. 013) 在标准压力下,90℃的液态水气化为90℃的水蒸汽,体系的熵变为:( )A.∆S体 >0B. ∆S体 <0C. ∆S体 =0D. 难以确定14) 在101.325kPa下,385K的水变为同温下的水蒸汽。
对于该变化过程,下列各式中哪个正确:( )A.∆S体+∆S环> 0B. ∆S体+∆S环 < 0C.∆S体+∆S环 = 0D. ∆S体+∆S环的值无法确定15) 在标准压力p∅和268.15K时,冰变为水,体系的熵变∆S体应:( )A. 大于零B. 小于零C. 等于零D. 无法确定16) 1mol理想气体从p1,V1,T1分别经:(1) 绝热可逆膨胀到p2,V2,T2;(2) 绝热恒外压下膨胀到p2′,V2′,T2′,若p2 = p2′则:( )A.T2′= T2, V2′= V2, S2′= S2B.T2′> T2, V2′< V2, S2′< S2C.T2′> T2, V2′> V2, S2′> S2D.T2′< T2, V2′< V2, S2′< S217) 理想气体在恒温条件下,经恒外压压缩至某一压力,此变化中体系的熵变∆S体及环境的熵变∆S环应为:( )A. ∆S体> 0, ∆S环< 0B. ∆S体 < 0, ∆S环 > 0C. ∆S体 > 0, ∆S环 = 0D. ∆S体< 0,∆S环= 018) 理想气体在绝热条件下,经恒外压压缩至稳定,此变化中的体系熵变∆S体及环境熵∆S环应为:( )A. ∆S体 > 0, ∆S环< 0B. ∆S体 < 0,∆S环 > 0C. ∆S体> 0, ∆S环= 0D. ∆S体< 0, ∆S环= 019) 在101.3kPa下,110℃的水变为110℃水蒸气,吸热Q p,在该相变过程中下列哪个关系式不成立?( )A. ∆S体 > 0B. ∆S环不确定C. ∆S体+∆S环 > 0D. ∆G体< 020) 一个由气相变为凝聚相的化学反应在恒温恒容下自发进行,问下列各组答案中哪一个是正确的:( )A. ∆S体> 0, ∆S环 < 0B. ∆S体 < 0, ∆S环 > 0C. ∆S体 < 0, ∆S环 = 0D. ∆S体> 0, ∆S环= 021) 1mol范德华气体从T1、V1绝热自由膨胀至T2、V2,设容热容C V为常数,则过程的熵变为:( )A.∆S = C V ln(T2/T1)B.∆S = nR ln[(V2-b)/(V1-b)]C.∆S = C V ln(T2/T1) + nR ln[(V2-b)/(V1-b)]D.∆S = 022) 263K的过冷水凝结成263K的冰,则:( )A. ∆S < 0B. ∆S > 0C. ∆S = 0D. 无法确定23) 理想气体由同一始态出发,分别经(1)绝热可逆膨胀;(2)多方过程膨胀,达到同一体积V2,则过程(1)的熵变∆S(1)和过程(2)的熵变∆S(2)之间的关系是:( )A.∆S(1) > ∆S(2)B.∆S(1) < ∆S(2)C.∆S(1) = ∆S(2)D.两者无确定关系24) 从多孔硅胶的强烈吸水性能说明在多孔硅胶吸水过程中,自由水分子与吸附在硅胶表面的水分子比较,两者化学势的高低如何?( )A. 前者高B. 前者低C. 相等D. 不可比较25) 一绝热容器分成两部分,分别置入同温同压的1molO2和3molN2(均为理想气体),抽去隔板使两气体混合达到平衡,则终态与始态热力学概率之比(Ω2/Ω1)为:( )A.exp(13.5×1023)B.exp(27.0×1023)C.exp(54.0×1023)D. exp(6.75×1023)26) 在300℃时,2mol某理想气体的吉布斯自由能G与赫姆霍兹自由能F的差值为:( )A. G-F = 1.247kJB. G-F = 2.494kJC. G-F = 4.988kJD. G-F = 9.977kJ27) 理想气体从状态I经自由膨胀到状态II,可用哪个热力学判据来判断该过程的自发性?( )A.∆HB.∆GC.∆S隔离D.∆U28) 理想气体从状态p1,V1,T等温膨胀到p2,V2,T,此过程的∆F与∆G 的关系为( )A. ∆F > ∆GB. ∆F < ∆GC. ∆F = ∆GD.无确定关系29) 在一简单的(单组分,单相,各向同性)封闭体系中,恒压只做膨胀功的条件下,吉布斯自由能值随自由能如何变化?( )A.(∂G/∂T)p > 0B. (∂G/∂T)p < 0C. (∂G/∂T)p =0D. 视具体体系而定30) 在标准压力p∅下,383.15K的水变为同温下的蒸汽,吸热Q p。
对于该相变过程,以下哪个关系式不能成立?( )A. ∆G < 0B.∆H = Q pC.∆S ise < 0D. ∆S ise > 031) 某气体的状态方程为p[(V/n)-b]=RT,式中b为常数,n为物质的量。
若该经一等温过程,压力自p1变至p2,则下列状态函数的变化,何者为零?( )A. ∆UB. ∆HC. ∆SD. ∆G32) 下列四个关系式中哪一个不是麦克斯韦关系式?( )A. (∂T/∂V)S = (∂V/∂S)pB. (∂T/∂p)S = (∂V/∂S)pC.(∂S/∂V)T =(∂p/∂T)V D. (∂S/∂p)T =-(∂V/∂T)p33) 在理想气体的S - T 图上,任一条恒容线与任一条恒压线的斜率之比,在恒温时的含义是:( )A.(∂S/∂T)V / (∂S/∂T)p= 0B. (∂S/∂T)V / (∂S/∂T)p = ∞C.(∂S/∂T)V / (∂S/∂T)p = C p/C VD.(∂S/∂T)V / (∂S/∂T)p = C p/C V34) 在下列状态变化中,哪些可以应用公式 d U =T d S - p d V ? ( )A.NO2气体缓慢膨胀,始终保持化学平衡NO2⇔ NO + (1/2)O2B.NO2气体以一定速度膨胀,解离出来的NO + (1/2)O2总是低于平衡组成C.SO3气体在不解离为SO2+ (1/2)O2的条件下膨胀D.水在-10℃时等温结冰35) 对临界点性质的下列描述中,哪一个是错误的:( )A.液相摩尔体积与气相摩尔体积相等B.液相与气相的界面消失C.气化热为零D.固,液,气三相共存36) 下述说法中哪一个正确?当温度恒定时:( )A.增加压力有利于液体变为固体B.增加压力不利于液体变为固体C.增加压力不一定有利于液体变为固体D.增加压力与液体变为固体无关37) 对于平衡态的凝聚相体系,压力p表示什么含义?( )A. 101.3kPaB. 外压C.分子间引力总和D.分子运动动量改变的统计平均值38) 用130℃的水蒸汽(蒸汽压2.7p∅)与1200℃的焦炭反应生成水煤气:( )C + H2O → CO + H2,如果通入的水蒸汽反应掉70%,问反应后混合气体中CO的分压是多少?设总压2.7p∅不变。
