专项练习二与圆有关的角
和圆有关的角(含答案)
OFE CBAOE DCBA和圆有关的角与圆有关的角我们学习了圆心角、圆周角、弦切角以及它们的大小与它们所对（或夹）的弧的度数之间的关系.角的顶点和边与圆位置关系在运动和变化过程中也可能形成另外的两种角.•如果角的顶点在圆内,则称这样的角为圆内角,如图1中所示的∠AEB 即为圆内角.圆内角的大小究竟与弧有何关系呢?延长AE 、BE 分别交圆于C 、D 两点,再连结AD,•则∠AEB=∠A+∠D.∵∠A 的度数等于12CD ,∠D 的度数等于12AB ,∴∠AEB 的度数等于12(•AB +CD ).即圆内角的度数等于它和它的对顶角所对的两弧度数和的一半,其中圆心角是特殊的圆内角.E DCBAEDCBA（1） (2)如果角的顶点在圆外,且角的两边都与同一个圆相交,则称这样的角为圆外角,•如图2所示,∠AEB 即为圆外角,圆外角又有什么性质呢?连结AD,则∠E=∠CAD-∠D,•∵∠CAD 的度数等于12CD ,∠D 的度数等于12AB ,∴∠E 的度数等于 12(CD -AB ).即圆外角的度数等于它所夹的两弧度数的差的绝对值的一半.圆心角、圆周角、弦切角、圆内角和圆外角，弧是联系它们的中介，即“由角看弧，由弧看角”是促使它们互相转化的基本方法。
例1 已知:如图,△ABC 内接于⊙O,∠A=60°,∠B=80°,E 是BC 上一点,F•是AC 的中点,求∠BEF 的度数.解析 ∵∠C=∠AEB,∠C=180°-(∠BAC+∠ABC)=180°-(60°+80°)=40°, ∴∠AEB=40°. ∵AF FC ,∴∠ABF=12∠ABC=40°. 又∵∠AEF=∠ABF=40°. ∴∠BEF=∠AEB+∠AEF=80°.点评若所求的角是与圆有关的角,如圆心角、圆周角、弦切角、•内接四边形的内角和外角，要设法利用相关的定理进行计算，若所求的角与圆无关，要设法转化为与圆有关的角去解决。
圆周角定理练习题
圆周角定理练习题在数学中，圆周角定理是一个非常重要的定理，它关于圆周角和圆心角的关系进行了阐述。
理解和掌握这个定理对于解决与圆相关的问题非常有帮助。
那么，现在我们来进行一些圆周角定理的练习题，以便加深对该定理的理解和运用能力。
练习题一：已知半径为r的圆上的弧AB所对的圆周角为θ，求弧AB的长度。
解答：根据圆周角定理可知，圆周角θ所对的弧的长度等于半径r乘以圆周角的弧度。
即弧AB的长度为rθ。
练习题二：已知弧CD的长度为s，求弧CD所对的圆周角。
解答：根据圆周角定理可知，弧CD所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题三：已知圆O的半径为r，圆弧AB所对的圆周角为θ，求圆O的周长。
解答：根据圆周角定理可知，圆周角θ所对的弧AB的长度为rθ。
因为圆O的周长等于圆周率π乘以直径d，而直径d等于半径r的两倍，所以圆O的周长为2πr。
练习题四：已知半径为r的圆上的弧AB的长度为s，求弧AB所对的圆周角。
解答：根据圆周角定理可知，弧AB所对的圆周角的弧度等于弧长s除以半径r。
即圆周角θ等于s/r。
练习题五：已知圆O的半径为r，圆上的弧AB所对的圆周角为θ，求弧AB所对的圆心角。
解答：根据圆周角定理可知，圆周角θ所对的圆心角的度数为360°乘以θ/2π。
通过以上练习题，我们可以更好地理解和应用圆周角定理。
掌握这个定理对于解决与圆有关的各种问题非常重要。
希望通过练习能够加深你对圆周角定理的理解，并培养你的数学思维和解题能力。
小升初专项练习几何图形圆与立体图形
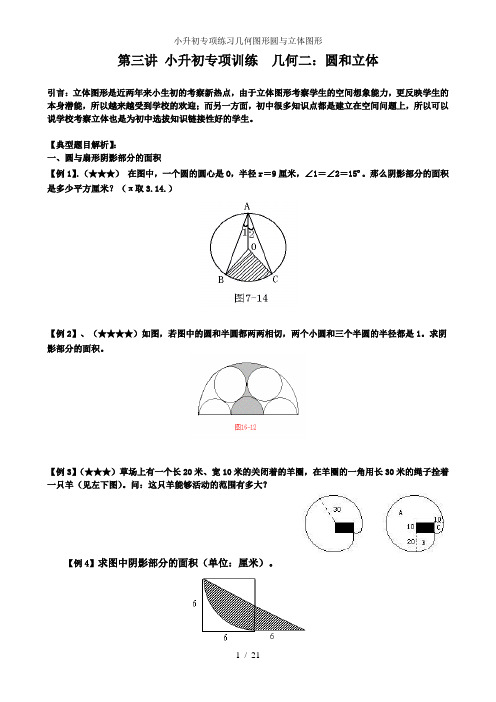
第三讲小升初专项训练几何二：圆和立体引言：立体图形是近两年来小生初的考察新热点，由于立体图形考察学生的空间想象能力，更反映学生的本身潜能，所以越来越受到学校的欢迎；而另一方面，初中很多知识点都是建立在空间问题上，所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
【典型题目解析】：一、圆与扇形阴影部分的面积【例1】．（★★★）在图中，一个圆的圆心是O，半径r＝9厘米，∠1＝∠2＝15º。
那么阴影部分的面积是多少平方厘米？（π取3.14.）【例2】、（★★★★）如图，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径都是1。
求阴影部分的面积。
【例3】（★★★）草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊（见左下图）。
问：这只羊能够活动的范围有多大？【例4】求图中阴影部分的面积（单位：厘米）。
【例5】求图中阴影部分的面积（单位：厘米）。
【分析】阴影部分通过翻折移动位置后，构成了一个新的图形（如图所示）。
从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半。
3.14×42×1/4－4×4÷2÷2＝8.56（平方厘米）【例6】如图19－10所示，两圆半径都是1厘米，且图中两个阴影部分的面积相等。
求长方形ABOO的面积。
1【分析】因为两圆的半径相等，所以两个扇形中的空白部分相等。
又因为图中两个阴影部分的面积相等，所以扇形的面积等于长方形面积的一半（如图19－10右图所示）。
所以 3.14×12×1/4×2＝1.57（平方厘米）【例7】如图所示，图中圆的直径AB是4厘米，平行四边形ABCD的面积是7平方厘米，∠ABC＝30度，求阴影部分的面积（得数保留两位小数）。
【分析】阴影部分的面积等于平行四边形的面积减去扇形AOC的面积，再减去三角形BOC的面积。
半径：4÷2＝2（厘米）扇形的圆心角：180－（180－30×2）＝60（度）扇形的面积：2×2×3.14×60/360≈2.09（平方厘米）三角形BOC的面积：7÷2÷2＝1.75（平方厘米）7－（2.09+1.75）＝3.16（平方厘米）【例8】如图所示，求图中阴影部分的面积。
圆心角与圆周角的专题练习
圆周角和圆心角的练习题一、选择题1．圆周角是24°，则它所对的弧是________ A．12°；B．24°；C．36°；D．48°．2．在⊙O中，∠AOB=84°，则弦AB所对的圆周角是________A．42°；B．138°；C．84°；D．42°或138°．3．如图，圆内接四边形ABCD的对角线AC，BD把四边形的四个角分成八个角，这八个角中相等的角的对数至少有___________．（）A．1对；B．2对；C．3对；D．4对．4．如图，AC是⊙O的直径，AB，CD是⊙O的两条弦，且AB∥C D．如果∠BAC=32°，则∠AOD=___[ ] A．16°；B．32°；C．48°；D．64°．二、计算题6．如图，AD是△ABC外接圆的直径，AD=6cm，∠DAC=∠AB C．求AC的长．7．已知：△DBC和等边△ABC都内接于⊙O，BC=a，∠BCD=75°（如图）．求BD 的长．8．如图，半圆的直径AB =13cm ，C 是半圆上一点，CD ⊥AB 于D ，并且CD =6cm ．求AD 的长．、9．如图，圆内接△ABC 的外角∠MAB 的平分线交圆于E ，EC =8cm ．求BE 的长．10．已知：如图，AD 平分∠BAC ，DE ∥AC ，且AB =a ．求DE 的长．11．如图，在⊙O 中，F ，G 是直径AB 上的两点，C ，D,E 是半圆上的三点，如果弧AC 的度数为60°，弧BE 的度数为20°，∠CFA =∠DFB ，∠DGA =∠EG B ．求∠FDG 的大小． 12．如图，⊙O 的内接正方形ABCD 边长为1，P 为圆周上与A ，B ，C ，D 不重合的任意点．求PA 2＋PB 2＋PC 2＋PD 2的值．13．如图，在梯形ABCD 中，AD ∥BC ，∠BAD =135°，以A 为圆心，AB 为半径作⊙A 交AD ，BC 于E ，F 两14．如图，⊙O 的半径为R ，弦AB =a ，弦BC ∥OA ，求AC 的长．15．如图，在△ABC 中，∠BAC ，∠ABC ，∠BCA 的平分线交△ABC 的外接圆于D ，E 和F ，如果，，分别为m °，n °，p °，求△ABC 的三个内角．16．如图，在⊙O 中，BC ，DF 为直径，A ，E 为⊙O 上的点，AB =AC ，EF =21DF ．求∠ABD +∠CBE 的值．17．如图，等腰三角形ABC 的顶角为50°，AB =AC ，以数．第二页18．如图，AB是⊙O的直径，AB=2cm，点C在圆周上，且∠BAC=30°，∠ABD=120°，CD⊥BD于D．求BD的长．19．如图，△ABC中，∠B=60°，AC=3cm，⊙O为△ABC的外接圆．求⊙O的半径．20．以△ABC的BC边为直径的半圆，交AB于D，交AC于E，EF⊥BC于F，AB=8cm，AE=2cm，BF∶FC=5∶1（如图）．求CE的长．21．已知等腰三角形的腰长为13cm，底边长为10cm，求它的外接圆半径．22．如图，△ABC中，AD是∠BAC的平分线，延长AD交△ABC的外接圆于E，已知AB=a，BD=b，BE=c．求AE的长．23．如图，△ABC中，AD是∠BAC的平分线，延长AD交△ABC的外接圆于E，已知AB=6cm，BD=2cm，BE=2．4cm．求DE的长．24．如图，梯形ABCD内接于⊙O，AB∥CD，的度数为60°，∠B=105°，⊙O的半径为6cm．求BC的长．25．已知：如图，AB是⊙O的直径，AB=4cm，E为OB的中点，弦CD⊥AB于E．求CD的长．26．如图，AB为⊙O的直径，E为OB的中点，CD为过E点并垂直AB的弦．求∠ACE 的度数．27．已知：如图，在△ABC 中，∠C =90°，∠A =38°，以C 为圆心，BC 为半径作圆，交AB 于D ，求的度数．第三页28．如图，△ABC 内接于圆O ，AD 为BC 边上的高．若AB =4cm ，AC =3cm ，AD =2．5cm ，求⊙O 的半径．29．设⊙O 的半径为1，直径AB ⊥直径CD ，E 是OB 的中点，弦CF 过E 点（如图），求EF 的长．30．如图，在⊙O 中直径AB ，CD 互相垂直，弦CH 交AB 于K ，且AB =10cm ，CH =8cm ．求BK ∶AK 的值．31．如图，⊙O 的半径为40cm ，CD 是弦，A 为的中点，弦AB 交CD 于F ．若AF =20cm ，BF =40cm ，求O 点到弦CD 的弦心距．32．如图，四边形ABCD 内接于以AD 为直径的圆O ，且AD =4cm ，AB =CB =1cm ，求CD 的长． 三、证明题33．如图，已知△ABC 内接于半径为R 的⊙O ，A 为锐角． 求证：ABCsin =2R34．已知：如图，在△ABC中，AD，BD分别平分∠BAC和∠ABC，延长AD交△ABC 的外接圆于E，连接BE．求证：BE=DE．35．如图，已知D为等边三角形ABC外接圆上的上的一点，AD交BC边于E．求证：AB为AD和AE的比例中项．36．已知：如图，在△ABC中，AB=AC，以AB为直径的圆交BC于D．求证：D为BC 的中点．第四页37．已知：如图，⊙O是△ABC的外接圆，AD⊥BC于D，AE平分∠BAC交⊙O于E．求证：AE平分∠OA D．38．已知：如图，△ABC的AB边是⊙O的直径，另两边BC和AC分别交⊙O于D，E 两点，DF⊥AB，交AB于F，交BE于G，交AC的延长线于H．求证：DF2=HF·GF．39．已知：如图，圆内接四边形ABCD中，BC=C D．求证：AB·AD+BC2=AC2．40．已知：如图，AB是半圆的直径，AC是一条弦，D是中点，DE⊥AB于E，交AC于F，DB交AC于G．求证：AF=FG．41．如图，AB是⊙O的弦，P是AB所对优弧上一点，直径CD⊥AB，PB交CD于E，延长AP交CD的延长线于F．求证：△EPF∽△EO A．42．已知：如图，AB是⊙O的直径，弦CD⊥AB于E，M为上一点，AM的延长线交DC于F．求证：∠AMD=∠FM C．43．已知：如图，AB，AC分别为⊙O的直径与弦，CD⊥AB于D，E为⊙O外一点，且AE=AC，BE交⊙O于F，连结ED，CF．求证：∠ACF=∠AE D．44．如图，⊙O的半径OD，OE分别垂直于弦AB和AC，连结DE交AB，AC于F，G．求证：AF2=AG2=DF·GE．45．如图，△ABC内接于圆，D是AB上一点，AD=AC，E是AC延长线上一点，AE=AB，连接DE交圆于F，延长ED交圆于G．求证：AF=AG．第五页46．已知：如图，⊙O的两条直径AB⊥CD，E是OD的中点，连结AE，并延长交⊙O 于M，连结CM，交AB于F．求证：OB=3OF．47．已知：如图，△ABC是等边三角形，以AC为直径作圆交BC于D，作DE⊥AC交圆于E．（1）求证：△ADE是等边三角形；（2）求S△ABC∶S△ADE．48．已知：如图，半径都是5cm的两等圆⊙O1和⊙O2相交于点A，B，过A作⊙O1的直径AC与⊙O2交于点D，且AD∶DC=3∶2，E为DC的中点．（1）求证：AC⊥BE；（2）求AB的长．一、填空题:1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.4.如图4,A 、B 、C 为⊙O 上三点，若∠OAB=46°,则∠ACB=_______度.BA(4) (5) (6)5.如图5,AB 是⊙O 的直径, BC BD ,∠A=25°,则∠BOD 的度数为________.第六页6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______. 二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对9.如图9,D 是AC 的中点,则图中与∠ABD 相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个 10.如图10,∠AOB=100°,则∠A+∠B 等于( ) A.100° B.80° C.50° D.40°11.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )A.40°B.50°C.70°D.110°三、解答题:13.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.A14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.15.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值.16.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.第七页17.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B，如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素) 18.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢?。
圆心角与弧弦的关系专项练习60题(有答案)ok
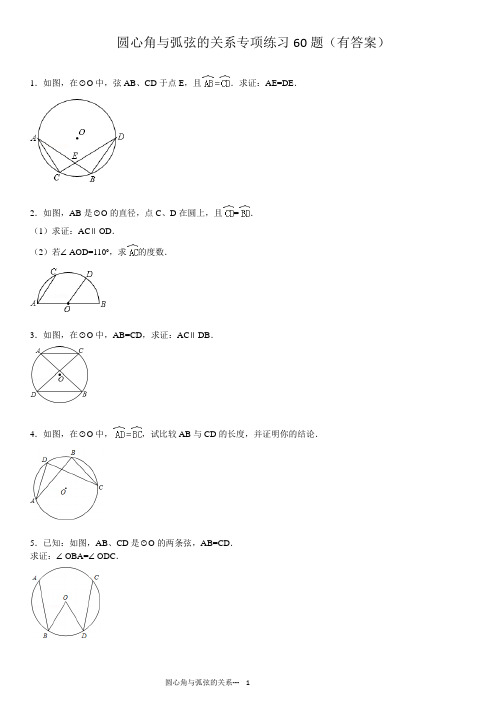
圆心角与弧弦的关系专项练习60题（有答案）1．如图，在⊙O中，弦AB、CD于点E，且．求证：AE=DE．2．如图，AB是⊙O的直径，点C、D在圆上，且=．（1）求证：AC∥OD．（2）若∠AOD=110°，求的度数．3．如图，在⊙O中，AB=CD，求证：AC∥DB．4．如图，在⊙O中，，试比较AB与CD的长度，并证明你的结论．5．已知：如图，AB、CD是⊙O的两条弦，AB=CD．求证：∠OBA=∠ODC．6．如图，在⊙O中，与相等，OD⊥BC，OE⊥AC，垂足分别为D、E，且OD=OE，那么△ABC是什么三角形，为什么？7．如图，在⊙O中，弦AB与弦CD相交于点E，且AB=CD．求证：BE=DE．8．如图，已知在⊙O中，∠ABD=∠CDB．（1）求证：AB=CD；（2）顺次连接ACBD四点，猜想得到的四边形是哪种特殊的四边形？并证明你的猜想．9．如图，在⊙O中，AD=BC．（1）比较与的长度，并证明你的结论；（2）求证：DE=BE．10．如图，点A、B、C、D在⊙O上，AB与OC、OD分别相交于E、F，AE=BF，说明AC=BD的理由．11．已知：⊙O中，OB、OC是半径，DF⊥OC于F，AE⊥OB于E，若AB=CD，求证：AE=DF．12．如图，⊙O中，弦AB=CD．求证：∠AOC=∠BOD．13．如图四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若再增加一个条件，就可使四边形ABCD成为等腰梯形，你所增加的条件是（只写出一个条件，图中不再增加其他的字母和线段．（给出证明）14．如图，D、E分别为⊙O半径OA、OB的中点，C是的中点，CD与CE相等吗？为什么？15．如图，平行四边形ABCD中，以A为圆心，AB为半径的圆分别交AD、BC于F、G，延长BA交圆于E．求证：=．16．如图，C是的中点，D、E分别是半径OA、OB上的点，且AD=BE．求证：∠CDO=∠CEO．17．如图，半径为2的⊙O内有互相垂直的两条弦AB、CD相交于P点．（1）求证：PA•PB=PC•PD；（2）若AB=8，CD=6，求OP的长．18．如图，M为⊙O上一点，弧MA=弧MB，MD⊥OA于D，ME⊥OB于E，求证：MD=ME．19．如图，OA、OB、OC都是⊙O的半径，∠AOB=2∠BOC．探索∠ACB与∠BAC之间的数量关系，并说明理由．20．如图，C是劣弧AB的中点，过点C分别作CD⊥OA，CE⊥OB，D、E分别是垂足，试判断CD、CE的大小关系，并证明你的结论．21．如图，Rt△ABC中，∠BAC=90°，CD是∠ACB的平分线，过A，C，D三点的圆与斜边BC交于点E，连接DE．（1）求证：AC=EC；（2）若AC=，△ACD外接圆的半径为1，求△ABC的面积．22．如图，已知∠APC=30°，的度数为30°，求和∠AEC的度数．23．如图，AD，BC是⊙O的两条弦，且AD=BC，求证：AB=CD．24．如图所示，M、N分别是⊙O的弦AB、CD的中点，AB=CD．求证：∠AMN=∠CNM．25．如图，⊙O中，C为的中点，CD⊥OA，CE⊥OB，求证：AD=BE．26．AB、CD为⊙O内两条相交的弦，交点为E，且AB=CD．则以下结论中：①AE=EC、②AD=BC、③BE=EC、④AD∥BC，正确的有_________．试证明你的结论．27．如图，，C、D分别是半径OA、OB的中点，连接PC、PD交弦AB于E、F两点．求证：（1）PC=PD；（2）PE=PF．28．已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．29．如图，D、E分别是⊙O的半径OA、OB的中点，点C是的中点．求证：CD=CE．30．如图，⊙O中两条不平行弦AB和CD的中点M，N．且AB=CD，求证：∠AMN=∠CNM．31．如图，AB，CD是⊙O的两条直径，过点A作AE∥CD交⊙O于点E，连接BD，DE，求证：BD=DE．32．已知：如图，A、B、C、D是⊙O上的点，∠1=∠2，AC=3cm．（1）求证：=；（2）求BD的长．33．如图，点A、B、C、D是直径为AB的⊙O上四个点，C是劣弧BD的中点，AC交BD于点E，AE=2，EC=1．（1）求证：△DEC∽△ADC；（2）试探究四边形ABCD是否是梯形？若是，请你给予证明并求出它的面积；若不是，请说明理由．34．已知：如图，AB是⊙O的直径，弦AD∥OC．求证：．35．如图，⊙O中，=，∠C=75°，求∠A的度数．36．如图，已知AB、CD为⊙O的两条弦，，求证：AB=CD．37．⊙O的一条弦AB分圆周长为3：7两部分，若圆的半径为4cm，试求：（1）优弧的长；（2）弦所对的圆周角的度数．38．如图⊙O中，AB、CD是两条直径，弦CE∥AB，弧EC的度数是40°，求∠BOD的度数．39．已知：如图，在⊙O中，弦AB和CD相交，连接AC、BD，且AC=BD．求证：AB=CD．40．已知如图所示，A，B，C是⊙O上三点，∠AOB=120°，C是的中点，试判断四边形OACB形状，并说明理由．41．如图，半径为2的半圆O中有两条相等的弦AC与BD相交于点P．（1）求证：PO⊥AB；（2）若BC=1，求PO的长．42．如图所示，在⊙O中，AB与CD是相交的两弦，且AB=CD，求证：．43．如图所示，以平行四边形ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，延长BA交⊙A于G，求证：．44．如图在⊙O中，AC=BC，OD=OE，求证：∠ACD=∠BCE．45．如图，AB是⊙O的直径，E是⊙O上的一点，的度数为40°，过点O作OC∥BE交⊙O于点C，求∠BCO 的度数．46．如图，A、B、C都是⊙O上的点，，CD⊥OA于D，CE⊥OB于E．求证：OD=OE．47．如图，在⊙O是中A、B、C、D在圆上，AD=BC．求证：BD=AC．48．如图，⊙O中，AB是直径，半径CO⊥AB，D是CO的中点，DE∥AB，求证：=2．49．如图所示，已知F是以O为圆心，BC为直径的半圆上任一点，A是弧BF的中点，AD⊥BC于点D，求证：AD=BF．50．如图，AB、AC、BC都是⊙O的弦，∠CAB=∠CBA，∠COB与∠COA相等吗？为什么？51．如图所示，⊙O中弦AB=CD，求证：．52．已知：如图，⊙O中弦AB=CD．求证：．53．如图所示，已知在⊙O中，半径OC垂直弦AB于D，证明：AC=BC．54．已知图所示，AB是半圆O的直径，，AB=4cm，求四边形ABCD的面积．55．如图所示，以等边三角形ABC的边BC为直径作⊙O交AB于D，交AC于E，判断，，之间的大小关系，并说明理由．56．已知：如图，在△ABC中，∠ACB=90°，∠B=25°，以点C为圆心、AC为半径作⊙C，交AB于点D，求的度数．57．已知如图所示，P为直径AB上一点，EF，CD为过点P的两条弦，且∠DPB=∠EPB；（1）求证：；（2）求证：CE=DF．58．如图，在⊙O中弦AB⊥CD于点E，过E作AC的垂线交BD于点Q，P为垂足，求证Q为BD的中点．59．如图所示，⊙O在△ABC三边截得的弦长相等，∠A=70°，求∠BOC．60．如图，AB为⊙O的直径，弦CD与AB的延长线交于点P，且DP=OB，若∠P=29°，求弧AC的度数．参考答案：1．方法一：连接AD，∵=∴AC=BD，∴∠BAD=∠CDA，∴AE=BE．方法二：∵=，∴﹣=﹣，=，∴AC=BD在△ACE与△DBE中，∵，∴△ACE≌△DBE（ASA），∴AE=DE．2．（1）证明：如图，连接AD．∵=，∴=2∴∠CAB=2∠DAB．又∵∠DOB=2∠DAB，∴∠CAB=∠DOB，∴AC∥OD；（2）解：如图，连接OC．∵∠AOD=110°，∴∠DOB=70°．又∵=，∴∠COD=∠DOB=70°，∴∠AOC=∠AOD﹣∠COD=110°﹣70°=40°，∴=40°．3．∵在⊙O中，AB=CD，∴=，∴﹣=﹣，即=，∴∠ACD=∠BDC，∴AC∥DB（内错角相等，两直线平行）．4．AB=CD．理由如下：∵，∴+=+，即=，∴AB=CD．5．过点O分别作OE⊥AB于点E，OF⊥CD于点F．∵AB=CD，∴OE=OF．又∵BO=DO，∴Rt△BOE≌Rt△DOF（HL），∴∠OBA=∠ODC．6．△ABC为等边三角形．理由如下：连OC，∵=，∴AB=BC，∵OD⊥BC，OE⊥AC，∴CE=AC，CD=BC，∠ODC=∠OEC=90°∵在Rt△ODC和Rt△OEC中，，∴Rt△ODC≌Rt△OEC（HL）∴CD=CE，∴BC=AC，∴AB=AC=CB，∴△ABC为等边三角形．7．先连接BC、AD，∵AB=CD，∴=，∵=，∴BC=AD，在△BEC与△DEA中，∵，∴△BEC≌△DEA（ASA），∴BE=DE．8．（1）证明：∵∠ABD=∠CDB，∴弧AD=弧BC，∴弧AD+弧AC=弧BC+弧AC，∴弧AB=弧CD，∴AB=CD；（2）四边形ACBD是等腰梯形．理由如下：如图，连AC，CB，AD，∵弧AD=弧BC，∴AD=CB，∠1=∠2，∴AC∥BD，且AC≠BD，∴四边形ACBD是等腰梯形．9．（1）∵AD=BC，∴=，∴=；（2）∵=，∴AB=CD，在△ADE与△CBE中，∵∠DAB=∠BCD，AD=BC，∠ADC=∠ABC，∴△ADE≌△CBE，∴DE=BE，∵AB=CD，∴DE=BE10．∵OA=OB（同圆的半径相等），∴∠A=∠B（等角对等边）．在△AOE和△BOF 中，，∴△AOE≌△BOF（SAS）…（1分）∴∠AOC=∠BOD（全等三角形对应角相等）．∴AC=BD（同圆中，相等的圆心角所对的弧相等）．11．连接OA、OD，∵AB=CD，∴∠AOB=∠COD，∵AE⊥OB，DF⊥OC，∴∠OEA=∠OFD=90°，又∵OA=OD，∴△AOE≌△DOF，∴AE=DF．12．∵弦AB=CD（已知），∴=；∴∠AOB=∠COD，∴∠AOB﹣∠BOC=∠COD﹣∠BOC，即∠AOC=∠BOD．13．添加的条件为=；证明：∵四边形ABCD是圆的内接四边形，∴∠A+∠C=180°；∵=，∴=；∴∠A=∠B；∴∠B+∠C=180°；∴AB∥CD；∵，∴AD=BC；又∵AB＞CD，∴四边形ABCD是等腰梯形．14．CD=CE，理由如下：（1分）连接OC，∵D、E分别为⊙O半径OA、OB的中点，∴OD=，，∵OA=OB，∴OD=OE，（2分）∵C 是的中点，∴，∴∠AOC=∠BOC，（4分）∴△DCO≌△ECO，（5分）∴CD=CE．（6分）故答案为：CD=CE．15．连接AG．∵A为圆心，∴AB=AG，∴∠ABG=∠AGB，（2分）∵四边形ABCD为平行四边形，∴AD∥BC，∠AGB=∠DAG，∠EAD=∠ABG，（4分）∴∠DAG=∠EAD，（5分）∴=．（6分）16．连接OC，∵OA=OB，又∵AD=BE，∴OD=OE，又∵∠AOC=∠BOC，∴OC=OC，∴△DOC≌△EOC（AAS）．∴∠CDO=∠CEO．17．（1）连接AD，BC，∵∠A、∠C所对的圆弧相同，∴∠A=∠C，∴Rt△APD∽Rt△CPB，∴，∴PA•PB=PC•PD；（2）作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，由垂径定理得：OM2=（2）2﹣42=4，ON2=（2）2﹣32=11，∵弦AB、CD互相垂直，∴∠DPB=90°，∵OM⊥AB于M，ON⊥CD于N，∴∠OMP=∠ONP=90°∴四边形MONP是矩形，∴OP=．18．连接MO（1分）∵∴∠MOD=∠MOE（4分）又∵MD⊥OA于D，ME⊥OB于E∴MD=ME（7分）19．∠ACB=2∠BAC．证明：∵∠ACB=∠AOB，∠BAC=∠BOC；又∵∠AOB=2∠BOC，∴∠ACB=2∠BAC．20．CD=CE…（1分）理由：连接CO．∵C是弧AB 的中点，∴=，∴∠COD=∠COE…（2分），∵CD⊥AO、CE⊥BO，∴∠CDO=∠CEO=90°…（3分），又∵CO=CO…（4分），∴△COD≌△COE…（5分），∴CD=CE…（6分）．21．（1）证明：∵∠BAC=90°，∴∠DEC=∠BAC=90°，又∵CD是∠ACB的平分线，∴∠ACD=∠ECD．∴∠ADC=∠EDC．∴．∴AC=EC．（2）解：∵∠BAC=90°，CD=2，AC=，∴AD=1．∴∠ACD=∠ECD=30°，∴∠ACB=60°．在Rt△ABC中，AB=AC•tan60°=3，又∵AC=，∴S△ABC =×3×=22．连接AC，∵=30°，∴∠1=∠2==15°，∵∠APC=30°，∠ADC是△APD的外角，∴∠ADC=∠1+∠APC=15°+30°=45°，∴=2ADC=90°；∵∠AEC是△CDE的外角，∴∠AEC=∠ADC+∠2=45°+15°=60°．故答案为：90°，60°．23．：∵AD=BC，∴弧AD=弧BC，∴弧AD+弧BD=弧BC+弧BD，即弧AB=弧CD．∴AB=CD24．连接OM、ON，∵O为圆心，M、N分别为弦AB、CD的中点，∴OM⊥AB，ON⊥CD．∵AB=CD，∴OM=ON．∴∠OMN=∠ONM．∵∠AMN=90°﹣∠OMN，∵∠CNM=90°﹣∠ONM，∴∠AMN=∠CNM．25．∵点C是的中点，∴∠AOC=∠BOC；∵CD⊥OA，CE⊥OB，∴∠ODC=∠OEC，又∵OC=OC，∴△COD≌△COE（AAS）．∴OD=OE，∵OA=OB，∴AD=BE．26．③BE=EC、④AD∥BC；∵AB=CD，∴弧AB=弧CD．∴弧AB﹣弧AD=弧CD﹣弧AD．即弧AC=弧BD．∴∠B=∠C．∴BE=EC．故③正确．由弧AC=弧BD得∠A=∠B，∴AD∥BC．故④正确．27．（1）连接PO，∵，∴∠POC=∠POD．∵C、D分别是半径OA、OB的中点，∴OC=OD．∵PO=PO，∴△PCO≌△PDO．∴PC=PD．（2）∵△PCO≌△PDO，∴∠PCO=∠PDO．∵OA=OB，∴∠A=∠B．∴∠AEC=∠BFD．∴∠PEF=∠PFE．∴PE=PF．28．∵AD=BC，∴．∴．∴．∴AB=CD．29．∵点C 是的中点，∴∠AOC=∠BOC；∵D、E分别是⊙O的半径OA、OB的中点，∴OD=OE=OA；又∵OC=OC，∴△COD≌△COE（SAS）．∴CD=CE．30．连OM，ON，如图，∵M，N分别为AB，CD的中点，∴OM⊥AB，ON⊥CD，∴∠AMO=∠CNO=90°，∵AB=CD，∴OM=ON，∴∠OMN=∠ONM，∴∠AMN=∠CNM．31．连接OE，如图，∵OA=OE，∴∠A=∠OEA，∵AE∥CD，∴∠BOD=∠A，∠DOE=∠OEA，∴∠BOD=∠DOE，∴BD=DE．32．（1）证明：∵∠1=∠2，∴=，∴+=+，∴=；（2）解：∵=，∴AC=BD，而AC=3cm，∴BD=3cm．33．（1）∵C为劣弧BD的中点，∴=，∴∠DAC=∠BAC，又∠DAC和∠BDC 对的弧都为，∴∠DAC=∠BDC．∴∠BAC=∠BDC，又∠DCA=∠DCA，∴△DEC∽△ADC．（2）由（1）知，△DEC∽△ADC，∴EC：DC=DC：AC．∴DC2=3，DC==BC．∵AB是直径，∴∠ACB=90°．在Rt△BCE中，CE=1，BC=，∴BE=2，∴∠CBE=30°，∴∠BAC=∠DAC=30°．∴劣弧BD的度数为2×2×30°=120°，劣弧AD的度数为60°．即∠DCA=30°=∠CAB．∴CD∥AB，且CD≠AB．∴四边形ABCD是上底为DC，下底为AB，高为直角三角形斜边AB边上的高的梯形．∵AC=AE+EC=3，BC=，根据勾股定理得AB=2，则∠CAB=30°，∴直角三角形斜边AB 边上的高为，∴S梯形ABCD ==．34．连接AC、OD．∵AD∥OC（已知），∴∠DAB=∠COB（两直线平行，同位角相等）；又∵∠CAB=∠COB（同弧所对的圆周角是所对的圆心角的一半），∴∠DAB=∠CAB（等量代换），∵∠DAC=∠CAB，∠DAC=∠DOC（同弧所对的圆周角是所对的圆心角的一半），∴∠DOC=∠COB（等量代换）∴．35．∵⊙O 中，=，∠C=75°，∴∠B=∠C=75°，∴∠A=180°﹣75°×2=30°36．∵，∴，即：，∴AB=CD．37．（1）弦AB分圆周长为3：7两部分，则分圆心角也为3：7两部分．故优弧的圆心角为360×∴优弧AB==cm；（3分）（2）弦AB所对圆周角也被分成了3：7两部分．弦AB所对圆周角的度数为180°．故分别为54°或126°．38．连接DE，∵DC是圆的直径，∴∠DEC=90°．∵弧EC的度数是40°，∴∠EDC=40°．∴∠ECD=50°．∵CE∥AB，∴∠AOD=∠ECD=50°．∴∠BOD=130°39．∵AC=BD，∴．∴．∴AB=CD．40．AOBC是菱形．证明：连OC∵C 是的中点∴∠AOC=∠BOC=×120°=60°∵CO=BO（⊙O的半径），∴△OBC是等边三角形∴OB=BC同理△OCA是等边三角形∴OA=AC又∵OA=OB∴OA=AC=BC=BO∴AOBC是菱形．41．（1）证明：连接AD．∵AB是直径，∴∠ACB=∠ADB=90°．∵AC=BD，AB=BA，∴△ABC≌△ABD．∴∠BAC=∠ABD，从而PA=PB．∵O是AB中点，∴PO⊥AB；（4分）（2）解：∵∠AOP=∠ACB=90°，∠OAP=∠CAB，∴△AOP∽△ACB．∴．∵AB=4，BC=1，∴AC==．∴OP==．42．在⊙O中，∵AB=CD，∴．∴．∴．43．连接AF，∵AB=AF，∴∠ABF=∠AFB．∵四边形ABCD是平行四边形，∴AD∥BC．∴∠DAF=∠AFB，∠GAE=∠ABF．∴∠GAE=∠EAF．∴．44．连接OC，∵AC=BC，∴∠AOC=∠BOC，∵在△AOC和△BOC中，，∴△AOC≌△BOC（SAS），∴∠A=∠B，∵OD=OE，∴AD=BE，∵在△ACD和△BCE中，，∴△ACD≌△BCE（SAS），∴∠ACD=∠BCE．45．连接OE，∵的度数为40°，∴∠BOE=40°，∵OB=OE，∴∠OBE=∠OEB=（180°﹣40°）÷2=70°，∵OC∥BE，∴∠C=∠1，∵CO=BO，∴∠2=∠C，∴∠1=∠2，∴∠BCO=∠1=∠OBE=35°46．∵，∴∠AOC=∠BOC，又∵CD⊥OA，CE⊥OB，∴∠CDO=∠CEO=90°，在△ODC和△OEC中，，∴△ODC≌△OEC（AAS），∴OD=OE．47．∵AD=BC，∴=，∴+=+，∴=，∴BD=AC．48．连接OE，∵AB⊥OC，DE∥AB，∴DE⊥OC，∴∠EDO=90°，∵D为OC中点，∴OD=OC=OE，∴∠DEO=30°，∴∠EOC=90°﹣30°=60°，∵OC⊥AB，∴∠AOC=90°，∴∠AOE=90°﹣60°=30°，即∠AOE=30°，∠COE=60°，∴=2（圆心角的度数等于它所对的弧的度数）．49．连接OA，交BF于点E，∵A是弧BF的中点，O为圆心，∴OA⊥BF，∴BE=BF，∵AD⊥BC于点D，∴∠ADO=∠BEO=90°，在△OAD与△OBE 中，，∴△OAD≌△OBE（AAS），∴AD=BE，∴AD=BF．50．∠COB=∠COA，理由是：∵∠CAB=∠CBA，∴AC=BC，∴弧AC=弧BC，∴∠COB=∠COA．51．连接AD，BD，CB，∵AB=CD，∴=，∴=，∴AD=BC．52．∵AB=CD，∴，∴﹣=﹣，∴．53．∵OC⊥AB，∴（垂径定理）．∴AC=BC（同圆中相等的弧所对的弦相等）54.∵，∴都为60°．连接DO，CO，∴∠AOD=∠DOC=∠BOC=60°．∴△AOD≌△DOC≌△COB．∴S△AOD =AO•ODsin60°=×22=．∴四边形ABCD面积为3．55．相等．如右图所示，连接OD，OE，∵OB=OD=OE=OC，∠B=∠C=60°∴△BOD与△COE都是等边三角形∴∠BOD=∠COE=60°∠DOE=180°﹣∠BOD﹣∠COE=60°∴∠DOE=∠BOD=∠COE∴56．解法一：（用垂径定理求）如图，过点C作CE⊥AB于点E ，交于点F，∴，又∵∠ACB=90°，∠B=25°，∴∠FCA=25°，∴的度数为25°，∴的度数为50°；解法二：（用圆周角求）如图，延长AC交⊙C于点E，连接ED，∵AE是直径，∴∠ADE=90°，∵∠ACB=90°，∠B=25°，∴∠E=∠B=25°，∴的度数为50°；解法三：（用圆心角求）如图，连接CD，∵∠ACB=90°，∠B=25°，∴∠A=65°，∵CA=CD，∴∠ADC=∠A=65°，∴∠ACD=50°，∴的度数为50°．圆心角与弧弦的关系--21 57．（1）作ON ⊥EF ，OM ⊥CD ，∵∠DPB=∠EPB ；∴ON=OM ，∴CD=EF ， ∴=，﹣=﹣， 即．；； （2）证明：∵∴CE=DF ．58．∵AB ⊥CD 于点E ，过E 作AC 的垂线交BD 于点Q ，∴三角形ACE 、三角形PCE 、三角形APE 、三角形BED 都是直角三角形．∴∠DEQ=∠CEP （对顶角相等）．∠CEP=∠A （同角的余角相等）．又∵∠A=∠D （同弧所对的圆周角相等），∴∠DEQ=∠D ，∴EQ=QD （等角对等边）． 又∵∠QEB=∠B （等角的余角相等），∴EQ=QB ．∴EQ=QD=QB ，即Q 为BD 的中点．59．过O 作OM ⊥AB ，ON ⊥AC ，OP ⊥BC ，垂足分别为M ，N ，P ，∵DE=FG=HI∴OM=OP=ON∴O 是∠B ，∠C 平分线的交点∵∠A=70°，∴∠B+∠C=180°﹣∠A=110°，又∵O 是∠B ，∠C 平分线的交点，∴∠BOC=180°﹣（∠B+∠C ）=180°﹣×110°=125°60．作直径DE ．∵OB=OD ，OB=PD ，∴DO=DP ，∵∠P=29°，∴∠DOP=∠DOP=29°=∠AOE ，∴弧AE 的度数是29°，∠CDE=∠P+∠DOP=58°， ∴弧CAE 的度数是2×58°=116°，∴弧AC 的度数是116°﹣29°=87°．。
新人教版九年级数学(上)——与圆有关的角(圆周角、圆心角)
OA BE FCD课前回顾1、垂径定理的概念及其推论：2、回顾练习：如图：AB 是的直径，CD 是弦，过A 、B 两点作CD 的垂线，垂足分别为E 、F ，若AB=10，AE=3，BF=5，求EC 的长。
知识点一、圆心角1、圆心角的定义：顶点在圆心的角叫做圆心角。
2、圆心角的度数与它所对的弧的度数之间的关系：圆心角的度数等于它所对弧的度数。
3、圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。
4、圆心角定理推论：在同圆或等圆中，两个圆心角、两条弦、两条弧、两条弦的弦心距中有一组量相等，其余各组量都相等。
例题讲练例题一、概念理解1．______________的______________叫做圆心角． 2．如图，若长为⊙O 周长的nm，则∠AOB =____________．与圆有关的角——圆心角、圆周角3．在同圆或等圆中，两个圆心角及它们所对的两条弧、两条弦中如果有一组量相等，那么_ _____________________．4．在圆中，圆心与弦的距离(即自圆心作弦的垂线段的长)叫做弦心距，不难证明，在同圆或等圆中，如果两条弦相等，那么它们的弦心距也______．反之，如果两条弦的弦心距相等，那么_____________________．5. 求证：在同圆或等圆中，两条弦相等，那么它们的弦心距也相等。
例题二、基础应用6．已知：如图，A、B、C、D在⊙O上，AB=CD．求证：∠AOC=∠DOB．7．已知：如图，P是∠AOB的角平分线OC上的一点，⊙P与OA相交于E，F点，与OB 相交于G，H点，试确定线段EF与GH之间的大小关系，并证明你的结论．8．如图，AB为⊙O的直径，C，D为⊙O上的两点，且C为的中点，若∠BAD=20°，求∠ACO的度数．例题三：综合应用9．⊙O中，M为的中点，则下列结论正确的是( )．A．AB>2AM B．AB=2AMC．AB<2AM D．AB与2AM的大小不能确定10．如图，⊙O中，AB为直径，弦CD交AB于P，且OP=PC，试猜想与之间的关系，并证明你的猜想．11．如图，⊙O中，直径AB=15cm，有一条长为9cm的动弦CD在上滑动(点C与A，点D与B不重合)，CF⊥CD交AB于F，DE⊥CD交AB于E．(1)求证：AE=BF；(2)在动弦CD滑动的过程中，四边形CDEF的面积是否为定值?若是定值，请给出证明并求这个定值；若不是，请说明理由．CAB1、圆周角的定义：顶点在圆上，两条边与圆相交的角叫做圆周角．2、圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等；都等于这条弧所对的圆心角的一半。
2022年中考数学大题圆证明切线的两种常用方法及专项练习题汇总
2022中考数学圆综合大题证明切线的两种常用方法类型1直线与圆有交点方法归纳：直线过圆上某一点，证明直线是圆的切线时，只需“连半径，证垂直，得切线”．“证垂直”时通常利用圆中的关系得到90°的角，如直径所对的圆周角等于90°等．【例1】如图，AB＝AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M.求证：DM与⊙O相切．1．(朝阳中考)如图，AB是⊙O的弦，OA⊥OD，AB，OD交于点C，且CD＝BD.(1)判断BD与⊙O的位置关系，并证明你的结论；(2)当OA＝3，OC＝1时，求线段BD的长．2．(德州中考)如图，已知⊙O的半径为1，DE是⊙O的直径，过D作⊙O的切线，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．(1)求AD的长；(2)BC是⊙O的切线吗？若是，给出证明，若不是，说明理由．3．(毕节中考)如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC＝FC.(1)求证：AC是⊙O的切线；(2)已知圆的半径R＝5，EF＝3，求DF的长．类型2不确定直线与圆是否有公共点方法归纳：直线与圆没有已知的公共点时，通常“作垂直，证半径，得切线”．证明垂线段的长等于半径常用的方法是利用三角形全等或者利用角平分线上的点到角的两边的距离相等．【例2】如图，AB＝AC，D为BC中点，⊙D与AB切于E点．求证：AC与⊙D相切．4．如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC 相切于点M，与AB，AD分别相交于点E，F.求证：CD与⊙O相切．5．如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE＝DC，以D为圆心，DB长为半径作⊙D，AB＝5，EB＝3.(1)求证：AC是⊙D的切线；(2)求线段AC的长．参考答案【例1】 证明：法一：连接OD.∵AB ＝AC ，∴∠B ＝∠C.∵OB ＝OD ，∴∠BDO ＝∠B.∴∠BDO ＝∠C.∴OD ∥AC.∵DM ⊥AC ，∴DM ⊥OD.∴DM 与⊙O 相切．法二：连接OD ，AD. ∵AB 是⊙O 的直径，∴AD ⊥BC.∵AB ＝AC ，∴∠BAD ＝∠CAD.∵DM ⊥AC ，∴∠CAD ＋∠ADM ＝90°.∵OA ＝OD ，∴∠BAD ＝∠ODA.∴∠ODA ＋∠ADM ＝90°.即OD ⊥DM ，∴DM 是⊙O 的切线．1.(1)连接OB ，∵OA ＝OB ，∴∠OAC ＝∠OBC.∵OA ⊥OD ，∴∠AOC ＝90°.∴∠OAC ＋∠OCA ＝90°.∵DC ＝DB ，∴∠DCB ＝∠DBC.∵∠DCB ＝∠ACO ，∴∠ACO ＝∠DBC.∴∠DBC ＋∠OBC ＝90°.∴∠OBD ＝90°.∵点B 是半径OB 的外端，∴BD 与⊙O 相切．(2)设BD ＝x ，则CD ＝x ，OD ＝x ＋1，OB ＝OA ＝3，由勾股定理得：32＋x 2＝(x ＋1)2.解得x ＝4.∴BD ＝4.2.(1)连接BD ，则∠DBE ＝90°.∵四边形BCOE 是平行四边形，∴BC ∥OE ，BC ＝OE ＝1.在Rt △ABD 中，C 为AD 的中点，∴BC ＝12AD ＝1.∴AD ＝2.(2)BC 是⊙O 的切线，理由如下：连接OB ，由(1)得BC ∥OD ，且BC ＝OD.∴四边形BCDO 是平行四边形．又∵AD 是⊙O 的切线，∴OD ⊥AD.∴四边形BCDO 是矩形．∴OB ⊥BC ，∴BC 是⊙O 的切线．3.(1)连接OA ，OD ，∵D 为BE 的下半圆弧的中点，∴∠FOD＝90°.∵AC＝FC，∴∠CAF＝∠AFC.∵∠AFC＝∠OFD，∴∠CAF＝∠OFD.∵OA＝OD，∴∠ODF＝∠OAF.∵∠FOD＝90°.∴∠OFD＋∠ODF＝90°.∴∠OAF＋∠CAF＝90°，即∠OAC＝90°.∴AC与⊙O相切．(2)∵半径R＝5，EF＝3，∴OF＝OE－EF＝5－3＝2.在Rt△ODF中，DF＝52＋22＝29.【例2】法一：连接DE，作DF⊥AC，垂足为F.∵AB是⊙D的切线，∴DE⊥AB.∵DF⊥AC，∴∠DEB＝∠DFC＝90°.∵AB＝AC，∴∠B＝∠C.∵BD＝CD，∴△BDE≌△CDF.∴DF＝DE.∴F在⊙D上．∴AC是⊙D的切线．法二：连接DE，AD，作DF⊥AC，F是垂足．∵AB与⊙D相切，∴DE⊥AB.∵AB＝AC，BD＝CD，∴∠DAB＝∠DAC.∵DE⊥AB，DF⊥AC，∴DE＝DF.∴F在⊙D上，∴AC与⊙D相切．4.证明：连接OM，过点O作ON⊥CD，垂足为N，∵⊙O与BC相切于M，∴OM⊥BC.∵正方形ABCD中，AC平分∠BCD，又∵ON⊥CD，OM⊥BC，∴OM＝ON.∴N在⊙O上．∴CD与⊙O相切．5.(1)证明：过点D作DF⊥AC于F.∵∠ABC＝90°，∴AB⊥BC.∵AD平分∠BAC，DF⊥AC，∴BD＝DF.∴点F在⊙D上．∴AC是⊙D的切线．(2)在Rt△BDE和Rt△FDC中，∵BD＝DF，DE＝DC，∴Rt△BDE≌Rt△FDC(HL)，∴EB＝FC.∵AB＝AF，∴AB＋EB＝AF＋FC，即AB＋EB＝AC，∴AC＝5＋3＝8.2022年中考数学复习专题---圆中阴影面积计算班级：___________姓名：___________学号：___________1．如图，直线y kx b=+经过点M(1，√3)和点N(1−，3√3)，A、B是此直线与坐标轴的交点．以AB为直径作⊙C，求此圆与y轴围成的阴影部分面积．2．如图，AAAA是⊙OO的直径，CC,DD是圆上两点，且有BD�=CCDD�，连结AADD,AACC，作DDDD⊥AACC的延长线于点DD．(1)求证：DDDD是⊙OO的切线；(2)若AADD=2√3,∠AADDDD=60∘，求阴影部分的面积．（结果保留ππ）3．如图，AAAA是圆OO的直径，AACC⊥AAAA，DD为圆OO上的一点，AACC=DDCC，延长CCDD交AAAA的延长线于点DD.(1)求证：CCDD为圆OO的切线.(2)若OOFF⊥AADD，OOFF=1，30∠=o，求圆中阴影部分的面积.(结果保留ππ)OAF4．如图，⊙OO是等边ΔAAAACC的外接圆，连接AAOO并延长至点PP，且AAAA=AAPP．（1）求证：PPAA是⊙OO的切线；（2）若AAAA=2√3，求图中阴影部分的面积．（结果保留ππ和根号）5．如图，OO为等边△AAAACC的外接圆，DD为直径CCDD延长线上的一点，连接AADD，AADD=AACC．（1）求证：AADD是⊙O的切线；（2）若CCDD=6，求阴影部分的面积．6．如图，AC为圆O的直径，弦AD的延长线与过点C的切线交于点B，E为BC中点，AC= 4√3，BC=4.（1）求证：DE为圆O的切线；（2）求阴影部分面积.7．已知AB是⊙O的直径，点C是圆O上一点，点P为⊙O外一点，且OP∥BC，∠P＝∠BAC．（1）求证：P A为⊙O的切线；（2）如果OP＝AB＝6，求图中阴影部分面积．8．如图，AAAA为⊙OO的直径，弦CCDD⊥AAAA，垂足为DD，CCDD=4√5，连接OOCC,OODD=2DDAA,FF为圆上一点，过点FF作圆的切线交AAAA的延长线于点GG，连接AAFF,AAFF=AAGG．（1）求⊙OO的半径；（2）求证：AAFF=FFGG；（3）求阴影部分的面积．9．如图，△ABC中，∠C=90º，∠ABC=2∠A，点O在AC上，OA=OB,以O为圆心，OC为半径作圆．（1）求证：AB是⊙O的切线；（2）若BC=3，求图中阴影部分的面积．10．如图，在△ABC中，∠CC=60∘，⊙OO是△ABC的外接圆，点P在直径BD的延长线上，且AB=AP．(1)求证：PA是⊙OO的切线；(2)若AB=2√3，求图中阴影部分的面积.(结果保留ππ和根号)11．如图，AB为圆O的直径，射线AD交圆O于点F，点C为劣弧BF的中点，过点C作CE⊥AD，垂足为E，连接AC(1)求证：CE是圆O的切线(2)若∠BAC＝30°，AB＝4，求阴影部分的面积12．如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD于G,OG:OC=3:5,AB=8.(1)求⊙O的半径；(2)点E为圆上一点,∠ECD=15º,将弧CE沿弦CE翻折,交CD于点F,求图中阴影部分的面积.13．如图，已知⊙O是△ABC的外接圆，AC是直径，∠A＝30°，BC＝4，点D是AB的中点，连接DO并延长交⊙O于点P．（1）求劣弧PC的长（结果保留π）；（2）过点P作PF⊥AC于点F，求阴影部分的面积（结果保留π）.14．如图，四边形ABCD内接于圆O，对角线AC是圆O的直径，DB平分∠ADC，AC长10cm．（1）求点O到AB的距离；（2）求阴影部分的面积．15．如图，在矩形ABCD中，AB=8cm，BC=4cm，以点A为圆心，AD为半径作圆与BA 的延长线交于点E，连接CE，求阴影部分的面积．16．如图，∠APB的平分线过点O，以O点为圆心的圆与PA相切于点C，DE为⊙O的直径．（1）求证：PB是⊙O的切线；（2）若∠CPO＝50°，∠E＝25°，求∠POD；（3）若⊙O的半径为2，CE＝2√3，求阴影部分的面积．17．如图，点P在圆O外，PA与圆O相切于A点，OP与圆周相交于C点，点B与点A 关于直线PO对称，已知OA=4，∠POA=60°求：（1）弦AB的长；（2）阴影部分的面积（结果保留π）．18．如图，⊙O是Rt△ABC的外接圆，直径AB＝4，直线EF经过点C，AD⊥EF于点D，∠ACD＝∠B．（1）求证：EF是⊙O的切线；（2）若AD＝1，求BC的长；（3）在（2）的条件下，求图中阴影部分的面积．。
人教版数学九年级上学期课时练习- 圆及有关概念(人教版)
专题24.2 圆及有关概念（专项练习）一、单选题1．如图所示，在⊙O 中，点A ，O ，D 以及点B ，O ，C 分别在一条直线上，则图中的弦有( )A ．2条B ．3条C ．4条D ．5条2．⊙O 的半径为5cm ，点A 到圆心O 的距离OA ＝3cm ，则点A 与⊙O 的位置关系为( ) A ．点A 在⊙O 上 B ．点A 在⊙O 内C ．点A 在⊙O 外D ．无法确定3．如图，一枚圆形古钱币的中间是一个正方形孔，已知圆的直径与正方形的对角线之比为3：1，则圆的面积约为正方形面积的（ ）A ．27倍B ．14倍C ．9倍D ．3倍4．把地球看成一个表面光滑的球体，假设沿地球赤道绕紧一圈钢丝，然后把钢丝加长，使钢丝圈沿赤道处处高出球面16cm ，那么钢丝大约需要加长A ．102cmB ．104cmC ．106cmD ．108cm5．在平面直角坐标系xOy 中，已知点A （4，3），以原点O 为圆心，5为半径作⊙O ，则（ ）A ．点A 在⊙O 上B ．点A 在⊙O 内C ．点A 在⊙O 外D ．点A 与⊙O 的位置关系无法确定6．已知,3,4ABC AC CB ==，以点C 为圆心r 为半径作圆，如果点A 、点B 只有一个点在圆内，那么半径r 的取值范围是（ ）A ．3r >B ．34r <<C ．34r <≤D ．34r ≤≤7．下列4个说法中：⊙直径是弦；⊙弦是直径；⊙任何一条直径所在的直线都是圆的对称轴；⊙弧是半圆； 正确的有（ ）A ．1个B ．2个C ．3个D ．4个8．一个圆的周长是10π，它的面积是（ ） A ．25πB ．5πC ．100πD ．10π9．矩形ABCD 中，AB ＝8，BC =P 在边AB 上，且BP ＝3AP ，如果圆P 是以点P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ）．A ．点B 、C 均在圆P 外；B ．点B 在圆P 外、点C 在圆P 内； C ．点B 在圆P 内、点C 在圆P 外；D ．点B 、C 均在圆P 内．10．若⊙O 的半径为5cm ，点A 到圆心O 的距离为4cm ，那么点A 与⊙O 的位置关系是A ．点A 在圆外B ．点A 在圆上C ．点A 在圆内D ．不能确定11．如图，四边形ABCD 为矩形，3AB =，4BC =．点P 是线段BC 上一动点，点M 为线段AP 上一点．ADM BAP ∠=∠，则BM 的最小值为（ ）A ．52B ．125C 32D 212．已知：等腰直角三角形ABC 的腰长为4，点M 在斜边AB 上，点P 为该平面内一动点，且满足PC ＝2，则PM 的最小值为（ ）A．2 B ．﹣2C ．D ．二、填空题13．已知O 的面积为25π．PO=，则点P在________；（1）若 5.5PO=，则点P在________；（2）若4（3）若PO=_________，则点P在O上．14．如图，⊙M的半径为4，圆心M的坐标为（5，12），点P是⊙M上的任意一点，P A⊙PB，且P A、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为_______．15．连接圆上任意两点的线段（如图中的______）叫做弦，经过圆心的弦（如图中的_____）叫做直径．【注意】凡直径都是弦，是圆中最长的弦，但弦____是直径．16．圆上任意两点间的部分叫做________，简称___．以A、B为端点的弧，记作__________，读作“圆弧AB”或“弧AB”．圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做_______．17．如图，以△ABC的顶点B为圆心，BA长为半径画弧，交BC于点D，连接AD．若⊙B＝40°，⊙C＝36°，则⊙DAC的大小为_____度．18．点P 是非圆上一点，若点P 到O 上的点的最小距离是4cm ，最大距离是9cm ，则O 的半径是______．19．如图，OA 、OB 是O 的半径，点C 在O 上，30AOB ∠=︒，40OBC ∠=︒，则OAC ∠=______︒．20．我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点(2,1)A 到以原点为圆心，以1为半径的圆的距离为_____．21．如图，用等分圆的方法，在半径为OA 的圆中，画出了如图所示的四叶幸运草，若OA ＝2，则四叶幸运草的周长是________．22．如图，在Rt ABC 中，⊙ACB=90°，AC=BC=2，以BC 为直径的半圆交AB 于D ，P是CD上的一个动点，连接AP，则AP的最小值是_____．23．如图,在△ABC中,⊙ACB=90°,AB=5,BC=3,P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是________．24．如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A，B，C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是__________．三、解答题25．如图所示，AC BC⊥，试证明：A、B、C、D在同一圆上．⊥，AD BD26．在平面直角坐标系中，作以原点O 为圆心，半径为4的O ，试确定点()2,3(4,2),,(A B C ----与O 的位置关系．27．如图，在图中求作⊙P ，使⊙P 满足以线段MN 为弦且圆心P 到⊙AOB 两边的距离相等．（要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔加黑）28．如图，点C 是以AB 为直径的半圆O 内任意一点，连接AC ，BC ，点D 在AC 上，且AD ＝CD ，请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．(1)在图（1）中，画出ABC 的中线AE ； (2)在图（2）中，画出ABC 的角平分线AF ．29．已知A 为O 上的一点，O 的半径为1，O 所在的平面上另有一点P ． （1）如果PA P 与O 有怎样的位置关系？（2）如果PA =P 与O 有怎样的位置关系？30．如图，菱形ABCD 的对角线,AC BD 相交于点O ，四条边,,,AB BC CD DA 的中点分别为,,,E F G H ．这四个点共圆吗？圆心在哪里？参考答案1．B 【分析】根据弦的定义进行分析，从而得到答案． 解：图中的弦有AB ，BC ，CE 共三条， 故选B ．【点拨】本题主要考查了弦的定义，熟知定义是解题的关键：连接圆上任意两点的线段叫弦．2．B解：将点到圆心的距离记为d ，圆的半径记为r ,⊙d =OA =3,⊙d <r ， ⊙点A 在圆内， 故选：B ． 3．B 【分析】设OB =x ，则OA =3x ，BC =2x ，根据圆的面积公式和正方形的面积公式，求出面积，进而即可求解．解：由圆和正方形的对称性，可知：OA =OD ，OB =OC ，⊙圆的直径与正方形的对角线之比为3：1， ⊙设OB =x ，则OA =3x ，BC =2x ， ⊙圆的面积=π(3x )2=9πx 2，正方形的面积=()2122x =2x 2， ⊙9πx 2÷2x 2=9142π≈，即：圆的面积约为正方形面积的14倍，故选B ．【点拨】本题主要考查圆和正方形的面积以及对称性，根据题意画出图形，用未知数表示各个图形的面积，是解题的关键．4．A解：设地球半径为：rcm ，则地球的周长为：2πrcm ，假设沿地球赤道绕紧一圈钢丝，然后把钢丝加长，使钢丝圈沿赤道处处高出球面16cm ，故此时钢丝围成的圆形的周长变为：2π（r+16）cm ，⊙钢丝大约需要加长：2π（r+16）﹣2πr≈100（cm ）=102（cm ）． 故选：A ． 5．A 【分析】先求出点A 到圆心O 的距离，再根据点与圆的位置依据判断可得．解：⊙点A （4，3）到圆心O 的距离5OA ，⊙OA ＝r ＝5， ⊙点A 在⊙O 上， 故选：A ．【点拨】本题考查了对点与圆的位置关系的判断．关键要记住若半径为r ，点到圆心的距离为d ，则有：当dr 时，点在圆外；当d r =时，点在圆上，当d r <时，点在圆内，也考查了勾股定理的应用．6．C 【分析】由于3AC =，4CB =，当以点C 为圆心r 为半径作圆，如果点A 、点B 只有一个点在圆内时，那么点A 在圆内，而点B 不在圆内．当点A 在圆内时点A 到点C 的距离小于圆的半径，点B 在圆上或圆外时点B 到圆心的距离应该不小于圆的半径，据此可以得到半径的取值范围．解：当点A 在圆内时点A 到点C 的距离小于圆的半径，即：3r >；点B 在圆上或圆外时点B 到圆心的距离应该不小于圆的半径，即：4r ； 即34r <． 故选：C ．【点拨】本题考查了点与圆的位置关系，解题的关键是明确半径的大小与位置关系的关系．7．B【分析】根据弧的分类、圆的性质逐一判断即可．解：⊙直径是最长的弦，故正确；⊙最长的弦才是直径，故错误；⊙过圆心的任一直线都是圆的对称轴，故正确；⊙半圆是弧，但弧不一定是半圆，故错误，正确的有两个，故选B．【点拨】本题考查了对圆的认识，熟知弦的定义、弧的分类是本题的关键．8．A【分析】根据圆的周长公式，由已知的周长求出圆的半径，利用圆的面积公式即可求出所求圆的面积．解：设圆的半径为r，⊙圆的周长为10π，⊙2πr=10π，即r=5，则圆的面积S=πr2=25π．故选：A．【点拨】此题考查了圆的周长公式，以及圆的面积公式，根据周长求出圆的半径是解本题的关键．同时要求学生熟练掌握圆中的有关计算公式．9．C解：⊙AB=8，点P在边AB上，且BP=3AP⊙AP=2，⊙根据勾股定理得出，，，⊙PB=6＜r，PC=9＞r⊙点B在圆P内、点C在圆P外,故选C．【点拨】点与圆的位置关系的判定，难度系数中等，此题应根据点与圆心之间的距离和圆的半径的大小关系作出判断10．C【分析】要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系；利用d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内判断出即可．解：⊙⊙O的半径为5cm，点A到圆心O的距离为4cm，⊙d＜r，⊙点A与⊙O的位置关系是：点A在圆内，故选C．11．D【分析】证明=90AMD︒∠，得出点M在O点为圆心，以AO为半径的园上，从而计算出答案．解：设AD的中点为O，以O点为圆心，AO为半径画圆⊙四边形ABCD为矩形⊙+=90BAP MAD︒∠∠⊙ADM BAP∠=∠⊙+=90MAD ADM︒∠∠⊙=90AMD︒∠⊙点M在O点为圆心，以AO为半径的园上连接OB交圆O与点N⊙点B为圆O外一点⊙当直线BM过圆心O时，BM最短⊙222 BO AB AO=+，1==22AO AD⊙29413 BO=+=⊙BO=⊙2BN BO AO=-=故选：D．【点拨】本题考查直角三角形、圆的性质，解题的关键是熟练掌握直角三角形和圆的相关知识．12．B【分析】根据等腰直角三角形的性质得到斜边AB＝，由已知条件得到点P在以C为圆心，PC为半径的圆上，当点P在斜边AB的中线上时，PM的值最小，于是得到结论．解：⊙等腰直角三角形ABC的腰长为4，⊙斜边AB＝⊙点P为该平面内一动点，且满足PC＝2，⊙点P在以C为圆心，PC为半径的圆上，当点P在斜边AB的中线上时，PM的值最小，⊙⊙ABC是等腰直角三角形，⊙CM＝1AB＝，2⊙PC＝2，⊙PM＝CM﹣CP＝﹣2，故选：B．【点拨】本题考查线段最小值问题，涉及等腰三角形的性质和点到圆的距离，解题的关键是能够画出图形找到取最小值的状态然后求解．13．圆外圆内5【分析】（1）先求出O的半径，再根据PO的长度和圆的半径进行比较即可得；（2）根据PO的长度和圆的半径进行比较即可得；（3）根据点在圆上得点到圆心的距离等于半径，即可得．解：设O的半径为r，225=，rππr，=5（1）⊙PO=5.5>5，⊙点P在圆外；（2）⊙PO=4<5，⊙点P在圆内；（3）若要点P在O上，则PO=r=5；故答案为：（1）圆外；（2）圆内；（3）5．【点拨】本题考查了点与圆的位置关系，解题的关键是判断点与圆的位置关系的方法．14．18【分析】△中AB＝2PO，若要使AB取得最小值，则PO 连接OP，因为P A⊙PB，所以在Rt APB需取得最小值，连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，据此求解即可得．解：如图所示，连接OP，⊙P A⊙PB，⊙⊙APB＝90°，⊙AO＝BO，⊙AB＝2PO，若要使AB取得最小值，则PO需取得最小值，连接OM，交⊙M于点P′，当点P位于P′位置时，OP′取得最小值，过点M作MQ⊙x轴于点Q，则OQ ＝5，MQ ＝12，在Rt MQB 中，根据勾股定理，得13OM =，又⊙MP ′＝4，⊙OP ′＝9，⊙AB ＝2OP ′＝18，故答案为：18．【点拨】本题考查了点与圆的位置关系，关于圆点对称的点的坐标和勾股定理，解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB 取得最小值时点P 的位置．15． AC AB 不一定略16． 圆弧 弧 AB 半圆略17．34【分析】先根据同圆的半径相等可得AB BD =，再根据等腰三角形的性质可得70BAD BDA ∠=∠=︒，然后根据三角形的外角性质即可得．解：由同圆的半径相等得：AB BD =，11(180)(18040)7022BAD BDA B ∴∠=∠=︒-∠=⨯︒-︒=︒， 36C ∠=︒，34DAC BDA C ∴∠=∠-∠=︒，故答案为：34．【点拨】本题考查了圆的性质、等腰三角形的性质等知识点，熟练掌握同圆的半径相等是解题关键．18．6.5cm 或2.5cm【分析】分点P 在O 外和O 内两种情况分析；设O 的半径为xcm ，根据圆的性质列一元一次方程并求解，即可得到答案．解：设O 的半径为xcm当点P 在O 外时，根据题意得：429x +=⊙ 2.5x cm =当点P 在O 内时，根据题意得：294x =+⊙ 6.5x cm =故答案为：6.5cm 或2.5cm ．【点拨】本题考查了圆、一元一次方程的知识；解题的关键是熟练掌握圆的性质，从而完成求解．19．25【分析】连接OC ，根据等腰三角形的性质和三角形内角和定理得到⊙BOC =100°，求出⊙AOC ，根据等腰三角形的性质计算．解：连接OC ，⊙OC =OB ，⊙⊙OCB =⊙OBC =40°，⊙⊙BOC =180°-40°×2=100°，⊙⊙AOC =100°+30°=130°，⊙OC =OA ，⊙⊙OAC =⊙OCA =25°，故答案为：25．【点拨】本题考查的是圆的基本性质、等腰三角形的性质，三角形内角和定理，掌握三角形内角和等于180°是解题的关键．201【分析】连接OA ，与圆O 交于点B ，根据题干中的概念得到点到圆的距离即为OB ，再求出OA ，结合圆O 半径可得结果.解：根据题意可得：点到圆的距离为：该点与圆上各点的连线中，最短的线段长度，连接OA，与圆O交于点B，可知：点A和圆O上点B之间的连线最短，⊙A（2，1），⊙圆O的半径为1，⊙AB=OA-1，⊙点(2,1)A到以原点为圆心，以11，1.【点拨】本题考查了圆的新定义问题，坐标系中两点之间的距离，勾股定理，解题的关键是理解题意，利用类比思想解决问题.21．．【分析】由题意得出：四叶幸运草的周长为4个半圆的弧长=2个圆的周长，求出圆的半径，由圆的周长公式即可得出结果．解：由题意得：四叶幸运草的周长为4个半圆的弧长＝2个圆的周长，⊙四叶幸运草的周长＝π×2＝；故答案为．【点拨】本题考查了正多边形和圆、正方形的性质以及圆周长公式；由题意得出四叶幸运草的周长=2个圆的周长是解题的关键．221.【分析】找到BC 的中点E ，连接AE ，交半圆于P 2，在半圆上取P 1，连接AP 1，EP 1，可见，AP 1+EP 1＞AE ，即AP 2是AP 的最小值，再根据勾股定理求出AE 的长，然后减掉半径即可．解：找到BC 的中点E ，连接AE ，交半圆于P 2，在半圆上取P 1，连接AP 1，EP 1，可见，AP 1+EP 1＞AE ，即AP 2是AP 的最小值，⊙AEP 2E =1，⊙AP 21.1.23．1试题分析：在Rt⊙ABC 中，由勾股定理可知：，由轴对称的性质可知：BC=CB′=3，⊙CB′长度固定不变，⊙当AB′+CB′有最小值时，AB′的长度有最小值．根据两点之间线段最短可知：A 、B′、C 三点在一条直线上时，AB′有最小值，⊙AB′=AC ﹣B′C=4﹣3=1．故答案为1．【点拨】1．翻折变换（折叠问题）；2．动点型；3．最值问题；4．综合题．24．35r <<.试题分析：根据勾股定理可求得BD=5，三个顶点A 、B 、C 中至少有一个点在圆内,点A 与点D 的距离最近，点A 应该在圆内，所以r>3，三个顶点A 、B 、C 中至少有一个点在圆外，点B 与点D 的距离最远，点B 应该在圆外，所以r<5，所以r 的取值范围是35r <<.【点拨】勾股定理；点和圆的位置关系.25．见分析【分析】利用直角三角形斜边上的中线等于斜边的一半，得出AE BE CE DE ===进而得出答案．解：如图，取AB 的中点E ，连接CE ，DE ，⊙AC BC ⊥，AD BD ⊥，⊙ABC 和ABD △为直角三角形， ⊙12CE AB AE BE ===，12DE AB =， ⊙AE BE CE DE ===，⊙A ，B ，C ，D 四点都在以点E 为圆心，AE 长为半径的圆上．【点拨】本题主要考查了四点共圆和直角三角形的性质，得出AE BE CE DE ===是解题的关键．26．点A 在O 内；点B 在O 外；点C 在O 上．【分析】连接OA 、OB 、OC ，根据点的坐标，分别求出OA 、OB 、OC 的长，和⊙O 的半径4比较即可得出答案．解：连接OA 、OB 、OC ，⊙()2,3A --，由勾股定理得 OA =4，⊙点A 与O 的位置关系是点A 在O 内；⊙(4,2)B -，由勾股定理得OB=4，⊙点B与O的位置关系是点B在O外；⊙(2)C-，由勾股定理得OC4=4，⊙点C与O的位置关系是点C在O上．【点拨】本题考查了点与圆的位置关系，勾股定理．点与圆的位置关系有三种：⊙当d=r 时，点在圆上；⊙当d>r时，点在圆外；⊙当d<r时，点在圆内．27．见分析．试题分析：先做出⊙AOB的角平分线，再求出线段MN的垂直平分线就得到点P．试题解析：【点拨】尺规作图角平分线和线段的垂直平分线、圆的性质．28．(1)见分析(2)见分析【分析】（1）连接CO、BD，CO交BD于点G，连接AG并延长交BC于E，线段AE即为所求作；（2）利用（1）的中点E，过点E作半径OH，连接AH交BC于点F，则线段AF即为所求作．(1)解：如图（1），线段AE即为△ABC的中线；；根据三角形三条中线交于一点即可证明；(2)解：如图（2），线段AF即为△ABC的角平分线；证明：⊙OA=OH，⊙⊙HAO=⊙H，⊙点O是AB的中点，点E是BC的中点，⊙OE是⊙ABC的中位线，⊙OE⊙AC，⊙⊙CAH=⊙H，⊙⊙CAF=⊙BAF，⊙AF为⊙ABC的角平分线．【点拨】本题考查了作图-复杂作图，三角形中位线定理，三角形三条中线交于一点，圆的半径相等，等边对等角，平行线的性质，解题的关键是灵活运用所学知识解决问题．29．（1）点P在O外；（2）点P可能在O外，也可能在O内，还可能在O上，实际上，点P位于以A【分析】（1）点P和圆的位置关系有：⊙在圆外，⊙在圆上，⊙在圆内，再逐个判断即可；（2）点P和圆的位置关系有⊙在圆外，⊙在圆上，⊙在圆内，再逐个判断即可．解：（1）5PA=O的直径为2∴点P的位置只有一种情况在圆外，即点P与O的位置关系是点在圆外．（2）3PA=O的直径为2∴点P的位置有三种情况：⊙在圆外，⊙在圆上，⊙在圆内．即点P可能在O外，也可能在O内，还可能在O上，实际上，点P位于以A为圆【点拨】本题考查了圆的认识的应用，解题的关键是做注意多种情况的考虑，注意：点和圆有三种位置关系：点在圆外，点在圆上，点在圆内．30．共圆，圆心在点O处【分析】根据三角形中位线的性质，证出四边形EFGH是平行四边形，根据菱形性质证出四边形EFGH是矩形，根据矩形性质可得E，F，G，H到矩形中心的距离相等，从而得出结论．解：点E，F，G，H四点共圆，圆心在点O处．理由如下：连接HE，EF，FG，GH，OH，OE，OF，OG．⊙E，F，G，H分别是AB，BC，CD，DA的中点，⊙EF平行且等于12AC, HG平行且等于12AC，⊙EF平行且等于GH⊙四边形EFGH是平行四边形，////,HE GF BD∴又⊙四边形ABCD是菱形⊙AC BD⊥⊙⊙AOB＝90°∴⊙HEF＝90°，⊙四边形EFGH是矩形，⊙E，F，G，H到矩形中心的距离相等⊙这个矩形的四个顶点在同一个圆上，圆心即为点O．【点拨】考核知识点：点和圆的位置关系．理解矩形、菱形的判定和性质和点和圆的位置关系是解题关键．。
与圆有关的角(解析版)
专题08 与圆有关的角知识网络重难突破知识点一圆心角1.圆心角：顶点在圆心的角叫做圆心角.圆心角的度数等于它所对的弧的度数．2.圆心角性质定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各组量都相等．【典例1】（2020•项城市三模）如图，圆O通过五边形OABCD的四个顶点．若＝150°，∠A＝75°，∠D＝60°，则的度数为何？（）A．25°B．40°C．50°D．60°【点拨】连接OB，OC，由半径相等得到△OAB，△OBC，△OCD都为等腰三角形，根据∠A＝75°，∠D＝60°，求出∠1与∠2的度数，根据的度数确定出∠AOD度数，进而求出∠3的度数，即可确定出的度数．【解析】解：连接OB、OC，∵OA＝OB＝OC＝OD，∴△OAB、△OBC、△OCD，皆为等腰三角形，∵∠A＝75°，∠D＝60°，∴∠1＝180°﹣2∠A＝180°﹣2×75°＝30°，∠2＝180°﹣2∠D＝180°﹣2×60°＝60°，∵＝150°，∴∠AOD＝150°，∴∠3＝∠AOD﹣∠1﹣∠2＝150°﹣30°﹣60°＝60°，则的度数为60°．故选：D．【点睛】此题考查了圆心角、弧、弦的关系，多边形内角与外角，弄清圆心角、弧、弦的关系是解本题的关键．【变式训练】1．（2019秋•鹿城区月考）一个圆的内接正多边形中，一边所对的圆心角为72°，则该正多边形的边数是（）A．6 B．5 C．4 D．3【点拨】根据正多边形的中心角＝计算即可．【解析】解：设正多边形的边数为n．由题意＝72°，∴n＝5，故选：B．【点睛】本题考查正多边形的有关知识，解题的关键是记住正多边形的中心角＝．2．（2019秋•余杭区期中）如图，在△ABC中，∠C＝90°，的度数为α，以点C为圆心，BC长为半径的圆交AB于点D，交AC于点E，则∠A的度数为（）A．45°﹣αB．αC．45°+αD．25°+α【点拨】连接OD，求得∠DCE＝α，得到∠BCD＝90°﹣α，根据等腰三角形的性质和三角形的内角和即可得到结论．【解析】解：连接OD，∵的度数为α，∴∠DCE＝α，∵∠ACB＝90°，∴∠BCD＝90°﹣α，∵BC＝DC，∴∠B＝（180°﹣∠BCD）＝（180°﹣90°+α）＝45°+α，∴∠A＝90°﹣∠B＝45°﹣α，故选：A．【点睛】本题考查了圆心角，弧，弦，直角三角形的性质，等腰三角形的性质，正确的作出辅助线是解题的关键．3.（2019秋•鄞州区期末）如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AC＝12，AE＝3，则⊙O的直径长为（）A．10 B．13 C．15 D．16【点拨】连接OF，首先证明AC＝DF＝12，设OA＝OF＝x，在Rt△OEF中，利用勾股定理构建方程即可解决问题．【解析】解：如图，连接OF．∵DE⊥AB，∴DE＝EF，＝，∵点D是弧AC的中点，∴＝，∴＝，∴AC＝DF＝12，∴EF＝DF＝6，设OA＝OF＝x，在Rt△OEF中，则有x2＝62+（x﹣3）2，解得x＝，∴AB＝2x＝15，故选：C．【点睛】本题考查垂径定理，圆心角，弧，弦之间的关系等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．4．（2019春•西湖区校级月考）如图，AB是⊙O的直径，M、N分别是AO，BO的中点，CM⊥AB，DN⊥AB，则的度数60°．【点拨】根据圆心角、弧、弦的关系和含30°的直角三角形的性质解答．【解析】解：∵AB是⊙O的直径，M、N分别是AO，BO的中点，∴2OM＝OC，2ON＝OD，∵CM⊥AB，DN⊥AB，∴∠CMO＝∠DNO＝90°，∴∠MCO＝∠NDO＝30°，∴∠MOC＝∠NOD＝60°，∴∠COD＝180°﹣60°﹣60°＝60°，∴的度数是60°，故答案为：60°【点睛】此题考查圆心角、弧、弦，关键是根据圆心角、弧、弦的关系和含30°的直角三角形的性质解答．5.（2018秋•丽水期中）如图，已知OA、OB、OC是⊙O的三条半径，点C是弧AB的中点，M、N分别是OA、OB的中点．求证：MC＝NC．【点拨】根据弧与圆心角的关系，可得∠AOC＝∠BOC，又由M、N分别是半径OA、OB的中点，可得OM＝ON，利用SAS判定△MOC≌△NOC，继而证得结论．【解析】证明：∵弧AC和弧BC相等，∴∠AOC＝∠BOC，又∵OA＝OB，M、N分别是OA、OB的中点∴OM＝ON，在△MOC和△NOC中，，∴△MOC≌△NOC（SAS），∴MC＝NC．【点睛】此题考查了弧与圆心角的关系以及全等三角形的判定与性质；证明三角形全等是解决问题的关键．知识点二圆周角1.圆周角：顶点在圆上，两边分别和圆相交的角叫做圆周角．圆周角的度数等于它所对弧上的圆心角度数的一半．2.圆周角性质定理：一条弧所对的圆周角等于它所对的圆心角的一半．推论1：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．推论2：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．【典例2】（2019秋•义乌市期末）如图，已知AB为半圆O的直径，AC，AD为弦，且AD平分∠BAC．（1）若∠ABC＝28°，求∠CBD的度数；（2）若AB＝6，AC＝2，求AD的长．【点拨】（1）利用圆周角定理得到∠C＝∠ADB＝90°，则根据互余计算出∠CAB＝62°，再根据角平分线的定义得到∠CAD＝∠CAB＝31°，然后根据圆周角定理得到∠CBD的度数；（2）连接OD交BC于E，如图，先利用勾股定理计算出BC＝4，由∠CAD＝∠BAD得到＝，根据垂径定理得到OD⊥BC，BE＝CE＝BC＝2，则OE＝1，然后根据勾股定理计算出BD，接着计算出AD．【解析】解：（1）∵AB是⊙O的直径，∴∠C＝∠ADB＝90°，∴∠CAB＝90°﹣28°＝62°，∵AD平分∠BAC，∴∠CAD＝∠CAB＝31°，∴∠CBD＝∠CAD＝31°；（2）连接OD交BC于E，如图，在Rt△ACB中，BC＝＝4，∵AD平分∠BAC，∴∠CAD＝∠BAD，∴＝，∴OD⊥BC，∴BE＝CE＝BC＝2，∴OE＝AC＝×2＝1，∴DE＝OD﹣OE＝3﹣1＝2，在Rt△BDE中，BD＝＝2，在Rt△ABD中，AD＝＝2．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．【变式训练】1．（2019秋•海曙区期末）如图，点A，B，C，D在⊙O上，AC是⊙O的直径，若∠CAD＝25°，则∠ABD 的度数为（）A．25°B．50°C．65°D．75°【点拨】先根据圆周角定理得到∠ADC＝90°，∠ABD＝∠ACD，然后利用互余计算出∠ACD，从而得到∠ABD的度数．【解析】解：∵AC是⊙O的直径，∴∠ADC＝90°，∴∠ACD＝90°﹣∠CAD＝90°﹣25°＝65°，∴∠ABD＝∠ACD＝65°．故选：C．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．2．（2020•绍兴）如图，点A，B，C，D，E均在⊙O上，∠BAC＝15°，∠CED＝30°，则∠BOD的度数为（）A．45°B．60°C．75°D．90°【点拨】首先连接BE，由圆周角定理即可得∠BEC的度数，继而求得∠BED的度数，然后由圆周角定理，求得∠BOD的度数．【解析】解：连接BE，∵∠BEC＝∠BAC＝15°，∠CED＝30°，∴∠BED＝∠BEC+∠CED＝45°，∴∠BOD＝2∠BED＝90°．故选：D．【点睛】此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．3. （2020•温州一模）如图，四边形ABCD内接于⊙O，若∠AOC＝∠B，则∠D的度数为60°．【点拨】根据圆周角定理得到∠AOC＝2∠D，根据题意得到∠B＝2∠D，根据圆内接四边形的对角互补列式计算，得到答案．【解析】解：由圆周角定理得，∠AOC＝2∠D，∵∠AOC＝∠B，∴∠B＝2∠D，∵四边形ABCD内接于⊙O，∴∠D+∠B＝180°，∴∠D+2∠D＝180°，解得，∠D＝60°，故答案为：60．【点睛】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．4.（2019春•西湖区校级月考）如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交BC、AC于点D、E连接EB、DE，EC＝2，BC＝6，则⊙O的半径为 4.5．【点拨】连接BE，AD，求出CD，根据圆周角定理求出∠CAD＝∠CBE，证△CAD∽△CBE，得出比例式，求出AC，即可得出答案．【解析】解：连接BE，AD，∵AB为⊙O的直径，∴∠ADB＝90°，即AD⊥BC，∵BC＝6，AB＝AC，∴CD＝BD＝3，∵由圆周角定理得：∠CAD＝∠CBE，∵∠C＝∠C，∴△CDA∽△CEB，∴＝，∴＝，解得：AC＝9，∵AB＝AC，∴AB＝9，∴⊙O的半径为＝4.5，故答案为：4.5．【点睛】本题考查了等腰三角形的性质，圆周角定理，相似三角形的性质和判定等知识点，能综合运用定理进行推理是解此题的关键．5.（2019秋•温州期末）如图，点A、B、C、D、E都在⊙O上，AC平分∠BAD，且AB∥CE，求证：＝．【点拨】由于AC平分∠BAD则∠BAC＝∠DAC，再利用平行线的性质得∠BAC＝∠ACE，所以∠DAC ＝∠ACE，然后根据圆周角定理得到结论．【解析】证明：∵AC平分∠BAD，∴∠BAC＝∠DAC，∵AB∥CE，∴∠BAC＝∠ACE，∴∠DAC＝∠ACE，∴＝．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．6.（2018秋•西湖区校级期中）如图，在△ABC中，AB＝AC，以AC为直径的⊙O交AB于点D，交BC于点E．（1）求证：BE＝CE；（2）若∠B＝75°，求弧DE的度数；（3）若BD＝3，BE＝4，求AC的长．【点拨】（1）连结AE，如图，由圆周角定理得∠AEC＝90°，而AB＝AC，则根据等腰三角形的性质即可判断BE＝CE；（2）连结OD、OE，如图，在Rt△ABE中，利用互余计算出∠BAE＝15°，再根据圆周角定理得∠DOE ＝2∠DAE＝30°，然后根据圆心角的度数等于它所对的弧的度数即可得到弧DE的度数为30°；（3）连结CD，如图，BC＝2BE＝8，设AC＝x，则AD＝x﹣3，由圆周角定理得∠ADC＝90°，在Rt △BCD中，利用勾股定理得CD2＝55，然后在Rt△ADC中再利用勾股定理得到（x﹣3）2+55＝x2，接着解方程求出x即可．【解析】解：（1）证明：连结AE，如图，∵AC为直径，∴∠AEC＝90°，∴AE⊥BC，∵AB＝AC，∴BE＝CE；（2）解：连结OD、OE，如图，在Rt△ABE中，∠BAE＝90°﹣∠B＝90°﹣75°＝15°，∴∠DOE＝2∠DAE＝30°，∴弧DE的度数为30°；（3）解：连结CD，如图，BC＝2BE＝8，设AC＝x，则AD＝x﹣3，∵AC为直径，∴∠ADC＝90°，在Rt△BCD中，CD2＝BC2﹣BD2＝82﹣32＝55，在Rt△ADC中，∵AD2+CD2＝AC2，∴（x﹣3）2+55＝x2，解得x＝，即AC的长为．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质．知识点三圆内接四边形1.圆的内接四边形：如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆．2. 圆内接四边形的性质：圆的内接四边形的对角互补．【典例3】（2018秋•崇川区校级月考）如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．（1）若∠E＝∠F，求证：∠ADC＝∠ABC；（2）若∠E＝∠F＝40°，求∠A的度数；（3）若∠E＝30°，∠F＝40°，求∠A的度数．【点拨】（1）根据外角的性质即可得到结论；（2）根据圆内接四边形的性质和等量代换即可求得结果；（3）连结EF，如图，根据圆内接四边形的性质得∠ECD＝∠A，再根据三角形外角性质得∠ECD＝∠1+∠2，则∠A＝∠1+∠2，然后根据三角形内角和定理有∠A+∠1+∠2+∠E+∠F＝180°，解方程即可．【解析】解：（1）∠E＝∠F，∵∠DCE＝∠BCF，∠ADC＝∠E+∠DCE，∠ABC＝∠F+∠BCF，∴∠ADC＝∠ABC；（2）由（1）知∠ADC＝∠ABC，∵∠EDC＝∠ABC，∴∠EDC＝∠ADC，∴∠ADC＝90°，∴∠A＝90°﹣40°＝50°；（3）连结EF，如图，∵四边形ABCD为圆的内接四边形，∴∠ECD＝∠A，∵∠ECD＝∠1+∠2，∴∠A＝∠1+∠2，∵∠A+∠1+∠2+∠E+∠F＝180°，∴2∠A+30°+40°＝180°，∴∠A＝90°﹣＝55°．【点睛】本题考查了圆内接四边形的性质：圆内接四边形的对角互补；圆内接四边形的性质是沟通角相等关系的重要依据，在应用此性质时，要注意与圆周角定理结合起来．在应用时要注意是对角，而不是邻角互补．【变式训练】1．（2019秋•越城区期末）如图，四边形ABCD内接于⊙O，若∠A：∠C＝5：7，则∠C＝（）A．210°B．150°C．105°D．75°【点拨】根据圆内接四边形对角互补可得∠C＝180°×＝105°．【解析】解：∵∠A+∠C＝180°，∠A：∠C＝5：7，∴∠C＝180°×＝105°．故选：C．【点睛】此题主要考查了圆内接四边形，关键是掌握圆内接四边形对角互补．2．（2020•仙居县模拟）如图，四边形ABCD是⊙O的内接四边形，若∠BCD＝143°，则∠BOD的度数是（）A．77°B．74°C．37°D．43°【点拨】根据圆内接四边形的性质求出∠A，再根据圆周角定理解答即可．【解析】解：∵四边形ABCD为⊙O的内接四边形，∠BCD＝143°，∴∠A＝180°﹣∠BCD＝37°，由圆周角定理得，∠BOD＝2∠A＝74°，故选：B．【点睛】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．3．．如图，已知ABCD是一个以AD为直径的圆内接四边形，分别延长AB和DC，它们相交于P，若∠APD ＝60°，AB＝5，PC＝4，则⊙O的面积为（）A．25πB．16πC．15πD．13π【点拨】连接AC，由圆周角定理可得出∠ACD＝90°，再由圆内接四边形的性质及三角形内角和定理可求出∠P AC＝30°，由直角三角形的性质可求出AP、AC的长，由相似三角形的判定定理及性质可得出CD的长，再根据勾股定理接可求出AD的长，进而求出该圆的面积．【解析】解：连接AC，∵AD是⊙O的直径，∴∠ACD＝90°，∵∠APD＝60°，∴∠P AC＝30°，∴AP＝2PC＝2×4＝8，∵AB＝5，∴PB＝8﹣5＝3，∵四边形ABCD是以AD为直径的圆内接四边形，∴∠BAD+∠BCD＝180°，∵∠BCD+∠PCB＝180°，∴∠BAD＝∠PCB，∠APD＝∠APD，∴△PCB∽△P AD，∴＝，即＝，PD＝6，∴CD＝PD﹣PC＝6﹣4＝2，∴AC＝＝＝4，在Rt△ACD中，AD＝＝＝2．∴OA＝AD＝，∴⊙O的面积＝π×（）2＝13π．故选：D．【点睛】本题考查的是相似三角形的判定与性质、圆内接四边形的性质、勾股定理，解答此题的关键是作出辅助线，构造出直角三角形求解．4．（2019秋•萧山区期中）如图，四边形ABCD内接于⊙O，AE⊥CB交CB的延长线于点E，若BA平分∠DBE，AD＝5，CE＝，则AE＝2．【点拨】连接AC，由圆内接四边形的性质和圆周角定理得到∠BAE＝∠CDA，∠ABD＝∠ACD，从而得到∠ACD＝∠CDA，得出AC＝AD＝5，然后利用勾股定理计算AE的长．【解析】解：连接AC，如图，∵BA平分∠DBE，∴∠ABE＝∠ABD，∵∠ABE＝∠CDA，∠ABD＝∠ACD，∴∠ACD＝∠CDA，∴AC＝AD＝5，∵AE⊥CB，∴∠AEC＝90°，∴AE＝＝＝2．故答案为：2．【点睛】本题考查了圆内接四边形的性质、等腰三角形的判定、圆周角定理、勾股定理、角平分线定义等知识；熟练掌握圆周角定理和圆内接四边形的性质是解题的关键．6.（2019•黄埔区一模）如图，四边形ABCD内接于⊙O，AD，BC的延长线交于点E，F是BD延长线上一点，∠CDE＝∠CDF＝60°．（1）求证：△ABC是等边三角形；（2）判断DA，DC，DB之间的数量关系，并证明你的结论．【点拨】（1）根据圆内接四边形的性质得到∠CDE＝∠ABC＝60°，根据圆周角定理、等边三角形的判定定理证明；（2）在BD上截取PD＝AD，证明△APB≌△ADC，根据全等三角形的性质证明结论．【解析】（1）证明：∵∠CDE＝∠CDF＝60°，∴∠CDE＝∠EDF＝60°，∵四边形ABCD内接于⊙O，∴∠CDE＝∠ABC＝60°，由圆周角定理得，∠ACB＝∠ADB＝∠EDF＝60°，∴△ABC是等边三角形；（2）解：DA+DC＝DB，理由如下：在BD上截取PD＝AD，∵∠ADP＝60°，∴△APD为等边三角形，∴AD＝AP，∠APD＝60°，∴∠APB＝120°，在△APB和△ADC中，，∴△APB≌△ADC（AAS），∴BP＝CD，∴DB＝BP+PD＝DA+DC．【点睛】本题考查的是圆内接四边形的性质、等边三角形的性质、全等三角形的判定和性质，掌握圆内接四边形的性质是解题的关键．巩固训练1．（2019秋•福田区期末）下图中∠ACB是圆心角的是（）A．B．C．D．【点拨】根据圆心角的概念判断．【解析】解：A、∠ACB不是圆心角；B、∠ACB是圆心角；C、∠ACB不是圆心角；D、∠ACB不是圆心角；故选：B．【点睛】本题考查的是圆心角的概念，掌握顶点在圆心的角叫作圆心角是解题的关键．2．（2019秋•诸暨市期末）用直角三角板检查半圆形的工件，下列工件哪个是合格的（）A．B．C．D．【点拨】根据90°圆周角所对的弦是直径即可判断．【解析】解：根据90°的圆周角所对的弦是直径得到只有C选项正确，其他均不正确；故选：C．【点睛】本题考查圆周角定理、解题的关键是灵活运用圆周角定理解决问题，属于中考常考题型．3．（2019秋•拱墅区校级期末）下列语句中，正确的是（）①相等的圆周角所对的弧相等；②同弧或等弧所对的圆周角相等；③平分弦的直径垂直于弦，并且平分弦所对的弧；④圆内接平行四边形一定是矩形．A．①②B．②③C．②④D．④【点拨】根据圆周角定理、垂径定理、圆内接四边形的性质定理判断．【解析】解：①在同圆或等圆中，相等的圆周角所对的弧相等，本说法错误；②同弧或等弧所对的圆周角相等，本说法正确；③平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧，本说法错误；④圆内接平行四边形一定是矩形，本说法正确；故选：C．【点睛】本题考查的是命题的真假判断，掌握圆周角定理、垂径定理、圆内接四边形的性质定理是解题的关键．4．（2019春•西湖区校级月考）圆的内接四边形ABCD的四个内角之比∠A：∠B：∠C：∠D的可能的值是（）A．1：2：3：4 B．4：2：3：1 C．4：3：1：2 D．4：1：3：2【点拨】因为圆的内接四边形对角互补，则两对角的和应该相等，比值所占份数也相同，据此求解．【解析】解：∵圆的内接四边形对角互补，∴∠A+∠C＝∠B+∠D＝180°，∴∠A：∠B：∠C：∠D的可能的值是4：3：1：2．故选：C．【点睛】要掌握圆的内接四边形对角互补的特性．5．（2018秋•句容市校级月考）如图，AB，CD是⊙O的直径，弦CE∥AB，弧CE的度数为40°，∠AOC 的度数70°．【点拨】连接OE，由弧CE的度数为40°，得到∠COE＝40°，根据等腰三角形的性质和三角形的内角和定理可求出∠OCE＝（180°﹣40°）÷2＝70°，而弦CE∥AB，即可得到∠AOC＝∠OCE＝70°．【解析】解：连接OE，如图，∵弧CE的度数为40°，∴∠COE＝40°，∵OC＝OE，∴∠OCE＝∠OEC，∴∠OCE＝（180°﹣40°）÷2＝70°，∵弦CE∥AB，∴∠AOC＝∠OCE＝70°．【点睛】本题考查了在同圆或等圆中，如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等，则另外两组量也对应相等，等腰三角形的性质和平行的性质以及三角形的内角和定理．6．（2020•浙江自主招生）如图，MN是⊙O的直径，MN＝2，点A在⊙O上，∠AMN＝30°，B为弧AN 的中点，P是直径MN上一动点，则P A+PB的最小值为．【点拨】首先利用在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点P的位置，然后根据弧的度数发现一个等腰直角三角形计算．【解析】解：作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．此时P A+PB最小，且等于AC的长．连接OA，OC，∵∠AMN＝30°，∴∠AON＝60°，∴弧AN的度数是60°，则弧BN的度数是30°，根据垂径定理得弧CN的度数是30°，则∠AOC＝90°，又OA＝OC＝1，则AC＝．【点睛】此题主要考查了确定点P的位置，垂径定理的应用．7．（2019春•西湖区校级月考）如图，在⊙A中，弦BC、ED所对的圆心角分别是∠BAC，∠EAD，已知DE＝6，BC＝9，∠BAC+∠EAD＝180°，则⊙A的直径等于3．【点拨】延长CA，交⊙A于点F，易得∠BAF＝∠DAE，由圆心角与弦的关系，可得BF＝DE，由圆周角定理可得：∠CBF＝90°，然后由勾股定理求得弦CF的长即可．【解析】解：作直径CF，连结BF，如图，∵∠BAC+∠EAD＝180°，而∠BAC+∠BAF＝180°，∴∠DAE＝∠BAF，∴，∴DE＝BF＝6，∵CF是直径，∴∠CBF＝90°，∴CF＝＝＝3，故答案为：3．【点睛】此题考查了圆周角定理、垂径定理、三角形中位线的性质以及勾股定理．正确作出辅助线是解题的关键．8．（2019秋•香坊区校级期中）如图，AB为 ⊙O的弦，半径OC，OD分别交AB于点E，F．且＝．（1）求证：OE＝OF；（2）作半径ON⊥AB于点M，若AB＝8，MN＝2，求OM的长．【点拨】（1）连接OA、OB，证明△AOE≌△BOF（ASA），即可得出结论；（2）连接OA，由垂径定理得出AM＝AB＝4，设OM＝x，则OA＝ON＝x+2，在Rt△AOM中，由勾股定理得出方程，解方程即可．【解析】（1）证明：连接OA、OB，如图1所示：∵OA＝OB，∴∠A＝∠B，∵＝，∴∠AOE＝∠BOF，在△AOE和△OBF中，，∴△AOE≌△BOF（ASA），∴OE＝OF；（2）解：连接OA，如图2所示：∵OM⊥AB，∴AM＝AB＝4，设OM＝x，则OA＝ON＝x+2，在Rt△AOM中，由勾股定理得：42+x2＝（x+2）2，解得：x＝3，∴OM＝3．【点睛】本题考查了圆心角、弧、弦的关系，等腰三角形的性质，全等三角形的判定与性质，垂径定理，勾股定理等知识；熟练掌握圆心角、弧、弦的关系和垂径定理是解题的关键．9．（2019秋•滨江区期中）如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC 交于点E．（1）若∠B＝70°，求弧CD的度数；（2）若AC＝24，DE＝8，求半圆O的半径．【点拨】（1）根据直径所对的圆周角是直角求出∠BAC的度数，根据平行线的性质求出∠AOD的度数，然后求出∠DOC的度数可确定弧CD的度数；（2）先证明OE⊥AC得到AE＝CE＝AC＝12，设半径为r，则OE＝r﹣8，然后利用勾股定理得到（r ﹣8）2+122＝r2，然后解方程即可．【解析】解：（1）连接OC，如图，∵AB是半圆O的直径，∴∠ACB＝90°，又∠B＝70°，∴∠BAC＝20°，∵OD∥BC，∴∠AOD＝∠B＝70°，又OD＝OA，∴∠OAD＝55°，∴∠DAC＝35°，∴∠DOC＝2∠DAC＝70°，∴的度数是70°；（2）∵OD∥BC，∴∠OEA＝∠ACB＝90°，∴OE⊥AC，∴AE＝CE＝AC＝12，设半径为r，则OE＝r﹣8，在Rt△AOE中，（r﹣8）2+122＝r2，解得r＝5，即半圆O的半径为5．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．10．（2020•雅安）如图，四边形ABCD内接于圆，∠ABC＝60°，对角线BD平分∠ADC．（1）求证：△ABC是等边三角形；（2）过点B作BE∥CD交DA的延长线于点E，若AD＝2，DC＝3，求△BDE的面积．【点拨】（1）根据三个内角相等的三角形是等边三角形即可判断；（2）过点A作AE⊥CD，垂足为点E，过点B作BF⊥AC，垂足为点F．根据S四边形ABCD＝S△ABC+S△ACD，分别求出△ABC，△ACD的面积，即可求得四边形ABCD的面积，然后通过证得△EAB≌△DCB（AAS），即可求得△BDE的面积＝四边形ABCD的面积＝．【解析】（1）证明：∵四边形ABCD内接于圆．∴∠ABC+∠ADC＝180°，∵∠ABC＝60°，∴∠ADC＝120°，∵DB平分∠ADC，∴∠ADB＝∠CDB＝60°，∴∠ACB＝∠ADB＝60°，∠BAC＝∠CDB＝60°，∴∠ABC＝∠BCA＝∠BAC，∴△ABC是等边三角形．（2）过点A作AM⊥CD，垂足为点M，过点B作BN⊥AC，垂足为点N．∴∠AMD＝90°，∵∠ADC＝120°，∴∠ADM＝60°，∴∠DAM＝30°，∴DM＝AD＝1，AM＝＝＝，∵CD＝3，∴CM＝CD+DM＝1+3＝4，∴S△ACD＝CD•AM＝×＝，Rt△AMC中，∠AMD＝90°，∴AC＝＝＝，∵△ABC是等边三角形，∴AB＝BC＝AC＝，∴BN＝BC＝，∴S△ABC＝×＝，∴四边形ABCD的面积＝+＝，∵BE∥CD，∴∠E+∠ADC＝180°，∵∠ADC＝120°，∴∠E＝60°，∴∠E＝∠BDC，∵四边形ABCD内接于⊙O，∴∠EAB＝∠BCD，在△EAB和△DCB中，，∴△EAB≌△DCB（AAS），∴△BDE的面积＝四边形ABCD的面积＝．【点睛】本题考查圆内接四边形的性质，等边三角形的判定和性质，勾股定理，三角形的面积等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．。
人教版 九年级数学上册 24.1 圆的概念和性质专项练习(包含答案)
圆的概念和性质专项练习【例1】 判断题：（1）直径是弦 ( ) （2）弦是直径 ( ) （3）半圆是弧 ( ) （4）弧是半圆 ( ) （5）长度相等的两条弧是等弧 ( ) （6）等弧的长度相等 ( ) （7）两个劣弧之和等于半圆 ( ) （8）半径相等的两个圆是等圆 ( ) （9）两个半圆是等弧 ( ) （10）圆的半径是R ，则弦长的取值范围是大于0且不大于2R ( )【答案】（1）√；（2）×；（3）√；（4）×；（5）×；（6）√；（7）×；（8）√；（9）×；（10）√．【举一反三】如图，在两半径不同的同心圆中，''60AOB A OB ∠=∠=︒，则（ ）A ．''AB A B = B ．''AB A B >C ．AB 的度数=''A B 的度数D ．AB 的长度=''A B 的长度【解析】因为在圆中，圆心角的度数与它所对的弧的度数相等，而''60AOB A OB ∠=∠=︒，所以AB 的度数＝''A B 的度数．所以答案是C ．【答案】C【例2】 如图，点A D G M 、、、在半圆O 上，四边形ABOC DEOF HMNO 、、均为矩形，设BC a =，EF b =，NH c =则下列格式中正确的是( )A ．a b c >>B ．a b c ==C ．c a b >>D ．b c a >>【解析】连结OM OD OA 、、由矩形对角线相等可知OM NH c OD EF b OA BC a ======，，， 又OM OD OA ==，ON MHG FE DC B A∴a b c ==． 选B ．【答案】B【举一反三】如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为216cm ，则该半圆的半径为______．【解析】如图，连两条半径由已知小正方形半径为4cm ，设大正方形半径为2x则()222544x x =++，整理得2280x x --=解得1242x x ==-，(舍去) ∴大正方形半径为8cm则半圆的半径为．【答案】【例3】 如图①，，，，为四个等圆的圆心，A ，B ，C ，D 为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点是 ；如图②，，，，，为五个等圆的圆心，A ，B ，C ，D ，E 为切点，请你在图中画出一条直线，将这五个圆．．．分成面积相等的两部分，并说明这条直线经过的两个点是 ．【解析】略【答案】（1），，如图①(提示：答案不惟一，过与交点O 的任意直线都能将四个圆分成面积相等的两部分)；1O 2O 3O 4O 1O 2O 3O 4O 5O 图1图1图2图21O 3O 31O O 42O O（2），，如图②（提示：答案不惟一，如，，，等均可）．二、圆的性质定理1. 圆周角定理【例4】 如图，80AOB ∠=︒，则弧AB 所对圆周角ACB ∠的度数是（ ）A ．40︒B ．45︒C ．50︒D ．80︒【解析】略 【答案】A ．【举一反三】如图，O ⊙是ABC ∆的外接圆，已知50ABO ∠=︒，则ACB ∠的大小为__________．【解析】略 【答案】40︒．【例5】 如下左图，四个边长为1的小正方形拼成一个大正方形，A B O 、、是小正方形顶点，O ⊙的半径为1，P 是O ⊙上的点，且位于右上方的小正方形内，则APB ∠等于__________．【解析】略 【答案】45︒【例6】 如图，量角器外沿上有A B 、两点，它们的度数分别是7040︒︒、，则1∠的度数为_________．5O O 4AO 3DO 2EO 1CO PO BA【解析】()117040152∠=︒-︒=︒【答案】略【举一反三】如图，量角器外缘边上有A P Q，，三点，它们所表示的读数分别是180︒，70︒，30︒，则PAQ∠的大小为（）A．10︒B．20︒C．30︒D．40︒【解析】考察同弧所对圆心角是圆周角的2倍．答案选B．【答案】B【例7】如图，O⊙是ABC∆的外接圆，已知60B∠=︒，则CAO∠的度数是（）A．15︒B．30︒C．45︒D．60︒【解析】略【答案】B【举一反三】如图，AB是O的直径，CD是⊙O的弦，连接AC AD，，若35CAB∠=︒，则ADC∠的度数为．【解析】直径所对圆周角是90︒且同弧所对圆周角相等．所以得55︒．【答案】55︒【例8】如图所示的半圆中，AD是直径，且32AD AC==，，则sin B的值是________．【解析】略．DCAB【举一反三】如图，AB 是O ⊙的直径，CD AB ⊥，设COD α∠=，则2sin 2AB AD α⋅=_____________．【解析】略 【答案】1【例9】 如图，AB 为O ⊙的直径，CD 是O ⊙的弦，AB CD 、的延长线交于点E ，若218AB DE E =∠=︒，，求AOC ∠的度数．【解析】连结OD∵AB 是直径，2AB DE =，∴12DE AB OD ==∴18DOE E ∠=∠=︒，∴36ODC DOE E ∠=∠+∠=︒∵OC OD =，∴36OCD ODC ∠=∠=︒， ∴54AOC OCD E ∠=∠+∠=︒．【答案】54︒．【举一反三】如图所示CD 是O ⊙的直径，87EOD ∠=︒，AE 交O ⊙于B ，且A B O C =，求A ∠的度数．【解析】连结OB∵AB OC =，OBOC =，∴OB AB = 设A x ∠=，则BOA x ∠=． ∴2OBE BOA A x ∠=∠+∠=． ∵OE OB =，EEDD∴2OEA OBE x ∠=∠=．∴387EOD E A x ∠=∠+∠==︒ ∴29x =︒，即29A ∠=︒．【答案】29︒．【例10】 如图，在O ⊙中，AOB ∠的度数为m ，C 是ACB 上一点，D E 、是AB 上不同的两点(不与A B 、两点重合)，则D E ∠+∠的度数为____________．【解析】()136018022mD E m ∠+∠=︒-=︒- 【答案】1802m ︒-【举一反三】如图，AB 是O ⊙的直径，弦PC 交OA 于点D ，弦PE 交OB 于点F ，且OC DC OF EF ==，．若C E ∠=∠，则CPE ∠=___________．【答案】40︒【例11】 如图所示，在ABC ∆中，45C ∠=︒，4AB =，则O ⊙的半径为（ ）B.4C. D.5【解析】如右图所示连接OA 、OB ，因为45C ∠=︒，290AOB C ∠=∠=︒4AB =，所以半径为OA OB ==【答案】【举一反三】如图，ABC △的三个顶点都在O ⊙上，302cm C AB ∠=︒=，，则O ⊙的半径O PFEDCBA BABA为______cm ．【解析】连接OA ，OB∵30C ∠=︒，∴260O C ∠=∠=︒，又∵OA OB =，∴OAB ∆为等边三角形， ∴2OA AB ==，即O 的半径为2．【答案】2【举一反三】如图AB 是半圆O 的直径，点C D 、在弧AB 上，且AD 平分CAB ∠，已知106AB AC ==，，求AD 的长．【解析】延长AC 交BD 的延长线于E ，∵AB 是半圆的直径，AD 平分CAB ∠， 则可得10AE AB ==，BD ED =， ∴4CE AE AC =-=，∵90ACB ∠=︒，∴8BC =，在Rt BCE ∆中，BE =，∴BD DE ==，∴AD =．【答案】【例12】 如图，ABC △是O 的内接三角形，点C 是优弧AB 上一点(点C 不与A B ，重合)，设OAB α∠=，C β∠=．（1）当35α=︒时，求β的度数；（2）猜想α与β之间的关系，并给予证明．【答案】（1）解：连接OB ，则OA OB =，∴35OBA OAB ∠=∠=︒．∴180110AOB OAB OBA ∠=︒-∠-∠=︒．∴1552C AOB β=∠=∠=︒．（2）答：α与β之间的关系是90αβ+=︒．证一：连接OB ，则OA OB =．OBA OAB α∴∠=∠=． ∴1802AOB α∠=︒-．∴11(1802)9022C AOB βαα=∠=∠=︒-=︒-．∴90αβ+=︒．证二：连接OB ，则OA OB =． ∴22AOB C β∠=∠=．过O 作OD AB ⊥于点D ，则OD 平分AOB ∠．∴12AOD AOB β∠=∠=．在Rt AOD △中，90OAD AOD ∠+∠=︒， ∴90αβ+=︒证三：延长AO 交O 于E ，连接BE ， 则E C β∠=∠=．∵AE 是O 的直径，∴90ABE ∠=︒． ∴90BAE E ∠+∠=︒，∴90αβ+=︒．【举一反三】如图，O ⊙与P ⊙相交于B 、C 两点，BC 是P ⊙的直径，且把O ⊙分成度数比为12∶的两条弧，A 是BmC 上的动点(不是B 、C 重合)，连结AB 、AC 分别交P ⊙于D 、E 两点．（1）当ABC ∆是钝角三角形时，判断PDE ∆的形状． （2）当ABC ∆是直角三角形时，判断PDE ∆的形状．（3）当ABC ∆是锐角三角形时，判断PDE ∆的形状．这种情况加以证明．【解析】三种情况下，PDE ∆的形状都是等边三角形．如图，连结CD ，显然30ACD ∠=︒，所以PDE ∆是等边三角形．【答案】PDE ∆是等边三角形【例13】 圆1S 及2S 相交于点A 及B ．圆1S 的圆心O 落在2S 的圆周上，圆1S 的弦AC 交2S 于点D （如图），证明：线段OD 与BC 是互相垂直的．【答案】作线段AB 、OB 及OC ．这时有BAD BOD ∠=∠，另一方面有12BAD BOC ∠=∠，ABC D OS 1S 2S 2S 1OD C B A所以12BOD BOC ∠=∠，即BOD DOC ∠=∠，而BO CO =，故OD BC ⊥．【举一反三】两圆相交于A 、B ，P 是大圆O 上一点，过A 、P 和B 、P 分别作直线交小圆于C 、D ，过O 、P 作直径PE ．求证：PE CD ⊥【答案】证法一：设直线CD 交大圆于F ，连接BA 并延长，则CAB CDB PDF ∠=∠=∠，∴12m DPO BE ∠，()12m PDF CAB AP AB ∠=∠=+．∴()119022m m DPO PDF BE AP AB PABE ∠+∠=++==︒，∴CD PE ⊥．证法二：如图，设CD 交圆O 于G 、F ，连接AB 、PG 、BG ， 则ACD ABD ∠=∠．APG ABG ∠=∠．∴ACD APG ABD ABGJ GBP ∠+∠=∠+∠=∠． 而PGF ACD APG ∠=∠+∠， ∴PGF GBP ∠=∠．∴PF PG =，∴PE CD ⊥．证法三：如图，设CD 交圆O 于G 、F ，连接BA 并延长．∵CDB CAB ∠=∠，又()12m CDB BG PF ∠=+．()()1122m CAB PA AG BG PG BG ∠++=+，∴PF PG =．∴PE CD ⊥．【例14】 如图，已知AB 是O ⊙的直径，点C 是O ⊙上一点，连结BC AC 、，过点C 作直线CD AB ⊥于点D ，点E 是AB 上一点，直线CE 交O ⊙于点F ，连结BF ，与直线CD 交于点G ．求证：2BC BG BF =⋅．PG FEDCBAE FCOD G BAPEPABG D OCF【答案】解法一：连结AF∵AB 是直径，∴90ACB AFB ∠=∠=︒，∵CD AB ⊥，∴2BC BD AB =⋅，90BDG ∠=︒∴BDG BFA ∆∆∽，∴BD BGBF BA=， ∴BG BF BD BA ⋅=⋅， ∴2BC BG BF =⋅．解法二：延长AG 交O ⊙于H ，∵AG BD ⊥，且BD 是直径，∴AB BH =， ∴BAG C ∠=∠，∵ABG CBA ∠=∠，∴ABG CBA ∆∆∽， ∴AB BG CB BA=，即2AB BG BC =⋅．【举一反三】如图，已知：在O ⊙中，直径4AB =，点E 是OA 上任意一点，过E 作弦CD AB ⊥，点F 是BC 上一点，连接AF 交CE 于H ，连接AC CF BD OD 、、、． ⑴ 求证：ACH AFC ∆∆∽；⑵ 猜想：AH AF ⋅与AE AB ⋅的数量关系，并说明你的猜想； ⑶ 探究：当点E 位于何处时，:1:4AEC BOD S S ∆∆=？并加以说明．【解析】⑴ ∵AB 是直径，且AB CD ⊥，∴AC AD =，∴AFC ACD ∠=∠，∵CAH FAC ∠=∠，∴ACH AFC ∆∆∽． ⑵ AH AF AE AB ⋅=⋅解法一：由⑴ACH AFC ∆∆∽可得：2AC AH AF =⋅， 连结BC ，∵C 在O ⊙上，∴90ACB ∠=︒， 又CD AB ⊥，∴2AC AE AB =⋅， ∴AH AF AE AB ⋅=⋅． 解法二：连结FB∵F 在O ⊙上，∴90AFB ∠=︒，又EAH FAB ∠=∠，∴AEH AFB ∆∆∽，∴AE AHAF AB=，即AH AF AE AB ⋅=⋅． ⑶ 12AEC S AE CE ∆=⋅，12BOD S BO DE ∆=⋅，∵:1:4AEC BOD S S ∆∆=，∴112142AEC BOD AE CE S AE S BO BO DE ∆∆⋅===⋅，∵4AB =，∴122OB AB ==， ∴1142AE OB ==，∴当12AE =时，:1:4AEC BOD S S ∆∆=．【答案】见解析【例15】 如图，AB ，AC ，AD 是圆中的三条弦，点E 在AD 上，且AB AC AE ==．请你说明以下各式成立的理由：（1）2CAD DBE ∠=∠；（2）22AD AB BD DC -=⋅．【解析】（1）如图，连接BC ，∵AB AC AE ==， ∴52∠=∠，236∠+∠=∠． 又45623∠+∠=∠=∠+∠， ∴43∠=∠．而143∠=∠+∠，∴124∠=∠．即2CAD DBE ∠=∠． （2）设BC 与AD 的交点为G ， ∵25∠=∠，BAG DAB ∠=∠，∴BAG DAB ∆∆∽，∴2AB AG AD =⋅． ∴222AD AB AD AG AD -=-⋅ ()AD AD AG =-AD DG =⋅．又∵5ADC ∠=∠，1DBG ∠=∠， ∴BDG ADC ∆∆∽． ∴DB DG AD DC=，AD DG BD DC ⋅=⋅． ∴22AD AB BD DC -=⋅．【举一反三】在ABC ∆中，60ABC ∠=︒，点O 、H 分别是ABC ∆的外心、垂心．点D 、E分别在边BC 、AB 上，使得BD BH =，BE BO =，已知1BO =．求B D E ∆的面积．【解析】如图，作ABC ∆外接圆的直径AF ，联结CF 、BF 、CH ． 因为BH AC ⊥，FC AC ⊥， 所以，BH FC ∥． 同理，CH FB ∥．E DC BAG654321A BCDE 图 12HOFE DCBA故四边形BHCF 是平行四边形．又因FO CO =，60AFC ABC ∠=∠=︒ 所以，FOC ∆是正三角形．于是，BD BH CF CO BO BE =====． 故BDE ∆也是正三角形．由已知1BO =，知BDE S ∆=。
第二讲 与圆有关的角度和线段
第二讲与圆有关的角度和线段圆中的角包括圆周角、圆心角等，线段有包括直径、半径在内的弦。
在全国中考试题中，利用角的数量关系和位置关系探究相似三角形和全等三角形是常用的方法，进而可以进行线段的计算和证明。
一、圆周角与圆心角：1.如图，四边形ABCD中，AB=AC=AD，若∠CAD=76°，则∠CBD=度．2.如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点．若⊙O的半径为7，则GE+FH 的最大值为．3.如图，△ABC内接于⊙O，AD⊥BC，OE⊥BC，OE=BC．将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H．①∠BAC=45°；②四边形AFHG是正方形；③BC=BG+CF；④若BD=6，CD=4，则AD=10．以上说法正确的有（）1二、圆周角与等腰三角形：1.如图，△ABC中，AB=AC，以AB为直径的⊙O交AC于点D，E为AB上一点，EF BC于F，且∠DEF=45°，求证：BD=BE.2.如图，⊙O是以等腰三角形ABC的底边BC为直径的外接圆，BD平分∠ABC 交⊙O于D，且BD与OA、AC分别交于点E、F延长BA、CD交于G．（1）试证明：BF=CG．（2）线段CD与BF有什么数量关系？为什么？（3）试比较线段CD与BE的大小关系，并说明理由．3.△ABC是⊙O的内接三角形，AC=BC，D为⊙O中弧AB上一点，连接DA并延长至点E，使∠ACB=∠ECD．（1）求证：AE=BD；（2）若AC⊥BC，求证：AD+BD=CD．2三、圆周角与等边三角形：1.△ABC是⊙O的内接正三角形，P为弧BC上一点，求证：AP=BP+CP。
2.如图，△ABC是圆内接正三角形，P为劣弧BC上一点，已知AB=，PA=6．（1）求证：PB+PC=PA；（2）求PB、PC的长（PB＜PC）．四、圆周角与直角三角形：1.如图，已知△ABC内接于半径为r的半圆内，直径AB为其一边，设AC+BC=S，则有（）A．S2≤8r2B．S2≥8r2C．S2≤6r2D．S2≥6r22．如图，△ABC中，∠BAC=90°，AD⊥BC于D，△ABC，△ABD，△ACD的外接圆半径分别为R，R1，R2，那么有（）A．R=R1+R2B．R=C．R2=R1R2D．R2=R12+R22343.如图，AB 是⊙O 的直径，弦BC=4cm ，F 是弦BC 的中点，∠ABC=60°．若动点E 以2cm/s 的速度从A 点出发沿着A →B →A 的方向运动，设运动时间为t （s ）（0≤t ＜6），连接EF ，当△BEF 是直角三角形时，t 的值为 ．4.如图，已知A 、B 两点的坐标分别为（4，0）、（0，2），P 是△AOB 外接圆上的一点，且∠AOP=45°，反比例函数图象经过点P ，则k的值为．5.在⊙O 的内接△ABC 中，AD ⊥BC 于D ，（1）①图1中，若作直径AP ，求证：AB •AC=AD •AP ；②已知AB +AC=12，AD=3，设⊙O 的半径为y ，AB 的长为x ．求y 与x 的函数关系式，及自变量x 的取值范围；（2）图2中，点E 为⊙O 上一点，且=，求证：CE +CD=BD ．。
人教版九年级数学上册 《圆中的求线段长度的相关计算》必考题型专项分类专题练习
《圆中的求线段长度的相关计算》必考经典题型专项分类专题练习（专题分类练习+详细解析）题型一：垂径定理中的线段长度计算1. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在MN⏜上,且不与M,N重合,当P点在MN⏜上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( )A.逐渐变大B.逐渐变小C.不变D.不能确定2. 如图,AB是☉O的直径,AB=6,OD⊥AB,弧BC为30°,P是直径AB上的点,则PD+PC的最小值是________.3. ☉O过等边△ABC的各个顶点,且AB=2,则☉O的半径为( )A.1B.√3C.2√33D.√324. 如图,点A,N在半圆O上,四边形ABOC,DNMO均为矩形,BC=a,MD=b,则a,b的关系为( )A.a>bB.a=bC.a<bD.a≤b5. 已知,如图,☉O的弦AB,CD相交于点P,PO平分∠APD.求证:AB=CD.题型二：和圆周角、圆心角相关的线段长度计算1. 如图,在☉O中,弦AC=2√3,点B是圆上一点,且∠ABC=45°,则☉O的半径R=________.2. 如图所示,☉O的两条弦AB,CD交于点P,连接AC,BD,若S△ACP ∶S△DBP=16∶9,则AC∶BD=________.3. 如图,小正方形的边长均为1,则∠1的正切值为( )A.15B.14C.13D.124. 如图,☉O的半径为4,△ABC是☉O的内接三角形,连接OB,OC,若∠BAC和∠BOC互补,则弦BC的长度为( )A.3√3B.4√3C.5√3D.6√35. 正方形ABCD的四个顶点都在☉O上,点E是☉O上的一点.(1)如图①,若点E在AB⏜上,点F是DE上的一点,DF=BE.求证:△ADF≌△ABE.(2)在(1)的条件下,小明还发现线段DE,BE,AE之间满足等量关系:DE-BE=√2AE.请你说明理由.(3)如图②,若点E在AD⏜上.写出线段DE,BE,AE之间的等量关系.(不必证明)题型三：和切线有关的线段长度计算1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.383.如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E.则AD为( )A.2.5B.1.6C.1.5D.13. 如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E两点,经测量发现AD和BE的长恰是方程x2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.4. 如图,已知:射线PO与☉O交于A,B两点,PC,PD分别切☉O于点C,D.(1)请写出两个不同类型的正确结论.(2)若CD=12,tan∠CPO=1,求PO的长.2题型四：扇形、多边形中的线段长度计算1. 已知正六边形的边长为2,则它的内切圆的半径为( )A.1B.√3C.2D.2√32. 粉笔是校园中最常见的必备品.现有一盒刚打开的六角形粉笔,总支数为50支.如图是它的横截面(矩形ABCD),已知每支粉笔的直径为12mm,由此估算矩形ABCD的周长约为________mm.⏜的中点,连接BM,CM.3. 如图,正方形ABCD内接于☉O,M为AD(1)求证:BM=CM.⏜的长.(2)当☉O的半径为2时,求BM4. 如图,已知等边△ABC内接于☉O,BD为☉O内接正十二边形的一边,CD=5√2cm,求☉O的半径R.《圆中的求线段长度的相关计算》必考经典题型专项分类专题练习（专题分类练习+详细解析）（解析版）题型一：垂径定理中的线段长度计算⏜上,且不与M,N重合, 1. 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在MN⏜上移动时,矩形PAOB的形状、大小随之变化,则PA2+PB2的值( ) 当P点在MNA.逐渐变大B.逐渐变小C.不变D.不能确定【解析】选C.连接OP,∵在直角三角形PAB中,AB2=PA2+PB2,又∵在矩形PAOB 中,OP=AB, ∴PA 2+PB 2=AB 2=OP 2.2. 如图,AB 是☉O 的直径,AB=6,OD ⊥AB,弧BC 为30°,P 是直径AB 上的点,则PD+PC 的最小值是________.【解析】作C 点关于AB 的对称点C ′,连接DC ′交AB 于P 点,过D 点作直径DE,连接EC ′,如图, ∴BC⏜=BC′⏜=30°,PC=PC ′, ∴DC ′是PD+PC 的最小值.又∵弧EC ′的度数=90°-30°=60°,∴∠D=30°, 而DE=AB=6,在Rt △DEC ′中,EC ′=12DE=3, DC ′=√3EC ′=3√3.即PD+PC 的最小值是3√3.答案:3√33. ☉O 过等边△ABC 的各个顶点,且AB=2,则☉O 的半径为 ( )A.1B.√3C.2√33D.√32【解析】选C.连接OB,OC,过点O 作OD ⊥BC 于点D. ∵△ABC 为等边三角形, ∴AB=BC=AC,∴AB⏜=BC ⏜=AC ⏜, ∴∠BOC 为120°. 又OD ⊥BC,OB=OC,∴∠COD=60°,∠COD=30°,CD=12BC=1, ∴cos ∠OCD=CDOC , ∴OC=CD cos∠OCD =√32=2√33. 4. 如图,点A,N 在半圆O 上,四边形ABOC,DNMO 均为矩形,BC=a,MD=b,则a,b 的关系为 ( )A.a>bB.a=bC.a<bD.a ≤b【解析】选B.连接ON,OA,如图,∵点A,N在半圆上,∴ON=OA,∵四边形ABOC,DNMO均为矩形,∴ON=MD,OA=BC,∴BC=MD,即a=b.5. 已知,如图,☉O的弦AB,CD相交于点P,PO平分∠APD.求证:AB=CD.【证明】过点O作OM⊥AB于点M,ON⊥CD于点N.∵PO平分∠APD,OM⊥AB,ON⊥CD.∴OM=ON,连接OA,OD,在Rt△AOM中,AM=√OA2−OM2,在Rt△DON中,DN=√OD2−ON2,又∵OA=OD,OM=ON,∴AM=DN,∴2AM=2DN,即AB=CD.题型二：和圆周角、圆心角相关的线段长度计算1. 如图,在☉O中,弦AC=2√3,点B是圆上一点,且∠ABC=45°,则☉O的半径R=________.【解析】∵∠ABC=45°,∴∠AOC=90°,∵OA=OC=R,∴R2+R2=(2√3)2,解得R=√6. 答案:√62. 如图所示,☉O的两条弦AB,CD交于点P,连接AC,BD,若S△ACP ∶S△DBP=16∶9,则AC∶BD=________.【解析】由题干图可知∠C=∠B,∠A=∠D, ∴△ACP∽△DBP,∴S△ACPS△DBP =(ACBD)2,即(ACBD)2=169,∴AC∶BD=4∶3.答案:4∶33. 如图,小正方形的边长均为1,则∠1的正切值为( )A.15B.14C.13D.12【解析】选D.如图,∵∠1=∠2,∴tan∠1=tan∠2=12.4. 如图,☉O的半径为4,△ABC是☉O的内接三角形,连接OB,OC,若∠BAC和∠BOC互补,则弦BC的长度为( )A.3√3B.4√3C.5√3D.6√3BC.【解析】选B.过点O作OD⊥BC于点D,则BD=CD=12∠BOC,∵∠BAC+∠BOC=180°,∠BAC=12∴∠BOC=120°,∠BAC=60°,∴∠BOD=60°.在Rt△BOD中,BD=OBsin60°=2√3,∴BC=4√3.5. 正方形ABCD的四个顶点都在☉O上,点E是☉O上的一点.⏜上,点F是DE上的一点,DF=BE.求证:△ADF≌△ABE.(1)如图①,若点E在AB(2)在(1)的条件下,小明还发现线段DE,BE,AE之间满足等量关系:DE-BE=√2AE.请你说明理由.⏜上.写出线段DE,BE,AE之间的等量关系.(不必证明) (3)如图②,若点E在AD【解析】(1)在正方形ABCD中,AB=AD.⏜,∴∠1=∠2,∵∠1和∠2所对的弧都是AE在△ADF和△ABE中,{AD=AB,∠1=∠2, DF=BE,∴△ADF≌△ABE(SAS).(2)由(1)得△ADF≌△ABE,∴AF=AE,∠3=∠4.在正方形ABCD中,∠BAD=90°,∴∠BAF+∠3=90°,∴∠BAF+∠4=90°,∴∠EAF=90°.∴△EAF是等腰直角三角形.∴EF2=AE2+AF2,∴EF2=2AE2.∴EF=√2AE.∵DE-DF=EF,∴DE-BE=√2AE.(3)BE-DE=√2AE.题型三：和切线有关的线段长度计算1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.38【解析】选B.如图,根据切线长定理可知,AE=AH,BE=BF,CF=CG,DG=DH.所以AE+DG=AH+DH=AD,BE+CG=BF+CF=BC,所以AB+BC+CD+DA=AE+BE+BC+CG+DG+DA=2AD+2BC=2×7+2×10=34.3.如图,Rt △ABC 中,∠ACB=90°,AC=4,BC=6,以斜边AB 上的一点O 为圆心所作的半圆分别与AC,BC 相切于点D,E.则AD 为 ( )A.2.5B.1.6C.1.5D.1【解析】选B.连接OD,OE,OC,设OD=r,∵AC,BC 切☉O 于D,E, ∴∠ODC=∠OEC=90°,OD=OE, ∵S △AOC +S △BOC =S △ABC ,即12OD ·AC+12OE ·BC=12BC ·AC,12r ·4+12r ·6=12×6×4,r=2.4,AD=AC-r=1.6.3. 如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E 两点,经测量发现AD 和BE 的长恰是方程x 2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.【解析】连接OD,OE.解方程x2-25x+150=0,得x1=10,x2=15,∴设AD=10,BE=15,半径为r,∴AB=AD+BE=25,∴(AD+r)2+(BE+r)2=AB2,即(10+r)2+(15+r)2=252,解得:r=5.答案:54. 如图,已知:射线PO与☉O交于A,B两点,PC,PD分别切☉O于点C,D.(1)请写出两个不同类型的正确结论.(2)若CD=12,tan∠CPO=12,求PO的长.【解析】(1)不同类型的正确结论有:①PC=PD,②∠CPO=∠DPO,③CD⊥BA,④∠CEP=90°,⑤PC2=PA·PB.(2)连接OC,∵PC,PD分别切☉O于点C,D∴PC=PD,∠CPO=∠DPA,∴CD⊥AB,∵CD=12,∴DE=CE=12CD=6.∵tan∠CPO=12,∴在Rt△EPC中,PE=12,∴由勾股定理得CP=6√5,∵PC切☉O于点C,∴∠OCP=90°.在Rt △OPC 中,∵tan ∠CPO=12, ∴OC PC =12,∴OC=3√5, ∴OP=√OC 2+PC 2=15.题型四：扇形、多边形中的线段长度计算1. 已知正六边形的边长为2,则它的内切圆的半径为 ( ) A.1B.√3C.2D.2√3【解析】选B.如图,由正六边形的性质知,三角形AOB 为等边三角形,所以,OA=OB=AB=2,AC=1,由勾股定理,得内切圆半径OC=√3.2. 粉笔是校园中最常见的必备品.现有一盒刚打开的六角形粉笔,总支数为50支.如图是它的横截面(矩形ABCD),已知每支粉笔的直径为12mm,由此估算矩形ABCD 的周长约为________mm.【解析】作B ′M ′∥C ′D ′,C ′M ′⊥B ′M ′于点M ′.粉笔的半径是6mm.则边长是6mm. ∵∠M ′B ′C ′=60°,∴B ′M ′=B ′C ′·cos60°=6×12=3(mm), C ′M ′=B ′C ′sin60°=6×√32=3√3(mm). 则题干图中,AB=CD=11×3√3=33√3(mm). AD=BC=5×6+5×12+3=93(mm).则周长是:2×33√3+2×93=(66√3+186)mm. 答案:(66√3+186)3. 如图,正方形ABCD 内接于☉O,M 为AD ⏜的中点,连接BM,CM. (1)求证:BM=CM.(2)当☉O 的半径为2时,求BM⏜的长.【解析】(1)∵四边形ABCD 是正方形, ∴AB=CD, ∴AB⏜=CD ⏜, ∵M 为AD ⏜的中点, ∴AM ⏜=DM ⏜,∴AB ⏜+AM ⏜=CD ⏜+DM ⏜,即BM⏜=CM ⏜,∴BM=CM.(2)∵☉O 的半径为2, ∴☉O 的周长为4π, ∴BM⏜的长=38×4π=32π.4. 如图,已知等边△ABC 内接于☉O,BD 为☉O 内接正十二边形的一边,CD=5√2cm,求☉O 的半径R.【解析】连接OB,OC,OD,∵等边△ABC 内接于☉O,BD 为内接正十二边形的一边, ∴∠BOC=13×360°=120°,∠BOD=112×360°=30°, ∴∠COD=∠BOC-∠BOD=90°, ∵OC=OD,∴∠OCD=45°,∴OC=CD ·cos 45°=5√2×√22=5(cm). 即☉O 的半径R=5cm.学海迷津：数学学习十大方法1、配方法所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。
人教版数学九年级上学期课时练习-弧、弦、圆心角(巩固篇)(人教版)
专题24.9 弧、弦、圆心角（巩固篇）（专项练习）一、单选题类型一、圆心角概念1．已知下列命题：①长度相等的两条弧所对的圆心角相等． ①直径是圆的最长的弦，也是圆的对称轴． ①平分弦的直径垂直于这条弦．①在同圆或等圆中，相等的弦所对的圆周角相等． 其中错误命题的个数为（ ） A ．1个B ．2个C ．3个D ．4个2．已知①ABC 内接于①O ，若①AOB =120°，则①C 的度数是( ) A ．60°B ．120°C ．60°或120°D ．30°或150°3．如图， AB 为①O 的直径，弦CD ①AB 于点E ，连接AC ，OC ，OD ，若①A ＝20°，则①COD 的度数为（ ）A ．40°B ．60°C ．80°D ．100°类型二、圆心角与它所对弧的度数4．如图，已知△ABC 是圆O 的内接三角形，AB ＝AC ，①ACB ＝65°，点C 是弧BD 的中点，连接CD ，则①ACD 的度数是（ ）A ．12°B ．15°C ．18°D ．20°5．如图，扇形AOB 中，90AOB ∠=︒，半径6,OA C =是AB 的中点，//CD OA ，交AB 于点D ，则CD 的长为（ ）A．2B C．2D．66．如图，已知O的半径为5，弦AB，CD所对的圆心角分别是AOB∠，COD∠∠，若AOB AB=，则弦CD的长为（）与COD∠互补，弦8A．6B．8C．D．5类型三、用弧、弦、圆心角关系求解⊥于点7．如图，在以AB为直径的①O中，点C为圆上的一点，2=，弦CD ABBC ACE，弦AF交CE于点H，交BC于点G，若点H是AG的中点，则CBF∠的度数为（）A．18°B．21°C．22.5°D．30°8．如图，在①O中，AB是①O的直径，AB＝10，AC=CD=DB，点E是点D关于AB 的对称点，M是AB上的一动点，下列结论：①①BOE=30°；①①DOB=2①CED；①DM①CE；①CM+DM的最小值是10，上述结论中正确的个数是（）A ．1B ．2C ．3D ．49．如图，①O 的半径为9cm ，AB 是弦，OC ①AB 于点C ，将劣弧AB 沿弦AB 折叠交于OC 的中点D ，则AB 的长为（ ）A ．B ．C ．D ．类型四、用弧、弦、圆心角关系证明10．有一直径为AB 的圆，且圆上有C 、D 、E 、F 四点，其位置如图所示．若6AC =，8AD =，5AE =，9AF =，10AB =，则下列弧长关系何者正确？（ ）A ．AC AD AB +=，AE AF AB += B ．AC AD AB +=，AE AF AB +≠ C ．AC AD AB +≠，AE AF AB +=D ．AC AD AB +≠，AE AF AB +≠11．在锐角ABC 中，60ACB ∠=︒，①BAC 、①ABC 的角平分线AD 、BE 交于点M ，则下列结论中错误的是（ ）A ．120AMB ∠=︒ B ．ME MD =C ．AE BD AB += D ．点M 关于AC 的对称点一定在ABC 的外接圆上 12．如图，AB 、CD 分别是①O 的直径，连接BC 、BD ，如果弦DE AB ∥，且①CDE ＝62°，则下列结论错误的是（ ）A ．CB ①BD B ．①CBA ＝31°C ．AC AE =D ．BD ＝DE二、填空题类型一、圆心角概念13．在①O 中，AB 是直径，AB ＝2，C 是AB 上一点，D 、E 分别是AC 、BC 的中点，M 是弦DE 的中点，则CM 的取值范围是__________________．14．把一个圆分成4个扇形，它们分别占整个圆的10%，20%，30%，40%，那么这四个扇形的圆心角分别是_______.15．已知点A 、B 、C 、D 在圆O 上，且FD 切圆O 于点D ，OE CD ⊥于点E ，对于下列说法：①圆上AbB 是优弧；①圆上AbD 是优弧；①线段AC 是弦；①CAD ∠和ADF ∠都是圆周角；①COA ∠是圆心角，其中正确的说法是________．类型二、圆心角与它所对弧的度数16．如图，在以AB 为直径的半圆中，AD =EB ，CD①AB ，EF①AB ，CD=CF=1，则以AC 和BC 的长为两根的一元二次方程是________．17．已知半径为2的①O 中，弦AC=2，弦AD ＝①AOD ＝________，①COD ＝_________．18．如图，AB 是O 的直径，弦,CD AB ⊥连接CO 并延长交O 于点,E 连接BD 交CE于点,F 若32,DBE ∠=︒则DFE ∠的度数是________________．类型三、用弧、弦、圆心角关系求解19．如图，点A 、B 、C 、D 均在O 上，若65AOD ∠=︒，AO DC ∥，则①B 的度数为______．20．如图，点A 、B 、C 、D 、E 都是圆O 上的点，AC AE =，①B ＝116°，则①D 的度数为______度．21．如图，①O 的直径AB 过CD 的中点A ，若①C ＝30°，AB 、CD 交于点E ，连接AC 、BD ，则AEBE＝________________．类型四、用弧、弦、圆心角关系证明22．如图，AB、CE是圆O的直径，且AB＝4，弧BD＝弧CD＝弧AC，点M是AB上一动点，下列结论：正确的数是___（写出所有正确结论的序号）①BOD；①①CED＝12①DM①CE；①CM+DM的最小值为4；①设OM为x，则S△OMC．23．在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧______;所对的弦__________, 所对弦的弦心距____________．24．如图，AB是①O的直径，CD是弦，若①ABC＝63°，则①D的度数是__．三、解答题25．如图是半径为2的圆，（1）在其中画两个不重叠的扇形AOB和扇形BOC，使扇形AOB的圆心角为120度，扇形BOC的圆心角为90度，（2）求第三个扇形AOC的面积．26．如图，AB是①O的一条弦，OD①AB，垂足为C，交①O于点D，点E在①O上．（1）若①AOD=52°，求①DEB的度数；（2）若AB=24，CD=8，求①O的半径长．27．阅读与应用请阅读下列材料，完成相应的任务：托勒密是“地心说”的集大成者，著名的天文学家、地理学家、占星学家和光学家．后人从托勒密的书中发现一个命题：圆内接四边形对边乘积的和等于对角线的乘积．下面是对这个命题的证明过程．如图1，四边形ABCD内接于O．⋅+⋅=⋅．求证：AB DC AD BC AC BD∠=∠交BD于点E．证明：如图2，作BAE CAD①AD AD =，①ABE ACD ∠=∠．（依据） ①ABE ACD ∽△△．①AB BEAC CD=．AB DC AC BE ⋅=⋅． …①ABC AED ∽△△． ①AC BCAD ED=．①AD BC AC ED ⋅=⋅． ①AB DC AC BE ⋅=⋅，①()AB DC AD BC AC BE AC ED AC BE ED AC BD ⋅+⋅=⋅+⋅=+=⋅． ①AB DC AD BC AC BD ⋅+⋅=⋅． 任务：(1)证明过程中的“依据”是______； (2)补全证明过程；(3)如图3，O 的内接五边形ABCDE 的边长都为2，求对角线BD 的长．28．如图，在①O 中，弦AB ，CD 互相垂直，垂足为M ，F 是BD 上的一点，且BF BC =，AF分别与CD，BD相交于点E，N，连接FD，MN．(1)求证：DE＝DF；(2)若①O的半径为8，①BAF＝22.5°，求线段MN的长．参考答案1．D【分析】根据圆心角定理、直径的性质、垂径定理、圆周角定理逐个判断即可．解：等弧所对的圆心角相等，但长度相等的两条弧不一定是等弧，则命题①错误直径是圆的最长的弦，但不是圆的对称轴，圆的对称轴是直径所在直线，则命题①错误平分弦（非直径）的直径垂直于这条弦，则命题①错误在同圆或等圆中，相等的弦所对的圆周角相等或互补，则命题①错误综上，错误命题的个数为4个故选：D．【点拨】本题考查了圆心角定理、直径的性质、垂径定理、圆周角定理，熟记各定理是解题关键．2．C【分析】根据圆周角定理可以得出同弧所对的圆周角等于圆心角的一半，此时分两种情况进一步分析讨论即可.解：①当点C与线段AB位于圆心的两侧时，①C=12①AOB=60°；①当点C与线段AB位于同侧时，与上一种情况所得的度数互补；即此时的①C=120°．故选：C．【点拨】本题主要考查了圆周角定理的应用，熟练掌握相关概念是解题关键.3．C【分析】利用圆周角与圆心角的关系得出①COB=40°，再根据垂径定理进一步可得出①DOB=①COB，最后即可得出答案.解：①①A=20°，①①COB=2①A=40°，①CD①AB，OC=OD，①①DOB=①COB=40°，①①COD=①DOB+①COB=80°.故选：C.【点拨】本题主要考查了圆周角、圆心角与垂径定理的综合运用，熟练掌握相关概念是解题关键.4．B【分析】如图，连接AO，BO，CO，DO，由等腰三角形的性质可求①ABC＝①ACB＝65°，①BAC ＝50°，由圆周角定理可求①AOC＝2①ABC＝130°，①BOC＝2①BAC＝100°，可求①AOD＝30°，即可求解．解：如图，连接AO，BO，CO，DO，①AB＝AC，①ACB＝65°，①①ABC＝①ACB＝65°，①①BAC＝50°，①①AOC＝2①ABC＝130°，①BOC＝2①BAC＝100°，①点C是弧BD的中点，①BC CD，①①BOC＝①COD＝100°，①①AOD＝30°，①①AOD＝2①ACD，①①ACD＝15°，故选：B．【点拨】本题主要考查了圆周角定理，熟练掌握圆周角、圆心角、弧的关系是解题的关键．5．D【分析】连接OC，延长CD交OB于点E，如图，易得①AOB、①COE、①BDE都是等腰直角三角形，然后根据等腰直角三角形的性质求出CE与DE的长，从而可得答案．解：连接OC，延长CD交OB于点E，如图，①90∠=︒，C是AB的中点，AOB①①COE=45°，①//∠=︒，AOBCD OA，90①CE①OB，①①OCE=①COE=45°，==6①BE=OB－OE=6-，①OA=OB，90AOB∠=︒，①①ABO=45°，①①BDE=①ABO=45°，①EB=ED=6--=．①CD=CE－DE=(66故选：D．【点拨】本题考查了圆心角和弧的关系、等腰直角三角形的判定和性质等知识，属于常考题型，熟练掌握等腰直角三角形的判定和性质是解此题的关键．6．A【分析】延长AO交①O于点E，连接BE，由①AOB+①BOE=①AOB+①COD知①BOE=①COD，据此可得BE=CD，在Rt①ABE中利用勾股定理求解可得．解：如图，延长AO交①O于点E，连接BE，则①AOB+①BOE=180°，又①①AOB+①COD=180°，①①BOE=①COD，①BE=CD，①AE为①O的直径，则AE=10，①①ABE=90°，；故选择：A.【点拨】本题主要考查圆心角定理，解题的关键是掌握圆心角定理和圆周角定理．7．D【分析】由圆周角定理可求①ACB=90°，由弧的关系得出角的关系，进而可求①ABC=30°，①CAB=60°，由直角三角形的性质可求①CAH=①ACE=30°，即可求解．解：①AB是直径，①①ACB=90°，①①ABC+①CAB=90°，①2=，BC AC①①CAB=2①ABC，①①ABC=30°，①CAB=60°，①CD①AB，①①AEC=90°，①①ACE=30°，①点H是AG的中点，①ACB=90°，①AH=CH=HG，①①CAH=①ACE=30°，①①CAF=①CBF，①①CBF=30°，故选：D．【点拨】本题考查了圆周角定理，圆心角、弧、弦的关系，直角三角形的性质，求出①CAB 的度数是本题的关键．8．B【分析】根据AC=CD=DB和点E是点D关于AB的对称点，求出①DOB=①COD=①BOE=60°，求出①CED，即可判断①①；根据圆周角定理求出当M和A重合时①MDE=60°即可判断①；求出M点的位置，根据圆周角定理得出此时DF是直径，即可求出DF长，即可判断①．解：①AC=CD=DB，点E是点D关于AB的对称点，①BD=BE，①①DOB=①BOE=①COD=13×180°=60°，①①错误；①CED=12①COD=12×60°=30°=12①DOB，即①DOB=2①CED；①①正确；①BE的度数是60°，①AE的度数是120°，①只有当M和A重合时，①MDE=60°，①①CED=30°，①只有M和A重合时，DM①CE，①①错误；作C关于AB的对称点F，连接CF，交AB于N，连接DF交AB于M，此时CM+DM 的值最短，等于DF长，连接CD，①AC=CD=DB=AF，并且弧的度数都是60°，①①D=12×120°=60°，①CFD=12×60°=30°，①①FCD=180°-60°-30°=90°，①DF是①O的直径，即DF=AB=10，①CM+DM的最小值是10，①①正确；综上所述，正确的个数是2个．故选：B．【点拨】本题考查了圆周角定理，轴对称-最短问题等知识点，能灵活运用圆周角定理求出各个角的度数和求出M的位置是解此题的关键．9．D【分析】圆周角定理；翻折变换（折叠问题）；勾股定理；垂径定理；圆心角、弧、弦的关系；连接OA，求出OC，根据勾股定理求出AC，可得结论．解：连接OA，①将劣弧AB沿弦AB折叠交于OC的中点D，①OC23=r＝6（cm），OC①AB，①AC＝CB=cm），①AB＝2AC＝cm），故选：D．【点拨】本题主要考查了圆的基本性质，垂径定理，勾股定理，关键是学会添加常用辅助线，构造直角三角形解决问题．10．B【分析】连接BD ，BF ，先求解6AC BD ==， 可得AC BD =，AC AD AB +=，再求解19,BF可得AE BF ≠， AE AF AB +≠，从而可得答案.解：连接BD ，BF ，AB 直径，10AB =，8AD =，90,6ADB BD ∴∠=︒=，6AC =，AC BD ∴=，∴AC BD =，∴AC AD AB +=，AB 直径，10AB =，9AF =，90,AFB BF ∴∠=︒=5AE =，∴AE BF ≠，∴AE AF AB +≠，所以B 符合题意，故选：B ．【点拨】本题主要考查了圆中弧、弦的关系和直径所对的圆周角是直角，熟练掌握相关定理是解答本题的关键．11．D【分析】利用三角形内角和定理以及角平分线的定义求出①MAB +①MBA =60°，推出①AMB =120°，可判断A ，证明C ，E ，M ，D 四点共圆，利用圆周角定理可判断B ；在AB 上取一点T ，使得AT =AE ，利用全等三角形的性质证明BD =BT ，可判断C ；无法判断M 与①ABC 互补，可判断D．解：如图，①①ACB=60°，①①CAB+①CBA=120°，①AD，BE分别是①CAB，①CBA的角平分线，①①MAB+①MBA=12（①CAB+①CBA）=60°，①①AMB=180°-（①MAB+①MBA）=120°，故A符合题意，①①EMD=①AMB=120°，①①EMD+①ECD=180°，①C，E，M，D四点共圆，①①MCE=①MCD，① EM DM，①EM=DM，故B符合题意，四边形CEMD是O的内接四边形，60,AME ACB BMD在AB上取一点T，使得AT=AE，在①AME和①AMT中，AE ATMAE MAT AM AM，①①AME①①AMT（SAS），①①AME=①AMT=60°，EM=MT，①①BMD=①BMT=60°，MT=MD，在①BMD和①BMT中，MD MTBMD BMT BM BM，①①BMD①①BMT，①BD=BT，①AB=AT+TB=AE+BD，故C符合题意，①M，M'关于AC对称，①M=①AMC，①11802AMC CAB ACB11801802ABC=90°+12①ABC，①M与①ABC不一定互补，①点M'不一定在①ABC的外接圆上，故D不符合题意，故选D．【点拨】本题考查三角形的外接圆，四点共圆，圆周角定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．12．D【分析】根据直径所对的圆周角是直角，即可判断A，根据圆周角定理可判断B选项，根据圆周角与弧的关系可判断C，根据CDE CDB∠≠∠判断D选项．解：①AB、CD分别是①O的直径，90CBD∴∠=︒，①CB①BD，故A选项正确，如图，连接BE，DE AB∥，且①CDE＝62°，62BOD CDE∴∠=∠=︒，1312BCD BOD ∴∠=∠=︒， OC OB =，31CBO BCO ∴∠=∠=︒，62AOC ∴∠=︒，62CBE CDE ∠=∠=︒，31ABC ABE ∴∠=∠=︒，∴AC AE =，故B ，C 选项正确，31,90BCD CBD ∠=︒∠=︒，59BDC ∴∠=︒，62CDE ∠=︒，CDE CDB ∴∠≠∠，∴BD ≠DE ，故D 选项不正确，故选D ．【点拨】本题考查了圆周角定理，直径所对的圆周角是直角，掌握圆周角定理是解题的关键．13．1CM 【分析】如图，连接OD 、OC 、OE ，先计算出①DOC +①COE ＝90°，则可判断①ODE 为等腰直角三角形，所以DE OD 则OM ＝12DE 由C 点在弧DE 上，则0≤①COM ＜45°，根据三角形的性质，①COM 越大，CM 越长，当O 、M 、C 共线时CM 最小，C 在点A 或点B 时CM 最长，即OC -OM ≤CM ＜ME ；解：如图，连接OD 、OC ，①AB 为直径，①①AOC+①BOC＝180°，①D、E分别是AC、BC的中点，①①AOD＝①COD，①COE＝①BOE，①①DOC+①COE＝1（①AOC+①BOC）＝90°，2①①ODE为等腰直角三角形，OD①DE①M是弦DE的中点，DE①OM＝12①C点在弧DE上，①0≤①COM＜45°，①OMC中，OM，OC的长度确定，①①COM越大，CM越长，①O、C、M共线时CM最小，C在点A或点B时CM最长；①CM≥1﹣，2当C点在A点或B点时，CM①CM的取值范围是1≤CM．【点拨】本题考查了圆心角的概念，三角形的三边关系；根据三角形的性质判断CM的长度是解题关键．14．36°，72°，108°，144°【分析】根据扇形所占的百分比乘以360°进行解答即可．解：四个扇形的圆心角分别是360°×10%=36°；360°×20%=72°；360°×30%=108°；360°×40%=144°.故答案为36°，72°，108°，144°.【点拨】考查了扇形圆心角的度数问题，注意周角的度数是360°．15．①①①①【分析】根据优弧的定义，弦的定义，圆周角的定义，圆心角的定义逐项分析判断即可解：AbB ，AbD 都是大于半圆的弧，故①①正确，,A C 在圆上，则线段AC 是弦；故①正确；,,C A D 都在圆上，∴CAD ∠是圆周角而F 点不在圆上，则ADF ∠不是圆周角故①不正确；O 是圆心，,C A 在圆上∴COA ∠是圆心角故①正确故正确的有：①①①①故答案为：①①①①【点拨】本题考查了优弧的定义，弦的定义，圆周角的定义，圆心角的定义，理解定义是解题的关键．优弧是大于半圆的弧，任意圆上两点的连线是弦，顶点在圆上，并且两边都和圆相交的角叫做圆周角，顶点在圆心，并且两边都和圆相交的角叫做圆心角．16．0152=+-x x【分析】连接OD ，OE ，因为AD =EB ，根据等弧所对的圆心角相等可得①DOC=①EOF ，因为CD①AB ，EF①AB ，所以①DCO=①EFO=90°，又因为DO==EO ，所以Rt①DOC①Rt①EOF ，所以CO=OF=12，在Rt①DOC 中，，所以，，BC=AB -，所以以AC 和BC 的长为两根的一元二次方程是（x ）(x )=0，整理，得0152=+-x x ． 解：连接OE ，OD ，①AD =EB ，①①DOC=①EOF ，①CD①AB ，EF①AB ，①①DCO=①EFO=90°，又①DO=EO ，①Rt①DOC①Rt①EOF ， ①CO=OF=12，①在Rt①DOC 中，，AC=AO -，BC=AB - =，①以AC 和BC 的长为两根的一元二次方程是（x ）(x )=0，整理，得0152=+-x x ．故答案为：x 2．【点拨】本题考查圆心角定理及其推论，全等三角形的判定与性质以及根与系数的关系．此题属于开放题，注意数形结合与方程思想的应用．17． 90° 150°或30°【分析】如图，在①AOD 中，根据勾股定理的逆定理即可求出①AOD 的度数；连接OC ，易得△AOC 是等边三角形，从而可得∠AOC ＝60°，进一步利用角的和差即可求出①COD 的度数．解：如图，在①AOD 中，∵2222228OA OD +=+=，(228AD ==，①222OA OD AD +=，∴①AOD =90°；连接OC ，∵OA ＝OC ＝AC =2，∴△AOC 是等边三角形，∴∠AOC ＝60°．∴∠COD ＝∠AOC +∠AOD ＝60°+90°＝150°或∠COD ＝∠AOD ﹣∠AOC ＝90°－60°＝30°．故答案为：90°；150°或30°．【点拨】本题考查了圆心角、勾股定理的逆定理、等边三角形的判定与性质以及分类的数学思想，依照题意画出图形、熟练掌握相关知识是解题的关键．18．93【分析】根据圆周角定理的推论，得①DCE=32°，由CD AB⊥结合三角形外角的性质，得①BOC 的度数，从而得①BDC的度数，进而即可求解．解：①①DCE和①DBE是同弧所对的圆周角，①①DCE=①DBE=32°，①CD AB⊥，①①BOC=90°+①DCE=90°+32°=122°，①①BDC=12①BOC=12×122°=61°，①DFE∠=①DCE+①BDC=32°+61°=93°．故答案是：93°．【点拨】本题主要考查圆周角定理及其推论，三角形外角的性质，掌握“同弧或等弧所对的圆周角相等”，“同弧或等弧所对的圆周角等于圆心角的一半”，是解题的关键．19．57.5°【分析】根据平行线的性质得出①ODC=①AOD=65°，根据等腰三角形的性质和三角形内角和定理求出①ODA=①OAD=12（180°-①AOD）=57.5°，求出①ADC的度数，根据圆内接四边形的性质得出①B+①ADC=180°，再求出答案即可．解：连接AD，①①AOD=68°，AO①DC，①①ODC=①AOD=65°，①①AOD=65°，OA=OD，①①ODA=①OAD=1（180°-①AOD）=57.5°，2①①ADC=①ODA+①ODC=57.5°+65°=122.5°，①四边形ABCD是①O的内接四边形，①①B+①ADC=180°，①①B=57.5°，故答案为：57.5°．【点拨】本题考查了圆内接四边形的性质，圆周角定理，圆心角、弧、弦之间的关系，等腰三角形的性质等知识点，能求出①ADC的度数是解此题的关键．20．128【分析】连接AD．首先证明①ADC=①ADE，再利用圆内接四边形的性质求出①ADC即可解决问题．解：连接AD．①AC AE，①①ADC=①ADE，①①B+①ADC=180°，①①ADC=180°-116°=64°，①①CDE=2×64°=128°，故选：128．【点拨】本题考查圆心角，弧，弦的关系，圆周角定理，圆内接四边形等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．21．1 3【分析】根据已知条件得出①DCA=①DBA=30°，设DE=EC=x，由在直角三角形中，30°所对的直角边等于斜边的一半可以得出AE和BE的长，然后代入要求的式子进行计算即可得出答案．解：①①O的直径AB过CD的中点A，①AC＝AD，①DE＝EC，①AB是①O的直径，①①BED＝①CEA＝90°，①①C＝30°，①①DCA＝①DBA＝30°，设DE＝EC＝x，①①C＝30°，①AE，①①DBA＝30°，①BE，①AEBE13；故答案为：13．【点拨】本题主要考查了圆心角、弧、弦的关系以及圆周角定理，掌握在直角三角形中，30°所对的直角边等于斜边的一半是解题的关键．22．①①【分析】①由BD CD =，可得①COD =①BOD ，据此根据圆周角定理即可得结论；①由点M 是直径AB 上一动点，而CE 的位置是确定的，因此DM ①CE 不一定成立，可得结论；①由题意可得点D 和点E 关于AB 对称，因此CM +DM 的最小值是在点M 和点O 重合时取到，即CE 的长；①过点C 作CN ①AO 于点N ，利用解直角三角形可求得CN ，利用三角形面积公式求解即可．解：①BD CD =，COD BOD ∴∠=∠，12CED COD ∠=∠， 12CED BOD ∴∠=∠，故①正确； ①点M 是直径AB 上一动点，而CE 确定，∴DM ①CE 不一定成立，故①错误；①BD CD AC ==，60BOE AOC COD BOD ∠=∠=∠=∠=∴︒，①CED =30°，∴DE ①AB ，∴点D 和点E 关于AB 对称，∴CM +DM 的最小值是在点M 和点O 重合时取到，即CE 的长，AB =4，∴CE =AB =4，故①正确；①连接AC ，BD CD AC ==，∴①COA =60°，则①AOC 为等边三角形，边长为2，过点C 作CN ①AO 于N ，则sin 602CN OC =⋅︒==，在①COM 中，以OM 为底，OM 边上的高为CN ，1122COM S OM CN x ∴=⋅==△，故①错误； 综上，①①正确，故答案为：①①．【点拨】本题考查了圆周角定理，最小值问题，等边三角形判定和性质，三角形面积等知识，解题的关键是灵活运用所学知识解决问题．23． 越长 越长 越短【分析】根据圆心角定理解答即可.解：在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧越长，所对的弦越长，所对弦的弦心距越短．故答案为越长；越长；越短.【点拨】本题考查了圆心角定理及其推理，解此题的关键在于熟练掌握其知识点. 24．27°【分析】根据题意易得①ACB ＝90°，然后根据圆的性质及直角三角形的两个锐角互余可求解． 解：①AB 是①O 的直径，①①ACB ＝90°，①①A ＝90°﹣①ABC ＝90°﹣63°＝27°，①①D ＝①A ＝27°．故答案为27°．【点拨】本题主要考查圆的基本性质，熟练掌握圆的性质是解题的关键．25．（1）作图见分析；（2）53π 试题分析：（1）根据扇形定义及题目要求画出即可；（2）根据扇形的面积公式S=2360n rπ计算即可．解：（1）如图所示：（2）①①AOB=120°，①BOC=90°，①①AOC=150°，故S扇形AOC=2150253603ππ⨯⨯=．26．（1）26；（2）13【分析】（1）连接OB，结合OD①AB，根据垂径定理，推导得①AOD；再根据圆心角、圆周角的性质，即可得到答案；（2）结合题意，根据垂径定理性质，计算得AC；再结合OD①AB，通过勾股定理即可计算得①O的半径．解：（1）连接OB①⊥OD AB①AD BD=①52AOC BOD∠=∠=①12DEB BOD ∠=∠①26DEB∠=（2）①⊥OD AB①112412 22AC AB==⨯=设OA x =，则8OC x =-在Rt ACO 中，()222128x x =+-①13x =①O 的半径长为13．【点拨】本题考查了圆的知识；解题的关键是熟练掌握垂径定理、圆心角、圆周角、勾股定理的性质，从而完成求解．27．(1)同弧所对的圆周角相等；(2)见分析；1；【分析】（1）根据同弧所对的圆周角相等可得ABE ACD ∠=∠；（2）由BAE CAD ∠=∠可得BAC EAD ∠=∠，再由ACB ADE ∠=∠可得ABC AED ∽△△； （3）连接AD ，BE ，由2AB BC CD DE EA =====可得AB BC CD DE BA ====，进而BE AD BD ==，BE =AD =BD ，再由AB DE AE BD BE AD ⋅+⋅=⋅解方程即可；(1)解：①同弧所对的圆周角相等，AD AD =，①ABE ACD ∠=∠；故答案为：同弧所对的圆周角相等；(2)解：①BAE CAD ∠=∠，①BAE EAC CAD EAC ∠+∠=∠+∠，①BAC EAD ∠=∠，①AB AB =，①ACB ADE ∠=∠；(3)解：如图，连接AD ，BE ，①2AB BC CD DE EA =====，①AB BC CD DE BA ====，①AB AE AE ED CD CB +=+=+，①BE AD BD ==，①BE =AD =BD ，①四边形ABDE 是O 的内接四边形，①AB DE AE BD BE AD ⋅+⋅=⋅，①2AB DE EA ===，①2222BD BD ⨯+=，解得：1BD =或1BD =，①对角线BD 1；【点拨】本题考查了圆内接多边形，圆心角、弧、弦关系，相似三角形的判定和性质，一元二次方程等知识；掌握在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等是解题关键．28．(1)见分析(2)【分析】（1）根据AB CD ⊥得，90AME DMB ∠=∠=︒，根据等弧或同弧所对的圆周角相等可得BDC BAF ∠=∠，DBA DFA ∠=∠，根据等角的余角相等可得AEM DBM ∠=∠，进而可得DFA DEF ∠=∠，根据等角对等边即可得证；（2）连接,,,OF OC CF AC ，根据①BAF ＝22.5°，证明COF 是直角三角形，勾股定理求得CF ，进而证明MN 是ECF △的中位线，即可求解．解：(1)BF BC =，BDC BAF ∴∠=∠，AB CD ⊥，90AME DMB ∴∠=∠=︒，90,90BAF AEM CDB DBM ∴∠+∠=︒∠+∠=︒，AEM DBM ∴∠=∠，AD AD =，DBA DFA ∴∠=∠，AEM DEN ∠=∠，DFA DEF ∴∠=∠，DE DF ∴=；(2)如图，连接,,,OF OC CF AC ，BF BC =，22.5CDB BDF BAF ∠=∠=∠=∴︒， 45CDF CDB BDF ∴∠=∠+∠=︒， CF CF =，290COF CDF ∴∠=∠=︒，在Rt COF △中，CF == 由（1）得，DE DF =，DEF ∴是等腰三角形， CDB BDF ∠=∠，EN FN ∴=，N ∴是EF 的中点，BF BC =，BAF BAC ∴∠=∠，AB CD ⊥，AM EC ∴⊥，EM MC ∴= ，∴12MN CF == 【点拨】本题考查了圆周角定理，同弧所对的圆周角相等，等腰三角形的性质与判定，勾股定理，三角形中位线的性质与判定，掌握以上知识是解题的关键．。
与圆有关的性质练习题
圆的练习题一1、半径为R 的圆中，垂直平分半径的弦长等于（ ）A ．43RB ．23R C ．3R D ．23R2．如图1，半圆的直径AB=4，O 为圆心，半径OE ⊥AB ，F 为OE 的中点，CD ∥AB ，则弦CD 的长为（ ）A ．23B ．3C ．5D ．253．已知：如图2，⊙O 的直径CD 垂直于弦AB ，垂足为P ，且AP=4cm ，PD=2cm ，则⊙O 的半径为（ ）A ．4cmB ．5cmC ．42cmD ．23cm3．如图3，同心圆中，大圆的弦AB 交小圆于C 、D ，已知AB=4，CD=2，AB 的弦心距等于1，那么两个同心圆的半径之比为（ ）A ．3：2B ．5：2C ．5：2D ．5：44、在⊙O 中，圆心角∠AOB=90°，点O 到弦AB 的距离为4，则⊙O 的直径的长为（ ）A ．42B ．82C ．24D ．165、下列命题中，正确的有（ ） A ．圆只有一条对称轴B ．圆的对称轴不止一条，但只有有限条C ．圆有无数条对称轴，每条直径都是它的对称轴D ．圆有无数条对称轴，经过圆心的每条直线都是它的对称轴 6．下列说法中，正确的是（ ） A ．等弦所对的弧相等B ．等弧所对的弦相等C ．圆心角相等，所对的弦相等D ．弦相等所对的圆心角相等7．⊙O 中，M 为的中点，则下列结论正确的是( )． A ．AB >2AM B ．AB =2AMC ．AB <2AMD ．AB 与2AM 的大小不能确定8、如图所示，圆O 的弦AB 垂直平分半径OC ．则四边形OACB 是（ ）A ．正方形 B.长方形C ．菱形D ．以上答案都不对9、如图，AB 是⊙O 的弦，OC AB ⊥于点C ，若8cm AB =，3cm OC =，则⊙O 的半径为 cm ．10.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示，已知AB ＝16m ，半径 OA ＝10 m ，高度CD 为_ ____m ．11、如图所示，AB 是圆O 的直径，弦CD ⊥AB ，E 为垂足，若AB=9，BE=1，则CD=_________________12. ⊙O 的半径是3cm ，P 是⊙O 内一点，PO=1cm ，则点P 到⊙O 上各点的最小距离是 ．13. 一点和⊙O 上的最近点距离为4cm ，最远距离为9cm ，则这圆的半径是 cm ．14. 若圆的半径为2cm ，圆中的一条弦长23cm ，则此弦中点到此弦所对弧的中点的距离为 ．15. AB 为圆O 的直径，弦CD ⊥AB 于E ，且CD=6cm ，OE=4cm ，则AB= ． 16．半径为5的⊙O 内有一点P ，且OP=4，则过点P 的最短的弦长是 ，最长的弦长是 ．17.如图，弦DC 、FE 的延长线交于⊙O 外一点P ，直线PAB 经过圆心O ，请你根据现有圆形，添加一个适当的条件： ，使∠1=∠2．18.已知：⊙O 半径为6cm ，弦AB 与直径CD 垂直，且将CD 分成1∶3两部分,求：弦AB 的长．第8题第9题第10题19. 如图，AB、CD、EF都是⊙O的直径，且∠1=∠2=∠3，弦AC、EB、DF是否相等？为什么？20、已知：如图，A、B、C、D在⊙O上，AB=CD．求证：∠AOC=∠DOB．21、如图所示，以ABCD的顶点A为圆心，AB为半径作圆，作AD，BC于E，F，•延长BA交⊙O于G，求证：GE=EF22、 如图，⊙O 直径AB 和弦CD 相交于点E ，AE=2，EB=6，∠DEB=30°，求弦CD 长．23.⊙O 的直径为50cm ，弦AB ∥CD ，且AB=40cm ，CD=48cm ，求弦AB 和CD 之间的距离．24、 如图所示，破残的圆形轮片上，弦AB 的垂直平分线交弧AB 于点C ，交弦AB 于点D 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专项练习二与圆有关的角圆心角定理、圆周角定理为圆中角的等量关系提供了丰富的理论依据，圆中确定角相等一般按弧所对角来确定，要特别注意直径与直角的关系．1.如下图，AE∥CD，连结AO，∠AOC=40°，那么所对的圆心角的度数为(A).A.40°B.50°C.60°D.30°(第1题)(第2题)(第3题)(第4题)2.如下图，AB是⊙O的一条弦，且OD⊥AB于点C，所对的圆周角∠DEB=35°，那么∠AOD的度数是(C).A.35°B.55°C.70°D.110°3AB，那么弦AB3.如下图，在⊙O中，圆心O到弦AB的距离OD=6所对圆心角的度数为(C).A.60°B.90°C.120°D.1 50°4.如下图，量角器的外缘边上有A，P，Q三点，分别表示读数180°，70°，30°，那么∠PAQ的度数为(D).A.10°B.30°C.40°D.20°5.如下图，在△ABC中，AB=AC，以AB为直径的⊙O分别交BC，A C于点D，E，那么以下判断：①BD=CD；②BD=DE；③AE=DE；④△AB C为锐角三角形.其中正确的判断有(C).A.1个B.2个C.3个D.4个(第5题)(第6题)(第7题)(第8题)6.如下图，⊙O的圆心O在正方形网格的格点上，A，B两点在⊙O上，并且也在格点上，C为⊙O上一点，那么∠ACB= 45°．7.如下图，，AD为⊙O的弦，假设∠BAD=50°，那么∠A ED= 75°．8.如下图，AC为⊙O的直径，B，D，E都是⊙O上的点，那么∠A+∠B+∠C= 90°．图1图2〔第9题〕9.如下图，在⊙O中，半径OA与弦BD垂直，点C在⊙O上，∠AO B=80°.(1)假设点C在优弧BD上，求∠ACD的大小.(2)假设点C在劣弧BD上，直接写出∠ACD的大小.【答案】(1)∵AO⊥BD，∴=.∴∠AOB=2∠ACD.∵∠AOB=80°，∴∠ACD=40°.〔第9题答图〕(2)①如答图所示，当点C1在上时，∠AC1D=∠ACD=40°.②如答图所示，当点C2在上时，∵∠AC2D+∠ACD=180°，∴∠AC2D=140°.综上所述，∠ACD=140°或40°.(第10题)10.如下图，在平面直角坐标系中，以点M(0，3)为圆心，23为半径作⊙M交x轴于A，B两点，交y轴于C，D两点，连结AM并延长交⊙M于点P，连结PC交x轴于点E、(1)求点C，P的坐标．(2)求证：BE=2OE、〔第10题答图〕【答案】(1)如答图所示，连结PB.∵PA是⊙M的直径，∴∠PBA=90°.∵MO⊥AB，∴PB∥MO,OB=OA=3.∴PB=2OM=23.∴点P坐标为(3，23).∵MC=23.OM=3,∴OC=MC-OM=3.∴点C的坐标为(0，-3).(2)如答图所示，连结AC.∵AM=MC=23，AO=3，OC=3.∴AM=M C=AC=23.∴△AMC为等边三角形.∵AP为⊙M的直径，∴∠ACP=90°.∴∠OCE=30°.∴OE=1.∴BE=OB-OE=2.∴BE=2OE.11.如下图，过等腰三角形ABC三边的中点D，F，G作⊙O，并与两腰AB，AC分别相交于点H，E，假设∠B=72°，那么∠BDH等于(C).A.32°B.34°C.36°D.72°(第11题)(第12题)(第13题)12.如下图，A，B，C是⊙O上的三个点，∠AOB=2∠BOC，那么以下说法中，正确的选项是(D).A.∠OBA=∠OCAB.四边形OABC内接于⊙OC.AB=2BCD.∠OBA+∠BOC=90°13.如下图，四边形ABCD为矩形，△ACE为以AC为底的等腰直角三角形，连结BE分别交AD，AC于点F，N，CM平分∠ACB交BN于点M.给出以下结论：①BE⊥ED；②AB=AF；③EM=EA；④AM平分∠BAC.其中正确的结论有(D).A.1个B.2个C.3个D.4个14.如下图，AB是⊙O的直径，的度数是60°，的度数是20°，且∠AFC=∠BFD，∠AGD=∠BGE，那么∠FDG的度数为50°．(第14题) (第15题)15.如下图，AB=AC=AD，∠ABD=50°，∠BDC=30°，那么∠CBD= 10°.16.如下图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AC，点D为垂足，E是BC上一点，G是DE的中点，OG的延长线交BC于点F．(1)线段OD，BC所在直线有怎样的位置关系？写出你的结论，并给出证明过程．(2)线段BE，EF，FC三者之间有怎样的数量关系？写出你的结论，并给出证明过程．(第16题)【答案】(1)OD∥BC.证明：∵AB是⊙O直径，C是⊙O上一点，∴∠ACB=90°，即BC⊥AC.∵OD⊥AC，∴OD∥BC.(2)EF=BE+FC.证明：∵OD ⊥AC ，∴AD=DC.∵O 为AB 的中点，∴O D 是△ABC 的中位线.∴BC=2OD.∵∠ODG=∠FEG ，DG=EG ，∠GOD=∠GFE ，∴△ODG ≌△FEG.∴O D=EF.∴BC ＝BE+EF+FC=2OD=2EF.∴EF=BE+FC.17.如下图，是劣弧，M 是的中点，B 为上任意一点.自点M 向BC 引垂线，垂足为点D ，求证：AB+BD=DC 、(第17题)〔第17题答图〕 【答案】如答图所示，在CD 上取点N ，使CN=AB ，连结CM ，MN.∵M 是的中点，∴. ∴AM=CM.∵AB ＝CN ，∠BAM=∠BCM ，AM ＝CM ，∴△ABM ≌△CNM.∴BM=MN.∵MD ⊥BN ，∴BD=DN.∴AB+BD=CN+DN ＝CD.(第18题)18.如下图，A ，B 是⊙O 上的两个定点，P 是⊙O 上的动点(不与点A ，B 重合)，我们称∠APB 是⊙O 上关于点A ，B 的滑动角．(1)∠APB 是⊙O 上关于点A ，B 的滑动角.①假设AB 是⊙O 的直径，那么∠APB= 90° .②假设⊙O 的半径是1，AB=2，求∠APB 的度数．(2)O2是⊙O1外一点，以点O2为圆心作一个圆与⊙O1交于A ，B 两点，∠APB 是⊙O1上关于点A ，B 的滑动角，直线PA ，PB 分别交⊙O2于点M ，N(点M 与点A ，点N 与点B 均不重合)，连结AN ，试探索∠AP B 与∠MAN ，∠ANB 之间的数量关系．【答案】 (1)①90°②如答图1所示，连结AB ，OA ，OB.在△AOB 中，∵OA=OB=1,AB =2，∴OA2+OB2=AB2.∴∠AOB=90°.当点P 在优弧APB 上时，∠APB=21∠AOB=45°.当点P 在劣弧AB 上时，∠AP ′B=21 (360°-∠AOB)=135°.(2)根据点P 在⊙O1上的位置分为以下四种情况.图1图2图3图4图5〔第18题答图〕①如答图2所示，点P在⊙O2外，且点A在点P与点M之间，点B 在点P与点N之间.∵∠MAN=∠APB+∠ANB，∴∠APB=∠MAN-∠ANB.②如答图3所示，点P在⊙O2外，且点A在点P与点M之间，点N 在点P与点B之间.∵∠MAN=∠APB+∠ANP=∠APB+(180°-∠ANB)，∴∠APB=∠MA N+∠ANB-180°.③如答图4所示，点P在⊙O2外，且点M在点P与点A之间，点B 在点P与点N之间.∵∠APB+∠ANB+∠MAN=180°，∴∠APB=180°-∠MAN-∠ANB.④如答图5所示，点P在⊙O2内.∠APB=∠MAN+∠ANB.(第19题)19.如下图，AB是⊙O的直径，点C在⊙O上，CD⊥AB于点D，且∠COD=60°，E为上一动点(不与点B，C重合)，过点E分别作于EF⊥AB于点F，EG⊥OC于点G．现给出以下四个命题：①∠GEF=60°；②CD=GF；③△GEF一定为等腰三角形；④点E在上运动时，存在某个时刻使得△GEF为等边三角形．其中正确的命题是①②④(写出所有正确命题的序号).〔第20题〕〔第20题答图〕20.【上海】如下图，⊙O是△ABC的外接圆，，点D在边BC 上，AE∥BC，AE=BD.(1)求证：AD=CE.(2)如果点G在线段DC上(不与点D重合)，且AG=AD，求证：四边形AGCE是平行四边形.【答案】(1)在⊙O 中，∵，∴AB=AC.∴∠B=∠ACB.∵AE ∥B C ，∴∠EAC=∠ACB.∴∠B=∠EAC.在△ABD 和△CAE 中，∵⎪⎩⎪⎨⎧=∠=∠=AE BD EAC B CA AB ，∴△ABD ≌△CAE(SAS).∴AD=CE. (2)如答图所示，连结AO 并延长，交边BC 于点H.∵，OA 为半径，∴AH ⊥BC.∴BH=CH.∵AD=AG ，∴DH=HG.∴BH -DH=CH -GH ，即BD=CG.∵BD=AE ，∴C G=AE.∵CG ∥AE ，∴四边形AGCE 是平行四边形.21.如图1所示，AB 是⊙O 的直径，C 是上的一个动点(点C 与点A ，B 不重合)，连结AC ，D 是的中点，作弦DE ⊥AB ，垂足为点F. (1)假设点C 和点E 不重合，连结BC ，CE 和EB ，当△BCE 是等腰三角形时，求∠CAB 的度数.(2)假设点C 和点E 重合，如图2所示，试探索AB 与AC 的数量关系并说明理由.图1图2〔第21题〕图1 图2 〔第21题答图〕【答案】(1)连结OC ，当△BCE 是等腰三角形时，分两种情况：①当时，如答图1所示，∴CE=BC.设的度数为x °，那么的度数为x °，的度数为2x °.∵DE ⊥AB ，AB 为直径，∴.∴的度数为3x °.∵D 是的中点，∴的度数为6x °∴的度数为2x °+3x °=5x °.又∵AB 的度数为180°，∴5x=180，解得x=36.∴∠CAB=21×36°=18°.②当CE=BE 时，如答图2所示.∴.设的度数为x °，那么的度数为x °.∵DE ⊥AB ，AB 为直径，∴.∴的度数为3x °.∵D 是的中点，∴的度数为6x °.∴的度数为4x °.又的度数为180°，∴4x=180，解得x=45.∴的度数为90°.∴∠CAB=21×90°＝45°. 综上所述，当△BCE 是等腰三角形时，∠CAB 的度数是18°或45°. (2)AC=23AB.理由如下：设的度数为x °，那么的度数为x °.∵D 是的中点，∴,且其度数为2x °.∴的度数为3x °.∵的度数为180°，∴3x=180，解得x=60.∴∠A=30°.∵AB 为⊙O 的直径，∴A C=23AB.。