常见的连续型随机变量
连续型随机变量及其概率密度

(3) 计算落入各子区间内观测值频数 ni 频率 fi = ni / n, i = 1, 2, ···, m;
子区间 (127.5, 131.5) 频数 6 频率 0.06
(131.5, (135.5, (139.5, (143.5, (147.5, (151.5,
135.5) 139.5) 143.5) 147.5) 151.5) 155.5)
设连续型随机变量 X 的分布函数为
x a, 0, x F ( x ) A B arcsin , a x a , a x a. 1, 求 : (1) 系数 A, B 的值; a ( 2) P{ a X }; 2 ( 3) 随机变量 X 的概率密度.
例1 某工厂生产一种零件,由于生产过程中各 种随机因素的影响,零件长度不尽相同。现测 得该厂生产的100个零件长度(单位: mm)如下:
129, 132, 136, 145, 140, 145, 147, 142, 138, 144, 147, 142, 137, 144, 144, 134, 149, 142, 137, 137, 155, 128, 143, 144, 148, 139, 143, 142, 135, 142, 148, 137, 142, 144, 141, 149, 132, 134, 145, 132, 140, 142, 130, 145, 148, 143, 148, 135, 136, 152, 141, 146, 138, 131, 138, 136, 144, 142, 142, 137, 141, 134, 142, 133, 153, 143, 145, 140, 137, 142, 150, 141, 139, 139, 150, 139, 137, 139, 140, 143, 149, 136, 142, 134, 146, 145, 130, 136, 140, 134, 142, 142, 135, 131, 136, 139, 137, 144, 141, 136.
概率论总结及例题
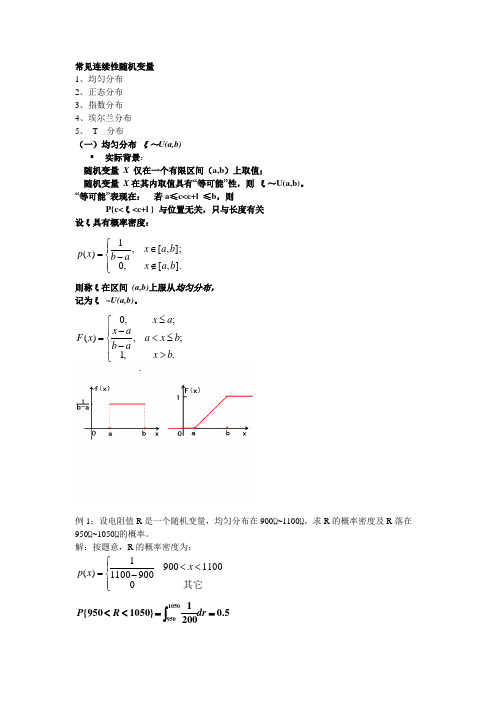
常见连续性随机变量1、均匀分布2、正态分布3、指数分布4、埃尔兰分布5、 T 分布(一)均匀分布 ξ~U(a,b)▪ 实际背景:随机变量 X 仅在一个有限区间(a,b )上取值;随机变量 X 在其内取值具有“等可能”性,则 ξ~U(a,b)。
“等可能”表现在: 若a ≤c<c+l ≤b ,则P{c<ξ<c+l } 与位置无关,只与长度有关设ξ具有概率密度:则称ξ在区间 (a,b)上服从均匀分布,记为ξ ~U(a,b)。
例1:设电阻值R 是一个随机变量,均匀分布在900Ώ~1100Ώ,求R 的概率密度及R 落在 950Ώ~1050Ώ的概率。
解:按题意,R 的概率密度为:⎪⎩⎪⎨⎧∉∈-=].,[,0];,[,1)(b a x b a x a b x p ⎪⎩⎪⎨⎧>≤<--≤=.,1;,;,0)(b x b x a a b a x a x x F ⎪⎩⎪⎨⎧<<-=其它0110090090011001)(x x p 5.02001}1050950{1050950==<<⎰dr R P例2 ξ ~ U (2, 5). 现在对 ξ 进行三次独立观测,试求至少有两次观测值大于 3 的概率.解:记 A = { ξ > 3 },则 P (A ) = P ( ξ> 3) = 2/3设 Y 表示三次独立观测中 A 出现的次数,则 Y ~ B (3, 2/3),所求概率为P (Y ≥2) =P (Y =2)+P (Y =3)=20/27(二)正态分布(normal distribution )记为ξ ~ N (μ, σ2),其中σ >0, μ 是任意实数.➢ μ 是位置参数➢ σ 是尺度参数.正态分布的性质(1) p (x ) 关于μ 是对称的. 在μ 点 p (x ) 取得最大值.(2) 若σ 固定, μ 改变, p (x )左右移动, 形状保持不变.(3) 若μ 固定, σ 改变,σ 越大曲线越平坦; σ 越小曲线越陡峭标准正态分布N (0, 1)密度函数记为 ϕ(x ),分布函数记为 Φ(x ).Φ(x ) 的计算(1) x ≥ 0 时, 查标准正态分布函数表.(2) x < 0时, 用 若 ξ ~ N (0, 1), 则(1) P (ξ < a ) = Φ(a );(2) P (ξ≥a ) =1-Φ(a );(3) P (a ≤ξ<b ) = Φ(b )Φ-(a );(4) 若a ≥ 0, 则P (|ξ|<a ) = P (-a <ξ<a ) = Φ(a )Φ-(-a ) = Φ(a )- [1- Φ(a )] = 2Φ(a )-1230233*********C C =+⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2()(),22x p x x μσ⎧⎫-⎪⎪=--∞<<∞⎨⎬⎪⎪⎩⎭R x dt e x F x t ∈=⎰∞---,21)(222)(σμσπ1(1) (0),2Φ=(2)()1()x x Φ-=-Φ()1().x x Φ=-Φ-例2.5.1 设 ξ ~ N (0, 1), 求P (ξ>-1.96) , P (|ξ|<1.96)解: P (ξ>-1.96)= 1- Φ(-1.96) = 1-(1- Φ(1.96)) = Φ(1.96)= 0.975 (查表得)P (|ξ|<1.96)= 2 Φ(1.96)-1= 2 ⨯0.975-1= 0.95例2.5.2 设 ξ ~ N (0, 1), P (ξ ≤ b ) = 0.9515, P (ξ ≤ a ) = 0.04947, 求 a , b . 解: Φ(b ) = 0.9515 >1/2,所以 b > 0,反查表得: Φ(1.66) = 0.9515,故 b = 1.66而 Φ(a ) = 0.0495 < 1/2,所以 a < 0,Φ(-a ) = 0.9505, 反查表得:Φ(1.65) = 0.9505,故 a = - 1.65一般正态分布的标准化 结论1 设 ξ ~ N (μ, σ 2), 结论2:若 ξ ~ N (μ, σ 2), 则 若 ξ ~ N (μ, σ2), 则P (ξ<a ) = , P (ξ>a ) = 例2.5.3 设ξ ~ N (10, 4), 求 P (10<ξ<13), P (|ξ-10|<2).解: P (10<ξ<13) = Φ(1.5)Φ-(0) = 0.9332 - 0.5= 0.4332P (|ξ -10|<2) = P (8<ξ<12)= 2Φ(1)-1= 0.6826例2.5.4 设 ξ ~ N (μ, σ 2), P (ξ ≤ -5) = 0.045,P (ξ ≤ 3) = 0.618, 求 μ 及 σ.解:μ = 1.76σμξη-=()x F x μσ-=Φ⎛⎫ ⎪⎝⎭a μσ-⎛⎫Φ ⎪⎝⎭1a μσ-⎛⎫-Φ ⎪⎝⎭5 1.6930.3μσμσ+⎧=⎪⎪⎨-⎪=⎪⎩σ =4课堂练习(1)已知ξ~ N(3, 22), 且P{ξ>k} = P{ξ≤k}, 则k = ( ).课堂练习(2)设ξ~ N(μ, 42), η~ N(μ, 52), 记p1 = P{ξ≤μ-4},p2 = P{η≥μ +5}, 则( )①对任意的μ,都有p1 = p2②对任意的μ,都有p1 < p2③只个别的μ,才有p1 = p2④对任意的μ,都有p1 > p2课堂练习(3)设ξ~ N(μ , σ2), 则随σ的增大,概率P{| ξ-μ | <σ} ( )①单调增大②单调减少③保持不变④增减不定▪例假设在设计公共汽车车门的高度时,要求男子的碰头机会在1%以下,设男子的身高ξ(cm)服从正态分布,ξ~ N (170,36),问车门高度至少应为多高?实际背景:如果一个随机现象是由大量微小的相互独立的因素共同构成,那么描述这种随机现象的随机变量通常被认为服从或近似服从正态分布.在自然现象和社会现象中,大量随机变量都服从或近似服从正态分布。
概率统计中的离散型随机变量与连续型随机变量

概率统计中的离散型随机变量与连续型随机变量概率统计是数学的一个分支,用于研究随机现象的规律性和不确定性。
在概率统计中,随机变量是一个非常重要的概念。
随机变量可以分为离散型随机变量和连续型随机变量两种类型。
本文将介绍这两种类型的随机变量以及它们的特点和应用。
一、离散型随机变量离散型随机变量是指在一定范围内取有限个或可列个值的随机变量。
它的特点是在定义域内的每个值都有一定的概率与之对应。
离散型随机变量的概率可以通过概率分布函数来描述。
概率分布函数是一个将随机变量的取值映射到概率的函数。
离散型随机变量常见的例子有抛硬币的结果、掷骰子的点数、抽奖的中奖号码等。
这些随机变量的取值都是有限个或可列个,每个取值的概率可以通过实验或统计数据得到。
离散型随机变量的期望值和方差是衡量其分布特征的重要指标。
期望值表示随机变量的平均取值,方差表示随机变量取值的离散程度。
通过计算期望值和方差,可以更好地理解和描述离散型随机变量的分布特征。
离散型随机变量在实际应用中有着广泛的应用。
例如,在市场调研中,我们可以将消费者的购买行为看作是一个离散型随机变量,通过统计分析不同购买决策的概率分布,可以了解不同消费者的购买偏好和市场需求。
二、连续型随机变量连续型随机变量是指在一定范围内可以取任意实数值的随机变量。
与离散型随机变量不同,连续型随机变量的取值是连续的,无法一一列举出来。
连续型随机变量的概率可以通过概率密度函数来描述。
概率密度函数是一个描述随机变量概率分布的函数,它可以表示在某个取值范围内随机变量出现的概率密度。
与离散型随机变量的概率分布函数不同,连续型随机变量的概率密度函数在定义域内的每个点上的函数值并不表示该点的概率,而是表示该点附近的概率密度。
连续型随机变量常见的例子有身高、体重、温度等物理量。
这些随机变量的取值可以是任意的实数,通过概率密度函数可以描述它们的概率分布情况。
与离散型随机变量类似,连续型随机变量也有期望值和方差这两个重要指标。
3.2常见的一维连续型随机变量-PPT文档

a
b x
返回主目录
2019年2月5日星期二
返回
3.2
均匀分布的分布函数
常用连续型随机变量
若 随 机 变 量 X 服 从 区 间 ab , 上 的 均 匀 分 布 , 则 X 的 分 布 函 数 为
0 xa x a Fx a x b b a b x 1
a b
由此可知,
2019年2月5日星期二
1 dx 1 . ba a 1 a x b f xba 确是密度函数. 其它 0 返回主目录
1
目录 上页 下页 返回
3.2
均匀分布的概率背景
常用连续型随机变量
如果随机变量 X 服从区间 a , b 上的均匀分布, 变量
1.
由此可知,
ex f x 0
2019年2月5日星期二 8
确是一密度函数.
目录 上页
ቤተ መጻሕፍቲ ባይዱ
返回主目录
下页
返回
3.2
常用连续型随机变量
指数分布的分布函数
若随机变量 X服从参数 指数分布, 则 X 的分布函数为
x0 0 x x F 1 e x 0
2019年2月5日星期二
11
目录
上页
返回主目录
下页
返回
3.2
密度函数的验证
常用连续型随机变量
2 设 X ~ N , , f x 是其密度函数
1 f x e 2
x 2
2 2
0
下面验证:
x
x 2 2
2
1 f x dx e 2
2019年2月5日星期二 12
连续型随机变量及其概率密度

1. 均匀分布
设连续型随机变量
X
具有概率密度f
(
x)
b
1
a
,
a x b,
0,
其它,
则称 X 在区间 (a, b) 区间上服从均匀分布,记为 X ~ U (a, b).
说明:
对c, l R, 如果(c, c l ) (a, b), 则
cl
l
P(c X c l ) c
f ( x)dx ba
1
( x )2
e , 2 2
2
x
, ( 0)为常数, 则称X服从正态分布,记作:X : N(, 2).
0, 1时, X : N (0,1)
概率密度: ( x)
1
x2
e2
2
说明:
f(x)满足概率条件: f(x) 0,
+ f(x)dx 1 -
证明(2): 令 x- t, 则x t, dx dt
解 : (1) 由概率密度的定义 :
f ( x)dx 1
-
f ( x)dx
3 C(9 x2 )dx 1
-
-3
C 1 36
(2)
P{ X 0}
0 -3
1 36
(9
x2 )dx
1 36
(9x
x3 3
)
|03
1 2
P{1 X 1} 1 1 (9 x2 )dx 13
-1 36
k 0
n大,p小,np=3,用=np=3的泊松近似
上式 1 N 3k e3 0.01
k0 k !
N 3k e3 0.99
k0 k !
查泊松分布表,最小N=8。至少配8名维修工。
常见的连续型随机变量

02 均匀分布
定义和性质
定义
均匀分布是一种连续型概率分布,在 概率论和统计学中,均匀分布也叫矩 形分布,它是对称概率分布,在相同 长度间隔的分布概率是等可能的。
性质
均匀分布具有等可能性、对称性、均 匀性等特点。其分布函数是一条斜线 ,概率密度函数是一个常数。
概率密度函数和分布函数
概率密度函数
均匀分布的概率密度函数是一个常 数,表示为f(x) = 1/(b-a),其中a 和b是区间的端点,x属于[a, b]。
伽玛分布的概率密度函数具有指数函数和幂函数的乘积形式,形状 参数和尺度参数分别控制分布的形状和尺度。
性质
伽玛分布具有可加性,即多个独立同分布的伽玛随机变量的和仍然 服从伽玛分布。
贝塔分布
定义
贝塔分布是一种在[0,1]区间上的连续型概率分布,常用于描述比例、概率等随机变量的分布情况。
概率密度函数
贝塔分布的概率密度函数具有幂函数和Beta函数的乘积形式,形状参数控制分布的形状。
跨学科交叉融合
连续型随机变量的研究涉及数学、统 计学、计算机科学等多个学科领域。 未来,跨学科交叉融合将成为推动连 续型随机变量研究发展的重要趋势。 通过整合不同学科的优势和资源,我 们可以更深入地理解连续型随机变量 的本质和规律,为解决实际问题提供 更有效的手段和方法。
THANKS FOR WATCHING
均匀分布
在某一区间内,每个取值的可能性都 相等。
03
指数分布
描述某些随机事件发生的时间间隔的概率分 布,如放射性元素的衰变时间、电话交换台
的呼叫间隔时间等。
05
04
正态分布
一种钟形曲线分布,具有广泛的应用 背景,如自然和社会科学中的各种测 量误差、产品质量控制等。
连续型随机变量

5
0
20 1 1 dx dx 15 30 30
1 3
2. 指数分布 若连续型随机变量 X 具有概率密度 f (x)为:
x 1 x0 e f ( x ) 0 其它 其中 0 为常数 则称 X 为服从参数 的指数分布
注: ▲ 易证 f ( x ) 满足:
1 . f ( x) 0 , 2 . f ( x )dx 1
0
0
▲ 由分布函数定义可得:若X 服从指数分布,则 X 的分布函数为:
x 1 e F ( x) 0
x0 其它
若X 服从指数分布,则: 对任意的 s , t 0 有:
P {X s t X s } P { X t }
由分布函数定义可得:若X 服从均匀分布,则 ▲ X 的分布函数为:
0 x a F ( x) x a a x b ba 1 x b
图形:
1
F ( x)
a
0
b
x
例7.某公共汽车站从上午7时起,每15分钟来一班 车,即 7:00,7:15,7:30, 7:45 等时刻有汽车 到达此站,如果乘客到达此站时间 X 是7:00 到 7:30 之间的均匀随机变量 试求: (1) 乘客候车时间少于 5 分钟的概率 (2) 乘客候车时间超过10分钟的概率
P {10 X 15} P {25 X 30} 15 1 30 1 1 dx dx 10 30 25 30 3
候车时间超过10分钟,则乘客必须在7:00到7:05或 7:15到7:20之间到达车间
P ( 0 x 5) P (15 x 20)
高斯
2.4连续型随机变量及其概率密度函数

-?
a b- a
连续型随机变量及概率密度函数
注
蝌 P{c < X ? c l} = c+l f ( x)dx = c+l 1 dx = l
c
c b- a b- a
随机变量 X 落在任一长度为 l 的子区间(c,c + l],(a ? c c + l ? b)
内的可能性是相同的.
均匀分布的分布函数为
2
解 (2)X的分布函数为
ì
0,
ï
ï
ò ï
x x dx = x2 ,
F
(
x
)
=
ï í
ï
蝌 ï
ï
3 x dx + 06
06
x 3
骣 琪 琪 桫2
-
x 2
12 x2
dx = - 3 + 2x - , 4
ï î
1,
x <0 0? x 3 3? x 4
x³ 4
连续型随机变量及概率密度函数
例 1 设随机变量 X 具有概率密度
f
(x)
=
ì ï í
1 5
,0
<
x
<
5,
ï î
0,
其他
ì 0,
ï
蝌 F ( x) =
x
ï f ( x)dx = í
x dt = x ,
-?
ï 05 5
ï î
1,
x£ 0 0< x <5
x³ 5
(2)随机变量 X 的取值不小于 2,即
蝌 ò P{ X ? 2} = +? f ( x)dx = 5 1 dx + ? 0dx 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
31
标准正态分布的计算
如果随机变量 X ~ N 0, 1 ,则 X 的密度函数为
x
1
x2
e2
2
x .
其分布函数为
x
x tdt
1
x t2
e 2 dt
2
x .
教材的附录中给出了x 在某些点处的值.
对于 x 0,我们可以直接查表求出x PX x的
某些值.
第五节 常见的连续型随机变量
率为 0.
⑵ 随机变量 X 在区间 a, b 内的任一子区间上取值
的概率仅与该子区间的长度成正比,而与该子区间的形
状及子区间在 a, b内的位置无关.
第五节 常见的连续型随机变量
4
均匀分布的分布函数
如果随机变量 X 服从区间 a, b 上的
均匀分布,则 X 的分布函数为
0
F
x
x b
1
a a
为 f
1
2 ,可知当 越小时,曲线 y f x 的图形就越
陡,因而随机变量 X 落在点 附近的概率就越大;反之,
当 越大时,曲线 y f x 的图形就平坦,因而随机变量 X 的
取值就越分散.
第五节 常见的连续型随机变量
30
正态分布的重要性
正态分布是概率论中最重要的分布.这是因为:
⑴ 自然界及大量的科学、工程、技术、经济、社会中
a
b
a
0dx
b a
b
1
a
dx
0dx
b
1
.
这表明, f x 满足密度函数的条件.
第五节 常见的连续型随机变量
3
均匀分布的概率背景
如果随机变量 X 服从区间 a, b上的均匀分布,则随 机变量 X 在区间 a, b上取值是“等可能”的,即:
⑴ 随机变量 X 只在区间 a, b内取值,而不在a, b 外取值.或者说,随机变量 X 在区间 a, b外取值的概
§2.3 常见的连续型随机变量 (continuous random variable)
第五节 常见的连续型随机变量
1
1.均匀分布(uniform distribution)
如果随机变量 X 的密度函数为
f
x
b
1
a
a xb
0
其它
则 称 随 机 变 量 X 服 从 区 间 a, b 上 的 均 匀 分
上的均匀分布.
第五节 常见的连续型随机变量
6
例 1(续)
其密度函数为
f
x
1 60
0
0 x 60
其它 .
令 B 被带往甲地 .
开往甲地汽车的到达时间:
7:00, 7:15, 7:30, 7:45, 8:00; 开往乙地汽车的到达时间:
7:10, 7:25, 7:40, 7:55, 8:10.
2
12
第五节 常见的连续型随机变量
11
2.指数分布(exponential distribution)
如果随机变量 X 的密度函数为
f
x
ex
x0
0 x0
其中 0 为参数,则称随机变量 X 服从参
数为 的指数分布.
第五节 常见的连续型随机变量
12
密度函数的验证
对于函数
f
x
ex
0
x0
x 0 ,我们有
即随机变量
T
的分布函数为
FT
t
0 1
et
t0
t 0 ,因此T 的
密度函数为
fT
t
FT t
0
et
从参数为 的指数分布.
t0
t 0 .这表明,随机变量 T 服
第五节 常见的连续型随机变量
19
指数分布的数学期望与方差
如果随机变量 X 服从参数为 的指数分布,则
X 的数学期望与方差分别为
EX
1
正态分布也称为 Gauss 分布.
第五节 常见的连续型随机变量
21
标准正态分布(standard normal distribution)
如果 0, 1,称 N 0, 1 为标准正态
分布.标准正态分布的密度函数为
x
1
x2
e2
2
x .
第五节 常见的连续型随机变量
22
正态分布与标准正态分布的分布函数
y
x
O
第五节 常见的连续型随机变量
27
正态分布密度函数的图形性质
对于正态分布的密度函数
f x
1
e
x 2
2 2
2
x ,
由一元函数微积分中的知识,我们有如下结论:
⑴ 曲线 y f x 关于直线 x 对称.这表明,对于
任意的 h 0 ,有
P h X P X h.
2 2
0
2
⑵ 下面证明: f xdx
. 1
e
x 2
2 2
dx
1
2
我们首先验证: xdx
, 1
x2
e 2 dx 1
2
x2
或证: I e 2 dx 2 .
第五节 常见的连续型随机变量
24
密度函数的验证(续)
为此,我们只需证明: I 2
e
x2 2
dx
2
2
.
的许多指标都服从或者近似服从正态分布.可以证明:
如果一个随机指标受到许多随机因素的影响,但其中任
何一个随机因素的影响都不起决定性作用,则该随机指
标一定服从或者近似服从正态分布.
⑵ 正态分布有着许多良好的性质,这些性质是其它分
布所不具备的.
⑶ 正态分布可以作为许多其它分布的近似分布.
第五节 常见的连续型随机变量
2 2
dx
1
2
第五节 常见的连续型随机变量
25
密度函数的验证(续)
作变换 u
x
,则 du
dx
,则
. 1
e
x 2
2 2
dx
2
1
u2
e 2 du
2
1 2 1 2
综上所述,有
f x
1
e
x 2
2 2
2
x
确实是一个密度函数.
第五节 常见的连续型随机变量
26
正态分布密度函数的图形
一般正态分布与标准正态分布之间的关系
根据上面的讨论,我们得到以 下重要的结论:
如果随机变量 X ~ N , 2 ,则
X ~ N 0,
1 .
第五节 常见的连续型随机变量
29
正态分布密度函数的图形性质(续)
⑶ 曲线 y f x 在 x 处有拐点.曲线 y f x 以 x 轴
为水平渐近线.
⑷ 若 固定,而改变 的值,则曲线 y f x 沿 x 轴水平 移动,但其形状不改变.因此曲线 y f x 的位置由参数
所确定.
⑸ 若 固定,而改变 的值,由于函数 y f x 的最大值
x
f
t
dt
1
0 ex
x0
x0.
第五节 常见的连续型随机变量
14
指数分布的无记忆性
如果随机变量 X 服从参数为 的指数分布,则对于任意的
s 0, t 0,有
PX s t X s PX t.
解:
PX
s
t
X
s
PX
s tX PX s
s
PX s PX
t s
1 F s t 1 F s
I 2
e
x2 2
d
2
x
e
x2 2
d
x
e
y2 2
d
y
x2 y2
e 2d
x
d
y
作极坐标变换 x r cos, y r sin ,则有
. I 2
2
r2
d e 2 rdr
r2
2 e 2 rdr
r2
2e 2
2
0
0
0
0
下面验证: . 1
e
x 2
X
20
20 1 10 10
x
e 10dx
e1
e2
0.2325 .
第五节 常见的连续型随机变量
17
例4
设在长度为 t 的时间间隔内某一随机事件 A 发生的 次数 X 服从参数为 t 的 Poisson 分布.试求在相邻 两次事件发生之间的等待时间T 的密度函数.
解: 随机变量 X 的分布律为
PX k tk et
布.记作 X ~ U a, b.
注释:类似地,可以定义区间 a, b、 a, b、
a, b上的均匀分布.
第五节 常见的连续型随机变量
2
密度函数的验证
对于
f
x
b
1
0
a
a xb
其它 ,我们有
⑴ 对任意的 x ,有 f x 0 ;
a
b
⑵ f xdx f xdx f xdx f xdx
xa a xb
.
xb
第五节 常见的连续型随机变量
5
例1
设公共汽车站从上午 7 时起每隔 15 分钟有一辆开往
甲地的汽车,从上午 7 时 10 分起每隔 15 分钟有一辆开
往乙地的汽车.某乘客到达该车站的时间是 7 时到 8 时
之间的均匀随机变量,而且他见车就上,求该乘客被带
往甲地的概率.
解:
设该乘客于 7 时 X 分到达车站,则 X 服从区间0, 60
P 1 或者 2
