分子的对称性3
第三章分子对称性和点群
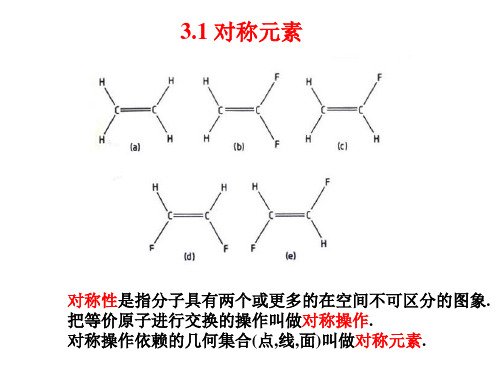
A(c) A(a) A( f ) 0 1
0
0
001
cos 4
3
sin 4
3 0
sin 4
3
cos 4
3 0
0 0Βιβλιοθήκη cos 43sin 4
3
1 0
sin 4
3
cos 4
3 0
0
0
1
A (a) 1
A (b) 1
A (c) 1
表示的分类:
(1)等价表示 若A(g)是群G的一个表示, X是一正交变换矩阵, 则 B(g)=X-1A(g)X
规则二. 点群中所有不可约表示的维数的平方和等于群的阶 n. l12 l22 lk 2 n
在 D3中, l12 l22 l32 6
从而 l1 l2 1, l3 2
规则三. 点群中不可约表示特征标间的正交关系:
k
h j r (R j ) * s (R j ) n rs
j 1
对不可约表示: (R) 2 n
3
y2 a21 a22 a23 x2 , yi aij x j
y3 a31 a32 a33 x3
j 1
(i=1,2,3)
矩阵的迹 (trace) 或特征标 (character):
( A) TrA aii
i
相似变换:
A S1AS
TrA TrA
(S为正交矩阵) St S SSt E
3.1 对称元素
对称性是指分子具有两个或更多的在空间不可区分的图象. 把等价原子进行交换的操作叫做对称操作. 对称操作依赖的几何集合(点,线,面)叫做对称元素.
3.1.1 n重对称轴, Cn (转动)
转角 2 / n
分子的对称性的概念和性质

分子的对称性的概念和性质
分子的对称性是指分子内部的元素和化学键的排列方式能够使分子具有某种对
称性质,例如轴对称、面对称或中心对称等。
分子的对称性具有以下性质:
1. 对称性越高,分子越稳定。
高对称性的分子能更好地分散电荷,使电子对于分子的外界环境的影响降低,从而提高其稳定性。
2. 对称性决定了部分分子性质。
例如,分子的光学旋光性、通过红外光谱确定的基团、共振能力和一些电学性质,都与其对称性有关。
3. 不同的分子对称性能够使分子之间的相互作用发生变化。
例如,对称性相同的分子之间的吸引力强于对称性不同的分子,因为它们之间的电场相互作用更强。
4. 分子的对称性还决定了它们在不同状态下的性质。
例如,具有闭壳层分子轨道的分子具有惰性,而具有非闭壳层分子轨道的分子具有较强的反应性和化学活性。
分子的对称性

4.1.1 旋转轴和旋转操作
1. 基转角:能够得到等价构型的最小旋转角。
轴次(n):
C4:
特殊的旋转轴: C∞轴
2. 主轴:一般来说,一个分子中轴次最高的旋转轴。
3. 付轴:除主轴外其余的旋转轴。
S4点群
S6(C3i)点群 1
2. D点群 Dn点群:
D2点群
D3点群 [Co(en)3]3+ 三草酸合铁(III)
Dnh点群
D2h点群 CH2=CH2 对-二氯苯
D3h点群 BF3
环丙烷
பைடு நூலகம்
D4h点群
(PtCl4)2-
D5h点群 (二茂铁) D6h点群 (苯)
Dnd点群
D2d点群 丙二烯
分子的对称性
对称的世界
4.1 对称操作和对称元素
1. 对称操作: 不改变分子中任何两原子间的距离而使其成为等价构 型的操作或动作。 2. 对称元素: 对称操作进行时所依据的几何元素。 3. 复原:分子经过某种动作后,所有同类的原子都与 动作前完全重合,无法区分分子构型是动作前还是动 作后。
等价构型:物理上不可区分的构型。 恒等构型:物理上不可区分且化学上不可区分的构 型,是等价构型的特例。
SF6:
主轴:C4 副轴:C3,C2 对称操作的矩阵表示:
4.1.2 对称中心和反演操作
对称中心 i
4.1.3 镜面(对称面)和反映操作
镜面σ
σv:通过主轴的对称面 σd:通过主轴且平分两个副轴C2的夹角的对称面 σh:垂直主轴的对称面
三种镜面 σv σd 和 σh
第四章分子的对称性

有机化学中的判据:分子含有不对称C原子时可产生旋光性。 但有例外:无不对称C,也可能有旋光性(六螺烯分子); 有不对称C,也可能没有旋光性(分子内消旋)。
H2O2中的C2
(旋转轴上的椭圆形为C2的图形符 号。类似地,正三角形、正方形、 正六边形分别是C3、C4和C6的图形
符号)
3、镜面和反映操作
分子中若存在一个平面,将分子两半部分互相反映 而能使分子复原,则该平面就是镜面σ,这种操 作就是反映. (1)分类:A:包含主轴的镜面v
C2
O
v1
H
H
v2
[B6H6]2-
10、Ih :120阶群, 是目前已知的分子中对称性最高的
对称操作:
E 12C5 12C52 20C3 15C2
i 12S10 12S103 20S6 15σ
C60
n=120
四、分子点群的确定
分子
线形分子:
Cv , Dh
Td , Th , Oh , I h ...
C1 , Ci , Cs
(2) C2 群:
R2
R1
R2
R1
(3)C3群
C3通过分子中心且垂直于荧光屏
2、 Cnv群 :除有一条n次旋转轴Cn外,还有包含主轴的 n个镜面σ 元素: Cn + nv
v
ˆ k (k 1 ˆ,C ˆv ,n 1 ), n 操作: E n
阶数:2n
C2v群:
H2O中的C2和两个σv
结构化学 第三章 分子的对称性chap3
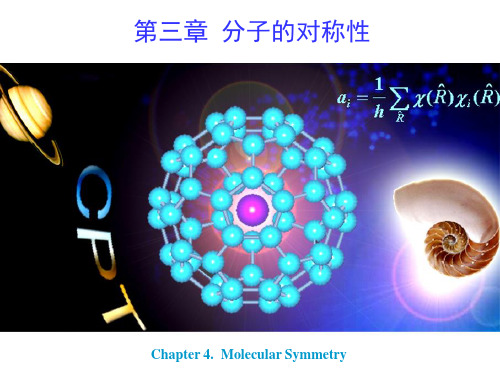
何其相似!
C2
唯一的C3旋转轴从xyz轴连成的 正三角形中心穿过, 通向Co; 三条C2旋转轴分别从每个N–N 键中心穿过通向Co. z C2 x y
C2
Dnh : 在Dn 基础上,还有垂直于主轴的镜面σh .
元素 操作 阶
E,nC2Cn ˆ ,C ˆ 2 ,,C ˆ n1, nC ˆ ˆ,C E
试观察以下分子模型并比较:
(1) 重叠型二茂铁具有
(2) 甲烷具有S4,所以, 只有C2与S4共轴,但C4和与 之垂直的σ并不独立存在.
S5, 所以, C5和与之垂直
的σ也都独立存在;
CH4中的映轴S4与旋转反映操作
•
注意: C4和与之垂直的σ都不独立存在
交叉式C2H6
S6=C3 + i
对称操作与对称元素
的镜面σd.
D2d : 丙二烯
元素 E,nC2Cn 操作 阶
n
ˆ ,C ˆ ,,C ˆ ˆ,C E
2 n
n1 n
ˆ , nC 2
2n
丙二烯(CH2=C=CH2)
对称元素 3C2 , 2 d
D2d群
D2d : B2Cl4
D3d : 乙烷交错型
D4d :单质硫
俯视图
D5d : 交错型二茂铁
Z
对称操作,共有9个对称操作. 但每条S4必然也是C2,
S42与C2对称操作等价,所以将3个S42划归C2,
穿过正四面体每条 棱并将四面体分为 两半的是一个σd ,
Y X
共有6个σd 。
从正四面体的每个顶点到 对面的正三角形中点有一 条C3穿过, 所以共有4条C3, 可作出8个C3对称操作。
分子的对称性

第四章 分子的对称性§4.1 对称性操作和对称元素§ <1>分子对称性概念原子组成分子构成有限的图形,具有对称性。
与晶体的对称性不同。
晶体的主要对称性是点阵结构,而分子的对称性主要是指分子骨架在空间的对称性以及分子轨道(波函数)的对称性。
○1分子对称性:指分子的几何图形(原子骨架和原子、分子轨道空间形状)中有相互等同的部分,而这些等同部分互相交换以后,与原来的状态相比,不发生可辨别的变化,即交换前后图形复原。
○2对称操作:不改变物体内部任何两点间的距离,使图形完全复原的一次或连续几次的操作。
(借助于一定几何实体)○3对称元素:对图形进行对称操作,所依赖的几何要素,如:点,线,面及其组合。
<2>对称元素及相应的对称操作○1恒等元素和恒等操作,(E ) ΛE 所有分子图形都具有。
○2旋转轴(对称轴)和旋转操作,Λn n C C ,;对称轴是一条特定的直线。
绕该线按一定方向(逆时针方向为正方面)进行一个角度θ旋转,nπθ2=如:H 2O : πθ21==n 。
分子中可能有 n 个对称轴,其中n 最大的称为主轴,其它称为非主轴,如:BF 3 ,主轴C 3 ,三个C 2垂直于C 3 与分子平面平行。
n C 将产生n 个旋转操作:E =-nn n n n n C C C C ,,,,12逆时旋转为正操作,k n C ;顺时旋转为逆操作,k n C -。
)(k n nk n C C --= 分子图形完全复原的最少次数称操作周期,旋转操作的周期为 n ;分子中,nC的轴次不受限制,n 为任意整数。
如: E =→332333,,C C C C○3对称和反映操作。
Λσσ, :对称面是一个特定的镜面,把分子图形分成两个完全相等的对称部分,两部分之间互为镜中映像,对称操作是镜面的一个反映。
图形中相等的部分互相交换位置,其反映的周期为2。
E =Λ2σ。
对称面可分为:v σ面:包含主轴; h σ面:垂直于主轴;d σ面:包含主轴且平分相邻'2C 轴的夹角(或两个v σ之间的夹角)。
结构化学 第四章 分子对称性
等组合而得,故I3可看作由C3和 i 组合得到:
i I3= C3 +
I4对称元素包括下列操作: I14iC14 ,I42C12 , I43iC43 , I44E
I4轴包括C2轴,但是并不具有C4轴,也不具有i, I4不等于C4和i两个对称元素的简单加和,I4是一 个独立的对称元素。 在CH4中包含3个互相垂直相交的I4轴。
同核双原子分轴 反轴In的基本操作:绕轴转360/n,接着按轴上的 中心点进行反演。
I1niC1n 是操作C1n 和i相继进行的联合操作。 I1的对称元素等于i I2的对称元素等于h I3包括6个对称操作: I31iC31 ,I32C32, I33i,I34C31, I35iC32, I36E
反轴In与映轴Sn及它们与其他对称元素的关系:
I1S2 i
I2 S1
I3 S6 C3 i
S1I2
S2 I1 i
S3 I6 C3
I 4 S4 I5 S10 C5 i
S4 I 4
S5 I10 C5
I6 S3 C3
S6 I3 C3 i
逆操作: 按原途径退回的操作.
实操作:能具体操作,直接实现。 旋转操作
第4章 分子的对称性
分子的对称性
1. 对称操作和对称元素 2. 对称操作群及对称元素的组合 3. 分子的点群 4.分子的偶极矩和分子的结构 5.分子的手性和旋光性
掌握分子对称性的意义:
1. 它能简明地表达分子的构型。 2. 可简化分子构型的测定工作。 3. 帮助正确地了解分子的性质。 4. 指导化学合成工作。
推论: 一个偶次旋转轴与对称中心组合,必定有一个垂直 于这个轴的镜面。
第三章 分子的对称性
逆元素
I--- I C3+---C3– v1--- v1 v2---v2 v3 ---v3
封闭性
结合律 v1(v2 v3) = v1 C3+ = v2
(v1v2)v3 = C3+ v3 = v2
3.5 群的表示
矩阵乘法 矩阵 方阵 对角元素
分子的所有对称操作----点群
如果每一种对称操作可以用一个矩阵(方阵)表示, 矩 阵集合满足群的要求,矩阵乘法表与对称操作乘法表
相似, 矩阵集合---群的一个表示
恒等操作I
矩阵
C2v: I C2 v v
特征标: 对角元素和 9
特征标3
特征标 1
特征标 -1
单位矩阵
I 矩阵, C2 矩阵, v 矩阵, v 矩阵 满足群的要求, 是C2v 点群的一个表示
集合G 构成群
1 –1, 乘法
1X1=1, 1X(-1)= -1 (-1)X1= -1, (-1)X(-1)=1 封闭性 恒等元素1 逆元素 1---1, -1--- -1,
群的乘法表 I A I A
I
I
IA
AA
I
I
A
?
A AI
A A
交叉线上元素 = 行元素 X 列元素
已知,I,A,B构成群, I 为恒等元素, 写出群的乘法表
3) 如果对称中心上无任何原子, 则同类原子是成双出现的.
例如: 苯中C, H
NH3 有无对称中心, 为什么? C2H3Cl有无对称中心, 为什么?
(b) 旋转轴Cp
绕轴旋转3600/p, 等价构型 水分子----绕轴旋转1800, 等价构型 C2轴 C3轴 360/2=180
BF3, 旋转1200, 等价构型 360/3=120
第三章-分子的对称性
对称操作只能产生等价构型分子,不能改变其 物理性质(偶极矩)。因此,分子的偶极矩必定在 分子的每一个对称元素上。
(1) 若分子有一个Cn轴,则DM必在轴上; (2) 若分子有一个σ面,则DM必在面上; (3) 若分子有n个σ面,则DM必在面的交线上; (4) 若分子有n个Cn轴,则DM必在轴的交点上,DM=0; (5) 分子有对称中心 i ( Sn ),则DM=0。
群的乘法表
把群元素的乘积列为表,则得到乘法表。乘 积为列×行,行元素先作用,列元素后作用。群 的元素数目 n为群的阶数。 例:H2O,对称元素,C2, σv, σv’ ,对称操作
ˆ ˆ ˆ ˆ C2,σv ,σv ', E , 属4阶群。
C2v
ˆ E ˆ C2 ˆ σv ˆ σv'
ˆ E ˆ ˆ σv σv' ˆ ˆ σv' σv
判据:若分子中有对称中心或有两个对称元素相交 于一点, 则分子不存在偶极矩。 推论:只有属于Cn 和Cnv(n=1,2,3,…,∞)这两类点群 的分子才具有偶极矩,而其他点群的分子偶极矩为 0。因C1v≡C1h≡Cs,Cs点群也包括在Cnv之中。
H C Cl
H C Cl
1,2 -二氯乙烯(顺式) , C2v,有
C60
闭合式[B12H12]2-
非真旋轴群: 包括Cs 、Ci 、S4 只有虚轴(不计包含在Sn中的Cn/2. 此外, i= S2 , σ = S1, 只有n为4的倍数时Sn是独立的).
Cs 群 : 只有镜面 Ci 群: 只有对称中心 S4 群: 只有四次旋映轴
亚硝酸酐 N2O3
分子点群的确定
起点 线性分子
2
ˆ E ˆ E ˆ C
ˆ C2 ˆ C
结构化学:分子的对称性
对称元素:对称操作所依据的几何元素(点、线、面) 分子中的对称元素有:
1. 恒等元素E 和恒等操作
ˆ E
恒等元素E是所有分子几何图形都有的,其相应的操作是恒等操 作 E。对分子施行这种操作后,分子保持完全不动,即分子中各原子 的位置及其轨道方位完全不变。
恒等操作对向量(x, y, z)不产生任何影响。
6. 映轴 Sn 和旋转反映
ˆ S n
对应的操作为
ˆ ˆ ˆ hC S n n
当对分子施行 轴的 S k次操作
n
时 Sn
k
k ˆk ˆk ˆ S n n Cn
k k ˆ ˆ ˆ S C n n k ˆ C ˆk S n n
当k为奇数时
当k为偶数时 当n为奇数时 当n为偶数时
4. 对称中心 i 和反演(倒反)操作
iˆ
5. 反轴 In 和旋转反演
ˆ I n
若将分子绕某轴旋转2/n角度后,再经对称中心反演产生分 子的等价图形,该对称操作称为反演,表示为 ,相应的 对称元素称反轴,用In表示。
ˆ I n
旋转反演是一种复合操作,且先反演后旋转( 转后反演(
),和先旋
ˆi ˆ C n
4.1.1 分子的对称性
对称性是物质内部分子结构对称性的反映。在
分子中,原子可以看做是固定在其平衡位置上的, 分子的结构参数,如键长、键角等决定了分子的几 何构型和分子的对称性。许多分子的几何构型具有 一定的对称性。
分子的对称性
对称操作和相应的对称元素
4.1.2 对称操作和相应的对称元素
对称操作:指不改变物体内部任何 两点间的距离而使物体复原的操作。
例: CH4 (放在正方体中)
ˆ I n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分子中常遇到的反轴有 1, 2, 3, 4,5,6 等,但实际
上只有 4 是独立存在的,其它几种反轴都可用 i,m,n或其组合来代替,因此,在反轴中只要重点 认识 4 就可以了。
1i 3 3i 6 3 mh
2 mh 5 5i
所以,只有 4 是独立存在的。 可以普遍的证明,对于n重反轴有: n+i n为奇数 m为奇数 m为整数 2n阶 n阶 n阶
NH3 H H
正三棱锥
H
H
HCCl3
C Cl Cl Cl
对称类型:将具有相同种类和个数的对称元素的
图形划归为一类,称为一种对称类型。
有限图形可能有些什么样的对称类型呢?乍 一想起来,花样一定极其繁多。但事实并非如此, 因为这些对称元素并不可以任意的组合在一起, 它们互相制约着,其个数及相对位置都要符合一 定的规则。下面介绍其中四个定理:
定理二:两个夹角为 Cn。
2 2n
的镜面的交线必为一n次轴
推论:若有一个镜面包含一个n重轴,则必有n个
2 镜面包含这个n次轴,且相邻镜面间的夹角为 2n
。
由以上两定理推知,单独存在两个或两个以上 的镜面的对称类型是不存在的。这是因为如果一个 图形存在两个镜面,则这两个镜面必相交,而其交 线必为一旋转轴。
例如,CH4分子,有四重反轴。
4
4
L( ) 2
4
I
先进行C41(沿 4 旋转 L( )) ,接着按中心进行反演 2 1 2 I IL ( ) 这一复合动作 I,分子能复原,也就是经 n n 后能够复原,且先旋转后反演或先反演后旋转的 效果相同,与这两个操作进行的先后次序无关,
即 IL( ) L( ) I
心,记为i。
由于每一个原子通过对称中心的反演操作可
以得到另一个相同原子,所以除位于对称中心i上
的原子外,其它原子必定成对地出现。
相对于同一对称中心进行两次或偶数次反演等 于不动操作,进行奇次反演等于一次反演,
即:
In =
E I
n为偶数 n为奇数
对称中心所对应的独立对称操作只有I和I2=E, 其阶次为2。 具有对称中心这一对称元素的分子为中心对称 分子。如苯,反式ClHC=CHCl,O=C=O,SF6, C2H4等。没有对称中心的分子,称为非中心对称 分子,如CH4,H2O,NH3,CO等。
定理一:一个有限图形所具有的任何对称元素必通过 物体的质心。 分子在对称操作作用下只是分子中周围环境完全 相同的原子互相串换了一下位置,变换成了与原来构 型不可分辨的构型,其物理性质是不变的,因而其质 量中心的位置在对称操作前后的位置是不改变的。对 于旋转,只有位于旋转轴上的点不改变位置,反映只 不改变位于对称面上点的位置,反演只不改变位于对 称中心上的点的位置,因此一个分子所具有的任何对 称元素必须通过分子的质心。 推论:一个有限图形所具有的所有对称元素必相交于 一点, 该点就是质心。
六、旋转反演与反轴
旋转反演:图形中每一点先凭借某一线转动某一角
度а之后,接着凭借此轴上的中心点进行反演的复
合操作称为旋转反演,记作In。是旋转与反演的联
合操作。
反轴:施行旋转反演所凭借的轴称为反轴。n重反 轴记为 n 。 基本对称操作:
2 2 I IL ( ) L( ) I n n
1 n
N NH3 H H
(4)C6H6有6个σv,和一个与C6轴垂直的σh。
H
(5)丙二烯,有两个σd,
2
H
H C H C C H H d
2
H
C
C
C
H
H
丙二烯立体模型
(6)HCN有无穷多个σv。
(7)CO2有无穷多个σv和1个垂直于C∞轴的σh。
五、反演和对称中心
反演:将图形中各点移到某点相反方向相等距离 处的操作,称为反演或倒反,记为I。 对称中心:进行反演所凭借的几何点称为对称中
IL ( ) 2
4 有一个特点,即在 4 的方向,必有2,因为
接连进行两次之后, I 进行了两次相当于不起
2 1 IL ( ) L ( ) I L ( ) C 2 2 2
2 2
作用,这个动作等于 L( ),可用式子表示为:
M
n为奇数
镜面所对应的独立的对称操作只有M和M2=E, 其阶次为2。
例如:
(1)反式ClHC=CHCl,O-N-Cl等平面型分子至
少有一个平面,就是分子平面。
Cl H N O H Cl
C2
Cl
(2)H2O有两个σv,它们 彼此垂直相交,交线为C2轴。
H O H
v1
v2
( 3 ) NH3 分子有 3 个 σv, 他们彼此成 2π/3 相交,交 线为C3轴。
。
关于反轴,要注意据以旋转的轴和据以反演的中 心,是不可分割的整体,其动作是一个联合操作。
) 对甲烷单独施行旋转操作L ( 或只进行反演操作I后 2
都不能复原,只有联合两个操作才能复原。这就
是说一个包含 4对称性的分子,并不是具有C4轴, 4 也不是有i,即 不等于 C4和i两个对称元素的简单 加和, 是一个独立的对称元素。 4
演,虚操作。
4.2 对称操作群与对称元素的组合
一、群的概念
1. 群:是按照一定规律相互联系着的一些元素的
集合。
2. 群中元的数目为有限的群称为有限群,元素的
数目为无限的群称为无限群。
3. 群的阶:群元素的数目称为群的阶,常用 h表示。
二、对称元素的组合
N
NH3具有1×3, 3×σv(一个三 重轴和三个镜面),正三棱锥具有 1×3, 3×σv, 三氯甲烷分子 (CHCL3)具有1×3, 3×σv。我 们发现,NH3、正三棱锥和CHCL3 虽然是不同的东西,但他们所具有 的对称元素的种类、数目却是完全 相同的,就其对称性来说两者毫无 差别。所以我们将有限图形按其对 称性分类。
n
=
n mh n=2m 2
n
n=4m
从上式可以看出只有4m 轴是独立存在的,且4m和2m
轴同时存在并ቤተ መጻሕፍቲ ባይዱ合。
七、旋转反映和映轴
旋转反映:图形中每一点先凭借某一轴线旋转某一 角度α之后,接着凭借与此轴线垂直的平面进行反 映操作的复合操作称为旋转反映。记做Sn。 映轴:施行旋转反映所凭借的轴线称为映轴。也记 做 S n。 CH4分子中有3个4次映轴,分子中不具有4和σh,
镜面:进行反映所凭借的平面称为镜面,记为σ 或m。 根据镜面和旋转轴在空间分布方式的不同,常以 不同的下标表示。 σh:凡镜面与主轴垂直者称为水平镜面,以σh表示。 σv:凡镜面包含主轴者称为垂直镜面,以σv表示。 σd:凡镜面通过主轴,等分两个副轴的夹角,称为等 分镜面,以σd表示。
镜面是平分分子的平面,要求镜面外的原子成 对出现且位于镜面的两侧,位于镜面上的原子不 受此限,如分子中某个原子只有一个,它必须位 于镜面上,但某种原子有两个,就不一定必须在 镜面外。相对于同一镜面进行两次或偶数次反映 等于不动操作。进行奇次反映等于一次反映, 即: Mn = E n为偶数
但经MC4这一复合操作后能够复原。
S n h Cn Cn h
先旋转后反映和先反映后旋转的效果是相同的。 除四重映轴外,其他映轴均可用
n, m, i
或其组
合来代替,而且映轴和反轴可以互相代替。例如:
S1 h 2 S3 3 h 6 S 5 5 h 10
S2 i 1 S4 4 S6 3 i 3
上述这些对称操作及相应的对称元素可 分为两大类,旋转操作属第一类,为实操作, 其特点是能具体操作,直接实现。反映、反 演,旋转反演等属第二类,为虚操作,其特
点是操作只能在想象中实现。
第一类对称操作:旋转,实操作;
第二类对称操作:反映、反演、旋转反
定理三:若有两个2轴以2π/2n角相交;则通过其 交点且垂直于这两个2轴的直线必为一Cn轴。 推论:若有一个2轴与一个n轴垂直,则在垂直于 n轴的平面内必有n个2轴,且相邻两个2轴间的夹 角为2π/2n。 定理四:i,σ和与σ垂直 的偶次轴2n三者之中, 任何两者的组合都产生 第三者。
