第5章__受弯构件正截面受力性能详解
合集下载
混凝土结构设计原理 课件 第5章-受剪
f yv ft
rsvfyv/ft
fc 1 (0.2~0.25c f -0.7) 1.25 t
矩形、T形和工形截面的一般受弯构件
第五章 受弯构件斜截面受剪承载力
Vu ft bh0
fc ft
0.2~0.25c
Vu
0.94 0.70 0.68 0.44 0.24
f t bh 0
1 . 75
1
Asv1 S
V
bh 0
b
r sv Asv bs Nhomakorabea
nA sv 1 bs
（2）配箍率对承载力的影响
rsvfyv
当配箍在合适范围时，受剪承载力随配箍量的 增多、箍筋强度的提高而增长，且呈线性关系。
第五章 受弯构件斜截面受剪承载力
4、纵筋配筋率
纵筋配筋率越大， 剪压区面积越大，
V
f t bh 0
纵筋的销栓作用越大，
第五章 受弯构件斜截面受剪承载力
第五章 受弯构件斜截面承载力 5.1 概述
受弯构件有三类破坏形态:
正截面受弯破坏（M）
斜截面受剪破坏（M、V）
斜截面受弯破坏（M、V）
计算和构造保证
构造保证
第五章 受弯构件斜截面受剪承载力
▲本章要解决的主要问题
建工
0S R
道桥
V Vu
Vu ?
0S R
2、混凝土强度
（1）为什么影响承载力？
剪压破坏是由于剪压区混凝土达到复合应力状态 下的强度而破坏； 斜拉破坏是由于混凝土斜向拉坏而破坏； 斜压破坏是由于混凝土斜向短柱压坏而破坏。 （2）如何影响承载力？ 砼强度越大，抗剪强度也越大。
第五章 受弯构件斜截面受剪承载力
第五章 受弯构件正截面承载力答案
5.方茴说：“那时候我们不说爱，爱是多么遥远、多么沉重的字眼啊。
我们只说喜欢，就算喜欢也是偷偷摸摸的。
”6.方茴说：“我觉得之所以说相见不如怀念，是因为相见只能让人在现实面前无奈地哀悼伤痛，而怀念却可以把已经注定的谎言变成童话。
”7.在村头有一截巨大的雷击木，直径十几米，此时主干上唯一的柳条已经在朝霞中掩去了莹光，变得普普通通了。
8.这些孩子都很活泼与好动，即便吃饭时也都不太老实，不少人抱着陶碗从自家出来，凑到了一起。
9.石村周围草木丰茂，猛兽众多，可守着大山，村人的食物相对来说却算不上丰盛，只是一些粗麦饼、野果以及孩子们碗中少量的肉食。
1.“噢，居然有土龙肉，给我一块！”2.老人们都笑了，自巨石上起身。
而那些身材健壮如虎的成年人则是一阵笑骂，数落着自己的孩子，拎着骨棒与阔剑也快步向自家中走去。
第五章 钢筋混凝土受弯构件正截面承载力计算一、填空题：1、钢筋混凝土受弯构件，随配筋率的变化，可能出现 少筋、 超筋 和 适筋 等三种沿正截面的破坏形态。
2、受弯构件梁的最小配筋率应取 %2.0m i n =ρ 和 y t f f /45min =ρ 较大者。
3、钢筋混凝土矩形截面梁截面受弯承载力复核时，混凝土相对受压区高度b ξξ ，说明 该梁为超筋梁 。
4．受弯构件min ρρ≥是为了____防止产生少筋破坏_______________；max ρρ≤是为了___防止产生超筋破坏_。
5．第一种T 形截面梁的适用条件及第二种T 形截面梁的试用条件中，不必验算的条件分别是____b ξξ≤___及__min ρρ≥_______。
6．T 形截面连续梁，跨中按 T 形 截面，而支座边按 矩形 截面计算。
7、混凝土受弯构件的受力过程可分三个阶段，承载力计算以Ⅲa 阶段为依据，抗裂计算以Ⅰa 阶段为依据，变形和裂缝计算以Ⅱ阶段为依据。
8、对钢筋混凝土双筋梁进行截面设计时，如s A 与 's A 都未知，计算时引入的补充条件为 b ξξ=。
工程结构 5 受弯构件正截面
1 0.8，1 1.0
当50N / mm 2 f cuk 80N / mm 2时，
1 0.8 0.002( f cuk 50) 1 1.0 0.002( f cuk 50)
三、最大配筋率ρmax和最小配筋率ρmin
截面有效高度h0： 一排： h0 =h-a= h –35； 两排： h0 =h-a= h –60 相对受压区高度 ξ=x/h0
45 f t f y 且不小0.2
现浇板和基础底板沿每个受力方向的受 拉钢筋
0.15
5.3 单筋矩形截面正截面承载力计算
一、基本公式 根据力和力矩 平衡条件可建 立方程如下：
x 0
f y As 1 f c bx
x M u 1 f c bx h0 2 x 或M u f y As h0 2
第5章 受弯构件(Bending member)
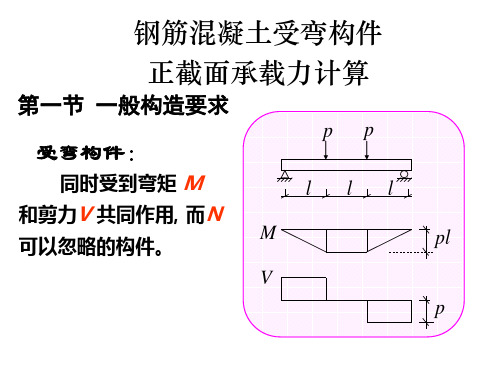
受弯构件概述 在外荷载作用下，截面上只产生弯矩和剪力的构 件，称为受弯构件。 1. 受弯构件的截面内力：M、V； 变形：横向弯曲变形为主 2. 实际工程中的受弯构件：梁、板 3. 受弯构件的设计要求： 正截面抗弯承载力； 斜截面抗剪和抗弯承载力。
5.1 受弯构件的受力特点
配置受压钢筋， 减少受压区高度x， 可提高截面的延性， 抗震有利。
1
1
HPB235
b
HRB335 HRB400 HRB400
0.518
0.508
0.499
0.490
0.481
0.472
0.463
max与 b的关系
界限破坏时: 根据平衡条件:
x xb b h0
f y As ,max 1 f c b b h0
第五章 受压构件的截面承载力
12
3.受压短柱承载力
N 混凝土压碎 钢筋凸出
钢筋屈服
混凝土压碎
N
达到最大承载力时混凝土压坏。 o
l
c' f c 应变 c' 0
如果 y 0则钢筋已经屈服 s' f y' 如果 y 0则钢筋未屈服但 f
' s ' y
fc f y As
(注意f y' 取值原则）
6e0 N 弹性材料 （ 1 ) A h
钢筋混凝土偏心受压构件的破坏形态与 偏心距e0和纵向钢筋配筋率有关
20
一、偏心受压短柱的破坏形态
（一）受拉破坏（大偏心受压破坏）
条件：偏性距较大且As不过多。 靠近纵向力一侧受压，远离纵向力一侧受拉。截面受拉侧混 凝土较早出现裂缝，As的应力随荷载增加发展较快，首先达 到屈服强度。此后，裂缝迅速开展，受压区高度减小，压区 混凝土压碎而达到破坏。受压侧钢筋A‘s 一般能受压屈服。
普通箍筋柱：
螺旋箍筋柱：箍筋的形状为圆形， 且间距较密，其对混凝土的约束作 用较强。
9
纵筋的作用：
◆ ◆ ◆
协助混凝土受压减小截面尺寸、改善截面延性。
承担弯矩作用
减小持续压应力下混凝土收缩和徐变的影响。
箍筋的作用： 与纵筋组成空间骨架，避免纵筋受压外凸。
10
一、配有纵向钢筋和普通箍筋柱
1.试验分析
混凝土：混凝土强度等级对受压构件的承载影响较大，一 般应采用强度等级较高的混凝土。目前我国一般结构中柱 的混凝土强度等级常用C30~C40，在高层建筑中， C50~C60级混凝土也经常使用。 钢筋：纵筋：HRB400 HRB500。箍筋：HRB400 HPB300。
受弯构件正截面承载能力计算教学内容
（3）适筋梁的塑性铰
当加载到受拉钢筋屈服时，弯矩为My，相应的曲率为φy。荷载继续增加，裂缝向上发展，混凝土受压区减小，中和轴上升，弯矩达极限抵抗弯矩Mu，曲率为φu。当受压区混凝土达极限压应变值时，构件丧失承载能力。在此破坏过程中，位于梁内拉压塑性变形集中的区域，形成一个性能特异的铰。
计算步骤如下：
①确定截面有效高度h0
②判断梁的破坏类型：先求出
③计算截面受弯承载力Mu
适筋梁
超筋梁
④判断截面是否安全：若M≤Mu，则截面安全。
（2）截面设计
己知：弯矩设计值M，混凝土强度等级fc，钢筋级别fy， 构件截面尺寸b×h。求：所需受拉钢筋截面面积As= ？
③当 2a′≤x ≤xb 时，直接代入公式计算Mu。
3.截面设计（一）
已知：弯矩设计值M，截面b、h、a和a’，材料强度fy、 fy ’、 fc 求：截面配筋（ As和 As’均未知的情况）
未知数：x、 As 、 As’ 基本公式：两个
按单筋截面计算
是
否
按总用钢量最少原则补充方程 x= ξbh0
双筋截面在满足构造要求的条件下，截面达到Mu的标志仍然是受压边缘混凝土应变达到εcu。 受压区混凝土的应力仍可按等效矩形应力考虑。当相对受压区高度x ≤xb时，截面受力的平衡方程为：
1.基本计算公式及其适用条件
适用条件
① 防止超筋脆性破坏
②保证受压钢筋强度充分利用
双筋截面一般不会出现少筋破坏情况，故可不必验算最小配筋率。
钢筋的弯起角度一般为45°，梁高h＞800mm时可采用60°
④纵向构造钢筋及拉筋
二、受弯构件正截面受力性能
纵向受拉钢筋配筋率：
1.正截面破坏形态
建筑结构和受力分析-之-正截面受弯构件
土梁其破坏弯矩等于同样截面尺寸的素砼梁的所
承担的弯矩所确定的。
《规范》规定：
防止少筋破坏
( f ; ) 0.45 t 0.2%
f min
max
y
h min h0
2.公式的适用条件
1)防止超筋破坏
max b 1 b
fc f
y
x xb hb 0
2)防止少筋破坏
b
h min h0
1.受压区混凝土合力大小不变
2.受压区混凝土合力作用点不变
1
等效应力图形的应力与受压区 混凝土最大应力的比值
1
x xc
系数
1
和
1
也仅与混凝土应力-应变曲线
有关,称为等效矩形应力图形系数。
表4－2 混凝土受压区等效矩形应力图形系数
强度等级 ≤ C50 C55 C60 C65 C70 C75 C80
bh0
h0
h
As b
纵向受力钢筋截面面积As与 截面有效面积bh0 的百分比
2、梁的纵向受力钢筋
h0－梁截面有效高度；
一排钢筋时 两排钢筋时
h0=h-(35~40) (mm) h0=h-(65~75) (mm)
至少2根。梁跨度较大时，一般不少于3根；常用直径10~28mm， 种类不宜过多，且同一截面不同直径相差不应小于2mm；若排两 排时，上下对齐；架立筋设置在梁的受压区，用来固定箍筋并与 受力钢筋形成钢筋骨架.
➢ 验算公式的适用条件 x xb ( b)
➢ 由基本公式 求As
As
bh0
验算 As minbh
➢ 选择钢筋直径和根数, 布置钢筋
(二)截面复核
➢求x (或)
➢ 验算适用条件 As minbh和x xb (或 b ) ➢求Mu ➢ 若Mu M，则结构安全；否则，结构不安全
承担的弯矩所确定的。
《规范》规定：
防止少筋破坏
( f ; ) 0.45 t 0.2%
f min
max
y
h min h0
2.公式的适用条件
1)防止超筋破坏
max b 1 b
fc f
y
x xb hb 0
2)防止少筋破坏
b
h min h0
1.受压区混凝土合力大小不变
2.受压区混凝土合力作用点不变
1
等效应力图形的应力与受压区 混凝土最大应力的比值
1
x xc
系数
1
和
1
也仅与混凝土应力-应变曲线
有关,称为等效矩形应力图形系数。
表4－2 混凝土受压区等效矩形应力图形系数
强度等级 ≤ C50 C55 C60 C65 C70 C75 C80
bh0
h0
h
As b
纵向受力钢筋截面面积As与 截面有效面积bh0 的百分比
2、梁的纵向受力钢筋
h0－梁截面有效高度；
一排钢筋时 两排钢筋时
h0=h-(35~40) (mm) h0=h-(65~75) (mm)
至少2根。梁跨度较大时，一般不少于3根；常用直径10~28mm， 种类不宜过多，且同一截面不同直径相差不应小于2mm；若排两 排时，上下对齐；架立筋设置在梁的受压区，用来固定箍筋并与 受力钢筋形成钢筋骨架.
➢ 验算公式的适用条件 x xb ( b)
➢ 由基本公式 求As
As
bh0
验算 As minbh
➢ 选择钢筋直径和根数, 布置钢筋
(二)截面复核
➢求x (或)
➢ 验算适用条件 As minbh和x xb (或 b ) ➢求Mu ➢ 若Mu M，则结构安全；否则，结构不安全
混凝土结构设计原理-受弯构件正截面承载力精选全文
求：截面配筋As
2.已知：矩形截面钢筋混凝土简支梁，计算跨度为6000mm， as=35mm, 作用均布荷载25 kN/m，混凝土强度等级C20，钢筋HRB335级。 （ fc =9.6 N/mm2 ， ft =1.1 N/mm2 ， fy =300 N/mm2 ）
试设计此梁
3.已知：矩形截面梁尺寸b＝200mm、h＝450mm，as=35mm。混凝土 强度等级C70，钢筋HRB335级，实配4根20mm的钢筋。 （ fc =31.8 N/mm2 ， ft =2.14 N/mm2 ， fy =300 N/mm2 ）
b
max
b
1 fc
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
m in
As bh
0.45
ft fy
且同时不应小于0.2%
受弯构件正截面承载力计算
造价
总造价
混凝土
钢
经济配筋率
经济配筋率 板：0.4~0.8%
矩形梁：0.6~1.5% T形梁：0.9~1.8%
受弯构件正截面承载力计算
小相等； 2. 等效矩形应力图形与实际抛物线应力图形的形心位置相同，即合
力作用点不变。
受弯构件正截面承载力计算
表 5.1 混凝土受压区等效矩形应力图系数
≤C50 C55
C60
C65
C
0.8
0.99 0.98 0.97 0.96 0.95 0.94 0.79 0.78 0.77 0.76 0.73 0.74
钢筋与混凝土的材料强度比，是反映构件中两种材料配比的本质参数。
基本方程改为：
N 0, M 0,
1 fcb h0 s As M u 1 fcbh02 (1 0.5 )
2.已知：矩形截面钢筋混凝土简支梁，计算跨度为6000mm， as=35mm, 作用均布荷载25 kN/m，混凝土强度等级C20，钢筋HRB335级。 （ fc =9.6 N/mm2 ， ft =1.1 N/mm2 ， fy =300 N/mm2 ）
试设计此梁
3.已知：矩形截面梁尺寸b＝200mm、h＝450mm，as=35mm。混凝土 强度等级C70，钢筋HRB335级，实配4根20mm的钢筋。 （ fc =31.8 N/mm2 ， ft =2.14 N/mm2 ， fy =300 N/mm2 ）
b
max
b
1 fc
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
m in
As bh
0.45
ft fy
且同时不应小于0.2%
受弯构件正截面承载力计算
造价
总造价
混凝土
钢
经济配筋率
经济配筋率 板：0.4~0.8%
矩形梁：0.6~1.5% T形梁：0.9~1.8%
受弯构件正截面承载力计算
小相等； 2. 等效矩形应力图形与实际抛物线应力图形的形心位置相同，即合
力作用点不变。
受弯构件正截面承载力计算
表 5.1 混凝土受压区等效矩形应力图系数
≤C50 C55
C60
C65
C
0.8
0.99 0.98 0.97 0.96 0.95 0.94 0.79 0.78 0.77 0.76 0.73 0.74
钢筋与混凝土的材料强度比，是反映构件中两种材料配比的本质参数。
基本方程改为：
N 0, M 0,
1 fcb h0 s As M u 1 fcbh02 (1 0.5 )
第五章 钢筋混凝土受弯构件(三)
特点： 特点：裂缝下宽上窄
（2）腹剪斜裂缝 ） 中和轴附近，正应力小，剪应力大， 中和轴附近，正应力小，剪应力大，主拉 应力方向大致为45 当荷载增大， 应力方向大致为 0，当荷载增大，拉应变达 到混凝土的极限拉应变时，混凝土开裂。 到混凝土的极限拉应变时，混凝土开裂。
特点： 特点：腹剪斜裂缝中间宽 两头细，呈枣核形， 两头细，呈枣核形，常见 于薄腹梁中。 于薄腹梁中。
研究中同时采用无腹筋梁和有腹筋梁进行分析
一、无腹筋梁的斜截面受剪性能研究
1、斜裂缝的类型 、 （1）弯剪斜裂缝 ） 在剪弯区段截面的下边缘，主拉应力还是水平向的。 在剪弯区段截面的下边缘，主拉应力还是水平向的。 所以在这些区段仍可能首先出现一些短的垂直裂缝， 所以在这些区段仍可能首先出现一些短的垂直裂缝，然后 延伸成斜裂缝，向集中荷载作用点发展，这种由垂直裂缝 延伸成斜裂缝，向集中荷载作用点发展， 引申而成的斜裂缝的总体，称为弯剪斜裂缝。 引申而成的斜裂缝的总体，称为弯剪斜裂缝。
4、最小配箍率及配箍构造
◆ 当配箍率小于一定值时，斜裂缝出现后，箍筋因不能 当配箍率小于一定值时，斜裂缝出现后，
承担斜裂缝截面混凝土退出工作释放出来的拉应力， 承担斜裂缝截面混凝土退出工作释放出来的拉应力， 而很快达到屈服，其受剪承载力与无腹筋梁基本相同。 而很快达到屈服，其受剪承载力与无腹筋梁基本相同。
Vcs =Vc +Vsv
矩形、 矩形、T形和工形截面的一般受弯构件
Vcs = 0.7 f t bh0 + 1.25 f yv
集中荷载作用下的独立梁
Asv h0 s
Asv 1.75 Vcs = f t bh0 + f yv h0 λ + 1.0 s
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t c c
s cb
b
sAs
y n h0
t c
X 0
(1 n )h0 t 0.5 b n h0 s As Es s As Es c As n h0
t c
E
1 n
n
ct As
n2 2 E n 2 E 0
sAs
s=
y
fyAs
fyAs
s>y
四、受弯构件的试验研究
2. 试验结果
适筋破坏
四、受弯构件的试验研究
2. 试验结果
当配筋很多时----超筋梁的破坏 过程
P
L/3 L
L/3
c
t
c
t
c
t
(ct=cu)
ct
MI
Mcr
MII
Mu
sAs tb<ft
sAs tb=ft(tb=tu) s<y
M cr 0.292(1 2.5 A ) ft bh
2
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹性阶段
ct
xn=n h0 M较小时， c可以认为 是按线性分布，忽略拉 区混凝土的作用
ct c
C yc xn
A
s
h0 h
y
M
y c Ec c E n h0
荷载-位移关系
•配置最小配筋率的梁的变形能力
L/3 L L/3 P
最好！
M 超筋 平衡 III II I 少筋 P
超筋 平衡
适筋
II
III
适筋
最小配筋率
I
O
少筋
最小配筋率
O
五、受弯构件正截面受力分析
1. 基本假定
平截面假定----平均应变意义上
As’
dy y
h0 h P
as’
c c
L/3
t
少筋破坏
四、受弯构件的试验研究
2. 试验结果
结论一
•适筋梁具有较好的变形能力，超
L/3 L L/3 P
筋梁和少筋梁的破坏具有突然性， 设计时应予避免
M 超筋 III II I 少筋 P
超筋 III II
适筋
适筋
O
I
少筋
O
四、受弯构件的试验研究
2. 试验结果
结论二
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢
d 10 ~ 28mm(桥梁中 14 ~ 40mm)
三、截面尺寸和配筋构造
1. 板
分布钢筋
h0
c15mm d 70mm
h
d 8 ~ 12 mm
h150mm时， 200mm h>150mm时， 250mm 1.5h
板厚的模数为10mm
四、受弯构件的试验研究
1. 试验装置
荷 载 分 配梁 P 外加荷 载 应 变 计 数据采集 系统
L/3 L
s’ nh0
(1-n)h0
As
as
s
tb
b
ct c s ' s n h0 y n h0 as ' (1 n )h0
五、受弯构件正截面受力分析
1. 基本假定
P
钢筋的应变和相同位置处混凝 土的应变相同----假定混凝土与钢
筋之间粘结可靠
筋屈服的同时，混凝土压碎，是区分适筋破坏和超筋破坏的 定量指标
平衡破坏（界限破坏，界 限配筋率）
四、受弯构件的试验研究
2. 试验结果
结论三
•在适筋和少筋破坏之间也存在一种“界限”破坏。其破坏特
征是屈服弯矩和开裂弯矩相等，是区分适筋破坏和少筋破坏 的定量指标
最小配筋率
ቤተ መጻሕፍቲ ባይዱ
四、受弯构件的试验研究
2. 试验结果
n h0
1 ct f c 2 2 E s 1 n 0 0
2 n
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但ct<0
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
As
ct
xn = h h0 nh0
试 验 梁
h0
As b
h
L/3 L
位 移 计
L/3
As bh0
四、受弯构件的试验研究
2. 试验结果
当配筋适中时----适筋梁的破坏 过程
P
L/3 L
L/3
c
t
c
t
c
t
ct
(Mu) MIII
(ct=cu)
ct
MI
Mcr
MII
My
sAs tb<ft
sAs tb=ft(tb =tu) s<y
h xcr
t c
xcr
s
h0 xcr
Ec c s Es s
t c
t
ft
ft 0.5Ec tu
o t0 2t0
t
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
xn=n h0
c
ct
C M T
c
X 0
A
s
xn=xc
r
h0 h
0.5 bxcr 0.5Ec tub(h xcr )
0 t f c n2 1 E 1 s n c 3 t c
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但0 <ct< cu
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
h0 h xn= nh y0 y
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但ct<0
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
As
ct
xn = h h0 nh0
ct c
C M yc xn Ts=sA
s
y
s c
b
n h0 c c2 ct ct 2 2 C f c b 2 dy f b 2 y y c 2 2 h dy 0 0 h 0 n 0 0 0 n 0 0 ct ct 2 t f c b n h0 c 2 f c b n h0 0 3 0 n h0
L/3 L
L/3
五、受弯构件正截面受力分析
1. 基本假定
混凝土受压时的应力-应 变关系
1 n 2 ( f cu 50), 当n 2时，取 n 2 60
当应力较小时，如 c 0.3 f c时，可取
c Ec c
c
fc
n c c f c 1 1 0
t t E c
s s E
s
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct c
xn h0 h M
s
As b
tb
sAs
（E-1）As 用材料力学的方法求解
s t
Es s Es s t E t Ec
T s As E As t
t c
s
b
t0 tb= tu
sAs
s As
设 E Es , 近似认为 s tu Ec
2 E As 1 bh h xcr A 1 E s 2 bh
对一般钢筋混凝土梁 As / bh 0.5 ~ 2%,
xcr 0.5h
E 6 ~ 7
将钢筋等效成混凝土
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
当tb =tu时，认为拉区混凝土开裂并退出工作（约束受拉）
ct
xn=n h0
c
ct
C M T
c
xn=xc
r
A
s
h0 h
s
b
t0 tb= tu
ft
sAs
为了计算方便用矩形应力 分布代替原来的应力分布
tu
ct c
C M yc xn Ts=sA
s
y
s
c
b
ct 1 t t2 3 12 c c 0 M f c b n h02 1 n 2 t c 0 3 0 1 3 0 ct 1 2 3 12 0 s As h0 1 n ( s f y ) ct 1 3 0
sAs
s <y
sAs
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
当配筋很少时----少筋梁的破坏 过程
cb
Mcr= My
P
L/3 L
L/3
cb
MI
sAs tb<ft
sAs tb=ft(t b=tu)
四、受弯构件的试验研究
2. 试验结果
b
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但0 <ct< cu
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
h0 h As xn= nh y0 y
0
ct
fc
c 0
M
C
yc xn
s cb
b
sAs
y n h0
t c
X 0
(1 n )h0 t 0.5 b n h0 s As Es s As Es c As n h0
t c
E
1 n
n
ct As
n2 2 E n 2 E 0
sAs
s=
y
fyAs
fyAs
s>y
四、受弯构件的试验研究
2. 试验结果
适筋破坏
四、受弯构件的试验研究
2. 试验结果
当配筋很多时----超筋梁的破坏 过程
P
L/3 L
L/3
c
t
c
t
c
t
(ct=cu)
ct
MI
Mcr
MII
Mu
sAs tb<ft
sAs tb=ft(tb=tu) s<y
M cr 0.292(1 2.5 A ) ft bh
2
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹性阶段
ct
xn=n h0 M较小时， c可以认为 是按线性分布，忽略拉 区混凝土的作用
ct c
C yc xn
A
s
h0 h
y
M
y c Ec c E n h0
荷载-位移关系
•配置最小配筋率的梁的变形能力
L/3 L L/3 P
最好！
M 超筋 平衡 III II I 少筋 P
超筋 平衡
适筋
II
III
适筋
最小配筋率
I
O
少筋
最小配筋率
O
五、受弯构件正截面受力分析
1. 基本假定
平截面假定----平均应变意义上
As’
dy y
h0 h P
as’
c c
L/3
t
少筋破坏
四、受弯构件的试验研究
2. 试验结果
结论一
•适筋梁具有较好的变形能力，超
L/3 L L/3 P
筋梁和少筋梁的破坏具有突然性， 设计时应予避免
M 超筋 III II I 少筋 P
超筋 III II
适筋
适筋
O
I
少筋
O
四、受弯构件的试验研究
2. 试验结果
结论二
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢
d 10 ~ 28mm(桥梁中 14 ~ 40mm)
三、截面尺寸和配筋构造
1. 板
分布钢筋
h0
c15mm d 70mm
h
d 8 ~ 12 mm
h150mm时， 200mm h>150mm时， 250mm 1.5h
板厚的模数为10mm
四、受弯构件的试验研究
1. 试验装置
荷 载 分 配梁 P 外加荷 载 应 变 计 数据采集 系统
L/3 L
s’ nh0
(1-n)h0
As
as
s
tb
b
ct c s ' s n h0 y n h0 as ' (1 n )h0
五、受弯构件正截面受力分析
1. 基本假定
P
钢筋的应变和相同位置处混凝 土的应变相同----假定混凝土与钢
筋之间粘结可靠
筋屈服的同时，混凝土压碎，是区分适筋破坏和超筋破坏的 定量指标
平衡破坏（界限破坏，界 限配筋率）
四、受弯构件的试验研究
2. 试验结果
结论三
•在适筋和少筋破坏之间也存在一种“界限”破坏。其破坏特
征是屈服弯矩和开裂弯矩相等，是区分适筋破坏和少筋破坏 的定量指标
最小配筋率
ቤተ መጻሕፍቲ ባይዱ
四、受弯构件的试验研究
2. 试验结果
n h0
1 ct f c 2 2 E s 1 n 0 0
2 n
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但ct<0
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
As
ct
xn = h h0 nh0
试 验 梁
h0
As b
h
L/3 L
位 移 计
L/3
As bh0
四、受弯构件的试验研究
2. 试验结果
当配筋适中时----适筋梁的破坏 过程
P
L/3 L
L/3
c
t
c
t
c
t
ct
(Mu) MIII
(ct=cu)
ct
MI
Mcr
MII
My
sAs tb<ft
sAs tb=ft(tb =tu) s<y
h xcr
t c
xcr
s
h0 xcr
Ec c s Es s
t c
t
ft
ft 0.5Ec tu
o t0 2t0
t
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
xn=n h0
c
ct
C M T
c
X 0
A
s
xn=xc
r
h0 h
0.5 bxcr 0.5Ec tub(h xcr )
0 t f c n2 1 E 1 s n c 3 t c
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但0 <ct< cu
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
h0 h xn= nh y0 y
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但ct<0
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
As
ct
xn = h h0 nh0
ct c
C M yc xn Ts=sA
s
y
s c
b
n h0 c c2 ct ct 2 2 C f c b 2 dy f b 2 y y c 2 2 h dy 0 0 h 0 n 0 0 0 n 0 0 ct ct 2 t f c b n h0 c 2 f c b n h0 0 3 0 n h0
L/3 L
L/3
五、受弯构件正截面受力分析
1. 基本假定
混凝土受压时的应力-应 变关系
1 n 2 ( f cu 50), 当n 2时，取 n 2 60
当应力较小时，如 c 0.3 f c时，可取
c Ec c
c
fc
n c c f c 1 1 0
t t E c
s s E
s
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct c
xn h0 h M
s
As b
tb
sAs
（E-1）As 用材料力学的方法求解
s t
Es s Es s t E t Ec
T s As E As t
t c
s
b
t0 tb= tu
sAs
s As
设 E Es , 近似认为 s tu Ec
2 E As 1 bh h xcr A 1 E s 2 bh
对一般钢筋混凝土梁 As / bh 0.5 ~ 2%,
xcr 0.5h
E 6 ~ 7
将钢筋等效成混凝土
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
当tb =tu时，认为拉区混凝土开裂并退出工作（约束受拉）
ct
xn=n h0
c
ct
C M T
c
xn=xc
r
A
s
h0 h
s
b
t0 tb= tu
ft
sAs
为了计算方便用矩形应力 分布代替原来的应力分布
tu
ct c
C M yc xn Ts=sA
s
y
s
c
b
ct 1 t t2 3 12 c c 0 M f c b n h02 1 n 2 t c 0 3 0 1 3 0 ct 1 2 3 12 0 s As h0 1 n ( s f y ) ct 1 3 0
sAs
s <y
sAs
四、受弯构件的试验研究
2. 试验结果
超筋破坏
四、受弯构件的试验研究
2. 试验结果
当配筋很少时----少筋梁的破坏 过程
cb
Mcr= My
P
L/3 L
L/3
cb
MI
sAs tb<ft
sAs tb=ft(t b=tu)
四、受弯构件的试验研究
2. 试验结果
b
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
压区混凝土处于弹塑性阶段，但0 <ct< cu
(以混凝土强度等级不大于C50的钢筋混凝土受弯构件为例 )
h0 h As xn= nh y0 y
0
ct
fc
c 0
M
C
yc xn