杆的扭转定理和公式
材料力学 第03章 扭转

sin 2 , cos 2
由此可知:
sin 2 , cos 2
(1) 单元体的四个侧面( = 0°和 = 90°)上切 应力的绝对值最大; (2) =-45°和 =+45°截面上切应力为零,而 正应力的绝对值最大;
[例5-1]图示传动轴,主动轮A输入功率NA=50 马力,从 动轮B、C、D输出功率分别为 NB=NC=15马力 ,ND=20马 力,轴的转速为n=300转/分。作轴的扭矩图。
解:
NA 50 M A 7024 7024 1170 N m n 300 NB 15 M B M C 7024 7024 351 m N n 300 NC 20 M D 7024 7024 468N m n 300
第3章
扭
转
§3.1
一、定义 二、工程实例 三、两个名词
概
述
一、定义
Me Me
扭转变形 ——在一对大小相等、转向相反的外力偶矩
作用下,杆的各横截面产生相对转动的
变形形式,简称扭转。
二、工程实例
1、螺丝刀杆工作时受扭。
Me
主动力偶
阻抗力偶
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
公式的使用条件:
1、等直的圆轴, 2、弹性范围内工作。
圆截面的极惯性矩 Ip 和抗扭截面系数Wp
实心圆截面:
2 A
I p d A (2π d )
2
d 2 0
O
2 π(
4
d /2
4
)
0
πd 4 32
d
d A 2π d
工程力学C-第9章 扭转

max
84.88MPa
16
min max
10 42.44MPa 20
§9-6 圆轴扭转破坏与强度条件
一、圆轴扭转时的破坏现象
脆性材料扭转破坏
沿450螺旋曲面被拉断
塑性材料扭转破坏
沿横截面被剪断
二、圆轴扭转的强度条件
D 1.192 得: d1
2
D2
A空 A实 4
(1 0.8 )
d1
4
2
0.512
例6 传动轴AB传递的功率为 P =7.5kW, 转速n=360r/min。轴的 AC 段为实心圆轴, CB 段为空心圆轴。已知:D =30mm,d =20mm。试计算AC段的最大剪应力,CB 段横截面上内、外缘处的剪应力。 解: (1)计算外力偶矩和扭矩 P AC段最大剪应力: m 9549 198.9N m n Tmax D 1max 37.5 10 6 Pa 37.5MPa T m 198.9N m I P1 2 (2)计算极惯性矩 CB段上内外缘的剪应力: D 4 T d 8 4 AC段:I P1 7.95 10 m 2内 I P2 2 32 D 4 4 31.2 10 6 Pa 31.2MPa (1 ) CB段:I P 2 T D 32 2外 8 4 6.38 10 m I P2 2 46.8 10 6 Pa 46.8MPa (3)计算应力
A
ρτ
ρ
dA T
d 2 G ρ dA T dx A
令:
ρ dA I P
2 A
极惯性矩
d G IP T dx
(仅供参考)第十九章-扭转的强度与刚度计算
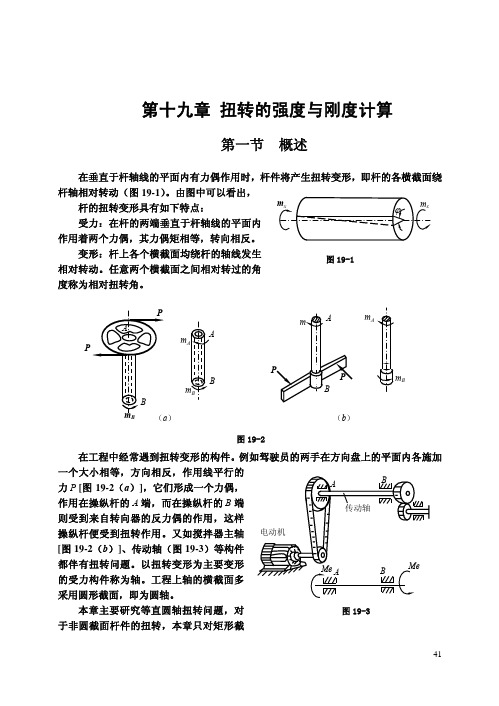
一、外力偶矩的计算
前面已经指出 ,使轴产生扭转变形的是外力偶矩。但是作用于轴上的外力偶矩往
往不是直接给出的,而是给定轴所传递的功率和轴的转速。以图 19-3 所示的传动轴为例,
由电动机的转速和功率可以求出传动轴 AB 的转速及通过皮带轮输入的功率。功率由皮
带轮传到轴 AB 上,再经右端的齿轮输出。设通过皮带轮给 AB 轴输入的功率为 N(kW),
因为 1kW=1000N·m/s 因此每秒钟输入功应为 : W = N ×1000(N ⋅ m)
(a)
电动机是通过皮带轮以力偶矩 Me 作用于 AB 轴上的,若 AB 轴的转速为每分钟 n 转,
则力偶矩 Me 在每秒内完成的功应为 :
W = 2π × n × Me(N ⋅ m)
(b)
60
因为 Me 所完成的功也就是皮带轮给 AB 轴输入的功,故(a)、(b)两式应相等,这
据微元的平衡要求,不仅左右一对面上有大小相等,方向相反的剪应力 τ ,在上下一对
面也必须有剪应力τ ′ ,而且由力矩平衡条件 ∑ mz = 0 有:
(τtdy)dx = (τ ′tdx)dy
由此得到:
τ =τ′
(19-2)
这表明,在相互垂直的两个微面上,剪应力总是成对出现的,它们数值相等,而方
向均垂直于两微面的交线,或指向或背离这一交线。这就是剪应力互等定理。
利用第三节中的(b)式和(c)式,上式可以写成:
φ
φ
图 19-9
u = 1 τγ 2
再由剪切胡克定律(式 19-3)得:
u = 1 τγ = τ 2 2 2G
46
第四节 圆轴扭转时的应力与变形
一、横截面上剪应力计算公式
圆轴扭转时,在已知横截面上的扭矩后,还应进一步研究横截面上的应力分布规律,
材料力学第四章 扭转

max
T GI p
180
(/m)
×
例5 图示圆轴,已知mA =1kN.m, mB =3kN.m, mC
=2kN.m;l1 =0.7m,l2 =0.3m;[]=60MPa,[ ]=0.3°/m,
G=80GPa;试选择该轴的直径。
mA
mB mC 解: ⑴按强度条件
A
l1
B l2 C
max
9.55
200 300
6.37
(kN m)
×
n D
m2 1 m3 2 m1 3 m4
n A 1 B 2 C 3D
②求扭矩(扭矩按正方向假设)
m 0 , T1 m2 0, T1 m2 4.78kN m m 0; T2 m1 m2 0
T2 m2 m3 (4.78 4.78) 9.56kN m
T
2 r02
t
T 2 A0
t
T
A0为平均半径所作圆的面积。
×
三、切应力互等定理:
´
a
b
dy
´
c
z
dx
d t
mz 0; t dxdy t dxdy
'
这就是切应力互等定理:在单元体相互垂直的两个截面
上,切应力必然成对出现,且数值相等,两者都垂直于两平
面的交线,其方向或共同指向交线,或共同背离交线。
垂直,则杆件发生的变形为扭转变形。
A
B O
A
BO
m
m
——扭转角(两端面相对转过的角度)
——剪切角,剪切角也称切应变。
×
§4–2 扭转的内力—扭矩与扭矩图
一、扭矩 圆杆扭转横截面的内力合成
结果为一合力偶,合力偶的力偶 矩称为截面的扭矩,用T 表示之。 m
材料力学第3章扭转

τ ρ = Gγ ρ
=G
ρdϕ
dx
22
C)静力平衡关系 C)静力平衡关系
T = ∫ A dA ⋅ τ ρ ⋅ ρ
2 dϕ = ∫ A Gρ dA dx
τ ρ = Gγ ρ
=G
dA
ρdϕ
dx
ρ
O
=G
dϕ ∫ A ρ 2dA dx
令
dϕ T = GI p dx
dϕ T = dx GIp
I p = ∫ A ρ 2dA
由公式
Pk/n
11
§3-2、外力偶矩 扭矩和扭矩图
(2)计算扭矩 (2)计算扭矩
(3) 扭矩图
12
§3-3、纯剪切
1、薄壁圆筒扭转:壁厚 、薄壁圆筒扭转:
t≤
1 r0 10
为平均半径) (r0:为平均半径)
A)观察实验: )观察实验:
实验前: 实验前: ①绘纵向线,圆周线; 绘纵向线,圆周线; ②施加一对外力偶 m。 。
16
纯剪切的概念: 纯剪切的概念:
当单元体的侧面上只有剪应力而无正应力时, 当单元体的侧面上只有剪应力而无正应力时, 就称为纯剪切。 就称为纯剪切。
3、剪应变与扭转角
设轴长为L,半径为R 设轴长为L 半径为R Φ称为扭转角,是用来表示轴变形的量; 称为扭转角,是用来表示轴变形的量; 且的剪应变 γ Φ的关系如下: 与 的关系如下:
∑ mz = 0
a dy
γ τ´
dx
τ´
b
τ ⋅ t ⋅ dxdy = τ ′ ⋅ t ⋅ dxdy
故
τ
c z
τ
d t
τ =τ′
上式称为剪应力互等定理。 上式称为剪应力互等定理。 为剪应力互等定理
第三章扭转

T=Fs×r
材料力学
0
Fs=2 r
0
扭转/圆轴扭转时的应力
一.圆轴扭转时的应力分布规律
T
T
材料力学
扭转/圆轴扭转时的应力
1. 单元格的变化
A
B
C
A B
C
D
D
现象一: 方格的左右两边发生相对错动
横截面上存在切应力
方格的左右两边距离没有发生改变 现象二:
材料力学
横截面上没有正应力
2. 半径的变化
材料力学
扭转/纯剪切
§3.3 纯剪切
材料力学
相关概念
纯剪切:单元体各个面上只承受切应力而没有正应力。
单元体:是指围绕受力物体内一点截取一边长为无限小 的正立方体,以表示几何上的一点。
材料力学
扭转/纯剪切
一.薄壁圆筒扭转时的切应力
纯剪切的变形规律通过薄壁圆筒的纯扭转进 行研究。 受扭前,在薄壁圆筒的表面上用圆周线和 纵向线画成方格。
扭转/圆轴扭转时的变形
两横截面间相对扭转角的计算:
=TL/GIP
T:扭矩;
L:两横截面间的距离; G:切变模量; IP:极惯性矩。
材料力学
扭转/圆轴扭转时的变形
=TL/GIP
GIP越大,则越小。 GIP称为抗扭刚度。
材料力学
扭转/圆轴扭转时的变形
`=/L
`:单位长度扭转角(rad/m)。
思路:
最大扭矩
最大切应力
max
校核强度
相等
强度相同,则两轴的最大切应力 求出实心轴直径
材料力学
两轴面积比即为重量比
扭转/圆轴扭转时的应力
计算Wt:
3 Wt=D
材料力学 第4章_扭转

d x d z d y d y d z d x 0
返回
4. 切应力互等定理
切应力互等定理: 也称切应力双生定理, 指在单元体相互垂直的两 个面上,切应力必成对存 在,且数值相等;两者都 垂直于两个平面的交线, 方向共同指向或背离这一 交线。
纯剪切
BC B
TCD mB mC 700N m
(b)
TDA mA 1146N m
可见:主动轮与从动轮位置不 同,轴内最大扭矩也不同,显 然(a)方案比(b)方案合理。
返回
§4.3 圆轴扭转时的应力与强度条件
返回总目录
一、薄壁圆筒扭转时的切应力 1. 变形现象 圆周线大小、形状、间距 不变,纵向线相同倾斜。 2. 横截面上应力分析 因纵向纤维无正应变, 有角应变,因此横截面上 无,有, 与圆周相切。 又因壁很薄,可近似认 为沿壁厚应力相等。
第4章 扭转
第4章 扭转
§4.1 扭转的概念 §4.2 外力偶矩、扭矩和扭矩图
§4.3 圆轴扭转时的应力与强度条件
§4.4 圆杆扭转时的变形及刚度条件
§4.5 非圆截面杆的扭转概念
§4.1 扭转的概念
返回总目录
工程中的受扭转杆件
拧紧螺母的工具杆产生扭转变形
返回
工程中的受扭转杆件
返回
工程中的受扭转杆件
r
d dx
横截面上任一点的 ⊥半 径,并与该点到轴线的距离 成正比。
返回
4. 应力公式 静力关系
T
dA
横截面上分布内力系对 圆心的矩等于扭矩T。
T d A A d d 2 G d A G d A A dx dx A
材料力学 第三章 扭 转

T2
T1
d
T3
Mx1=0.5kN· m
Mx2 =0.32kN· m lAB=300mm G=80GPa d=50mm
B
T2
φAB
lAB
A T1
lAC d φAC
C T3
B
lAB
A
lAC
C
M x1l AB j AB = GI P 500 0.3 = 9 80 10 0.054 32
r O
Mx
几何分析
变 形 应变分布
物理关系
应力分布
平面假定 静力学方程
应力公式
1. 变形几何关系
周线
a b c d
T
周线
a c d
γ
T
φ
b
纵线
dx
纵线
dx
a
c
a
γ
c c' d d'
b
d
b
(1)变形后所有圆周线的大小、形状和间距均不变,绕杆轴线相对转动。 (2)所有的纵线都转过了同一角度g。
T
周线
A
dρ
ρ o
ρ2dA
∫ 0ρ2·2πρdρ =
π d = 32
4
d/2
d
3 Ip π d Wp = r = 16
2. 空心圆截面
π D 4 - π d 4 π D 4(1-α4) Ip= 32 32 = 32 α=d/D
ρ o
dρ
π D3 Wp = 16 (1-α4)
d D
3.薄壁圆环截面
I P = 2r0
故该轴满足切应力强度要求。
二、刚度计算 等直圆杆扭转的刚度条件为
θ max = Mxmax ≤[θ] GI
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆截面杆的扭转之公保含烟创作外力与内力|| 圆杆扭转切应力与强度条件|| 圆杆扭转变形与刚度条件|| 圆杆的非弹性扭转杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶(图2·2-1a),其变形特点是在任意两个截面绕轴线发作相对转动.轴类构件常有扭转变形发作.作用在传动轴上的外力偶矩m通常是依据轴所传递的功率N和转速n(r/min)来计算.当N的单元为千瓦(kW)时当N的单元为马力(HP)时扭转时的内力为扭矩T,用截面法求得.画出的内力图称为扭矩图(或T图),如图2·2-1b所示图2·2-1 圆杆的扭转当应力不超越资料的剪切比例极限rp时,某横截面上任意C点(图2·2-2)的切应力公式为式中T——C 点所在横截面上的扭矩p——C点至圆心的间隔Lp——横截面对圆心的极惯性矩,见表2-2-1 等直杆扭转时的截面几何性质.图2·2-2 切应力散布圆杆横截面上的切应力r沿半径呈线性散布,其方向垂直于半径(图2·3-2).模截面上的最年夜切应力在圆周各点上,其计算公式为等截面杆的最年夜切应力发作在Tmax截面(危险截面)的圆周各点(危险点)上.其强度条件为式中,[τ]为许用扭转切应力,与许用拉应力[σ]的关系为:[τ]=(0.5~0.6)[σ] (塑性资料)或[τ]=(0.5~0.6)[σ](脆性资料)在比弹性范围内,圆杆在扭矩T作用下,相中为L的两截面间相对扭转角为或式中G——资料的切变模量单元扭转角公式为或式中GLp——抗扭刚度圆杆上与杆轴间隔为p外(图2·2-2)的切应变r为圆杆概略处的最年夜切应酿成式中,r——圆杆的半径等截面圆杆的最年夜单元扭转角,发作在Tmax一段内,其刚度条件为式中,[θ]为圆杆的许用单元扭转角(°)/m讨论圆杆扭转时切应力超越资料的比例极限并进入塑性状态的情况.关于加工硬化资料,如果资料的应力-应变图为已知(图2·3-3a),则杆中任一点处的切应力r就可以确定.位于横截面边缘处应酿成rmax,其相应的切应力rmax可以从应力-应变图求得.整个横截面上切应力的(图2·3-3b)与应力-应变图的形状相同.使圆杆发作单元扭转角所必需的扭矩T,可依据静力学方程求得(见图2·2-3b)为图2·2-3 圆杆的非弹性扭转将式(2-2-10)代入式(2-2-13)得式中Rmax=rθ依据式(2·2-14),可以失掉T与θ的关系曲线,依据该曲线,可以确定对给定T值的θ和Tmax.如果圆杆的资料具有明显的屈服极限rs,则可使应力-应变图理想化,如图2·2-4a所示,此资料弹塑性资料.此时,只要杆中最年夜应变小于rs 时,杆就属于弹性的.当横截面边缘处的应变超越rs 时,横截面上的应力散布如图2·2-4b所示,此图标明屈服开端于边缘,当应变增年夜时,屈服区例向里边开展.如果资料的屈服极限为rs ,弹塑性鸿沟为PS =C 时,则扭矩为图2·2-4 理想弹塑性资料杆的扭转式中d——圆杆的直径当整个横截面都面到屈服时,其应力将接近平均散布,如图2·3-4c所示,相应的扭矩为杆的塑性极限扭矩,其值为当扭矩到达此值时,扭矩不再增加而杆将持续变形杆中最初开端屈服时的弹性极限扭矩T s ,由式(2·2-3)得比拟式(2-2-16)和式(2-2-17),可得塑性极限扭矩与弹性极限扭矩之比为由此可知,杆中开端屈服后,只要扭矩增年夜三分之一,就将使杆到达极限承载能力.非圆截面杆的抟转与薄膜比拟等直杆扭转时的应力与变形|| 薄膜比拟|| 非弹性扭转杆非圆截面杆扭转时,其横截面将发作曲.横截面可以自由翘曲的扭转,称为自由扭转.此时,由于各截面的翘曲水平相同,故横截面收只在切而没有正奕力.例如,图2·2-5所示的工钢薄壁杆件,在两端作用一对扭转偶矩,杆的两个翼缘将相对转动,但翼缘的轴线仍为直线,不发作弯曲变形,也不发作正.图2·2-5 自由扭转若由于约束或受力条件的限制,造成杆件各截面的翘曲水平分歧时,则横截面上除有切应力外还有正应力.这种情况称为约束扭转.例如,图2·2-6a,所示的工字钢杆,一端固定,另一端作用扭转力偶矩.在固定端截面为平面,不能翘曲,但它限制了相邻截面的翘曲,离固定越远,翘曲受到的限制也越小,到自由端酿成了可以自由翘曲.由于相邻两截面的翘曲分歧,则引起这两个截面间纵向纤维长度的改动,于是横截面上发作正应力.又如图2·2-6b抽示两端简支工字钢杆,在跨度中点截面上作用一个扭转力偶矩.两端铰支座不允许端截面绕杆轴旋转,但可自由翘曲.由于对称,跨度中点截面应坚持为平面,离中点截面越远,翘曲越年夜.关于象工字钢、槽钢等薄壁杆件,在约束扭转时,横截面上的正应力往往很年夜我行我素厍以思索.但关于一些袂体杆件,如截面为矩形、椭圆形等杆件,因约束扭转而引起的正应力数值很小,可疏忽不计.图2·2-6 约束扭转具有任意形状的无限长等截面直杆,在绕扭转时,在与Z轴正交的截面上,要发作切应力rxz 和rxz (图2·2-7).为了确定应力和变形,设应力函数φ (X,Y),使其满足下列各式,即φs=C1(对单联域截面,可取C1=0)式中C、C1——常数φs——沿截面周边上的φ值AI——多联域时各孔的面积,单联域时,AI=0切应力和应力函数的关系为等直杆扭转时最年夜切应力为单元长度扭转角为式中,Jk 、Wk为截面抗几何特性,见表2-2-1 等直杆扭转时的截面几何性质.图2·2-7 等值杆的扭转关于任意实体截面(拜会表2-2-2 任意实心截面的Jk公式),最年夜切应力位于或十分接近于最年夜内切圆与鸿沟的切点之一(除非在鸿沟的其他点上有引起很高局部应力的锋利凹角),以及位于鸿沟曲率代数值为最小的点上.关于凸面,鸿沟曲率为正:关于凹面,鸿沟曲率为负(图2·2-8).最年夜切应力可近似地用下式计算,即图2·2-8 任意实体截面式中的C分下列两种情形求得:(1)在曲率为正(截面鸿沟是直或凸的)的点上式中D——最年夜内切圆直径r——该点上的鸿沟曲率半径(此时为正)A——截面面积(2)在曲率为负(截面鸿沟是凹的)的点上式中,ψ为鸿沟切线绕过凹部时所转过的角度,(见图2-2-8),其单元为弧度(这里的r为负)而D、r和A的含义同前.一些任意实体截面的Jh值,见表2-2-2 任意实心截面的Jk公式应用薄膜实际与弹性扭转实际的数学相似性,通过实验确定扭转切应力是比拟方便的.用一块平均薄膜,张在与截面相似的鸿沟上,然后从薄膜的一侧施加微小的气体压力,使薄膜鼓成曲面,如图2-2-9所示.该曲面与扭转切应力等有着下述关系,即图2-2-9 薄膜比拟(1)薄膜曲面上任一点的斜率,与截面相应点的扭转切应力的年夜小成正比.(2)曲面的等高线即这切应力线(3)薄腊鼓起的体积的两倍相当于扭矩.由薄膜比拟可知,一般情况下切应力散布有的规律为(1)实心轴最年夜扭转切应力,必发作在外周边上,且在最年夜内切圆切点或其左近,或有凹角处.(2)内外周边上的切应力都是沿周边切线方向作用.(3)在凸角的顶点上切应力为零.当杆的一局部资料的应力超越弹性极限而发作塑性变形时,即在弹塑性变形情况下,如仍引用与前一节情况相同应力函数,则关于非硬化资料,在塑性区域要满足.由上式可知,在塑性区域内,φ曲面斜率为一常数.在弹塑性区的接壤处,φ 是延续的.当到达极限状态即发作全面塑性变形时,则可由截面鸿沟上筑起具有等倾角为rs 的“屋顶”(自然倾斜概略即砂堆比拟法).由该“屋顶”与底面所围成的体积即等于塑性极限扭矩的一半.例如,图2-2-10所示边长这2a的方形截面,其应力函数是高为ars 的角锥体.当发作全面塑性变形时,其极限扭矩的一半等于角锥体的体积,其年夜小等于底面积乘以高度的1/3.因此可得图2-2-10 方形截面的全塑性应力函数曲面表2-2-3 常常使用截面的θs、Ts、Tp和Tp/Ts列出了几种常常使用的塑性极限扭矩,并与弹性极限扭矩停止比拟.由表看出,若使屈服扩展至整个截面,则杆件的承载能力将年夜年夜提高.表2-2-4 常常使用组合截面的Tp列出了某些常常使用组合截面的塑性极限扭矩近似公式.表中末列出弹性极限据矩,是因为凹角处很高的应力集中系数对初始屈服有影响.计算空心截面扭杆的塑性极限扭矩时,关于等壁厚的空心扭杆,其极限据矩Tp等于具有外截面鸿沟的实心扭杆的极限扭矩Tps 减去与空心内截面的实心扭杆的极限扭矩MpH 即薄壁截面杆的自由扭转启齿截面|| 杜口截面|| 多闭室杜口截面薄壁截面可分为启齿截面和杜口截面.轧制的型钢或挤压成形的型材,如工字钢、槽钢、角钢或T形、Z形等为“启齿”截.这种截面可看成是由一些等宽度的狭矩形组成.狭矩形能够是直的或是弯的,如图2-2-11所示.在对一个弯的启齿狭矩形截面杆的自由扭转停止应力和变形计算时,可用同宽同长的直的狭矩形截面杆来替代.图2-2-11 启齿截面单元长度扭有角的变卦为式中T——扭矩G——切变模量Jk——自由扭转的截面抗几何特性其中a——截面形状修正系数,见表2-2-5ti——每个狭矩形的厚度或平均厚度di——每个狭矩形的长度表2-2-5 截面形状系数α的平均值截面形状系数工字钢槽钢角钢T型钢Z型钢α每个狭矩形长边中点左近的切应力最年夜切应力式中,tmax为最年夜厚度.杜口截面可分为单闭室和多闭室截面.薄壁管和空心矩形截面杆等属于单闭室截面.它们在自由扭转时,单元长度扭转角的变卦为应力或剪流公式为由式(2-2-27)和式(2-2-28)的如由N个闭室构成的一个杜口截面扭杆,设各闭室的剪流辨别为qⅠ、qⅡ……、qN.这时,隔板上的剪流应辨别为qⅠ -qⅡ(向上) 、qⅡ-qⅢ(向上)、…… .可树立(N+1)个方程组,解出(N+1)个末知数:qⅠ、qⅡ……qN 和dθ/dz .其中N个方程是由各闭室的单元长度扭转角公式(2-2-30)得出,另一个方程由平衡条件图2-2-12 杜口截面得出.。
