薄壁杆件习题
材料力学第3 章 扭 转习题及答案

第 三 章 扭 转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
( × ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
( × ) 3.圆杆扭转变形实质上是剪切变形。
( √ ) 4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
( √ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
( × ) 6.切应力互等定理,仅适用于纯剪切情况。
( × ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
( √ ) 9.受扭圆轴的最大切应力只出现在横截面上。
( × ) 10. 因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( √ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径( 小 )。
2. 当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3. 直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4. 一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5. 直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是( 相 )同的,扭转角φ是( 不 )同的。
6. 等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
郑州大学材料力学习题集_【有答案】
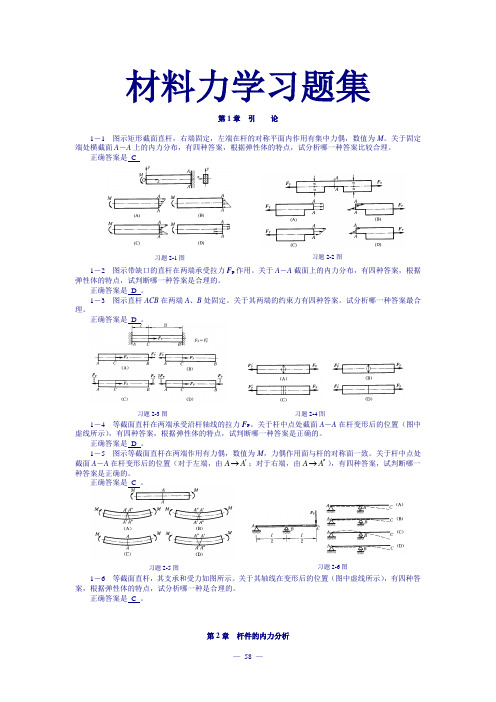
习题2-1图习题2-2图习题2-3图习题2-4图习题2-5图习题2-6图材料力学习题集第1章引论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M。
关于固定端处横截面A-A上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C1-2 图示带缺口的直杆在两端承受拉力F P作用。
关于A-A截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是D 。
1-3 图示直杆ACB在两端A、B处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P。
关于杆中点处截面A-A在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M,力偶作用面与杆的对称面一致。
关于杆中点处截面A-A在杆变形后的位置(对于左端,由AA'→;对于右端,由AA''→),有四种答案,试判断哪一种答案是正确的。
正确答案是C 。
1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是C 。
第2章杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图A BABC)(ql 2lM QF QF 454141(a-1) (b-1)AD EC MABCB 2M2M 34122-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A d Q F d M(B )(d x q x -=,Q d F x -=; (C )(d d Q x q x F -=,Q d d F x M=; (D )(d d Q x q x F =,Q d d F xM-=。
材料力学_范钦珊_习题参考解答
OB
B F P 60kN
Ea
1 .2 m
A
FP
x
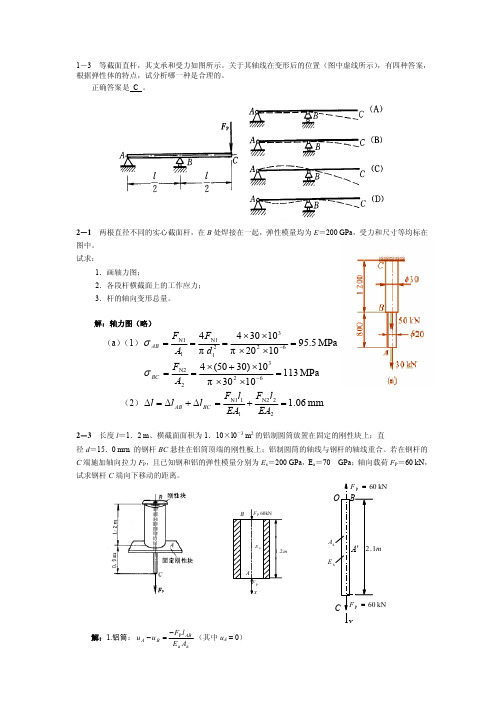
解:1.铝筒: u A − u B
=
−FPl AB Ea Aa
(其中 uA = 0)
As
A' 2.1m
Es
C FP = 60 kN
x
uB
=
60 ×103 ×1.2 ×103 70 ×103 ×1.10 ×10−3 ×106
= 0.935 mm
Mx1= Mx2 2.确定轴和薄壁管横截面上的最大剪应力 设轴受 T = 73.6N·m 时,相对扭转角为 ϕ0 ,于是,有
dφ0 = M x = T dx GIp1 GIp1
(a)
焊接后卸载,管承受扭转,其相对扭转角为 ϕ 2 ,轴上没有恢复的相对扭转角为 ϕ1 = ϕ0 − ϕ2 ,即
其中
ϕ1 + ϕ2 = ϕ0
×103 × 10 −6
= 95.5 MPa
σ BC
=
FN2 A2
=
4 × (50 + 30) ×103 π × 302 ×10−6
= 113 MPa
(2) ∆l = ∆l AB
+ ∆lBC
=
FN1l1 EA1
+ FN2l2 EA2
= 1.06 mm
2-3 长度 l=1.2 m、横截面面积为 1.10×l0-3 m2 的铝制圆筒放置在固定的刚性块上;直 径 d=15.0 mrn 的钢杆 BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。若在钢杆的 C 端施加轴向拉力 FP,且已知钢和铝的弹性模量分别为 Es=200 GPa,Ea=70 GPa;轴向载荷 FP=60 kN, 试求钢杆 C 端向下移动的距离。
工程力学材料力学部分课后习题详解
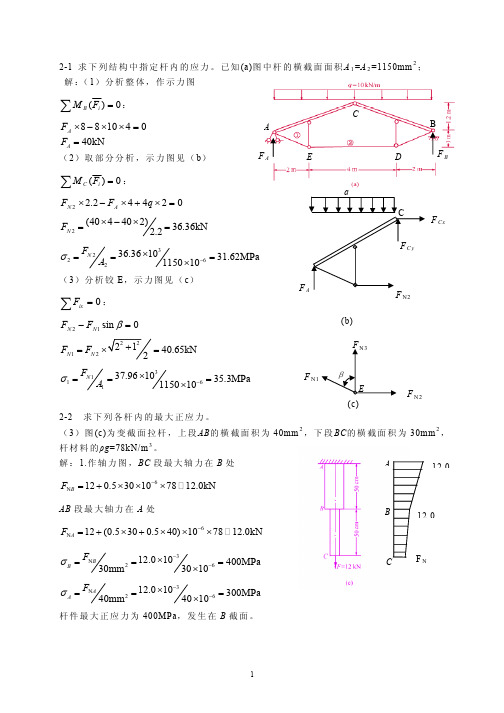
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:CB 041088=××−×A F AF N1F N2(c)40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×(3)分析铰E ,示力图见(c )∑=0ix F :0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ,发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比µ。
材料力学习题

材料⼒学习题材料⼒学习题训练22-1.求图⽰阶梯状直杆横截⾯1-1﹑2-2和3-3上的轴⼒,并作轴⼒图。
如横截⾯⾯积,,,求各横截⾯上的应⼒。
2-5.图⽰结构中,已知杆之横截⾯为的矩形,当杆横截⾯上的最⼤正应⼒为时,求此时的值。
2-6.直杆在两侧⾯受有沿轴线⽅向均匀分布的载荷(仅在段),其集度为;在端受集中⼒作⽤,。
已知杆横截⾯⾯积,,材料的弹性模量。
求:1、画出轴⼒图; 2、两截⾯的铅垂位3、过两点与轴线夹⾓斜截⾯上的螺杆所⽤材料的屈服点MPa,规定的安全系数n=1.5。
(1)试按强度要求选择⽴柱的直径D;(2)若螺杆的内径d=40mm试校核其强度。
3-1 夹剪如图所⽰。
销⼦C的直径d=5mm。
当加⼒P=0.2kN,剪直径与销⼦直径相同的铜丝时,求铜丝与销⼦横截⾯的平均剪应⼒。
已知a=30mm,b=150mm。
3-2 结构受⼒如图所⽰,若已知⽊材的许⽤切应⼒,试校核⽊接头剪切强度是否安全。
3-3 ⽊梁由柱⽀撑如图所⽰,今测得柱中的轴向压⼒为,若已知⽊梁所能承受的许⽤挤压应⼒。
确定柱与⽊梁之间垫板的尺⼨。
3-4 ⽊构件和由两⽚层合板⽤胶粘接在⼀起,承受轴向载荷作⽤,3-5 ⽔轮发电机组的卡环尺⼨如图所⽰。
已知轴向荷载P=1450kN,卡环材料的许⽤剪应⼒=80MPa,许⽤挤压应⼒=150MPa。
试对卡环进⾏强度校核。
3-6 拉⼒P=80kN的螺栓连接如图所⽰。
已知b=80mm,t=10mm,d=22mm,螺栓的许⽤剪应⼒=130MPa,钢板的许⽤挤压应⼒=300MPa,许⽤拉应⼒ =170MPa。
试校核该接头的强度。
3-7 ⼀托架如图所⽰。
已知外⼒P=35kN,铆钉的直径d=20mm,铆钉都受单剪。
求最危险的铆钉横截⾯上剪应⼒的数值及⽅向。
3-8 销钉式安全离合器如图所⽰,允许传递的外⼒偶矩m=30kN·cm,销钉材料的剪切强度极限=360MPa,轴的直径3-9 图⽰为测定剪切强度极限的试验装置。
(整理)郑大材料力学习题集

(整理)郑⼤材料⼒学习题集习题1-1图⽰拆卸⼯具的⽖钩(见图),若已知顶压⼒F=20kN ,求m-m 截⾯上的内⼒. 1-2试求图⽰m-m ,n-n 截⾯上的内⼒.习题1-2图 1-3 图⽰简易托架横梁上有吊车移动。
试求截⾯1-1和2-2(位于集中⼒F 左侧)上的内⼒及其最⼤值.1-4图⽰圆形薄板半径为R=100mm,变形后半径R 的增量为ΔR=2×10.3mm,.分别求出沿半径和外圆周两个⽅向的平均应变。
1-5图⽰三⾓形薄板受外⼒作⽤⽽变形,⾓点B 垂直向上位移为0.06mm, AB 和OB 仍保持为直线.试求:1)OB 的平均应变; 2)AB 和OB 两边在B 点的⾓度改变。
考 2-1 若杆件横截⾯上各点处的正应⼒都相等,则该截⾯上的法向分布内⼒的合⼒必通过横截⾯形⼼吗?⼜若杆件法向分布内⼒的合⼒通过横截⾯形⼼,横截⾯上各点处的正应⼒必相等吗?、B 两点间距离为a,材料的横向变形系数ν。
试证明该两点距离改变量为aAB νεδ-=。
2-3试说明公式A F N =σ, EA lF l N=?的应⽤条件,并说明E 的物理意义和量纲。
2-4 三根杆件尺⼨相同但材料不同,材料的εσ-曲线如图所⽰,试问哪⼀种(1)强度⾼?(2)刚度⼤?(1)塑性好? 2-5 杆件弹性模量E =210GPa ,⽐例极限σp =200MPa; 在轴向拉⼒作⽤下,纵向线应变为ε=8×10—4,求此时横截⾯上的正应⼒。
若拉⼒加⼤使杆件的纵向线应变增加到ε=5×10—3,问此时横截⾯上的正应⼒能否再由胡克定律确定? 2-6 若已测得受⼒物体内x 和y 两⽅向均有线应变,问在x 和y 两⽅向是否都必有正应⼒? 若测得x 和y 两⽅向均⽆线应变,则在x 和y 两⽅向是否都必⽆正应⼒? 2-7 低碳钢试样的拉伸图中,拉断时的应⼒为何⽐强度极限低?2-8 两根杆件,同样材料制成但横截⾯积不同,它们的强度极限相同吗? 2-9 脆性材料制成的轴向拉伸矩形截⾯杆,若有⽅向平⾏于轴线的裂纹,问杆的强度是否因此降低?若裂纹⽅向垂直于轴线,杆的强度是否因此降低?2-10 在图⽰杆系中,钢杆1和铜杆2的许⽤应⼒分别为[]1σ和[]2σ,横截⾯⾯积分别为A 1 和A 2 ;且[]1σ>[]2σ,⽽A 2 >A 1; 能断定铜杆2先破坏吗?若根据节点C 的平衡条件ΣY=0求结构的许可荷载,则02201130cos ][45cos ][][A A F σσ+=,这种结论对吗?思考题2-4图达到材料的许⽤应⼒值?习题Array 2-2 图⽰托架的AC横梁上有吊车移动。
材料力学典型例题与详解(经典题目)
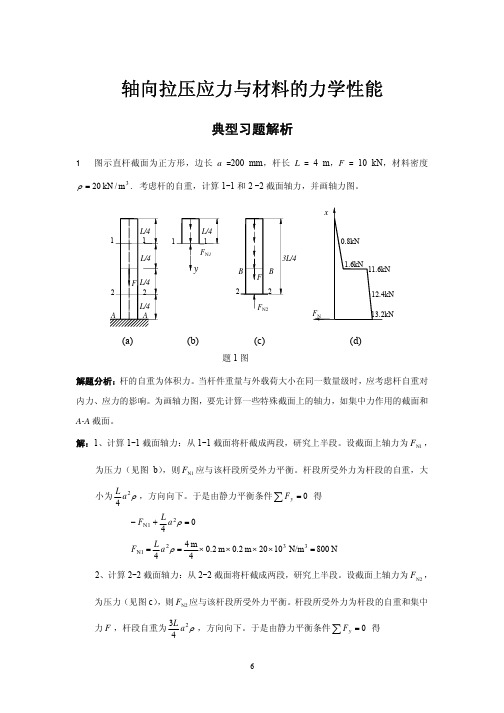
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
材料力学知到章节答案智慧树2023年山东科技大学

材料力学知到章节测试答案智慧树2023年最新山东科技大学第一章测试1.材料力学的研究方法与理论力学的研究方法完全相同。
参考答案:错2.内力只作用在杆件截面的形心处。
参考答案:错3.杆件某截面上的内力是该截面上应力的代数和。
参考答案:错4.确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
参考答案:对5.根据各向同性假设,可认为材料的弹性常数在各方向都相同。
参考答案:对6.根据均匀性假设,可认为构件的弹性常数在各点处都相同。
参考答案:对7.若物体各部分均无变形,则物体内各点的应变均为零。
参考答案:对8.外力就是构件所承受的载荷。
参考答案:错9.构件的强度、刚度和稳定性问题均与材料的力学性能有关。
参考答案:对10.可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
参考答案:对11.材料力学的研究对象为杆件。
参考答案:对12.题图所示直杆初始位置为ABC,作用力P后移至AB’C’,但右半段BCDE的形状不发生变化。
试分析哪一种答案正确。
参考答案:AB、BC两段都产生位移;13.根据各向同性假设,可认为构件的()沿各个方向相同。
参考答案:材料的弹性常数14.关于确定截面内力的截面法的适用范围,有下列说法正确的是()。
参考答案:不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况15.下列结论中是正确的是()。
参考答案:若物体各点均无位移,则该物体必定无变形16.以下结论中正确的是()。
参考答案:应力是内力的集度17.根据均匀性假设,可认为构件的下列各量中的哪个量在各点处都相同。
参考答案:材料的弹性常数18.材料力学的四个基本假设是()参考答案:连续性;各向同性;均匀性;小变形19.工程构件的基本类型是()参考答案:壳;板;杆件;块体20.下列描述正确的是()参考答案:应力是构件破坏的决定因素;应力是指内力的分布集度;应变是描述构件变形程度的量第二章测试1.因为轴力要按平衡条件求出,所以轴力的正负与坐标轴的指向一致。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其他问题:
(1)注意单位 (2)保留至少三位有效数字 (3)修改结果半途而废? (4)计算器使用 (5)将数字代入表达式,不要直接写结果
习题3-6 计算开闭混合截面和双室闭合截面的自由 扭转,并比较
(1)开闭混合截面开口部分截面的自由扭转惯性矩 (2)闭合截面无需计算开口部分截面的自由扭转惯性矩 (3)开口与闭合截面计算剪应力不同 (4)缺少二者结果比较
第三章习题
习题3-8 计算开闭混合截面杆件的自由扭转
(1)开口部分截面的自由扭转惯性矩 (2)取线模型计算
习题3-9 计算开闭混合截面杆件的自由扭转
(1)最大剪应力可以写成与外扭矩相关的函数 (2)圆管直径的选取 (3)取线模型计算
第三章习题
习题3-12 计算有加劲肋闭合截面杆件的扭转常数
(1)注意a0i的计算
习题3-13 计算有加劲肋闭合截面杆件的自由扭转
第四章习题
习题4-1 计算工字形截面主扇性坐标
习题2-12 计算截面的剪切中心
(1)板件绕向 (2)找主轴再计算?
第三章习题
习题3-1 计算闭合方形管状截面杆件的自由扭转
习题3-2 计算习题3-1开口截面杆件的自由扭转
(1)缺少开口、闭合截面扭-5 计算箱形截面杆件的翘曲值
(1)可采用公式(3.17)或简化公式(3.29)进行计算 (2)缺少图,计算起始点(例3-3)
习题2-8 计算单室闭合截面的弯曲剪力流
(1)计算线模型,截面特性计算 (2)切口选在对称轴上 (3)剪力流图包括大小、方向
第二章习题
习题2-11 确定两室闭合截面的剪切中心
(1)开口不同,计算所得的静定剪力流和超静定剪力流会 有所不同,但最终的叠加结果相同 (2)开口不同,不能随意套用例2-16
(1)线模型的选取(截面高度512mm) (2)辅助极点不宜选在形心处
习题4-2 计算弯曲扭转正应力
(1)计算扇性惯性矩图乘错误、单位换算错误
习题4-3 证明槽形截面扇性惯性矩公式
第四章习题
习题4-6 计算槽形截面悬臂梁的弯扭力矩
(1)偏心压力作用处的扇性坐标 (2)双力矩的定义,及与弯扭力矩的关系 (3)初参数法写出杆件的双力矩函数
第二章习题
习题2-3 确定剪切中心位置
(1)计算线模型,截面特性计算 (2)计算公式,计算方向
习题2-4 绘制剪力流变化图,确定剪切中心位置
(1)计算线模型,截面特性计算,最大剪力Q(位置) (2)剪力流变化图包括大小、方向 (3)计算剪切中心时参考点位置
第二章习题
习题2-6 习题2-7 证明等式
第四章习题
习题4-8 计算槽形截面固端梁的约束扭转
(1)主扇性特征的计算 (2)最大正应力(双力矩)在支座处,注意对称性 (3)最大弯扭力矩作用位置 (4)最大剪应力应考虑弯扭力矩和自由扭转力矩产生之和 (5)自由扭转力矩和扭转率有关 (6)注意初参数解中初参数的正负
第四章习题
习题4-11 应用扇性坐标计算剪切中心
