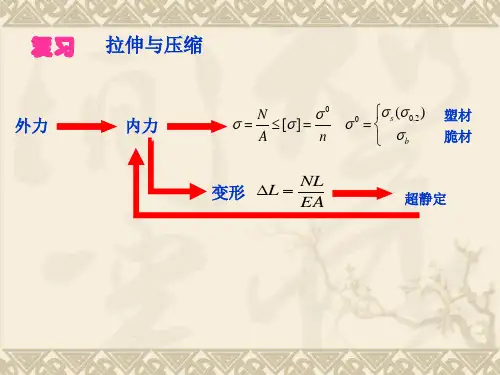
矩形截面杆、薄壁杆的扭转
矩形截面杆自由扭转时的应力和变形

矩形截面杆自由扭转时的应力和变形
在土建工程中还经常会遇到非圆截面杆,例如 矩形截面杆的扭转问题。在图3-13(a)所示 矩形截面杆的表面画上若干纵向线和横向线, 则在扭转后可看到所有横向线都变成了曲线 [图3-13(b)],这说明横截面不再保持为 平面而变为曲面,这种现象称为翘曲。试验表 明,非圆截面杆扭转时都会发生翘曲,圆轴扭 转时的平面假设不再成立,应力和变形的计算 公式也不再适用。
图3-13
当非圆截面杆不受任何约束时,横截面能自由翘曲,各截面翘曲 的程度相同(图3-13),此时横截面上只有切应力而没有正应 力,这种扭转称为自由扭转。若杆件受到约束,例如一端固定, 则各截面的翘曲受到限制,横截面上不仅有切应力,而且还有正 应力,这种扭转称为约束扭转。
对于实体截面杆,由约束扭转所引起的正应力数值很小,可忽略 不计;而对于薄壁截面杆,这种正应力往往较大,不能忽略。
非圆截面杆的扭转,必须用弹性力学的方法来研究。下面仅简单 介绍矩形截面杆自由扭转的主要结论:
1) 矩形截面杆自由扭转时横截面上切应力的分布规律如图314所示。截面周边各点处的切应力平行于周边且与扭矩方向一 致;在对称轴上,各点的切应力垂直于对称轴;其他各点的切应
力是斜向的;角点及形心处的切应力为零;最大切应力τmax发生 在长边中点处;短边中点处有较大的切应力τ1。
θmax=T/Gβhb3×180/π=4×103N·m/80×109Pa ×0.299×100×10-3×(50×10-3)3m4×180/可见此杆满足强度和刚度要求。
材料力学
图3-14
2) 计算公式。最大切应力为
τmax=T/Wp=T/αhb2 (3-17 短边中点处的切应力为
τ1=γτmax
(3-18
材料力学-第三章扭转
3、物理方程 mA a mA a AC 2GI p GI p
BC
2 mB a GI p
4 解得: m A 7 T 3 mB T 7
AB AC BC 0
例:由实心杆 1 和空心杆 2 组成的组合轴,受扭矩 T, 两者之间无相对滑动,求各点切应力。 T 解: 设实心杆和空心杆承担的扭矩分别为 G 2 Ip 2 M n 1 、 M n2 。 R2
二 刚度条件
M 180 刚度 n 0.50~1.0 / m 一般轴 l G Ip 条件
0.25~0.5 / m 精密轴
1.0 ~3.0 / m 粗糙轴
例 传动主轴设计,已知:n = 300r/m,P1 = 500kW,P2=200kW P3=300kW,G=80GPa [ ] 40MPa , [] 0.3 求:轴的直径d 解:1、外力分析
圆轴扭转的强度条件
max
Mn D Mn I p 2 Wp
Wp
2I p D
Mn
D 3 D 3 Wp 1 4 抗扭截面系数Wp : W p 16 16
强度条件:
Mn max Wp
例 已知汽车传动主轴D = 90 mm, d = 85 mm [ ] 60MPa, T = 1.5 kNm
Mn d
3
圆形优于矩形
Aa
= 0.208
3
a
3
4
3
d 0.886 d
2
Mn
a
2
Mn 0.208 0.886 d
b
6.913
材料力学第四章 扭转

max
T GI p
180
(/m)
×
例5 图示圆轴,已知mA =1kN.m, mB =3kN.m, mC
=2kN.m;l1 =0.7m,l2 =0.3m;[]=60MPa,[ ]=0.3°/m,
G=80GPa;试选择该轴的直径。
mA
mB mC 解: ⑴按强度条件
A
l1
B l2 C
max
9.55
200 300
6.37
(kN m)
×
n D
m2 1 m3 2 m1 3 m4
n A 1 B 2 C 3D
②求扭矩(扭矩按正方向假设)
m 0 , T1 m2 0, T1 m2 4.78kN m m 0; T2 m1 m2 0
T2 m2 m3 (4.78 4.78) 9.56kN m
T
2 r02
t
T 2 A0
t
T
A0为平均半径所作圆的面积。
×
三、切应力互等定理:
´
a
b
dy
´
c
z
dx
d t
mz 0; t dxdy t dxdy
'
这就是切应力互等定理:在单元体相互垂直的两个截面
上,切应力必然成对出现,且数值相等,两者都垂直于两平
面的交线,其方向或共同指向交线,或共同背离交线。
垂直,则杆件发生的变形为扭转变形。
A
B O
A
BO
m
m
——扭转角(两端面相对转过的角度)
——剪切角,剪切角也称切应变。
×
§4–2 扭转的内力—扭矩与扭矩图
一、扭矩 圆杆扭转横截面的内力合成
结果为一合力偶,合力偶的力偶 矩称为截面的扭矩,用T 表示之。 m
第八章 扭转问题

直杆的扭转
扭转问题中应力和位移 椭圆截面的扭转 扭转问题的薄膜比拟
矩形截面杆的扭转
薄壁杆的扭转
扭转问题的位移解法
扭转问题中应力和位移
问题: (1)等截面直杆,截面形状可以任意; (2)两端受有大小相等转向相反的扭矩 M ; (3)两端无约束,为自由扭转,不计体力 ; 求:杆件内的应力与位移?
l xz s m yz s 0
将 、 l、m 代入上述边界条件,有
dy dx ( )( ) 0 y ds x ds
dy dx 0 y ds x ds
dy dx 0 y ds x ds
d 0 ds
2 f1 0, 2 z 2 f2 0, 2 x
2 f2 0 2 z 2 f1 0, 2 y
f1 u0 y z z y K1 yz
f 2 v0 z x x z K 2 zx f f 又由: 2 1 0 得: x y z K 2 z z K1 z 0
zx 0 z zy 0 z xz yz 0 x y
基本方程的求解
2 yz 0
(a)
2 zx 0
(b)
—— 扭转问题的相容方程
—— 平衡方程
由式(a)的前二式,得
zx zx ( x, y) zy zy ( x, y ) —— 二元函数
分部积分,得:
yX xY dxdy y x dxdy y y x x dxdy
zx zy
y C D
同理,得:
B y dy dx A y
内容提要矩形截面直杆的扭转

第十二章 扭转与弯曲的几个补充问题一、 内容提要1. 矩形截面直杆的扭转 ab c t W 1max τντ= (12.2)杆件上相距为l 的两截面相对扭转角为3tTl TG hb GI ϕβ== (12.3) 3t I h b β=t I 称为矩形截面的扭转惯性矩。
以上各式中的系数α、ν、β和矩形截面的长边与短边的比值/h b 有关,其数值已列入教材表12.1中。
当h b >10时,截面成狭长矩形。
这时13αβ=≈。
如以δ狭长矩形的短边长度,则tW 和t I 分别为2t 13W h δ= , 3t 13I h δ= (12.4)2.薄壁杆件的自由扭转 a . 开口薄壁杆件的自由扭转由图12.4所示,开口薄壁截面可以看成若干狭长的矩形所组成的组合截面,则截面扭转惯性矩为3t t 1113nn i i i i i I I h δ====∑∑ (12.5)组合截面的最大切应力将发生在壁最厚的矩形的长边上,其值为maxmax tT I δτ=(12.6) 对于各种型钢,由于圆角及壁厚不均匀的影响,t I 还要给予修正,其修正公式为3t 113n i i i I h ηδ==∑b .闭合薄壁杆件的自由扭转其横截面上任意一点处切应力的计算公式为02TA τδ=(12.7) 式中0A 为薄壁中线所围成的面积,δ为该点处的壁厚。
由于壁厚δ沿中线是变化的,则最大切应力应发生在壁厚最薄处,即max 0max2TA τδ=(12.8)闭合薄壁杆件上相距为l 的两截面相对扭转角为2d 4sTl sGA ϕδ=⎰(12.9)若杆件的壁厚δ不变,上式化为3.非对称弯曲情况。
纯弯曲力偶矩在xy当前讨论的纯弯曲问题,仍采用§3.8中提出的两各假设,即⑴平面假设;⑵纵向纤维间无正应力。
从而可推得在xy 平面内作用纯弯曲力偶矩z M 时,横截面上任一点的正应力为2()z y yz y z yzM I y I z I I I σ-=- (12.12)同理可得在xz 平面内作用纯弯曲力偶矩y M 时,横截面上任一点的正应力为2()y z yz y z yzM I z I y I I I σ-=- (12.13)对于一般性问题,即在包含杆件轴线得任意纵向平面内,作用一对纯弯曲力偶M 。
弹性力学第8章—柱体扭转问题

n
n
A
扭转刚度
KT = 2G ∑ ki Ai + 2G ∫∫ ψ dxdy
i =1 A
8.2 基本方程 (3)应力函数表示的应力、应变和翘曲函数
∂ψ ∂ψ τ zx = Gθ , τ zy = −Gθ ∂y ∂x
合力
⎛ ∂ψ ⎞ ⎛ ∂ψ ⎞ 2 2 τ = τ zx + τ zy = Gθ ⎜ +⎜ ⎟ ⎟ ∂ ∂ y x ⎠ ⎝ ⎠ ⎝
8.3 矩形截面柱体的扭转
用应力函数方法求解,只要确
b/ 2
y
D
C
定应力函数,就可以进一步求出剪 应力和单位长度的相对扭转角。 应力函数方程
∇2ψ = −2
边界条件
b/ 2
O
x
B
A
a/ 2
a/ 2
b a x = ± 或 y = ± 时, ψ =0 2 2 上述问题称为泊松方程的第一边值问题,其解可由通解ψ 0和 特解 ψ 1 组成
A A
⎝ ∂x
∂y
⎠
对于柱体横截面是单连通域情况,利用斯托克斯公式,可得
⎛ ∂ψ ∂ψ ⎞ M T = −Gθ ∫∫ ⎜ x+ y ⎟ dxdy A ∂y ⎠ ⎝ ∂x ⎡∂ ⎤ ∂ = −Gθ ∫∫ ⎢ ( xψ ) + ( yψ ) ⎥ dxdy + 2Gθ ∫∫ ψ dxdy A ∂x A ∂y ⎣ ⎦ = −Gθ v ∫ ψ ( xl + ym ) ds + 2Gθ ∫∫ ψ dxdy
T
8.2 基本方程
8.2.1 基本关系式
位移表达式 圆柱上距离轴线为 r 的任 一点P的位移
u = − ( rθ z ) sin α = − yθ z ⎫ ⎪ v = ( rθ z ) cos α = xθ z ⎬ w = w ( x, y ) = θϕ ( x, y ) ⎪ ⎭
薄壁截面杆件的自由扭转变形能力比较
薄壁截面杆件的自由扭转变形能力比较刘晓红【摘要】近些年建筑行业对薄壁杆件的应用在迅猛增加,冷弯形成的各种杆件以及焊接、热轧薄壁杆件在钢结构中比比皆是.本文进行对比研究相同材料用量下工字形、T形开口薄壁截面杆和圆形、箱型、三角形闭口薄壁截面杆在自由扭转时的变形能力,分析了相同材料用量下工字形、箱形和三角形薄壁截面杆高宽比对截面扭转变形能力的影响.【期刊名称】《四川建材》【年(卷),期】2016(042)008【总页数】3页(P55-57)【关键词】薄壁截面杆件;自由扭转;扭转变形能力;高宽比【作者】刘晓红【作者单位】宁夏建设职业技术学院,宁夏银川 750021【正文语种】中文【中图分类】U442钢结构杆件在满足强度、刚度、稳定性要求的前提下,如能选择最佳截面来减少钢材损耗量、降低造价,将带来良好的经济效益和社会效益。
而薄壁结构杆件恰好具有重量轻、强度大、能充分利用材料的特点,所以各发达国家先后制定了关于薄壁结构的设计规范,我国也于1969年颁布了《弯曲薄壁型钢结构技术规范(草案)》,1975年又颁布了TJ18-75《薄壁型钢结构技术规范》,1987年颁布了GBJ18-87《冷弯薄壁型钢结构技术规范》和2002年颁布的GB5008-2002《冷弯薄壁型钢结构技术规范》共计4个版本。
国家体育场“鸟巢”主结构和次结构均采用焊接扭曲薄壁箱型截面,对此我国专家首次在国内外提出复杂扭曲薄壁箱型构件的设计理论与工程构型方法,可见薄壁杆件应用前景广阔。
扭转是工程中较为常见的一种现象,对薄壁截面扭转性能的研究是在试验和理论分析的基础上发展起来的。
无论是开口截面还是闭合截面,根据支撑情况和加载方式的不同,扭转分为两类:自由扭转(轴向位移是自由的)和约束扭转(轴向位移受到约束)。
针对薄壁杆件自由扭转问题,鲁汉银、郭建华[1] 已经做出了相关研究,本文与其不同之处在于:①鲁汉银等的研究仅限于三种闭合截面薄壁杆件,而本文增加了两种开口截面薄壁杆件工字型截面杆[2-5]和T形截面杆的研究,五种薄壁杆件自由扭转性能形成更鲜明对比;②鲁汉银等的文章从抗扭承载力方面研究薄壁截面杆件的扭转性能,而本文从扭转变形能力方面进行研究,通过变形能力可以使薄壁截面杆件的扭转性能对比更有说服力。
材料力学 第三章 扭 转
T2
T1
d
T3
Mx1=0.5kN· m
Mx2 =0.32kN· m lAB=300mm G=80GPa d=50mm
B
T2
φAB
lAB
A T1
lAC d φAC
C T3
B
lAB
A
lAC
C
M x1l AB j AB = GI P 500 0.3 = 9 80 10 0.054 32
r O
Mx
几何分析
变 形 应变分布
物理关系
应力分布
平面假定 静力学方程
应力公式
1. 变形几何关系
周线
a b c d
T
周线
a c d
γ
T
φ
b
纵线
dx
纵线
dx
a
c
a
γ
c c' d d'
b
d
b
(1)变形后所有圆周线的大小、形状和间距均不变,绕杆轴线相对转动。 (2)所有的纵线都转过了同一角度g。
T
周线
A
dρ
ρ o
ρ2dA
∫ 0ρ2·2πρdρ =
π d = 32
4
d/2
d
3 Ip π d Wp = r = 16
2. 空心圆截面
π D 4 - π d 4 π D 4(1-α4) Ip= 32 32 = 32 α=d/D
ρ o
dρ
π D3 Wp = 16 (1-α4)
d D
3.薄壁圆环截面
I P = 2r0
故该轴满足切应力强度要求。
二、刚度计算 等直圆杆扭转的刚度条件为
θ max = Mxmax ≤[θ] GI
(整理)杆的扭转定理和公式
圆截面杆的扭转外力与内力 || 圆杆扭转切应力与强度条件 || 圆杆扭转变形与刚度条件 || 圆杆的非弹性扭转1.外力与内力杆件扭转的受力特点是在垂直于其轴线的平面内作用有力偶(图2·2-1a),其变形特点是在任意两个截面绕轴线发生相对转动。
轴类构件常有扭转变形发生。
作用在传动轴上的外力偶矩m通常是根据轴所传递的功率N和转速n(r/min)来计算。
当N的单位为千瓦(kW)时当N的单位为马力(HP)时扭转时的内力为扭矩T,用截面法求得。
画出的内力图称为扭矩图(或T图),如图2·2-1b所示图2·2-1 圆杆的扭转2.圆杆扭转切应力与强度条件当应力不超过材料的剪切比例极限r p时,某横截面上任意C点(图2·2-2)的切应力公式为式中T——C 点所在横截面上的扭矩p——C点至圆心的距离L p——横截面对圆心的极惯性矩,见表2-2-1 等直杆扭转时的截面几何性质。
图2·2-2 切应力分布圆杆横截面上的切应力r沿半径呈线性分布,其方向垂直于半径(图2·3-2)。
模截面上的最大切应力在圆周各点上,其计算公式为等截面杆的最大切应力发生在T max截面(危险截面)的圆周各点(危险点)上。
其强度条件为式中,[τ]为许用扭转切应力,与许用拉应力[σ]的关系为:[τ]=(0.5~0.6)[σ] (塑性材料)或[τ]=(0.5~0.6)[σ](脆性材料)3.圆杆扭转变形与刚度条件在比弹性范围内,圆杆在扭矩T作用下,相中为L的两截面间相对扭转角为或式中G——材料的切变模量单位扭转角公式为或式中GL p——抗扭刚度圆杆上与杆轴距离为p外(图2·2-2)的切应变r为圆杆表面处的最大切应变为式中,r——圆杆的半径等截面圆杆的最大单位扭转角,发生在T max一段内,其刚度条件为式中,[θ]为圆杆的许用单位扭转角(°)/m4.圆杆的非弹性扭转讨论圆杆扭转时切应力超过材料的比例极限并进入塑性状态的情况。
材料力学 扭转(2)
1
M d n1 dx 1 GIp
2
M d n2 dx 2 GI p
M n1 d 因 M n1 M n 2 故 max 1 GI p dx max
max
180 N m 180 0.43 ( ) / m [ ] (80109 Pa)(3.0 105 10-12 m 4 ) π
§4-5 扭转扭转时的变形和刚度条件
一、圆轴扭转时的变形计算 1、扭转变形(相对扭转角)
d M n dx GI P Mn d dx GI P d M n dx GI P
扭转变形与内力计算式
Mn Mn
Mn L dx GI P
rad m ——单位长度的扭转角
扭转角单位:弧度(rad) GIP——抗扭刚度。
2.绘扭矩图
7640 N m
3.直径d1的选取 按强度条件
d1
A M e1
( )
M e2
d 2 M e3
C
max
3
16M n 3 d1
3
B
4580 N m
16M n d1 π[ ]
16 7640 π 70 106
82.2 103 m 82.2mm
n
3)等直圆杆受分布扭矩 t 作用,t 的单位为 N m m。
从中取 dx 段,dx 段两相邻截面的扭转角为:
M n x dx AB 截面相对扭转角为: l d l GI p
M n x dx d GI p
4)变截面圆杆,A、B 两端直径 分别为 d1、d2 。
解: 1.外力
P M e1 9549 1 n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、泊松方程:2F 2 (在柱形杆横截面所组成区域R内)。
2、边界条件:F(x, y) k(在横截面的周界C上)。
对于矩形截面杆件的扭转问题,能否像椭圆截面杆件扭 转问题一样假设扭转应力函数为其横截面的周界方程 ?
3 a2
a2
a3
a3
图3
设 ai 及 i分别表示扭杆横截面的第i个狭矩形的长度和宽度,
Ti表示该矩形截面上承受的扭矩,T表示整个横截面上的扭矩, i代表该矩形长边中点附近的剪应力, 为单 位长度扭转角。则
由狭长矩形的结果,得
3Ti
Gai
3 i
(2-1)
由式(2-1)得
i
3Ti
ai i 2
(2-2)
4G
13s2
A2 1
2
3
s1
A2 2
12s3 (
A1
A2
)2
(2-14) (2-15) (2-16)
例2 两个截面完全相同的变厚度薄壁杆如图8所示,其
中(a)为闭口,(b)为开口,试分析两杆件在抗扭转 刚度和最大剪应力方面的特点。
解(1)开口薄壁杆
由式(2-6),得单位长度扭转角:
G
3T
ai
1
4
T
图4
(2-6)
T
T
(2-6)
T
(2-6) T
(2-6) T
二 闭口薄壁杆件的扭转
对于闭口薄壁杆件的扭转问题,可以通过薄膜比拟
法求得近似解答。如图5所示,假想在薄杆横截面的外边
界上张一张膜,保证薄膜外边界的垂度为零,内边界处
的垂度为常量。由于杆壁厚度很小,所以沿壁的厚度方
向薄膜的斜率可视为常量。于是,在杆壁的厚度 处,剪
2b
得到应力函数
F ( x,
y)
b2 4
y2
8b2 π3
n0
(1)n1chn x cos n y (2n 1)3ch (2n 1) a
2b
由式(1-2),可求得
D 2
Fdxdy ab3[1 64 a
th (2n 1)πa 2b ]
R
3 π5 b n0 (2n 1)5
由此得
T GD
ab3G[1 3
答:不能。假设扭转应力函数为
F (x, y) B(x2 a2 )( y2 b2 )
显然这个应力函数虽然满足边界条件,但不 满足泊松方程。由于根据边界条件难以直接确定 满足基本方程的扭转应力函数,因此首先简化扭 转问题的基本方程。
一 狭长矩形截面杆的扭转
设矩形截面的边长为a和b。若a/b的值很大 (图1示), 则称为狭长矩形。由薄膜比拟法可以推断,应力函数F 在横截面的绝大部分上几乎与坐标x无关,于是有
GD Gab3
(1-1) (1-2)
(1-3)
由式(1-1)求得应力分量
zx
aG
F y
6T ab3
y
zy
aG
F x
0
(1-4)
这个应力表达式除在狭长矩形截面的短边附近外,对截面 的大部分区域都是正确的。由薄膜比拟法可知,最大剪应力 发生在矩形截面的长边上,即 y , 其b大小为
2
max |
zx
yb 2
|
3T ab2
(1-5)
二 任意边长比的矩形截面杆的扭转
在狭长矩形截面扭杆应力函数(1-1)的基础上,加上修正 项F1,即
F ( x,
y)
b2 4
y2
F1 ( x,
y)
(1-6)
函数F应满足方程 2F 2,将式(1-6)代入,得到F1满足方程
2F1 2F1 0 x2 y2
(1-7)
(2-12)
再分别对两根中心闭合线ACBA和ABDA求应力环量,有
ACB1ds
BA
3ds
2G
A1
BDA
2
ds
AB
3ds
2G
A2
(2-13)
若 1、 2 为常数,则式(2-13)可变为
1s1 2s2
3s3 3 s3
2G A1 2G A2
求得
1
2
T[3s2 A1 2s3 ( A1 A2 )]
(2n 1)5
]
(2-20)
将式(1-19)和式(1-20)分别写成
T ab3G
(2-21)
max
T
ab2
(2-22)
其中 和 都是仅与比值 有a关/ b的参数,这两个因子通过计
算可以表示如下:
图2
由表可见,对于很狭长矩形截面的扭杆, a / b 很大,
则 和 都趋近于1/3,这时式(2-21)和(2-22)分别简化为
Ti
G
ai
3 i
3
这个横截面上的扭转为
T
Ti
G
3
ai
3 i
(2-3) (2-4)
由式(2-3)和式(2-4)消去 ,得
Ti
aii3 T aii3
代回式(2-3)和式(2-4),我们得到
G
3T
ai
3 i
(2-5)
i
3T i
ai
3 i
(2-6)
值得注意的是:由上述公式给出的狭矩形长边中点的剪应 力已相当精确,然而,由于应力集中的存在,两个狭矩形 的连接处,可能存在远大于此的局部剪应力。
XY
其中, 为任意常数。
由此得方程
X 2 X 0
Y 2Y 0
(1-9) (1-10) (1-11)
(1-12) (1-13)
解之得方程(1-12)和(1-13)的通解 X (x) B1ch x B2sh x
Y ( y) C1cos y C2sin y
根据薄膜比拟法,应力函数为坐标x和y的偶函数。所以
64 π5
a b
T
n0
th (2n 1)πa 2b
(2n 1)5
]
(1-17) (1-18) (1-19)
由薄膜比拟可以推断,最大剪应力发生在矩形截面长边的中 点,其值为
T [1
5 π2
n0
1 (2n 1)2 th (2n 1)πa
]
max
2b
ab2[1
3
64 π5
a b
n0
th (2n 1)πa 2b
T 4 A2G
截面扭转刚度:
GD T 4A2G /
剪切力:
T 2 A
最大剪切力:
max
T
2 Amin
最大剪切力发生在宽度最小处。
(3)闭口截面与开口截面的扭杆的刚度比为
GD闭口 =(12A2 ) / 3ds
GD开口
12 A2
2s2
1
此式表明,闭口截面扭杆的刚度远远大于开口截面扭 杆的刚度。
应力的大小应等于薄膜的斜率,即
h
(2-7)
其中,h为杆壁厚度 薄膜的垂度。
设外边界所包围面积的平均值 (即薄壁杆件截面中线所包围的面 积)为A,于是有
T 2Ah (2-8)
图5
由此得 代入式(2-7)得
h T 2A
T 2 A
(2-9)
可见,剪应力与杆壁的厚度成反比,最大的剪应力 发生在杆壁最薄处。
n0
Anch
(2n 1)πa 2b
cos
(2n 1)π b
y
y2
b2 4
(1-16)
等式两边同时乘以cos (2m 1)π ydy,并在区间(-b/2,b/2)积分,得
b
An
π3 (2n
(1)n18b2 1)3ch (2n
1) a
2b
代入式(1-16),得
F1 ( x,
y)
8b2 π3
n0
(1)n1chn x cos n y (2n 1)3ch (2n 1) a
F
F dF
0,
a
x
y dy
则
2 F 2
b
o
x
y
变为常微分方程
d 2F dy 2
2
图1
而边界条件为 此时,方程的解为 代入
F(y b) 0 2
F ( y2 b2 ) 4
D 2 Fdxdy
得 于是
D 2
Fdxdy
R
2
a
2 a
2
b
2 b
(
y
2
2
b2 4
)dy
dx
ab3 3
T 3T
13s2
A2 1
2
3
s1
A2 2
12s3 ( A1
A2 )2
2
T[3s1A2 1s3 ( A1 A2 )]
2
13s2
A2 1
2
3
s1
A2 2
12s3 ( A1
A2
)2
3
2
1
3
s2
A2 1
T[1s2 A1 2s1A2 ]
2
3
s1
A2 2
12s3 ( A1
A2 )2
T (s1s23 s1s32 s2s31)
另外,应力函数F在矩形截面的边界处满足如下边界条件
F( a , y) 0, F(x, b) 0
2
2
(1-8)
所以,修正函数F1的边界条件为
F1 (
a 2
,
y)
y2
b2 4
F1 (
x,
b 2
)
0
设
F1(x, y) X (x)Y ( y)
将(1-10)代入(1-7)中,有 X Y 2
中 为圆角半径。
