第4章 薄壁杆件弯扭屈曲

Ex l2 2 π EI y PEy = l2 2 π EIω 1 PE β = 2 GJ + r0 l 2 =
π 2 EI x
(14)
由式(5)得 由式 得：
EIω β Ⅵ − ( GJ − Pr02 − R ) β ′′ = 0 EI y u Ⅵ + Pu ′′ = 0 EI y vⅥ + Pv′′ = 0
Π = ∫ F ( u′, u′′, v′, v′′, β ′, β ′′ ) dz (12) 0
l
由变分法可知，弹性体系处于平衡状态的条件： 由变分法可知，弹性体系处于平衡状态的条件：δΠ = 0
∂F d ∂F d 2 ∂F − + 2 ′′ = 0 ∂u dz ∂u ′ dz ∂u ∂F d ∂F d 2 ∂F − + 2 =0 ∂v dz ∂v′ dz ∂v′′ ∂F d ∂F d 2 ∂F − + 2 ′′ = 0 ∂β dz ∂β ′ dz ∂β
(2)
将 σ =P
A 代入式(2)，得： 代入式(2)， (2)
A q y = ∫ dq y = − P ( v′′ − x0 β ′′ ) A 2 m( z ) = ∫ dm( z ) = P ( y0u ′′ − x0 v′′ ) + Pr0 β ′′ A Ix + I y 2 2 2 其中： 其中： r0 = A + x0 + y0
l πz v = B sin l πz β = C sin l u = A sin
πz
(16) 满足边界条件： 满足边界条件：
将式(16)代入式 ，可得： 代入式(5)，可得： 将式 代入式
P − P Ey 0 − Py0 0 PEx − P Px0 A 0 B = 0 (17) 0 2 C ( PEβ − P ) r0 − Py0 Px0
第4章 薄壁杆件的弯扭屈曲
任课老师： 任课老师：强士中 卫 星
第4章 薄壁杆件的弯扭屈曲
薄壁杆件弯扭屈曲特点 中心受压开口薄壁杆件的弯扭屈曲 偏心受压开口薄壁杆件的弯扭屈曲× 纯弯梁的侧向屈曲 工字梁侧向屈曲的近似分析×
4.1 薄壁杆件弯扭屈曲特点
屈曲形式： 屈曲形式：
弯曲屈曲、 弯曲屈曲、扭转屈曲及弯扭屈曲
(18)
方程的3个根中最小者即屈曲临界荷载 方程的 个根中最小者即屈曲临界荷载 讨论： P <P <P <P <Pβ <P 讨论：1) PEx < PEy < PEβ
1 Ex 2 Ey E
3
2)
PE β < PEx < PEy
P < PE β < PEx < P2 < PEy < P3 1
结论： 结论：非对称截面开口薄壁杆件的弯扭屈 曲临界荷载总是小于纯弯曲屈曲和 和纯扭转屈曲临界荷载中的最小者。 和纯扭转屈曲临界荷载中的最小者。
PEy − P 0 − Py0 0 PEx − P Px0 − Py0
所以： 所以：
(P
Px0
ห้องสมุดไป่ตู้Eβ
− P ) r02
=0
2 2 r02 ( PEx − P ) ( PEy − P ) ( PE β − P ) − P 2 y0 ( PEx − P ) − P 2 x0 ( PEy − P ) = 0
单轴对称截面 y为对称轴，则x0=0，由式 为对称轴， 可得： 为对称轴 ，由式(18)可得： 可得 解之得： 解之得：
( PEx − P ) ( PEy − P ) ( PE β − P ) − P 2 y02
P = PEx = 1
π 2 EI x
l2
2
r02 = 0
P2,3 =
( PEy + PEβ ) r02 ±
(21)
(22)
(23) 式中： 式中：
将式(21)(22)(23)代入式 ，可得： 代入式(1)，可得： 将式 代入式 (24)
对于两端铰支杆，将式 代入式(24)，可得： 对于两端铰支杆，将式(16)代入式 代入式 ，可得：
P −P 0 − P ( y0 − ex ) Ey A 0 B = 0(25) 0 PEy − P P ( x0 − ey ) 2 − P ( y0 − ex ) P ( x0 − ey ) r0 ( PEβ − P ) − 2P ( ex a y + ey ax ) C 0
qx = ∫ dqx = − P ( u ′′ + y0 β ′′ )
(3)
将式(3)代入式(1)， 将式(3)代入式(1)，得： (3)代入式(1)
EIω β Ⅵ − ( GJ − Pr02 ) β ′′ + Py0u ′′ − Px0 v′′ = 0 EI y u Ⅵ + P ( u ′′ + y0 β ′′ ) = 0 EI y vⅥ + P ( v′′ − x0 β ′′ ) = 0
EIω β Ⅵ − ( GJ − Pr02 − R ) β ′′ + Py0u ′′ − Px0 v′′ = 0 EI y u Ⅵ + P ( u ′′ + y0 β ′′ ) = 0 EI y vⅥ + P ( v′′ − x0 β ′′ ) = 0
(5)
式中： 式中：
(13)
4.2.2 中心受压开口薄壁杆件弯扭屈曲临界荷载
双轴对称截面 剪力中心与截面形心重合， 剪力中心与截面形心重合，x0=0，y0=0 由式(4)得 由式 得： P
EIω β Ⅵ − ( GJ − Pr02 ) β ′′ = 0 EI y u Ⅵ + Pu ′′ = 0 EI y v Ⅵ + Pv′′ = 0
R = ∫ σ r ( x 2 + y 2 )dA
A
(6)
II 能量法 薄壁杆件的应变能： 薄壁杆件的应变能：
1 l 1 l 2 2 U = ∫ EI y ( u ′′ ) dz + ∫ EI x ( v ′′ ) dz 2 0 2 0 1 l 1 l 2 2 + ∫ GJ ( β ′ ) dz + ∫ EI ω ( β ′′ ) dz 2 0 2 0
(4)
若考虑残余应力的影响，截面上的法向应力： 若考虑残余应力的影响，截面上的法向应力： σ = P A +σr (s) 残余应力是自相平衡的应力体系： 残余应力是自相平衡的应力体系：
∫ σ dA = ∫ σ
A r A
r
xdA = ∫ σ r ydA = 0
A
考虑残余应力的弯扭屈曲平衡方程式： 考虑残余应力的弯扭屈曲平衡方程式：
所以： 所以：
π 2 EA = λ02 2
(20)
结论： 结论：单轴对称截面开口薄壁杆件可能在截面对称平面 内发生弯曲屈曲或者离开对称平面发生弯扭屈曲。 内发生弯曲屈曲或者离开对称平面发生弯扭屈曲。
4.3 偏心受压薄壁杆件的弯扭屈曲
M 偏心弯矩： 偏心弯矩： M x = Pex ， y = Pey
σM =
P Mxy Myx + + A Ix Iy
基本假定： 基本假定：
(1) 屈曲时杆件仍处于弹性工作状态和小变形状态； 屈曲时杆件仍处于弹性工作状态和小变形状态； (2) 尽管杆件各截面可能产生垂直于截面的翘曲，但其在 尽管杆件各截面可能产生垂直于截面的翘曲， 自身平面内的投影始终保持固定形状“ 自身平面内的投影始终保持固定形状“横截面形状不 变假设” 变假设”； (3) 荷载作用线的方向保持不变。 荷载作用线的方向保持不变。
PEx = l2 2 π EI y PEy = l2 π 2 EIω 1 PE β = 2 GJ − R + r0 l 2
π 2 EI x
(15)
非对称截面 两端铰支杆，位移函数可用正弦函数表示： 两端铰支杆，位移函数可用正弦函数表示：
l
纤维缩短量： 纤维缩短量：
1 l 2 2 ′ ′ ∆ = s − l = ∫ ( uM ) + ( vM ) dz 2 0
(9)
将式(9)代入式 ，可得： 将式 代入式(8)，可得： 代入式
1 l 2 2 ′ ′ V = − ∫ σ∆dA = − ∫ ∫ σ ( uM ) + ( vM ) dAdz A 2 0 A
4.2 中心受压薄壁杆件的弯扭屈曲
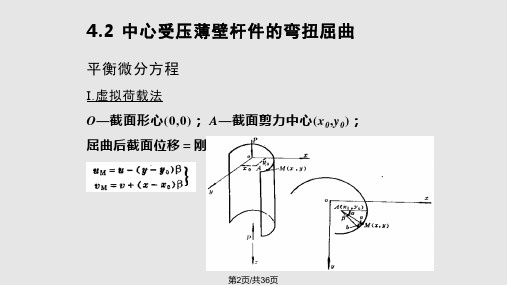
4.2.1 平衡微分方程
I.虚拟荷载法 O—截面形心 截面形心(0,0)； A—截面剪力中心 0,y0)； 截面剪力中心(x 截面形心 ； 截面剪力中心 ； 屈曲后截面位移＝刚体平动＋ 屈曲后截面位移＝刚体平动＋绕剪力中心的转动
如右图a)所示梁屈曲时平衡微分方程： 如右图a)所示梁屈曲时平衡微分方程： a)所示梁屈曲时平衡微分方程 如右图b)所示梁屈曲时平衡微分方程： 如右图b)所示梁屈曲时平衡微分方程： b)所示梁屈曲时平衡微分方程
l2 2 π EI y PEy = l2 其中： 其中： 2 π EI 1 PE β = 2 GJ − R + 2 ω r0 l PEx =
π 2 EI x
A、B、C不全为 ，则式 不全为0，则式(17)中系数行列式须等于零： 中系数行列式须等于零： 不全为 中系数行列式须等于零
A、B、C不全为 ，则式 不全为0，则式(17)中系数行列式须等于零： 中系数行列式须等于零： 不全为 中系数行列式须等于零