二次函数初高中衔接
初高中衔接二次函数专题

3 二次函数 基础知识1.二次函数的三种表示方式: (1)一般式:y=ax 2 +bx+c ;(2)顶点式:y=a(x-m)2 +n (常用,便于求最值、画图); (3)交点式: y=a(x-x 1 )(x-x 2 ) (△≥0时) .2.若函数y=f(x)的对称轴是x=h,则对f(x)定义域内的任意x,都有f(h+x)=f(h-x);反之也成立。
3.二次方程根的分布问题,限制条件较多时可用相应抛物线位置,限制条件较少时可用韦达定理解决。
4.二次函数的最值问题(1)二次函数2(0)y ax bx c a =++≠的最值.二次函数在自变量x 取任意实数时的最值情况:当0a >时,函数在2bx a=-处取得最小值244ac b a -,没有最大值;当0a <时,函数在2b x a=-处取得最大值244ac b a -,没有最小值.求二次函数最大值或最小值的步骤:第一步确定a 的符号,a >0有最小值,a <0有最大值; 第二步配方求顶点,顶点的纵坐标即为对应的最大值或最小值. (2)求二次函数在某一范围内的最值.二次函数在某区间上的最值须用配方法,含字母的函数最值可借助图象分析。
如:求2y ax bx c =++在m x n ≤≤(其中m n <)的最值的步骤: 第一步:先通过配方,求出函数图象的对称轴:0x x =;第二步:讨论:(请同学们画出图像理解)(1)若0a >时求最小值或0a <时求最大值,需分三种情况讨论: ①0x m <,即对称轴在m x n ≤≤的左侧; ②0m x n ≤≤,即对称轴在m x n ≤≤的内部; ③0x n >,即对称轴在m x n ≤≤的右侧。
(2) 若0a >时求最大值或0a <时求最小值,需分两种情况讨论: ①02m nx +≤,即对称轴在m x n ≤≤的中点的左侧;②02m nx +>,即对称轴在m x n ≤≤的中点的右侧。
初高中数学衔接知识复习二次函数

初、高中数学衔接知识复习:二次函数一.要点回顾1. 二次函数y =ax 2+bx +c (a ≠0)配方得:y =ax 2+bx +c =a (x 2+b x a )+c =a (x 2+b x a+224b a )+c -24b a 224()24b b ac a x a a-=++, 所以,y =ax 2+bx +c (a ≠0)的图象可以由函数y =ax 2的图象作左右平移、上下平移而得到。
2.二次函数y =ax 2+bx +c (a ≠0)的性质:[1] 当a >0时,函数y =ax 2+bx +c 图象开口向 ;顶点坐标为 ,对称轴为直线 ;当x 时,y 随着x 的增大而 ;当x 时,y 随着x 的增大而 ;当x 时,函数取最小值 .[2] 当a <0时,函数y =ax 2+bx +c 图象开口向 ;顶点坐标为 ,对称轴为直线 ;当x 时,y 随着x 的增大而 ;当x 时,y 随着x 的增大而 ;当x 时,函数取最大值 .3.二次函数的三种表示方式[1]二次函数的三种表示方式:(1).一般式: ; (2).顶点式: ; (3).交点式: . 说明:确定二此函数的关系式的一般方法是待定系数法,在选择把二次函数的关系式设成什么形式时,可根据题目中的条件灵活选择,以简单为原则.二次函数的关系式可设如下三种形式:①给出三点坐标可利用一般式来求;②给出两点,且其中一点为顶点时可利用顶点式来求.③给出三点,其中两点为与x 轴的两个交点)0,(1x .)0,(2x 时可利用交点式来求.2 二次函数图像的变换----------平移二次函数y =a (x +h )2+k (a ≠0)中,a 决定了二次函数图象的开口大小及方向;h 决定了二次函数图象的左右平移,而且“h 正左移,h 负右移”;k 决定了二次函数图象的上下平移,而且“k 正上移,k 负下移”. 选择题:(1)下列函数图象中,顶点不在坐标轴上的是 ( )(A )y =2x 2 (B )y =2x 2-4x +2(C )y =2x 2-1 (D )y =2x 2-4x(2)函数y =2(x -1)2+2是将函数y =2x 2( )(A )向左平移1个单位、再向上平移2个单位得到的 (B )向右平移2个单位、再向上平移1个单位得到的 (C )向下平移2个单位、再向右平移1个单位得到的 (D )向上平移2个单位、再向右平移1个单位得到的(3)把函数y =-(x -1)2+4的图象向左平移2个单位,向下平移3个单位,所得图象对应的解析式为 ( )(A )y = (x +1)2+1 (B )y =-(x +1)2+1(C )y =-(x -3)2+4 (D )y =-(x -3)2+二.题型演练例1.抛物线()21252y x =--+的顶点坐标是_________,对称轴是_________,开口向_____,当x =_______时,y 有最______值,最大值为 ________。
借助二次函数衔接初高中数学

借助二次函数衔接初高中数学【摘要】初高中数学教育的重要性不言而喻,而二次函数作为数学学科中重要的一部分,在初高中阶段更是发挥着关键作用。
本文通过探讨二次函数的基本性质,以及初中和高中数学知识与二次函数的联系,揭示了借助二次函数实现初高中数学知识的有效衔接的必要性和可能性。
通过案例分析,展示了如何利用二次函数来衔接不同阶段的数学知识,从而确保学生学习的连贯性和深度。
结论部分强调了二次函数在数学教育中的重要作用,并呼吁进一步完善使用二次函数衔接初高中数学的方法和策略,以促进学生数学学科的全面发展和学习效果的最大化。
通过借助二次函数,可以有效地实现初高中数学知识的衔接,为学生的数学学习提供更好的支持和指导。
【关键词】初高中数学教育、二次函数、衔接工具、基本性质、联系、案例分析、有效衔接、重要作用、方法、策略、未来。
1. 引言1.1 初高中数学教育的重要性数学是一门具有普适性的学科,它不仅在自然科学领域有着广泛的应用,还在工程技术、经济管理等领域发挥着重要作用。
初中数学教育和高中数学教育的衔接至关重要。
只有通过系统性的学习和逐层深化,学生才能建立起完整的数学知识体系,为将来的学习和工作打下坚实的基础。
在整个教育体系中,数学是一个贯穿始终的主题。
初高中数学教育的衔接非常重要,可以帮助学生更好地理解和应用数学知识。
通过借助二次函数作为衔接工具,可以有效地提高学生的数学学习能力,促进他们的全面发展和素质提升。
1.2 二次函数在数学学科中的地位和应用二次函数是数学中非常重要的一个概念,它在数学学科中有着特殊的地位和广泛的应用。
二次函数是代数学中最基本的函数之一,其形式为y=ax^2+bx+c,是一种二次多项式函数。
在数学学科中,二次函数不仅在初中阶段就开始学习,而且在高中数学中也是重要的内容之一。
掌握二次函数可以帮助我们更好地理解函数的概念和性质,为进一步学习数学打下坚实的基础。
二次函数在数学学科中有着丰富的应用。
(初高中衔接教材)专题三 二次函数
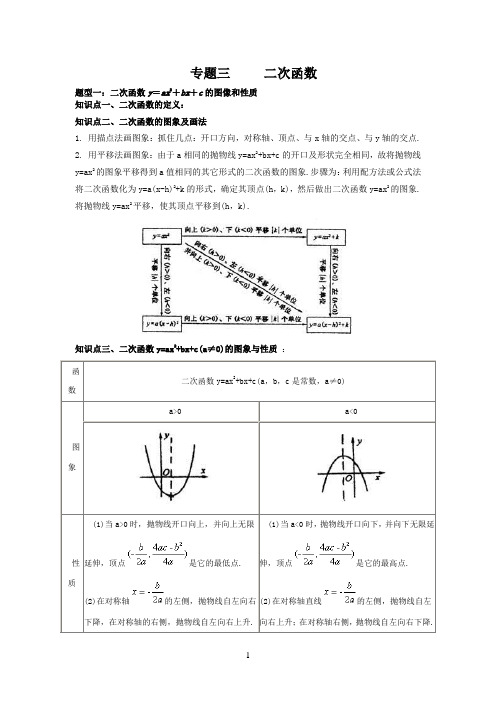
专题三二次函数题型一:二次函数y=ax2+bx+c的图像和性质知识点一、二次函数的定义:知识点二、二次函数的图象及画法1. 用描点法画图象:抓住几点:开口方向,对称轴、顶点、与x轴的交点、与y轴的交点.2. 用平移法画图象:由于a相同的抛物线y=ax2+bx+c的开口及形状完全相同,故将抛物线y=ax2的图象平移得到a值相同的其它形式的二次函数的图象.步骤为:利用配方法或公式法将二次函数化为y=a(x-h)2+k的形式,确定其顶点(h,k),然后做出二次函数y=ax2的图象.将抛物线y=ax2平移,使其顶点平移到(h,k).知识点三、二次函数y=ax2+bx+c(a≠0)的图象与性质:函数二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象a>0 a<0性质(1)当a>0时,抛物线开口向上,并向上无限延伸,顶点是它的最低点.(2)在对称轴的左侧,抛物线自左向右下降,在对称轴的右侧,抛物线自左向右上升.(1)当a<0时,抛物线开口向下,并向下无限延伸,顶点是它的最高点.(2)在对称轴直线的左侧,抛物线自左向右上升;在对称轴右侧,抛物线自左向右下降.知识点四、抛物线y=ax 2+bx+c 中a 、b 、c 的作用a ,b ,c 的代数式 作用字母的符号图象的特征a1. 决定抛物线的开口方向;2. 决定增减性a>0开口向上 a<0 开口向下 c决定抛物线与y 轴交点的位置,交点坐标为(0,c)c>0交点在x 轴上方 c=0抛物线过原点 c<0交点在x 轴下方 决定对称轴的位置,对称轴是直线ab>0 对称轴在y 轴左侧 ab<0 对称轴在y 轴右侧 b 2-4ac决定抛物线与x 轴公共点的个数b 2-4ac>0抛物线与x 轴有两个交点例题讲解1、下列函数中,是二次函数的是 .①y=x 2-4x+1; ②y=2x 2; ③y=2x 2+4x ; ④y=-3x ;⑤y=-2x -1; ⑥y=mx 2+nx+p ; ⑦y =(4,x) ; ⑧y=-5x 。
初高中衔接二次函数专题

3 二次函数 基础知识1.二次函数的三种表示方式:(1)一般式:y=ax 2+bx+c ;(2)顶点式:y=a(x-m)2+n (常用,便于求最值、画图);(3)交点式: y=a(x-x 1 )(x-x 2 ) (△≥0时) .2.若函数y=f(x)的对称轴是x=h,则对f(x)定义域内的任意x,都有f(h+x)=f(h-x);反之也成立。
3.二次方程根的分布问题,限制条件较多时可用相应抛物线位置,限制条件较少时可用韦达定理解决。
4.二次函数的最值问题(1)二次函数2(0)y ax bx c a =++≠的最值.二次函数在自变量x 取任意实数时的最值情况:当0a >时,函数在2bx a=-处取得最小值244ac b a -,没有最大值;当0a <时,函数在2b x a=-处取得最大值244ac b a -,没有最小值.求二次函数最大值或最小值的步骤:第一步确定a 的符号,a >0有最小值,a <0有最大值; 第二步配方求顶点,顶点的纵坐标即为对应的最大值或最小值. (2)求二次函数在某一范围内的最值.二次函数在某区间上的最值须用配方法,含字母的函数最值可借助图象分析。
如:求2y ax bx c =++在m x n ≤≤(其中m n <)的最值的步骤: 第一步:先通过配方,求出函数图象的对称轴:0x x =;第二步:讨论:(请同学们画出图像理解)(1)若0a >时求最小值或0a <时求最大值,需分三种情况讨论: ①0x m <,即对称轴在m x n ≤≤的左侧; ②0m x n ≤≤,即对称轴在m x n ≤≤的内部; ③0x n >,即对称轴在m x n ≤≤的右侧。
(2) 若0a >时求最大值或0a <时求最小值,需分两种情况讨论: ①02m nx +≤,即对称轴在m x n ≤≤的中点的左侧;②02m nx +>,即对称轴在m x n ≤≤的中点的右侧。
衔接2二次函数

m2 3
是二次函数, 且图像开
口向上,则 m 的值为_
5 二次函数 y ax bx c 的顶点
2
坐标为(0,3) ,且经过点(-2,-1) , 则其解x bx c 的图象如图 例 1 二次函数
1 所示,则下列结论正确的是( A. a 0,b 0,c 0 B. a 0,b 0,c 0 C. a 0,b 0,c 0 D. a 0,b 0,c 0 图1
D
y ax b 体验 2 已知二次函数 与
2
y 3x 4 的图象关于 x 轴对称,
2
则a
,b
例 2 已知二次函数 y=ax +bx+c 的图象 与 x 轴交于 A(1,0),B(3,0)两点, 与 y 轴交于点 C (0,3),则二次函数 的解析式是 .
2
体验 3 二次函数 y 3x 4 与一次函数 y x b 只有唯一公共点,则 b
2
已知抛物线 y=x -2x-8. (1)试说明该抛物线与 x 轴一定有 两个交点. (2)若该抛物线与 x 轴的两个交点 分别为 A、B(A 在 B 的左边),且点 P 为 抛物线在 x 轴下方上的任意一点, 求 △ABP 的面积的最大值.
2
)
体验 1
物体在地球的引力作用下做自由下
1 2
2
落运动, 它的运动规律可以表示为: s= gt . 其中 s 表示自某一高度下落的距离,t 表示 下落的时间, g 是重力加速度.若某一物体从 一固定高度自由下落,其运动过程中下落的 距离 s 和时间 t 函数图象大致为( )
s s s s O O t O t O t t
2 若函数 y=4x +1 的函数值为 5, 则自变 量 x 的值应为( ) A.1 B.-1
初高中二次函数衔接内容

1、二次函数的定义定义: y=ax ² + bx + c ( a 、 b 、 c 是常数, a ≠ 0 ) 定义要点:①a ≠ 0 ②最高次数为2 ③代数式一定是整式练习:1、y=-x ²,y=2x ²-2/x ,y=100-5 x ²,y=3 x ²-2x ³+5,其中是二次函数的有____个。
2.当m_______时,函数y=(m+1)χ - 2χ+1 是二次函数?2、二次函数的图像及性质例2:已知二次函数(1)求抛物线开口方向,对称轴和顶点M 的坐标。
(2)设抛物线与y 轴交于C 点,与x 轴交于A 、B 两点,求C ,A ,B 的坐标。
(3)x 为何值时,y 随的增大而减少,x 为何值时,y 有最大(小)值,这个最大(小)值是多少?(4)x 为何值时,y<0?x 为何值时,y>0?抛物线 顶点坐标 对称轴 位置 开口方向 增减性 最值y=ax2+bx+c(a>0)y=ax 2+bx+c (a<0)由a,b 和c 的符号确定由a,b 和c 的符号确定 a>0,开口向上a<0,开口向下在对称轴的左侧,y 随着x 的增大而减小. .在对称轴的左侧,y 随着x 的增大而增大. 在.⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22abx 2-=直线abx 2-=直线mm -223212-+=x x y【考题1】(2009、贵阳).抛物线y =-4(x +2)2+5的对称轴是______ 【考题2】(2009、宁安)函数y= x 2-4的图象与y 轴的交点坐标是( ) A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)【考题3】(2009、贵阳)已知抛物线21(4)33y x =-- 的部分图象(如图1-2-1),图象再次与x轴相交时的坐标是( ) A .(5,0) B.(6,0) C .(7,0) D.(8,0)【考题4】(深圳)二次函数c bx ax y ++=2图像如图所示,若点A(1,1y ),B(2,2y )是它的图像上两点,则1y 与2y 的大小关系是()A.1y <2y B.1y =2y C.1y >2y D.不能确定练习1.抛物线y=x 2-4x +5的顶点坐标是( ) A .(-2,1) B .(-2,-1) C .(2,l ) D .(2,-1)2.二次函数 y=2(x -3)2+5的图象的开口方向、对称轴和顶点坐标分别为( ) A .开口向下,对称轴x =-3,顶点坐标为(3,5) B .开口向下,对称轴x =3,顶点坐标为(3,5) C .开口向上,对称轴x =-3,顶点坐标为(-3,5) D .开口向上,对称轴x =-3,顶点(-3,-5)3.二次函数c bx x y ++=2的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )A . 4=x B. 3=x C. 5-=x D. 1-=x4.已知二次函数c bx ax y ++=21(a ≠0)与一次函数y 2=kx+m(k ≠0)的图象相交于点A (-2,4),B(8,2),如图1-2-7所示,能使y 1>y 2成立的x 取值范围是_______三.二次函数的图象与系数的关系1、a 的符号:a 的符号由抛物线的开口方向决定.抛物线开口向上,则a >0;抛物线开口向下,则a <0.2、b 的符号由对称轴决定,若对称轴是y 轴,则b=0;若抛物线的顶点在y 轴左侧,顶点x=-3yO的横坐标-2b a <0,即2ba>0,则a 、b 为同号;若抛物线的顶点在y 轴右侧,顶点的横坐标-2b a >0,即2ba<0.则a 、b 异号.间“左同右异”. 3.c 的符号:c 的符号由抛物线与y 轴的交点位置确定.若抛物线交y 轴于正半,则c >0,抛物线交y 轴于负半轴.则c <0;若抛物线过原点,则c=0.4.△的符号:△的符号由抛物线与x 轴的交点个数决定.若抛物线与x 轴只有一个交点,则△=0;有两个交点,则△>0.没有交点,则△<0 .5、a+b+c 与a -b+c 的符号:a+b+c 是抛物线c bx ax y ++=2(a ≠0)上的点(1,a+b+c )的纵坐标,a -b+c 是抛物线c bx ax y ++=2(a ≠0)上的点(-1,a -b +c )的纵坐标.根据点的位置,可确定它们的符号.【考题1】(2009、潍坊)已知二次函数c bx ax y ++=2的图象如图 l -2-2所示,则a 、b 、c 满足( ) A .a <0,b <0,c >0 B .a <0,b <0,c <0 C .a <0,b >0,c >0 D .a >0,b <0,c >0【考题2】(2009、天津)已知二次函数c bx ax y ++=2(a≠0)且a <0,a -b+c >0,则一定有( )A .b 2-4ac >0B .b 2-4ac =0C .b 2-4ac <0D .b 2-4ac≤0 【考题3】(2009、重庆)二次函数c bx ax y ++=2的图象如图1-2-10,则点(b ,c a )在( )A .第一象限B .第二象限C .第三象限D .第四象限练习1.已知函数c bx ax y ++=2的图象如图1-2-11所示,给出下列关于系数a 、b 、c 的不等式:①a <0,②b <0,③c >0,④2a +b <0,⑤a +b +c >0.其中正确的不等式的序号为___________-2.已知抛物线c bx ax y ++=2与x 轴交点的横坐标为-1,则a +c=_________.四、抛物线解析式的三种方法的互相转化1、一般式:已知抛物线上的三点,通常设解析式为________________ y=ax2+bx+c(a ≠0)2,顶点式:已知抛物线顶点坐标(h, k ),通常设抛物线解析式为_______________求出表达式后化为一般形式. y=a(x-h)2+k(a ≠0)3,交点式:已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________ 例 将下列二次函数的解析式转化成其他两种形式 (1)y =x 2-x -6· (2)y =21x 2+3 x +256二次函数与一元二次方程的关系一元二次方程根的情况与b ²-4ac 的关系我们知道:代数式b2-4ac 对于方程的根起着关键的作用.二次函数y=ax ²+bx +c 的图象和x 轴交点的横坐标,便是对应的一元二次方程ax ²+bx +c=0的解。
初高中衔接04二次函数的图象与性质

课题:《初高中衔接04二次函数图象与性质》一 教学目标:①掌握二次函数的概念及性质;②能根据二次函数的性质作出简图;③会用配方法研究二次函数的性质;二 教学重点:用配方法研究二次函数的性质与图像;三 教学难点:研究二次函数的性质与图像的一般方法;四 教学过程:1开口向 ,并向上无限延伸。
开口向 ,并向下无限延伸。
对称轴是x = , 顶点坐标是 对称轴是x = ,顶点坐标是 2、例题分析例1、已知二次函数6421)(2++=x x x f . (1)利用配方求()f x 的最值、顶点坐标、对称轴. (2)求()f x 与x 轴的交点.(3)列表作()y f x =的图象. (4)指出()f x 的单调区间. 例2 已知将二次函数2()f x x bx c =++的图象向上平移2个单位,再向左平移4个单位,得到函数2x y =的图象,求b 、c 的值.变式:求把二次函数1422+-=x x y 的图象经过下列变换后得到的图象所对应的函数解析式:⑴、向右平移2个单位,向下平移1个单位;⑵、关于直线1-=x .《初高中衔接04二次函数的图象与性质》作业班级 学号 姓名1. 函数2)12(-=x y 的顶点是 ( )(A )(1,0) (B )(-1,0) (C )(21,0) (D )(-21,0) 2. 抛物线c x x y +-=422的顶点在x 轴上,则c 值为 ( )(A )0 (B )1 (C )2 (D )43. 若0<a ,则函数522-+=ax x y 的图形的顶点在 ( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 4. 函数2)1(22+-=x y 是将函数22x y = ( )(A )左移1个单位、上移2个单位得到的 (B )右移2个单位、上移1个单位得到的(C )下移2个单位、右移1个单位得到的 (D )上移2个单位、右移1个单位得到的 5. 设二次函数)1(,0)(,)(2+<-+-=m f m f a x x x f 则若的值为 ( )(A )正数 (B )正、负与m 有关 (C )负数 (D )正、负与a 有关 6. 函数3222--=x x y 的单调区间是 ( )(A )(∞-,1] (B )(∞-,-1] (C )21,(-∞] (D )),21[+∞- 7. 二次函数122++-=x x y 的图像与x 轴交点的个数为 ( )(A )3个 (B )2个 (C )1个 (D )0个8. 二次函数422++-=x x y ,则函数 ( )(A )对称轴为x=1,最大值为3 (B )对称轴为x=-1,最大值为5(C )对称轴为x=1, 最大值为5 (D )对称轴为x=-1,最小值为39. 已知函数c bx ax y ++=2) (A )321212--=x x y (B )321212+-=x x y (C )321212-+-=x x y (D )321212+--=x x y 10. 二次函数c bx ax y ++=2图像顶点为(2,1)-,与y轴交点坐标为(0,11),则( )(A )a=1,b=-4,c=-11 (B )a=3,b=12,c=11(C )a=3,b=-6,c=-11 (D )a=3,b=-12,c=1111. 函数)3(2x x y -=的图像可能是 ( )12. 若32)1()(2++-=mx x m x f 为偶函数,则)(x f 在区间(3,1)-上 () (A )单调递增 (B )单调递减 (C )先增后减 (D )先减后增 13. 已知,0,0<<b a 那么抛物线22++=bx ax y 的顶点在 () (A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限 14. 用配方法将函数12212+-=x x y 写成k h x a y +-=2)(的形式是 () (A )1)2(212--=x y (B )1)1(212--=x y(C )3)2(212--=x y (D )3)1(212--=x y15. 已知二次函数的图像经过点(1,0),(2,0),(0,2),则该函数的解析式为 () (A )222++=x x y (B )232++=x x y(C )322+-=x x y (D )232+-=x x y16. 已知抛物线的顶点坐标为(3,-2),且与x 轴的两个焦点的距离为4.(1)求这个二次行数的解析式;(2)写出抛物线的开口方向、对称轴、顶点坐标及最值.A. B. C.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Байду номын сангаас2 2
2.一元二次方程的根与系数的关系 定理:如果一元二次方程 ax2 bx c 0 (a 0) 的两个根为 x1 , x2,那么:
x1 x2 , x1x2
例1.(1)已知方程 5x2 kx 6 0 的一个根是2,求它的另一个根及k的 值.
(2)已知关于的一元二次方程,根据下列条件,分别求出的范围: (1)方程有两个不相等的实数根; (2)方程有两个相等 的实数根 (3)方程有实数根; (4)方程 无实数根.
1.一元二次方程、一元二次函数、一元二次不等式的区别与联系。
一元二次方程根的判别式 一元二次方程 ax bx c 0 (a 0),用配方法将其变形为 _____________ . 对于一元二次方程 ax bx c 0 (a 0) 有 (1)当Δ > 0时,方程有两个不相等的实数根: ; (2)当Δ = 0时,方程有两个相等的实数根: ; (3)当Δ < 0时,方程没有实数根.
