1坐标系伸缩变换
平面直角坐标系伸缩变换课件

伸缩变换的矩阵表示
伸缩变换
将平面中的点按照某个方向进行缩放,通常称为放缩变换。
伸缩变换矩阵
放缩变换可以通过一个二阶实对称矩阵来实现,该矩阵称为伸缩变 换矩阵。
伸缩变换矩阵的性质
具有正定的对角线元素,并且其特征值分别对应于放缩变换的两个 方向上的缩放因子。
平面直角坐标系伸 缩变换的优缺点及 展望
平面直角坐标系伸缩变换的优点
便于解决几何问题
通过伸缩变换,可以将复杂的几 何问题转化为简单的代数问题,
从而更便于解决。
丰富数学内容
伸缩变换是一种新的数学方法,可 以丰富数学的教学内容,提高学生 的学习兴趣。
应用广泛
伸缩变换在物理学、工程学等领域 都有广泛的应用,可以帮助学生更 好地理解这些领域的基础知识。
平面直角坐标系伸缩 变换课件
目录
CONTENTS
• 平面直角坐标系基础 • 伸缩变换的基本原理 • 伸缩变换的应用 • 伸缩变换的数学模型 • 伸缩变换的实现方法 • 平面直角坐标系伸缩变换的优缺
点及展望
01
平面直角坐标系基 础
定义与性质
定义
平面直角坐标系是一个二维的数 轴系统,它由两个互相垂直的坐 标轴构成。
伸缩变换的逆变换与等价变换
01
02
03
04
逆变换
如果一个变换可以通过逆变换 还原到原始状态,那么这个变
换就称为可逆的。
等价变换
两个变换可以相互转换,并且 它们对所有点的作用相同,那
么它们称为等价的。
伸缩变换的逆变换
通过伸缩变换矩阵的逆矩阵可 以获得逆变换矩阵。
等价变换的证明
讲坐标系平面直角坐标系中的伸缩变换

2023讲坐标系平面直角坐标系中的伸缩变换contents •引言•平面直角坐标系的基本概念•伸缩变换的基本原理•伸缩变换的应用实例•平面直角坐标系中的伸缩变换•结论与展望目录01引言伸缩变换是指对平面直角坐标系中的点进行有比例的放大或缩小,可以用一个矩阵来表示这种变换。
伸缩变换的主要特点是,原点保持不变,且每个轴上的单位长度发生了变化。
伸缩变换的定义伸缩变换在图像处理、计算机视觉和机器学习等领域具有广泛应用。
通过伸缩变换,可以将图像或数据集的大小调整为适合分析或处理的要求,从而提高算法的准确率和效率。
伸缩变换的重要性伸缩变换的应用场景图像缩放01在图像处理中,通过伸缩变换可以调整图像的大小,以满足不同应用的需求。
数据预处理02在机器学习中,为了提高算法的准确性,通常需要对数据进行预处理,其中包括对数据进行缩放。
通过伸缩变换,可以将数据调整为同一尺度,减少计算误差。
计算机视觉03在计算机视觉中,伸缩变换被广泛应用于目标检测、识别和跟踪等领域。
通过对图像进行伸缩变换,可以增强目标特征,提高检测准确率。
02平面直角坐标系的基本概念在平面直角坐标系中,每个点都可以由两个数值,即横坐标和纵坐标,来表示。
例如,点A的坐标为(3,4)。
点的坐标表示点的坐标平面直角坐标系的原点是(0,0)。
原点平面直角坐标系中有两条相互垂直的坐标轴,分别是x轴和y轴。
坐标轴点到点的距离在平面直角坐标系中,两点之间的距离可以通过欧几里得距离公式来计算。
例如,点A(3,4)到点B(1,2)的距离是[(3-1)^2 + (4-2)^2]^0.5 = 2.8284。
向量的模一个向量的模等于其终点与原点之间的距离。
例如,向量OA的模是[(3^2 + 4^2)^0.5] = 5。
距离与向量的计算平面几何的基本定理勾股定理在直角三角形中,勾股定理表述了两条直角边的平方和等于斜边的平方。
平行线之间的距离两条平行线之间的距离等于两直线上的对应点之间的距离。
1坐标系伸缩变换

高二数学导学案§1.1平面直角坐标系与伸缩变换一、三维目标1、知识与技能:回顾在平面直角坐标系中刻画点的位置的方法2、能力与与方法:体会坐标系的作用3、情感态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识。
二、学习重点难点1、教学重点:体会直角坐标系的作用2、教学难点:能够建立适当的直角坐标系,解决数学问题三、学法指导:自主、合作、探究四、知识链接问题1:如何刻画一个几何图形的位置?问题2:如何研究曲线与方程间的关系?五、学习过程一.平面直角坐标系的建立某信息中心接到位于正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到一声巨响,正东观测点听到巨响的时间比它们晚了4s。
已知各观测点到中心的距离是1020m,试确定巨响发生的位置(假定声音传播的速度是340m/s,各观测点均在同一平面上)问题1:思考1:问题1:用什么方法描述发生的位置?思考2:怎样建立直角坐标系才有利于我们解决问题?问题2:还可以怎样描述点P的位置?B例1.已知△ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,CF上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。
探究:你能建立不同的直角坐标系解决这个问题吗?比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?小结:选择适当坐标系的一些规则:如果图形有对称中心,可以选对称中心为坐标原点如果图形有对称轴,可以选对称轴为坐标轴使图形上的特殊点尽可能多地在坐标轴上二.平面直角坐标系中的伸缩变换思考1:怎样由正弦曲线y=sinx 得到曲线y=sin2x?坐标压缩变换:设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x 缩为原来 1/2,得到点P’(x’,y’).坐标对应关系为: ⎪⎩⎪⎨⎧==yy x x ''21通常把上式叫做平面直角坐标系中的一个压缩变换。
思考2:怎样由正弦曲线y=sinx 得到曲线y=3sinx?写出其坐标变换。
伸缩变换-高中数学知识点讲解

伸缩变换
1.伸缩变换
【知识点的知识】
将每个点的横坐标变为原来的k1 倍,纵坐标变为原来的k2 倍,(k1、k2 均不为 0),这样的几何变换为伸缩变换.变换的坐标公式和二阶矩阵为:
【解题方法点拨】
1.几种常见的线性变换
(1)恒等变换矩阵M=;
(2)旋转变换Rθ对应的矩阵是M=;
(3)反射变换要看关于哪条直线对称.例如若关于x 轴对称,则变换对应矩阵为M1=;若关于y 轴对称,则变换对应矩阵为M2=;若关于坐标原点对称,则变换对应矩阵M3=;
(4)伸压变换对应的二阶矩阵M=,表示将每个点的横坐标变为原来的k1 倍,纵坐标变为原来的k2 倍,k1,k2 均为非零常数;
(5)投影变换要看投影在什么直线上,例如关于x 轴的投影变换的矩阵为M=;
1/ 2
(6)切变变换要看沿什么方向平移,若沿x 轴平移|ky|个单位,则对应矩阵M=,若沿y 轴平移|kx|个单位,则对应矩阵M=.(其中k 为非零常数).
2.线性变换的基本性质
设向量α=,规定实数λ与向量α的乘积λα=;设向量α=,β=,规定向量α与β的和α+β=.
(1)设M是一个二阶矩阵,α、β是平面上的任意两个向量,λ是一个任意实数,则①M(λα)=λMα,②M
(α+β)=Mα+Mβ.
(2)二阶矩阵对应的变换(线性变换)把平面上的直线变成直线(或一点).
2/ 2。
直角坐标系伸缩变换(最终)
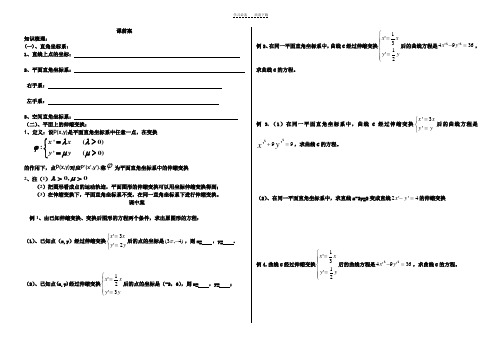
课前案知识梳理:(一)、直角坐标系:1、直线上点的坐标:2、平面直角坐标系:右手系:左手系:3、空间直角坐标系: (二)、平面上的伸缩变换:1、定义:设P(x,y)是平面直角坐标系中任意一点,在变换的作用下,点P(x,y)对应P’(x’,y’).称ϕ为平面直角坐标系中的伸缩变换2、注(1) (2)把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到; (3)在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。
课中案例1、由已知伸缩变换、变换后图形的方程两个条件,求出原图形的方程:(1)、已知点(x,y )经过伸缩变换⎩⎨⎧==y y xx 2'3'后的点的坐标是)4,3(-π,则x= ,y= .(2)、已知点(x,y)经过伸缩变换⎪⎩⎪⎨⎧==yy xx 3'21'后的点的坐标是(-2,6),则x= ,y= ; 例2、在同一平面直角坐标系中,曲线C 经过伸缩变换⎪⎪⎩⎪⎪⎨⎧==y y x x 21'31'后的曲线方程是36'9'422=-y x ,求曲线C 的方程。
例 3.(1)在同一平面直角坐标系中,曲线C 经过伸缩变换'3'x xy y=⎧⎨=⎩后的曲线方程是2299''y x +=,求曲线C 的方程。
(2)、在同一平面直角坐标系中,求直线x-2y=2变成直线2''4x y -=的伸缩变换例4.曲线C 经过伸缩变换⎪⎪⎩⎪⎪⎨⎧==y y x x 21'31'后的曲线方程是36'9'422=-y x ,求曲线C 的方程。
'(0):'(0)x x y y λλϕμμ=>⎧⎨=>⎩0,0λμ>>课后案1.将点(2,3)变成点(3,2)的伸缩变换是( )A.⎪⎪⎩⎪⎪⎨⎧==y y x x 23'32'B.⎪⎪⎩⎪⎪⎨⎧==y y x x 32'23' C.⎩⎨⎧==x y y x '' D.⎩⎨⎧-=+=1'1'y y x x 2.将点),(y x P 的横坐标伸长到原来的2倍,纵坐标压缩为原来的31,得到点P '的坐标为( ) A.)3,2(y x B.)3,2(y x C.)2,3(y x D.)2,3(y x3.曲线C 经过伸缩变换⎪⎩⎪⎨⎧='='y y xx 31后得到曲线C '的方程为)2(log 2+=x y ,则曲线C 的方程为 ( ) A.)2(log 312+=x y B.)2(log 32+=x yC.)231(log 2+=x y D.)23(log 2+=x y4.把函数sin 2y x =的图像作怎样的变换能得到sin(2)3y x π=+的图像 ( )A .向左平移6π B .向右平移6π C .向左平移3π D .向右平移3π5.将()y f x =的图像横坐标伸长到原来的3倍,纵坐标缩短到原来的31,则所得函数的解析式为( )A .3(3)y f x = B. 1(3)3y f x =C. 13()3y f x =D. 11()33y f x = 6.点),(y x 经过伸缩变换⎪⎩⎪⎨⎧==yy x x 3'21'后的点的坐标是(-2,6),则=x ,=y ; 7.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 . 8.为了得到函数R x x y ∈+=),63sin(2π的图像,只需将函数R x x y ∈=,s i n 2的图像上所有的点( )A.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) B.向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) C.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) D.向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)9.曲线)6s i n (π+=x y 经过伸缩变换⎩⎨⎧==y y x x 2'3'后的曲线方程是 ; 10.曲线0222=+-x y x 变成曲线0'4'16'22=+-x y x 的伸缩变换是 .11.曲线364922=+y x 经过伸缩变换⎪⎪⎩⎪⎪⎨⎧==y y x x 31'21'后的曲线方程是 .12.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 .13.函数R x x x x y ∈++=,1c o s s i n 23c o s 212. (1)当函数y 取得最大值时,求自变量x 的集合;(2)该函数的图像可由)(s i n R x x y ∈=的图像经过怎样的平移和伸缩变换得到?1.点)1,2(π经过伸缩变换⎩⎨⎧==yy xx 3'2'后的点的坐标是 ; 3.在伸缩变换⎩⎨⎧==y y x x '2'与⎩⎨⎧==yy x x 2'2'的作用下,单位圆122=+y x 分别变成什么图形?4. 函数31x y x =-,经过怎样的平移变换与伸缩变换才能得到函数1y x=? 1.点),(y x 经过伸缩变换⎩⎨⎧==y y xx 2'3'后的点的坐标是)4,3(-π,则=x ,=y .2.将直线22=-y x 变成直线4''2=-y x 的伸缩变换是 . 3.为得到函数R x x y ∈+=),63sin(2π的图像,需将R x x y ∈=,sin 2的图像上所有的点( ) A.向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变)B.向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变)C.向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)D.向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)4.曲线)6sin(π+=x y 经过伸缩变换⎩⎨⎧==y y xx 2'3'后的曲线方程是 ;5.将曲线0222=+-x y x 变成曲线0'4'16'22=+-x y x 的伸缩变换是 . 6.函数()f x 的图像是将函数2log (1)x +的图像上各点的横坐标变为原来的13,纵坐标变为原来的12而得到的,则与()f x 的图像关于原点对称的图像的解析式是 。
平面直角坐标系知识点平面直角坐标系中的伸缩变换坐标系的作用

一、平面直角坐标系中的伸缩变换设点P(x,y)是平面直角坐标系中任意一点,在变换的作用下,点P(x,y)对应到P'(x',y'),称为平面直角坐标系中的伸缩变换。
在平面上取两条互相垂直并选定了方向的直线,一条称为x轴,一条称为y轴,交点O为原点。
再取一个单位长度,如此取定的两条互相垂直的且有方向的直线和长度单位构成平面上的一个直角坐标系,即为xOy。
数轴(直线坐标系):在直线上取定一点O,取定一个方向,再取一个长度单位,点O,长度单位和选定的方向三者就构成了直线上的坐标系,简称数轴.如图,平面直角坐标系:在平面上取两条互相垂直并选定了方向的直线,一条称为x轴,一条称为y轴,交点O为原点。
再取一个单位长度,如此取定的两条互相垂直的且有方向的直线和长度单位构成平面上的一个直角坐标系,即为xOy。
如图:建立坐标系必须满足的条件:任意一点都有确定的坐标与它对应;反之,依据一个点的坐标就能确定这个点的位置.坐标系的作用:①坐标系是刻画点的位置与其变化的参照物;②可找到动点的轨迹方程,确定动点运动的轨迹(或范围);③可通过数形结合,用代数的方法解决几何问题。
平面直角坐标系知识点(1)平面直角坐标系:在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称直角坐标系。
(2)两条数轴分别置于水平位置与垂直位置,取向右与向上的方向分别为两条数轴的正方向。
水平的数轴叫做x轴或横轴,垂直的数轴叫做y轴或纵轴,x轴y轴统称为坐标轴,它们的公共原点O称为直角坐标系的原点。
(3)x轴y轴将坐标平面分成了四个象限,右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。
第一、三象限角平分线上的点横、纵坐标相等;第二、四象限角平分线上的点横、纵坐标互为相反数。
(4)坐标平面内的点与有序实数对一一对应。
有序数对:有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b)。
平面直角坐标系及伸缩变换

=4.动圆 M 与圆 O1 内切,又与圆 O2 外切,建立适当的坐标系,
求动圆圆心 M 的轨迹方程,并说明轨迹是何种曲线.
解: 如图所示,以 O1O2 的中点 O 为原点,O1O2 所在直线为
x 轴建立平面直角坐标系.
y
由由|O|O1O1O2|=2|=4,4,得得OO11((- -22, ,00)),、OO2(22(,20,0))..
A1(- a,0),A2(a,0)
ec (e1) a
y b x a
A1(0,-a),A2(0,a)
ec (e1) a
y a x b
图形 ly
OF x
标准方程
y2=2px (p>0)
焦点坐标 准线方程
( p ,0 ) x p
2
2
二 抛
物
yl
FO
y2=-2px x (p>0)
( p ,0) 2
lll和和和lll的的的距距距离离离的的的最最最小小小值值值为为为|1|122||1±5±52441|±5.2|.45|.4 | .
O
x
∴∴∴点点点QQQ与与与ll的l的的最最最小小小值值值为为为88558555..5.
题 型 三 定义法求轨迹方程
【例 3】已知两个定圆 O1和 O2,它们的半径分别是 1 和 2,且|O1O2|
所以有 x02
4
把①代入②,
y02
得
4
1.
(2x)2
②
(2y)2 1,
4
整理, 得 x24y21.
MP
O
x
所以点M的轨迹方程是 x24y21.
课堂小结
平面直角坐标系建系时,根据几何特点选 择适当的直角坐标系。
1.1 直角坐标系中的平移变换与伸缩变换

1.1 直角坐标系中的平移变换与伸缩变换目标:平移变换与伸缩变换的应用与理解一.直角坐标系1.直线上,取定一个点为原点,规定一个长度为单位长度,规定直线的一个方向为正方向。
这样我们就建立了直线上的坐标系 (即数轴)。
它使直线上任意一点P 都可以由惟一的实数x 来确定。
2.平面上,取定两条互相垂直的直线作为x 、y 轴,它们的交点作为坐标原点,并规定好长度单位和这两条直线的正方向。
这样我们就建立了平面直角坐标系。
它使平面上任意一点P 都可以由惟一的二元有序实数对),(y x 来确定。
3.在空间中,选择三条两两垂直且交于一点的直线,以这三条直线分别作为x 、y 、z 轴,它们的交点作为坐标原点,并规定好长度单位和这三条直线的正方向。
这样我们就建立了空间直角坐标系。
它使空间中任意一点P 都可以由惟一的三元有序实数对),,(z y x 来确定。
事实上,直线上所有点的集合与全体实数的集合一一对应;平面上所有点的集合与全体二元有序数对),(y x 的集合一一对应;空间中所有点的集合与全体三元有序数对),,(z y x 的集合一一对应.二.平面直角坐标系中图形的平移变换 1.平移变换在平面内,将图形F 上所有点按照同一个方向,移动同样长度,称为图形F 的平移。
若以向量a表示移动的方向和长度,我们也称图形F 按向量a平移.在平面直角坐标系中,设图形F 上任意一点P 的坐标为),(y x ,向量),(k h a =,平移后的对应点为),(y x P '''.则有:),(),(),(y x k h y x ''=+即有:⎩⎨⎧'=+'=+y k y x h x .因此,我们也可以说,在平面直角坐标系中,由⎩⎨⎧'=+'=+y k y x h x 所确定的变换是一个平移变换。
因为平移变换仅改变图形的位置,不改变它的形状和大小.所以,在 平移变换作用下,曲线上任意两点间的距离保持不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二数学导学案主备人:备课时间:组长签字:
§ 1.1平面直角坐标系与伸缩变换
一、三维目标
1、知识与技能:回顾在平面直角坐标系中刻画点的位置的方法
2、能力与与方法:体会坐标系的作用
3 、情感态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识。
二、学习重点难点
1、教学重点:体会直角坐标系的作用
2、教学难点:能够建立适当的直角坐标系,解决数学问题
三、学法指导:自主、合作、探究
四、知识链接
问题1:如何刻画一个几何图形的位置?
问题2:如何研究曲线与方程间的关系?
五、学习过程
一.平面直角坐标系的建立
某信息中心接到位于正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到
一声巨响,正东观测点听到巨响的时间比它们晚了4s。
已知各观测点到中心的距离是1020m,试确定巨响发生的位置(假定声音传播的速度是340m/s,各观测点均在同一平面上)
问题1:
思考1:问题1 :用什么方法描述发生的位置?
思考2:怎样建立直角坐标系才有利于我们解决问题?
问题2:还可以怎样描述点P的位置?
B例1•已知△ ABC的三边a,b,c满足b2+c2=5a2,BE,CF分别为边AC,CF上的中线,建立适当的平面直角坐标系探究BE与CF的位置关系。
探究:你能建立不同的直角坐标系解决这个问题吗?比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意什么问题?
小结:选择适当坐标系的一些规则:如果图形有对称中心,可以选对称中心为坐标原点如果图形有对称轴,可以选对称轴为坐标轴使图形上的特殊点尽可能多地在坐标轴上
二.平面直角坐标系中的伸缩变换
思考1:怎样由正弦曲线y=sinx得到曲线y=sin2x?
坐标压缩变换:
设P(x,y)是平面直角坐标系中任意一点,保持纵坐标不变,将横坐标x缩为原来1/2,得到点
''1
X = — X
{ 2
P' (x '坐标对应关系为:y' = y通常把上式叫做平面直角坐标系中的一个压缩变换。
思考2:怎样由正弦曲线y=sinx得到曲线y=3sinx?写出其坐标变换。
设P(x,y)是平面直角坐标系中任意一点,保持横坐标x不变,将纵坐标y伸长为原来3倍,得到
「'
x =x
点P'(X',坐标对•应关系为:jy=3y通常把上式叫做平面直角坐标系中的一个伸长变换。
思考3:怎样由正弦曲线y=sinx得到曲线y=3sin2x? 写出其坐标变换。
十x=九x (九>0)
定义:设P(x,y)是平面直角坐标系中任意一点,在变换® :」,八的作用下,点P(x,y)对
畀=4y,(y = 0)
应P' (x ' ,y ').称「为平面直角坐标系中的伸缩变换。
六、达标检测 A1.求下列点经过伸缩变换
(1) (1, 2);
X 2X
后的点的坐标:
y'=3y
(2) ( -2,-1)
X‘ = 1 X 一
A2 .点(x,y )经过伸缩变换<
2 后的点的坐标是(-2, 6),则x= ________ , y = (y' =
3 y
A3.将点(2, 3)变成点(3, 2)的伸缩变换是( )
A4.将直线x -2y =2变成直线2x'-y'=:4的伸缩变换是 .
B6.在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换
(1) 2x 3y =0 ;
(2)x 2 y 2 -1.
B5.为了得到函数 y =2sin (- -), ^ R 的图像,只需将函数 3 6 () A. 向左平移二个单位长度,再把所得各点的横坐标缩短到原来的 6 B. 向右平移一个单位长度,再把所得各点的横坐标缩短到原来的 6 C. 向左平移一个单位长度,再把所得各点的横坐标伸长到原来的
6 D. 向右平移一个单位长度,再把所得各点的横坐标伸长到原来的
6
y = 2sin x, x • R 的图像上所有的点
1 、 一、 倍(纵坐标不变)
3
1 、 一、 倍(纵坐标不变) 3
3倍(纵坐标不变)
3倍(纵坐标不变)
x'=
A. «
y'=
B.
2y
.3 x' x 2 .2
八尹
C.
r
i x' = y y' = x
D.
,= X+1 y'=y_1
2x
后的图
B8.教材P8 习题1.1 第4, 5,6
七、学习小结
八、课后反思。
