2019届一轮复习人教版 绳上的活结、死结问题与活动杆、固定杆问题 学案
12“死结与活结”的两个问题—【新教材】人教版(2019)高一上学期期末复习易错点精讲精练
12“死结与活结”的两个问题--高一期末复习易错点精讲精练我们知道杆既可以发生拉伸或压缩形变也可以发生弯曲或扭转形变，因此杆的弹力不一定沿杆的方向．对于杆与铰链连接的结构，杆产生的弹力必定沿杆方向时，杆才能平衡；对于杆的一端固定(即杆不能绕杆上一点转动)时，杆平衡时，杆产生的弹力不一定沿杆，现在通过下面两个“形同质异”的问题来了解一下． 例1、如图甲所示，轻绳AD 跨过固定在水平横梁BC 右端的定滑轮挂住一个质量为10 kg 的物体，∠ACB ＝30°；图乙中轻杆HP 一端用铰链固定在竖直墙上，另一端P 通过细绳EP 拉住，EP 与水平方向也成30°，轻杆的P 点用细绳PQ 拉住一个质量也为10 kg 的物体．g 取10 N/kg ，求：(1)轻绳AC 段的张力F AC 与细绳EP 的张力F EP 之比； (2)横梁BC 对C 端的支持力； (3)轻杆HP 对P 端的支持力．答案 (1)1：2(2)100 N ，方向与水平方向成30°角斜向右上方(3)173 N ，方向水平向右解析 题图甲和乙中的两个物体M1、M2都处于平衡状态，根据平衡条件可判断，与物体相连的细绳拉力大小等于物体的重力．分别取C 点和P 点为研究对象，进行受力分析如图甲和乙所示．(1)图甲中轻绳AD 跨过定滑轮拉住质量为M1的物体，物体处于平衡状态，绳AC 段的拉力FAC ＝FCD ＝M1g图乙中由FEPsin30°＝FPQ ＝M2g得FEP ＝2M2g ，所以得FAC FEP ＝M12M2＝12. (2)图甲中，根据几何关系得：FC ＝FAC ＝M1g ＝100 N ，方向和水平方向成30°角斜向右上方．(3)图乙中，根据平衡方程有FEPsin30°＝M2gFEPcos30°＝FP所以FP ＝M2gcot30°＝3M2g≈173 N ，方向水平向右．[错因分析]误认为“死结”分开的两段绳子上的弹力一定相等，而由“活结”分开的两段绳子上弹力的大小不一定相等，所以两段绳子合力的方向一定沿杆的方向。
专题09绳的活结与死结模型动杆和定杆模型(原卷版)
2024年高考物理一轮复习热点重点难点夯练与提升专题09 绳的活结与死结模型、动杆和定杆模型【特训典例】一、绳子类的“死结”问题1．如图所示，质量为m=2.4kg的物体用细线悬挂处于静止状态。
细线AO与天花板之间的夹角为53︒，细线BO水平，若三根细线能承受最大拉力均为100N，重力加速度g取10m/s2，不计所有细线的重力，sin37︒=0.6，cos37︒=0.8。
下列说法正确的是（）A．细线BO上的拉力大小30NB．细线AO上的拉力大小18NC．要使三根细线均不断裂，则细线下端所能悬挂重物的最大质量为8kgD．若保持O点位置不动，沿顺时针方向缓慢转动B端，则OB绳上拉力的最小值为19.2N2．如图所示，两个质量均为m的小球a和b套在竖直固定的光滑圆环上，圆环半径为R，一不可伸长的细。
用竖直向上的力F拉细线中点O，可使两小球保持等高静止在线两端各系在一个小球上，细线长为圆上不同高度处。
当a、b时，力F的大小为（重力加速度为g）（）A ．2mgB ．3mgC ．D ．3．如图所示为一拔桩机的设计示意图，绳CDE 与绳ACB 连接于C 点。
在D 点施加竖直向下的力F 可将桩拔起。
保持CD 段绳水平，AC 段绳竖直，更省力的措施是（ ）A ．减小α角，增大β角B ．减小α角，减小β角C ．增大α角，增大β角D ．增大α角，减小β角4．如图，悬挂甲物体的细线拴牢在一不可伸长的轻质细绳上O 点处，绳的一端固定在墙上的A 点，另一端跨过光滑定滑轮B 与物体乙相连，AB 、等高，且OA AB ，系统处于平衡状态。
下列说法正确的是（ ）A ．减小物体乙的质量，绳OB 与竖直方向的夹角减小B ．减小物体乙的质量，绳OA 的拉力减小C．当轻绳OB 与竖直方向的夹角为30°D．当轻绳OB 与竖直方向的夹角为30°二、绳子类的“活结”问题5．如图所示，竖直墙壁上的M N 、两点在同一水平线上，固定的竖直杆上的P 点与M 点的连线水平且垂直MN ，轻绳的两端分别系在P N 、两点，光滑小滑轮吊着一重物可在轻绳上滑动。
(新课标)高考物理大一轮复习物理模型2“动杆”、“定杆”和“死结”、“活结”模型
A．当m一定时，θ越大，轻杆受力越小 B．当m一定时，θ越小，滑块对地面的压力越大 C．当θ一定时，M越大，滑块与地面间的摩擦力越大 D．当θ一定时，M越小，可悬挂重物C的质量m越大
解析：选A.将与C相连的绳子的拉力按照作用效果分解，如 1 mg 2 mg 图所示．根据平行四边形定则有F1＝F2＝ ＝ ， sin θ 2sin θ
故m一定时，θ越大，轻杆受力越小，选项A正确；对A、 2M＋m B、C组成的整体分析可知，对地面压力为FN＝ g，与θ无 2 关，选项B错误；对A受力分析，受重力、杆的推力、支持力和 mg 向右的静摩擦力，根据平衡条件有f＝F1cos θ＝ ，与M无 2tan θ 关，选项C错误；只要动摩擦因数足够大，即可满足F1cos θ≤μF1sin θ，不管m多大，滑块都不会滑动，选项D错误．
解析：选C.对C点受力分析，如图所示，C点受向下的拉力，沿 CA方向的拉力F1及沿BC方向的支持力F2；三力 的合力为零；A上移，使AC、CD的夹角变大， 由于ACD为同一根绳，所以绳的拉力大小相等 即F1＝G，故细绳的拉力不变，两绳对C点的作 用力的合力减小，即BC杆所受压力变小，故选 项C正确．
[典例]
如图甲所示，轻绳AD跨过固定的水平横梁BC右端
的定滑轮挂住一个质量为M1的物体，∠ACB＝30° ；图乙中轻杆 HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG 与水平方向也成30° ，轻轩的G点用细绳GF拉住一个质量为M2的 物体，求：
(1)轻绳AC段的张力FTAC与细绳EG的张力FTEG之比； (2)轻杆BC对C端的支持力； (3)轻杆HG对G端的支持力．
解析：选D.细线上的弹力处处相等，因此细线BO对天花板 的拉力大小是G，选项A错误．两段细线上弹力均为G，构成菱 形，合力为2Gsin 30° ＝G，大小等于a杆对滑轮的作用力，选项B 错误、D正确．a杆和细线对滑轮的合力大小是0，选项C错误．
高中物理：专题11 “活结”和“死结”、“动杆”和“定杆”模型-高一上学期同步重难讲练之相互作用
重难讲练1.“活结”和“死结”问题(1)活结：当绳绕过光滑的滑轮或挂钩时，由于滑轮或挂钩对绳无约束，因此绳上的力是相等的，即滑轮只改变力的方向不改变力的大小，例如图乙中，两段绳中的拉力大小都等于重物的重力.(2)死结：若结点不是滑轮，是固定点时，称为“死结”结点，则两侧绳上的弹力不一定相等.“死结”一般是由绳子打结而形成的，“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点：a.绳子的结点不可随绳移动b.“死结”两侧的绳子因打结而变成两根独立的绳子，因此由“死结”分开的两端绳子上的弹力不一定相等2.“动杆”和“定杆”问题(1)动杆：若轻杆用光滑的转轴或铰链连接，当杆处于平衡时杆所受到的弹力方向一定沿着杆，否则会引起杆的转动.如图甲所示，若C为转轴，则轻杆在缓慢转动中，弹力方向始终沿杆的方向.(2)定杆：若轻杆被固定不发生转动，则杆所受到的弹力方向不一定沿杆的方向.如图乙所示.【典例1】(2016·全国卷Ⅲ·17)如图所示，两个轻环a和b套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时，a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量为( )A.m 2B.32m C.mD.2m【☆答案☆】 C 【解析】 如图所示，【典例2】 如图所示，一轻绳的两端分别固定在不等高的A 、B 两点，现用另一轻绳将一物体系于O 点，设轻绳AO 、BO 相互垂直，α>β，且两绳中的拉力分别为F A 、F B ，物体受到的重力为G ，下列表述正确的是( )A．F A一定大于G B．F A一定大于F BC．F A一定小于F B D．F A与F B大小之和一定等于G【☆答案☆】 B【解析】分析O点受力如图所示，由平衡条件可知，F A与F B的合力与G等大反向，因F A⊥F B，故F A、F B均小于G；因α>β，故F A>F B，B正确，A、C错误；由三角形两边之和大于第三边可知，|F A|＋|F B|＞G，D错误．【典例3】如图甲所示，轻绳AD跨过固定的水平横梁BC右端的定滑轮挂住一个质量M1的物体，∠ACB＝30°；图乙中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°，轻杆的G点用细绳GF拉住一个质量M2的物体，求：(1)轻绳AC段的张力F T AC与细绳EG的张力F T EG之比；(2)轻杆BC对C端的支持力；(3)轻杆HG对G端的支持力．【☆答案☆】(1)M12M2(2)M1g方向和水平方向成30°指向右上方(3)3M2g方向水平向右【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态，根据平衡的条件，首先判断与物体相连的细绳，其拉力大小等于物体的重力；分别取C点和G点为研究对象，进行受力分析如图甲和乙所示，根据平衡规律一一求解．【跟踪训练】1. 如图所示，将一细绳的两端固定于两竖直墙的Ａ、Ｂ两点，通过一个光滑的挂钩将某重物挂在绳上，下面给出的四幅图中有可能使物体处于平衡状态的是（ ）【☆答案☆】C2．如图所示，当重物静止时，节点O 受三段绳的拉力，其中AO 沿水平方向，关于三段绳中承受拉力的情况，下列说法中正确的是A ． AO 承受的拉力最大B ． BO 承受的拉力最大C ． CO 承受的拉力最大D ． 三段绳承受的拉力一样大 【☆答案☆】B【解析】以结点O 为研究对象，分析受力情况，受力分析如图：由平衡条件得： 1tan T G θ=，2cos GT θ=，故T1小于T2，G 小于T2；所以BO 承受的拉力最大；故B 正确。
绳上的活结、死结问题与活动杆、固定杆问题-高考物理一轮复习热点专题突破
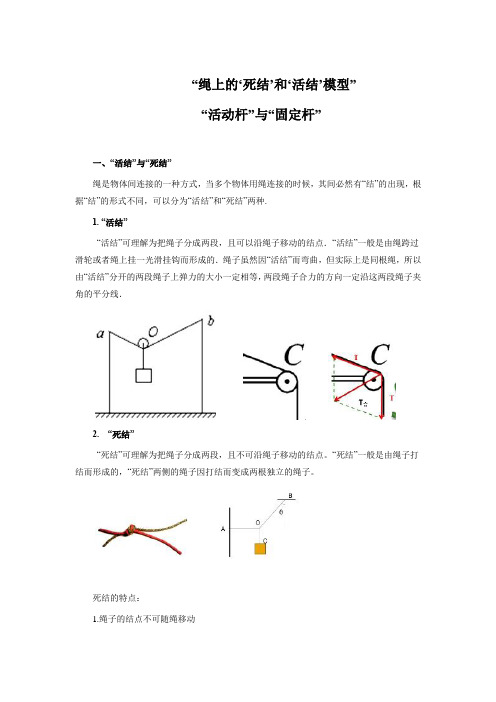
“绳上的‘死结’和‘活结’模型”“活动杆”与“固定杆”一、“活结”与“死结”绳是物体间连接的一种方式，当多个物体用绳连接的时候，其间必然有“结”的出现，根据“结”的形式不同，可以分为“活结”和“死结”两种.1. “活结”“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．2. “死结”“死结”可理解为把绳子分成两段，且不可沿绳子移动的结点。
“死结”一般是由绳子打结而形成的，“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点：1.绳子的结点不可随绳移动2.“死结”两侧的绳子因打结而变成两根独立的绳子，因此由“死结”分开的两端绳子上的弹力不一定相等【典例1】如图所示，将一细绳的两端固定于两竖直墙的Ａ、Ｂ两点，通过一个光滑的挂钩将某重物挂在绳上，下面给出的四幅图中有可能使物体处于平衡状态的是（）【答案】C【解析】由于重物是通过一个光滑的挂钩挂在绳上，绳子张力处处相等，而两边绳子的合力大小等于物体的重力，方向竖直向上，由对称性可知两边绳子与竖直方向的夹角相等，所以C正确。
【典例2】如图所示，一轻绳的两端分别固定在不等高的A、B两点，现用另一轻绳将一物体系于O点，设轻绳AO、BO相互垂直，α>β，且两绳中的拉力分别为F A、F B，物体受到的重力为G，下列表述正确的是( )A．F A一定大于GB．F A一定大于F BC．F A一定小于F BD．F A与F B大小之和一定等于G【答案】B【典例3】如图所示，在水平天花板的A点处固定一根轻杆a，杆与天花板保持垂直．杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处，细线跨过滑轮O，下端系一个重为G的物体，BO段细线与天花板的夹角为θ＝30°.系统保持静止，不计一切摩擦．下列说法中正确的是( )GA．细线BO对天花板的拉力大小是2GB．a杆对滑轮的作用力大小是2C．a杆和细线对滑轮的合力大小是GD．a杆对滑轮的作用力大小是G【答案】D二、“活动杆”与“固定杆”轻杆是物体间连接的另一种方式，根据轻杆与墙壁连接方式的不同，可以分为“活动杆”与“固定杆”.所谓“活动杆”，就是用铰链将轻杆与墙壁连接，其特点是杆上的弹力方向一定沿着杆的方向；而“固定杆”就是将轻杆固定在墙壁上（不能转动），此时轻杆上的弹力方向不一定沿着杆的方向。
专题10 活结与死结绳模型、动杆和定杆模型和受力分析(原卷版)-2024年高考物理一轮综合复习
2024年高考物理一轮大单元综合复习导学练专题10活结与死结绳模型、动杆和定杆模型和受力分析导练目标导练内容目标1活结与死结绳模型目标2动杆和定杆模型目标3受力分析【知识导学与典例导练】一、活结与死结绳模型1．“活结”模型【例1】如图所示，一根不可伸长的光滑轻质细绳通过轻滑轮挂一重物，细绳一端系在竖直墙壁的A点，另一端系在倾斜墙壁的B点，现将细绳右端从B点沿倾斜墙壁缓慢向下移动到与A点等高的B′点。
在移动过程中，关于细绳拉力大小变化情况正确的是（）A．先变小后变大B．变大C．变小D．不变【例2】在如图所示装置中，两物体质量分别为1m和2m，滑轮直径大小可忽略。
设动滑轮P两侧的绳与竖直方向夹角分别为α和β。
整个装置能保持静止。
不计动滑轮P的质量和一切摩擦。
则下列法正确的有（）A．α一定等于βB．1m一定大于2m C．1m一定小于2m D．1m可能大于22m2．“死结”模型【例3】如图所示，将三段轻绳相结于O点，其中OA绳的一端拴在墙上，OB绳的下方悬挂甲物体，OC绳跨过光滑定滑轮悬挂乙物体。
OC绳与竖方向的夹角为α=70°。
OA绳与竖直方向的夹角为β（未知）。
若甲、乙两物体的质量均为m=2kg，重力加速度g取10m/s2，sin55°≈0.82。
根据所学的知识，不需计算，推理出OA绳的拉力约为（）A ．16NB ．23NC ．31ND ．41N二、动杆和定杆模型1．动杆模型模型结构模型解读模型特点轻杆用光滑的转轴或铰链连接，轻杆可围绕转轴或铰链自由转动当杆处于平衡时，杆所受的弹力方向一定沿杆【例4】如图所示，A 、B 为竖直墙面上等高的两固定点，AO BO 、为长度相等的两根轻绳，CO 为一根轻杆，铰链C 在AB 中点D 的正下方，AOB 在同一水平面内，120AOB ∠=︒，60COD ∠=︒，若在O 点处悬挂一个质量为m 的物体，则平衡后绳AO 所受的拉力和杆OC 所受的压力分别为（）A ．3mg ，2mg B ．mg ，2mg C．3mg，3mg D ．3mg ，3mg 2．定杆模型模型结构模型解读模型特点轻杆被固定在接触面上，不发生转动杆所受的弹力方向不一定沿杆，可沿任意方向【例5】水平横梁一端A 插在墙壁内，另一端装有一小滑轮B ，轻绳的一端C 固定于墙壁上，另一端跨过滑轮后悬挂一重力为100N G =的重物，30CBA ∠=︒，如图所示，则滑轮受到轻绳的作用力的大小为（）A．50N B．C．100N D．三、受力分析1.受力分析的一般顺序：先分析场力(重力、电场力、磁场力)，再分析接触力(弹力、摩擦力)，最后分析其他力．2.研究对象选取方法：整体法和隔离法．(1)当分析相互作用的两个或两个以上物体整体的受力情况及分析外力对系统的作用时，宜用整体法．(2)在分析系统内各物体(或一个物体各部分)间的相互作用时常用隔离法．(3)整体法和隔离法不是独立的，对一些较复杂问题，通常需要多次选取研究对象，交替使用整体法和隔离法．3.受力分析的六个注意点(1)不要把研究对象所受的力与研究对象对其他物体的作用力混淆。
2019版高考物理一轮复习核心素养微专题二轻绳与轻杆模型问题课件
2.如图所示,质量为m的杂技演员进行 钢索表演,当演员走到钢索中点时,钢 索与水平面成θ角,此时钢索最低点 拉力大小为(重力加速度为g) (
)
1 A. mg 2sin
cos B. mg 2
tan C. mg 2
1 D. mg 2
【解析】选A。以人为研究对象,分析受力情况,作出受 力图,根据平衡条件: 两绳子合力与重力等大反向,则有: 2Fsin θ =mg 解得:F= mg,故A正确,B、C、D错误。
质量以及相互之间的摩擦均不计,绳子不可伸长。若整 个系统平衡时∠AOB为α,则两物块的质量的比值 为 ( ) A.cos C.sin B.2sin D.2cos
m1 m2
2 2
2 2
【点睛】题目中轻绳跨过光滑滑轮,所以绳两端的张力大小相等,故而可以沿绳方向列 平衡方程。
【解析】选B。对小环进行受力分析,如图所示,小环受上面绳子的拉力m1g,下面绳子 的拉力m2g,以及圆环对它沿着OA向外的支持力,将两个绳子的拉力进行正交分解,它 们在切线方向的分力应该相等:
G F F1 3 F 5
2
2 1
即方向与竖直方向成37°角斜向下,这个力与轻绳的拉力恰好在同一条直线上。根据物 体平衡的条件可知,轻杆对小球的作用力大小为5 N,方向与竖直方向成37°角斜向右上 方。
答案:5 N,方向与竖直方向成37°角斜向右上方
【强化训练】 1.如图,弹性杆AB的下端固定,上端固定一个质量为m的小球,用水平向右的力F缓慢拉球, 使杆发生弯曲。逐步增加水平力F的大小,则弹性杆AB对球的作用力的方向 ( )
(1)图中轻绳AD跨过定滑轮拉住质量为M的物体,物体处于平衡状态,绳AC段的拉力大 小为: FAC=FCD=Mg=10×10 N=100 N (2)由几何关系得:FC=FAC=Mg=100 N 方向和水平方向成30°角斜向右上方。
高考物理大一轮复习 物理模型2“动杆”、“定杆”和“死结”、“活结”模型课件
(2)图1中，三个力之间的夹角都为120°，根据平衡规律有FNC ＝FTAC＝M1g，方向和水平方向成30°，指向右上方．
(3)图2中，根据平衡方程有FTEGsin 30°＝M2g，FTEGcos 30° ＝FNG，所以FNG＝M2gcot 30°＝ 3M2g，方向水平向右．
答案
(1)
M1 2M2
解析 如题图甲和乙中的两个物体M1、M2都处于平衡状 态，根据平衡的条件，首先判断与物体相连的细绳，其拉力大小 等于物体的重力；分别取C点和G点为研究对象，进行受力分析 如下图1和2所示，根据平衡规律可求解．
(1)图1中轻绳AD跨过定滑轮拉住质量为M1的物体，物体处于 平衡状态，轻绳AC段的拉力
FTAC＝FTCD＝M1g 图2中由于FTEGsin 30°＝M2g，得FTEG＝2M2g. 所以FFTTEAGC＝2MM12.
2．“活结”和“死结”问题 (1)当绳绕过滑轮或挂钩时，由于滑轮或挂钩对绳无约束，因 此绳上力的大小是相等的，即滑轮只改变力的方向，不改变力的 大小．例如图乙中，两段绳中的拉力F1＝F2＝mg.(2)若结点不是 滑轮，是称为“死结”的结点，则两侧绳上的弹力不一定相 等．例如图甲中，B点固定，B点下面绳中的拉力大小始终等于 mg，而B点上侧绳AB中的拉力随杆的转动而变化．
[典例] 如图甲所示，轻绳AD跨过固定的水平横梁BC右端 的定滑轮挂住一个质量为M1的物体，∠ACB＝30°；图乙中轻杆 HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG 与水平方向也成30°，轻轩的G点用细绳GF拉住一个质量为M2的 物体，求：
ቤተ መጻሕፍቲ ባይዱ
(1)轻绳AC段的张力FTAC与细绳EG的张力FTEG之比； (2)轻杆BC对C端的支持力； (3)轻杆HG对G端的支持力．
“动杆”与“定杆”问题“活结”与“死结”
滑轮模型与死结模型问题的分析1．跨过滑轮、光滑杆、光滑钉子的细绳两端张力大小相等．2．死结模型：如几个绳端有“结点”，即几段绳子系在一起，谓之“死结”，那么这几段绳中的张力不一定相等．3．同样要注意轻质固定杆的弹力方向不一定沿杆的方向，作用力的方向需要结合平衡方程或牛顿第二定律求得，而轻质活动杆中的弹力方向一定沿杆的方向．1．如图甲所示，细绳AD 跨过固定的水平轻杆BC 右端的定滑轮挂住一个质量为M 1的物体，∠ACB ＝30°；图乙中轻杆HG 一端用铰链固定在竖直墙上，另一端G 通过细绳EG 拉住，EG 与水平方向也成30°，在轻杆的G 点用细绳GF 拉住一个质量为M 2的物体，求：(1)细绳AC 段的张力F T AC 与细绳EG 的张力F T EG 之比；(2)轻杆BC 对C 端的支持力；(3)轻杆HG 对G 端的支持力。
2．(2017·天津)(多选)如图所示，轻质不可伸长的晾衣绳两端分别固定在竖直杆M 、N 上的a 、b 两点，悬挂衣服的衣架挂钩是光滑的，挂于绳上处于静止状态．如果只人为改变一个条件，当衣架静止时，下列说法正确的是( )A ．绳的右端上移到b ′，绳子拉力不变B ．将杆N 向右移一些，绳子拉力变大C ．绳的两端高度差越小，绳子拉力越小D ．若换挂质量更大的衣服，则衣架悬挂点右移3．(2016·全国Ⅲ)如图，两个轻环a 和b 套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m 的小球．在a 和b 之间的细线上悬挂一小物块．平衡时，a 、b 间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为( )A ．m 2B ．32m C ．m D ．2m4．(2016·全国Ⅰ)(多选)如图，一光滑的轻滑轮用细绳OO ′悬挂于O 点；另一细绳跨过滑轮，其一端悬挂物块a ，另一端系一位于水平粗糙桌面上的物块b 。
外力F 向右上方拉b ，整个系统处于静止状态。
绳的活结与死结模型、动杆和定杆模型(解析版)--2024年高考物理一轮复习热点重点难点
绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1绳子类的“死结”问题(1T -4T )目标2绳子类的“活结”问题(5T -8T )目标3有关滑轮组的“活结”问题(9T -12T )目标4定杆和动杆问题(13T -16T )【特训典例】一、绳子类的“死结”问题1如图所示，质量为m =2.4kg 的物体用细线悬挂处于静止状态。
细线AO 与天花板之间的夹角为53°，细线BO 水平，若三根细线能承受最大拉力均为100N ，重力加速度g 取10m/s 2，不计所有细线的重力，sin37°=0.6，cos37°=0.8。
下列说法正确的是()A.细线BO 上的拉力大小30NB.细线AO 上的拉力大小18NC.要使三根细线均不断裂，则细线下端所能悬挂重物的最大质量为8kgD.若保持O 点位置不动，沿顺时针方向缓慢转动B 端，则OB 绳上拉力的最小值为19.2N 【答案】C【详解】AB ．以结点O 为研究对象，受到重力、OB 细线的拉力和OA 细线的拉力，如图所示根据平衡条件结合图中几何关系可得细线BO 上的拉力大小为F BO =mg tan37°=18N 同理，可解得细线AO 上的拉力大小F AO =mgcos37°=30N 故AB 错误；C ．若三根细线能承受的最大拉力均为100N ，根据图中力的大小关系可得，只要OA 不拉断，其它两根细线都不会拉断，故有m max g =F max cos37°解得m max =F max cos37°g =100×0.810kg =8kg ，故C 正确；D ．当OB 与OA 垂直时，OB 细线的拉力最小，根据几何关系结合平衡条件可得F min =mg sin37°=2.4×10×0.6N =14.4N 故D 错误。
故选C 。
2如图所示，两个质量均为m 的小球a 和b 套在竖直固定的光滑圆环上，圆环半径为R ，一不可伸长的细线两端各系在一个小球上，细线长为23R 。
高考物理一轮复习核心素养微专题二轻绳与轻杆模型问题课件
A.水平向左 B.斜向右下方,与竖直方向夹角增大 C.斜向左上方,与竖直方向夹角减小 D.斜向左上方,与竖直方向夹角增大
【解析】选D。对球受力分析,受重力、 拉力和杆的弹力,根据平衡条件,杆的 弹力与拉力、重力的合力等值、反向、共线;拉力方向 不变、大小变大,重力大小和方向都不变,根据平行四 边形定则,两个力的合力大小逐渐增大,方向向右下方, 根据平衡条件,杆的弹力斜向左上方,与竖直方向夹角 增大,故D正确,A、B、C错误。
3.针对两种模型的三点提醒: (1)这两种模型均可以发生突变。 (2)轻绳和轻杆都是理想化模型。 (3)分析轻杆上的弹力时可结合物体的运动状态利用牛顿第二定律或共点力平衡分析 弹力方向。
【典例突破】 【典例1】粗铁丝弯成如图所示半圆环的形状, 圆心为O,半圆环最高点B处固定一个小滑轮, 小圆环A用细绳吊着一个质量为m2的物块并套在半圆环 上。一根一端拴着质量为m1的物块的细绳,跨过小滑轮 后,另一端系在小圆环A上。设小圆环、滑轮、绳子的
(1)图中轻绳AD跨过定滑轮拉住质量为M的物体,物体处于平衡状态,绳AC段的拉力大 小为: FAC=FCDபைடு நூலகம்Mg=10×10 N=100 N (2)由几何关系得:FC=FAC=Mg=100 N 方向和水平方向成30°角斜向右上方。
答案:(1)100 N (2)100 N 方向与水平方向成30°角斜向右上方
1 2sin
3.如图所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10 kg的物 体,∠ACB=30°,g取 10 m/s2,求: (1)轻绳AC段的张力FAC的大小。 (2)横梁BC对C端的支持力的大小及方向。
【解析】物体M处于平衡状态,根据平衡条件可判断,与物体相连的轻绳拉力大小等于 物体的重力,取C点为研究对象,进行受力分析,如图所示。
02活结与死结、定杆与动杆
【例题1】 如图(a)所示，轻绳AD 跨过固定在水平轻杆BC 右端的定滑轮(重力不计)挂住一个质量为M 1的物体，∠ACB ＝30°；如图(b)所示，轻杆HG 一端用铰链固定在竖直墙上，另一端G 通过轻绳EG 拉住，EG 与水平方向也成30°角，一轻绳GI 悬挂在轻杆的G 端并拉住一个质量为M 2的物体，重力加速度为g ，则下列说法正确的是( D )A ．图(a)中BC 杆对滑轮的作用力大小为M 1g2B ．图(b)中HG 杆受到的作用力大小为M 2gC ．轻绳AC 段的张力T AC 与轻绳EG 段的张力T EG 的大小之比为M 1∶M 2D ．轻绳AC 段的张力T AC 与轻绳EG 段的张力T EG 的大小之比为M 1∶2M 2(1)像滑轮这样的“活结”，结点两侧绳的拉力相等．(2)像图(b)中的“死结”，结点两侧绳的拉力一般不同，各自的大小可以采用正交分解法或矢量三角形法求出．(3)图(a)中水平直杆左端固定于竖直墙上，是“定杆”，杆对结点弹力的方向可以不沿杆的方向． (4)图(b)中轻杆左端用铰链固定，是“动杆”，轻杆在缓慢转动的过程中，弹力方向始终沿杆的方向． 【例题2】如图所示，一根粗糙的水平横杆上套有A 、B 两个轻环，系在两环上的登场细绳拴住的书本处于静止状态，现将两环距离变小后书本仍处于静止状态，则 A. 杆对A 环的支持力变大 B. B 环对杆的摩擦力变小 C. 杆对A 环的力不变D. 与B 环相连的细绳对书本的拉力变大 【答案】B【例题3】如图，一粗糙斜面固定在地面上，斜面顶端装有一光滑定滑轮。
一细绳跨过滑轮，其一端悬挂物块N 。
另一端与斜面上的物块M 相连，系统处于静止状态。
现用水平向左的拉力缓慢拉动N ，直至悬挂N 的细绳与竖直方向成45°。
已知M 始终保持静止，则在此过程中 A ．水平拉力的大小可能保持不变 B ．M 所受细绳的拉力大小一定一直增加 C ．M 所受斜面的摩擦力大小一定一直增加 D ．M 所受斜面的摩擦力大小可能先减小后增加【答案】BD【例题4】如图所示，轻质不可伸长的晾衣绳两端分别固定在竖直杆M 、N 上的a 、b 两点，悬挂衣服的衣架钩是光滑的，挂于绳上处于静止状态。
高中物理“动杆”和“定杆”与“活结”和“死结”问题 —人教版高一暑假综合易错点、易混淆点突破专题讲义
七、“动杆”和“定杆”与“活结”和“死结”问题--易错点、易混淆点突破1．“动杆”和“定杆”问题(1)动杆：若轻杆用光滑的转轴或铰链连接，当杆处于平衡时杆所受到的弹力方向一定沿着杆，否则会引起杆的转动．如图甲所示，若C为转轴，则轻杆在缓慢转动中，两绳对BC杆弹力方向：始终沿BC杆的方向．(2)定杆：若轻杆被固定不发生转动，图乙中，轻杆是插入墙中的，则杆所受到的弹力方向不一定沿杆的方向，即C Bm对轻杆A B的作用力就不一定沿BA方向。
2．“活结”和“死结”问题(1)“死结”可理解为把绳子分成两段，且不可以沿绳子移动的结点。
“死结”两侧的绳因“结”而变成了两根独立的绳，因此由“死结”分开的两段绳子上的弹力不一定相等。
(2)“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点。
“活结”一般由绳跨过滑轮或者绳上挂一光滑挂钩而形成。
绳子虽然因“活结”而弯曲，但实际上“活结”两侧的绳子是同一根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的角平分线。
1．(2020·天津市南开中学月考)如图为两种形式的吊车的示意图，OA为可绕O点转动的轻杆，重量不计，AB为缆绳，当它们吊起相同重物时，杆OA在图(a)、(b)中的受力分别为F a、F b，则下列关系正确的是()A．F a＝F b B．F a>F bC．F a<F b D．大小不确定答案：A解析：对题图中的A点受力分析，则由图(a)可得F a＝F a′＝2mg cos 30°＝3mg，由图(b)可得tan30°＝mgF b′，则F b＝F b′＝3mg，故F a＝F b，A正确．2.(多选)如图所示，质量均可忽略的轻绳与轻杆，A端用铰链固定，滑轮在A点正上方(滑轮大小及摩擦均可不计)，B端吊一重物．现将绳的一端拴在杆的B端，用拉力F将B端缓慢上拉，在AB杆达到竖直前()图11A．绳子拉力不变B．绳子拉力减小C．AB杆受力增大D．AB杆受力不变答案：BD解析：以B点为研究对象，受力分析如图所示，B点受重物的拉力F T1(等于重物的重力G)、轻杆的支持力F N和绳子的拉力F T2由平衡条件得，F N和F T2的合力与F T1大小相等、方向相反，根据三角形相似可得：F N AB ＝F T2BO ＝F T1AO 又F ＝F T2，F T1＝G 解得：F N ＝AB AO ·G ，F ＝BO AO·G∠BAO 缓慢变小时，AB 、AO 保持不变，BO 变小，则F N 保持不变，F 变小，故选项B 、D 正确．3．如图所示，两个轻环a 和b 套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m 的小球．在a 和b 之间的细线上悬挂一小物块．平衡时，a 、b 间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为( )A ．m 2B ．32m C ．m D ．2m答案：C解析：如图所示，圆弧的圆心为O ，悬挂小物块的点为c ，由于ab ＝R ，则△aOb 为等边三角形，同一条细线上的拉力相等，F T ＝mg ，合力沿Oc 方向，则Oc 为角平分线，由几何关系知，∠acb ＝120°，故细线的拉力的合力与物块的重力大小相等，则每条细线上的拉力F T ＝G ＝m ′g ，所以小物块质量为m ′＝m ，故C 对．4.如图甲所示 , 细绳AD 跨过固定的水平轻杆BC 右端的光滑定滑轮挂住一个质量为M 1的物体， ∠ACB ＝30°； 图乙中轻杆HG 一端用铰链固定在竖直墙上，另一端G 通过细绳EG 拉住，EG 与水平方向也成30°角，轻杆的G 点用细绳GF 拉住一个质量为M 2的物体，重力加速度为g ，求：(1)细绳AC 段的张力F T AC 与细绳EG 的张力F T EG 之比； (2)轻杆BC 对C 端的支持力； (3)轻杆HG 对G 端的支持力．解析：(1)图甲中细绳AD 跨过定滑轮拉住质量为M 1的物体，物体处于平衡状态， 细绳AC 段的拉力F T AC ＝F T CD ＝M 1g ，图乙中由F T EG sin 30°＝M 2g ，得F T EG ＝2M 2g ， 所以F T AC F TEG ＝M 12M 2.(2)图甲中，三个力之间的夹角都为120°，根据平衡条件有F N C ＝F T AC ＝M 1g ，方向与水平方向成30°角指向右上方．(3)图乙中，根据平衡条件有 F T E G sin 30°＝M 2g ， F T E G cos 30°＝F N G ，所以F N G ＝M 2g tan 30°＝3M 2g ，方向水平向右．答案：(1)M 12M 2(2)M 1g ，与水平方向成30°角指向右上方 (3) 3M 2g ，方向水平向右【题后反思】 (1)轻绳中的“活结”两侧实际是同一根轻绳，“死结”两侧是两根不同的轻绳． (2)轻杆模型中，杆顶端所受的各力中，除杆的弹力外，如果其他力的合力沿着杆的方向，则杆的弹力也必然沿着杆，如果其他力的合力不沿着杆，则杆的弹力也不会沿着杆．。
高考物理一轮复习 第2章 相互作用 第2节 核心素养 科学思维—“活结”和“死结”及“动杆”和“定
学习资料科学思维-“活结”和“死结”及“动杆”和“定杆"模型“活结"和“死结”模型模型概述模型示例“死结”：理解为绳子的结点是固定的，“死结”两侧的是两根独立的绳，两根绳产生的弹力不一定相等，如图中OA和OB。
“活结”：理解为绳子的结点可以移动,一般是由绳跨过滑轮或光滑挂钩而形成的.“活结”两侧的两个弹力大小一定相等，它们合力的方向一定沿两绳的角平分线。
桌面上；小滑轮P被一根斜拉短线系于天花板上的O点;O′是三根线的结点，bO′水平拉着B物体,cO′沿竖直方向拉着弹簧;弹簧、细线、小滑轮的重力和细线与滑轮间的摩擦力均可忽略,整个装置处于平衡静止状态,g取10 m/s2。
若悬挂小滑轮的斜线OP的张力是20错误! N，则下列说法中不正确的是( ）A．弹簧的弹力为10 NB．重物A的质量为2 kgC．桌面对B物体的摩擦力为10错误! ND．OP与竖直方向的夹角为60°D[O′点是三根线的结点，属于“死结”，而小滑轮重力不计且与细线间的摩擦力可忽略，故P处为“活结”。
由m A g＝F O′a，F OP＝2F O′a cos 30°可解得:F O′a＝20 N，m A＝2 kg，选项B正确；OP的方向沿绳子张角的角平分线方向，故OP与竖直方向间的夹角为30°，选项D错误；对O′受力分析，由平衡条件可得:F弹＝F O′a sin 30°，F O′b＝F O′a cos 30°，对物体B有：f B＝F O′b,联立解得：F弹＝10 N，f B＝10错误! N，选项A、C均正确。
］“动杆"和“定杆”模型模型概述模型示例“动杆”：是可以绕轴自由转动的轻杆。
当杆处于平衡时，杆所受到的弹力方向一定沿着杆。
“定杆”：被固定了的不发生转动的轻杆.杆所受到的弹力方向可以沿着杆，也可以不沿杆AD BC住一个质量为10 kg的物体M1，∠ACB＝30°;图乙中轻杆HP一端用铰链固定在竖直墙上,另一端P通过细绳EP拉住,EP与水平方向也成30°，轻杆的P点用细绳PQ拉住一个质量也为10 kg的物体M2.g取10 m/s2，求：甲乙（1)轻绳AC段的张力F AC与细绳EP的张力F EP之比；（2)横梁BC对C端的支持力；（3)轻杆HP对P端的支持力。
力学4(死结、活结、死杆活杆)—高三物理一轮复习讲义
力学4（死结、活结、死杆活杆）1.轻绳、轻杆模型①轻绳，m=0，没有惯性，任何状态下F合=0；同一根绳子两端的力等大反向；轻绳的弹力只可能沿着绳且指向绳收缩的方向；②轻杆：m=0，没有惯性，任何状态下F合=0；；刚性杆的受力可以沿着任意方向，因此杆的弹力可以沿着任意方向，取决于具体情景：2.“活杆”和“死杆”；①活杆（铰链连接）：由F合=0，故弹力只能沿着杆方向，可以是拉力（等同细绳）也可以是支持力。
②死杆：需要什么力就能提供什么方向的力，“供可变型”。
3. “活结”和“死结”、①活结模型：活结两端仍然是同一根细绳，两端的力大小相等，合力大小为：F＝2F1cos θ2，合力方向在角平分线上。
常见的有：一根细绳绕过光滑的滑轮，光滑的钉子；一个光滑圆环套在一根细绳上等。
②死结模型：不是同一段细绳，各段细绳的力大小也不相等。
口诀：绳杆有死活，弹簧有双解例1.如图所示，一重为10 N的球固定在支杆AB的上端，今用一段绳子水平拉球，使杆发生弯曲，已知绳的拉力为7.5 N，则AB杆对球的作用力？例2.如图所示，求：细绳AC段的张力F TAC与细绳EG的张力F TEG之比；例3.已知m＝10 kg，求杆的弹力？例4.比较四幅图中木杆受到的弹力大小？例5.（多选）如图所示为位于水平面上的小车，固定在小车上的支架的斜杆与竖直杆的夹角为θ，在斜杆下端固定有质量为m的小球。
下列关于杆对球的作用力F的判断中，正确的是（）A．小车静止时，F＝mgsin θ，方向沿杆向上B．小车静止时，F＝mgcos θ，方向垂直于杆向上C．小车向右匀速运动时，一定有F＝mg，方向竖直向上D．小车向右匀加速运动时，一定有F＞mg，方向可能沿杆向上例6.如图所示，a、b两个小球穿在一根光滑的固定杆上，并且通过一条细绳跨过定滑轮连接。
已知b球质量为m，杆与水平面成θ角，不计所有摩擦，重力加速度为g。
当两球静止时，Oa段绳与杆的夹角也为θ，Ob段绳沿竖直方向，则下列说法正确的是（）A．a可能受到2个力的作用B．b可能受到3个力的作用C．绳子对a的拉力等于mg D．a的重力为mgtan θ例7.F向右移动一小段距离，θ怎么变，F怎么变？高分冲刺-力学4（死结、活结、死杆活杆）习题课1.如图所示，杆BC的B端用铰链接在竖直墙上，另一端C为一滑轮．重物G上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙缓慢向下移（BC杆、滑轮、绳的质量及摩擦均不计），则（）A、绳的拉力增大，BC杆受绳的压力增大B、绳的拉力不变，BC杆受绳的压力增大C、绳的拉力不变，BC杆受绳的压力减小D、绳的拉力不变，BC杆受绳的压力不变2.如图所示，晾晒衣服的绳子轻且光滑，悬挂衣服的衣架的挂钩也是光滑的，轻绳两端分别固定在两根竖直杆上的A、B两点，衣服处于静止状态．如果保持绳子A端位置不变，将B端分别移动到不同的位置．下列判断正确的是（）A．B端移到B 1 位置时，绳子张力不变B．B端移到B 2 位置时，绳子张力变小C．B端在杆上位置不动，将杆移动到虚线位置时，绳子张力不变D．B端在杆上位置不动，将杆移动到虚线位置时，绳子张力变大3.如图所示．用钢筋弯成的支架，水平虚线MN的上端是半圆形，MN的下端笔直竖立．一不可伸长的轻绳通过动滑轮悬挂一重物G．现将轻绳的一端固定于支架上的A点，另一端从最高点B处沿支架缓慢地向C点靠近（C点与A点等高），则绳中拉力（）A．先变大后不变 B．先不变后变大C．先不变后变小 D．保持不变4.如图所示，重量为G的均匀链条，两端用等长的轻绳连接挂在等高的地方，绳与水平线成θ角，试求：（1）绳子的张力：（2）链条最低点的张力。
死结、活结与固定杆、活动杆学案、试题、答案
绳子死结、活结与固定杆、活动杆一、“活结”与“死结”1. “活结”“活结”一般是由绳跨过滑轮、光滑钉子或者绳上挂一光滑挂钩而形成的，结点可以沿绳子移动。
绳子虽然因“活结”而弯曲，但实际上是同根绳，两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线。
2.“死结”“死结”一般是由绳子打结而形成的，结点不可沿绳子移动。
可理解为绳子因打结而变成两根独立的、拉力可不相同的绳子。
1、如图，一个重为G 的吊椅用三根轻绳AO 、BO 固定，绳AO 、BO 相互垂直，α＞β，且两绳中的拉力分别为FA 、FB ，物体受到的重力为G ，则（ ）A ．F A 一定大于GB ．F A 一定大于F BC ．F A 一定小于F BD ．F A 与F B 大小之和一定等于G2、如图所示，A 、B 两物体的质量分别为、，且，整个系统处于静止状态，滑轮的质量和一切摩擦均不计，如果绳一端由Q 点缓慢地向左移到P 点，整个系统重新平衡后，绳的拉力F 和两滑轮间绳、水平方向的夹角θ与物体A 的高度变化情况是( )A ．F 变大，θ角变大，A 升高B ．F 变小，θ角变小，A 升高C ．F 不变，θ角变小，A 降低D ．F 不变，θ角不变，A 升高3、如图，将一根不可伸长、柔软的轻绳左、右两端分别系于A 、B 两点上，一物体用动滑轮悬挂在轻绳上，达到平衡时，两段绳子间的夹角为1θ，绳子张力为1F ；将绳子右端移到C 点，待系统达到平衡时，两段绳子间的夹角为2θ，绳子张力为2F ；将绳子右端再由C 点移到D 点，待系统达到平衡时，两段绳子间的夹角为3θ，绳子张力为3F ，不计摩擦，并且BC 为竖直线，则（ ）A.123θθθ==B.123θθθ=<C.123F F F >>D.123F F F =>二、“活动杆”与“固定杆”1.“活动杆”“活动杆”就是用铰链或者转动轴将轻杆与墙壁连接，其特点是杆上的弹力方向一定沿着杆的方向；2.“固定杆”“固定杆”就是将轻杆固定在墙壁上（不能转动），此时轻杆上的弹力方向不一定沿着杆的方向。
第五讲死结与活结,死杆与活杆
第五讲：绳上的‘死结’和‘活结’杆中的“活杆”与“死杆”模型一、“活结”与“死结”绳是物体间连接的一种方式，当多个物体用绳连接的时候，其间必然有“结”的出现，根据“结”的形式不同，可以分为“活结”和“死结”两种.1. “活结”“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．2. “死结”“死结”可理解为把绳子分成两段，且不可沿绳子移动的结点。
“死结”一般是由绳子打结而形成的，“死结”两侧的绳子因打结而变成两根独立的绳子。
死结的特点：1.绳子的结点不可随绳移动2.“死结”两侧的绳子因打结而变成两根独立的绳子，因此由“死结”分开的两端绳子上的弹力不一定相等【典例1】如图所示，将一细绳的两端固定于两竖直墙的Ａ、Ｂ两点，通过一个光滑的挂钩将某重物挂在绳上，下面给出的四幅图中有可能使物体处于平衡状态的是（）【典例2】如图所示，一轻绳的两端分别固定在不等高的A、B两点，现用另一轻绳将一物体系于O点，设轻绳AO、BO相互垂直，α>β，且两绳中的拉力分别为F A、F B，物体受到的重力为G，下列表述正确的是( )A．F A一定大于G B．F A一定大于F BC．F A一定小于F B D．F A与F B大小之和一定等于G第2题图第3题图【典例3】如图所示，在水平天花板的A点处固定一根轻杆a，杆与天花板保持垂直．杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处，细线跨过滑轮O，下端系一个重为G的物体，BO段细线与天花板的夹角为θ＝30°.系统保持静止，不计一切摩擦．下列说法中正确的是( )A．细线BO对天花板的拉力大小是2G B．a杆对滑轮的作用力大小是2G C．a杆和细线对滑轮的合力大小是G D．a杆对滑轮的作用力大小是G 【典例4】如图所示，长为5 m的细绳的两端分别系于竖立在地面上的相距为4 m的两杆的顶端A、B，绳上挂一个光滑的轻质挂钩，其下连着一个重为12 N的物体，平衡时绳中的张力F T为多大？当A点向上移动少许，重新平衡后，绳与水平面夹角、绳中张力如何变化？.【典例5】如图所示，AO、BO和CO三根绳子能承受的最大拉力相等，O为结点，OB与竖直方向夹角为θ，悬挂物质量为m。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
“绳上的‘死结’和‘活结’模型”
“活动杆”与“固定杆”
一、“活结”与“死结”
绳是物体间连接的一种方式，当多个物体用绳连接的时候，其间必然有“结”的出现，根据“结”的形式不同，可以分为“活结”和“死结”两种.
1. “活结”
“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．
2. “死结”
“死结”可理解为把绳子分成两段，且不可沿绳子移动的结点。
“死结”一般是由绳子打结而形成的，“死结”两侧的绳子因打结而变成两根独立的绳子。
学.
死结的特点：
1.绳子的结点不可随绳移动
2.“死结”两侧的绳子因打结而变成两根独立的绳子，因此由“死结”分开的两端绳子上的弹力不一定相等
【典例1】如图所示，将一细绳的两端固定于两竖直墙的Ａ、Ｂ两点，通过一个光滑的挂钩将某重物挂在绳上，下面给出的四幅图中有可能使物体处于平衡状态的是（）
【答案】C
【解析】由于重物是通过一个光滑的挂钩挂在绳上，绳子张力处处相等，而两边绳子的合力大小等于物体的重力，方向竖直向上，由对称性可知两边绳子与竖直方向的夹角相等，所以C正确。
【典例2】如图所示，一轻绳的两端分别固定在不等高的A、B两点，现用另一轻绳将一物体系于O 点，设轻绳AO、BO相互垂直，α>β，且两绳中的拉力分别为F A、F B，物体受到的重力为G，下列表述正确的是()
A．F A一定大于G
B．F A一定大于F B
C．F A一定小于F B
D．F A与F B大小之和一定等于G
【答案】 B
【典例3】如图所示，在水平天花板的A点处固定一根轻杆a，杆与天花板保持垂直．杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处，细线跨过滑轮O，下端系一个重为G的物体，BO 段细线与天花板的夹角为θ＝30°.系统保持静止，不计一切摩擦．下列说法中正确的是()
A ．细线BO 对天花板的拉力大小是G
2
B ．a 杆对滑轮的作用力大小是G
2
C ．a 杆和细线对滑轮的合力大小是G
D ．a 杆对滑轮的作用力大小是G 【答案】 D
二、“活动杆”与“固定杆”
轻杆是物体间连接的另一种方式，根据轻杆与墙壁连接方式的不同，可以分为“活动杆”与“固定杆”.
所谓“活动杆”，就是用铰链将轻杆与墙壁连接，其特点是杆上的弹力方向一定沿着杆的方向； 而“固定杆”就是将轻杆固定在墙壁上（不能转动），此时轻杆上的弹力方向不一定沿着杆的方向。
【典例1】 甲、乙两图中的杆都保持静止，试画出甲、乙两图O 点受杆的作用力的方向．(O 为结点)
图2－1－8
【答案】 如解析图所示
【解析】甲为自由杆，受力一定沿杆方向，如下图甲所示的F N1.乙为固定杆，受力由O 点所处状态决定，此时受力平衡，由平衡条件知杆的支持力F N2的方向与mg 和F 1的合力方向相反，如下图乙所示．
【典例2】如图甲所示，轻绳AD 跨过固定的水平横梁BC 右端的定滑轮挂住一个质量M 1的物体，∠ACB ＝30°；图乙中轻杆HG 一端用铰链固定在竖直墙上，另一端G 通过细绳EG 拉住，EG 与水平方向也成30°，轻杆的G 点用细绳GF 拉住一个质量M 2的物体，求：
(1)轻绳AC 段的张力F T AC 与细绳EG 的张力F T EG 之比； (2)轻杆BC 对C 端的支持力； (3)轻杆HG 对G 端的支持力．
【答案】(1)M 1
2M 2
(2)M 1g 方向和水平方向成30°指向右上方 (3)3M 2g 方向水平向右
【解析】 题图甲和乙中的两个物体M 1、M 2都处于平衡状态，根据平衡的条件，首先判断与物体相连的细绳，其拉力大小等于物体的重力；分别取C 点和G 点为研究对象，进行受力分析如图甲和乙所示，根据平衡规律一一求解．
(3)图乙中，根据平衡方程有F T EG sin 30°＝M 2g ，F T EG cos 30°＝F NG ，所以F NG ＝M 2g cot 30°＝3M 2g ，方向水平向右．。