不同雷诺数下方柱绕流的数值模拟
不同雷诺数下的圆柱绕流数值模拟研究

不同雷诺数下的圆柱绕流数值模拟研究引言:圆柱绕流是流体力学领域中一个经典的、被广泛研究的问题。
在众多的工业应用中,圆柱绕流的研究对于风力发电机组的设计优化、管道内部液体运动的控制等方面具有重要实际意义。
雷诺数是描述流体流动的一个无量纲参数,它与流体的流速、流体的粘性有关。
本文将对不同雷诺数下的圆柱绕流进行数值模拟研究。
方法:数值模拟是一种有效的研究流体力学问题的方法,它能够通过计算机模拟得到流体的速度场、压力场等关键参数,从而进一步分析流体的特性。
在本文中,我们将使用计算流体力学方法进行圆柱绕流的数值模拟研究。
结果与讨论:我们选取了不同雷诺数的圆柱绕流作为研究对象,分别为200、400、600、800和1000,通过数值模拟得到了不同雷诺数下的圆柱绕流的速度场和压力场等关键参数。
首先,我们分析了速度场的分布。
通过数值模拟可以得到圆柱绕流过程中流体速度的分布情况。
随着雷诺数的增加,流体速度场呈现出不同的特征。
在雷诺数较低的情况下,流体绕圆柱流动的速度场分布较为简单,流速主要集中在圆柱前部和尾部。
随着雷诺数的增加,流体速度场呈现出更复杂的结构,流速分布更加均匀。
其次,我们研究了压力场的分布。
通过数值模拟可以得到圆柱绕流过程中流体压力的分布情况。
在不同雷诺数下,圆柱周围存在不同的压力区域。
当雷诺数较低时,圆柱前后表面存在较大的压差,压力分布较为不均匀。
而当雷诺数增加时,压力分布更加均匀,圆柱表面的压力变化较小。
最后,我们研究了绕流过程中的阻力情况。
通过数值模拟得到了不同雷诺数下圆柱绕流过程中的阻力系数。
我们发现,随着雷诺数的增加,阻力系数逐渐增大。
这是因为当雷诺数较低时,流体绕圆柱流动的速度较低,阻力较小;而当雷诺数增加时,流体流动速度较高,阻力也逐渐增大。
结论:本文通过数值模拟的方式研究了不同雷诺数下的圆柱绕流问题。
通过分析速度场、压力场和阻力系数等关键参数,我们得出了以下结论:随着雷诺数的增加,流体速度场更加复杂,流速分布更加均匀;压力场分布更加均匀,圆柱表面的压力变化较小;阻力系数随着雷诺数的增大而增加。
雷诺数为22000的二维方柱绕流仿真计算

图 15-1-3 网格划分结果
图 15-1-3 给出了网格划分结果,在划分网格时,约束整个面的网格尺寸为 10mm, 并且定义入口、 出口、 上下边界、 方柱表面的名称集 (Named Selections) , 以方便在 Fluent 中定义边界条件。
图 15-1-4 局部网格示意
图 15-1-4 给出了局部网格示意图,从图中可以看出,在方柱表面的网格高 度是较高的, 使用尺度化近壁面函数法时并没有划分很细的边界层网格。最后共 得到 48900 个网格,网格最大长宽比为 1.0069,满足仿真计算的网格要求。
(3)对于存在较高导热率的共轭传热问题; (4)对于流场网格长宽比较大的问题。 在本算例中,虽然不存在以上问题,但仍采用双精度 4 核并行计算求解。 在进行计算时, 先进行稳态计算,然后将稳态计算的结果作为瞬态计算的初 场,再进行瞬态计算。 求解器采用压力基求解器,并进行湍流模型的设置。
图 15-1-6 湍流模型的选择
关于雷诺数 22000 方柱绕流 (关于壁面函数法、湍流粘度比的计算等概念可以参考 文献十六)
15.1.1 RNG 模型与尺度化壁面函数在方柱绕流中的应用
图 15-1-1 分析流程
图 15-1-1 给出了二维方柱绕流问题的分析流程, 在 Workbench 中建立模型, 然后使用 Mesh 模块进行分网,最后提交到 Fluent 中进行计算。
图 15-1-15 方柱表面的 Y+值分布范围
仿真后可以知道,近壁面 Y+值的分布范围为 7.07-68.6,在 Fluent 的官方 文献中推荐壁面函数法的 Y+值适用范围为 30-500,对于尺度化壁面函数,由于 在近壁面使用了预防 Y+值过小导致结果恶化的技术,其 Y+值范围下限可以适当 放宽, 但仍应尽量取在 11.25 以上。 过大或过小的 Y+值都可能引起结果的恶化。
不同雷诺数下的圆柱绕流数值模拟研究

2 01 5在
中
国
水
运
VoI .1 5 Jul Y
No. 7
7月
Ch i n a Wa ter Tr a ns p or t
2 01 5
不 同雷诺数下 的圆柱绕流数值模拟研究
陈 禹,李 强 ,郭廷 凯
( 浙江海洋 学院 船舶与海洋I - 程系 ,浙江 舟 山 3 1 6 0 2 2 ) 摘 要:通过 a b a q u s的 CF D 模 块 ,在水动力作用下 ,对刚性 圆柱 展开了绕流三维仿真计算 ,同时也对 圆柱绕 流
的水动力特性进行了研究 。通过仿真计算得到了漩涡脱落形态、升力系数、 阻力系数 曲线 以及斯特劳哈尔数 ,经过 分析 比较可以看出 ,不同雷诺数情况下圆柱绕流在性质上存在着 比较大 的差异 。结果表 明,随着雷诺数 的增大 ,层 流变为紊 流 ,升力以及阻力系数 的变化 幅度出现 了不稳 定性 ,漩 涡的脱落 形态 也变得 不规则。 关键 词:圆柱 绕流 ;数值模 拟 ;升力 系数 ;阻力系数 ;漩涡 脱落 中图分类号:T H 3 1 1 文献标识码 :A 文章编号:1 0 0 8 - 7 9 7 3( 2 0 1 5 )0 7 — 0 0 8 8 — 0 3
王亚玲等为得到较高雷诺数 时圆柱绕流 的三维特性 , 采
用有限体积 法 , 选取 了 Re = 1 0 。 和 Re =1 0 , 对黏性 不可 压缩 流场条件下 的圆柱绕流展开 了了三维仿真 试验『 6 】 。苏铭德和 康 钦军 选取 Re = 1 0 和 2X 1 0 ,使 用大涡模拟 的方法 ,对 圆
收稿 日期 :2 0 1 5 — 0 5 — 0 3 作者简介 :陈
a
不同雷诺数下倾斜圆柱绕流三维数值模拟研究

不同雷诺数下倾斜圆柱绕流三维数值模拟研究近年来,研究倾斜圆柱绕流特性引起了学界的广泛关注。
圆柱绕流可分为水平和垂直两类,其中倾斜圆柱绕流为一种特殊的二维绕流状态,它在一定雷诺数范围内具有更复杂的流场结构特性,并且受水文物理过程的影响更为显著,研究其特性更为重要。
本研究使用时间和空间设置,以带边界流作为边界条件,利用基于六边形网格的数值模拟方法研究不同雷诺数下的倾斜圆柱绕流特性。
实验参数包括:倾斜角度α=20°,Re=1000 ~ 10000,向心轴比例范围为0.5 ~ 2.0,圆柱入口处外提升速度Um=0.3 ~ 0.8,及空气密度ρ=1。
有鉴于此,本研究根据不同雷诺数和向心轴比例,计算出倾斜圆柱绕流特性。
首先,主要考察不同雷诺数Re下倾斜圆柱绕流的流态特性,包括在不同位置的压力梯度,流场动量,温度梯度,流态结构以及涡度等信息。
其次,重点考察不同向心轴比例和轴向外提升速度下倾斜圆柱绕流的流态特性,包括压降,动量,温度梯度,以及不同方向的涡度分布。
结果表明,不同的雷诺数和向心轴比例会对倾斜圆柱绕流的流动特性产生明显不同的影响。
随着雷诺数的增大,压力梯度增大,动量梯度减小,温度梯度增大,涡度明显减少,圆柱内部的流场会变得更加复杂,气泡变小,而且其会从一种混合流场演变为一种逆流的流场结构。
另外,随着向心轴比例的增加,轴向外提升速度的变化会出现显著影响,但随着向心轴比例的增加,压力梯度会逐渐减小,动量梯度增大,温度梯度变化不大,涡度分布也会有较大变化。
研究结果表明,在不同雷诺数和向心轴比例范围内,倾斜圆柱绕流的流动特性会发生明显的变化。
本研究对于进一步理解流动特性和确定流动行为有重要的理论意义,同时也为实际工程的设计提供了参考。
总的来说,本研究通过应用数值模拟方法研究不同雷诺数下倾斜圆柱绕流特性,得出上述结论。
未来可以将此模拟实验方法应用于建立更复杂物理系统的研究,以更深入地理解绕流特性和其流动性质。
方柱绕流的数值模拟

价值 . 是能够 将方 柱或 其 它类 似 的障碍 物对 流 但 场 的 影 响 , 别 是 流 体 撞 击 障碍 物后 的 流 场 分 特
布 , 力分 布 以及 障碍 物后 方 的流 动状态 等等 清 压 晰地 展 示 出来 的方 法是 罕 见 的 . 日常 生 活 中 , 在
收稿 日期 : 2 0 0 6—0 4—1 7
式 中 , 为 Y 向流 速 ;1 为 z 向 流速 ; 为 , / P
压力 ; p为流体 密度 ; 为流体 动 力学粘 性 系数 . 方 柱周 围 的流 场 利用 F UE T 求 得 , 用 L N 利
作者 简介 : 王建( 9 9 , , 17 一)男 辽宁开原人 , 士研究生在读 , 硕 主要从事流体计算 的研究
区长 度 和 Re的关 系 , 后通 过 与 其 他文 献 数 据 最
的 比较 , 明本 文 模 拟结 果 的正确 性 . 证 同时 对方 柱位 于流场 中央 的情 况 进 行 模 拟 , 析 当 Re 分 = 2 0时形 成 的漩 涡 变化情 况 . 0
象 是方 柱位 于流场 的 中央 , 因此可 用方柱 绕 流 的 计算 来模 拟风 载 荷 或水 载 荷 对 建 筑物 的作 用 力 大小 、 应力 分 布等 . 如果 经 过 分析 可 以全 面 的并
维普资讯
第2 1卷
20 6 0 7.
第 2期
沈
阳
化
工
学
院
学
报
V 12 N0 2 o. 1 . Jn20 u .0 7
J RN HE OU AL OF S NYA NS TU F C E I A C OL NG I TI TE O H M C L TE HN OGY
高雷诺数下双圆柱绕流的数值模拟_廖俊

A辑第16卷第1期 水动力学研究与进展 Ser.A,V ol.16,N o.1 2001年3月 JOURNAL OF HYDRODYNAM ICS M ar.,2001文章编号:1000-4874(2001)01-0101-10高雷诺数下双圆柱绕流的数值模拟廖 俊1, 景思睿2(1.华中理工大学能源科学与工程学院,湖北武汉430074;2.西安交通大学能源与动力工程学院,陕西西安710049) 摘 要: 本文使用表面涡法研究高雷诺数下不同排列方式双圆柱绕流的流动状态。
计算了双圆柱在并列、串列及级列的情况下的各种流动结构,涡街的变化及作用在圆柱上的受力情况。
本文结果清楚地描述了双圆柱绕流复杂的流动状况,计算结果与实验显示的流动状况十分相似,斯特罗哈数和阻力系数与实验结果符合得很好。
关 键 词: 表面涡方法;圆柱绕流;数值模拟;涡街中图分类号: O357.1 文献标识码:A1 引言对多圆柱的绕流研究在工程实际中有很重大的意义,例如管束的热交换,反应堆,高大建筑物,海洋平台及桥梁等。
当流体流过圆柱体时,由于涡的脱落,使圆柱体上产生交变作用力。
这种作用力导致柱体的振动及材料的疲劳,而使结构损坏,产生严重的后果。
如水电站的蒸发塔,就曾经由于安装位置不正确,导致多个塔之间强烈影响、振动并使塔损坏,悬索桥也发生过类似事例,悬索共振而使桥倒塌。
由于多个柱体流动状况复杂、多变,导致对于柱体上作用力大小和方向极其复杂,实验测量非常困难,在实际工程中就需要用数值模拟的方式确定其流动状况,估计出柱体上的作用力大小、方向,以便工程参数的确定。
在多圆柱绕流研究中最多的是双圆柱绕流,双圆柱绕流按圆柱的不同排列方式可以分为三类:串列,两圆柱相对来流方向呈前后排列;并列,两圆柱相对来流方向呈并排排列;级列,两圆柱呈前后交叉排列。
对于柱体绕流的数值模拟方式可以分两大类,一类为网格法,另一类为无网格法。
网格法主要有有限差分法、有限元法。
不同雷诺数下倾斜圆柱绕流三维数值模拟研究

87
向流影响ꎬ其尾流形态特征、受力特性及旋涡脱落频率与竖直圆柱相比存在明显差异ꎮ 近年来ꎬ针对倾斜圆
柱绕流的研究受到海洋工程界和学术界的广泛关注ꎮ
第 38 卷第 1 期
2020 年 1 月
ቤተ መጻሕፍቲ ባይዱ
海
洋
工
程
THE OCEAN ENGINEERING
Vol. 38 No. 1
Jan. 2020
文章编号:1005 ̄9865(2020)01 ̄0086 ̄15
不同雷诺数下倾斜圆柱绕流三维数值模拟研究
高洋洋1 ꎬ张演明1 ꎬ刘 彩1 ꎬ王 滨2
(1. 浙江大学 海洋学院ꎬ浙江 舟山 316021ꎻ 2. 中国电建集团华东勘测设计研究院有限公司ꎬ浙江 杭州
在海洋工程中ꎬ钢悬链线立管因其结构简单、经济可靠及对上部平台运动更好的适应性越来越多的被应
用于深水油气资源开发中ꎮ 钢悬链线立管近触底区由于倾斜角度变化大ꎬ在流体绕流倾斜立管的过程中ꎬ尾
涡相互干扰机制更加复杂ꎬ更易导致立管发生疲劳破坏ꎮ 然而目前基于竖直圆柱的尾涡特性研究因忽略轴
收稿日期:2019 ̄05 ̄06
cylinder at different Reynolds numbers
GAO Yangyang 1 ꎬ ZHANG Yanming 1 ꎬ LIU Cai 1 ꎬ WANG Bin 2
(1. Ocean Collegeꎬ Zhejiang Universityꎬ Zhoushan 316021ꎬ Chinaꎻ 2. Power China Huadong Engineering Corporation Limitedꎬ
Reynolds numbers ( Re = 100ꎬ 1 500 and 3 900) and inclined angles (  ̄60° ≤ α ≤ 60°) based on the computational fluid dynamics
FLUENT仿真计算不同雷诺数下的圆柱绕流
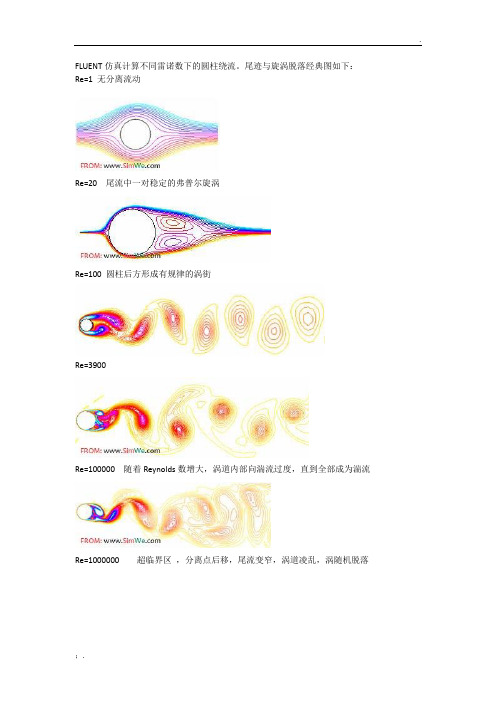
FLUENT仿真计算不同雷诺数下的圆柱绕流。
尾迹与旋涡脱落经典图如下:Re=1 无分离流动Re=20 尾流中一对稳定的弗普尔旋涡Re=100 圆柱后方形成有规律的涡街Re=3900Re=100000 随着Reynolds数增大,涡道内部向湍流过度,直到全部成为湍流Re=1000000 超临界区,分离点后移,尾流变窄,涡道凌乱,涡随机脱落Re=10000000 极超临界区,分离点继续后移,尾流变窄,湍流涡道重新建立。
图3 Cd随Re的变化曲线图3中实曲线是由Wieselsberger,A.Roshko以及G.W.Jones和J.J.Walker测量数据绘制得到,图中圆点部分是FLUENT计算值在Re=106(超临界区),从经典数据和我们的计算结果都可以看到,圆柱体的平均阻力系数急剧下降。
这是因为在Re=3×105附近,边界层流动由层流状态转变为湍流状态,虽然湍流边界层流动的摩擦阻力较层流边界层大,但它从物面的分离较晚,所以形成较小的尾流区。
由于钝体绕流的阻力主要是压差阻力,所以此时物体的总阻力有了一个明显的下降。
入口VELOCITY_INLET,出口OUTFLOW,上下WALL.Re=1,20,100,二维层流模型。
Re=3900后,三维大涡模型计算不准与网格划分与一些参数设置有关。
1。
圆柱中心离上下边界(wall)的距离大于10D(D为圆柱直径),影响较小。
2。
湍流模型采用大涡模型(LES)。
是目前最复杂,最完善的一种湍流模型。
试验曲线来自,《Boundary-Layer Theory》, Dr.HERMANN SCHLICHTING, Translated by Dr.J.KESTIN,Seventh Edition,用MATLB绘制4.阻力系数的求法请参考此论坛我发的教程FLUENT三分立系数的求法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
计算结果与讨论
分别对雷诺数为 100, 1 103 , 1 104 和 2 2
3 4
计算得到了方柱上的阻力系数和升力系数. 阻力系数 C D 与升力系数 C L 的定义分别为: CD = FD , 1 L 2 U2 2 CL = FL 1 L 2 U2 2 ( 12)
104 时的情况进行了计算 . 当 Re = 100 时, 直接采 用 N S 方程进行计算 ; 当 Re = 1 10 , 1 10 和 2 2 10 4 时 , 则引入 k 湍流模型进行计算. 下面 给出不同雷诺数下的计算结果 . 图 2 给出了计算得到的涡线图 . 在 4 个不同 的雷诺数下, 都会在柱体的尾部出现规则的旋涡 脱落 , 尾涡交替的甩在方柱上下两侧的壁面上 , 这 就是著名的卡门涡街 . 同时我们可以发现, 方柱后 尾涡的形态会随雷诺 数的变化而产 生一定的变 化. 当雷诺数较低时 ( Re = 100) , 尾涡会拖得比较
[ 6]
图1
计算模型
各边界条件分别为: 入口 : 给定无量纲速度, u = 1, v = 0 . 出口 : 给定无量纲压力 p = 0 , 速度采用 u / x = 0, v / x = 0 . 固壁 : 采用无滑移边界条件, 即 u = 0, v = 0 . 上下边界 : u = 1, v = 0. 不可压缩牛顿流体运动的控制方程 N S 方 程可表示为: ui = 0 xi u i + uj t 式( 2 ) 中 ui = - 1 xj p + xi ui xj xj
[ 4]
得到了绕流的速度场以及柱体上的受力参数. 总 结了方柱后的涡脱落形式和流场的动力学参数随 雷诺数的变化规律 , 并将计算结果与前人的实验 和计算结果进行了对比.
1
计算方法
计算区域为一 60 D 20 D 的矩形区域 , 如图
1 所示. 上游长度为 10 D, 下游长度为 50 D. 流向 速度和垂向速度分别定义为 u 和 v .
105 , 3 6
106
数. 以 上 方 程无 量 纲 化后 , 引 入 雷 诺数 Re = UD/ , U 是流动的特征速度, D 为流动的特征长 度, 即方柱的边长. 处理湍流问题时, 引入平均 N S 方程 , 将瞬 时速度分解为平均速度与脉动速度之和 , u i = U i + u i . 则可得到如下的控制方程 :
[ 7]
对绕流雷诺数为 2 2
10 的方
4
( 1) ( 2)
柱绕流流场进行了大涡模拟, 并对应用不同模型 的计算结果进行了比 较. L o et al [ 8] 应用 DES 湍 流模型, 数值研究了高雷诺数下的圆柱和方柱的 绕流流场 , 计算雷诺数分别为 1 4 和2 2
4
是流体的密度 , 是流体的运动粘性系
Ui = 0 xi Ui Ui 1 + Uj =t xj p + xi xj Ui - u iu xj
j
10 . 前人的计算结果都较好地反映了方
柱绕流流场在相应的计算雷诺数下的流动特性, 但往往都是在单个雷诺数下的计算, 不能反映流 场随雷诺数的变化规律 . 笔者将力求在不同的雷 诺数下更全面地反映方柱绕流的特性 , 进而考察 方柱绕流流场随雷诺数的变化规律 . 笔者对雷诺数分别为 100, 1 2 2
2
湍 流模
对高雷诺数下钝体绕流进
行了数值模拟, 较好地模拟出了方柱后的涡街脱 落. 另 外, 大 涡 模 拟 ( Larg e Eddy Sim ulat ion, LES) 和 分离 涡 模 拟 ( Det ached eddy sim ulat ion DES) 也在近几年被相当广泛地应用于湍流模拟. Sohankar et al
Abstract: Flow ar ound a square cylinder is numer ically simulated at different R eynolds number s. T he R ey nolds number s of comput ation are selected to be 100, 1 10 3 , 1 10 3 , 1 104 and 2 2 104 , a k 10 4 and 2. 2 10 4 . F or the lo wer Reynolds num ber, R e = 100, N S equatio ns are directly used in t he simulation. Fo r the higher Rey no lds number s, Re = 1 based model of turbulence is applied to so lv e the tur bulent problem. Var ia tional fo rm of t he numerical sy stem is discr et ized w ith the Galerkin finite element method and no n linear cou pling terms in the equatio ns are treated sepa rately at differ ent fractional time steps, by an o per ator splitting time stepping metho d. T he shedding modes o f the K arman vo rtex streets after the cylinder at different Reyn o lds number s wer e calculated o ut. When the R eynolds number is smaller, the for ming length o f the vo rtex in the near w ake of the cylinder is long er. I ncreased Reyno lds number r esults in short ened for ming length. T he force coefficients and the Str ouhal number are calculated out and co mpa red w ith the pr ev ious experimental and numerical data. T hese results are in g ood ag reement. Key words: Rey no lds number; Galerkin finite element method; K arman vo rtex str eets; fo rce co eff icients; St rouhal number
【 收稿日期 】 2005 12 26 【 作者简介 】 刘 宇 ( 1981- ) , 男 , 辽宁葫芦岛人 , 硕士研究生 . 主要研究方向为计算流体力学 .
第1期
刘
宇 , 等 : 不同雷诺数下方柱绕流的数值模拟
41
钝体绕流问题广泛存在于桥梁工程、 海洋工 程、 兵器工业工程和现代宇航工程等工程科学领 域中 . 例如 , 海洋平台、 斜拉桥、 原子能反应堆中的 换热器等都存在类似的流体与结构相互作用的情 况. 当流体以一定的速度流过柱形钝头物体时 , 会 在物体尾部形成规则的旋涡脱落, 即著名的卡门 涡街 . 方柱是一种典型的钝头柱体 , 关于方柱绕流 问题的研究一直是流 体力学领域的 热点问题之 一. 关于方柱绕流问题的实验研究也已进行得相 当广泛, 有很多作者通过实验的方式对方柱绕流流 场和柱体受力 情况进行 了测量 , 如 Lyn et al [ 1] , Norberg [ 2] , Bearman & Obasaju [3] 等. 大量的 实验 数据为我们提供了重要的比对依据 . 数值模拟是解决钝体绕流问题的一种有效手 段, 许多作者用数值的方法研究了方柱绕流问题, 可诸见于文献[ 4~ 12] . 王广超
Numerical simulation of flow around square cylinders at different Reynolds numbers
L IU Yu, SU Z ho ng di
( C ol lege of M et rolorolgical T echnology & Engineering, Chin a Jiliang U niversit y, H angzhou 310018, China)
4
( 3) ( 4)
10 , 1
3
10 和
4
10 的方柱绕流情况进行了数值模拟 . 计算
42
中
国
计
量
学 院
学
报
第 17 卷
采用 k 湍流模型来模拟高雷诺数下的绕流, 引入湍动能 k 和耗散比 的概念: k= = k 和 的方程 :
k k + Uj = Gt xj + Uj = C1 + xj
2
长, 在方柱下游较远处才形成规则的涡街脱落; 随 着雷诺数的增 加 ( Re = 1 10 , 1 10 , 2 2 4 10 ) , 尾涡长度会随之变短, 从而在近壁区域就会 出现规则的卡门涡街脱落 .
j j
t
可用 k 和
ij
表示 : Ui + xj ( 11)
= 2k 3
-
t
方程( 7) 、 ( 8) 、 ( 9) 中的各系数的取值为: C = 0 09, C 1 = 1 44, C 2 = 1 92,k来自= 1 0和= 1 3.
采用 Galer kin 有限元法 对上述各式 进行离 散, 利用分离时间步长法处理式中的非线性项进 行. 计算采用六结点三角形非均匀网格 , 方柱壁面 附近采用较密集的网格, 最小网格间距为 D/ 30. 总网格数在 49 000 以上, 此时可确保计算公差在 0 5% 以内.
