数列与不等式知识点及练习(唐)
[高一数学]不等式知识点归纳与总结
![[高一数学]不等式知识点归纳与总结](https://img.taocdn.com/s3/m/3b1c8088dd88d0d232d46a11.png)
授课教案教学标题 期末复习(三) 教学目标 1 、不等式知识点归纳与总结 教学重难点重点:不等式基础知识点的熟练掌握难点:不等式在实际应用中的相互转换上次作业检查授课内容:一、数列章节知识点复习1 等差数列(1)性质:a n =an+b ,即a n 是n 的一次性函数,系数a 为等差数列的公差;(2) 等差{n a }前n 项和n d a n d Bn An S n ⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=+=22122 即S n 是n 的不含常数项的二次函数;若{a n },{b n }均为等差数列,则{a n ±n n },{∑=k1i ka},{ka n +c}(k ,c 为常数)均为等差数列;当m+n=p+q 时,a m +a n =a p +a q ,特例:a 1+a n =a 2+a n-1=a 3+a n-2=…;当2n=p+q 时,2a n =a p +a q ; ① 等差数列依次每k 项的和仍成等差数列,其公差为原公差的k 2倍...,,232k k k k k S S S S S --; ② 若等差数列的项数为2()+∈N n n ,则,奇偶nd S S =-1+=n na a S S 偶奇;等差数列等比数列 定义 d a a n n =-+1)0(1≠=+q q a a nn 递推公式 d a a n n +=-1;()n m a a n m d =+-q a a n n 1-=;m n m n q a a -= 通项公式 d n a a n )1(1-+=11-=n n q a a (0,1≠q a )中项2kn k n a a A +-+=(*,,0n k N n k ∈>>))0( k n k n k n k n a a a a G +-+-±=(*,,0n k N n k ∈>>)前n 项和)(21n n a a nS +=d n n na S n 2)1(1-+=()⎪⎩⎪⎨⎧≠--=--==)1(111)1(111q q qa a qq a q na S n n n 重要性质),,,,(*q p n m N q p n m a a a a qp n m +=+∈+=+),,,,(*q p n m N q p n m a a a a qp n m +=+∈⋅=⋅③ 若等差数列的项数为()+∈-N n n 12,则()n n a n S 1212-=-,且n a S S =-偶奇, 1-=n n S S 偶奇 (4)常用公式:①1+2+3 …+n =()21+n n ②()()61213212222++=+++n n n n③()2213213333⎥⎦⎤⎢⎣⎡+=++n n n[注]:熟悉常用通项:9,99,999,…110-=⇒n n a ; 5,55,555,…()11095-=⇒nna .2 等比数列 (1)性质当m+n=p+q 时,a m a n =a p a q ,特例:a 1a n =a 2a n-1=a 3a n-2=…,当2n=p+q 时,a n 2=a p a q ,数列{ka n },{∑=k1i ia}成等比数列。
高三数学复习专题四数列与不等式

高三数学专题四(数列与不等式)第一讲递推公式与通项公式数列是高中数学很重要的内容之一,是高考的热点和重点。
数列中蕴含着丰富的数学思想,而递推公式的 通项问题具有很强的逻辑性,是考查逻辑推理和转化化归能力的好素材,因此也成为近几年高考的热点。
类型 1 (已归纳常见题型)(1) a 1.=a n ■ f (n);(2) a n 1 =a n f (n) ; (3)a1 — pa n q ;(4)a n 1 = pa n • r q n ;(5)a n 1. =pa “ r p n ; (6)(a n 1 ■ q^ p (a n q)r ;(7) a n 2 = ' a n 1uanG u =1)类型 2 : af(n)ang(n)a nn(n)这种类型一般是等式两取倒数后转化为类型( 3)3nan丄(n > 2),求数列{ a n }的通项公式.2a n 1亠n【解析】由已知,得丄=_? n -1a n 3n 3na n 丄至此可知:数列{a n }的各项的值依次为0,- 3, ■■ 3,0,_ 3, ■. 3,0,……周而复始例1 •已知数列{a n }满足a =?,且a12 '[n 口 2(n > 2). a n 1 3 n , . 1 n —1 m 设 a n 一3(訂」(n ‘2),n _1 a n口 _±(n > 2),3-1,二{丄_门是首项为_!,公比为1的等比数列, a n3 3解得a n类型3:周期型这种类型与函数的周期性相类似,应推导对任意 n • N *有a n k =a n (k ・N *)例2•已知数列{ a n }满足a ’=0,a(3(n 詁),则a 20 =()n朽a n 北则k 为数列的周期c . 3【解析】选B.• a 1 二 0,口3 =0,1 1 n 1 -3 々■.这种类型一般通过构造方程,利用“不动点”知识处理.例3 •已知数列{ a n }满足a’ =£,an *=2a n 46,求数列{ a n }的通项公式.n 1a n 比【解析】设方程x -2x 6,则X 2 -x -6 =0= x =3或X - _2 x 比两式相除,得:务1 -3 a n 十 +24 a n +220 -:-3 =6 余 2类型4:an 1pa n q ra n sa n 1由(1 )知S ’ =a 」.S 2=创a J 丄二2.由(*)可得s 3仝.由此猜想S n =丄,n =1,2,3, ■■-22 634 n -1下面用数学归纳法证明这个结论 ①n =1时已知结论成立.②假设n=k 时结论成立,即 S1 _ .即s .故n =k 出时结论也成立.kSk1_k 2又当n=1时,目丿二丄,所以{a n }的通项a =一1一(n 乏N *).2 1汇2 nn (n+1)•- a nX ,则 b n A —S n ,b,注a n2 4a 1 2 =2二 b n =Eq n 丄=2x(_:)n1 41314 U-)n13=2 (-;)口 Vn— 1-2 ( -^)4 3 (/)n 丄-(/严牙类型 5: a n -.-a n 1 =pn .q 或; 这种类型一般可转化为{ a 2n J 与{ a 2n }是等差或等比数列求解. a n a n 1 = p例 4. (1)在数列{a n }中,q =1,a n1 =6n_a n ,求乱; v=3n ,求 a n .(2)在数列{a n }中,耳=1 ,a n a n【解析】(1)v a n 亠a 1 =6n ,二 O n 1 ' a n 2 =6(n T),两式相减,得 a, [n二{ a 2n 1}与{ a 2n }均为公差为6的等差数列,易求得_pn —2a"3n_12_an=6 .(n 为奇数) (n 为偶数)(2)类似(1)的方法易求 a =』3nn —n32(n 为奇数) (n 为偶数)类型6:归纳猜想法例5•设数列{务}的前n 项和为S n ,且方程 (2 )求{a n }的通项公式.2Xa nx- a n=0 有一根为 & —1, n =1,2,3, (1)求 ^ ,爲;【解析】(1)当n=1时, x 2 —qx —a_, =0有一根为 S = =d —1,于是佝一1)2 —a^a t —1) —% =0.解得 a1 =丄2当n =2时, x 2(2)由题设①-1)2 -a当n > 2时,a n =£ 一S n 丄,代入上式得:-a 2X 一日2 =0有一根为S -12(日2 —1 )「日2(日2 J )「日2 =0,解得日2 =-2 2 6(*)当n =k 出时,则(*)得S k + = 2 -S综上,由①、②可S 二丄对所有正整数n 都成立.于是当n > 2时, nn 力a n-Snn -1 _ 1 n n(n •1)练习:1 •已知数列{ a n}中,a1 =4,3a n =3a“ 1- "2,则使a“a n2 :::0成立的n 是(D )A. 21 或22B. 22 或23C. 22 D . 21学习必备64362已知f (x )是定义在(0,;)上的增函数,对任意的X, y 有f (xy^f (x ) - f (y )且f ( 6) -I ;定义数列 { a n }满足:a 1 =a 2 =5, f (a n 讥一a n ) =f (a n 』1(n > 2,n ^N ),若{ a n n a n }为等比数列.(1 )求,的 所有值及{耳}的通项公式;(2)当k 为奇数时,求证:丄食;(3)求证:丄.丄.....丄a k ak -13 a 1 a2-3n _ (一 2J )I 丄 2n22 •若数列{ a n }中,a 1 =3,且对任意的正整数m 、n 者有二 a m a n,则a n 等于A . 3n "B . 2 3n 13 •给定正整数n ( n >2)按下图方式构成三角 形数表:第一行依次写上数1, 2, 3, ......... , n ,在下面一行的每相邻两个数的正中间上方写上这两 个数之和,得到上面一行的数(比下一行少1个数), 依次类推,最后一行(第 n 行)只有一个数,例如 n = 6时数表如图所示,则当n = 2009时最后一行的 数是(C ) A . 251 X 22009251 X 220083n204812112 28162011 56C . 2010 X 22007 2009 X 22007数列{ a n }满足2anan丰=< an—11(0 < an ::-)若 1(-< a n :::1) 2耳,则a 20的值是7设数列{ a n }的前n 项和S n=^a ―1 X2n +£,n =1,2,3,,■”求数列{ a n }的通项公式.(a “3 n 3 3=4 -2n )1 1<a n 2学习必备64362n 项和T en . 得 21°(S 30 -S 20) =S20 -^0 , ''+日20 , 得 2 q (日11 +日12 * …+日20 )=日11 *日12 + …*320 ,町-、) 1_ n =2^ 卍=_丄,nS n =n -12nT n =(1 2 亠亠n)-(--)牛扣2 — n )甘寺一牙^弄例1 •设正项等比数列第二讲}的首项a数列的通项与前n 项和(教师用)n项和为 S n ,且 210S 30 —(210 V)S 20 £10 =0.因为a n 0,所以210q 10 ",解得q 冷,因而"2 彳(n =1,2, ■■). (1)求{a n }的通项;(2)求{n &}的前 (2)因为{ a n }是首项a,4,公比qW 的等比数列,故S 则数列{ nS, }31故a山乜心匚⑴b 「b)"1—2①—②得: T L =](1 • 2 .….n) _(]-丄学…2 2 2 2n1na 2, a 4, a 6, a 8,…是公比为2的等比数列,二a n =a 2 27- =2^ .n,n 为奇数,:• n.2jn 为偶数(2) b n =a 2n 丄 a 2n =(2 n —1) 2 , /• S n =1 2 322 5 23…丁(2n _1) 2n ,2( =1 22 - 323 - 5 24 ………(2n _1) 2n 1两式相减,得: -S n =2 2 22 2 2^亠2 2n _(2n _1) 2n 1=2H 1 -2_(2n -1)2n 1=(3 -2n) 2n 1 —6,二 S n1-2⑵由*1必「3,氛一4二迪£,心寸0,由-1bn丁a n •21 1n n(n -1)2(^2n)刃 4~2即T_n(n⑴.1. n2 1 n_ 2 2^1刃 _2例 2 •已知数列{a n }满足:a 1 =1,a 2 =2,2a . 2=[3 - (_1)n ]a^2[(-1)^1],n ・ N *.a 6的值及数列{ a n }的通项公式;(2 )设b n =a 2n【思路点拔】(1)先令n =1,2,3,4,再讨论n 的奇偶.(2)用错位相减法. 【解析】(1)(1)求 a 3,1 a2n,求数列{ b n }的前n 项和S n .当 n 为奇数时,2a n*=2a n +4,二 a n* =a n +2, 二a.!, a 3, a 5, a 7,…是公差为 2 的等差数列, 二a n =n. 当n 为偶数时,2a n 2 =4a n ,二 耳2 =2a ,已3 二3, a 4 —4,已5 二5,已6 二8 , 二数列{a n }的通项公式为a ann -1=(2n —3) 26.例 3 •数列{a n }满足 a, =1 且 8a n4a n _16a n ++2a n +5=0(n > 1),记-——(n > 1). (° 求 b 1、b 2、 2、b 4的值;(2)求数列{ b n }的通项公式及数列{ a n b n }的前n 项和S【解析】方法一:(1 )由d _1 ,得:a 二丄 1,代入递推关系式b n=1n 一b n 2 a n -2a nb n 8a n i a n -16a n 彳• 2a n • 5 =0,整理得一4bb i =2,所以b 2 =8, b 3 =4, b 4320 3所以{ b _4}是首项为2,公比q =2的等比数列,故 n 3一 b n4J -2n ,3 3即 b n_1 _3例4 •已知各项均为正数的数列{a n }满足:耳=3,且2an 1 _an =a n a n ’,n^N *. (1)求数列{ a n }的通项公2an —a n +式;⑵设S n -a -a f亠a 2,T n =4,A•…丄,求S nT n ,并确定最小正整数n ,使S n T n 为整数.a 1 a 22 •数列{a n }的前n 项和S n =q n -1(q >0且q 是常数),某同学研究此数列后,得出如下三个结论:①方法二:’ a n “詐 设方程:x — _8x _16 三—,则 8x 2_14x 5 =0二 x =丄或 x 2 1 -6a n +3 an 1十 2 8a n -J6an 1 ■十41把久15, 两式相除得ai 1 一㊁8a n _16_1"21 二 5 a n41a ___ 令: cn _2 ,则: Cn5a n1 Cn -1Cn21 a1-2--------- -25 日1 ----1 an '2 5 a n ——4n 2 —ann2 +4, 8 . . , 20 b 2 , G=4, b t332n -+5 a n bi3'S n 曲 g =1(1 2 2"丄) 5n 2n 5n -1 r --- = --------------- 3 32a n 1 - a n【解析】(1)条件化为a 1 _J n + a.所以a n -丄2 a n 3 —=2( a n1an・;2丄(n 三,因此{a _丄}为一个等比数列,其公比为2,首项为na n⑵由(1)有S n T n =佝一丄)2 G —丄)2… 何一I)2 2nai a 23i〈2)+,..,毛 2)(4 -n)in2N :*,为使=61(4n _1) 2n 为整数,当且仅当 J 为整数. 当n =1,2时,显然S n +T :不为整数,1 2 2 当 n > 3时,:4n -1 =(1,3)n -1 二C : 3 9: 32 '33(C"'-彳弋;).:只需 Cn 3 Cn 3 丿 31 一1 为整数, n nnn 9 227V 3n _1与3互质,二n 为9的整数倍.当n=9时,n9T _13为整数,故n 的最小正整数为2 -9.练习:1•数列{ a n }是公差不为零的等差数列,并且 a 13是等比数列{b n }的相邻三项,若b 2 =5,则 b n 等于(D ) A . 5 (5)n 丄C .3 n _L 3 c )n53n学习必备2 2153 .对于实数x ,用[x]表示不超过x 的最大整数,如】0.32] =0, [5.68] =5.若n 为正整数,列{a n }的前n 项和,则s 3n 2= .引5 3 4 5 6 7 8 9 10 11 12 13 14 1516 1724 •某资料室在计算机使用中,如下表所示, 编码以一定规则排列,且从左至右以及从上到下都是无限的.此表中,主对角线上数列1,2, 5,10,17,…的通项公式为 __________;编码100共出现 __________ 次.n 2-2n 2; 65.对正整数n ,设抛物线y 2 =2(2n +1)x ,过P(2n,0)任作直线I 交抛物线于 A n , &两点,则数列{OAl O B n }的前n 项和为n‘ 2(n +1)'-n(n T)n 都有 S + S2+ 亠 S n =丄S 成立.a 1 - 2 a 2 : 2 a n ^2 4(1)求证:S JafSg N *);⑵求数列{S n }的通项公式;4 2证T n <1. (S n =n(n ・ 1)) 9.已知数列{ a n }的通项公式为a n =常-5 (瞬数 ),求数列{ a n }的前n 项的和S n . 【解析】当n 为偶数2k(k 邛*)时,有S 2k =佝■日3亠亠a 2k 丄)■ (a ? ■日4亠Pk), .1 6 (1k A 1) 2 , 1 6(1 k A 1) =(k • & ( - 1) )6k —5k •15 152将k 』代入,得S ^3n _ _5n 芒n ,n 2 215当 n 为奇数 2k -1(k • N *)时,有瓦丄^S^「a2k=6k 2-5kJ6169 _42k =6k 2 -5k16 161715将k 工1代入得Sn 二3n2 +n —2丄军丄―16.11 1 1 1 1 123456 1 3 57 9 11 1 4 7 10 13 16 1 5 9 13 17 21 1611162126{a n }的通 (C )6.设各项均为正数的数列{a n }的前n 项和为S,,对于任意的正整数(3)记数列{丄}的前S 1n 项和为T n ,求项公式是a n =(q -1) q n1:②{a n}是等比数列;③当1时,S n S n 2 :::S;1.其中正确结论的个数是学习必备2215。
数列不等式知识点归纳总结

数列不等式知识点归纳总结数列不等式是数学中重要的一个分支,它与数列和不等式的结合使我们可以更深入地理解和解决实际问题。
在这篇文章中,我将对数列不等式的相关知识点进行归纳总结,希望能帮助读者更好地理解和应用数列不等式。
1. 数列的概念首先,我们需要了解数列的基本概念。
数列是按照一定的顺序排列的一组数,可以用常数项或通项公式来表示。
数列常用的表示方法有:通项公式、递推式和列表法。
通项公式表示第n项与n的关系,递推式表示后一项与前一项的关系,而列表法则将所有项罗列出来。
2. 数列不等式的性质数列不等式有一些基本的性质,对于求解不等式问题非常有用。
(1)同号性质:对于给定的数列,如果数列中相邻两项的差值同号,即大于零或小于零,那么这个数列就是同号数列。
(2)双边性质:对于同号数列,如果将数列中的每一项都乘以一个正数或负数,不等号的方向保持不变。
(3)单调性:对于数列a1, a2, a3, ...,如果对于任意的n,有an≤an+1或an≥an+1,则这个数列是递增数列或递减数列。
3. 数列不等式的解法接下来,我们将介绍一些常见的数列不等式的解法。
(1)柯西不等式:柯西不等式是指对于任意的实数ai和bi,有(a1b1 + a2b2 + ... + anbn)² ≤ (a₁² + a₂² + ... + an²) × (b₁² + b₂² + ... + bn²)。
柯西不等式在计算机科学、金融等领域有很广泛的应用。
(2)排序不等式:对于给定的数列,在求解不等式问题时,可以将数列按照大小顺序排序,然后根据排序后的数列性质来进行分析和推导。
(3)图形法:对于一些复杂的数列不等式问题,可以利用图形来进行辅助推导和分析。
例如,通过作图可以更直观地观察数列的趋势和规律,从而找到解决问题的方法。
4. 数列不等式的应用数列不等式的应用非常广泛,可以涉及到各个领域。
数列不等式知识点

数列1、数列:按照一定次序排列起来的一列数叫做数列.2、数列的项:数列中的每一个数叫做这个数列的项.3、有穷数列:项数有限的数列.4、无穷数列:项数无限的数列.5、递增数列:从第2项起,每一项都不小于它的前一项的数列.10n n a a +->6、递减数列:从第2项起,每一项都不大于它的前一项的数列.10n n a a +-<7、常数列:各项相等的数列.8、数列的通项:数列的第n 项n a 叫做数列的通项.9、数列的通项公式:表示数列{}n a 的第n 项与序号n 之间的关系的公式.10、等差数列:如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,则这个数列称为等差数列,这个常数称为等差数列的公差.即:若数列}{),(}{1n n n n a d a a a 则常数满足=-+称等差数列11、等差中项:由三个数a ,A ,b 组成的等差数列可以看成最简单的等差数列,则A 称为a 与b 的等差中项,记为A b a 2=+.12、等差数列的通项公式:若等差数列{}n a 的首项是1a ,公差是d ,则()11n a a n d =+-.13、等差数列的性质:设等差数列,,,,,:}{321n n a a a a a (1);23121 =+=+=+--n n n a a a a a a(2)若m n p q +=+w 2=(w 、m 、n 、p 、*q ∈N ),则m n p q a a a a +=+w a 2= (3)()n m a a n m d =+- (m 、n 都是正整数)(4)若)也成等差数列。
(成等差数列,则*,,,,,,N n p m a a a n p m n p m ∈ (5)数列}{b a n +λ,}{n n b a ±也是等差数列(其中λ、b 是常数,{n b }是等差数列) 14、等差数列的前n 项和的公式:①()12n n n a a S +=;②()112n n n S na d -=+.15、等比数列:如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,则这个数列称为等比数列,这个常数称为等比数列的公比.即:若数列q a a a nn n =+1}{满足(常数且不为零),则}{n a 称等比数列 注:等比数列中每一项都不为零。
专题复习六必修五《数列与不等式》知识要点

《等比数列与不等式》知识要点一.数列的概念与简单表示法.(1)数列是定义域为(或它的有限子集{1,2,…,n})的特殊函数,(2)数列的表示方法:解析法(通项公式法);列表法;图象法;递推法(递推公式法).(3)a n与S n的关系式:a n=二.等差数列(1)定义:.((2)公差为d的等差数列{a n}的通项公式:,等差数列中任意两项的关系:. 即:d =(3)等差中项:若a,A,b成等差数列,则A叫做a与b的等差中项,可表示成.(4)前n项和公式S n==.(5)等差数列的判断:定义法:等差中项法:<通项公式法:形如求和公式法:形如(6)等差数列的性质①若公差,则{a n}是递增等差数列;若公差 ,则{a n }是递减等差数列; 若 ,则{a n }是常数列.②若m +n =p +q (m ,n ,p ,q ∈N *),则 .%若m +n =2p (m ,n ,p ∈N *),则③若{a n }是等差数列,则S n ,S 2n -S n , ,…仍成等差数列,公差(7) 若{a n }是等差数列,S n 是{a n }的前n 项的和,T n 是{|a n |}的前n 项的和,若0n a 是正负项的分界项,它与1a 的符号一致。
前正后负:T n = ; 前负后正:T n = (8)等差数列前n 项和的最值 ①等差数列{a n }中,[a 1>0,d <0时,S n 有 ;a 1 ,d ,S n 有最小值. ②最值的求法配方或求二次函数最值的方法:等差数列{a n }前n 项和公式S n =na 1+nn -12d =d 2n 2+(a 1-d 2)n =An 2+Bn ,可通过 求得. 邻项变号法:.}当a 1>0,d <0时,满足 的n ,使S n 取最大值;当a1<0,d>0时,满足的n,使S n取最小值.三.等比数列(1)定义:(q为常数,且q≠0).(2)公比为q(q≠0)的等比数列{a n}的通项公式:,'等比数列中任意两项的关系:.(3)等比中项:若a,G,b成等比数列,则G叫做a与b的等比中项,可以表示成.(4)前n项和公式S n=(5)等比数列的判断: 定义法:等差中项法:&通项公式法:形如求和公式法:形如S n=(6)等比数列的性质①若m+n=p+q(m,n,p,q∈N*),则;若m+n=2(m,n,p∈N*),则;②若{a n}是等比数列,则S n,,,…仍成等比数列(当S n≠0时),且公比为(q≠-1).③如果{a n},{b n}均为等比数列,且公比分别为q1,q2,·那么数列⎩⎨⎧⎭⎬⎫1a n ,{ka n }(k ∈R ,且k ≠0),{a n ·b n },⎩⎨⎧⎭⎬⎫b n a n ,{|a n |}仍是等比数列,且公比分别为 , , , , .(7)在等比数列{a n }中,若q >0,则{a n }中的项 ;若q >0,则{a n }中的项的符号(8) 在等比数列{a n }中,q =1时,{a n }是 。
数列与不等式(解析版)
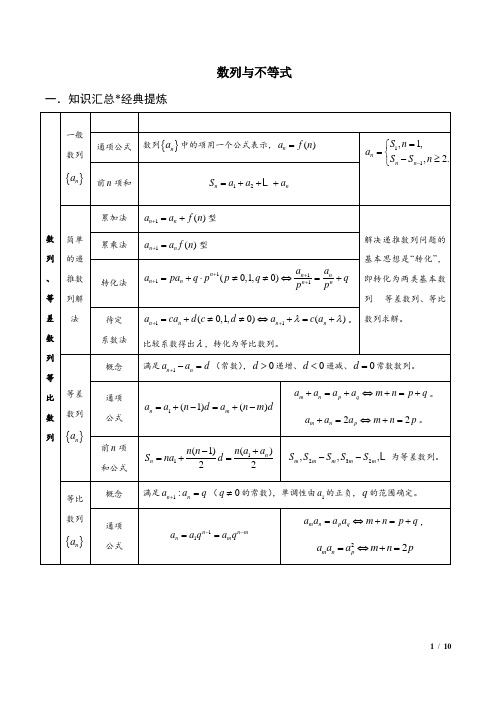
数列与不等式一.知识汇总*经典提炼二.核心解读*方法重温1.已知数列的前n 项和S n 求a n ,易忽视n =1的情形,直接用S n -S n -1表示.事实上,当n =1时,a 1=S 1;当n≥2时,a n =S n -S n -1.[回扣问题1] 在数列{a n }中,a 1+a 22+a 33+…+a nn=2n -1(n ∈N *),则a n =________.解析 依题意得,数列⎩⎨⎧⎭⎬⎫a n n 的前n 项和为2n -1,当n≥2时,a n n=(2n -1)-(2n -1-1)=2n -1,又a 11=21-1=1=21-1,因此a n n =2n -1(n ∈N *), 故a n =n·2n -1. 答案 n·2n -12.等差数列中不能熟练利用数列的性质转化已知条件,并灵活整体代换进行基本运算.如等差数列{a n }与{b n }的前n 项和分别为S n 和T n ,已知S n T n =n +12n +3,求a n b n时,无法正确赋值求解.[回扣问题2] 等差数列{a n },{b n }的前n 项和分别为S n ,T n ,且S n T n =3n -12n +3,则a 8b 8=________.解析a 8b 8=2a 82b 8=a 1+a 15b 1+b 15=S 15T 15=3×15-12×15+3=43. 答案 433.运用等比数列的前n 项和公式时,易忘记分类讨论.一定分q =1和q≠1两种情况进行讨论.[回扣问题3] 等比数列{a n }的各项均为实数,其前n 项和为S n ,已知S 3=74,S 6=634,则a 8=________.解析 设数列{a n }的公比为q ,若q =1, 则S 6=2S 3与题设矛盾,∴q≠1.则⎩⎪⎨⎪⎧S 3=a 1(1-q 3)1-q=74,S 6=a 1(1-q 6)1-q=634,解得⎩⎪⎨⎪⎧a 1=14,q =2,所以a 8=a 1q 7=14×27=32.答案 324.利用等差数列定义求解问题时,易忽视a n -a n -1=d(常数)中,n≥2,n ∈N *的限制,类似地,在等比数列中,b nb n -1=q(常数且q≠0),忽视n≥2,n ∈N *的条件限制. [回扣问题4] 已知数列{a n }中,a 1=a 2=1,a n +1=a n +12(n≥2),则数列{a n }的前9项和等于________.解析 由a 2=1,a n +1=a n +12(n≥2),∴数列{a n }从第2项起是公差为12的等差数列,∴S 9=a 1+a 2+a 3+…+a 9 =1+8a 2+8(8-1)2×12=23.答案 235.利用错位相减法求和,切忌漏掉第一项和最后一项;裂项相消求和,相消后剩余的前、后项数要相等. [回扣问题5] 已知等差数列{a n }的前n 项和为S n ,a 3=6,S 4=20. (1)求数列{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫1S n 的前n 项和T n .解 (1)设数列{a n }的公差为d , 由a 3=6,S 4=20,得⎩⎪⎨⎪⎧a 1+2d =6,2a 1+3d =10,解得⎩⎪⎨⎪⎧a 1=2,d =2, 因此a n =2+2(n -1)=2n.(2)由(1)知S n =(2+2n )n 2=n(n +1),从而1S n =1n (n +1)=1n -1n +1∴T n =⎝⎛⎭⎫1-12+⎝⎛⎭⎫12-13+…+⎝⎛⎭⎫1n -1n +1=1-1n +1=nn +1. 6.对于通项公式中含有(-1)n 的一类数列,在求S n 时,切莫忘记讨论n 为奇数、偶数;遇到已知a n +1-a n -1=d 或a n +1a n -1=q(n≥2),求{a n }的通项公式时,要注意对n 的讨论.[回扣问题6] 若a n =2n -1,b n =(-1)n -1a n ,则数列{b n }的前n 项和T n =________. 解析 b n =(-1)n -1a n =(-1)n -1(2n -1).当n 为偶数时,T n =a 1-a 2+a 3-a 4+…+a n -1-a n =(-2)×n2=-n.当n 为奇数时,T n =T n -1+b n =-(n -1)+a n =n.故T n =⎩⎪⎨⎪⎧-n ,n 为偶数,n ,n 为奇数.答案 ⎩⎪⎨⎪⎧-n ,n 为偶数,n ,n 为奇数7.解形如ax 2+bx +c>0的一元二次不等式时,易忽视系数a 的讨论导致漏解或错解,要注意分a>0,a<0,a =0进行讨论.[回扣问题7] 设命题甲:ax 2+2ax +1>0的解集是实数集R ;命题乙:0<a<1,则命题甲是命题乙成立的( ) A.充分不必要条件 B.充要条件C.必要不充分条件D.既不充分也不必要条件解析 由命题甲:ax 2+2ax +1>0的解集是实数集R 可知,当a =0时,原式=1>0恒成立,当a≠0时,需满足⎩⎪⎨⎪⎧a>0,Δ=(2a )2-4a<0,解得0<a<1,所以0≤a<1,所以由甲不能推出乙,而由乙可推出甲,因此命题甲是命题乙成立的必要不充分条件. 答案 C8.容易忽视使用基本不等式求最值的条件,即“一正、二定、三相等”导致错解,如求函数f(x)=x 2+2+1x 2+2的最值,就不能利用基本不等式求解最值. [回扣问题8] 若直线x a +yb =1(a>0,b>0)过点(1,2),则2a +b 的最小值为________.解析 依题意1a +2b =1(a>0,b>0),∴2a +b =(2a +b)⎝⎛⎭⎫1a +2b =4+b a +4ab ≥8, 当且仅当b a =4ab ,即a =2,b =4时,取等号.故2a +b 的最小值为8. 答案 89.求解线性规划问题时,不能准确把握目标函数的几何意义导致错解,如y -2x +2是指已知区域内的点(x ,y)与点(-2,2)连线的斜率,而(x -1)2+(y -1)2是指已知区域内的点(x ,y)到点(1,1)的距离的平方等. [回扣问题9] 若变量x ,y 满足⎩⎪⎨⎪⎧x +y≤2,2x -3y≤9,x≥0,则x 2+y 2的最大值是( )A.4B.9C.10D.12解析 满足条件⎩⎪⎨⎪⎧x +y≤2,2x -3y≤9,x≥0的可行域如图阴影部分(包括边界)所示,x 2+y 2是可行域上的动点(x ,y)到原点(0,0)距离的平方,显然,当x =3,y =-1时,x 2+y 2取得最大值,最大值为10.答案 C10.求解不等式、函数的定义域、值域时,其结果一定要用集合或区间表示,另外一元二次不等式的解集表示形式受到二次项系数符号的影响.[回扣问题10] 已知关于x 的不等式ax 2+bx +c<0的解集是⎩⎨⎧⎭⎬⎫x ⎪⎪x<-2,或x>-12,则ax 2-bx +c>0的解集为________.解析 ∵ax 2+bx +c<0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x<-2,或x>-12, ∴a<0,且c a =1,-b a =-52,∴b =52a ,c =a ,故ax 2-bx +c>0化为ax 2-52ax +a>0,由于a<0,得x 2-52x +1<0,解得12<x<2.答案 ⎝⎛⎭⎫12,2三.新题好题*保持手感1.(2020·涡阳县第九中学高三三模)已知数列{}n a 的前n 项和()2*23n S n n n N=+∈,则{}na 的通项公式为( ) A .21n a n =+ B .21n a n =- C .41n a n =+ D .41n a n =-【答案】C【解析】因为223n S n n =+,所以,当2n ≥时,22123[2(1)3(1)]41n n n a S S n n n n n -=-=+--+-=+,当1n =时,11235==+=a S ,上式也成立, 所以41n a n =+,故选C.2.(2020·湖南省长郡中学高三三模)若两个等差数列{}n a 、{}n b 的前n 项和分别为n A 、n B ,且满足2131n n A n B n -=+,则371159a a ab b +++的值为( ) A .3944B .58C .1516D .1322【答案】C【解析】11337117131135971313()3333213115213()22223131162a a a a a a A b b b b b B +++⨯-==⨯=⨯=⨯=++⨯+, 故选:C.3.(2020·曲靖市第二中学高三二模)等比数列{}n a 的前n 项和为n S ,若22S =,36S =-,则5S =( ) A .18 B .10C .-14D .-22【答案】D【解析】设等比数列{}n a 的公比为q ,显然1q ≠,由求和公式可得()212121a q S q-==-①,()313161a q S q-==--②②①可得3221163112q q q q q -++-===--+,解得2q =-, 代回①可得12a =-,()()()55152********a q S q⎡⎤----⎣⎦∴===----,故选D .4.(2020·全国高三三模)已知等差数列{}n a 的前n 项和为n S ,满足33a =,()21223n n n S S S n --+=+≥,则( )A .2n n S na n -= B .2n n S na n +=C .21n n S a n-=D .21n n S a n+=【答案】B【解析】由已知得31222S S S +=+,即123222222a a a a a ++=++, 所以2321a a =-=,则公差322d a a =-=, 所以()33223n a a n n =+-⨯=-,即11a =-,()()1122n n n n a a n a S +-==,得2n nS na n +=.故选:B. 5.(2020·海口市第四中学高三三模)当x ∈R 时,不等式210kx kx -+>恒成立,则k 的取值范围是( ) A .(0,)+∞ B .[)0,+∞C .[)0,4D .(0,4)【答案】C【解析】当0k =时,不等式210kx kx -+>可化为10>,显然恒成立;当0k ≠时,若不等式210kx kx -+>恒成立,则对应函数的图象开口朝上且与x 轴无交点,则240k k k >⎧⎨=-<⎩V 解得:04k <<,综上k 的取值范围是[)0,4,故选C.6.(2020·甘肃省张掖市第二中学高三三模)若直线l :20(0,0)ax by a b -+=>>过点(1,2)-,当21a b+取最小值时直线l 的斜率为( ) A .2 B .12CD .【答案】A【解析】因为直线l 过点()1,2-,所以220a b --+=,即212a b+=,所以21212141()(4)(44222a b b a a b a b a b ++=+=++≥+=g 当且仅当4b aa b =,即2a b =时取等号 所以斜率2ab=,故选A7.(2020·安徽省高三二模)已知数列{}n a 、{}n b 、{}n c 中,11a =,1121n n n a a +=+-,1n n b n a =+,11n n nc a b =-. (1)求证:数列{}n b 是等比数列,并求数列{}n a ,{}n b 的通项公式; (2)求数列{}n c 的前n 项和n S . 【答案】(1) 12n n a n =-,2nn b =.(2) 222nnn S +=- 【解析】(1)因为1121n n n a a +=+-,故1121122n n n n n n a a a +⎛⎫++=+=+ ⎪⎝⎭,即12n n b b +=,故{}n b 是以1112a +=为首项,2为公比的等比数列.故2n n b =. 所以1122n n n n n a a n +=⇒=-. 故12n na n=-,2n n b =. (2)由(1) 12112222n n n n nn n nc n-=-=-=-.所以123123...2222n nS n=++++23411231 (22222)12n n n n n S +-=+++++ 相减可得123411111111...2222222n n n n S +⎛⎫- ⎪⎝⎭=+++++- 故111122111222n n n n S +⎛⎫- ⎪⎝⎭=--,1112122n n nS n +=--.化简得222n n n S +=-8.(2020·山东省高三二模)已知数列{}n a 的前n 项和为0121n n n n n n S C C C C -=++++L ,数列{}n b 满足2log n n b a =,(1)求数列{}n a 、{}n b 的通项公式;(2)求()12222212341n n nT b b b b b +=-+-++-L . 【答案】(1)12n n a -=;1n b n =-(2)22,2,2n n n n T n n n ⎧-⎪⎪=⎨-⎪⎪⎩为偶数为奇数 【解析】(1)012121n nn n n n n S C C C C -=++++=-L ,当2n ≥时,112n n n n a S S --=-=,当1n =时,11a =也满足12n n a -=,所以12n n a -=,又数列{}n b 满足2log n n b a =,所以1n b n =-.(2)当2n k =,*k N ∈时,()()()2222221234212n k k T b b b b b b -=-+-++-L()122k b b b =-+++L ()()1221k ⎡⎤=-+++-⎣⎦L 22k k =-+;当21n k =-,*k N ∈时,()()()22222221234232221n k k k T b b b b b b b ---=-+-++-+L()()()2122341k k ⎡⎤=-+++-+-⎣⎦L 2231k k =-+.所以()()222,2231,21n k k n k T k k n k ⎧-+=⎪=⎨-+=-⎪⎩,*k N ∈,即22,2,2n n n n T n n n ⎧-⎪⎪=⎨-⎪⎪⎩为偶数为奇数.。
数列与不等式的综合-高中数学知识点讲解

数列与不等式的综合1.数列与不等式的综合【知识点的知识】证明与数列求和有关的不等式基本方法:(1)直接将数列求和后放缩;(2)先将通项放缩后求和;(3)先将通项放缩后求和再放缩;(4)尝试用数学归纳法证明.常用的放缩方法有:2푛1 12푛―12푛2푛+12푛<,2푛+12푛2푛―1>,2푛+1<2푛,11푛3<푛(푛2―1)=112[푛(푛―1)―1푛(푛+1)]1푛―1푛+1=111푛(푛―1)=푛(푛+1)<푛2<1푛―1―1(n≥2),푛11푛2<푛2―1=11(푛―1―21)(n≥2),푛+11푛2=4414푛2<4푛2―1=2(2푛―1―4푛2―1=2(2푛―1―12푛+1),2(푛+1―푛)=2푛+1―푛<1푛=22푛<2푛+푛―1= 2(푛―푛―1).1푛+1+1푛+2+⋯+12푛≥12푛+12푛+⋯+12푛=푛2푛=12푛+(푛+1)푛(푛+1)<.2【解题方法点拨】证明数列型不等式,因其思维跨度大、构造性强,需要有较高的放缩技巧而充满思考性和挑战性,能全面而综合地考查学生的潜能与后继学习能力,因而成为高考压轴题及各级各类竞赛试题命题的极好素材.这类问题的求解策略往往是:通过多角度观察所给数列通项的结构,深入剖析其特征,抓住其规律进行恰当地放缩;其放缩技巧主要有以下几种:1/ 4(1)添加或舍去一些项,如: 푎2 + 1>|a |; 푛(푛 + 1)>n ;(2)将分子或分母放大(或缩小);푛 + (푛 + 1)(3)利用基本不等式; 푛(푛 + 1)<;2(4)二项式放缩;(5)利用常用结论;(6)利用函数单调性.(7)常见模型:①等差模型;②等比模型;③错位相减模型;④裂项相消模型;⑤二项式定理模型;⑥基本不等式模型.【典型例题分析】题型一:等比模型푎1 ― 1 典例 1:对于任意的 n ∈N *,数列{a n }满足 21 + 1 +푎2 ― 2 22 + 1 +⋯ + 푎푛 ― 푛 2푛 + 1 = n +1. (Ⅰ)求数列{a n }的通项公式;2 (Ⅱ)求证:对于 n ≥2, 푎2 +2 푎3 +⋯ + 2 푎푛+1<1 ― 1 2푛. 푎1 ― 1 解答:(Ⅰ)由 21 + 1 +푎2 ― 2 22 + 1 +⋯ + 푎푛 ― 푛 2푛 + 1 = 푛 + 1①, 푎1 ― 1 当 n ≥2 时,得 21 + 1 +푎2 ― 2 22 + 1 +⋯ + 푎푛―1 ― (푛 ― 1) 2푛―1 + 1 = 푛②, 푎푛― 푛 ①﹣②得2푛 + 1 = 1(푛 ≥ 2).∴푎푛= 2푛 +1 + 푛(푛 ≥ 2). 푎1 ― 1又 1=7 不适合上式.21 + 1 = 2,得 a综上得푎푛= {7 ,푛 = 12푛 + 1 + 푛,푛 ≥ 2;2 (Ⅱ)证明:当 n ≥2 时,푎푛 =2 2 2푛 + 1 + 푛< 2푛 = 1 2푛―1.2/ 42 ∴ 푎2 + 2 푎3 +⋯ + 2 1 2 + 푎푛+1< 1 22 +⋯ + 1 2푛 = 1 1 2 (1 ― 2푛 1 ― 1 2) = 1 ― 1 2푛. 2 ∴当 n ≥2 时,푎2 + 2 푎3 +⋯ + 2 푎푛+1<1 ―1 2푛. 题型二:裂项相消模型典例 2:数列{a n }的各项均为正数,S n 为其前 n 项和,对于任意 n ∈N *,总有 a n ,S n ,a n 2 成等差数列.(1)求数列{a n }的通项公式;(2)设푏푛 = 1 푛푎2푛,数列{b n }的前 n 项和为 T n ,求证:푇푛> 푛 + 1.分析:(1)根据 a n =S n ﹣S n ﹣1,整理得 a n ﹣a n ﹣1=1(n ≥2)进而可判断出数列{a n }是公差为 1 的等差数列,根 据等差数列的通项公式求得答案.(2)由(1)知푏푛 = 1 1 1 푛2,因为 푛(푛 + 1) = 푛2> 1 푛 ―1 1 ,所以푏푛> 푛 ―푛 + 11,从而得证. 푛 + 1 解答:(1)由已知:对于 n ∈N *,总有 2S n =a n +a n 2①成立∴2푆푛―1 = 푎푛―1 + 푎푛―12(n ≥2)②①﹣②得 2a n =a n +a n 2﹣a n ﹣1﹣a n ﹣12,∴a n +a n ﹣1=(a n +a n ﹣1)(a n ﹣a n ﹣1)∵a n ,a n ﹣1 均为正数,∴a n ﹣a n ﹣1=1(n ≥2)∴数列{a n }是公差为 1 的等差数列又 n =1 时,2S 1=a 1+a 12,解得 a 1=1,∴a n =n .(n ∈N *)(2)解:由(1)可知푏푛 = 1 1 1 푛2∵ 푛(푛 + 1) = 푛2>푛2∵ 푛(푛 + 1) =1 푛 ― 1 푛 + 1 ∴푇푛>(1 ― 1 1 2) + (2 ― 1 1 3) + +(푛 ―1 푛 + 1) = 푛 푛 + 1 【解题方法点拨】(1)放缩的方向要一致.(2)放与缩要适度.(3)很多时候只对数列的一部分进行放缩法,保留一些项不变(多为前几项或后几项).3/ 4(4)用放缩法证明极其简单,然而,用放缩法证不等式,技巧性极强,稍有不慎,则会出现放缩失当的现象.所以对放缩法,只需要了解,不宜深入.4/ 4。
数列与不等式(有答案)

数列与不等式1. 不等式的解集是B. C. D.2. 已知实数,满足,则的最大值为.3. 已知,,,则的最小值为.4. 若,,且,则的最小值为.5. 记等差数列的前项和为.若,,,则正整数.6. 设是等差数列的前项和,,,则.7. 已知在各项都为正数的等比数列中,若首项,,则的值为.8. 设等比数列的前项和为,若,则.9. 若正实数,满足,则的最小值是.10. 设两个等差数列和的前项和分别为和,且,则.11. 已知为锐角,且.(1)求的值;(2)求的值.12. 在中,内角,,的对边分别为,,.已知.(1)求的值;(2)若,,求的面积.13. 为数列的前项和,已知,.(1)求的通项公式;(2)设,求数列的前项和.14. 设数列的前项和为.已知.(1)求的通项公式;(2)若数列满足,求的前项和.答案第一部分1. D 【解析】由,得,即.所以原不等式等价于即所以所以原不等式的解集是.第二部分4.5.【解析】因为,,所以公差.又因为,所以,所以.6.【解析】由题意得整理得解得所以7.【解析】由,,得由,解得,从而8.【解析】设等比数列的首项为,公比为,由,得,即,所以.9.【解析】根据题意,,满足,则即的最小值是.10.【解析】由题意,可设,,则,,所以.第三部分11. (1)已知为锐角,所以,由得,解得或,由为锐角,得.(2)且为锐角,,.故12. (1)由正弦定理得,,,所以,即,即有,即,所以.(2)由知:,即,又因为,所以由余弦定理得:,即,解得,所以,又因为,所以,故的面积为.13. (1)由题意得,所以.两式相减整理得.又,所以.又由得(负值舍去).所以是首项为,公差为的等差数列,故.(2)由(1)知.于是数列的前项和14. (1)因为,所以,故.当时,,此时,即,所以(2)因为,所以.当时,.所以;当时,,所以,两式相减,得所以.经检验,时也适合.综上可得.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列与不等式一、看数列是不是等差数列有以下三种方法:①),2(1为常数d n d a a n n ≥=--②211-++=n n n a a a (2≥n )③b kn a n +=(k n ,为常数). 二、看数列是不是等比数列有以下两种方法:①)0,,2(1≠≥=-且为常数q n q a a n n ②112-+⋅=n n n a a a (2≥n ,011≠-+n n n a a a )(2)在等差数列{n a }中,有关S n 的最值问题:(1)当1a >0,d<0时,满足⎩⎨⎧≤≥+001m m a a 的项数m 使得m s 取最大值. (2)当1a <0,d>0时,满足⎩⎨⎧≥≤+01m m a a 的项数m 使得m s 取最小值.在解含绝对值的数列最值问题时,注意转化思想的应用。
四.数列通项的常用方法:(1)利用观察法求数列的通项.(2)利用公式法求数列的通项:①;②{}n a 等差、等比数列{}n a 公式.(3)应用迭加(迭乘、迭代)法求数列的通项:①;②(4)造等差、等比数列求通项:;②;③;④.第一节通项公式常用方法题型1 利用公式法求通项例1:1.已知{a n }满足a n+1=a n +2,而且a 1=1。
求a n 。
2.已知为数列{}n a 的前项和,求下列数列{}n a 的通项公式: ⑴ ;⑵.总结:任何一个数列,它的前项和n S 与通项n a 都存在关系:⎩⎨⎧≥-==-)2()1(11n S S n S a n n n 若1a 适合n a ,则把它们统一起来,否则就用分段函数表示. 题型2 应用迭加(迭乘、迭代)法求通项例2:⑴已知数列{}n a 中,,求数列{}n a 的通项公式;⑵已知为数列{}n a 的前项和,,,求数列{}n a 的通项公式.总结:⑴迭加法适用于求递推关系形如“”; 迭乘法适用于求递推关系形如““;⑵迭加法、迭乘法公式:①⎩⎨⎧≥-==-)2()111n S S n S a n n n ()(1n f a a n n +=+).(1n f a a n n =+q pa a n n +=+1n n n q pa a +=+1)(1n f pa a n n +=+n n n a q a p a ⋅+⋅=++12n S n 1322-+=n n S n 12+=nn S n )2(12,211≥-+==-n n a a a n n n S n 11=a n n a n S ⋅=2)(1n f a a n n +=+)(1n f a a n n ⋅=+11232211)()()()(a a a a a a a a a a n n n n n n n +-++-+-+-=-----② . 题型3 构造等比数列求通项例3已知数列{}n a 中,,求数列{}n a 的通项公式. 总结:递推关系形如“” 适用于待定系数法或特征根法: ①令;② 在中令,;③由得,. 例4已知数列{}n a 中,,求数列{}n a 的通项公式.总结:递推关系形如“”通过适当变形可转化为:“”或“求解.数列求和的常用方法一公式法:适用于等差、等比数列或可转化为等差、等比数列的数列。
利用下列常用求和公式求和是数列求和的最基本最重要的方法. 1、 等差数列求和公式: 2、等比数列求和公式: 3.4、 5.二.裂项相消法:适用于其中{ }是各项不为0的等差数列,c 为常数;部分无理数列、含阶乘的数列等。
例2 求数列的前n 项和这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)如:1122332211a a a a a a a a a a a a n n n n n n n ⋅⋅⋅⋅⋅⋅=----- 32,111+==+n n a a a q pa a n n +=+1)(1λλ-=-+n n a p a q pa a n n +=+1pqx x a a n n -=⇒==+11∴)(1x a p x a n n -=-+q pa a n n +=+1q pa a n n +=-1∴)(11-+-=-n n n n a a p a a nn n a a a 32,111+==+nn n q pa a +=+1q pa a n n +=+1nn n n f a a )(1+=+d n n na a a n S n n 2)1(2)(11-+=+=⎪⎩⎪⎨⎧≠--=--==)1(11)1()1(111q q q a a qq a q na S n nn )1(211+==∑=n n k S nk n )12)(1(6112++==∑=n n n k S nk n 213)]1(21[+==∑=n n k S nk n ⎭⎬⎫⎩⎨⎧+1n n a a c n a )1(n 1+n(1)(2))121121(211)12)(12()2(2+--+=+-=n n n n n a n (3)])2)(1(1)1(1[21)2)(1(1++-+=+-=n n n n n n n a n三.错位相减法:可以求形如的数列的和,其中为等差数列,为等比数列.例1:求和:. 例2:数列1,3x ,5x 2,…,(2n-1)xn-1前n 项的和.小结:错位相减法类型题均为:nna b 等差数列等比数列连续相加。
四.常用结论1)1+2+3+...+n =2)1(+n n 2) 1+3+5+...+(2n-1) =2n 3)2333)1(2121⎥⎦⎤⎢⎣⎡+=+++n n n 4))12)(1(613212222++=++++n n n n 5)111)1(1+-=+n n n n )211(21)2(1+-=+n n n n重要不等式1、和积不等式:(当且仅当时取到“”).【变形】:①(当a = b 时,) 【注意】, 2、均值不等式:两个正数的调和平均数、几何平均数、算术平均数、均方根之间的关系,即“平方平均算术平均几何平均调和平均” *.若0x >,则12x x +≥ (当且仅当1x =时取“=”);若0x <,则12x x+≤- (当且仅当1x =-时取“=”)若0x ≠,则11122-2x x x xxx+≥+≥+≤即或 (当且仅当b a =时取“=”)111)1(1+-=+=n n n n a n ,a b R ∈⇒222a b ab +≥a b ==222()22a b a b ab ++≤≤222()22a b a b ab ++==(,)2a ba b R ++∈2()(,)2a b ab a b R +∈≤b a 、≥≥≥22“”112ab a b a b a b a b+===++时取)*.若0>ab ,则2≥+ab ba (当且仅当b a =时取“=”)若0ab ≠,则22-2a b a b a bb a b a b a+≥+≥+≤即或 (当且仅当b a =时取“=”) 3、含立方的几个重要不等式(a 、b 、c 为正数):(,); *不等式的变形在证明过程中或求最值时,有广泛应用,如:当0>ab 时,ab b a 222≥+同时除以ab 得2≥+b a a b 或baa b -≥-11。
*,,b a 均为正数,b a ba -≥22八种变式:①222b a ab +≤;②2)2(b a ab +≤;③2)2(222b a b a +≤+ ④)(222b a b a +≤+;⑤若b>0,则b a ba -≥22;⑥a>0,b>0,则b a b a +≥+411;⑦若a>0,b>0,则ab b a 4)11(2≥+;⑧若0≠ab ,则222)11(2111b a ba +≥+。
上述八个不等式中等号成立的条件都是“b a =”。
放缩不等式:①,则. 【说明】:(,糖水的浓度问题). 【拓展】:. ②,,则; ③; ④,. ⑤,函数()(0)bf x ax a bx=+>、图象及性质 (1)函数()0)(>+=b a xbax x f 、图象如图:3333a b c abc ++≥0a b c ++>等式即可成立时取等或0=++==c b a c b a 3a b c ++⇒3()3a b c abc ++≤3333a b c ++≤00a b a m >>>>,b m b b ma m a a m-+<<-+b b m a a m+<+0,0a b m >>>,则,,000>>>>n m b a ban b n a m a m b a b <++<<++<1,,a b c R +∈b d a c <b b d d a a c c+<<+n N +∈<<,1n N n +∈>21111111n n n n n-<<-+-ln 1x x -≤(0)x >1xe x +≥()x R ∈(2)函数()0)(>+=b a xbax x f 、性质: ①值域:),2[]2,(+∞--∞ab ab ;②单调递增区间:(,-∞,)+∞;单调递减区间:,[0) 最值定理(积定和最小)①,则当时和有最小值(和定积最大)②,则当是积有最大值. 【推广】:已知,则有.(1)若积是定值,则当最大时,最大;当最小时,最小.(2)若和是定值,则当最大时,最小;当最小时,最大.③已知,若,则有则的最小值为:④已知,若则和的最小值为:②.②应用基本不等式求最值的“八种变形技巧”:⑴凑系数(乘、除变量系数).例1.当时,求函的数最大值.⑵凑项(加、减常数项):例2.已知,求函数的最大值. ⑶调整分子:例3.求函数的值域; ⑷变用公式:基本不等式有几个常用变形,,不易想到,应重视; 例4.求函数的最大值;,0,x y x y >+≥由()xy P =定值x y =x y +,0,x y x y >+≥由()x y S +=定值x y =xy 214s R y x ∈,xy y x y x 2)()(22+-=+xy ||y x -||y x +||y x -||y x +||y x +||y x -||xy ||y x -||xy ,,,R a x by +∈1ax by +=21111()())by ax ax bya b a b ab a b x y x y x y+=++=+++++=≥04x <<(82)y x x =-54x <1()4245f x x x =-+-2710()(1)1x x f x x x ++=≠-+2a b +≥2a b+≥222()22a b a b ++≥15()22y x =<<⑸连用公式:例5.已知,求的最小值;⑹对数变换:例6.已知,且,求的最大值; ⑺三角变换:例7.已知,且,求的最大值;⑻常数代换(逆用条件):例8.已知,且,求的最小值 1、数列95,74,53,32,1的一个通项公式n a 是() A 、12+n n B 、12-n n C 、32-n n D 、32+n n2、已知等比数列{}n a 的公比为正数,且24282a a a =,11=a 则()A 、B 、2C 、22D 、213、已知等差数列{}n a 前n 项和为n S 且0>n a 已知02564=-+a a a 则=9S ()A 、17B 、18C 、19D 、20 4、已知)1,0(,21∈a a ,记21a a M =,121-+=a a N 则M 与N 的大小关系() A 、M<N B 、M>N C 、M=N D 、不确定5、若011<<b a ,则下列不等式:bc a c c b c a b a ab b a 22)4(,)3(,)2(,)1(<+>+><+中正确的是() A 、(1)(2) B 、(2)(3) C 、(1)(3) D 、(3)(4)6、不等式1213≥--x x 的解集是() A 、⎭⎬⎫⎩⎨⎧≤≤243x x B 、⎭⎬⎫⎩⎨⎧<≤243x x C 、⎭⎬⎫⎩⎨⎧≤>432x x x 或 D 、{}2<x x 7、设n S 是等差数列{}n a 的前n 项和,若59355,9a Sa S ==则()A 、1B 、1-C 、2D 、128、在的条件下,,00>>b a 三个结论:①22b a b a ab +≤+,②,2222b a b a +≤+ ③b a b a a b +≥+22,其中正确的个数是()A 、0B 、1C 、2D 、39、目标函数y x z +=2,变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ,则有 ()A 、3,12min max ==z zB 、,12max =z z 无最小值C 、z z ,3min =无最大值D 、z 既无最大值,也无最小值 10、在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立,0a b >>216()y a b a b =+-1,12x y >>xy e =ln (2)y t x =20y x π<<≤tan 3tan x y =t x y =-0,0a b >>21a b +=11t a b=+=2a 2则()A 、11<<-aB 、20<<aC 、2321<<-a D 、2123<<-a 二、填空题:(每小题5分,共25分)11、等比数列{}n a 公比,0>q 已知n n n a a a a 6,1122=+=++,则{}n a 的前4项和=4S ___________ 12、 等比数列{}n a 的前n 项和n S ,又2132S S S +=,则公比=q ___________ 13、若0>x ,0>y 且12=+y x ,则xy 的最大值为___________14、实数x 、y 满足不等式组⎪⎩⎪⎨⎧≥-≥≥001y x y x ,则W=x y 1-的取值范围是_____________15、关于x 的不等式211(1)0(0)x a x a a a a-++++<>的解集为三、解答题:16、(本小题满分12分)等比数列{}n a 中,已知16,241==a a , (1)求数列{}n a 的通项公式;(2)若53,a a 分别为等差数列{}n b 的第3项和第5项,试求数列{}n b 的通项公式及前n 项和n S .17、(本小题满分12分)已知数列{}n a 的前n 项和248n S n n =-(1) 求数列{}n a 的通项公式; (2) 求n S 的最大或最小值.18、(本小题满分12分)已知向量)sin ,2(cos θθn n a n =,),)(sin 2,1(*N n n b n ∈=θ若n n a C =·n n b 2+,(1)求数列{}n C 的通项公式; (2)求数列{}n C 的前n 项和n S .19、(本小题满分12分)在数列{}n a 中,n n n a a a 22,111+==+(1)设12-=n nn a b ,证明:数列{}n b 是等差数列;(2)求数列{}n a 的前n 项和n S . 20、(本小题满分13分)某房地产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元. (Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:①年平均利润最大时以 46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案盈利更多? 21、(本小题满分14分)已知数列{}n a 满足:1112,2--==n n a a a , ,4,3,2=n , (1) 求证:数列⎭⎬⎫⎩⎨⎧-11n a 为等差数列; (2) 求数列{}n a 的通项公式; (3)令∑=+=ni i i n a a T 11,求证:43+<n T nB A B BC BADCC 二、填空题:(每小题5分,共25分) 11、215 12、21- 13、81 14、 [-1,1) 15、1(1,)a a + 三、解答题: 16、解:(1)设公比为q ,则n n n q a a q q 2,2,216113==∴=∴=------------------------6分 (2)由(1)得,32,853==a a 则12,32,853===d b b2812-=∴n b n n n S n 2262-=-----------------------(12分) 17、解:(1)当n=1时,4711-==S a当n ≥2时,4921-=-=-n S S a n n n 故492-=n a n(2)由248n S n n =-576)24(2--=n ,于是n S 有最小值是-576,此时24=n ;无最大值。
