机器人操作臂动力学

合集下载

机器人概论(2004版)7-第五章操作臂动力学

（1）动力学基本理论：包括牛顿－欧拉方程（2）拉格朗日力学：特别是拉格朗日方程
此外还有应用高斯原理、阿佩尔（Appel）方程式、旋量对偶数法和凯恩（Kane）法等来分析动力学问题的。
2009-2-20
机电研究室－李挺 (http:// )
3
机器人概论
第五章操作臂动力学
c1θ&12
+
1 2
c2θ&22
x
外力做的功W
θ
(x1, y1)
d1 m1
r2
W = T1θ1 + T2θ2
2009-2-20
机电研究室－李挺 (http:// )
θ2 d2
(x2, y2)
m2
11
机器人概论
第五章操作臂动力学
牛顿-欧拉法求解动力学方程
d dt
(
∂K
∂θ&1
2m2 d1d 2
cosθ2 ]θ&&1
+
(m2d
2 2
+
m2 d1d 2
cosθ2 )θ&&2
+
c1θ&1
− 2m2d1d2 sinθ2θ&1θ&2 − m2d1d2 sinθ2θ&22 + (m1 + m2 )gd1 sinθ1 + m2 gd2 sin(θ1 +θ2 )
T2
=
(m2
d
2 2
+
m2 d1d 2
⎤ ⎥ ⎦
⎢⎣⎡θθ&&1222
⎤ ⎥ ⎦
+
⎡ ⎢ ⎣
D112 D212

机器人学速度和静力操作臂动力学习题

第5次速度和静力、操作臂动力学加*的题目（7道）是必做题，其它（2道）题目自己选择一道做即可。

Matlab习题要在文档中给出必要的证明解题过程和结果。

5.1[10]解释下列名词的含义（1）线速度（2）角速度（3）雅克比矩阵（4）奇异性解答：5.2[20]解答：5.3[10] *如错误！未找到引用源。

所示是具有两个转动关节的操作臂。

计算出操作臂末端的速度，将它表达成关节速度的函数。

用在坐标系{0}中表达的雅可比矩阵完成。

图5-2 两连杆操作臂解答：5.4 [15] 一般机构有时存在某些特定的位形，称作“各向同性点”，这时雅可比矩阵的各列正交且模相同。

对于错误！未找到引用源。

的两连杆操作臂，求出存在的各向同性点。

提示：对1l ，2l 有什么要求？解答：5.5 [20] * 如图5-3所示为平面3R 机器人，建立合适的坐标系，分别写出工具坐标系和基坐标系中的雅可比矩阵，并分别根据两个雅可比矩阵计算什么情况下该机器人会出现奇异点，计算结果是否相同？图5-3三连杆平面操作臂解答：5.6[30]*任何具有3个旋转关节且连杆长度非零的机构在其工作空间内一定有一条奇异点轨迹（a locus of singular points）的说法是否正确？解答：5.7[25]*求出图5-4所示的3自由度操作臂雅可比矩阵。

在坐标系{4}中写出此矩阵，坐标系{4}位于手部末端且与坐标系{3}的方位相同。

图5-4 3R 非平面操作臂解答： 5.8 [20] * Given0.6120.50.61210.3540.8660.35430.70700.70770001-⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦ If the velocity vector at the origin of {A} is 5130.900.5⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦Find the 6*1 velocity vector with reference point at the origin of {B}. 解答：5.9 [MATLAB 习题] *这个练习的重点是平面3自由度3R 机器人（见图5-3；DH 参数由表5-1给出）的雅可比矩阵及行列式、分布速度控制仿真和静力学逆解。

机器人操作臂动力学参数的动静态辨识方法研究

验验证了该辨识算法的正确性与可行性。关键词：动力学参数；动静态辨识；机械臂
中图分类号：ＴＨ１１３；ＴＰ２４１文献标志码：Ａ文章编号：１００１ — ４５５１（２０１４）０３— ０２８３— ０６
Ｓｔａｔｉｃａｎｄｄｙｎａｍｉｃｍｅｔｈｏｄｏｆｉｄｅｎｔｉｆｙｉｎｇｄｙｎａｍｉｃｐａｒａｍｅｔｅｒｓｏｆｍａｎｉｐｕｌａｔｅｒ
第３１卷第３期
２０１４年３月
机
电
工
程
Ｖｏ１．３ｌＮｏ．３Ｍａｒ．２０１４
ＪｏｕｒｎａｌｏｆＭｅｃｈａｎｉｃｌ＆ＥｌａｅｃｔｉｃｒｌａＥｎｇｉｎｅｅｒｉｎｇ
ＺＨＡＮＧＹａｎ
（ＣｈａｎｇｃｈｔｍＩｎｓｉｔｔｕｔｅｏｆＯｐｔｉｃｓ，ＦｉｎｅＭｅｃｈａｎｉｃｓａｎｄＰｈｙｓｉｃｓ，ＣｈｉｎｅｓｅＡｃａｄｅｍｙｏｆＳｃｉｅｎｃｅｓ，Ｃｈａｎｇｃｈｕｎ１３００３３，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ａｉｍｉｎｇａｔｔｈｅｐｒｏｂｌｅｍｏｆｉｎｅｒｔｉａｌｐａｒａｍｅｔｅｒｓｉｄｅｎｔｉｆｉｃａｔｉｏｎ，ｔｈｅｍｅｔｈｏｄｏｆｓｔａｔｉｃａｎｄｄｙｎａｍｉｃｉｄｅｎｔｉｆｉｃａｔｉｏｎｏｆｒｏｂｏｔｄｙｎａｍｉｃｓｐａ－ｒｍｅａｔｅｓｒｗａｓｐｒｅｓｅｎｔｅｄ．Ｉｎｔｈｅｐｈａｓｅｏｆｓｔａｔｉｃｉｄｅｎｔｉｆｉｃａｔｉｏｎ，ａｍｕｌｔｉｄｉｍｅｎｓｉｏｎａｌｍａｔｉｒｘｗａｓｃｏｎｓｔｉｔｕｔｅｄｔｈｒｏｕｇｈｔｒａｎｓｆｏｒｍｉｎｇｔｈｅｃｏｎｉｆｇｕｒａ — ｔｉｏｎｓｏｆｏｂｒｏｔａｒｍｓ．Ｔｈｅｎ，ｔｈｅｐｒｏｄｕｃｔｏｆｍａｓｓａｎｄｃｅｎｔｅｒ — ｏｆ－ｍａｓｓｃｏｏｒｄｉｎａｔｅｓｗａｓｓｏｌｖｅｄｂｙｕｓｉｎｇｔｈｅｌｅａｓｔｓｑｕａｒｅｍｅｔｈｏｄ．ＢａｓｅｄｏｎＮｅｗ— ｔｏｎ－Ｅｕｌｅｒｌｇａｏｉｔｒｈｍ，ｄｅｃｏｕｐｌｅｄｄｙｎｍｉａｃｅｑｕａｔｉｏｎｏｆｍｅｃｈｎｉａｃｌａａｒｌｎｓｄｙｎｍｉａｃｓｗａｓｄｅｄｕｃｅｄ．Ｉｎｔｈｅｐｈａｓｅｏｆｄｙｎａｍｉｃｉｄｅｎｔｉｆｉｃａｔｉｏｎ，ｓｐｅｃｉｆｉｃ

机器人学导论第六章

期望求出期望的关节力矩矢量τ。这个运动学公式对操作臂控制问题（第10章）很有用。第二个问题是计算施加在一组关节力矩的情况下关节如何运动。也就是已知一个关节矢量τ，计算出操作臂运动的
，和。这对操作臂的仿真很有用。
6.2 刚体的加速度
在任一瞬时对刚体的线速度和加速度进行求导，可分别得到线加速度和量矩阵， V θ,θ是n×1
的离心力和哥氏力矢量， Gθ 是重力矢量。上式
之所以成为状态空间方程，是因为式中 V θ,θ取
决于位置和速度。M θ和 Gθ 中的元素都是关于
操作臂所有关节位置θ的复杂函数，而 V θ,θ中的
元素都是关于和的复杂函数。
可以看出惯性张量是坐标系位姿的函数。众所周知的平行移轴定理就是在参考坐标系平移是惯性张量如何变化的计算方法。平行移轴定理描述了一个以刚体质心为原点的坐标系平移到另一个坐标系是惯性张量的变换关系。
假设{C}是以刚体质心为原点的坐标系，{A}为任意平移后的坐标系，则平行移轴定理可表示为
式中 PC xc yczc T 表示刚体质心在坐标系{A}中的位
机器人学导论
第6章操作臂动力学
第六章操作臂动力学
6.1概述到目前为止，我们只研究了操作臂的运动
学。我们已研究了静态位置、静态力和速度；但是从未考虑引起运动所需的力。在本章中，将考虑操作臂的运动学方程—— 由驱动器施加的力矩或施加在操作臂上的外力是操作臂运动。
与第一操个作臂问动题力，学已有知关一的个两轨个迹问点题有，待和解决。
计算速度和加速度的向外迭代法
为了计算作用在连杆上的惯性力，需要计算操作臂每个连杆在某一时刻的角速度、线加速度和角加速度。首先对连杆1进行计算，由第五章知识

第6章操作臂动力学

zc
1 2
w
l
h
C Izz
m (w2 12
l2 )
,
C Ixy 0
第 6 章: 操作臂动力学 6.3 质量分布
其它参量由对称性得出：
m 12
(l
2
h2
)
CI
0
0
0 m (w2 h2) 12
0
0
0
m 12
(l
2
w2
)
第 6 章: 操作臂动力学 6.3 质量分布
惯性张量的其他性质: ---如果由坐标系的两个坐标轴构成的平面为刚体质量分布的对称平面，则正交于这个对称平面的坐标轴与另一个坐标轴的惯量积为0. ---惯量距永远是正值，而惯量积可能正，可能负. ---三个惯量距的和保持不变. ---惯性张量的特征值为刚体的主惯量距，相应的特征矢量为主轴。
h2
)
AI
m wl 4
m hw 4
m wl 4
m (w2 h2) 3
m hl 4
m hw 4
m hl 4
m 3
(l 2
w2
)
惯性张量是坐标系位姿的函数.
第 6 章: 操作臂动力学 6.3 质量分布
平行移轴定理 :
A Izz C Izz m(xc2 yc2 ) A Ixy C I xy mxc yc
刻的角速度、线加速度和角加速度. 可应用迭代方法完成这些计算。首先对连杆1进行计算，接着计算下一个连杆，这样一直向外迭代到连杆n – 计算出每个连杆质心的线加速度和角加速度之后，运动牛顿欧拉公式计算出作用在连杆质心上的惯性力和力矩 .
第 6 章: 操作臂动力学 6.4 牛顿欧拉方程
角速度在连杆之间的“传递问题”:

六自由度机械臂动力学

六自由度机械臂动力学是研究六自由度机械臂运动规律的学科，主要包括六自由度机械臂的运动学和动力学两部分。

运动学主要研究六自由度机械臂的运动轨迹、速度、加速度等运动参数，不涉及力和受力的问题。

运动学方程通常采用正解运动学或者逆解运动学的方法进行求解。

动力学则需要考虑六自由度机械臂在运动过程中所受到的各种力，如重力、摩擦力、弹性力等，并研究这些力如何影响机械臂的运动状态，从而得出动力学方程。

动力学方程通常通过牛顿-欧拉方程或者拉格朗日方程进行求解。

六自由度机械臂的动力学问题是机器人学和控制理论中的重要问题之一。

对于复杂的实际应用，如工业自动化、医疗机器人、空间探索等，精确的六自由度机械臂动力学模型和控制算法对于实现高精度、高效率的机器人操作至关重要。

机器人学速度和静力操作臂动力学2习题

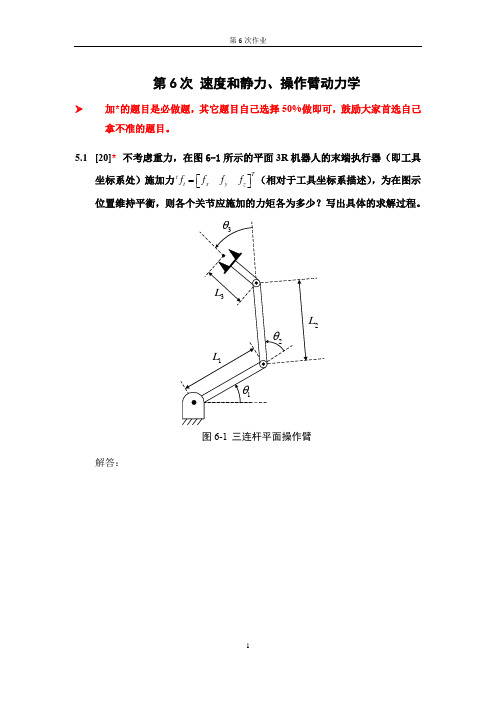
第6次速度和静力、操作臂动力学加*的题目是必做题，其它题目自己选择50%做即可，鼓励大家首选自己拿不准的题目。

5.1 [20]* 不考虑重力，在图6-1所示的平面3R 机器人的末端执行器（即工具坐标系处）施加力Tt t xyz f f f f ⎡⎤=⎣⎦（相对于工具坐标系描述），为在图示位置维持平衡，则各个关节应施加的力矩各为多少？写出具体的求解过程。

图6-1 三连杆平面操作臂解答：DH 参数表如下：变换矩阵如下:111101000000100001c s s cT -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦221221200000100001c s L s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 33233230000010001c s L s c T -⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦33410001000010001L T ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∙11100θω⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=00011υ 211122212222221212ˆ()0000000001R Z c s s c ωωθθθθθ-=⋅+⋅⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦21111122112221121221211()()0000(000)01000v R v P c s L L s s c L c ωθθθ-=⋅+⨯⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+⨯=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦32123332333333123123ˆ()0000000001R Z c s s c ωωθθθθθθθ-=⋅+⋅⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦⎣⎦3212223322333121233121123121312121231213121212()()000(00)0100[()][()]0v R v P c s L s L s c L c c L s s L c L s L s c L c L ωθθθθθθθθθθθθ-=⋅+⨯⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⨯⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤+++⎢⎥=-+++⎢⎥⎢⎥⎣⎦ 从上面的计算中可知，旋转矩阵为：11011122122233233334000010000100001100010001c s R s c c s R s c c s R s c R θθθθθθθθθθθθ-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦利用书中公式1111111i i i i i i ii i i ii i i i if R f n R n P f +++++++==+⨯由Tt t x y z f f f f ⎡⎤=⎣⎦ 有33T xyz f f f f ⎡⎤=⎣⎦33333000x y z z y L f n f L f f L f ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⨯=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 33332233330001x x y y xy z z c s f c f s f f s c f s f c f f f θθθθθθθθ--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦33233223333333333232330000010()x y z x y y z zz zy x y c s L c f s f n s c L f s f c f L f f s L f c L f L f L f L s f c f θθθθθθθθθθθθ⎡⎤--⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+⨯+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=--⎢⎥⎢⎥++⎣⎦223311223323323323323300001()()()()x y xy z x y x y x y x y z c s c f s f f s c s f c f f c c f s f s s f c f s c f s f c s f c f f θθθθθθθθθθθθθθθθθθθθ--⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦--+⎡⎤⎢⎥=-++⎢⎥⎢⎥⎣⎦22331122332323312332332332332332330001()()()0()()0()(zz z y x y x y x y x y x y z z c s s L f n s c c L f L f L f L s f c f L c c f s f s s f c f s c f s f c s f c f f c s L f s c L f θθθθθθθθθθθθθθθθθθθθθθθθ⎡⎤-⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦--+⎡⎤⎡⎤⎢⎥⎢⎥+⨯-++⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦+=22332332132331233233)()()()(()())z z z z z zy x y x y x y L f s s L f c c L f L f L f L f L s f c f L s c f s f c s f c f θθθθθθθθθθθθ⎡⎤+⎢⎥+--+⎢⎥⎢⎥+++-++⎣⎦5.2 [10] 求一个质量为m ，底面圆半径为r ，高为h ，坐标系的原点建立在其质心处的均质刚性圆柱体的惯性张量。

第5章-操作臂动力学

J
l1s1 l2s12
l1c1
l2c12
l2s12
l2c12
则该操作臂的力雅可比矩阵为：
JT
l1s1 l2
l2 s12
s12
l1c1 l2c12
l2c12
根据 JT F ，得：
1 2
l1s1 l2s12
l2 s12
l1c1 l2c12 Fx
l2c12
Fy
（2）已知关节驱动力矩，确定操作臂末端执行器对外界环境的作用力
F 或负荷的质量。这类问题是第一类问题的逆解。
此时有：
F
JT
1
【例5-1】
由图5-3所示的一个二自由度平面关节操作臂，已知末端点力为 F FX ,FY T
求相应于该末端点力的关节力矩（不考虑摩擦）。
解: 已知该操作臂的速度雅可比矩阵为
fi1,i fi,i1 mi g 0
ni1,i ni,i1 ri1,i ri,Ci fi1,i ri,Ci fi,i1 0
式中：ri1,i 为坐标系 i 的原点相对于坐标系i 1的位置矢量； ri,Ci 为质心相对于坐标系 i的位置矢量。
假设已知外界环境对操作臂末端执行器的作用力和力矩，那么可以由最后一个连杆向零连杆（基座）依次递推，从而计算出每个连杆上的受力情况。
动力学研究物体的运动和作用力之间的关系。操作臂动力学问题有两类：
（1）给出已知得轨迹点上的 q 、q及 q ，即机械臂关节位置、速度和加
或写为：
W T q FT X
根据虚位移原理，操作臂处于平衡状态的充分必要条件是对任意的符合几何
约束的虚位移，有
W 0
W Tq FT Jq
JT F

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A B A B B )B B0 S ( A Av R p S ( AB ) S ( AB ) B R p
二、刚体的速度和加速度
{B}相对于{A}移动，姿态不变
A
B 0 B 0, A
A
A B A B A B v p AvB0 B R v p S ( AB ) B R p AvB0 B R vp
图6.4表示了角速度为(t)的一个刚体。
图6.4 旋转矢量的变化率。当r(t)的顶端绕(t)轴旋转，它的轨迹是半径为|b|的圆。r(t)顶端的速度是|(t)||b|。
考虑在时刻 t 定义于世界空间的向量 r(t) 。假定该向量固定在刚体上， r(t) 与刚体一起在世界空间中移动。既然r(t) 是一个方向，它独立于任何平移，特别是， dr(t)/dt 独立于 v( t ) 。为了研究dr(t)/dt, 我们把r(t) 分解为矢量a 和 b, 其中a平行于(t)，b垂直于(t)。假使刚体保持一个恒定的角速度，结果r(t)的顶端划出一个中心在(t) 轴上的圆。
角速度、角加速度
A
C B R C
A A B B A A B A A B C B B R C S ( B ) B R C
A
三、旋转关节的连杆运动的传递
如图所示,连杆i＋1相对连杆i 转动的角速度是绕关节 i ＋ 1 运动引起的,
i 1
i 1 zi 1
根据矩阵的乘法规则，我们可以提取出公因子
r11 (t ) (t ) r R 21 r31
这是矩阵和矩阵的乘积。
r12 r22 r32
r13 r23 (t ) R (t ) r33
记
0 S ( ) z y
线速度
i
vi 1 i vi ii i pi 1
连杆i转动速度而产生的分量
在{i+1}坐标系中表示
i 1
vi 1 i i1R(i vi ii i pi 1 )
角加速度，线加速度
i
i 1 z i 1 ii i 1iR i 1 i 1
i 1 z i 1 z i 1 i i1Ri i i i1Rii i 1 i 1 i 1 i 1
图6.3 刚体的线速度v(t)和角速度(t)
让我们回顾一下 R(t) 的物理的含意。我们知道 R(t) 的列告诉我们在时刻 t 被转换的 x ， y 和 z 轴的方向。这意味着dR(t)/dt的列描述正在被转换的x，y和z轴的速度。为了发现 (t) 和 R(t) 之间的关系，我们首先检查刚体上任意向量的变化与角速度 (t)的关系。
{A}固定，刚体与{B}固结
B
p 0 p 0, B v p 0, B v
A
A B A B A B v p AvB0 B R v p S ( AB ) B R p AvB0 S ( AB ) B R p
A
A B A B A B A B B )B p Av B0 B p 2 S ( A B ) B v R v R v p S ( A R p S ( A B ) S ( A B ) B R p
为了简化上述表达式，使用下述算子。如果a和b是3维矢量，那么ab是矢量
a y bz b y a z a x bz bx a z a b b a x y x y
给定矢量a, 定义 a* 是矩阵那么，
a *b
0 az a y
{B}相对于{A}纯滚动，
A
B0 0 pB0 const, AvB0 0, Av
A
A B A B A B A B v p AvB0 B R v p S ( AB ) B R pB R v p S ( AB ) B R p
A
A B A B A B A B B )B p Av B0 B p 2 S ( A B ) B v R v R v p S ( A R p S ( A B ) S ( A B ) B R p
A
A B A B A B A B B )B p Av B0 B p 2 S ( A B ) B v R v R v p S ( A R p S ( A B ) S ( A B ) B R p
A B B0 B p Av R v
二、刚体的速度和加速度
S () R R
z 0
y x
0

x
(t ) (t ) R(t ) S () R R
二、刚体的速度和加速度
A A B p B R p ApB0
A
A B A B Ap B0 B B p R p R p
(t ) (t ) R(t ) S () R R
1 R (t ) 0 0
(6–3)
参照式(6–2)中R(t)的元素，有
1 r11 r R (t ) 0 21 0 r31
(6–4)
是R(t)的第一列。
R(t)的物理含意是当在时刻t转换到世界空间的时候，R(t) 第一列给出刚体的x轴的方向。同样地。R(t)的第二列和第三列，是在时刻t到世界空间中刚体y轴和z轴的方向。
r11 R r21 r31 r12 r22 r32 r13 r23 r33
(6–2)
其中，每一列向量表示{B}的一个主轴在{A}中的三个方向余弦。因此也把旋转矩阵R称为余弦矩阵。
另外，我们可以把物理含义赋予R(t)。考虑局部空间的x 轴向量（1，0，0），在时刻t，该向量在世界空间具有方向
0 0 i 1
关节角速度
Z轴单位向量
角速度
两关节角速度向量转换到同一坐标系中，有
i
i 1 z i 1 ii i 1iR i 1 i 1
在{i+1}坐标系中表示
i 1
i 1 z i 1 i i1Rii i 1 i 1
A B A B A B A B B )B p 2 S ( A B ) B B R v R v p S ( A R p S ( A B ) S ( A B ) B R p
若已知{C}相对{B}的转动角速度为BC，则{C}相对{A}的转动角速度和角加速度矢量为
A A B C AB B R C A A B A A B C B B R C S ( B ) B R C
ab

z

(t )简化为使用符号“* ”, 我们可以重新把R
r11 r12 r13 (t ) (t ) r (t ) r (t ) r R 21 22 23 r r r 31 32 33
A
二、刚体的速度和加速度
线速度、线加速度
A A B A B vp AvB0 B R vp S ( AB )B R p
A
A B A B A B A B p Av B0 B p 2S ( AB )B B )B v Rv R vp S ( A R p S ( AB )S ( AB )B Rp
r11 r 21 r31
r12 r13 r 和 22 r23 r32 r33
R [ x y z]
刚体不仅能平移，也能旋转。想象我们在空间中固定质心位置，因此刚体上的任何点的运动都是由刚体绕某个穿过质心的轴旋转造成的（除非质心本身被移动）。我们可以把旋转描写为向量(t)。(t)的方向给出旋转轴的方向（图6.3）， (t)量被称做角速度。线速度： x(t) 和 v(t) 的关系为 v(t)=dx(t)/dt. 如何表达 R(t) 和 (t) 的关系?
az 0 ax
ay ax 0
0 az a y
az 0 ax
a y bx ax by 0 b
a y bz by a z a x bz bx a z a b b a x y x y
这个圆的半径是 |b| 。因为矢量r(t)的尖瞬时地是沿着这个圆移动，r(t)的瞬时的改变是垂直于b和ω(t)两者的。因为r(t)的顶端正在沿着一个半径为 b 的圆移动， r(t) 的瞬时的速度具有模 |b||(t)| 。因为b 和 (t) 垂直，他们的叉积具有模
(t ) b (t ) b
A A B A B vp AvB0 B R vp S ( AB )B R p
A
A B A B A B A B p Av B0 B p 2S ( AB )B B )B v Rv R vp S ( A R p S ( AB )S ( AB )B Rp
二、刚体的速度和加速度
r 21 r31
在时刻 t ， R(t) 的第一列的导数恰恰是这个矢量的变化率：使用叉积规则，这个改变是
r11 (t ) r21 r 31
对于R(t)的其它两列是同样的。这意味着我们可以记
r11 r12 r13 R(t ) (t ) r21 (t ) r22 (t ) r23 r r r 31 32 33
(6-5)
既然 r(t)=a+b，且a平行于(t), (t)a =0 ，因此
(t ) (t ) b (t ) b (t ) a r (t ) (a b) (t ) r (t )