初中数学《函数》完整版 北师大版9
初中数学《函数》经典课件北师大版9

例5 已知 f(x)=
2x 1+2x
,
x∈R,
求
f-1(
1 3
)
的值.
初中数学《函数》经典课件北师大版9
初中数学《函数》经典课件北师大版9
课外练习.求下列函数的定义域
(1).y
log (3x 0.5
1)
(2).y
2 log (x 2 4
2x
3)
(3).y
log 3
x 3x
1 1
初中数学《函数》经典课件北师大版9
注:例2是利用对数函数的增减性比较两个对数 的大小的,对底数与1的大小关系未明确指出时,要分 情况对底数进行讨论来比较两个对数的大小.
初中数学《函数》经典课件北师大版9
初中数学《函数》经典课件北师大版9
例3 比较下列各组中两个值的大小:
⑴.log 67 , log 7 6 ; ⑵.log 32 , log 2 0.8 .
y log2 x
这就是本节课要学习的:
初中数学《函数》经典课件北师大版9
对数函数
定义函数 yloagx(a0,且 a 1)
叫做对数函数,其中x是自变量,函数的定
义域是(0,+∞)。
注意:对数函数的定义与指数函数类似,都是形式定义,
注意辨别.如:y 2lo2gx,y
log 5
x
5
都不是对数函数,而只能称其为对数型函数.
系呢?
关于x轴对称
初中数学《函数》经典课件北师大版9
初中数学《函数》经典课件北师大版9
2.(71页)探究:
画出对数函数 ylo3g x和 ylo1gx的图象。
y
1.函数图象分布在哪些 象限? 一、四
初中数学《函数》_PPT完整版【北师大版】4

(2)y=ax²+c ------ (a≠0,b=0,c≠0).
(3)y=ax²+bx ---- (a≠0,b≠0,c=0).
初中数学《函数》教学分析北师大版4 -精品 课件ppt (实用 版)
的阳光就会减少. 根据经验估计,每多 种一棵树,平均每棵 树就会少结5个橙子.
某果园有100棵橙子树,每一棵树平均结600个橙 子。现准备多种一些橙子树以提高产量,但是如 果多种树,那么树之间的距离和每一棵树所接受 的阳光就会减少。根据经验估计,每多种一棵树, 平均每棵树就会少结5个橙子。
①问题中有那些变量?其中哪些是自变量?哪些 是因变量? ②假设果园增种x棵橙子树,那么果园共有多少 棵橙子树?这时平均每棵树结多少个橙子?
60420
60420
60375
60375
想一想
亲历知识的发生和发展
银行的储蓄利率是随时间的变化而变化的,也就 是说,利率是一个变量.在我国,利率的调整是由 中国人民银行根据国民经济发展的情况而决定的.
设人民币一年定期储蓄的年利率是x,一年到 期后,银行将本金和利息自动按一年定期储蓄转 存.如果存款是100元,那么请你写出两年后的本 息和y(元)的表达式(不考虑利息税).
小结
拓展
回
初中数学《函数》教学分析北师大版4 -精品 课件ppt (实用 版)
味
无
穷
定义中应该注意的几个问题 :
2.定义的实质是:ax²+bx+c是整
式,自变量x的最高次数是二次,
自变量x的取值范围是全体实数.
初中数学《函数》免费课件北师大版9

初中数学《函数》免费课件北空数集,如果按照某个确定的对
应关系f,使对于集合A中的任意一个数x,在集合B中都有惟
一确定的数f(x)和它对应,那么就称f:A B为从集合A到集
合 B的函数。 2.函数的三要素
定义域 值域
定义域 决定值域
对应法则f 对应法则
初中数学《函数》免费课件北师大版9
这里的实数a与b都叫做相应区间的端点。
实数集R可以用区间表示为(-∞,+∞),“∞”读作“无 穷大”。满足x≥ a,x>a ,x ≤b, x<b的实数的集合分别 表示为[a, +∞)、(a, +∞)、(-∞,b]、(-∞,b).
初中数学《函数》免费课件北师大版9
初中数学《函数》免费课件北师大版9
设a,b是两个实数,而且a<b, 我们规定:
(1)、满足不等式a≤x≤b的实数x的集合叫做闭区间, 表示为 [a,b]
(2)、满足不等式a<x<b的实数x的集合叫做开区间, 表示为 (a,b)
(1)、满足不等式a≤x<b或a<x≤b的实数x的集合叫 做半开半闭区间,表示为 [a,b)或(a,b]
初中数学《函数》免费课件北师大版9
3.理解区间是表示数集的一种方法,会把不等式转化为区间。
初中数学《函数》免费课件北师大版9
(2)f(x)= 5-x x 3
(3)f(x)= (x-1)0 x2 x
初中数学《函数》免费课件北师大版9
初中数学《函数》免费课件北师大版9
两个函数相同:
( 1 ) 对 应 关 系 f , 定 义 域 , 值 域 都 相 同
定义域,定义域到值域的对应关系 相同
( 2 ) 两 个 函 数 的 图 像 完 全 相 同
初中数学课件-函数PPT精品课件北师大版9

底数不确定,需 进行分类讨论
⑸log34与log43
利用图象
初中数学课件-函数PPT精品课件北师 大版9( 精品课 件)
初中数学课件-函数PPT精品课件北师 大版9( 精品课 件)
例3. 设a log0.5 6.7,b log2 4.3,c log2 5.6,则C( ). A. b<c<a B. a<c<b C. a<b<c D. c<b<a
-2
3
y log 1 x
2
对数函数在第一象限越靠近x轴底数越大
初中数学课件-函数PPT精品课件北师 大版9( 精品课 件)
初中数学课件-函数PPT精品课件北师 大版9( 精品课 件)
例1 求下列函数定义域
(1) y logx22 x 2
(1) f x x 10 lg(x 2)
| x|x
图象
对数函数的图象和性质
a>1
0<a<1
y
y
O
(1,0)
x
f x loga xa 1
(1,0)
O
x
f(x)=logax (0<a<1)
(1) 定义域:(0,+∞),
(2) 值域:R,无最值
(3) 过点(1,0),即x=1时,y=0
(4) 在(0,+∞)上是增函数
性质 (5) 非奇非偶
(4) 在(0,+∞)上是减函数
示溶液中氢离子的浓度,单位是摩尔/升.
(1) 根据对数函数性质及上述pH的计算公式,说明溶液酸
碱度与溶液中氢离子的浓度之间的变化关系;
解:
(1)
根据对数的运算性质,有
pH
初中数学《函数》精品ppt北师大版9
特殊一点
6
,
sin
6
y
MPsin6
P
MA o
6
有向线段MP叫做正弦线
正弦函数
正弦线MP
MPsin6
, sin
6 6
利用弧PA长度
来做出点的横
x
坐标,用正弦
线来做出点的
6
纵坐标
lR,R1 l
即弧长 PA
6
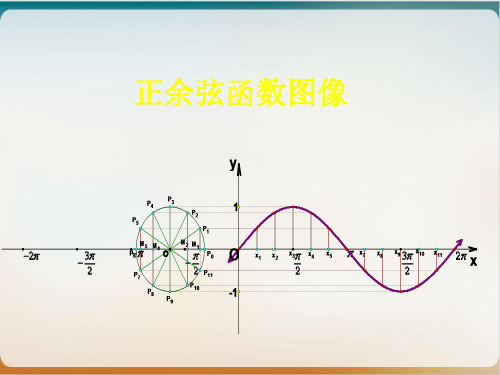
用正弦线作出 ysinx,x [0,2]
的图像
y
2 3 5
.6
7 6
4 3
正弦、余弦函数的图象
y
1
-
-
-
- o
4 3
2
-1
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象 y
1
-
-
-
- o
4 3
2
-1
2
3 4
5 6x
正弦曲线
形状完全一样 只是位置不同
余弦曲线
2
3 4
5 6x
试一试: ycos,xx[0,2π]
-
图象的最高点 (0,1) (2,1)
与x轴的交点
1
-1
x
典型例题
例1: (1)用五点法作出函数 y 1 sinx,x [0 ,2 ]的简图
解法1: 列表 描点
连线
y2
x
0
2
3 2
2
sin x 0 1 0 1 0
sinx1 1 2 1 0 1
1
y 1 sinx,x [0 ,2 ]
图了
像一
整个
2
体单 向位
初中数学《函数》优秀课件北师大版9

•
9.自信让我们充满激情。有了自信, 我们才 能怀着 坚定的 信心和 希望, 开始伟 大而光 荣的事 业。自 信的人 有勇气 交往与 表达, 有信心 尝试与 坚持, 能够展 现优势 与才华 ,激发 潜能与 活力, 获得更 多的实 践机会 与创造 可能。
感谢观看,欢迎指导!
温度
1 0 -3 0 3 5 7 8 6 3 2
(单位:°C)
T/℃ 8
(14,8)
·
把-3一0 个(4函·,4-数3)的自变量x1与21对4应时的间函数y的2值4分t/别时作为
点的横坐标和纵坐标,在直角坐标系中描出它的对应
点,所有这些点组成的图形叫做何明显优势?
•
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
•
3.把握好故事情节,是欣赏小说的基础, 也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点, 从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
观察一下
下表是根据测温仪显示记录的数据,它反映了 富阳去年12月14日的温度T如何随时间t的变化而变 化。你从表格中得到了哪些信息?
时间t(时) 0 1 4 6 8 10 12 14 16 20 24
温度T
1 0 -3 0 3 5 7 8 6 3 2
(单位:°C)
时间t(时) 0 1 4 6 8 10 12 14 16 20 24
有关直线相交的交点坐标的求解方法:
1.图象法: 2.解析式法:
直线与x轴交点坐标:令y=0
直线与y轴交点坐标:令x=0
练习:在同一直角坐标系中画出下列函数的图象,并写出
初中数学《函数》_PPT完整版【北师大版】10
所以 k1或2
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
7.已知 A 4,m 点 ,B1,n在反比 y8例 上函 ,
x
线 AB 的函数表达式为_
解析: 由已知可得:
m
8, 4
m 2;n
k<0 图象在第二和第四象限y,在每个 象限内y 随x的增大而增大。
S S 2、
1k
2 AOP BOP
S k 四边A形 OVP
A
P
oB
x
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
再见
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
经过三点分x轴 别引 向垂,交 线x轴于 A1,B1,C1三点 ,
边结 OA,OB,OC,记OA1A,OB1B,OC1C的
面积分别 S1,为 S2,S3,则有_A_.
y
A.S1 = S2 = S3 B. S1 < S2 < S3 C. S3 < S1 < S2 D. S1 > S2 >S3
A
S1
B C
(2)由 . 图可知, 6 当 x 0或x 4时,
一次函数的值例 大函 于数 反的 比值。
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
初中数学《函数》教学分析北师大版1 0-精品 课件pp t(实用 版)
知识小结:
1、反比例函数的图象和性质
k>0 图象在第一和第三象限,在每 个象限内y随x的增大而减小。
初中数学《函数》优秀ppt北师大版9
•3. 要得到函数 y=sin(x + π/3)的图象,只需将 y=sinx 图象( C) A. 向左平移π/6个单位 B. 向右平移π/6个单位 C. 向左平移π/3个单位 D. 向右平移π/3个单位
6.把y sin(2x )的图象向右平移 个单位,
3
6
这时图象所表示的函为数 D
A. y sin(2x )
2
B. y sin(2x )
6
C. y sin(2x 3) D. y sin2x
7.要得到函数 y s2in(x )的图象,可由y sinx
26
2
的图象 C
A. 向右平移
6
C. 向右平移
3
B. 向左平移
6
D. 向左平移
3
8.函数 yAsin(x)的定义域 R周 ,为期为,
2
初相为,值域为 1,3,
3
则其函数式的最 为简形A 式
A.y2sin4x()1B.y2sin4x()1
3
3
C.y2sin 4x()1D.y2sin 4x()1
3
3
小结
1.五点法作 yAsi nx ()一个周期上的函数图像
2
y sin x
4 x
y sin 1 x 2
总结 函数y=sinx(>0)图象: 周期变换
函数 y=sinx (>0且0) 的图象可以看作 是把 y=sinx 的图象上所有点的横坐标缩短 (当>1时)或伸长(当0< <1时)到原来的1/ 倍(纵坐标不变)而得到的.
初中数学《函数》完美课件 【北师大版】1
阿拉伯数学家 花拉子米(约7 80~约850)给 出了一次方程 和二次方程的 一般解法.
阿贝尔(1802~ 1829)挪威数学 家.证明了五次 以上一般方程 没有求根公式.
卡尔达诺,意大利数学家,他第一个发 表了三次代数方程一般解法的卡尔达诺 公式,也称卡当公式(解法的思路来自 塔塔利亚,两人因此结怨,争论多年)。 他的学生费拉里第一个求出四次方程的 代数解。
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
P143 例1 求方程f(x)=lnx+2x-6的实数解的个数.
解:令函数f(x)=lnx+2x-6,因为函数f(x)的定义域为(0,+∞)
f(2)=ln2+4-6=ln2-2=ln2-2lne=ln2-lne2<0, f(3)=ln3+6-6=ln3>0, 函数f(x)=lnx+2x-6在(2,3)上存在零点.
x
y=-2x +6
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
【变式提升】 求方程2-x =x的根的个数,并确定根所在
的区间[n,n+1](n∈Z).
解的: 根的求数形个方缺少数程数形,2-x时时即=少难x在的入直判根断微观的函,,个数数y,=x即与求y方 (程12)x
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
练习2:
请判断出函数f x x3 2x的零点个数
初中数学《函数》完美课件 北师大版1-精品课件ppt(实用版)
注:只有上述两个条件同时满足,才能判断函数在指定区间内存在零点。
北师大版九年级数学下册第二章二次函数第三节确定二次函数的表达式(无答案)
北师大版九年级数学下册第二章二次函数第三节确定二次函数的表达式(无答案)确定二次函数的表达式知识梳理知识点一:用配方法确定二次函数y =ax 2+bx +c 图象的对称轴、顶点坐标及最值 1.二次函数y =ax 2+bx +c 的配方一般地,对于二次函数y =ax ²+bx +c ,我们可以利用配方法推导出它的对称轴和顶点坐标. 例:求次函数y =ax ²+bx +c 的对称轴和顶点坐标. 配方:这个结果通常称为求顶点坐标公式. 2.二次函数y =ax ²+bx +c (a ≠0)的图象和性质(1)二次函数y =ax ²+bx +c 的图象是一条抛物线. 画二次函数图象的“三步骤” ①化:把一般式化成顶点式.②定:确定抛物线的开口方向、顶点坐标、对称轴. ③画:利用抛物线对称性列表、描点、连线.(2)二次函数y =ax ²+bx +c 写成顶点式为a b ac a b x a y 44222-+⎪⎭⎫ ⎝⎛+=。
(3)对称轴顶点坐标⎪⎭⎫ ⎝⎛++=c c x a b x a 2⎪⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛++=a c a b a b x a b x a 22222⎥⎥⎦⎤⎢⎢⎣⎡-+⎪⎭⎫ ⎝⎛+=222442a b ac a b x a .44222a b ac a b x a -+⎪⎭⎫ ⎝⎛+=(4)开口方向:当a>0时,抛物线的开口向上,有最小值为ab ac y 442min-=;当a<0时,抛物线的开口向下,有最大值为ab ac y 442max -=。
(5)增减性:① a>0,当x>a b 2-时,y 随x 的增大而增大,当x<a b 2-时,y 随x 的增大而减小. ②a<0,当x>a b 2-时,y 随x 的增大而减小,当x<ab2-时,y 随x 的增大而增大知识点二:抛物线位置与系数a ,b ,c 的关系:知识点三:用待定系数法求二次函数解析式 1.利用三点坐标确定二次函数的一般式①一般情况下,把三点的坐标代入解析式y =ax ²+bx +c ,列方程组. ②如果没有直接给出三点的坐标,可通过图象的性质求出其他点的坐标. 确定二次函数一般式的“四步骤”①设:设二次函数解析式为y =ax ²+bx +c (a ≠0). ②列:根据题意列方程组.北师大版九年级数学下册第二章二次函数第三节确定二次函数的表达式(无答案)③解:解方程组.④定:确定二次函数解析式.2.利用顶点式确定二次函数解析式用顶点式求解析式的“三种情况”①已知顶点坐标. ②已知对称轴或顶点的横坐标. ③已知二次函数的最大(小)值或顶点的纵坐标.3.利用交点式确定二次函数解析式当已知抛物线与x 轴的交点坐标(x1,0),(x2,0)时,则设抛物线的解析式为y=a(x-x1)(x-x2),再根据其他条件求出a的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
log 3 2 log 2 0.8
log 6 7 > log 6 6 = 1 log 7 6 < log 7 7= 1 log 6 7 > log 7 6
log 3 2 > log 3 1= 0 log 2 0.8 < log 2 1= 0 log 3 2> log 2 0.8
若底数、真数都不相同, 则常借助1、 0等中间量进行比较。
•
8.少年时阅历不够丰富,洞察力、理 解力有 所欠缺 ,所以 在读书 时往往 容易只 看其中 一点或 几点, 对书中 蕴含的 丰富意 义难以 全面把 握。
•
9.自信让我们充满激情。有了自信, 我们才 能怀着 坚定的 信心和 希望, 开始伟 大而光 荣的事 业。自 信的人 有勇气 交往与 表达, 有信心 尝试与 坚持, 能够展 现优势 与才华 ,激发 潜能与 活力, 获得更 多的实 践机会 与创造 可能。
2.2.2 对数函数及其性质
新课导入
有一种细胞分裂时,由1个分裂成2个,2个分裂成4
个,···1个这样的细胞分裂x次会得到多少个细胞?
指数函数
y 2x
如果知道了细胞的个数y如何确定分裂的次数x?
x log2 y 用y作自变量的函数
但习惯上仍用x表示自变量,y表示它的函数:
即
y log2 x
对数函数的定义
•
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
•
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
•
7.阅历之所以会对读书所得产生深浅 有别的 影响, 原因在 于阅读 并非是 对作品 的简单 再现, 而是一 个积极 主动的 再创造 过程, 人生的 经历与 生活的 经验都 会参与 进来。
-2
3
y log1 x
2
规律:在第一象限图象自左向右底数越来越大!
练习
函数 y log a x, y log b x, y log c x, y log d x
的图像如图所示,则下列式子中正确的是( C )
y A .0 a b 1 c d B .0 b a 1 d c
y logb x yloga x
练习 求下列函数的反函数: (1)y3x1(xR) (2)yx31(xR)
小 结:
求反函数的一般步骤分三步, 一解、二换、三注明.
练习 函数f(x)=loga (x-1)(a>0且a≠1) 的反函数的图象经过点(1, 4),求a的值.
小 结:
若函数y=f(x)的图象经过点(a, b), 则其反函数的图象经过点(b, a).
感谢观看,欢迎指导!
解(1 : )根据对数的 pH 运 lgH 算 []l性 gH[]质 1lg[得 H 1],
在 (0, )上[H , ]增大 [H 1, ]减小 lg[H , 1]也减小 pH , 减.即 小 所,以 [H]增,大 pH 减,小 即溶液中氢越 离,大 子 其的 酸浓 碱度 度 液酸碱度是通pH过刻画的.pH的计算公式:为pH lg[H ], 其中[H]表示溶液中氢离子度 的, 浓单位是摩/升 尔. (1)根据对数函数性质述 及p上 H的计算公式,说明酸 溶碱 液度 与溶液中氢离子的之 浓间 度的变化关系; (2)已知纯净水中氢离浓 子度 的为[H] 107摩尔/升,计算纯 净水的pH值.
解(2 : )当 [H ]1 0 7时p, H lg 1 0 77. 即纯p 净 是 H 7.水的
国家规定,饮的 用 pH纯 应净 该5.水 在 0~ 7.0之间 .
反函数
在指数函数 y 2x 中 ,以y为自变量, x为
因变量,可以得到一个新的函数吗?若可以,它 的对应关系是什么?它们之间有什么关系?
0
2
y
描
2
点
1
11
42
0 1 23 4
x
连
-1
线
-2
24 …
1 2…
…
x … 1/4 1/2 1
列 表
ylog2 x
y log1 x
… …
2
-2 2
-1 1
0 0
24 …
1 2… -1 -2 …
描 点
y 2
1 11
42
0 1 23 4
连
-1
线
-2
这两个函
数的图象
x
有什么关
系呢?
关于x轴对称
你能画出 f (x)log1 x和f(x)lo3gx
x∈(0, 1)时,y>0 x∈(1, +∞)时,y<0.
在(0,+∞)上是增函数 在(0,+∞)上是减函数
对数函数:y = loga x (a>0,且a≠ 1) 图象 随着a的取值变化图象如何变化?有规律吗?
y
2
y=1
1 11 42
0 1 23 4
ylog2 x
ylog3 x
x
-1
y log1 x
3. 已知函数y=f (x)= x 1,求f -1(3)的值.
一、对数函数的定义; 二、对数函数的图象和性质; 三、比较两个对数值的大小; 四、反函数.
作业
•
1.情节是叙事性文学作品内容构成的 要素之 一,是叙 事作品 中表现 人物之 间相互 关系的 一系列 生活事 件的发 展过程 。
•
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
它们的图象关于直线y=x对称。 它们的单调性相同。
对反函数定义的理解
(1) 原函数与反函数的法则互逆,它们互为 反函数,反函数也是函数;
(2) 不是每一个函数都有反函数;一个函数有 反函数的充要条件是它相应的映射是一一映射;
(3)原函数与反函数的定义域与值域互换; (4)原函数与反函数的图象关于直线y=x对称。 (5)原函数与反函数的单调性相同。
1. 求下列函数的反函数
(1) y=4x (x∈R) (2) y=0.25x (x∈R)
(3) y=( 1 ) x (x∈R) 3
(5) y=lgx (x>0)
(4) y=( 2 ) x (x∈R)
2. 函数y=3x的图象与函数y=log3x的图象关
于( D )
A. y轴对称 C. 原点对称
B. x轴对称 D. 直线y=x对称
xlog2 y 改写成 ylog2 x
它们的图象关于直线 y x 对称。
我们把具有上述特征的两个函数互称 为反函数。请给出反函数的定义。
反函数的概念
设A,B分别为函数y=f(x)的定义域和值域,
如果由函数y=f(x)所解得 x(y) 也是一个函
数(即对任意一个 yB,都有唯一的 xA与之
对应),那么就称函数 x(y) 是函数y=f(x)
y
解:∵ log 7 5 > log 7 2 >0
log log
2 5
7 7
1
1
log7 2 log7 5
o1
∴ log 2 7 > log 5 7
ylog2 x y log5 x
7x
同真数比较大小: 1.通过换底公式; 2.利用函数图象。
例4:比较下列各组数中两个值的大小:
log 6 7 log 7 6
x-1≠
∴ 所求函数的定义域为: (1,2) ∪
对数函数探y=究loga x (a>0,且a≠ 1)图象与性质
在同一坐标系中用描点法画出对数函数
ylo2gx和 ylo1gx的图象。
2
作图步骤: ①列表;②描点;③连线。
x … 1/4 1/2 1
列 表
ylog2 x
y log1 x
… …
-2
-1
当a1时 yloagx在( 0, )上是增函5.数 15, .9, 且 loag5.1loag5.9 ;
当a1时 yloagx在( 0, )上是增函5.数 15, .9, 且 loag5.1loag5.9 ;
当底数不确定时,要对底数a与1的大小进行 分类讨论.
例3:比较下列各组数中两个值的大小:
log 2 7 与 log 5 7
例5. 溶液酸碱度的测. 量 溶液酸碱度是通pH过刻画的.pH的计算公式:为pH lg[H ], 其中[H]表示溶液中氢离子度 的, 浓单位是摩/升 尔. (1)根据对数函数性质述 及p上 H的计算公式,说明酸 溶碱 液度 与溶液中氢离子的之 浓间 度的变化关系;
(2)已知纯净水中氢离浓 子度 的为[H] 107摩尔/升,计算纯 净水的pH值.
C .0 d c 1 b aO D .0 a b 1 d c
x y logd x
y logc x
例2 比较下列各组数中两个值的大小:
(1)lo23g.4, lo28g.5 (2)lo0.3g1.8, lo0.3g2.7 (3 )lo a5 .1 g ,lo a5 .9 g (a 0 ,a 1 )
(1) ylo2gx在0( , )上是且 增 3.4函 8.5, 数 lo2g3.4lo2g8.5;
(2) ylo0g.3x在0( , )上是减 且 1.8函 2.7数 , lo0g.31.8lo0g.32.7 ;
当底数相同时,利用对数函数的单调性比较大小
(3 )lo a5 .1 g ,lo a5 .9 g (a 0 ,a 1 )
•
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
