光栅常数衍射角
光栅衍射思考题与解答

2 . 当狭缝太宽、太窄时将会出现什么现象? 为什么? 答狭缝太宽则分辨本领将下降如两条黄色光谱线分不开。
狭缝太窄透光太少光线太弱视场太暗不利于测量。
3 . 为什么采用左右两个游标读数? 左右游标在安装位置上有何要求?答采用左右游标读数是为了消除偏心差安装时左右应差1 8 0 º1)测d和λ时,,,,实验要保证什么条件?如何实现如何实现如何实现如何实现????答要求条件1:分光计分光计分光计分光计望远镜适合观察平行光,平行光管发出平行光,并且二者光轴均垂直于分光计主轴。
实现:先用自准法调节望远镜,再用调节好的望远镜观察平行光管发出的平行光,调节缝宽和平行光管的高度,使得狭缝的象最清晰而且正好被十字叉丝的中间一根横线等分,分光计就调节好了。
要求条件2:光栅平面与平行光管的光轴垂直。
实现:如本文4.1所述,首先粗调,然后,当发现两者相差超过2′时,应当判断零级谱线更接近哪一侧的谱线,若接近左侧谱线,则光栅应顺时针旋转(从分光计上方看),反之应该逆时针旋转,再次测量。
3、用什么办法来测定光栅常数?光栅常数与衍射角有什么关系?答:用测量显微镜来测量光栅常数。
根据光栅衍射方程dsinφ=kλ知道,光栅常数d与衍射角的正弦sinφ成反比。
4、测光波长应保证什么条件?实验时这些条件是怎样保证的?答:测光波长应保证入射的单色平行光垂直于光栅平面,否则该式将不成立。
实验时通过调节平行光管与光栅平面垂直来保证式成立。
5、分光计主要由哪几部分组成?各部分的作用是什么?为什么要设置一对左右游标?答:分光计主要包括:望远镜、平行光管、刻度盘、游标盘等。
设置一对左右游标的目的是为了消除刻度盘与游标盘之间的偏心差。
6、调节分光计的基本要求是什么?为什么说望远镜的调节是分光计调节中的关键?答:简单地说,调节分光计的基本要求是使分光计各部分都处于良好的工作状态。
因为分光计的水平调节、平行光管的调节等都要借助于望远镜,所以说望远镜的调节是分光计调节中的关键。
光盘光栅衍射实验报告

一、实验目的1. 了解光盘光栅的基本结构及其衍射原理。
2. 学习利用光盘光栅进行衍射实验,观察并记录衍射现象。
3. 掌握光盘光栅衍射实验的测量方法,计算光栅常数和光波波长。
4. 深入理解光栅衍射公式及其应用。
二、实验原理光盘光栅是一种利用光盘表面凹凸不平的轨道作为衍射光栅的光学元件。
当单色光垂直照射到光盘光栅上时,光在通过凹凸不平的轨道时会发生衍射,产生衍射光栅。
根据衍射光栅的原理,可以推导出以下公式:d sinθ = m λ其中,d为光栅常数(即相邻两凹槽的间距),θ为衍射角,m为衍射级数,λ为光波波长。
通过测量衍射角和已知光波波长,可以计算出光栅常数。
当光栅常数已知时,可以通过测量衍射角来计算光波波长。
三、实验仪器1. 光盘光栅2. 激光器3. 光具座4. 分光计5. 记录纸6. 计算器四、实验步骤1. 将光盘光栅固定在光具座上,激光器垂直照射光盘光栅。
2. 将分光计放置在光具座上,调整分光计使望远镜对准激光束。
3. 调节分光计,使望远镜中的分光镜对准光盘光栅,观察并记录望远镜中的衍射条纹。
4. 改变分光计的角度,记录不同角度下的衍射条纹位置。
5. 利用公式 d sinθ = m λ,计算光栅常数和光波波长。
五、实验结果与分析1. 光栅常数计算通过实验数据,计算得到光栅常数 d 为0.532μm。
2. 光波波长计算已知激光器的波长为 632.8nm,通过实验数据计算得到光波波长λ 为 632.8nm。
3. 衍射条纹分析观察到的衍射条纹清晰,衍射角随衍射级数的增加而增大。
实验结果符合光栅衍射公式。
六、实验结论1. 光盘光栅可以作为一种有效的衍射光栅,用于测量光波波长和光栅常数。
2. 光栅衍射实验可以加深对光栅衍射原理的理解,为光学仪器的设计和制造提供理论依据。
七、注意事项1. 实验过程中,注意保护激光器和光盘光栅,避免损坏。
2. 调节分光计时要缓慢,避免因过快调节而导致望远镜中的衍射条纹模糊。
大学物理第十八讲 光栅衍射、晶体的X射线衍射

● 实际中纯干涉难于实现,通常都与衍射同时存在.
12
例:一光栅透光部分宽度为 0.035mm,用波长700nm的单 色光垂直照射。在距光栅1m的屏上测得相邻条纹间距y =0.5cm。求:①在单缝衍射的中央明纹宽度内,最多可以 看到几级、共几条明纹? ②光栅不透光部分宽度为多少?
2
2
4级明纹 3级明纹 2级明纹 1级明纹
d sin k
k 0,1,2,3...
光栅方程
决定各级主极大方向的方程.
或 用 图 解 法 求
d
中央明纹 -1级明纹
a
b
B
C
-2级明纹 -3级明纹 -4级明纹
BC d sin k
6
3.缺级现象 ●在某些方向,同时满足光栅衍射的明纹条件和单缝衍 射的暗纹条件,则该方向上的光栅衍射明纹将不会出现, 称这种现象为“缺级”。 第k级光栅衍射主极大:
a
a b 3a 3 10 cm
② kmax
4
ab
sin
2
k a 1 N 3333 / cm ab
kmax 5.5 5 (向前取整数)
14
共呈现5级,共9条谱线: k 0, 1, 2, 4, 5.
③ k 2, v 400nm, r 760nm
§11-6
光栅衍射
一、光栅 在透光或反光性能上具有周期性空间结构的光学元件.
平面光栅—在透明平面玻璃上刻成若干等间距的刻痕, 或在镀铬板上用光刻的办法刻出若干条刻痕做成的器 件。 透射光栅
反射光栅
大学物理实验教案(光栅的衍射)

大学物理实验教案实验项目光栅的衍射教学目的1. 观察光的衍射现象,了解光栅分光的原理。
2. 测定光栅常数和光波波长。
实验原理当光射到光栅面上时,在透光狭缝处光线可透过,而在不透光处则不能透过。
若这些透光狭缝的宽为。
相邻狭缝间不透光部分的宽度为,,称为光栅常数。
本实验装置产生的光栅衍射是夫琅和费衍射,因为衍射屏(光栅)与光源及观察屏之间的距离均为无穷远(入射光栅的入射光和出射光栅的衍射光均为平行光)。
根据夫琅和费衍射理论,当波长为λ的平行光束投射到光栅平面上时,光波将在两个透光狭缝处发生衍射,所有狭缝的衍射光又彼此发生干涉,其结果是在透镜的焦平面上得到一排明亮分立的光谱线。
当平行光垂直入射时,相邻两缝对应点出射的光束的光程差为式中d为光栅常数,称为衍射角。
根据衍射光的干涉条件,当衍射角满足下式时则该衍射角方向上的光将会得到加强,叫做主极大,其它方向的光或者完全抵消,或者强度很小在焦平面上形成暗背景。
我们把时所对应的主极大分别称为中央(0级)极大,正负第一级极大,正负第二级极大,……。
如果入射光不是单色光,而是包含几种波长的光,对于同一级次光的波长λ不同,其衍射角也各不相同,于是复色光将被分解,从而在不同的地方形成不同颜色的光谱线。
但是,在中央主极大位置上,即K=0,处,各颜色的光仍重叠在一起,形成中央明条纹。
在中央条纹两侧对称分布着级光谱,各级光谱线都按波长大小的顺序依次排列成一组彩色谱线,对同一级谱线来说,λ越大,衍射角也越大,λ越小,越小,即彩色谱线排列是长波谱线在外侧,短波谱线在内侧。
如果用分光计测出,则当λ已知时d可求,当d已知时λ可求。
衍射角为其中为望远镜对准所要测定的正级谱线时,A,B两游标读数。
为望远镜对准所要测定的负级谱线时,A,B两游标读数。
教学重点与难点重点:1. 分光计的调节(望远镜调焦、望远镜光轴调节、平行光管调节等);2. 光栅放置位置的要求;3. 衍射角测量方法。
难点:1. 分光计调节;2. 游标盘读数。
衍射光栅常数与光波长的测量讲义

右游标
ө'-k 66°45' 66°48' 67°55' 71°55' 77°2' 77°5'
左游标
ө+k 287°37' 287034' 286°26' 282°29' 277°18' 277°15'
右游标
ө'+k 107°37' 107°32' 106°25' 102°28' 97°19' 77°16'
2017626重庆邮电大学理学院物理实验中心17光栅1衍射实验数据处理级次左游标右游标左游标右游标望远镜转过的角度衍射角黄光224644?6645?28737?10737?4053?4052?2026?黄光124646?6648?28734?10732?4048?4044?2023?绿光24755?6755?28626?10625?3831?3830?1913?紫光25154?7155?28229?10228?3035?3033?1517?黄光22574?772?27718?9719?2014?2017?108?黄光12575?775?27715?7716?2010?2011?105?绿光25735?7738?27634?9633?1859?1855?929?紫光25935?7934?27438?9437?153?153?729?数据处理要求案例数据处理要求案例2017626重庆邮电大学理学院物理实验中心18级次黄光2黄光1绿光紫光黄光2黄光1绿光紫光5461埃衍射角2026?2023?1913?1517?108?105?929?729?sin03489480348130328981026346201758510174992501646780130172sin012176501211950108228006941200309240030622400271190016945906934?6937?7047?7443?7952?7955?8031?8231?cos09368640937169094407409644609842760984430109862160991387cos平方0877714087828508912760930182096880969102609726220982849光栅常数3319951331617843148e05光栅常数不确定度00004020001674710899e09光波波长埃5792448577887843734055803048580304834316729波长不确定度0000149000022900002050000403000040240000353波长不确定度埃0000433199000233162017626重庆邮电大学理学院物理实验中心19
课设-光栅常数测量

编号:专业工程设计说明书衍射光栅光栅常数测定题目:院(系):专业:学生姓名:学号:指导教师:职称:摘要光栅常数,是光栅两条刻线之间的距离,用d表示,是光栅的重要参数。
通常所说的衍射光栅是基于夫琅禾费多缝衍射效应工作的,当用不同波长的光照明光栅时,除零级外,不同波长的第一级主极大对应不同的衍射角,即发生了色散现象。
这表明了光栅的分光能力,是光栅分光的原理。
描述光栅结构与光的入射角和衍射角之间关系的公式叫“光栅方程”。
光栅是一维的栅状物体,通常测定其光栅常数时,多用分光计测量,但是分光计价格昂贵,并且操作麻烦,不易掌握,因此我们寻求一种更为简便的测定方法,能够测得光栅常数。
本文运用的是在已知光源波长的情况下,通过测得光栅到成像屏幕的距离和光栅0级和第一级主极大之间的距离计算。
该方法首先要对CCD定标,通过透镜成像后,能够得到物像体的像素值。
再计算光栅成像后通过CCD采集的像素值,即可得到真实光栅间距的大小。
关键词:光栅常数;CCD标定引言 (1)1 实验目的及要求 (1)1.1 课程设计的目的 (1)1.2 课程设计的任务 (1)1.3 课程设计的要求及技术指标 (1)2 方案设计和选择 (2)2.1 利用塔尔博特效应测量光栅常数原理 (2)2.2激光测定法原理 (3)2.3显微镜测光栅常数原理 (3)2.4 分光计测光栅常数 (3)2.5 测量光栅常数光路的选择 (4)3 各组成部分光路的实验原理 (5)3.1 衍射光栅的使用与分光原理 (5)3.2激光测定法光路工作原理 (5)3.3 对CCD进行标定原理 (6)3.4 电荷耦合器件CCD的工作原理 (6)3.4.1 CCD器件 (6)3.4.2 图像采集卡 (7)4 实际光路及测量步骤 (7)4.1 对CCD标定的实际光路及测量步骤 (7)4.1.1 实际光路图如图 (7)4.1.2定标步骤 (8)4.1.3实验结果 (8)4.2测量光栅常数的实际光路及测量步骤 (8)4.2.1实际光路图 (8)4.2.2测量步骤 (9)4.2.3实验结果 (9)5 数据处理及分析系统中各参数对测量结果的影响 (9)5.1 CCD标定的数据处理 (9)5.1.1用MATLAB处理标定图像及计算像素总数N (10)5.2测量光栅常数的数据处理 (11)5.2.1用MATLAB处理衍射光点图像及计算像素总数N (11)5.3 数据计算与误差分析 (12)5.3.1 数据的采集 (12)5.3.2 数据的计算 (12)5.3.3 数据的误差分析 (13)5.4 各参数对测量结果影响的分析 (14)6 结论 (14)谢辞 (15)参考文献: (16)附录 (17)引言光栅是由大量等宽等间距的平行狭缝构成的光学器件。
光栅衍射
EN
E
E2
E1
2 d sin
E1 E2
EN
由上式决定的明条纹称作主极大 上式又称光栅方程
I Imax ?
0 (k 0) 所确定的明纹称作中央主极大
I
sin I0(
)2 (sin N
)2
2 d sin
E
a sin
E
E2
E1
2 d sin
E1 E2
EN
I Imax ?
3. 光栅衍射光强公式
I
I
0
(
s
in
)2 (sin N
)2
a sin
4. 主极大
d sin
d sin k k 0,1,2.......N
2 d sin
3. 光栅衍射光强公式
I
I
0
(
s
in
)2 (sin N
)2
衍射因子
a sin
干涉因子
d sin
2k , k 0,1,2,...
d sin k k 0,1,2.......N
EN
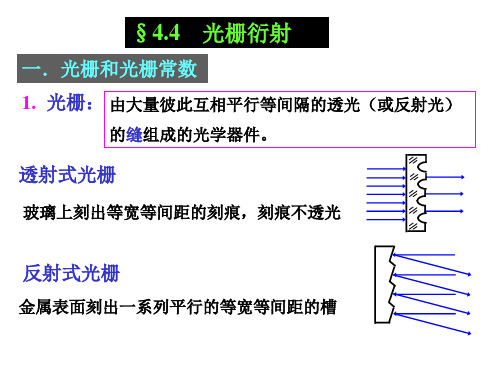
§4.4 光栅衍射
一.光栅和光栅常数 1. 光栅: 由大量彼此互相平行等间隔的透光(或反射光)
的缝组成的光学器件。
透射式光栅
玻璃上刻出等宽等间距的刻痕,刻痕不透光
反射式光栅
金属表面刻出一系列平行的等宽等间距的槽
光栅的衍射解析

望远镜焦距紧固螺钉
十字叉丝 12
e、采用“各半调节法”,调节载物台螺丝b或c和望远 镜的俯仰调节螺丝,使得绿色十字叉丝像与分划板的 上方叉丝重合。而且,旋转载物台180°之后也能够完 全重合。此时,望远镜光轴与分光计转轴相互垂直。
调 节 螺 丝
13
望远镜调节好的标志:
分划板
十字叉丝
14
实验步骤
16
c、调节平行光管俯仰螺丝,使狭缝像被分 划板中央水平叉丝线平分。
平行光管高度 调节螺钉
狭缝像
17
d、调节望远镜位置,使 狭缝像与分划板竖直叉 丝线重合。此时,可以 将望远镜的紧固螺丝锁 住,确保望远镜与平行 光管的光轴共轴。
18
平行光管调节好的标志:
19
实验步骤
3、调节光栅:
目的:使光栅面⊥平行光管的光轴; 且与分光计主轴平行。
23
光栅调节好的标志:需老师检查
分划板 狭缝像
十字叉丝
仪器调节时间到4:30
24
检查要点
1、狭缝是否被中央水平线平分; 保证平行光管光轴与望远镜光轴同轴。
2、绿色十字叉丝像和最上方叉丝重合; 保证平行光垂直入射光栅。
3、左右转动望远镜时所有谱线等高; 保证光栅上狭缝和分光计转轴平行。
25
4、光栅常数的测量:
k =-1
k=-2
波长(nm) 404.7 435.8 546.1 577.0 579.0
颜色
紫
蓝
绿 黄1 黄2
6
实验仪器
载物平台
汞灯
平行光管 刻度盘
游标盘
望远镜
7
实验步骤
1、调节望远镜:
目的:使分光计主轴⊥望远镜光轴;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
f
R L
第一暗纹的衍射角
b
P
f
o
x
1 arcsin
b
第一暗纹的衍射角 1 arcsin b b增大, 1减小 0, 1 0 b 一定 光直线传播 π 1增大 b , 1 b减小, 2
衍射最大
1越大,衍射效应越明显. b一定, 越大,
108
1012
1016
无线电波 3 10 m ~ 0.1cm
4
红 外 线 6 10 nm ~ 760nm
5
可 见 光 760nm ~ 400nm 紫 外 光
400nm ~ 5nm
x
射 线 5nm ~ 0.04nm
射 线 0.04nm
可见光的范围
: 400 ~ 760nm : 7.5 10 ~ 4.3 10 Hz
d
s1
r1
r2
d'
B
p
s
x
o
o
s2
r
d ' d
波程差
x r r2 r1 d sin d d'
sin tan x d '
d
实 s 验 装 置
s1
o
r1
r2
d'
加强
B
p
x
o
s2
r
x r d d'
(2k 1) 减弱 2
k
14 14
2 相干光
普通光源的发 光机制
激 发 态
En
E h
基态 原子能级及发光跃迁
1 2 P
普通光源发光特点: 原子发光是断续 的,每次发光形成一个短短的波列, 各原 子各次发光相互独立,各波列互不相干.
相干光的产生
振幅分割法
波阵面分割法
s1
光源 *
s2
四
实 验 装 置
杨氏双缝干涉实验
r E (r , t ) cos (t ) 4π r u 2 p0 sin r H (r , t ) cos (t ) u 1 4πr u
p0 2 sin
平面电磁波
E o H
E H
u x
u
x E E0 cos (t ) u x H H 0 cos (t ) u
已知 =589.3nm 求 (1) d=1mm时
d’=800nm
x ? (2) d=10mm时 x ?
解 (1) d=1mm时 d x 0.47mm d (2) d=10mm时 d x 0.047mm d
光程与波程讨论
光在真空中的速度 c 1 光在介质中的速度 u 1
n
s1 *
r1
r2
P
s 2*
n
波程差 r r2 r 1
t r2 t r1 相位差 2π ( ) 2π ( ) T ' T
r2 r1 2π ( ) '
2π (
s1 *
r1
r2
P
(1)光程:
nr2 r1
)
s 2*
n
媒质折射率与光的几何路程之积 nr = 物理意义:光程就是光在媒 质中通过的几何路程按相位差相 等折合到真空中的路程.
(2)中央明纹
( k 1 的两暗纹间)
角范围 sin b b 线范围 f x f b b
中央明纹的宽度 l0 2 x1 2
b
f
单缝宽度变化,中央明纹宽度如何变化?
入射波长变化,衍射效应如何变化 ?
1 越大,
越大,衍射效应越明显.
(3)条纹宽度(相邻条纹间距)
O O
x
dx
y
y dy
x x
x dW dVA sin (t ) u
2 2 2
体积元的总机械能
x dW dWk dWp dVA sin (t ) u
2 2 2
O O
x
dx
y
y dy
x x
讨 论 (1)在波动传播的媒质中,任一体 积元的动能、势能、总机械能均随 x, t 作周期性变化,且变化是同相位的. 体积元在平衡位置时,动能、势能 和总机械能均最大. 体积元的位移最大时,三者均为零.
紫外灾难
一
波动能量的传播
1 波的能量 波的传播是能量的传播,传播 过程中,媒质中的质点由不动到动, 具有动能 W K ,媒质形变具有势能 W P .
以固体棒中传播的纵波为例分析波动能量 的传播. 1 x 1 2 2 dWk dm v dV v y A cos (t ) u 2 2 y x v A sin (t ) t u 1 x 2 2 2 振动动能 dWk dVA sin (t ) 2 u
E
S
H
电磁波谱
电 磁 波 谱
10 10 10 10 10 10 10 10 10 10 10 10 10
频率 Hz
0 2 4 6 8 10 12 14 16 18 20 22 24
长波无线电波
红外线 紫外线 760nm
可见光 400nm
X射线
射线
短波无线电波 波长 m
108
104
100
104
变化的电磁场在空间以一定的速度传 播就形成电磁波. 1 T 2 π LC 2π LC
+ Q0 +
+
L
C
Q0
振荡电偶极子
不同时刻振荡电偶 极子附近的电场线
振荡电偶极子附近的电磁场线
p p0 cost
B
c
c
+ -
+ + + +
E
E
B
c
c
极轴
传播方向 E
H p0 r
(k 1,2,3,)
1、半波带法
b
缝长
A
R
A
A1
C
L
P
Q
B
o
L
b sin 2k 2
B
A
R
A1
/2
b
A
C
P
Q
b sin (2k 1) 2 k 1,2,3,
B
B
A2
o
/2
A
R
A1
C
L
P
Q
B
A2
/2
BC b sin k o 2 ( k 个半波带)
k 干涉相消(暗纹) 2 b sin (2k 1) 干涉加强(明纹) 2
r
'
nr
(2)光程差 (两光程之差) 光程差 Δ nr2 r1
Δ 相位差 Δ 2π λ
相位差=波数×光程差
s1 *
r1
r2
P
s 2*
n
五 单峰衍射--半波带法
夫 琅 禾 费 单 缝 衍 射
b
R
A
衍射角
L
f
P
Q
o
B
C
b sin
.)
(衍射角
:向上为正,向下为负
2
菲涅尔波带法 BC b sin k
又 u 1 /
H E
电磁波的能流密度(坡印廷)矢量 S E H
电磁波的能流密度(坡印廷)矢量 S E H
平面电磁波能流密度 1 平均值 S E0 H 0 2 振荡偶极子的平均 辐射功率 2 4 p0 4 p 12πu
O O
x
dx
y
y dy
x x
二
能流和能流密度
能流:单位时间内垂直通过某一面积 的能量. 平均能流:
u
P wu S
udt
S
能流密度 ( 波的强度 )I: 通过垂直于波传播方向的单位面 积的平均能流.
P I wu S
1 2 2 I A u 2
P wuS
u
udt
S
x dW dVA sin (t ) u (2) 任一体积元都在不断地接收和 放出能量,即不断地传播能量. 任一体 积元的机械能不守恒. 波动是能量传递 的一种方式 .
2 2 2
O O
x
dx
y
y dy
x x
能量密度:单位体积介质中的波动能量 dW x 2 2 2 w A sin (t ) dV u 平均能量密度:能量密度在一个周 期内的平均值 1 T 1 2 2 w wdt A T 0 2
平面电磁波的特性
x H H 0 cos (t ) H 0 cos(t kx) u x E E0 cos (t ) E0 cos(t kx) u
k 2π
(1)电磁波是横波, E u (2) E 和 H 同相位 (3)E 和 H 数值成比例
H u; E
例 证明球面波的振幅与离开其波源的 距离成反比,并求球面简谐波的波函数. 证 介质无吸收,通过两个球面的平均 能流相等. w1uS1 w2uS2 1 1 2 2 2 2 2 2 A u 4 π r A u 4 π r 即 1 1 2 2 2 2 A1 r2 s1 r s2 2 A2 r1
b f b
o
b f b
2
2
